Hybrid Stacking Model for Earthquake Magnitude Prediction in

Japan Using Time Series Data

(1970-2024)

Nandhini P S, Malarvizhi V, Nekelash I L, Kanishkar B and Malliga S

Department of Computer Science and Enginnering, Kongu Engineering College, Tamilnadu, India

Keywords: Ensemble Learning, Random Forest, Extra Trees, CatBoost, Linear Regression, Earthquake Magnitude

Prediction

Abstract: Seismic prognosis is considered as one of the most important scientific challenges. Among many nations,

Japan is in greatest need of such system due to the constant and frequent occurrence of strong earthquakes

caused by tectonic activity in the Pacific seismic zone. Therefore, the development of an advanced early

warning system is necessary to predict the earthquake in advance to prevent the disaster. For this purpose,

data related to earthquakes are collected from 1970 to 2024. This time-series data is trained using the hybrid

stacking model, based on Random Forest, Extra Trees and CatBoost as base models and Linear Regression

as a meta-model. The objective of the proposed model is to enhance the precision of earthquake magnitude

forecasting, focusing on significant earthquakes. The performance of the proposed model is evaluated using

two parameters i.e. R-Squared and Mean Square Error (MSE). The dataset is split in to 80:20 ratio for training

and testing data respectively. From the results, it is inferred that the developed hybrid model decreases error

rates with an R-squared value of 0.83 and MSE of 0.066. Thus, the proposed work helps to improve early

warning systems for earthquakes, minimizing risks in Japan.

1 INTRODUCTION

Japan situated at the intersection of four tectonic

plates (Pacific, Philippine Sea, Eurasian and others)

is one of the most seismic-sensitive countries. The

country has suffered from some of the worst

catastrophic earthquakes in history. They are the

Great Kanto Earthquake (1923), which claimed more

than 100,000 lives and the Tohoku Earthquake

(2011), which resulted in extensive destruction of

buildings and important infrastructure, such as

Fukushima nuclear reactor complex. These two

quakes highlight the fact that the world still requires

better and more efficient means of predicting

earthquakes in order to reduce the effects of future

ones.

Elastic movements in Japan are mainly caused by

the Benioff zones, where the Pacific Plate is being

pushed below both the Philippine Sea Plate and the

Eurasian Plate. This tectonic activity makes this area

highly susceptible to various types of earthquakes

such as megathrust earthquakes at the subduction

interface. While advancements have been made in

seismic monitoring and early warning systems,

accurate prediction of time, location and magnitude

of earthquakes still remains challenging. This is due

to their unpredictable and flexible nature. Among the

existing earthquake forecasting techniques, Seismic

Gap Theory and Historical seismicity have made

significant efforts to forecast earthquakes. However,

these approaches have not been successful in regions

with complex tectonic activities like those in Japan.

So, in this work to overcome the limitations,

hybrid stacking model is used to predict the

magnitude of Earthquakes. The models such as

Random Forest Regressor, Extra Trees Regressor and

CatBoost Regressor are used as the first-level models,

while a Linear Regression model is employed as the

second-level model in the stacking approach. For this,

time series data of Japan is collected from 1970 to

2024. The collected data is split into 80% for training

and the remaining 20% for testing. This approach

aims to improve the prediction of earthquake

magnitudes and enhance the understanding of how to

improve early warning systems in Japan. This extends

the existing work by integrating various Machine

756

P S, N., V, M., I L, N., B, K. and S, M.

Hybrid Stacking Model for Earthquake Magnitude Prediction in Japan Using Time Series Data (1970-2024).

DOI: 10.5220/0013585200004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 756-763

ISBN: 978-989-758-763-4

Learning models to hybrid models to improve the

potential for more accurate seismic forecasting.

The rest of the paper is organised as follows:

Section-II presents the Literature Review, Section-III

explains the proposed methodology, Section-IV

discusses the results and its comparison, Section-V

concludes the paper and outlines the Future work.

2 LITERATURE REVIEW

In (Joshi et al., 2023), the authors have outlined the

disadvantages of the classical form of early warning

systems. According to the authors, the disadvantage

is that the system provided delayed response. This is

due to the time required for data analysis from several

stations. In this paper, the authors have focused

particularly on the ability of ML models to improve

the predictive capabilities based on the multi-

parametric relationships within the collected data.

Feature engineering is also applied in this study

resulting in 29 features derived from the initial phase

of the P wave in relation to earthquake magnitude.

From the results, it is inferred that XGBoost model

effectively enhanced the performance by giving

better prediction results, for which the average error

is lower than conventional methods. In this paper

(Asim et al., 2017), authors focused on the analysis of

earthquake magnitude prediction for the Hindukush

region through a ML classifier based on historical

data of past seismicity. Eight physical characteristics

in accordance with geophysical concepts were used to

simulate future earthquakes, specifically those

exceeding a magnitude of shake of 5.5. The authors

have used various ML methods and evaluated the

performance of the models using sensitivity and

accuracy.

The XGBoost-SC model for ground motion

prediction was developed in this paper (Dang et al.,

2024) using 67,164 data records of shallow crustal

earthquakes that occurred in Japan between 1997 and

2019. Some of the features include magnitude, depth,

Vs30, hypo-central distance, altitude, and focal

mechanism. From the results, it is inferred that

XGBoost has shown to be more successful and

outperformed traditional approaches in terms of

accuracy and stability. The result of the SHAP

analysis confirmed the importance of features and

demonstrated the model's overall value in predicting

future disaster engineering, particularly with regard to

earthquakes. The primary objective of this paper

(Dutta et al., 2011) is to develop a standard

earthquake database for the South Asian region

(1905–2009) in the context of comparing seismic

risks in low-to-moderate seismicity regions.

Specifically, the accuracy of the magnitudes greater

than five was improved using linear regression to

model the relationship between earthquake

magnitude, latitude, longitude and depth. Weka had

better performance than SPSS in the prediction of

earthquake magnitude when data was smoothed. The

results suggested that WEKA is more suitable for this

task.

In this work (Ahmed et al., 2024), several ML

techniques were applied on data obtained from the US

Geological Survey to classify earthquake magnitudes.

During data pre-processing, it was found that more

than 10 percent of the data has NULL values. Suitable

actions such as imputation and removal of “null”

feature were taken. To improve the performance of

the model, features were encoded ‘one hot’ and

feature scaling was applied. With the better

hyperparameters, the SVM model achieved the most

accurate results, with MSE of 0.10 and a coefficient

determination of 0.93. In a recent study, the effects of

earthquakes, including ground movement and

economic losses were examined. The Researchers

have used a global dataset and shaped the same using

a technique called gradient boosting regressor to

forecast earthquake events with respect to date, time

and magnitude. They broke down the predictions into

smaller components and the results were improved to

86.1% for magnitude and 99.7% for depth, which

actually surpassed previous models.

In (Wang & Wang, 2024), the authors have also

tried to determine risk-free zones to minimize loss by

comparing actual and predicted values. In

(Sadhukhan et al., 2023) , the authors have explored

the use of DL algorithms for earthquake prediction,

focusing on significant seismic magnitudes from

regions such as Japan, Indonesia and Hindu-Kush

Karakoram Himalayan (HKKH) area. Three DNN

models such as LSTM, Bidirectional LSTM and

Transformer were used to analyze the correlations

between the seismic features and possible earthquake

activities. For Japan dataset, LSTM outperformed all

the other models, while Bi-LSTM outperformed all

other models for the Indonesia region and the

transformer model outperformed all other models for

the HKKH region. The models gave good results for

predicting earthquake magnitude in the range of 3.5

to 6.0. Various studies have focused on improving

earthquake prediction using ML models. The

limitations of the existing systems are:

 traditional system suffer from delayed

response

Hybrid Stacking Model for Earthquake Magnitude Prediction in Japan Using Time Series Data (1970-2024)

757

 current model still face challenges in

achieving accurate prediction and less error

rate.

3 PROPOSED METHODOLOGY

In the proposed work, the dataset is cleaned by

handling missing values and removing unnecessary

columns. The categorical features are labelled using

one-hot encoding. Further, the dataset is split into

80% for training and the remaining 20% for testing.

The data is then fed to base model and the output of

it is given to meta model as shown in Fig.1.

3.1 Dataset Pre-processing

The dataset consists of earthquake data from Japan

taken from the USGS, with 25,326 rows and 27

columns. After cleaning the data by removing

unnecessary columns ('id', 'updated', and 'place'),

categorical columns ('magType', 'net', 'type', 'status',

'locationSource', and 'magSource') were encoded

using LabelEncoder. Label encoding is applied to

convert categorical data into numerical values,

making it compatible with ML models for processing.

The dataset pre-processing for the collected data is

done as follows:

 Removing Unnecessary Columns: Columns

such as 'id', 'updated' and 'place' were

removed because they may not provide

relevant information for prediction. For

example, 'id' is a unique identifier and does

not contribute predictive value.

 Label Encoding: Categorical columns were

converted into numerical representations

using LabelEncoder. This is essential for

models like Random Forest and XGBoost

that work with numerical data. For instance,

'magType' may have values like 'mb', 'ms',

etc., which are transformed into numbers.

 Features: The cleaned data focuses on

numerical features like 'latitude', 'longitude',

'depth', 'mag', 'nst', and 'rms', along with

categorical ones like 'magType'.

3.2 Base Models

The pre-processed dataset is split into 80 % for

training data and the remaining 20% for testing data.

The pre-processed data is given as input to the base

models. The base models are

3.2.1 Random Forest Regressor

The Random Forest Regressor is an ensemble model

in ML that creates several decision trees while

training and then delivers the averaged results. It

builds on the method bootstrap aggregation were each

tree is learnt from a boot strap sample of the data.

During the splits in the trees, the candidate

features to be used for splitting are chosen randomly

so as to avoid proximity between individual trees and

enhance the generalization power of the entire

system. Random Forest outperforms single decision

trees when it comes to minimizing overfitting, and it

is exceptionally apt for regression problems as well

as classification (Al Banna et al., 2021). The model is

capable of analysing non-linear relationship in the

data; and since the output is an aggregation of many

trees it is less sensitive to noise in the data. In

mathematical terms, the prediction of a Random

Forest model is expressed as in Equation (1).

𝑦=





∑

𝑓





𝑥







(1)

where 𝑇 is the total number of trees in the forest

and

𝑓





𝑥



is the prediction made by the 𝑡

tree for a

given input x. Each decision tree in the forest is built

by recursively splitting the data based on certain

features, chosen to minimize a loss function, typically

the mean squared error (MSE) for regression tasks.

The model continues splitting the nodes of each tree

until a stopping criterion, such as a maximum depth

or a minimum number of samples per leaf, is met.

Random forest identifies non-linear patterns and

address issues regarding variance through

accumulation of outcome from a variety of classifier

trees. The bootstrapping mechanism assures the

existence of stability in the predictions even if there

is a high level of noises.

3.2.2 Extra Trees Regressor

Extra Trees Regressor (Extremely Randomized

Trees) is an ML algorithm that involves several

decision trees created randomly. In Extra Trees, the

splitting nodes that fractures at each node is randomly

chosen within a given range other than being chosen

at best split based on certain criterion such as the

mean squared error (Kumar et al., 2023).

This randomness both in the feature and in the

split selection also helps to lessen the variance of the

model and therefore generalizes well and does not

over fit. Extra Trees enhance the accuracies’

homogenization and generation speed in addition to

general stability by averaging the output of several

INCOFT 2025 - International Conference on Futuristic Technology

758

trees randomly constructed. Random split in Extra

Trees improves generality and resolves the overfitting

problem. It gives variance by aggregating the results

of an extremely randomized decision trees model.

3.2.3 CatBoost Regressor

CatBoost Regressor is actually a gradient boosting

model that is excellent when used with datasets that

contain both categorical and numerical variables

(Jozinović et al., 2022).

The key difference between the CatBoost model

and the other models is that while the gradient

boosting is used, ordered boosting is applied, which

helps to minimise the target leakage problem and to

prevent overfitting, which is characteristic of small

datasets (Mir et al., 2022).

The model continuous features are engineered

using “target statistics”, where a value is given to a

continuous variable based on the distribution of the

target variable by the categories of the dummy

variable (Kalavakunta & Parthipan, 2024). This

ordered boosting technique helps in preventing the

model to overlearn the training data as in the normal

boosting techniques of using part of the data set for

prediction in boosting. Therefore, CatBoost works

well with density data and offers stable performance

irrespective of significant feature transformation. The

prediction in CatBoost is calculated sequentially

according to the gradient boosting algorithm, when

new trees try to reduce the residual error of previous

predictions (Su & Zhang, 2020). The prediction at

iteration t is given by Equation (2)

𝑦







= 𝑦







+𝜂⋅𝑔









𝑥







where η is the learning rate, 𝑔









𝑥



is the

prediction from the new tree at iteration t and 𝑦







the prediction from the previous iteration.

In CatBoost, the model iteratively refines its

predictions by focusing on errors from previous

iterations, combining the strengths of boosting with

advanced handling of categorical data for superior

performance. This model adds a gradient-boosting

perspective to the stacking approach, complementing

the randomness of Random Forest and Extra Trees

models. Its ability to handle categorical features

natively provides an advantage when modeling

seismic data, which often includes discrete

categories. CatBoost ensures stable performance

irrespective of the nature of the dataset (dense, sparse,

or mixed).

3.3 Meta Model (Linear Regression)

Linear regression is a fundamental method of using

statistics in developing the relationship between one

or more variables. The advantages of this model are

simplicity, interpretability and strong predictive

performance on input features. The primary objective

of this model is to find a line that predicted values

(Varshney et al., 2023). This approach provides a

model that assumes a direct linear relationship,

minimises the deviations between the actual and the

allowing for clear inference on how changes in

predictor variables influence the outcome.

In the proposed hybrid stacking approach for

earthquake magnitude prediction, the Linear

Regression model serves as the meta-model,

combining the predictions from the base models such

as RF, ET and CatBoost. Instead of using the

predictions from these models directly, the Linear

Regression model treats them as features, optimising

the strengths of each algorithm (Roy et al., 2024).

This result in more accurate and reliable final

predictions compared to the case with each individual

model. This hybrid approach not only increases

prediction but also provides insights into how each

base model contributes to the final result, which is

particularly valuable in applications such as in

disaster response and earthquake vulnerability.

The mathematical formulation of the prediction in

a Linear Regression model is expressed in Equation

(3)

𝑦= 𝛽



+ 𝛽







𝑥







where 𝑦 represents the predicted earthquake

magnitude, 𝛽



is the intercept, 𝛽



are the coefficients

for each predictor 𝑥



(indicating the predictions from

the base models), and n is the total number of base

models (Katole et al., 2024).

The model coefficients are determined by

minimizing the Residual Sum of Squares (RSS),

defined as in Equation (4)

𝑅𝑆𝑆=

∑

𝑦



−𝑦













(4)

where 𝑦



is the actual target value and 𝑦



 is the

predicted value. Through this method, the stacking

approach effectively integrates the capabilities of

various models, ultimately leading to improved

predictions in earthquake magnitude forecasting.

Hybrid Stacking Model for Earthquake Magnitude Prediction in Japan Using Time Series Data (1970-2024)

759

Figure 1. Architecture of Proposed Methodology

Linear Regression determines weights of the base

models and comes up with the best weights that

complements each others strengths. The passthrough

mechanism helps Linear Regression to benefit from

the forecasts produced by base models and the

residual distribution in original features. The

coefficients of Linear Regression also allow for

interpreting directly the contribution of each base

model and original feature to the stacking framework.

Linear Regression does not require many

computations making it more appropriate for large

data sets or a situation where, an over-speed meta-

model training is required.

4 RESULTS AND DISCUSSION

4.1 Evaluation Metrics

In evaluating earthquake prediction models, various

performance metrics are employed to assess the

accuracy and reliability of predictions. These metrics

include Mean Squared Error (MSE), R-squared (R²),

Root Mean Squared Error (RMSE), and so on. Each

of which provides distinct insights into model

performance.

4.1.1 Mean Squared Error (MSE)

MSE measures the average squared difference

between actual and predicted values, offering a

penalization for larger errors. A lower MSE value

indicates better predictive accuracy as in Equation (5)

𝑀𝑆𝐸 =





∑

𝑦



−𝑦













(5)

where 𝑦



represents the actual value, 𝑦



 the

predicted value, and n is the total number of

predictions.

4.1.2 R-squared (𝑹

𝟐

)

R-squared

Evaluates the proportion of variance in

the target variable explained by the model. It ranges

from 0 to 1, with higher values signifying better

model fit as in Equation (6)

𝑅



=1−

∑



















∑















(6)

where 𝑦

is the mean of actual values.

4.1.3 Root Mean Squared Error (RMSE),

RMSE

a derivation of MSE, is the square root of

MSE. It retains the same scale as the target variable,

making it easier to interpret as in Equation (7)

𝑅𝑀𝑆𝐸 =

√

𝑀𝑆𝐸







∑

𝑦



−𝑦













(7)

4.1.4 Mean Absolute Error (MAE)

MAE

calculates the average magnitude of prediction

errors, without considering their direction. It is less

sensitive to outliers compared to MSE or RMSE is

shown as in Equation (8)

𝑀𝐴𝐸 =





∑

|𝑦



−𝑦



|





(8)

INCOFT 2025 - International Conference on Futuristic Technology

760

4.1.5 Mean Absolute Percentage Error

(MAPE)

MAPE quantifies prediction error as a percentage,

offering scale-independent insight. Its formula is

shown as in Equation (9)

𝑀𝐴𝑃𝐸 =





∑

|𝑦



−𝑦



|





 100 (9)

Together, these metrics provide a complete

evaluation of the accuracy of earthquake prediction

models. They highlight both prediction rate and the

error patterns to choose the model for prediction.

4.2 Experimental Results

In this paper, ML models such as XG Boost, Random

Forest, Gradient Boosting, Lasso, Ridge, SVM, KNN,

ElasticNet, Extra Trees and CatBoost are compared

and the results are presented in Table 1.

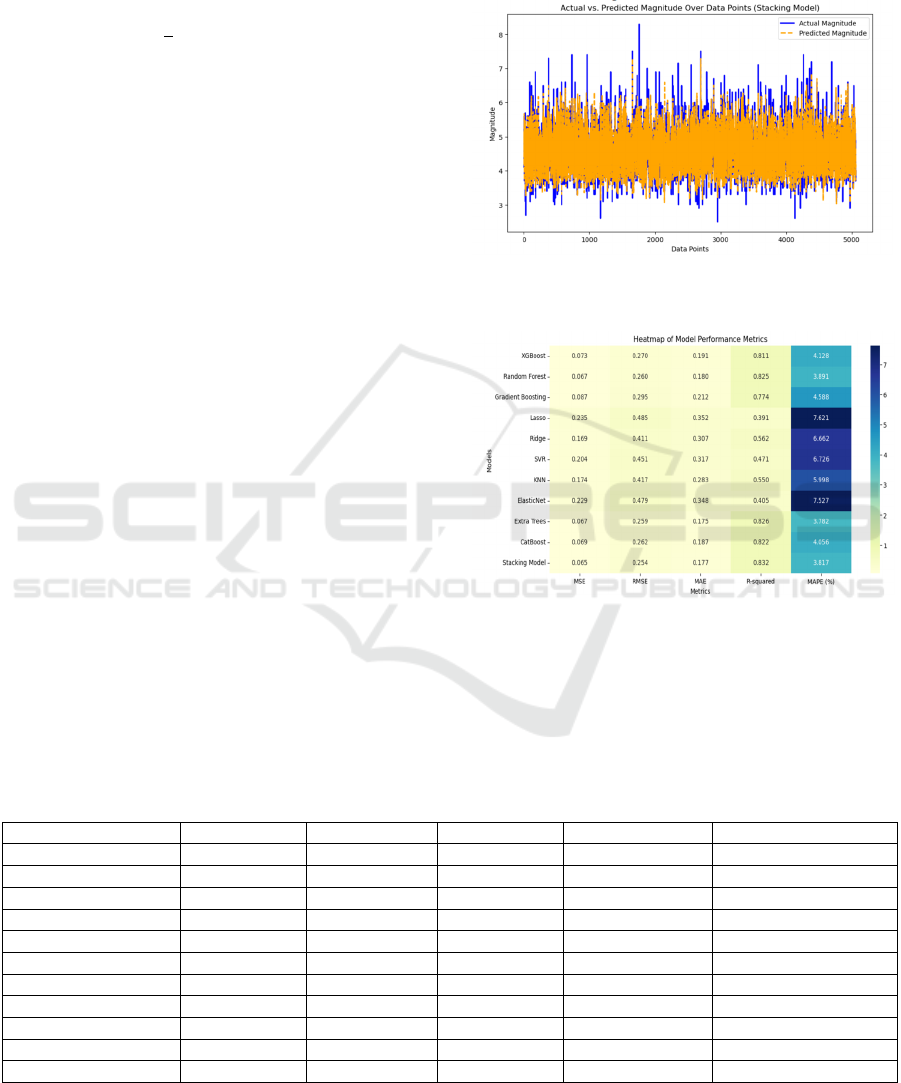
The actual earthquake magnitudes and those

expected based on the stacking model were also

compared as a way of testing the validity of the

model. The actual values the magnitudes are shown

as a blue/gray continuous curve, while the predicted

values are shown by the orange dashed line in Figure

2. The proximity of the two lines further supports the

fact that the stacking model can replicate actual

seismic data. There is a lack of variability, but this is

perfect for illustrating the ability of a model to

analyze the change in magnitude.

In addition to the gradient coloring, the heatmap

is also presented in Figure 3 for assessing the values

of each metric to that of the line plot.

By evaluating the models using MSE, RMSE,

MAE, MAPE and R-squared, the lower coefficients

and a higher R-squared value indicate better model

performance. Among these models tested with the

considered datasets, the stacking model provided the

least error estimations and the highest R² (0.832)

confirming its efficiency and high predictive abilities

as shown in in Figure 3.

Figure 2: Actual vs Predicted Magnitude prediction using

Proposed Method

Figure 3: Heatmap of Model Performance Metrics

The overall model comparison across Metrics is

shown in the Figure 4.

Table 1. Comparison of the performance of models

MODELS

MSE

RMSE MAE R-s

uared MAPE(%)

XGBoost

0.0727

0.2697 0.1910 0.8112 4.1281

Random Forest

0.0674

0.2596 0.1801 0.8251 3.8912

Gradient Boosting

0.0870

0.2949 0.2121 0.7743 4.5875

Lasso

0.2348

0.4845 0.3522 0.3909 7.6209

Rid

0.1689

0.4110 0.3067 0.5618 6.6623

SVR

0.2038

0.4514 0.3166 0.4712 6.7261

KNN

0.1735

0.4166 0.2826 0.5497 5.9979

ElasticNet

0.2292

0.4787 0.3480 0.4053 7.5265

Extra Trees

0.0669

0.2587 0.1749 0.8263 3.7788

CatBoost

0.0685

0.2617 0.1873 0.8222 4.0561

Stackin

Model

0.0648

0.2545 0.1768 0.8319 3.8219

Hybrid Stacking Model for Earthquake Magnitude Prediction in Japan Using Time Series Data (1970-2024)

761

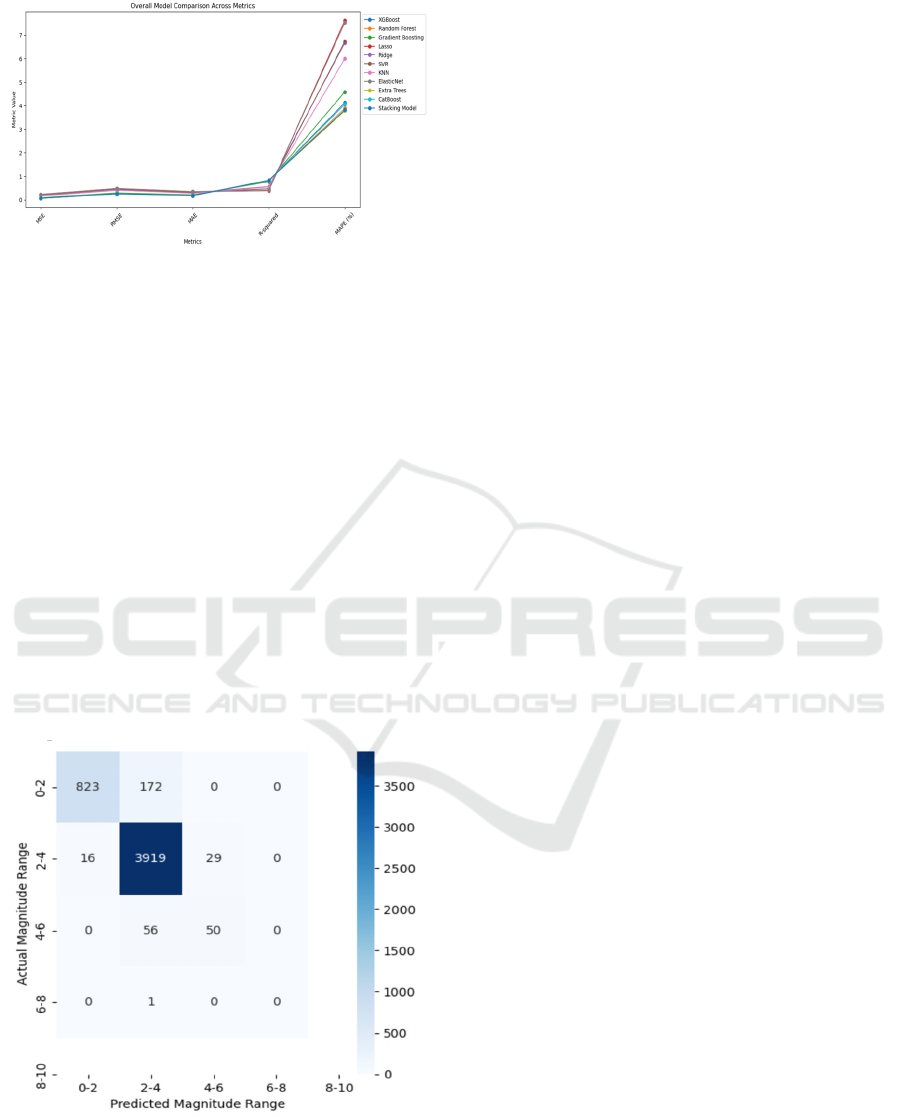
Figure 4. Overall Model Comparison Across Metrics

In the confusion matrix as shown in Figure 5,

results of the stacking model shows how well it

predicts the earthquake magnitude for various ranges.

The model shows high accuracy in the range between

2-4, where 3,919 instances were forecasted correctly,

therefore its capability in handling the most

frequently recurrent range of magnitude as shown in

the dataset. The experiments of the 0-2 range of

estimates had 823 correct and 172 wrong

classifications with the 2-4 range. The

misclassification is very low in the higher magnitude

zones suggesting that the model has a bias towards

lower and mid-range magnitudes. This distribution

means that although the stacking model is precise for

relative low and about average magnitude seismic

events, the quality of this work revealed that the

possibility exists to improve the accuracy of the

stacking model for more rare, higher magnitude

earthquakes.

Figure 5. Confusion Matrix for Stacking Model

5 CONCLUSION AND FUTURE

WORK

Thus, the proposed work on Earthquake prediction

has utilized statistical and ML techniques to predict

earthquake magnitudes accurately using a dataset

from the Japan region. The proposed model, which

combines Random Forest, Extra Trees, CatBoost in a

stacking ensemble, and Linear Regression,

demonstrated better results. Specifically, the model

achieved an MSE of 0.0647, RMSE of 0.2544, MAE

of 0.1766, R-squared value of 0.8321, and MAPE of

3.82%, confirming its ability to effectively model

complex seismic patterns. When compared to

individual models like XGBoost, Gradient Boosting

and CatBoost, the stacking model leveraged the

strengths of multiple algorithms to improve accuracy

and prediction reliability. The stacking ensemble

further enhanced generalization and reduced the risk

of misclassification, which is common with

standalone models. This work underscores the

importance of combining various models for seismic

analysis and hazard management. The proposed

model provides a robust foundation for earthquake

magnitude estimation, supporting the development of

early warning systems and improving preparedness.

The future work will focus on expanding the dataset

to include additional seismic features, incorporating

IoT for real-time predictions and applying this

methodology to other seismic regions. These

advancements will contribute to strengthening AI’s

role in enhancing global disaster resilience.

REFERENCES

Ahmed, F., Akter, S., Rahman, S. M., Harez, J. B.,

Mubasira, A., & Khan, R. (2024). Earthquake

Magnitude Prediction Using Machine Learning

Techniques. 2024 IEEE International Conference on

Interdisciplinary Approaches in Technology and

Management for Social Innovation (IATMSI)

Al Banna, M. H., Ghosh, T., Al Nahian, M. J., Taher, K. A.,

Kaiser, M. S., Mahmud, M., Hossain, M. S., &

Andersson, K. (2021). Attention-based bi-directional

long-short term memory network for earthquake

prediction. IEEE Access, 9, 56589-56603.

Asim, K., Martínez-Álvarez, F., Basit, A., & Iqbal, T.

(2017). Earthquake magnitude prediction in Hindukush

region using machine learning techniques. Natural

Hazards, 85, 471-486.

Dang, H., Wang, Z., Zhao, D., Wang, X., Li, Z., Wei, D., &

Wang, J. (2024). Ground motion prediction model for

shallow crustal earthquakes in Japan based on XGBoost

INCOFT 2025 - International Conference on Futuristic Technology

762

with Bayesian optimization. Soil Dynamics and

Earthquake Engineering, 177, 108391.

Dutta, P., Naskar, M., & Mishra, O. (2011). South Asia

earthquake catalog magnitude data regression analysis.

International Journal of Statistics and Analysis, 1(2),

161-170.

Joshi, A., Vishnu, C., Mohan, C. K., & Raman, B. (2023).

Application of XGBoost model for early prediction of

earthquake magnitude from waveform data. Journal of

Earth System Science, 133(1), 5.

Jozinović, D., Lomax, A., Štajduhar, I., & Michelini, A.

(2022). Transfer learning: Improving neural network

based prediction of earthquake ground shaking for an

area with insufficient training data. Geophysical

Journal International, 229(1), 704-718.

Kalavakunta, S., & Parthipan, V. (2024). Natural Disaster

Earthquake Prediction using Linear Regression

Algorithm Comparing with K-Nearest Neighbors

Algorithm. 2024 2nd International Conference on

Advancement in Computation & Computer

Technologies (InCACCT).

Katole, A., Batheja, V., Deshmukh, A., Dekate, F., & Soni,

A. (2024). Earthquake Prediction Using QSVM. 2024

IEEE International Students' Conference on Electrical,

Electronics and Computer Science (SCEECS).

Kumar, R., Gupta, M., Bedi, K. S., Upadhyay, A., & Obaid,

A. J. (2023). Earthquake Prediction Using Machine

Learning. 2023 5th International Conference on

Advances in Computing, Communication Control and

Networking (ICAC3N).

Mir, A. A., Çelebi, F. V., Alsolai, H., Qureshi, S. A.,

Rafique, M., Alzahrani, J. S., Mahgoub, H., & Hamza,

M. A. (2022). Anomalies prediction in radon time series

for earthquake likelihood using machine learning-based

ensemble model. IEEE Access, 10, 37984-37999.

Roy, S., Mandal, P., Chowdhury, A., Abdullah-AL-Wadud,

M., Seikh, A. H., Seikh, A. H., Ghosh, M., &

Mukhopadhyay, A. (2024). Utilizing machine learning

algorithms to predict accuracy of the Index of Relative

Tectonic Activity (IRTA), Dhansiri (North) River

Basin in India and Bhutan. IEEE Access.

Sadhukhan, B., Chakraborty, S., & Mukherjee, S. (2023).

Predicting the magnitude of an impending earthquake

using deep learning techniques. Earth Science

Informatics, 16(1), 803-823.

Su, Z., & Zhang, Q. (2020). Earthquake prediction based on

Bi-LSTM+ CRF model and Spatio-Temporal Data.

2020 IEEE 9th joint international information

technology and artificial intelligence conference

(ITAIC)

Varshney, N., Kumar, G., Kumar, A., Pandey, S. K., Singh,

T., & Singh, K. U. (2023). Machine learning based

algorithm for earthquake monitoring. 2023 IEEE 12th

International Conference on Communication Systems

and Network Technologies (CSNT)

Wang, H., & Wang, H. (2024). Research on earthquake

magnitude prediction method based on Resnet transfer

learning. 2024 36th Chinese Control and Decision

Conference (CCDC)

Hybrid Stacking Model for Earthquake Magnitude Prediction in Japan Using Time Series Data (1970-2024)

763