An Integrated Approach of Differential Privacy Using Cryptographic

Systems

Chitra M.

, Tvisha Prasad

and Anshuman Bangalore Suresh

Department of Electronics and Communication Engineering, Ramaiah Institute of Technology, Bangalore, India

Department of Artiﬁcial Intelligence and Machine Learning, Ramaiah Institute of Technology, Bangalore, India

Keywords:

Data Privacy, Differential Privacy, Cryptographic Systems, PATE, AES-GCM, Privacy-Preserving Machine

Learning.

Abstract:

Ensuring data privacy is critical in today’s data-driven world. Differential privacy provides a mathematical

framework to protect individual privacy while enabling data analysis. However, its integration with machine

learning introduces challenges in maintaining model accuracy and scalability. In this work, a novel approach is

proposed that combines differential privacy with cryptographic systems to enhance privacy and security. The

Private Aggregation of Teacher Ensembles (PATE) algorithm is employed to train models on the Canadian

Institute For Advanced Research (CIFAR) dataset and the Modiﬁed National Institute of Standards and Tech-

nology (MNIST) dataset. Privacy is achieved by aggregating noisy predictions from teacher models trained

on disjoint data subsets. To further secure datasets, the Advanced Encryption Standard-Galois/Counter Mode

(AES-GCM) encryption algorithm is utilized. Experimental results show that this method effectively balances

strong privacy and security with high model accuracy, highlighting the potential of integrating differential pri-

vacy with cryptographic techniques in machine learning applications.

1 INTRODUCTION

Differential privacy and encryption are two key con-

cepts used for protecting the privacy and conﬁden-

tiality of sensitive data. Differential privacy aims to

safeguard individual privacy while allowing for the

analysis of aggregate data by adding random noise

into the data. This ensures that the overall statistical

properties remain intact while making it signiﬁcantly

harder to identify individual records, thereby prevent-

ing attackers from learning speciﬁc information about

any individual (Papernot et al., 2018; Boenisch et al.,

2023). Homomorphic encryption, which enables

computations on encrypted data without decryption,

has also gained traction as a privacy-preserving ap-

proach for secure collaborative learning frameworks

(Fang and Qian, 2021). By combining differential pri-

vacy with encryption, data can be protected through-

out its lifecycle—during storage, transmission, and

analysis—offering a robust framework for ensuring

the privacy and conﬁdentiality of data across various

applications (Xu et al., 2021).

2 METHODOLOGY

This section details the implementation of privacy-

preserving machine learning methodologies, includ-

ing the Private Aggregation of Teacher Ensembles

(PATE) algorithm and Differentially Private Stochas-

tic Gradient Descent (DP-SGD), enhanced with AES-

GCM encryption. These approaches were evaluated

on the MNIST dataset.

2.1 Private Aggregation of Teacher

Ensembles (PATE)

PATE is a privacy-preserving technique designed to

train machine learning models on sensitive datasets. It

utilizes an ensemble of teacher models and a student

model to maintain individual data privacy (Papernot

et al., 2018). An overview of the PATE methodology

is shown in Figure 1.

2.1.1 Data Partitioning

The sensitive dataset is divided into non-overlapping

subsets, with each subset assigned to a distinct teacher

744

M, C., Prasad, T. and Suresh, A. B.

An Integrated Approach of Differential Privacy Using Cryptographic Systems.

DOI: 10.5220/0013584900004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 744-747

ISBN: 978-989-758-763-4

model. This ensures that no single model has com-

plete access to the dataset, preserving privacy.

2.1.2 Teacher Model Training

Each teacher model is trained on its respective data

subset using standard machine learning algorithms.

To protect privacy, noise is added to the models’ pre-

dictions, controlled by a privacy budget parameter,

which determines the balance between privacy and

accuracy (Wagh et al., 2021).

2.1.3 Aggregation of Predictions

The teacher models’ noisy predictions are aggregated

using a voting mechanism, which selects the most

commonly predicted label for each data point. This

process prevents individual data points from being di-

rectly inferred (Xu et al., 2021).

2.1.4 Student Model Training

The aggregated predictions are used to train a student

model, which learns from the collective knowledge of

the teacher models. As the aggregated predictions al-

ready include noise, the student model uses a smaller

privacy budget (Boenisch et al., 2023).

2.1.5 Evaluation

The student model is tested on a separate dataset to

evaluate its accuracy and ability to generalize.

Figure 1: Overview of PATE (Papernot et al., 2018)

2.2 Differentially Private Stochastic

Gradient Descent (DP-SGD)

DP-SGD ensures differential privacy during the train-

ing of machine learning models by adding noise to the

gradients (Papernot et al., 2018). While DP-SGD is

effective in preserving individual data privacy through

noise addition, integrating advanced techniques such

as homomorphic encryption can further enhance pri-

vacy by allowing computations to be performed on

encrypted data, thus minimizing the exposure of sen-

sitive gradients (Fang and Qian, 2021). This hybrid

approach can address speciﬁc attack vectors, such as

membership inference, that exploit plaintext gradient

information.

2.2.1 Gradient Computation and Clipping

Gradients are computed using stochastic gradient de-

scent (SGD) on randomly sampled data batches. To

limit the inﬂuence of individual data points, gradients

are clipped to a ﬁxed norm.

2.2.2 Adding Noise and Aggregation

Noise is added to the clipped gradients, adjusted

based on the privacy budget. These noisy gradi-

ents are aggregated to compute the average gradient,

which is used to update the model parameters.

2.2.3 Model Updating and Evaluation

The model parameters are iteratively updated using

the average noisy gradients. The trained model is

evaluated on a test dataset to measure accuracy and

privacy guarantees (Boenisch et al., 2023).

2.3 AES-GCM Encryption for Data

Security

AES-GCM is applied to enhance data security during

preprocessing (Das et al., 2019; Gueron and Krasnov,

2014). Its performance and security have been exten-

sively studied across different IoT-oriented microcon-

troller architectures, including 8-bit, 16-bit, and 32-

bit cores, where it was found to balance cryptographic

efﬁciency and resource constraints effectively (Sovyn

et al., 2019). This algorithm’s ability to resist side-

channel attacks, such as timing and power analysis,

makes it suitable for resource-constrained IoT envi-

ronments.

2.3.1 Data Pre-processing and Encryption

The MNIST dataset is normalized and split into train-

ing and testing sets. Selected data points are en-

crypted using AES-GCM, ensuring both conﬁdential-

ity and integrity during training. AES-GCM’s prac-

tical strengths, such as balancing speed and security,

have made it a suitable choice for ML applications

(Arunkumar and Govardhanan, 2018).

2.4 Dataset: MNIST

The MNIST dataset is a standard benchmark in ma-

chine learning, featuring 70,000 grayscale images of

handwritten digits ranging from 0 to 9. It includes

60,000 images for training and 10,000 for testing,

each sized at 28×28 pixels. This dataset was em-

ployed to validate the proposed methodologies.

An Integrated Approach of Differential Privacy Using Cryptographic Systems

745

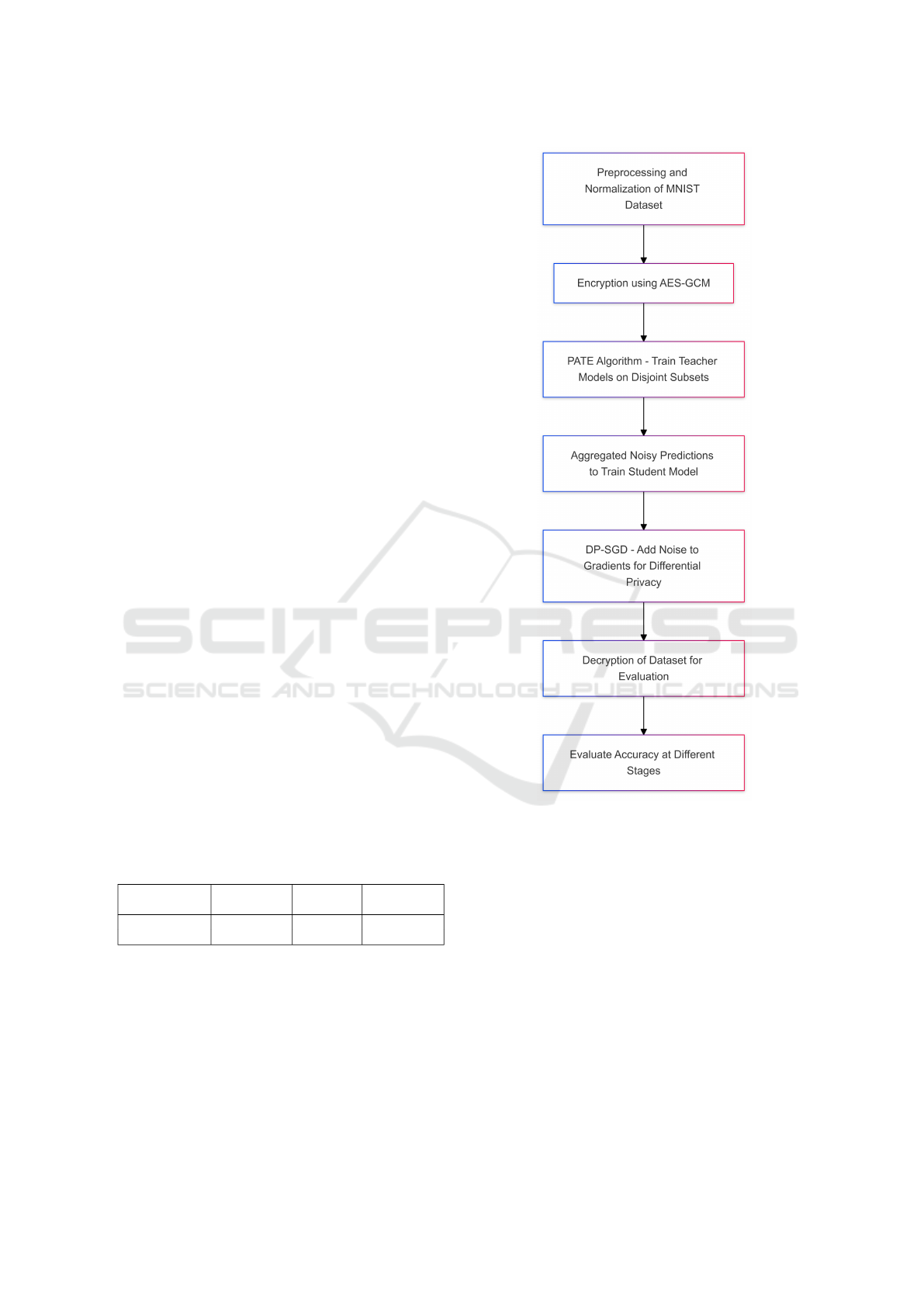
2.5 Integrated Approach and Accuracy

Calculation

The integration of differential privacy techniques with

cryptographic systems forms the core of this method-

ology. The process ensures robust privacy preserva-

tion and data security without signiﬁcant loss of ac-

curacy. The MNIST dataset is preprocessed, normal-

ized, and encrypted using AES-GCM, ensuring conﬁ-

dentiality and integrity of data throughout its lifecycle

(Bellare and Tackmann, 2016).

Next, the PATE algorithm is applied to train

teacher models on disjoint subsets of the dataset. Ag-

gregated noisy predictions from these teacher mod-

els are used to train a student model, ensuring that

the sensitive data remains private. DP-SGD is sub-

sequently employed to train the student model by

adding noise to gradients, further reinforcing differ-

ential privacy guarantees.

Finally, the encrypted dataset is decrypted post-

training for evaluation. Accuracy is measured at each

stage—baseline, after applying privacy techniques,

and post-decryption—to evaluate the trade-offs be-

tween privacy preservation and model performance.

This integrated approach demonstrates the feasi-

bility of combining cryptographic systems and differ-

ential privacy to secure machine learning applications

without compromising accuracy.

3 RESULTS AND DISCUSSION

The results of this study demonstrate the effective-

ness of privacy-preserving algorithms, namely PATE

and DP-SGD, in protecting sensitive data while main-

taining high accuracy levels. Table 1 summarizes the

accuracy achieved by these methods before and after

applying differential privacy and after decryption.

Table 1: Comparison of PATE and DP-SGD with AES-

GCM.

Methodology No Privacy After DP

After

Decryption

PATE 100% 97.15% 0%

DP-SGD 100% 97.30% 0%

When no privacy-preserving algorithm was ap-

plied, the model achieved an accuracy of 100%.

After applying the PATE algorithm, the accuracy

slightly decreased to 97.15%, attributed to the in-

troduction of noise during training to safeguard data

privacy. Despite this reduction, PATE successfully

balanced privacy and performance, with accuracy re-

maining within an acceptable range. Similarly, the

DP-SGD algorithm achieved an accuracy of 97.30%,

Figure 2: Workﬂow of the Integrated Approach

a marginal decrease compared to the non-private

model, reﬂecting the expected trade-offs in differen-

tial privacy frameworks. After decryption, both meth-

ods resulted in an accuracy of 0%, as the encrypted

data could no longer be interpreted without the origi-

nal key.

Visual representations of the performance of these

methods provide additional insights into their behav-

ior. Figure 3 illustrates the outcomes of applying the

PATE algorithm on the MNIST dataset.

Figure 4 presents results from the DP-SGD

method.

Overall, these visuals highlight the robustness of

both algorithms in preserving privacy while maintain-

ing high model usability. The introduction of noise in

PATE and the gradient-level noise in DP-SGD ensure

INCOFT 2025 - International Conference on Futuristic Technology

746

Figure 3: PATE results achieved. The left image shows the

original image (Label: 8), and the right image shows the

decrypted image before applying PATE.

Figure 4: DP-SGD results achieved. The top section shows

the training loss across epochs, and the bottom section dis-

plays the original image (Label: 2).

that sensitive data cannot be directly inferred. Despite

minor accuracy reductions, both methods maintain

strong performance, illustrating the potential of com-

bining differential privacy with cryptographic sys-

tems to address real-world privacy concerns in ma-

chine learning.

4 CONCLUSION

This paper demonstrated the effective integration

of differential privacy and cryptographic techniques,

speciﬁcally PATE and DP-SGD algorithms combined

with AES-GCM encryption, to ensure robust data se-

curity in machine learning applications. The approach

achieved high privacy guarantees with minimal im-

pact on model accuracy.

Future work will focus on exploring advanced

techniques such as homomorphic encryption, op-

timizing algorithm parameters to balance privacy

and accuracy, extending the methodology to larger

datasets and diverse models, conducting compre-

hensive security assessments, and developing user-

friendly tools for broader adoption. These advance-

ments aim to enhance the scalability, usability, and re-

silience of privacy-preserving solutions in real-world

applications.

REFERENCES

Arunkumar, B. and Govardhanan, K. (2018). Analysis of

aes-gcm cipher suites in tls. In International Con-

ference on Computational Intelligence and Networks

(CINE), pages 102–111. Springer.

Bellare, M. and Tackmann, B. (2016). The multi-user secu-

rity of authenticated encryption: Aes-gcm in tls 1.3. In

Robshaw, M. J. B. and Katz, J., editors, Advances in

Cryptology – CRYPTO 2016, volume 9815 of Lecture

Notes in Computer Science, pages 247–276. Springer,

Cham.

Boenisch, F., M

uhl, C., Rinberg, R., Ihrig, J., and Dziedzic,

A. (2023). Individualized pate: Differentially pri-

vate machine learning with individual privacy guar-

antees. Proceedings on Privacy Enhancing Technolo-

gies, 2023:158–176.

Das, P., Sinha, N., and Basava, A. (2019). Data pri-

vacy preservation using aes-gcm encryption in heroku

cloud. International Journal of Recent Technology

and Engineering (IJRTE), 8:7544–7548.

Fang, H. and Qian, Q. (2021). Privacy preserving machine

learning with homomorphic encryption and federated

learning. Future Internet, 13:94.

Gueron, S. and Krasnov, V. (2014). The fragility of aes-gcm

authentication algorithm. In 2014 11th International

Conference on Information Technology: New Gener-

ations, pages 333–337.

Papernot, N., Song, S., Mironov, I., Raghunathan, A., Tal-

war, K., and Erlingsson,

U. (2018). Scalable private

learning with pate.

Sovyn, Y., Khoma, V., and Podpora, M. (2019). Compar-

ison of three cpu-core families for iot applications in

terms of security and performance of aes-gcm. IEEE

Internet of Things Journal, PP:1–1.

Wagh, S., He, X., Machanavajjhala, A., and Mittal, P.

(2021). Dp-cryptography: Marrying differential

privacy and cryptography in emerging applications.

Communications of the ACM, 64:84–93.

Xu, R., Baracaldo, N., and Joshi, J. (2021). Privacy-

preserving machine learning: Methods, challenges

and directions. arXiv preprint.

An Integrated Approach of Differential Privacy Using Cryptographic Systems

747