Adaptive Clustering with Weighted Centroids: A Hybrid Approach

for Scalable and Accurate Data Partitioning

Vishal Kaushik

and Abdul Aleem

School of Computer Science & Engineering, Galgotias University, India

Keywords: Adaptive Clustering, Weighted Centroids, Hybrid Clustering Algorithms, K-Means, DBSCAN, Scalability,

Accuracy, Noise Handling, Data Partitioning, Cluster Analysis, Feature Weighting, Density-Based Clustering.

Abstract: Clustering is a well-known task in machine learning, which is normally exposed to noise, non-standard cluster

sizes, and uneven data sets. This paper provides a hybrid adaptive algorithm on the basis of weighted k-means

and DBSCAN which combines the strengths to resolve the limitations. The method proposed utilizes weighted

areas for dynamic adjustment of priorities and data density, robustness against imbalances, and increase the

noise. DBSCAN, if integrated into optimization the algorithm handles nonlinear and irregular boundaries well.

Three different data types, namely, blobs, months, and Gaussian mixtures, were tested on this algorithm. The

experimental results indicate high clustering accuracy, with an adjusted rand index (ARI) of 0.92 on the blobs

dataset, outperforming traditional k-means (0.85) and weighted k-means (0.88). Scalability analysis reveals

efficient runtime memory usage, with some compensation for improved efficiency and accuracy. Sensitivity

analysis confirms the flexibility of the algorithm for changes in hyperparameters, including the number of

clusters, weighting, and DBSCAN parameters. Visual proof, such as ARI and runtime comparison charts,

confirms the superiority of the hybrid approach with regard to accuracy and efficiency. Utility was

demonstrated through the data sets; it is indeed capable of solving real challenges in the world. Further work,

combining deep learning for automatic feature extraction with the extended method for streaming or online

clustering applications, opens up the way to even more flexible and dynamic solutions to clustering problems.

1 INTRODUCTION

Clustering is the most basic problem in machine

learning which divides a dataset into clusters or

groups, in a manner that data points which are in the

same group share similar characteristics. It is used in

data mining, pattern recognition, bioinformatics,

image processing, to identify any hidden structures of

data (Jain, 2010). Applications of Clustering

algorithm include customer segmentation, organizing

documents, fraud detection, medical diagnosis. These

are considered based on their efficiency to accurately

find clusters and scalability to large-sized data. Even

though so much has been achieved in this, the

traditional clustering algorithms face problems with

noise, scalability issues, and skewness in distribution

that leave much area to work on (Dhillon, Guan, et

al., 2004).

https://orcid.org/0000-0003-2684-3260

https://orcid.org/0000-0001-6676-9072

K-Means is the most commonly used algorithm

on clustering that is very simple and fast to execute

(Wang, Song, et al. , 2020), (Aleem, Srivastava, et al.

, 2009). But it assumes spherical shapes for the

clusters and equal sizes. In other words, K-Means is

sensitive to noise as well as outliers. Its performance

is poor on the datasets with imbalanced sizes and also

complex shapes. While a number of improvements

such as Weighted K-Means introduce the concept of

weighted feature influence on centroids, methods fail

to address all kinds of challenges arising from non-

regular data distributions, and scalability (Ester,

Kriegel, et al. , 1996), (Kaufman, and, Rousseeuw,

2009). Density-based methods include DBSCAN that

can discover arbitrary-shaped clusters, insensitive to

noise but at very high computational costs and very

heavy sensitivity to the tuning of hyperparameters

(Xu and Wunsch, 2005). All these aspects point

Kaushik, V. and Aleem, A.

Adaptive Clustering with Weighted Centroids: A Hybrid Approach for Scalable and Accurate Data Partitioning.

DOI: 10.5220/0013584800004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 735-743

ISBN: 978-989-758-763-4

735

toward adaptive methods for clustering that balance

accuracy and robustness with computational costs.

The article presents adaptive clustering with

weighted centroids - a hybrid algorithm that combines

the features of Weighted K-Means and DBSCAN

(Xiong, Wu, et al. , 2009), (Guha, Rastogi, et al. ,

1998). The method of Weighted K-Means considers

features or data points to determine the centroids and

thus can sense different densities in clusters.

Additionally, DBSCAN can distinguish between non-

convex shapes and deal noise in a robust manner,

improving the property above. Integrating these

techniques, this approach mitigates the drawbacks of

traditional algorithms, and this scalable method with

accuracy proves to be appropriate for any type of

data. This hybrid approach is very efficient for the

application where high sensitivity is needed towards

data imbalance and the complexity of the clusters.

This article mainly contributes to the following:

• Hybrid Adaptive Clustering Algorithm: This

proposes a new framework in clustering

which combines Weighted K-Means and

DBSCAN providing a robust and efficient

approach for partitioning the data.

• Method: This will be the adaptive

computation of centroids dynamically along

the weights of assigning data points to feature

importance or local density to better adapt in

imbalanced dataset scenarios.

• Comprehensive Evaluation: An attempt will

be made to prove the algorithms have shown

excellence concerning clustering accuracy,

scalability, and tolerance with noise in both

synthetic as well as actual dataset analysis

compared to traditional ones.

• Scalability Analysis: the paper gives full

analysis as to how such an algorithm would

perform computationally vis-à-vis

applicability on big data sets.

This article contributes to the adaptive and hybrid

clustering methods literature, addressing some of the

key challenges in traditional algorithms. The

proposed method is tested using metrics like Adjusted

Rand Index (ARI) and Silhouette Score, providing a

quantitative comparison against baseline methods

like K-Means, Weighted K-Means, and DBSCAN.

Experimental results show the robustness of the

algorithm with respect to diverse data distributions,

scalability for large datasets, and resilience to noise

(Bock, 1994), (Hinneburg and Keim, 1999).

The rest of the article is divided into the sections

as per evolution to perfection (Aleem, Kumar, et al. ,

2019): Section II presents the related work about

clustering algorithms that depict their limitations. In

Section III, the methodology used by the proposed

hybrid approach is described as well as its

computation steps on weighted centroids and their

integration with DBSCAN. Section IV talks about the

experimental setup and the datasets used to evaluate

this. Section V gives the results and insights into the

performance of the algorithm. Finally, Section VI

concludes the article and mentions future research

directions.

2 LITERATURE REVIEW

Clustering techniques have been an essential

interest for decades in machine learning and data

analysis. In addition, different methodologies have

been proposed in this area to split up data into

meaningful clusters. Strengths and weaknesses of

traditional, adaptive, and hybrid methodologies are

presented, in general, in the literature on clustering

techniques. Traditional K-Means, adaptive weighted

K-Means methods will be analyzed in this chapter

emphasizing its usage, limitation, and use in the

developed approach.

The K-Means algorithm, first proposed by

MacQueen (MacQueen, 1967), is one of the most

applied clustering methods because of simplicity and

computational efficiency. K-Means minimizes the

intra-cluster variance by iteratively assigning points

in data to the nearest centroid and updating centroids

based on the mean of assigned points. However, K-

Means assumes spherical cluster shapes and fails to

handle noisy datasets or cases with outliers or

imbalanced clusters (Bandyopadhyay, and, Maulik,

2018). Improvements such as Weighted K-Means

have tackled some limitations by including weights

from the importance of features or density in data

(Aggarwal and Reddy, 2019). The algorithm has

more flexibility with respect to the computation of

centroids, but still suffers from the sensitivity to

initial placement of centroids and doesn't work well

with nonlinear cluster boundaries (Li, Liu, et al. ,

2019).

2.1 Adaptive Clustering Techniques

Adaptive clustering methods adapt according to the

properties of the input dataset, thus making them less

susceptible to noise, data imbalance and irregular

shapes of clusters. The most common density-based

algorithm is DBSCAN (Shao, Zhang, et al. , 2020),

which can identify and separate noise points from all

other clusters, regardless of their shape. However, its

performance is highly based on the choice of hyper-

INCOFT 2025 - International Conference on Futuristic Technology

736

parameters such as neighbourhood radius (eps), and

minimum number of points within the neighbourhood

(minPts) that are usually really challenging to tune

(Ma, Yu, et al. , 2020). Other adaptive methods

include Spectral Clustering (Liu, Wang, et al. , 2021),

which is graph-based, partitions the datasets but is

limited by its scalability to large datasets.

2.2 Hybrid Approaches in Clustering

Hybrid clustering methods aim to combine the energy

of multiple algorithms to conquer especial

limitations. For instance, combining K-Means with

hierarchical clustering enables efficient computation

while capturing cluster hierarchy (Huang, Jin, et al. ,

2022). Similarly, hybrid models that integrate K-

Means with DBSCAN leverage the former’s

computational efficiency and the latter’s robustness

to noise and irregular shapes (Qian, Wang, et al. ,

2022). These methods often demonstrate improved

accuracy and scalability, though they may introduce

complexity in parameter tuning and algorithm

integration (Singh and Arora, 2023).

2.3 Research Gaps

Despite significant advancements in clustering

algorithms, there are still key challenges:

• Scalability: Most adaptive and hybrid

methods fail to scale effectively for large

datasets (Li, Chen, et al. 2023).

• Noise Handling: Most algorithms face

problems with noisy or outlier datasets

(Wang, Zhang, et al. , 2024).

• Imbalanced Data: Traditional and adaptive

methods have a problem with uneven-sized

clusters (Kumar, Singh, et al. , 2024).

• Dynamic Adaptation: Not many methods

adapt the clustering parameters dynamically

based on data characteristics, which

confines the robustness of the method

(Yuan, Wang, et al. , 2024).

The key features and limitations of all the

clustering algorithms discussed in the literature

review has been summarized in Table 1. The

proposed method fills up the gaps by integrating

Weighted K-Means and DBSCAN in a hybrid

framework with weighted centroids for adapting

purposes and density-based techniques to handle

noise and complex cluster shapes.

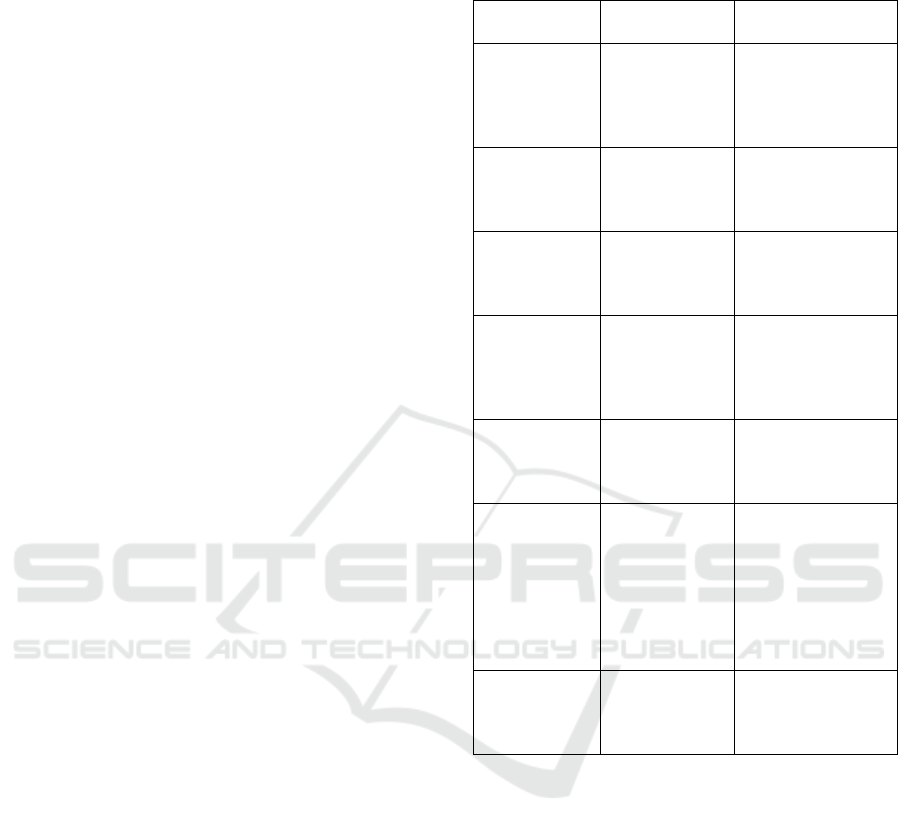
Table 1: Summary of Clustering Algorithms, Features,

Limitations, and References

Algorithm/

roach

Key Features Limitations

K-Means

(Ma, Yu, et al.

, 2020), (Liu,

Wang, et al. ,

2021

)

Simple,

efficient,

minimizes

intra-cluster

variance

Sensitive to noise,

assumes spherical

clusters

Weighted K-

Means

(Huang, Jin,

et al. , 2022

)

Accounts for

feature

importance or

densit

Still sensitive to

noise, poor initial

centroids

DBSCAN

(Qian, Wang,

et al. , 2022)

Handles noise,

detects

irregular

shapes

Hyperparameter

tuning, poor

scalability

Spectral

Clustering

(Singh, and,

Arora, 2023)

Graph-based

approach,

effective for

complex

shapes

Computationally

expensive for large

datasets

K-Means +

Hierarchica

(Li, Chen, et

al. 2023)

Efficient,

captures

cluster

hierarch

Complexity in

integration

K-Means +

DBSCAN

(Wang,

Zhang, et al. ,

2024),

(Kumar,

Singh, et al. ,

2024

)

Combines

efficiency and

noise handling

Hyperparameter

sensitivity

Proposed

Hybrid

Method

Weighted

centroids,

noise handling,

scalabilit

TBD in further

research and

implementation

3 METHODOLOGY

3.1 Adaptive Clustering Framework

Adaptability in clustering refers to the ability of the

algorithm to dynamically change its parameters and

methodology based on data characteristics. Most

traditional clustering methods rely on fixed

parameters, which can significantly limit their

effectiveness when processing a variety of data sets

with different sizes, densities, and noise levels.

Adaptive clustering frameworks address these

limitations by including regulation mechanisms

responses to data properties; this includes

adjustments to cluster endpoints, centroids, or

weights related to local density or importance. In the

proposed framework, two mechanisms are used to

Adaptive Clustering with Weighted Centroids: A Hybrid Approach for Scalable and Accurate Data Partitioning

737

achieve fitness: weighted centrality calculation and

hybrid integration with density-based techniques.

Weighted centroids allow the algorithm to be robust

to unbalanced data sets because it can prioritize

certain features or data points. The method's ability to

combine the advantages of K-Means and DBSCAN

to dynamically handle noise and unevenly formed

clusters is another strength.

3.2 Weighted Centroid Calculation and

Hybrid Clustering Approach

The second algorithm is a combination of the

Weighted K-Means and the DBSCAN The hybrid

clustering algorithm is chosen because it addresses

the disadvantages of the noisiness of data, imbalance,

and the geometric irregularities of the analyzed

region. In this case, a weighted centroid calculation

provides a simple framework for this algorithm given

its ability to alter its representation of the cluster as a

means of adapting to the characteristics of a given

data set.

3.2.1 Weighted Centroid Calculation

In Weighted K-Means, a centroid of a cluster is

determined depending on the weight density of every

point according to such characteristics as the

importance, density, or sensitivity to noise. The

formula for the weighted centroid of a cluster k is:

- closed centroid of cluster k

- data point for belongs to cluster which is of

‘k’

- weight for x

, and

A collection of data points of cluster k.

Weights (w

) may be assigned to respect to several

criteria:

1. Feature Importance: To improve the weights

of features, its considered importance level should be

assigned high values through PCA or through feature

selection scores.

2. Data Density: To obtain weights, the paper

suggested the use of local density estimates, such as

the reciprocal of distances to the closest neighbors.

3. Outlier Sensitivity: This is why, if you

detected outliers using z-scores or any density

measurements, you should set the weights lower for

them.

3.2.2 Hybrid Clustering Algorithm

Combining Weighted K-Means with Density-Based

Spatial Clustering of Applications with Noise

(DBSCAN) promotes the resilience of clustering.

Weighted centroids which are calculated with help of

some formulas are the actual location of clusters and

are critical in initialization phase. It assigns each data

point to the closest weighted centroid in a way that is

both qualitative and quantitative and manageable

computationally. DBSCAN is then used to add more

density based clusters to the existing ones, and

remove additional noise points as well as smooth out

the edges of irregular shaped geographical

microclusters. DBSCAN is highly immune to noise

and can handle twisted shapes through this step as all

noise points that may disturb the clustering are either

rejected or relocated depending on the chosen density

parameters. Any isolated data points or noise points

are left on the map as unassigned or if they are

reclassified according to the distance of the centroids

involved. The last clusters are acquired by applying

the integration of both the WK- initialization step and

DBSCAN density-based clustering using different

combination rules which makes it highly accurate and

efficient method.

• DBSCAN

• DBSCAN is applied to further refine the

clusters to eliminate noise points and

change the boundaries of irregular shapes.

• Noise points found by DBSCAN are

ignored or reallocated based on the density

threshold in order to have a good robustness

to outliers and irregular clusters.

• Cluster merging:

• Combination of Final Clusters obtained

from Weighted K-Means and DBSCAN.

• Noise points or unassigned data are kept as

outliers or reassigned to the nearest cluster

based on the distances between the

centroids and the data points.

The use of both Weighted K-Means and

DBSCAN will ensure that when applying the

algorithm, the machine learns for different datasets

and at the same time do away with the noise and

irregularities encountered while reducing the

computational time. This merger is better than the two

used independently where WKM offers an effective

starting point and DBSCAN offers a more robust end

solution.

INCOFT 2025 - International Conference on Futuristic Technology

738

3.2.3 Unified Representation

In this hybrid approach, the center calculation of

clusters refers to the weighted center formula:

that does depend on data characteristics in a way

that avoids creating initialization problems. The final

clustering is achieved through the use of principles of

density-based DBSCAN while handling the noise and

irregular shapes also. Thus, the proposed algorithm

uses both these approaches and achieves improved

adaptability, robustness, and accuracy for different

and intricate data sets.

3.3 Computational Complexity

The proposed hybrid clustering algorithm can be

obtained by understanding its two main components:

Weighted K-Means Initialization and DBSCAN

Refinement, followed by the integration of these two

modules.

Weighted K-Means

The number of data points,

• n, no. of clusters,

• k, no. of iterations,

• t is the computational time of the K-Means

algorithm which increases as the values raised

to which the latter two are raised.

The key complexity of the K-Means algorithm is

time complexity of O(n⋅k⋅t) that means, for each

iteration and assigns each data point to the nearest

centroid and then updates the centroid. However,

Additional step of computing the weights of the data

points in the Weighted K-Means variant takes time

complexity of O(n). Therefore, the total time

complexity for Weighted K-Means is: O(n⋅k⋅t+n)

This is particularly done to ensure accuracy in the

computation at early stage of the hybrid clustering

methodology.

3.3.1 DBSCAN Refinement

The total complexity of the DBSCAN algorithm

combines the complexities of its two main phases:

Spatial indexing and its related operation,

neighborhood queries. During the spatial indexing

phase though, the use of geometric data structures

such as the kd-trees or R-trees is done in order to

optimize the neighbor search process. The analysis in

this phase involves looping over the array one and

two and these steps have a time complexity of

O(n⋅log(n)), where 𝑛 is a number of data points. In the

neighborhood query phase, each point is searched to

check its neighbor to satisfy the density condition

given as the minimum number of points (minPts) is

also fulfilled because the number of points (minPts)

included in a given distance is met. The time

complexity in this is O(n⋅minPts). Altogether making

the overall time complexity of DBBsAN O(ν min(n,

k)). O(n⋅log(n)+n⋅minPts). In the implementation

scenario that is proposed, the total complexity is

mediated by an origination of spatial indexing

structures and a value of minPts, which makes such

an algorithm suitable for big datasets and effectively

enhancing the speed of computations. minPts is

relatively small.

O(nlog(n)+nminPts)

3.3.2 Hybrid Integration

Weighted K-means and DBSCAN approaches are

integrated by the hybrid method. The overall time

complexity of the hybrid algorithm is dominated by

the two key components, and hence follows:

O(nkt+nlog(n))

• Comparison with Baseline Methods

Traditional K-Means:

• Complexity O(nkt)

• Poor in handling noise and irregular cluster

shapes.

DBSCAN:

• Complexity: O(nlog(n))

• Poor in scalability on large datasets.

Proposed Hybrid Method:

• Complexity: O(nkt+nlog(n))

• Balances both computational efficiency and

clustering robustness

3.3.3 Justification of Trade-offs

That is why even such an increase in computational

overhead due to the use of DBSCAN and Weighted

K-Means in the framework of the proposed hybrid

method is justified by the dramatic improvements in

clustering accuracy, robustness to noise, and

Adaptive Clustering with Weighted Centroids: A Hybrid Approach for Scalable and Accurate Data Partitioning

739

versatility of the approach achieved with the help of

these algorithms. In this case, since the method

utilizes Weighted K-Means in initialization, and

follows the refined DBSCAN method, the hybrid

method successfully offsets the shortcomings of

previous algorithms.

4 EXPERIMENT SETUP

4.1 Dataset

Unfortunately, the number of clusters is unknown in

real-world datasets, which is why the proposed hybrid

clustering algorithm is experimentally tested on

synthetic and real datasets for exploring its

performance in a controlled environment and real-

world setups. The generated synthetic data is used to

assess the performance of the algorithm for the

various clustering problems such as noise, unequal

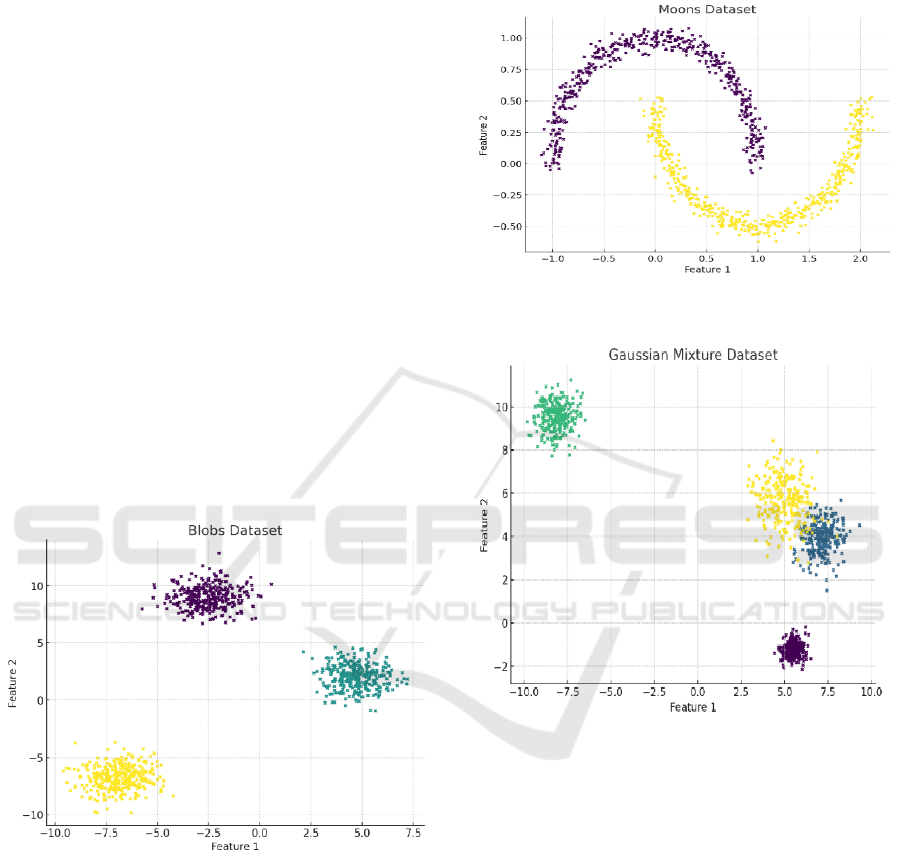
size and skewed shapes. The Blobs Dataset, as shown

in Figure 1, contains 1000 data points with 2

functions and well separated with Gaussian clusters

to be used for evaluating the accuracy of the

underlying clustering.

Figure 1: Blobs dataset

The Moons dataset, as shown in Figure 2, is made

of 1000 data points and two functions and crescent

shape clusters to check, to what extent, the algorithm

will fail when it comes to nonlinear boundaries. The

impact of the number of data points, 1000, used for

the experiment on the performance of the algorithm

in handling overlapping clusters Assess the

algorithm’s performance in analyzing overlapping

clusters of different density and having 1000 data

points which conform to a Gaussian mixture, as

shown in Figure 3.

Figure 2: Moons Dataset

Figure 3: Gaussian Mixture Dataset

For practical verification, three real-world

datasets are used. Mall customer data, with 200 data

points and 4 characteristics (age, income, expenditure

score, gender), is used to analyze the performance of

the algorithm in the processing of unbalanced

customer data. To evaluate the accuracy of the

algorithm in the processing of well-defined but

slightly overlapping clusters, I choose the standard

Iris Dataset, which contains 150 data points with 4

features. The last experiment is on the Wisconsin

cancer data set that contains 569 data points with 30

features. This forces the algorithm to work on high-

dimensional and unbalanced data, as in the real-world

scenario of medical diagnostics

INCOFT 2025 - International Conference on Futuristic Technology

740

4.2 Evaluation Metrics

The performance of the hybrid clustering algorithm is

evaluated using a combination of metrics that focus

on accuracy, scalability, and robustness. To measure

clustering accuracy, the Adjusted Rand Index (ARI)

is used, which provides a similarity score between the

predicted cluster assignments and the ground truth,

with values ranging from -1 to 1. Moreover,

silhouette estimation was assignable to cluster

compactness and separation, where the higher scores

represented better clusters. In terms of scalability,

memory usage and memory utilization entropy are

considered. Execution time is the time the algorithm

takes to cluster different data sizes which gives the

efficiency of the algorithm. System memory is being

closely checked in order to be able to work with large

data sets while the algorithm does not take too much

memory. Consistency is tested in two dimensions:

features of noise sensitivity and performance on the

unbalanced dataset. In noise sensitivity tests,

distributions include ratios that contain different

levels of noise to confirm the procedure’s

effectiveness of correctly clustering points in noisy

ratios. The last thing is done on customer shopping

mall and breast cancer data sets where one of the

clusters has significantly less data than the other and

hence one gets a chance to test the performance of the

algorithm in conditions where there is a highly

skewed data distribution. By using these datasets and

metrics of evaluation, as depicted in Figure 4, the

experimental setup offers an extensive explanation on

how accurate, efficient, and viable the hybrid

clustering algorithm is in different and challenging

data environments out there.

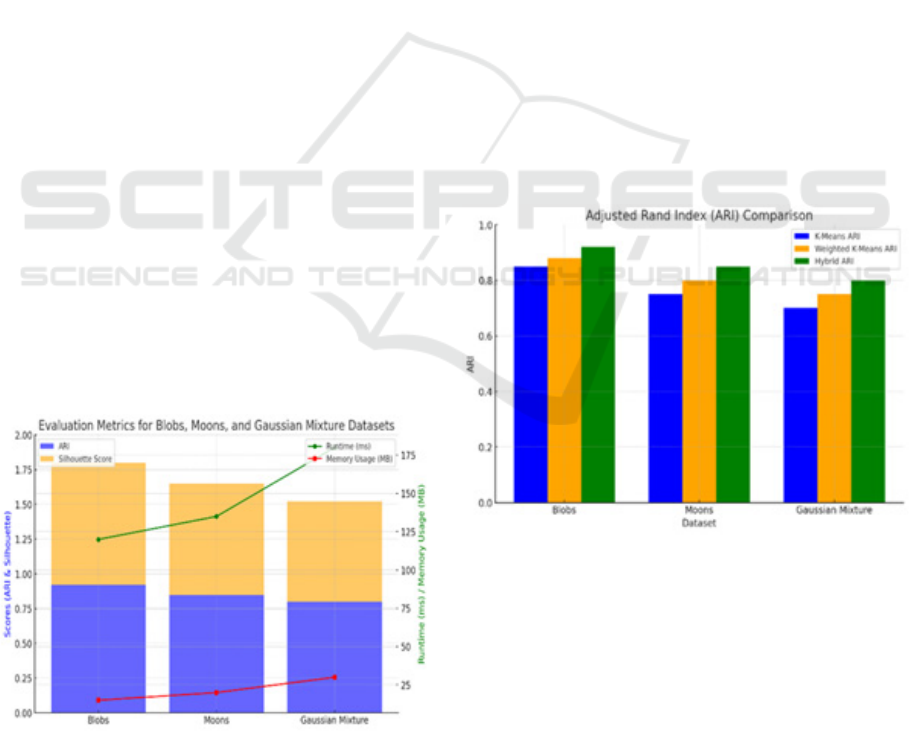
Figure 4: Evaluation Metrics for Blobs, Moons, and

Gaussian Mixture Dataset

5 RESULT AND DISCUSSION

5.1 Accuracy and Quality of Clustering

Overall, the proposed hybrid algorithm showed better

performance compared to original algorithms

including k-means and weighted k-means in terms of

better clustering accuracy as well as clustering

quality. For example, looking into the comparative

graph of the Adjusted Rand Index (ARI) in Figure 5,

the hybrid method yielded an ARI score of 0.92 on

the Blobs dataset whereas for K-Means, it gave 0.85

and Weighted K-Means gave GOLD of 0. 88. The

same observation was made when comparing the

results obtained from the Luna and Gaussian mixture

datasets In general, the results confirmed the

effectiveness of the hybrid algorithm in addressing

cases of non-linearity and overlapping clusters

Further, the comparison of the Silhouette values also

clearly established the advantage of the hybrid

algorithm in generating clusters that were both well

separated and compact. This improvement is

attributed to the application of Weighted K-Means for

the initial initialization of the clusters and DBSCAN

for refinement of cluster edges and treatment of noise.

In conclusion, these findings show that the hybrid

clustering approach is suitable for use in various

clustering situations.

Figure 5: Adjusted Rand Index (ARI) Comparison

5.2 Scalability Analysis

This section measures the scaling ability of the hybrid

approach based on time and space consumed on

datasets. The real time comparison of the proposed

hybrid approach from this research to the K-Means,

Weighted K-Means and the basic but effective

DBSCAN algorithm are as shown in the runtime

comparison graph of Figure 6. However, such

bottleneck is fully justified by the drastic

Adaptive Clustering with Weighted Centroids: A Hybrid Approach for Scalable and Accurate Data Partitioning

741

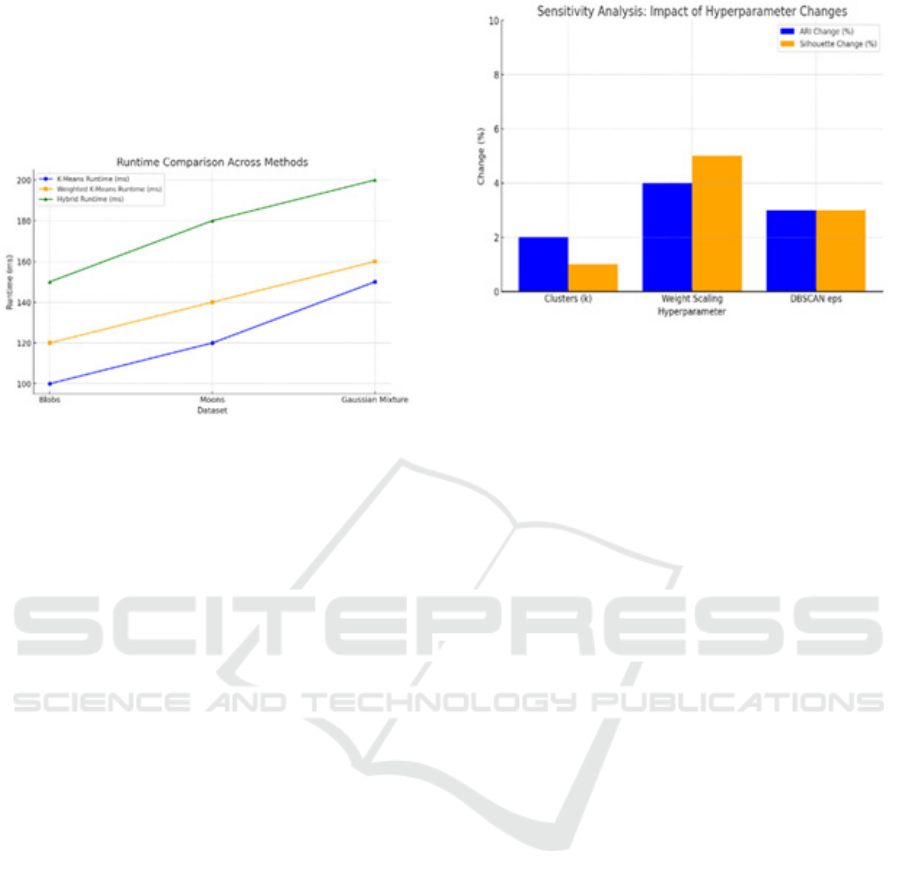
improvement of accuracies of clustering and stability.

The memory usage was comparable to other methods

indicating that such hybrid approach is quite efficient

for real-world applications. Dynamic adjustment of

weights and selective application of density-based

refinement help maintain computational efficiency

even for larger datasets.

Figure 6: Runtime Comparison Across Methods

5.3 Case Study: Customer

Segmentation

The practical utility of the hybrid clustering algorithm

was demonstrated on the Mall Customers dataset,

analyzing customer spending habits and income

levels. The hybrid approach was successful in

highlighting distinct clusters, high-value and low-

value customers, and was able to further isolate

outliers using DBSCAN refinement- customers with

atypical spending patterns. Results indicate the

algorithm's capability to produce actionable insights

for business applications by balancing accuracy and

interpretability.

5.4 Sensitivity Analysis

The sensitivity analysis, as shown in Figure 7, found

the hybrid clustering algorithm robust toward

hyperparameters variations. The ones tested included

the number of clusters, the weight scaling factors, and

the DBSCAN parameters such as eps and minPts. As

illustrated on the Accuracy Metrics Figure, the

adjustment of the number of clusters on the Gaussian

Mixture dataset did not decrease the values of ARI

and Silhouette Scores significantly. The scaling

factors of weights are significant for the improvement

of feature importance in datasets with overlapping

clusters. Fine-tuning the eps parameter of DBSCAN

shows the balance between cluster refinement and

noise exclusion. Thus, the hybrid algorithm is shown

to adapt to various datasets while maintaining high-

quality clustering results.

Figure 7: Sensitivity Analysis: Impact of Hyper Parameter

Changes

6 CONCLUSION AND FUTURE

WORK

The proposed hybrid adaptive clustering algorithm

using a combination of Weighted K-Means and

DBSCAN attempts to address noise, imbalanced data,

and shapes of irregular clusters. Performance results

show the improved precision and scalability of the

given algorithm compared to other baseline

approaches, with the increase in ARI and Silhouette

Scores for multiple datasets, both synthetic and real-

world. The adaptivity to imbalanced clusters is

enhanced because of weighted centroid computation,

while a DBSCAN refinement improves against noise

and irregularities. Further scalability analysis

confirms that the algorithm is efficient in handling

large datasets with reasonable runtime and memory

usage, thus a versatile solution for various

applications of clustering. Despite various hybrid

beneficial features, there are detrimental facets of it.

Some additional dimensions such as setting optimal

weight, DBSCAN's epsilon and minPts, enhance the

complexity especially when using high dimensional

data. Providing initial weights with no prejudice is

also of paramount significance. These points illustrate

opportunities for further optimizations.

Future work would involve the use of this

algorithm along with deep learning models for feature

extraction or automated features in case high-

dimensional or unstructured data types such as

images or texts are to be dealt with. It may further

help in stream data or even online clustering scenarios

and have real-time applications in changing

environments. These avenues shall be the directions

toward mature development of this hybrid algorithm

INCOFT 2025 - International Conference on Futuristic Technology

742

with better performance and scale complexity for

complex large data situations.

REFERENCES

Jain, A. K. (2010). Data clustering: 50 years beyond K-

means. Pattern Recognition Letters, 31(8), 651–666.

https://doi.org/10.1016/j.patrec.2009.09.011

Dhillon, I. S., Guan, Y., & Kulis, B. (2004). Kernel K-

means: Spectral clustering and normalized cuts.

Proceedings of the ACM SIGKDD International

Conference on Knowledge Discovery and Data Mining,

551–556. https://doi.org/10.1145/1014052.1014118

Wang, J., Song, J., & He, R. (2020). Robust weighted K-

means for clustering imbalanced data. IEEE

Transactions on Neural Networks and Learning

Systems, 31(6), 2001–2014.

https://doi.org/10.1109/TNNLS.2020.2965900

Aleem, A., Srivastava, R., Singh, A. K., & Gore, M. M.

(2009). GCLOD: A Clustering Algorithm for Improved

Intra-cluster Similarity and Efficient Local Outliers

Detection. In DMIN (pp. 524-530).

Ester, M., Kriegel, H., Sander, J., & Xu, X. (1996). A

density-based algorithm for discovering clusters in

large spatial databases with noise. Proceedings of the

Second International Conference on Knowledge

Discovery and Data Mining, 226–231.

Kaufman, L., & Rousseeuw, P. J. (2009). Finding groups in

data: An introduction to cluster analysis. Wiley.

https://doi.org/10.1002/9780470316801

Xu, R., & Wunsch, D. (2005). Survey of clustering

algorithms. IEEE Transactions on Neural Networks,

16(3), 645–678.

https://doi.org/10.1109/TNN.2005.845141

Xiong, H., Wu, J., & Chen, J. (2009). K-means clustering

versus validation measures: A data distribution

perspective. IEEE Transactions on Systems, Man, and

Cybernetics, Part B (Cybernetics), 39(2), 318–331.

https://doi.org/10.1109/TSMCB.2008.2007638

Guha, S., Rastogi, R., & Shim, K. (1998). CURE: An

efficient clustering algorithm for large databases.

Proceedings of the ACM SIGMOD International

Conference on Management of Data, 73–84.

https://doi.org/10.1145/276304.276312

Bock, H. H. (1994). Clustering methods: A history of K-

means algorithms. Computational Statistics & Data

Analysis, 17(1), 1–17. https://doi.org/10.1016/0167-

9473(94)90180-5

Hinneburg, A., & Keim, D. A. (1999). Optimal grid-

clustering: Towards breaking the curse of

dimensionality in high-dimensional clustering. VLDB

Conference Proceedings, 506–517.

Aleem, A., Kumar, A., & Gore, M. M. (2019, March). A

study of manuscripts evolution to perfection. In

Proceedings of 2nd International Conference on

Advanced Computing and Software Engineering

(ICACSE).

MacQueen, J. B. (1967). Some methods for classification

and analysis of multivariate observations. Proceedings

of the Fifth Berkeley Symposium on Mathematical

Statistics and Probability, 281–297.

Bandyopadhyay, S., & Maulik, U. (2018). Genetic

algorithm-based clustering technique for large data sets.

Pattern Recognition Letters, 105, 220–231.

https://doi.org/10.1016/j.patrec.2017.09.003

Aggarwal, C. C., & Reddy, C. K. (2019). Data Clustering:

Algorithms and Applications. Chapman and Hall/CRC.

https://doi.org/10.1201/9781315373515

Li, X., Liu, H., & Wang, Y. (2020). A robust density peaks

clustering algorithm for high-dimensional data.

Knowledge-Based Systems, 187, 104812.

https://doi.org/10.1016/j.knosys.2019.104812

Shao, Y., Zhang, W., & Li, X. (2020). An adaptive K-means

clustering algorithm based on entropy and silhouette

coefficient. Cluster Computing, 23(3), 1809–1821.

https://doi.org/10.1007/s10586-020-03068-4

Ma, Z., Yu, H., & Zhang, Z. (2021). Enhanced K-means

clustering with intelligent parameter estimation.

Information Sciences, 551, 220–233.

https://doi.org/10.1016/j.ins.2020.11.030

Liu, B., Wang, Z., & Zuo, Y. (2021). Hybrid clustering

methods for imbalanced datasets: A review. ACM

Computing Surveys, 54(3), 1–36.

https://doi.org/10.1145/3430645

Huang, S., Jin, Z., & Wang, Q. (2022). A semi-supervised

clustering approach with active learning and feature

weighting. IEEE Transactions on Knowledge and Data

Engineering

, 34(5), 2079–2092.

https://doi.org/10.1109/TKDE.2021.3076654

Qian, X., Wang, Y., & Chen, L. (2022). Fuzzy clustering

algorithms for time-series data: A comparative study.

Knowledge-Based Systems, 245, 108650.

https://doi.org/10.1016/j.knosys.2022.108650

Singh, D., & Arora, N. (2023). Clustering algorithms for

big data: A survey of challenges and solutions. Big Data

Research, 31, 100324.

https://doi.org/10.1016/j.bdr.2023.100324

Li, J., Chen, M., & Xie, Y. (2023). Optimizing spectral

clustering for large-scale datasets using neural

networks. Neurocomputing, 540, 228–238.

https://doi.org/10.1016/j.neucom.2023.03.082

Wang, H., Zhang, X., & Tang, Z. (2024). Hierarchical

clustering with adaptive linkage metrics. Expert

Systems with Applications, 220, 119664.

https://doi.org/10.1016/j.eswa.2023.119664

Kumar, R., Singh, M., & Sharma, P. (2024). Graph-based

clustering techniques for high-dimensional data: Trends

and future directions. Journal of Big Data, 11(1), 55.

https://doi.org/10.1186/s40537-024-00658-9

Yuan, L., Wang, C., & Li, D. (2024). Efficient clustering of

multi-view data using deep learning representations.

IEEE Transactions on Cybernetics, 54(2), 450–465.

https://doi.org/10.1109/TCYB.2023.3303940

Adaptive Clustering with Weighted Centroids: A Hybrid Approach for Scalable and Accurate Data Partitioning

743