Associating a Markov Process with Maude Executable Modules

Lorenzo Capra

Dipartimento di Informatica, Universit

a degli Studi di Milano, Via Celoria 18, Milan, Italy

Keywords:

Maude, Stochastic Petri Nets, Markov Process, Adaptive Distributed Systems.

Abstract:

In this paper, we explore a methodology for generating a Markov chain directly from executable modules in

Maude. Initially, we incorporate stochastic parameters in Maude speciﬁcations in a straightforward and ﬂexible

way. Then, we focus on accurately computing state transition rates, a challenging task due to the complexities

introduced by rewriting logic semantics. Our methodology is general and relies on a structured description of

states that includes the exact state transition rates. This capability allows for the complete automation of the

process, a crucial aspect of our ongoing research.

We illustrate this methodology using stochastic rewritable Petri nets, a powerful model for adaptive distributed

systems. Finally, we present some preliminary ﬁndings based on application examples.

1 INTRODUCTION

Maude (Clavel et al. (2007)) is a high-performance,

purely declarative language with rewriting logic se-

mantics (Bruni and Meseguer (2003)). It achieves ef-

ﬁciency and expressiveness through pattern-matching

modulo operator attributes, sub-typing, partiality,

generic types, and reﬂection. A Maude system mod-

ule is an executable speciﬁcation for a distributed sys-

tem. The Maude runtime engine provides various fa-

cilities for model checking, veriﬁcation of LTL for-

mulae, inﬁnite-state analysis, and symbolic reachabil-

ity. Additionally, Maude has been utilized as a logical

framework for other formalisms, such as Petri Nets

(PN), Automata, and Process Algebra. These for-

malisms, though powerful, lack the necessary features

for modeling adaptable systems intuitively.

In this paper, we introduce a new methodology to

generate a Markov process from user-deﬁned Maude

executable modules (including stochastic parameters)

directly and systematically. The process, based on

‘pre-processing” the original modules, is entirely au-

tomatable. Calculating the stochastic matrix exactly

is challenging due to rewriting logic semantics, which

obfuscates multiple state transitions. We will illus-

trate our methodology, which functions for any Maude

executable speciﬁcation, through a challenging ap-

plication domain: stochastic PN with a dynamically

changing structure. This application example outlines

all the potential issues related to the accurate deriva-

https://orcid.org/0000-0002-1029-1169

tion of a Markov process from Maude executable

modules.

Related Works. Several options exist for timed

and probabilistic analysis using Maude. (Meseguer

(2012)) presents a non-up-to-date survey. The frame-

work presented in (

Olveczky and Meseguer (2002))

enables deterministic time speciﬁcations for analyz-

ing real-time systems. A branching-time analysis

framework for Maude speciﬁcations is described in

(Rubio et al. (2021)). The approach detailed in (Agha

et al. (2006)), based on probabilistic rewrite theories

associated with actors, enables probabilistic discrete-

event simulation. Recently, (Rubio et al. (2023)) in-

troduced a comprehensive method for utilizing Maude

in stochastic analysis via a probabilistic extension of

its strategy language. Notably, this strategy language

operates at the ”object” level rather than the meta-

level.

Our approach and objectives signiﬁcantly differ

from other works. Essentially, we aim to equip any

executable speciﬁcation with time semantics, mark-

ing an important step toward fully automating the pro-

cess. The rewriting logic establishes a labelled transi-

tion system (TS) associated with ground terms of any

type. However, deriving a consistent Markov chain

for this TS presents challenges for three main rea-

sons: TS state transitions correspond to equivalence

classes of rewrites; equivalent rewrites may be logi-

cally indistinguishable and need to be united; and lo-

cal rewrites of subterms within a speciﬁc term may

106

Capra, L.

Associating a Markov Process with Maude Executable Modules.

DOI: 10.5220/0013567900003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 106-116

ISBN: 978-989-758-759-7; ISSN: 2184-2841

occur. To our knowledge, none of the mentioned tech-

niques addresses these issues. Our technique, which

deﬁnes a kind of meta-operators at the object level,

is simpler to use and much more efﬁcient than the

predeﬁned Maude meta-level modules and more ac-

curate than the Maude strategy language. Unfortu-

nately, for a comprehensive description, we need to

provide some details of the Maude syntax and the pat-

tern matching mechanism used by the Maude rewrit-

ing engine.

In the paper, we focus on continuous-time Markov

chains (the model underneath SPN). It is worth

noting that through straightforward rate normalisa-

tion, we can employ the same approach to derive a

deterministic-time Markov chain.

We begin integrating stochastic parameters into

a Maude speciﬁcation ﬂexibly and intuitively. Next,

we tackle the challenge of accurately calculating state

transition rates by methodically preprocessing exe-

cutable modules so that they generate an enhanced

description of states associated with terms. Thereby,

we obtain the corresponding CTMC generator ma-

trix through fundamental text processing. We illus-

trate this approach through the stochastic extension

of rewritable Petri Nets (Padberg and Kahloul (2018);

Capra (2022); Capra and K

ohler-Bußmeier (2024)), a

versatile model for adaptive distributed systems.

2 THE Maude SYSTEM

Maude syntax is based on (conditional) equations and

rules. Each side of a rule or equation is a term of a

certain kind, which may involve variables. Rules and

equations operate through intuitive rewriting, where

instances on the left side are replaced with instances

on the right. A functional module acts as a func-

tional program, deﬁning operations using equations

as simpliﬁcations. It outlines a equational theory

(Σ,E ∪A) of membership equational logic (Bouhoula

et al. (2000)): Σ is the signature, encompassing the

declaration of sorts, subsorts, kinds

and operators;

E contains equations and membership axioms; and A

contains the operator’s equational attributes (assoc,

comm, ide, idem). The model of (Σ,E ∪A) is the ini-

tial algebra T

Σ/E∪A

, mathematically corresponding to

the quotient of the ground-term algebra T

, formed

by the equivalence classes of the relation induced by

E ∪ A on T

Under Church-Rosser (conﬂuence), sort-

decreasing and termination conditions –modulo

Kinds are equivalence classes implicitly formed by

connected components of sorts under the subsort partial or-

der. Terms of a certain kind without a sort denote errors.

A– on theory (Σ,E) (Bouhoula et al. (2000)), any

ground term is rewritten through equations (used as

simpliﬁcation rules) to a unique canonical form that

has the least sort according to the sub-sort partial

order and is made up of constructors (operators with

the ctor attribute). These canonical forms deﬁne an

algebra isomorphic to the initial algebra, ensuring

consistency between mathematical and operational

semantics.

A Maude system module includes (in addition

to equations) rewrite rules representing local tran-

sitions in a concurrent system. It deﬁnes a gener-

alised rewrite theory (Bruni and Meseguer (2003))

R = (Σ,E ∪ A,R). Here, (Σ,E ∪ A) acts as the un-

derlying equational theory, and R is a set of rewrite

rules. This theory captures the behaviour of a con-

current system, with (Σ, E ∪ A) deﬁning the algebraic

structure of the states and R describing the concurrent

transitions. The initial model of R provides each kind

k with a labelled transition system (TS) where states

are elements of T

Σ/E∪A,k

and state transitions occur as

[t]

[α]

→ [t

′

], with [α] denoting an equivalence class of

rewrites. The crucial coherence property, discussed

in the next sections, ensures that a system module is

executable using the Maude rewriting engine.

3 (REWRITABLE) STOCHASTIC

PETRI NETS

This section ﬂexibly incorporates stochastic pa-

rameters into rewritable PT nets (RwPT) (Pad-

berg and Kahloul (2018); Padberg and Schulz

(2016); Capra (2022); Capra and K

ohler-Bußmeier

(2024)). This deﬁnition integrates and com-

pletes (Capra and K

ohler-Bussmeier (2023); Capra

and K

ohler-Bußmeier (2023); K

ohler-Bußmeier and

Capra (2024)) using a systematic approach.

All the concepts discussed hereinafter are based

on multisets: For a set D, a multiset (or bag) b in D is

deﬁned as a map b : D → N, where b(d) represents the

multiplicity of the element d in b. We denote the set

of all multisets in D by Bag[D]. Common arithmetic

and relational operators can be extended to multisets

element by element.

A PT net (Reisig (1985)) (Figure 1) is a ﬁnite,

non-empty bipartite multidigraph. Its nodes are di-

vided into two types: places (represented by circles),

which illustrate state variables, and transitions (repre-

sented by bars), which denote events that trigger local

state changes. A multiset m of places (m ∈ Bag[P]),

referred to as marking, represents a distributed state.

Edges may be classiﬁed as: Input edges (from places

Associating a Markov Process with Maude Executable Modules

107

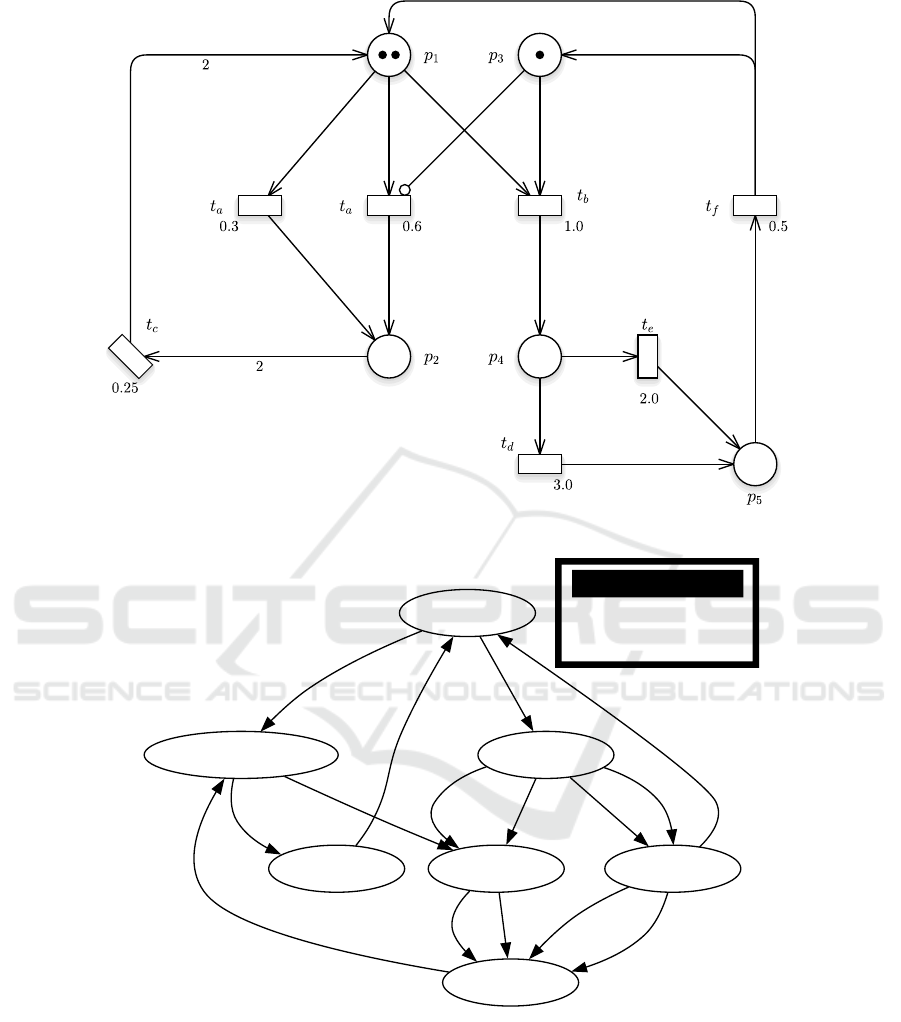
Figure 1: An example of SPN.

p1(2) p3(1)

p1(1) p2(1) p3(1)

ta2 (0.6)

p1(1) p4(1)

tb (1)

p2(1) p4(1)

tb (1)

p2(2) p3(1)

ta2 (0.3) ta1 (0.6) ta2 (0.3)

p1(1) p5(1)

te (2) td (3)

p2(1) p5(1)

te (2)td (3)

tc (0.25) tf (0.5)

ta2 (0.3)ta1 (0.6)

tf (0.5)

Reachability Graph

Showing all markings.

Total markings: 7

Figure 2: The CTMC generated by the SPN in ﬁgure 1.

to transitions), Output edges (the reverse), and in-

Hibitor edges (marked by a small circle endpoint).

The adjacency lists of transitions t ∈ T are also ex-

pressed with multisets in Bag[P]: I(t), O(t), H(t).

The interleaving PT behaviour is based on tran-

sition ﬁring rule: t is enabled in m if and only if:

I(t) ≤ m ∧ ∀p ∈ P : H(t)(p) = 0 ∨ H(t)(p) > m(p).

If t is enabled, it can reach m

′

= m + O(t) − I(t) (aka

m[t⟩m

′

). A PT system is a pair (N, m

) made up

of a net and a marking whose behaviour is deﬁned

by the reachability graph (RG), a labelled multidi-

graph (V,E) such that: m

∈ V ; m ∈ V ∧ m[t⟩m

′

⇒

′

∈ V ∧ m

−→ m

′

∈ E.

In stochastic PT nets (SPN) (Chiola et al. (1993)),

a CTMC is associated with the RG by assigning to

each transition t a negative exponential pdf with (pos-

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

108

sibly marking dependent) rate λ (t, m

). The generator

matrix is the following.

i, j

∑

t:m

[t⟩m

λ (t,m

), Q

i,i

:= 1 −

∑

j: j̸=i

i, j

The SPN depicted in Figure 1, along with its cor-

responding CTMC shown in Figure 2 (both illus-

trations generated using the GreatSPN toolset (Am-

parore et al. (2016)), serves as a basic model of a

distributed system with two processes on either side,

sharing resources at places p

and p

. All transitions

are modelled as ”inﬁnite servers”, with ﬁring rates

proportional to enabling degree. For example, the ﬁr-

ing rate of ta

in m

is 0.3 ∗ 2 as two instances of ta

are enabled concurrently.

3.1 Stochastic PT Nets in Maude

A rewritable PT (RwPT) (Padberg and Schulz (2016);

Padberg and Kahloul (2018); Capra and K

ohler-

Bußmeier (2024)) functions as an algebraic represen-

tation of a mutable PT, uniformly merging the ﬁring

rule with net rewrite rules. We will initially consider

the former and then generalise by including the latter.

We enhance RwPT by associating exponential

rates with rewriting rules using a method that can be

applied to any system module. We retain most of

the concepts of Capra and K

ohler-Bußmeier (2024)

while introducing ad-hoc changes. The formalisation

of stochastic RwPT includes a hierarchy of modules

available at https://github.com/lgcapra/rewpt. We in-

clude code excerpts for the reader’s convenience.

This formalisation is based on multisets which are

implemented as a rich data type (rather than a sim-

ple commutative monoid) for efﬁciency reasons. The

assoc,comm operator _+_, which is also marked as

a constructor, offers an intuitive description of multi-

sets as weighted sums. The Pbag sort (from module

BAG{Place}) holds multisets of places. For example,

the term 3. p(1) + 1. p(2) represents a multiset

with three occurrences of p

and one of p

The following excerpt from the PT-NET module

outlines the PT signature. It is parametric in the type

of node labels used. Transitions (terms of sort Tran)

are distinctly identiﬁed through labels linked to ad-

jacency lists, expressed as Pbag triples enclosed be-

tween [] (sort Tmatrix terms). Nets are deﬁned

in a modular fashion using the assoc,comm oper-

ator _;_ : Net Net -> Net, along with the sub-

sort relation Tran < Net (both inherited from the

predeﬁned MAP module). A term of kind [System]

comes from juxtaposing a Net and a Pbag (a mark-

ing). A conditional membership axiom ensures that

the System terms are built of non-empty nets

. Two

This choice enables the inclusion of the module MAP in

operators intuitively map the transition-enabling con-

dition and the ﬁring effect.

Listing 1: PT signature.

fmod PT−NET{L :: TRIV, PL :: TRIV} is

pr MAP{L,Tmatrix{PL}}

(sort Map{L,Tmatrix{PL

}} to Net, sort Entry{L,Tmatrix{PL}} to Tran,

op emptyM to emptyNet) .

***

renaming

sort System .

var L : L$Elt . var N : Net . vars M I O H : Pbag .

op __ : Net Pbag −> [System] [ctor] .

***

partial fun.

cmb N M : System if N =/= emptyNet .

op enabled : Tran Pbag −> Bool .

eq enabled(L |−> [I,O,H],M) = I <= M and−then H >

op fire : Tran Pbag −> Pbag .

eq fire(L |−> [I,O,H], M) = (M − I) + O .

endfm

The next excerpt is from module SPN, which inte-

grates stochastic parameters into PT-NET. Transition

labels include a String, a Float (the rate), and a Nat

(the ﬁring policy).

Listing 2: SPN signature.

fmod SPN is

pr PT−NET{Tlab, Nat} .

pr CONVERSION .

vars M M’ : Pbag . var B : NePbag . var P : Place .

var L : Tlab . var Q : Tmatrix . vars K K’ D : NzNat .

op firingRate : Tran Pbag −> [Float] .

eq firingRate(L |−> Q, M) = if pol(L) == 1 then

rate(L) else rate(L)

float(if pol(L) == 0 then

ed(I(Q), M) else min(pol(L), ed(I(Q), M)) fi) fi .

op ed : Pbag Pbag −> [NzNat] .

eq ed(nilP, M) = 1 .

eq ed(B, M) = $ed(B, M, MAXNAT) .

op $ed : Pbag Pbag NzNat −> [NzNat] .

eq $ed(K . P + M , K’ . P + M’, D) =

$ed(M , M’, min(D, K’ quo K)) .

eq $ed(nilP, M, D) = D .

endfm

A Tran term looks like:

t(S, R, P) |-> [I,O,H].

The firingRate operator deﬁnes state-

dependent ﬁring rates. This version is based on

the enabling degree (ed) of a transition in a marking,

which refers to the number of instances of a transition

that could be ﬁred simultaneously. Under the inﬁnite

server policy (0), the transition ﬁring rate is directly

proportional to ed. The k-server policy, with k > 0,

uses the smaller value between ed and k as the

multiplicative factor of the rate parameter. The

1-server policy maintains a constant ﬁring rate equal

to the rate parameter.

a protected way, that is, preserving its initial semantics.

Associating a Markov Process with Maude Executable Modules

109

The system module SPN-SYS adds the rewrite rule

firing to the PT signature. This rule includes the

topological aspect of transition ﬁring and the asso-

ciated rate. Notice the use of matching equations

in the rule’s condition: The free variables T, N’

are ﬁrst matched against the canonical term bound

to the variable N (and consequently bounded), and

then R:Float is bound to the canonical form of

firingRate(T, M).

Listing 3: SPN ﬁring rule

mod SPN−SYS is

inc SPN .

var M : Pbag . var T : Tran . vars N N’ : Net .

var R : Float

crl [firing] : N M => N fire(T, M) if T ; N’ := N /\

enabled(T, M) /\ R := firingRate(T, M) .

endm

This approach may be uniformly extended to any

system module M. We assume that each rewrite rule

r within M adheres to a similar pattern, where t

′′

sig-

niﬁes a Float term (if condition C is missing t

′′

is a

ground term):

r : t => t

′

i f C /\ R : Float := t

′′

This representation facilitates the automated con-

version of rules and the evaluation of different shapes

of state dependency simultaneously with the applica-

tion of rules.

We hereinafter suppose that a stochastic RwPT is

deﬁned by a system module M including SPN-SYS

and two constants (aliases): op net : -> Net and

op m0 : -> Pbag. The transition system generated

by the term net m0, denoted T S(net m0,M), con-

tains the reachability graph (RG).

The module SPN-EXE below contains the SPN sig-

nature in Figure 1, the system module SPN-EXE-SYS

includes the SPN signature and the firing rule. The

transition system T S(net m0, SPN-EXE-SYS) resem-

bles the RG described in Figure 2. However, it differs

by having single edges all marked firing. Figure

2 reveals multiple transitions between states (due to

two pairs of SPN transitions having the same effect),

which makes the layout of Maude TS inappropriate

for the derivation of a Markov process.

Listing 4: Signature of SPN in ﬁgure 1 and associated sys-

tem module.

fmod SPN−EXE is

pr SPN .

op net : −> Net . op m0 : −> Pbag .

eq net = t(”a”, 0.6, 0) |−> [1 . p(1), 1 . p(2), 1 . p(3)]

;

t(”a”, 0.3, 0) |−> [1 . p(1), 1 . p(2), nilP] ;

t(”b”, 1.0, 0) |−> [1 . p(1) + 1 . p(3), 1 . p(4), nilP

] ;

t(”c”, 0.25, 0) |−> [2 . p(2) , 2 . p(1), nilP] ;

t(”d”, 3.0, 0) |−> [1 . p(4) , 1 . p(5), nilP] ;

t(”e”, 2.0, 0) |−> [1 . p(4) , 1 . p(5), nilP] ;

t(”f”, 0.5, 0) |−> [1 . p(5) , 1 . p(1) + 1 . p(3),

nilP] .

eq m0 = 2 . p(1) + 1 . p(3) .

endfm

mod SPN−EXE−SYS is

inc SPN−EXE .

inc SPN−SYS .

endm

3.2 Rewritable SPN

The system module in listing 5 includes net transfor-

mations described by rewrite rules. The merge rule

combines two PT transitions sharing the tag when

both are enabled or disabled (e.g., those with tag "a"

in the listing 4). This merge relies on summing their

adjacency lists, resulting in a transition with a rate

parameter equal to the sum of the two. fold unites

two transitions with identical adjacency lists (e.g.,

those with tags "d" and "e"), resulting in a transition

whose rate parameter equals the sum of the originals.

Finally, aggr unites two transitions when the postset

of one aligns with the preset of the other, provided

that this is isolated from the rest of the net and the

second transition is not enabled (this makes the rule’s

formalisation a bit tricky). The resulting rate param-

eter is determined by the sum of the inverses of the

two original rate parameters. Each rule assumes that

the involved transitions share the ﬁring policy. Rules

have a constant rate for simplicity.

Notice that rules merge and aggr are marking-

dependent, while fold is merely structural. These

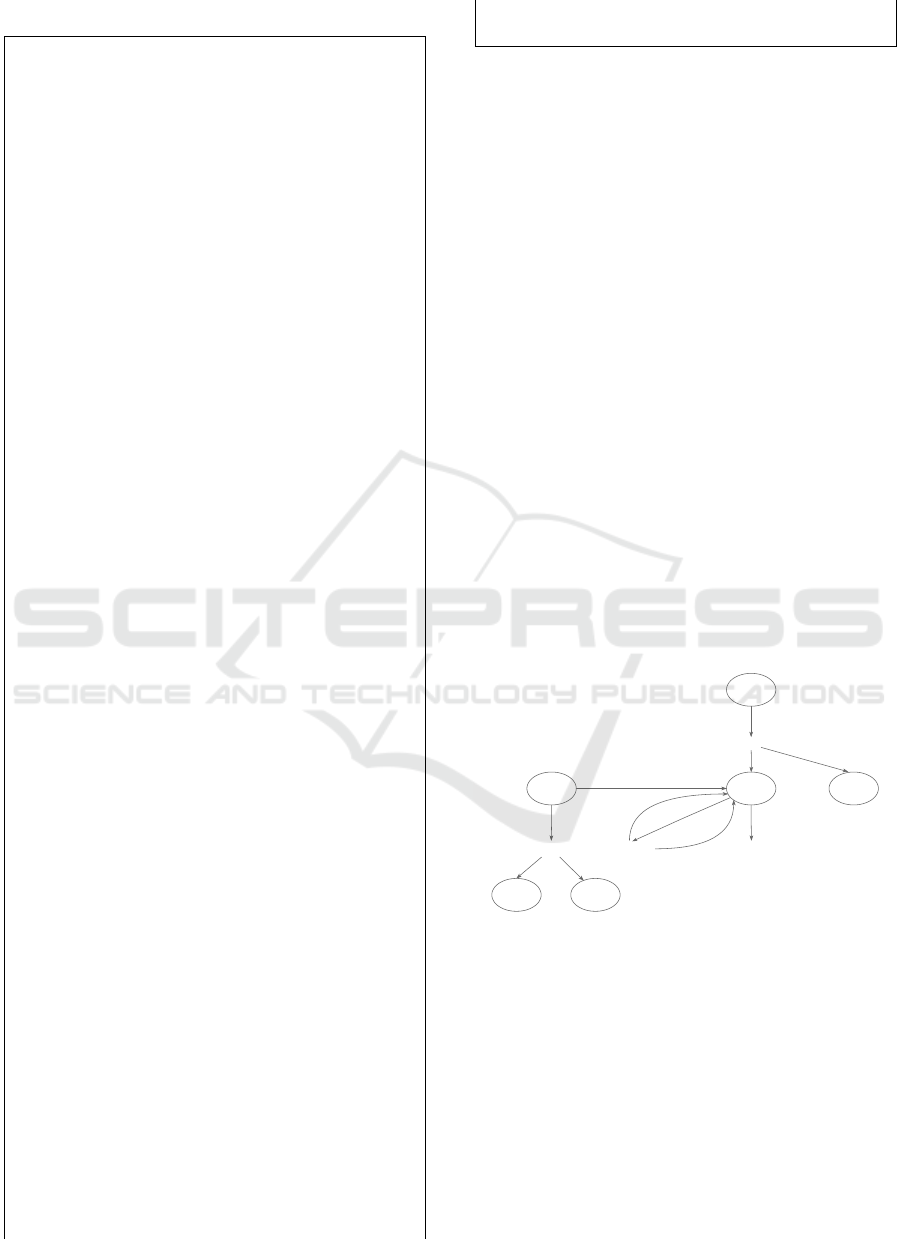
rules are illustrated in Figure 3, which refers to the

example SPN in Figure 2.

Listing 5: Example of rewritable SPN

mod SPN−EXE−SYS−REW is

inc SPN−EXE−SYS .

vars L L’ : Tlab . vars T T’ : Tran . var P : Place .

vars B B’ M I O : Pbag . vars r r’ R : Float . var N :

Net .

var W : String . var E : Nat . var Q : Tmatrix .

crl [merge] : (N ; T ; T’) M =>

(N ; merge(T, T’, t(W, rate(T) + rate(T’), E))) M

if W := tag(T) /\ W = tag(T’) /\ E := pol(T) /\ E = pol(T

’)

/\ enabled(T, M) = enabled(T’, M) /\ R := 0.01.

crl [fold] : L |−> Q ; L’ |−> Q =>

t(”fold”, rate(L) + rate(L’), E) |−> Q

if E := pol(L) /\ E = pol(L’) /\ R := 0.02 .

crl [aggr] : (N ; T ; T’) M =>

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

110

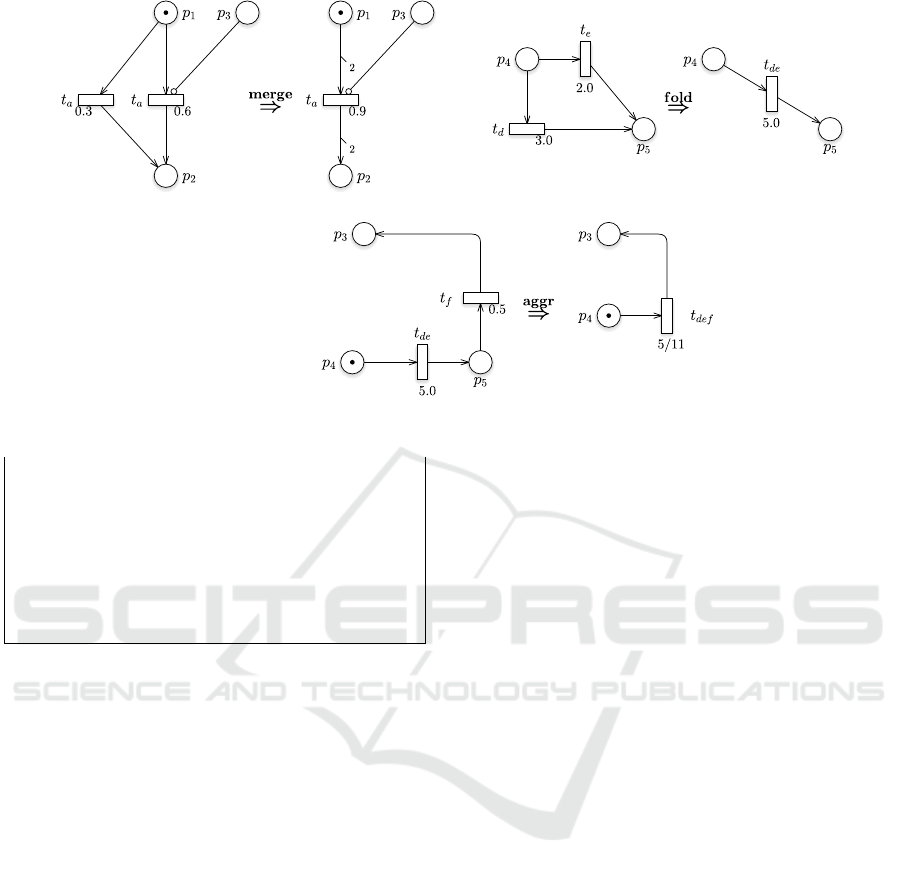
Figure 3: Net rewrites.

(N ; aggr(T, T’, t(tag(T) + ”−” + tag(T’),

r’ / (r + r’), E) ) ) M

if E := pol(T) /\ E = pol(T’) /\ enabled(T’, M) = false

/\ I := I(T’) /\ O := O(T) /\ O = I /\ support(I)

(places(N) U support(I(T) + H(T) + M + O(T’) + H(T’)

))

= empty /\ r := rate(T) /\ r’ := rate(T’) /\ R :=

0.05.

endm

4 ASSOCIATING A MC WITH A

SYSTEM MODULE

This section establishes the formal methodology for

associating a CTMC with the ground terms of a

Maude system module. Although rewriting logic the-

oretically supports concurrent application of rewrite

rules, our approach is directed towards a stochastic

interpretation by considering the interleaving seman-

tics adopted by the Maude rewrite engine.

Although we instantiate the methodology to the

formalisation of rewritable SPN provided in the pre-

vious section, we will provide general rigorous guide-

lines that function for any system module.

We ﬁrst recall some essential aspects of the pattern

matching mechanism (modulo A) used in Maude. Let

X encompass the variables utilised in R: Each x ∈ X is

associated with a particular kind or sort. By incorpo-

rating them into the signature Σ, one obtains a term al-

gebra T

(X) in which the terms may contain variables

from X and appear in equations and rules. A (well-

sorted) ground substitution is deﬁned as a mapping

σ : X → T

such that the minimal sort of σ (x) is less

than or equal to that of x. By performing term substi-

tution for variables conventionally, the substitution is

extended to a homomorphic function σ : T

(X) → T

Consider a term t ∈ T

(X), which corresponds to

the left-hand side of an equation or rule, and a subject

term u ∈ T

. We say that t matches u if there is a

substitution σ such that σ (t) ≡

u. In other words,

σ (t) and u are equivalent modulo the axioms A.

4.1 Matching and Rewrite: The

Congruence Property

The general structure of the rules is deﬁned by

t => t

′

i f C

∧ .. .C

wherein t and t

′

are terms (subsort decreasing) T

(X)

of the same kind, and C

may be a membership u

: s,

an equation u

= u

′

, or a match u

:= u

′

. The term t

′

can encompass ”free” variables that do not appear in

t, provided that they are bounded by a match u

:= u

′

and do not appear in any C

, j < i. In this regard, u

must constitute a pattern for E ∪ A. That is, if one ap-

plies a substitution of variables in u

using canonical

terms, the result should be a canonical term.

The rules R within the module M must be coherent

with the equations E modulo A: for any ground term

u, each one-step rewrite (modulo A) u → u

′

implies

that if ˆu is the canonical form of u, there is a one-step

rewrite ˆu → u

′′

such that u

′

E∪A

′′

′

and u

′′

have

the same canonical form). Coherence determines the

–otherwise impossible– decidability of rewriting un-

der theory E ∪ A. First, a term is reduced to its canon-

ical form using E ∪ A, followed by rewriting (modulo

A) this canonical form with R. In other words, any

Associating a Markov Process with Maude Executable Modules

111

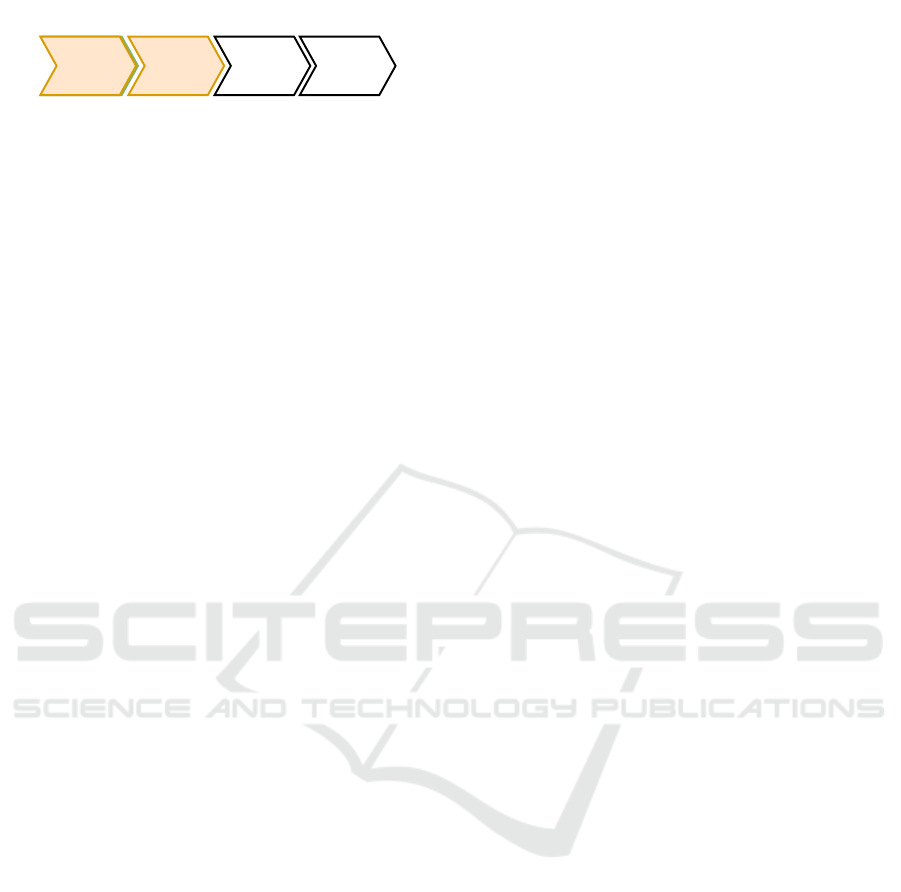
Derivation of a CTMC from a system module M

Step 2

preprocessing

(M*)

text processing

(Q)

stochastic

parameters

(M+)

CTMC solver

Figure 4: The steps to analyze a module M.

rewrite involving R on a term u can be emulated us-

ing u’s canonical form. This strategy, based on reduc-

ing terms to canonical forms before applying rules, is

sound and complete provided that it is supported by

a matching-modulo-A algorithm like that used by the

Maude engine, which implicitly relies on coherence.

A restrictive sufﬁcient condition for coherence is

that constructors do not appear as right terms in equa-

tions. This does not apply to our multiset deﬁnition,

where + is deﬁned through equations. The Maude sys-

tem provides a more general test for unconditional

rule s.

A broadly applicable condition for a rule r : t =>

′

i f cond to be coherent is that t is a pattern for

all variable substitutions σ that make cond provably

true. All Maude examples we have seen in the lit-

erature meet this criterion, easy to verify. We will

implicitly rely on this in the following discussion.

In this context, we should also ensure stochastic

coherence, which is guaranteed if for each rule r the

top operator in term t

′′

in the binding R : Float := t

′′

is a total function (its codomain is a sort, not a kind).

4.2 MC Deﬁnition and Related Issues

We aim to establish general criteria for obtaining a

Continuous-Time Markov Chain (CTMC) from the

transition system (TS) of a canonical ground term u of

a speciﬁed sort S within a system module M. These

criteria allow us to derive the generator matrix Q of

the CTMC, which is a crucial initial step toward au-

tomating the procedure. Our approach involves pre-

processing the module M to obtain an extended TS

that contains the necessary information to deﬁne Q.

This entire process is illustrated in Figure 4.

The deﬁnition of Q can be quite nonintuitive. In

the context of rewriting logic, a state transition u

[α]

→

(where u

and u

are the canonical representatives

of the equivalence classes [u

] and [u

]) represents

a group of equivalent rewrites. These rewrites cor-

respond to the interleaving of rule applications that

yield the same outcome.

In a stochastic setting, where the interleaving

semantics is applied—the approach adopted by the

Maude interpreter—the notation [α ] signiﬁes equiv-

alent single rewrites. Speciﬁcally, this means that

two matches (ground substitutions) are considered

equivalent, denoted as σ ≡

r,u

′

for a given rule

r : t ⇒ t

′

if cond, if and only if the following holds:

1. σ (t) = u

′

and σ

′

(t) = u

′′

, where u

′

and u

′′

are sub-

terms of u

. 2. Both σ (cond) and σ

′

(cond) are prov-

ably true. 3. The terms obtained by replacing the

subterm u

′

in u

with σ (t

′

), and the subterm u

′′

with

′

), respectively, are equal (with everything con-

sidered according to A ∪ E).

If u

′

and u

′′

coincide with u

, we state that rule r

applies to the top operator. We will start our discus-

sion with this common scenario.

To accurately deﬁne the transition rate from state

to state u

, we must consider the contributions of all

equivalent matches. Given two ground terms u

and

, let [α

] encompass the matches corresponding to

equivalent rewrites u

→ u

associated with r ∈ R (we

will omit the indices i and j). Furthermore, let λ

r,σ

de-

note the value assigned to the free variable R:Float

(appearing in the condition of each rule r) by substi-

tution σ . A plausible deﬁnition of matrix Q is:

Q[i, j] :=

∑

r∈R,σ ∈[α

]

r,σ

(1)

To obtain the Markov chain generator matrix, it is es-

sential to quantify all rewriting instances that corre-

spond to speciﬁc state transitions. We must address

three major issues:

1. The transition system (TS) generated by Maude’s

‘search‘ model checker can be visualised using

the ‘show search graph‘ command. This TS in-

cludes folded equivalent rewrites, with edges rep-

resenting state transitions annotated by the rules

that triggered those transitions. Matches for spe-

ciﬁc terms can only be obtained using the ‘match‘

command or the analogous metalevel operator.

2. Some matches that lead to equivalent rewrites

should be considered identical. This means that

although equation (1) is often sufﬁcient, it tends

to overestimate the rates of state transitions, as we

will demonstrate.

3. The possibility that a rewrite u

→ u

may result

from rewriting a local subterm adds complexity to

the computation of state transition rates.

Deﬁnition 1 Two equivalent matches σ and σ

′

of a

rule r are indistinguishable (

∼

) if one can be ob-

tained from the other through a permutation of vari-

ables of the same kind.

This concept induces the division of [α

] into sub-

classes. Consequently, we can modify Equation 1 ac-

cordingly (Equation 2 refers to the deﬁnition above):

Q[i, j] :=

∑

r∈R,[σ ]

∼

⊆[α

]

r,σ

(2)

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

112

5 GETTING THE MC

GENERATOR

This section describes how to preprocess a given sys-

tem module M to obtain extended modules that con-

tain all the necessary information to derive the associ-

ated Markov chain. We will illustrate this procedure

using the RwPT with its initial setup depicted in Fig-

ure 1. The fundamental concept involves rephrasing

each rewrite rule into an operator that emphasises the

potential matches of the rule, as formalised in the pre-

vious section. We use pre-deﬁned module templates,

some of which can be found in the listing 6.

Listing 6: Match enconding

fmod ANY−MATCH−CLASS is

sort AnyMatchClass .

endfm

view AnyMatchClass from TRIV to ANY−MATCH−

CLASS is sort Elt to AnyMatchClass .

endv

fmod MATCH−CLASS{X :: TRIV} is

pr ANY−MATCH−CLASS .

sorts MatchGroup{X} MatchClass{X} .

subsort X$Elt < MatchGroup{X} .

subsort MatchClass{X} < AnyMatchClass .

op _,_ : MatchGroup{X} MatchGroup{X} −>

MatchGroup{X} [ctor assoc comm prec 21] .

op {_} : MatchGroup{X} −> MatchClass{X} [ctor

prec 22] .

endfm

fmod MATCH is

pr LIST{AnyMatchClass}

(sort List{AnyMatchClass} to Match,

sort NeList{AnyMatchClass} to NeMatches,

op __ to _&_, op nil to emptyMatch) .

endfm

First, we consider the firing rule. Then we ap-

ply a uniform method for net rewrites. The operator

firing match takes a term s of the sort System and

produces the (System) state transitions obtained by

rewriting s with firing.

A StateTran{D} term, where D can be any sort,

is deﬁned as a triplet: Match --> D : Float. For-

mally, a Match is a list of MatchClass elements sep-

arated by &, representing variable substitutions. Each

MatchClass gathers variables of a speciﬁc sort, thus,

the arity of a Match term is inherently linked to the

variables involved in the rule. In our speciﬁc context

(as shown in listing 3), we have N:Net, M:Pbag, and

T:Tran (we can disregard free variables like N’ used

in the rule’s condition but not in the rule’s right side).

The auxiliary operator $firing-match parallels

the rule deﬁnition: It employs tail recursion to ex-

haustively generate, up to a ﬁxed point, all variable

substitutions that align with the rule’s left side and

satisfy the rule condition. Concurrently, it assigns the

target states and their corresponding state transition

rates. Notice that we could restrict the variables that

determine the rule’s matches to just T:Tran. How-

ever, this heuristic is more difﬁcult to automate.

Listing 7: Encoding of ﬁring rule for CTMC deﬁnition

fmod SPN−MC is

pr MATCH−CLASS{System} .

pr MATCH−CLASS{Pbag} .

pr MATCH−CLASS{Net} .

pr SPN−STATE−TRAN .

var T : Tran . vars M M’ : Pbag .

vars N N’ : Net . var S : System . var R : Float .

var X : Set{StateTran{System}}. var XM : Match.

op firing−match : System −> Set{StateTran{

System}} .

eq firing−match(S) = $firing−match(S,

noStateTranS) .

op $firing−match : System Set{StateTran{

System}} −> Set{StateTran{System}} .

ceq $firing−match(S, X) =

$firing−match(S, (XM −−> S’ : R) U X)

if (T ; N) M := S /\ enabled(T, M) /\

S’ := (T ; N) firing(T, M) /\ R := firing−rate(T, M)

XM := {N} & {T} & {M} /\ (XM −−> M’ : R) in X =

false.

eq $firing−match(S, X) = X [owise] .

endfm

In general, for a certain rule r:

r : t => t

′

i f C /\ R : Float := t

′′

of type D, we automatically introduce an operator

$r-match deﬁned by the following pair of equations

(we neglect any optimisations and assume that vari-

ables S and S

′

are of type D, while X is of type

Set{StateTran{D}}, with the operator’s arity and the

other variables’ types being appropriately deﬁned):

$r-match(S,X) = $r-match(S,(XM −− > S

′

: R)∪X)

i f C /\ t := S /\ S

′

:= t

′

/\ R := t

′′

/\ X M :=

VAR(r) /\ (XM − − > S

′

: R) in X = f alse .

$r-match(S,X) = X [owise] .

where the symbol VAR(r) denotes the term Match

that encompasses the list of signiﬁcant variables in

rule r.

Using this method, we can systematically and reli-

ably translate any rewrite rule. For example, Listing 8

illustrates the rephrase of the net rewrites merge and

fold, presented in Listing 4, as operators (the one of

aggr is similar).

Associating a Markov Process with Maude Executable Modules

113

Listing 8: Net rewrites of the example; Extended state de-

scription for MC.

fmod SPN−MC−EXE is

pr SPN−EXE .

pr SPN−MC .

pr MATCH−CLASS{Tlab} .

pr MATCH−CLASS{Tmatrix} .

pr SPN−STATE−TRAN .

var P : Place . vars T T’ : Tran .

var M : Pbag . var N : Net.

vars S S’ : System . var R : Float . var E : Nat .

vars L L’ : Tlab . var Q : Tmatrix . var W : String .

var X : Set{StateTran{System}} . var XM : Match .

op merge−match : System −> Set{StateTran{

System}} .

eq merge−match(S) =

$merge−match(S, noStateTranS) .

op $merge−match : System Set{StateTran{System

}} −> Set{StateTran{System}}.

ceq $merge−match(S, X) =

$merge−match(S, (XM −−> S’ : R) U X)

if (N ; T ; T’) M := S /\ W := tag(T) /\ W = tag(T’) /\

E := pol(T) /\ E = pol(T’) /\

enabled(T, M) = enabled(T’, M) /\ S’ :=

(N ; merge(T, T’, t(W, rate(T) + rate(T’), E))) M /\

R := 0.02 /\ XM := {T , T’} /\ (XM −−> S’ : R) in X =

false .

eq $merge−match(S, X) = X [owise] .

op fold−match : Net −> Set{StateTran{System

}}.

eq fold−match(S) = $fold−match(S, noStateTranS

) .

op $fold−match : System Set{StateTran{System

}} −> Set{StateTran{System}}.

ceq $fold−match(S, X) =

$fold−match(S, (XM −−> S’ : R) U X)

if (N ; L |−> Q ; L’ |−> Q) M := S /\

E := pol(L)/\ E = pol(L’) /\

S’ := (N ; t(”fold”, rate(L) + rate(L’), E) |−> Q) M

R := 0.02 /\ XM := {L , L’} & {Q} /\ (XM −−> S’ : R)

in X = false .

eq $fold−match(S, X) = X [owise] .

op aggr−match : System −> Set{StateTran{

System}} .

...

op rewriteS : System −> Set{STrate{System}} .

eq rewriteS(S) = cumrate(firing−match(S) U

fold−match(S) U merge−match(S) U aggr−

match(S)) .

op stateTranMC : System −> SpnStateTran .

eq stateTranMC(S) = SYS: S REW: rewriteS(S) .

endfm

mod SPN−STATE−TRAN−SYS is

inc SPN−MC−EXE .

vars S S’ : System . var RS : Set{STrate{System}}

rl [rew] : SYS: S REW: (RS U S’ : R:Float) =>

stateTranMC(S’) .

endm

This translation points out indistinguishable vari-

able substitutions - seen as distinct by the commands

match and metaMatch in Maude- that correspond to

variable permutations: T ↔T’ in merge and L↔L’

in fold.

The Match-Class constructor {_}, which en-

closes a commutative-associative, comma-separated

juxtaposition, is designed to implicitly recognise

potentially indistinguishable matches. This helps

prevent the overestimation of state transition rates.

In the deﬁnition of $merge-match, the Match

term is {T, T’}, while in $fold-match, it is

{L, L’} & {Q}. (Both deﬁnitions are optimised.)

It is important to note that the term Match, which

is part of $aggr-match (not displayed), also includes

a subterm {T, T’}. In this context, the ground sub-

stitutions associated with the permutation T↔T’ yield

distinct values for the rule condition.

The rule fold operates locally within the Net seg-

ment of a System term. When working with a canon-

ical term of type D, we need to identify all subterms

of type D

′

that can be rewritten using a corresponding

rule r

′

. We then wrap any instances of r

′

with an anal-

ogous rule of type D. The presence of equational at-

tributes for constructors and sub-sorts adds complex-

ity to this process.

Net

System

_ _

PbagTran

; (assoc, comm) emptyNet (ide)|->

Tlab Tmatrix

Figure 5: Digraph showing the structure of a System term.

An approach to effectively detect all possible lo-

cal applications of r

′

is to create an abstract semantic

graph for a generic term of type D, as demonstrated

in Figure 5 for terms of sort System and subterms of

sort Net. By embedding the rule fold (as shown in

the listing 2) into an ”equivalent” rule of type System,

we achieve the following result, where N and M are

variables of sorts Net and Pbag, respectively.

crl [fold−top] (N ; L |−> Q ; L’ |−> Q) M =>

(N ; t(”fold”,rate(L)+rate(L’),E) |−> Q) M

if E := pol(L) /\ E = pol(L’) /\ R := 0.02 .

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

114

The rule, once adorned, can be converted conven-

tionally. Matching modulo-A ensures that the rule

translation incorporates the speciﬁc scenario of a net

composed of two transitions, achieved by substituting

N with the term emptyNet, which is regarded as the

”identity” for net juxtaposition (;).

Using the conversion of rules into operators, we

can create a structured representation of states that

includes the CTMC generator matrix (see the ﬁnal

part of the listing 8). The operator cumrate com-

putes precise state transition rates, represented as

pairs consisting of a target state and a numerical

value. Meanwhile, the operator stateTranMC trans-

forms the standard state representation into an ex-

tended one, emphasising state transitions (we will

skip further details). The rule rew in the module

SPN-STATE-TRAN-SYS, which uses this extended de-

scription, synthesises the original rewrite rules.

5.1 Performance Metrics

Table 1 presents the experimental results related to the

(rewritable) Stochastic Petri Net shown in Figure 1.

These results were derived using the rules outlined in

listing 8. The model produces a CTMC with absorb-

ing states. By varying the initial marking parameter

k, we evaluate the time required to create the stan-

dard transition system (module SPN-EXE-SYS-REW)

using conventional hardware, in contrast to the time

needed to generate the extended transition system

(module SPN-STATE-TRAN-SYS). An online CTMC

solver was used. Although the overhead of the ex-

tended representation is generally acceptable, it be-

comes more pronounced as k increases. Additional

trials indicate that this overhead can be signiﬁcantly

reduced by considering the local effects of rewrites.

For example, we could exploit the locality of the

firing rule (by far the most frequently occurring)

that acts on the state of a PT System.

Table 1: Ordinary vs extended TS of the example–Mean

Time To Absorption (MTTA).

k · m

# states TS (sec) TS-ext (sec) MTTA

5 925 0 0 4

10 4685 2 2 123

20 28755 10 17 478

40 199095 58 156 1259

60 639035 169 745 3082

The second case study refers to a benchmark of a

distributed production system as discussed in Capra

and K

ohler-Bußmeier (2024), which presents mod-

elling challenges associated with structural and state

adaptation issues. The system comprises N Produc-

tion Line (PL) replicas that operate concurrently with

regulated degradation. Each PL is divided into K in-

terchangeable components. Following the occurrence

of a fault, each PL adapts itself to continue oper-

ating with diminished performance. The methodol-

ogy elucidated in Capra and K

ohler-Bußmeier (2024)

improves the rewritability of PT nets with process-

algebra operators, thus simplifying the work of mod-

elers and easing the management of large-scale mod-

els with nested components by exploiting their sym-

metries. A quotient transition system is constructed

using structured node labelling. This concise TS

conforms to the strong bisimulation property, which,

when applied to the stochastic extension of rewritable

PTs, aligns with the exact lumpability of the CTMC

associated with the TS (Buchholz (1994)). From a

technical perspective, this is achieved by embedding

the right side of each rewrite rule within a normalize

operator, which transforms a PT system (interpreted

as a coloured graph) into its canonical form. In this

framework, it is critical to accurately compute the

transition rates in the lumped CTMC by addressing

the issues discussed in Section 4. Speciﬁcally, a

canonical state is likely to reach several states corre-

sponding to the same canonical representative, which

remains undetectable using the original TS generated

by Maude.

Table 2 presents comparable data for this bench-

mark model

as the number of PL replicas increases,

alongside the system’s reliability at a speciﬁc point

in time (the generated CTMC in this instance also in-

cludes absorbing states). The values in the second and

third columns parallel those documented in Capra and

ohler-Bußmeier (2024). The overhead incurred by

extended TS construction is markedly lower than that

recorded in Table 1, which is attributed to exploiting

the locality inherent in the firing rewrite rule (we

omit further technical details on the Maude encoding).

Table 2: Ordinary vs extended TS of the production system

– R(t) := P(T TA) > t.

N # states TS (s) TS-ext (s) R(t = 10.000)

1 82 0 0 0.55

2 451 0.3 0.4 0.68

3 1153 1.1 1.9 0.74

4 2123 2.9 3.8 0.79

5 3357 4.7 7.5 0.83

6 4855 10 14 0.86

7 6617 18 25 0.88

8 8643 29 41 0.89

9 10933 48 62 0.90

10 13487 66 94 0.90

Notably, the states in this context are ”symbolic,”

meaning they represent equivalence classes. The conven-

tional state spaces, by contrast, are greater by several orders

of magnitude.

Associating a Markov Process with Maude Executable Modules

115

6 CONCLUSIONS

An organised methodology has been devised for con-

structing a coherent Markov process from executable

Maude modules that integrate stochastic parameters.

This approach tackles the difﬁculties related to the

accurate computation of state transition rates. The ef-

fectiveness of our method has been validated through

the speciﬁcation of rewritable stochastic Petri nets.

Present endeavours concentrate on fully automating

this procedure and reducing the overhead imposed by

the extended Transition System employed to generate

the Markov process. In particular, ongoing research

aims to minimize the redundancy introduced by pre-

processing in the state representation used to calculate

the Markov chain generator matrix exactly.

ACKNOWLEDGEMENTS

This work was partially funded by the MUR project

“T-LADIES” (PRIN 2020TL3X8X).

REFERENCES

Agha, G., Meseguer, J., and Sen, K. (2006). Pmaude:

Rewrite-based speciﬁcation language for probabilistic

object systems. Electronic Notes in Theoretical Com-

puter Science, 153(2):213–239. Proceedings of the

Third Workshop on Quantitative Aspects of Program-

ming Languages (QAPL 2005).

Amparore, E. G., Balbo, G., Beccuti, M., Donatelli, S., and

Franceschinis, G. (2016). 30 years of GreatSPN. In

Principles of Performance and Reliability Modeling

and Evaluation, pages 227–254. Springer.

Bouhoula, A., Jouannaud, J.-P., and Meseguer, J. (2000).

Speciﬁcation and proof in membership equational

logic. Theoretical Computer Science, 236(1):35–132.

Bruni, R. and Meseguer, J. (2003). Generalized rewrite the-

ories. In Baeten, J. C. M., Lenstra, J. K., Parrow, J.,

and Woeginger, G. J., editors, Automata, Languages

and Programming, pages 252–266, Berlin, Heidel-

berg. Springer-Verlag.

Buchholz, P. (1994). Exact and ordinary lumpability in ﬁ-

nite markov chains. Journal of Applied Probability,

31(1):59–75.

Capra, L. (2022). Rewriting logic and Petri nets: A natu-

ral model for reconﬁgurable distributed systems. In

Bapi, R., Kulkarni, S., Mohalik, S., and Peri, S.,

editors, Distributed Computing and Intelligent Tech-

nology, pages 140–156, Cham. Springer International

Pub.

Capra, L. and K

ohler-Bußmeier, M. (2023). Maude speci-

ﬁcation of nets-within-nets: A formal model of adapt-

able distributed systems. In Proceedings of the

38th ACM/SIGAPP Symposium on Applied Comput-

ing, SAC ’23, page 188–191, New York, NY, USA.

Association for Computing Machinery.

Capra, L. and K

ohler-Bussmeier, M. (2023). Modelling

adaptive systems with nets-within-nets in maude. In

Proceedings of the 18th International Conference on

Evaluation of Novel Approaches to Software Engi-

neering - Volume 1: ENASE,, pages 487–496. IN-

STICC, SciTePress.

Capra, L. and K

ohler-Bußmeier, M. (2024). Modular

rewritable petri nets: An efﬁcient model for dynamic

distributed systems. Theoretical Computer Science,

990:114397.

Chiola, G., Marsan, M. A., Balbo, G., and Conte, G. (1993).

Generalized stochastic Petri nets: A deﬁnition at the

net level and its implications. IEEE Trans. Software

Eng., 19:89–107.

Clavel, M., Dur

an, F., Eker, S., Lincoln, P., Oliet, N. M.,

Meseguer, J., and Talcott, C. (2007). All About Maude

- A High-Performance Logical Framework: How to

Specify, Program, and Verify Systems in Rewriting

Logic. Lecture Notes in Computer Science. Springer.

ohler-Bußmeier, M. and Capra, L. (2024). Modelling

and simulation of adaptive multi-agent systems with

stochastic nets-within-nets. In Proceedings of the 16th

International Joint Conference on Computational In-

telligence - Volume 1: ECTA, pages 313–320. IN-

STICC, SciTePress.

Meseguer, J. (2012). Twenty years of rewriting logic.

The Journal of Logic and Algebraic Programming,

81(7):721–781. Rewriting Logic and its Applications.

Padberg, J. and Kahloul, L. (2018). Overview of recon-

ﬁgurable petri nets. In Heckel, R. and Taentzer, G.,

editors, Graph Transformation, Speciﬁcations, and

Nets: In Memory of Hartmut Ehrig, pages 201–222.

Springer, Cham.

Padberg, J. and Schulz, A. (2016). Model checking recon-

ﬁgurable petri nets with maude. In Echahed, R. and

Minas, M., editors, Graph Transformation, pages 54–

70. Springer.

Reisig, W. (1985). Petri Nets: An Introduction. Springer-

Verlag New York, Inc., New York, NY, USA.

Rubio, R., Mart

ı-Oliet, N., Pita, I., and Verdejo, A. (2023).

Qmaude: Quantitative speciﬁcation and veriﬁcation in

rewriting logic. In Chechik, M., Katoen, J.-P., and

Leucker, M., editors, Formal Methods, pages 240–

259, Cham. Springer International Publishing.

Rubio, R., Mart

ı-Oliet, N., Pita, I., and Verdejo, A. (2021).

Strategies, model checking and branching-time prop-

erties in maude. Journal of Logical and Algebraic

Methods in Programming, 123:100700.

Olveczky, P. C. and Meseguer, J. (2002). Speciﬁcation of

real-time and hybrid systems in rewriting logic. Theo-

retical Computer Science, 285(2):359–405. Rewriting

Logic and its Applications.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

116