
New Integral Distinguishers and Security Reassessment of LTLBC
Abhilash Kumar Das
Indian Institute of Technology Jammu, India
Keywords:
Integral Cryptanalysis, Division Property, Lightweight Block Cipher, MILP, LTLBC, Cryptographic Security.
Abstract:
This paper presents an in-depth study of integral distinguishers for the LTLBC block cipher, a 14-round 64-bit
lightweight cryptographic scheme designed for low-latency applications in IoT environments. Leveraging the
division property technique introduced by Yosuke Todo, we employ a Mixed Integer Linear Programming
(MILP) approach to identify previously unpublished 6-round integral distinguishers for LTLBC. Additionally,
we studied the MixWord permutation phase and showed that the cyclic intermixing tweak to the input word
doesn’t yield any significant improvement. Instead, it reduces to the original MixWord operation. This obser-
vation is rigorously justified through an algebraic proof and further followed by linear and differential crypt-
analysis, leading to a revised active Sbox count for LTLBC. As a side contribution, we correct inaccuracies
in the reported division property propagations for the FUTURE Sbox, initially presented at AFRICACRYPT
2022. Our findings provide a deeper understanding of LTLBC’s security and offer valuable insights for the
design of future lightweight block ciphers.
1 INTRODUCTION
Integral cryptanalysis, originally introduced as the
Square attack by Daemen et al., has evolved into a
powerful method for analyzing symmetric-key prim-
itives through integral distinguishers (Todo, 2015).
The division property, introduced by Todo (Todo,
2015), enhanced this technique by modeling the
propagation of algebraic structures through crypto-
graphic operations. Despite its strength, early appli-
cations faced computational limitations, particularly
with large block ciphers.
To overcome these challenges, MILP-aided tech-
niques were adopted. Xiang et al. (Xiang et al., 2016)
demonstrated how MILP can automate the search for
integral distinguishers, significantly improving effi-
ciency. Later, Sun et al. (Sun et al., 2020) refined
this for bit-level analysis, extending its use to ciphers
with complex linear layers. Xu et al. (Xu et al., 2024)
recently emphasized the need for accurate modeling
in division property propagation, revealing flaws in
prior analyses of the FUTURE cipher.
In the context of lightweight cryptography, espe-
cially for IoT, integral cryptanalysis remains a key
evaluation tool. Mirzaie et al. (Mirzaie et al., 2023)
exposed vulnerabilities in Shadow-32 using MILP-
based analysis. Meanwhile, LTLBC (Sun et al.,
2024), a cipher with low-latency IoT applications, has
not yet been rigorously analyzed under integral crypt-
analysis. Our study addresses this gap, uncovering
potential weaknesses and proposing security enhance-
ments to better protect IoT-based cloud systems (Yalli
et al., 2025; Sasikumar and Nagarajan, 2024).
In this paper, we outline our key contributions.
1. We discovered new 6-round integral distinguish-
ers for LTLBC using MILP-based division prop-
erty analysis, giving details on best possible dis-
tinguishers.
2. We evaluate a structural property of MixWord ar-
chitecture, showing a reduction of a cyclic word
intermixing tweak to the original MixWord opera-
tion.
3. We revised some corrections in the proposed ac-
tive Sboxes count of the original cipher via linear
and differential cryptanalysis.
4. Correction of division property propagation for
the FUTURE Sbox published in AFRICACRYPT
2022.
2 PRELIMINARIES
This section provides an overview of the key crypto-
graphic concepts and techniques used in this paper,
including the division property, MILP-based crypt-
analysis, and integral distinguishers. These concepts
Das and A. K.
New Integral Distinguishers and Security Reassessment of LTLBC.
DOI: 10.5220/0013566600003979
In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 717-722
ISBN: 978-989-758-760-3; ISSN: 2184-7711
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
717

form the foundation for our analysis of LTLBC.
2.1 Division Property
The division property, introduced by Todo (Todo,
2015), is a generalized integral property that facil-
itates integral cryptanalysis by exploiting the alge-
braic structure of cipher components. It extends tra-
ditional integral properties by leveraging propagation
rules for basic operations such as XOR, AND, and n-
bit Sboxes. The division property offers a system-
atic framework for analyzing the propagation of inte-
gral properties across cryptographic functions, partic-
ularly Sboxes and linear transformations. Its primary
objective is to characterize how the division property
evolves through various cipher components.
2.1.1 Definitions
Definition 2.1 (u ≽ v,(Xiang et al., 2016)). We say
u ≽ v if and only if ∀i,u
i
≥ v
i
. Otherwise, u ̸≽ v i.e. at
least one element in u is strictly smaller than v coor-
dinate wise.
Definition 2.2 (Division Property (Todo, 2015)). Let
X be a multiset whose elements belong to F
n
2
. The
multiset X is said to have the division property D
n
k
if,
for all u ∈ F
n
2
satisfying u ̸≽ k, the parity of the sum
M
x∈X
n−1
∏
i=0
x
u
i
i
!
over all x ∈ X is always even. Otherwise, the parity
of the sum may or may not be even. Hence, we call it
unknown.
The k has the same dimension as that of u. The
notation of the division property depends on the in-
stance element, i.e. D
4
3
can be thought of as D
1,4
K
with
k
i
∈ K where k
i
can take one or more vectors from
K = {(0,1,1,1), (1,0, 1,1),(1,1,0, 1),(1, 1,1,0)}
However, they are not the same because of the dif-
ferent representations. The former is the finite field
representation, and the latter is the vectorial represen-
tation. It is easy to notice that the notation D
n,m
K
is jus-
tified using n = 1, m = 4 with the element take value
of F
n,m
2
. We give a suitable example to make a distinc-
tion. Note that we define the hamming weight hw(·)
as the number of non-zero elements in a vector v e.g.
let v = (1,0,1,0) then hw(v) = 2.
Example 2.1. Consider a multiset X of 4-bit ele-
ments:
X = 0x{9, 6, 7, 4, 4, a, 8, 4, 5, b}.
We analyze the division property by evaluating the
parity of the sum for all possible values of u. Notably,
the parity remains zero whenever hamming weight
hw(u) < 3, indicating that the division property of X
is D
4
3
.
However, we identify two specific vectors, k
0
and
k
1
, given by {(0111), (1011)}, that yield a parity
of 1. This implies the existence of a minimal set
K = {k
0
,k
1
}, where for any u ̸≽ k
0
,k
1
, the parity
over the multiset remains zero. To illustrate, consider
u = (1011). It is evident that u ̸≽ k
0
but u ≽ k
1
, which
confirms its inclusion in K. If u were not included, we
would observe a case where u ̸≽ k
0
while still produc-
ing a parity of 1 over X, contradicting the case. This
analysis establishes a clear criterion for defining the
division property of the given multiset.
Now, we explain the effect of division property in
the output multiset Y when passed through non-linear
transformation such as the Sbox S of lower algebraic
degree. According to the proposition given by Yosuke
Todo (Todo, 2015) for an Sbox with algebraic degree
d,
Proposition 2.1 (Propagation characteristic of divi-
sion property). If an input multiset X has the division
property D
n
k
, then the output multiset Y satisfies the
division property
D
n
k
S
−→ D
n
⌈k/d⌉
.
Furthermore, if S is a bijective Sbox, then the preser-
vation of the maximum degree implies
D
n
n
S
−→ D
n
n
.
So, the division property is preserved for the linear
layer since the algebraic degree is 1. It is clear that the
division property D
4
0
would be invalid if |X| is odd.
3 SPECIFICATION OF LTLBC
LTLBC is a lightweight block cipher designed for
low-latency applications, particularly in IoT en-
vironments. It follows a 14-round Substitution-
Permutation Network (SPN) structure, operating on
a 64-bit plaintext and using a 128-bit master key.
3.1 Notations
The notations used in LTLBC can be referred from
Table 1.
3.2 Encryption Algorithm
The encryption process of LTLBC consists of an ini-
tial key addition followed by 14 rounds of transfor-
mations. Each round includes PermuteBits (Pb),
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
718
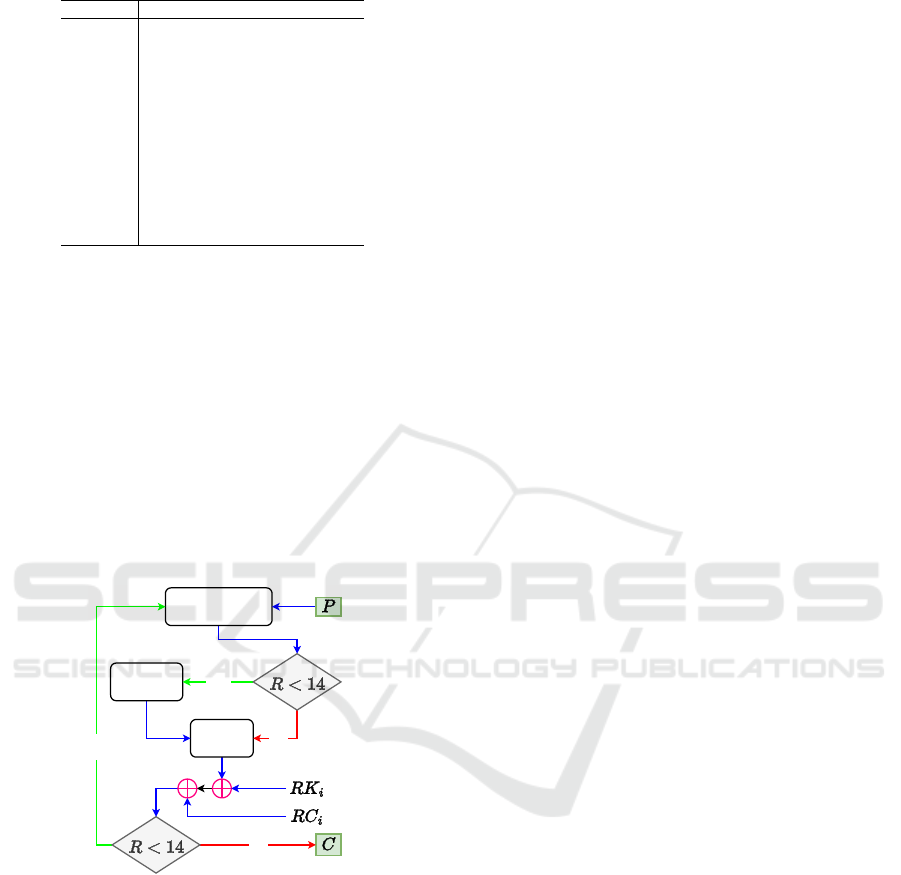
Table 1: Notations used in LTLBC.
Notation Description
P 64-bit plaintext
K 128-bit master key
C 64-bit ciphertext
T
(i)
Intermediate state after ith round
R
i
ith round number out of 14
RK
i
64-bit subkey for round i
RC
i
64-bit round constant for round i
X[i] ith bit of X
X[L : H] (H − L)-bit slice of X taken from
Lth bit to (H − 1)th bit
X||Y concatenation of X and Y
Op(X||Y ) Op(X)||Op(Y) if a valid operation
X
|<t|
t left cyclic shifts of X
MixWord (Mw), SubCell (Sb), AddRoundKey (Ak),
and AddRoundCon (Ac).
The final round excludes the MixWord operation,
and the resulting state T
(14)
is output as the cipher-
text C. The round function f
(i)
R
of ith round can be
expressed as (also shown in Figure 1)
T
(r)
=
(
Ac ◦ Ak ◦ Sb ◦ Pb(X), if r = 14,
Ac ◦ Ak ◦ Sb ◦ Mw ◦ Pb(X), else.
Finally, we express ciphertext C as
C = f
(14)
R
⃝
13
i=1
f
(i)
R
◦ (X ◦ K
0
)
PermuteBits
SubCell
MixWord
No
Yes
if
Yes
No
if
Figure 1: Structure of the LTLBC block cipher.
This section provides a complete overview of
LTLBC, including its round function and key sched-
ule, forming the foundation for further cryptanalysis
and security evaluation. The reader can refer to (Sun
et al., 2024) for more details.
4 SEARCHING THE INTEGRAL
DISTINGUISHERS
First, we provide all the known tools required to
model the cipher and then apply the searching tech-
nique to the LTLBC cipher.
4.1 MILP-Based Tool and Basic
Modelling Strategies
The LTLBC implements Sbox and XOR operation
in the entire encryption. The following MILP-based
bit-division property modelling can be used in our
case. To efficiently search for integral distinguish-
ers in block ciphers, the propagation of the division
property through fundamental operations like XOR
and Sboxes must be accurately modeled using MILP.
Modelling XOR (Xiang et al., 2016). The XOR oper-
ation is widely used in cryptographic structures, par-
ticularly in key addition and linear layers. When two
input bits x
0
,x
1
undergo XOR, the resulting output bit
y satisfies the relation
y = x
0
⊕ x
1
If the input multiset X = {(x
0
,x
1
) ∈ F
2
2
} has a division
property D
1,2
(k
0
,k
1
)
with vector k = (k
0
,k
1
) and k
0
,k
1
∈
F
2
, the output multiset follows D
1,1
(k
0
+k
1
)
. There can be
four division trails possible, namely,
D
1,2
(0,0)
−→ D
1,1
(0)
(valid)
D
1,2
(0,1)
−→ D
1,1
(1)
(valid)
D
1,2
(1,0)
−→ D
1,1
(1)
(valid)
D
1,2
(1,1)
−→ D
1,1
(2)
(invalid)
D
1,2
(k
0
,k
1
)
−→ D
1,2
k
0
or D
1,2
k
1
(invalid)
We give two examples of invalid division trails.
Example 4.1. Consider
X = {(0,0),(0,1),(0,1), (1,1), (0,0),(1,1)}
with D
1,2
(1,1)
and apply XOR y
i
= (x
0
⊕ x
1
)
i
for all i
giving Y = {0,1,1,0, 0,0} with D
1,1
2
that is invalid.
Example 4.2. Consider
X = {(0,0),(0,1),(0,1), (1,1), (1,1),(1,1)}
with D
1,2
(0,1)(1,0)
and apply XOR y
i
= (x
0
⊕ x
1
)
i
for all
i giving same Y = {0,1,1,0, 0,0} with invalid D
1,1
2
.
The linear layer always propagates the division prop-
erty, preserving the hamming weight of the input di-
vision.
Modelling Sbox (Xiang et al., 2016). Due to the non-
linearity of Sbox, we propagate input unknowns to
all the possible output unknowns. Suppose given the
input division property of n-bit Sbox is D
1,n
k
. This
implies that the parity of the sum is unknown when
u ≽ k. We propagate to the output division v if any
v ∈ {u|u ≽ k}.
New Integral Distinguishers and Security Reassessment of LTLBC
719

4.2 Integral Distinguishers
We report the best integral distinguishes in Table 2
with the least active bits in the input division prop-
erty across 1- to 6-rounds, giving all 64 balanced bits.
Additionally, we give a bound in the number of best
distinguishers.
Table 2: Input division D
1,64
k
across different rounds.
round input division k active log
2
(bound)
1 0x0000000000000003 2 10.97
2 0x00000000000003ff 10 37.14
3 0x0000000003ffffff 26 51.58
4 0x00001fffffffffff 45 47.18
5 0x0fffffffffffffff 60 63.35
6 0x7fffffffffffffff 63 22.86
We investigated the presence of balanced bits in a
half-round implementation of LTLBC but found none.
This suggests that LTLBC retains resistance beyond
half its rounds against integral cryptanalysis based on
the division property.
5 TWEAK TO MIXWORD
OPERATION
As discussed in Section 3.2, the MixWord layer takes
8-bytes input, out of which 4-bytes are given to a
symmetrically looking circuit with 5 and 9 left cyclic
shifts independently. However, We analyze the secu-
rity impact of interlinking all eight bytes in the circuit
at the input stage.
5.1 MixWord Modification
We modify the MixWord operation as under.
tmp
0
←− (X[0 : 16] ⊕ X[16 : 32])
|<t|
,
tmp
1
←− (X[16 : 32] ⊕ X[32 : 48])
|<t|
,
tmp
2
←− (X[32 : 48] ⊕ X[48 : 64])
|<t|
,
tmp
3
←− (X[48 : 64] ⊕ X[0 : 16])
|<t|
,
Y [0 : 16] ←− X[0 : 16] ⊕ tmp
0
,
Y [16 : 32] ←− X[16 : 32] ⊕ tmp
1
,
Y [32 : 48] ←− X[32 : 48] ⊕ tmp
2
,
Y [48 : 64] ←− X[48 : 64] ⊕ tmp
3
.
(1)
We observe the above equations are not involutary,
as proved in Lemma 5.1. Therefore, we propose a
different set of equations for both the encryption and
decryption, capturing the effect of all four words from
input. Here, two bytes is equal to one word.
Lemma 5.1. Consider a function f : (F
16
2
)
4
−→ (F
16
2
)
4
and
y
0
,y
1
,y
2
,y
3
= f (x
0
,x
1
,x
2
,x
3
)
associated with the MixWord layer with t left cyclic
shift in the circuit, then
y
0
= x
0
⊕ (x
0
⊕ x
1
)
|<t|
y
1
= x
1
⊕ (x
1
⊕ x
2
)
|<t|
y
2
= x
2
⊕ (x
2
⊕ x
3
)
|<t|
y
3
= x
3
⊕ (x
3
⊕ x
0
)
|<t|
if and only if
y
′
0
= x
0
⊕ (x
0
⊕ x
2
)
|<2t|
y
′
1
= x
1
⊕ (x
1
⊕ x
3
)
|<2t|
y
′
2
= x
2
⊕ (x
2
⊕ x
0
)
|<2t|
y
′
3
= x
3
⊕ (x
3
⊕ x
1
)
|<2t|
where y
′
0
,y
′
1
,y
′
2
,y
′
3
= f
2
(x
0
,x
1
,x
2
,x
3
) with twice the
original left cyclic shifts.
Proof. We use commutativity as a distribution rule
(a ⊕ b)
|<t|
= a
|<t|
⊕ b
|<t|
and rewrite the expression
y
′
0
,y
′
1
,y
′
2
,y
′
3
= f ◦ f (x
0
,x
1
,x
2
,x
3
). Now,
y
′
0
= y
0
⊕ (y
0
⊕ y
1
)
|<t|
= x
0
⊕ (x
0
⊕ x
1
)
|<t|
⊕ {x
0
⊕ (x
0
⊕ x
1
)
|<t|
⊕ x
1
⊕ (x
0
⊕ x
1
)
|<t|
}
|<t|
= x
0
⊕ x
|<2t|
0
⊕ x
|<2t|
2
= x
0
⊕ (x
0
⊕ x
2
)
|<2t|
Similarly,
y
′
1
= x
1
⊕ (x
1
⊕ x
3
)
|<2t|
y
′
2
= x
2
⊕ (x
2
⊕ x
0
)
|<2t|
y
′
3
= x
3
⊕ (x
3
⊕ x
1
)
|<2t|
This completes the proof.
The well-established set of equations 2 has an in-
volutary property with less number of gate counts
compared to the equation set 1.
tmp
0
←− (X[0 : 16] ⊕ X[32 : 48])
|<2t|
,
tmp
1
←− (X[16 : 32] ⊕ X[48 : 64])
|<2t|
,
Y [0 : 16] ←− X[0 : 16] ⊕ tmp
0
,
Y [16 : 32] ←− X[16 : 32] ⊕ tmp
1
,
Y [32 : 48] ←− X[32 : 48] ⊕ tmp
0
,
Y [48 : 64] ←− X[48 : 64] ⊕ tmp
1
.
(2)
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
720

The modified cyclic word input reduces to the origi-
nal MixWord operation, except with twice the previ-
ous left cyclic shifts t. This observation implies that
the diffusion achieved by the MixWord transformation
remains unchanged regardless of the permutation of
word inputs. The same is experimented with using
linear and differential cryptanalysis in Section 6.
6 LINEAR/DIFFERENTIAL
CHARACTERISTICS IN TWO
VERSIONS
We model the original LTLBC and compared it with
the tweaked version. We keep every element of the
model details as the original one and just replace the
MixWord architecture with new tweaked shift-pairs
(11,5) instead of (5,9) and input bytes
(x
0
x
1
x
2
x
3
)
modified to
−−−−−−→ (x
0
x
2
x
1
x
3
).
We analyze the linear and differential characteristics
of the cipher under the original and tweaked versions
and present the number of active Sboxes for 1- to 9-
rounds in Table 3. According to the security claim
of LTLBC, resisting linear and differential cryptanal-
ysis requires more than 31 active S-boxes. Here, n
A
(·)
Table 3: Active Sboxes in Linear and Differential Crypt-
analysis for both (5,9) and (11,5) MixWord architecture.
shift (5,9)
R 1 2 3 4 5 6 7 8 9
n
A
(l) 1 4 7 13 16 21 ⊥ ⊥ ⊥
n
∗
A
(l) 1 4 7 13 16 19 22 26 31
n
A
(d) 1 4 7 13 16 22 ⊥ ⊥ ⊥
n
∗
A
(d) 1 4 7 13 17 19 26 30 36
shift (11,5)
R 1 2 3 4 5 6 7 8 9
n
∗
A
(l) 1 4 7 13 16 18 21 26 31
n
∗
A
(d) 1 4 7 13 17 21
∗
24 29 36
⊥ - not recorded,
∗
- improved
and n
∗
A
(·) represent the proposed and the revised ac-
tive Sbox count respectively. The argument l or d
in n
A
(·) represents linear or differential cryptanalysis.
The red marked figures in the table were corrected,
which we believe to be inaccurate according to the
MILP model for original MixWord architecture using
the (5, 9) shifts. We use
˙
Ilter and Selc¸uk’s modelling
strategy for MixWord linear masking. Unlike linear
cryptanalysis, we adopt a straightforward modeling
approach to map the input differential to the output
differential directly.
We provide the best linear and differential trails
returned by Gurobi and a trail diagram for 3-round
linear trails in Figure 2 with A, B, and C denoting
the input trail to the PermuteBits, MixWord, and
SubCell. Moreover, we attach 6-round linear and dif-
ferential trails showing the number of active Sboxes in
MixWord
PermuteBits
MixWord
PermuteBits
MixWord
PermuteBits
MixWord
PermuteBits
Figure 2: 3-Round linear trail of LTLBC showing 7 active
Sboxes with red input-output mask.
Table 4: Linear and differential trail for 6-round LTLBC.
R I/O Linear Trail ±ε
A
Differential Trail p
A
1
A 0x7580800230810002
2
−7
0x0000002100000001
2
−3
B 0x8032866200010201 0x0000000010001008
C 0x0000065000000200 0x0000000000000008
2
A 0x0000028000000200
2
−8
0x0000000000000001
2
−12
B 0x0000000000040804 0x0000000010000000
C 0x0000000000000800 0x0000000010200020
3
A 0x0000000000000800
2
−12
0x0000000010800080
2
−35
B 0x0000000004000000 0x8020000008000000
C 0x0000000004020002 0x8430041008100010
4
A 0x0000000004020004
2
−25
0xc22008200a200020
2
−43
B 0x0401000000100000 0x400c220c00080408
C 0x0c21082008100800 0x0000620000000400
5
A 0x04c2082004400800
2
−31
0x0000140000000400
2
−46
B 0x0c008c0104000408 0x0000000000402040
C 0x0000800100000008 0x0000000000002000
6
A 0x0000100400000004
2
−32
0x0000000000008000
2
−55
B 0x0000000000102010 0x0000000002000000
C 0x0000000000002000 0x0000000002040004
A
+
0x0000000000004000 0x0000000002080004
∗
I/O represents the input-output trail.
the Table 4 with bolded hexadecimal digits and A
+
de-
noting the input trail to the 7th round. We compute the
probability bias ε
A
and propagation ratio p
A
of all the
active Sboxes n
A
using the Linear Approximation Ta-
ble (LAT) and Differential Distribution Table (DDT)
The notion of MILP modelling for linear cryptanaly-
sis can be found in (Das, 2024;
˙
Ilter and Selc¸uk, 2022)
and differential cryptanalysis in (Mouha et al., 2012).
7 FUTURE SBOX: REVISED
PROPAGATION
We take the Algebraic Normal Form (ANF) form of
FUTURE Sbox , displaying all the division propa-
New Integral Distinguishers and Security Reassessment of LTLBC
721

Table 5: All possible propagations v’s for every possible
input division property u for FUTURE Sbox.
u all output propagations v’s
0000 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
0001 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
0010 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
0011 1, 3, 5 , 6, 7, 8, 9, 10, 11 , 12, 13, 14, 15
0100 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
0101 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
0110 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15
0111 7, 9, 10, 11 , 13, 14, 15
1000 1, 2, 3, 4, 5, 6, 7 , 8, 9, 10, 11, 12, 13, 14, 15
1001 1, 2, 3, 5, 6, 7 , 8, 9, 10, 11, 12, 13, 14 , 15
1010 1, 3, 4, 5 , 6, 7 , 8, 9, 10, 11, 12, 13, 14, 15
1011 1, 3, 5 , 6, 7 , 8, 9, 10, 11 , 12, 13 , 14 , 15
1100 2, 3, 5, 6, 7 , 10, 11, 12, 13, 14, 15
1101 2, 3, 5, 6, 7 , 10, 11, 13, 14 , 15
1110 10, 11, 13, 14, 15
1111 15
gations. We correct the inaccuracies found in the
‘Security Analysis’ section of the integral attack. If
the propagations marked (.) are removed, then the
MILP-based search will struggle to find pathways to
the unit vector, giving an unbalanced bit with less
probability. Thereafter, the security against the in-
tegral attack would be in doubt. According to the
current literature, the 6th and 7th rounds of FUTURE
yield all 64-balanced bits (Xu et al., 2024).
8 DISCUSSION AND
CONCLUSION
This study underscores the critical role of robust
diffusion and strong S-box design in enhancing ci-
pher security. Through detailed MILP-based analy-
sis, we identified new 6-round integral distinguish-
ers for LTLBC by modeling its S-box and MixWord
layer, and refined active S-box estimates for linear and
differential attacks. While LTLBC shows resilience
against integral attacks up to 6 rounds, it remains vul-
nerable to other attacks by the 8th round. These in-
sights are valuable for strengthening lightweight en-
cryption in resource-constrained environments like
IoT and distributed systems.
Future Research. We will analyze LTLBC’s re-
sistance against quantum cryptanalysis, particularly
under Grover’s search and algebraic attacks and
consider hybrid approaches integrating LTLBC with
post-quantum cryptographic schemes.
REFERENCES
Das, A. (2024). Bit-Based MILP Modelling of Non-Bit-
Permutation Linear Layers for Linear Cryptanalysis.
In 2024 19th Asia Joint Conference on Information
Security (AsiaJCIS), pages 1–8. IEEE.
˙
Ilter, M. B. and Selc¸uk, A. A. (2022). Milp-aided crypt-
analysis of the future block cipher. In International
Conference on Information Technology and Commu-
nications Security, pages 153–167. Springer.
Mirzaie, A., Ahmadi, S., and Aref, M. R. (2023). Integral
cryptanalysis of round-reduced shadow-32 for IoT
nodes. IEEE Internet of Things Journal, 11(6):10592–
10599.
Mouha, N., Wang, Q., Gu, D., and Preneel, B. (2012).
Differential and linear cryptanalysis using mixed-
integer linear programming. In Information Security
and Cryptology: 7th International Conference, In-
scrypt 2011, Beijing, China, November 30–December
3, 2011. Revised Selected Papers 7, pages 57–76.
Springer.
Sasikumar, K. and Nagarajan, S. (2024). Comprehensive re-
view and analysis of cryptography techniques in cloud
computing. IEEE Access.
Sun, L., Wang, W., and Wang, M. Q. (2020). MILP-aided
bit-based division property for primitives with non-
bit-permutation linear layers. IET Information Secu-
rity, 14(1):12–20.
Sun, W., Li, L., and Huang, X. (2024). LTLBC: a low-
latency lightweight block cipher for internet of things.
Cluster Computing, 27(7):9783–9794.
Todo, Y. (2015). Structural Evaluation by Generalized Inte-
gral Property. In Oswald, E. and Fischlin, M., editors,
Advances in Cryptology – EUROCRYPT 2015, pages
287–314, Berlin, Heidelberg. Springer Berlin Heidel-
berg.
Xiang, Z., Zhang, W., Bao, Z., and Lin, D. (2016). Applying
MILP Method to Searching Integral Distinguishers
Based on Division Property for 6 Lightweight Block
Ciphers. In Cheon, J. H. and Takagi, T., editors, Ad-
vances in Cryptology – ASIACRYPT 2016, pages 648–
678, Berlin, Heidelberg. Springer Berlin Heidelberg.
Xu, Z., Cui, J., Hu, K., and Wang, M. (2024). Integral attack
on the full future block cipher. Tsinghua Science and
Technology.
Yalli, J. S., Hasan, M. H., Jung, L. T., Yerima, A. I., Aliyu,
D. A., Maiwada, U. D., Al-Selwi, S. M., and Shaikh,
M. U. (2025). A Systematic Review For Evaluating
IoT Security: A Focus On Authentication, Protocols
and Enabling Technologies. IEEE Internet of Things
Journal.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
722
