Exploring Image Search on Quantum Computing Systems

Hermann F

urntratt

, Werner Bailer

, Florian Krebs

, Roland Unterberger

and Herwig Zeiner

JOANNEUM RESEARCH Forschungsgesellschaft mbH, Graz, Austria

ﬁ

Keywords:

Image Search.

Abstract:

Image search based on descriptor similarities is a fundamental task in computer vision. These descriptors

are often highly quantised (e.g. binarised or ternarised). Quantum Computing (QC) has shown to have great

potential for a number of tasks including search. Especially Google’s new Quantum Processing Unit called

Willow reaches new milestones in error correction and durability and presents a benchmark that runs about

ﬁve minutes in the quantum domain while it would take more than 10

years on a state-of-the-art classical

supercomputer. The supposed reason that this achievement is not immediately claimed for quantum supremacy

is that Google also states that the benchmark — the so called Random Circuit Sampling (RCS) benchmark has

”not yet known real-world applications”. We therefore transform these benchmark results into the real world

by exploring the question: what hardware speciﬁcations are needed to execute a quantum implementation of

an image descriptor search algorithm more quickly than the fastest supercomputer available today? Hence,

two distinct implementations of the Compact Descriptor for Video Applications (CDVA) search, which uses

512-bit descriptors are compared to classical code running on a MI300A unit available in El Capitan, the

currently fastest supercomputer with AVX512-bit comands. The results indicate that the current key hardware

factors, including gate runtime, coherence time, error rate, and the number of qubits, are still considerably (by

orders of magnitude) below the performance levels necessary to compete with the El Capitan supercomputer,

but with the recent progress in error correction, we can expect the development of larger quantum systems in

the near future that reduces the performance gap between classical and quantum computers. Our source code

for simulation is available online at GitHub.

1 INTRODUCTION

Determining the similarity of images is a key aspect

of image search applications. A common requirement

is to compute a set of similarity scores between one or

a few query images and a much larger image database.

Depending on the speciﬁc application, it may be nec-

essary to identify the best match, the k-nearest neigh-

bor matches, or the similarity scores of all images in

the database (see Figure 1). In this process, images

are typically represented by descriptors — tradition-

ally hand-crafted, but increasingly learned — that are

optimised for efﬁcient indexing and matching, often

through techniques such as quantisation (e.g. binari-

sation or ternarisation).

https://orcid.org/0000-0002-1762-902X

https://orcid.org/0000-0003-2442-4900

https://orcid.org/0000-0001-5094-5748

https://orcid.org/0000-0002-9165-3749

https://orcid.org/0000-0002-6913-8046

Quantum computing has been shown to have great

potential for solving a number of challenging comput-

ing problems effectively, and search tasks are among

them (Portugal, 2018) (Rieffel and Polak, 2000). We

focus on the problem of matching a single binary im-

age descriptor (with size 512 bits) against a database

of 100 descriptors in order to obtain a complete list

of similarity scores. We assess implementations on

two different quantum computing frameworks. Qiskit

(IBM) (Research, 2024), which also provides the un-

derlying QASM circuit simulation, and Qrisp (Fraun-

hofer) (FOKUS, 2024a) as an important framework

of the German Qompiler project managed by Fraun-

hofer FOCUS. It represents Germany’s initiative to

create a European quantum software development

stack. While Qrisp provides higher levels of abstrac-

tion (F

urntratt et al., 2024) compared to Qiskit, it

still depends on the quantum simulation capabilities

of Qiskit.

Quantum algorithms are implemented as circuits,

where qubits serve as fundamental information units

Fürntratt, H., Bailer, W., Krebs, F., Unterberger, R. and Zeiner, H.

Exploring Image Search on Quantum Computing Systems.

DOI: 10.5220/0013562200004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 70-78

ISBN: 978-989-758-761-0

Figure 1: Example: get k-best keyframe matches depending on their (CDVA) similarity score.

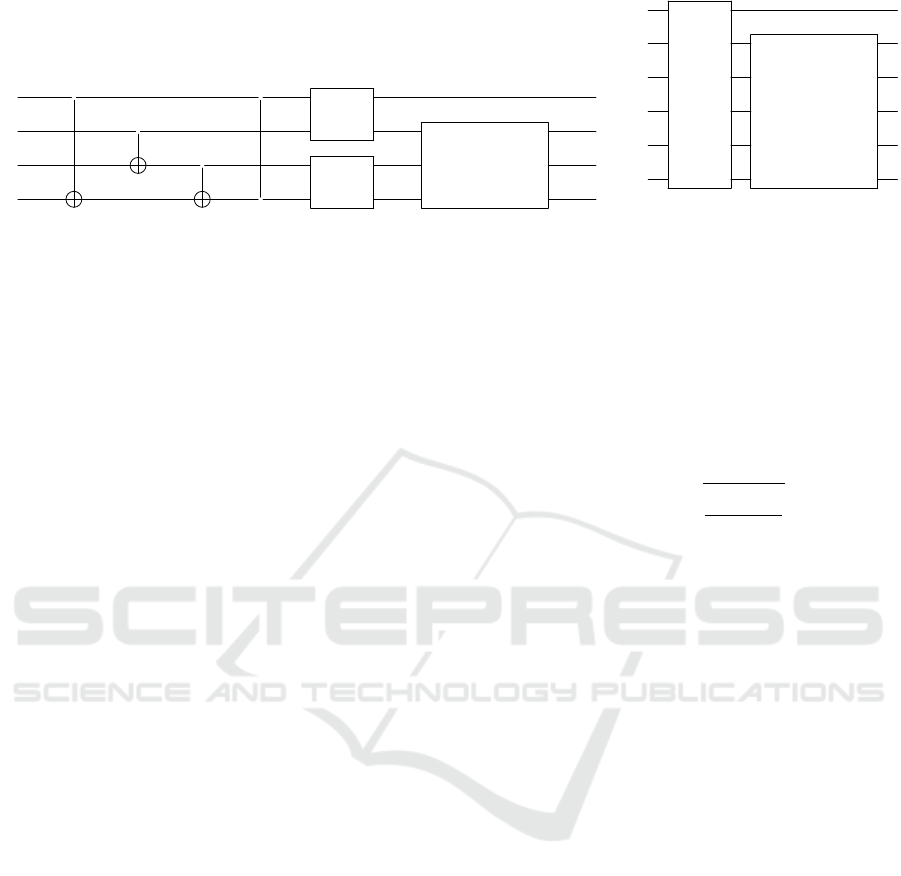
and gates manipulate the state of these qubits. In our

exploration, we present two distinct implementation

approaches to illustrate different circuit designs. The

ﬁrst approach uses Qiskit, featuring a small number of

qubits arranged in a conﬁguration with a large number

of gate layers. This setting results in a small but deep

circuit (SbD). The second approach uses Qrisp, which

allows for a large number of qubits but limits the cir-

cuit to a smaller number of gate layers. That set-

ting creates a wide but shallow conﬁguration (WbS).

The contrasting implementations allow us to evalu-

ate the performance and efﬁciency of quantum algo-

rithms under different circuit architectures and pro-

vide insights how qubit count and gate depth inﬂuence

computational capabilities.

In particular, we study under which conditions an

algorithm provides the same similarity ranking as ex-

act similarity computation in the classical domain,

and the complexity of the quantum implementation

depending on the descriptor size.

The main contributions of this paper are:

• We show that it is possible to reproduce exact

similarity matching results on quantum comput-

ers, given a sufﬁciently high number of shots (i.e.,

runs of the quantum computing algorithms in or-

der to obtain more stable results).

• We demonstrate two fundamental development

strategies for quantum computing algorithms,

which relate to the number of qubits used on the

one hand and the depth of the quantum circuit on

the other (small but deep (SbD) vs. wide but shal-

low (WbS)).

• We calculate the expected performance values

based on the Willow quantum hardware speciﬁ-

cation (AI, 2024b), the qubit count and the gate

layer depth and compare them with the expected

classical results on El Capitan’s AMD CI300A

unit (Laboratory, 2025).

The rest of this paper is organised as follows.

Section 2 introduces related work on compact de-

scriptors, quantum computing (QC) and frameworks,

along with similarity search using QC. Section 3 de-

scribes the proposed methods, and Section 4 the setup

for the performed experiments. The results are dis-

cussed in Section 5, and ﬁnally Section 6 concludes

the paper.

2 BACKGROUND

2.1 Highly Quantised Multimedia

Descriptors

Binarisation or ternarisation of descriptors, in or-

der to perform more efﬁcient indexing and match-

ing, has already been proposed in the era of hand-

crafted descriptors. While ternarisation makes han-

dling of descriptors more complex, it has the advan-

tage of discriminating cases where a value of the

descriptor vector is (almost) zero and where it has

a clear positive or negative value. Well-known ex-

amples include BRIEF (Calonder et al., 2011) and

BRISK (Leutenegger et al., 2011). A ternary variant

of BRIEF, named LTD, has also been proposed (Gao

et al., 2013), as well as ternary descriptors for au-

dio tasks (Adnan et al., 2018). Compact descrip-

tors for visual search (Duan et al., 2014) is a stan-

dard (ISO/IEC15938, 2019) for image and video de-

scription. It includes binary global descriptor com-

ponents based on hand-crafted and learned feature

descriptors. The hand-crafted components contain

interest-point based descriptors which are ternarised.

A learned descriptor is extracted using the last feature

layer of VGG16 (Simonyan and Zisserman, 2015).

In order to improve rotation invariance, the descrip-

tor is obtained by applying nested invariance pooling

(NIP) (Morere et al., 2017) to rotated versions of the

image. This descriptor is then normalised w.r.t. an av-

erage descriptor and then binarised. Binarising a net-

work trained for ﬂoating point output is suboptimal,

thus newer works propose to learn the binarisation

as part of the training process. One example is CD-

bin (Ye et al., 2019), which learns a descriptor using a

speciﬁc binarisation loss combined with triplet loss

for improved discriminability. DBLD (Xiao et al.,

2023) is a more recent approach, which proposes a bi-

nary transformation layer (BLT) that can be plugged

Exploring Image Search on Quantum Computing Systems

• •

gates

•

measurement

•

gates

•

(a) Small but deep circuit with large number of gates.

gates

measurement

(b) Wide but shallow circuit with

large number of qubits.

Figure 2: Distinct algorithm design pattern.

into any descriptor extraction backbone.

2.2 Quantum Computing Basics

2.2.1 The Qubit

Quantum computers use quantum mechanical entities

such as ions, photons, or atoms as their fundamental

information units, known as quantum bits or qubits

rather than classical bits. While qubits represent the

binary states of 0 and 1, similar to classical bits, they

can also enter a temporary state of superposition. In

this superposition phase, a qubit’s state becomes non-

deterministic and is described by a state vector com-

posed of complex probability amplitudes.

When a system contains m qubits in superposition,

the corresponding state vector includes 2

probability

amplitudes, representing all possible combinations of

the binary states of the qubits. Each amplitude in-

dicates the likelihood of measuring a speciﬁc basis

state. For instance, if m = 3, the state vector ψ in

bra-ket notation (Greenberger et al., 2009) can be ex-

pressed as a weighted sum of 2

= 8 basis states:

⟩

= α

000

⟩

+ α

001

⟩

+ . . . +α

111

⟩

(1)

The term |α

000

represents the probability of mea-

suring the basis state

000

⟩

. Quantum operations

performed on qubits during superposition manipu-

late this state vector in parallel, affecting all 2

en-

tries simultaneously. This ability to operate concur-

rently highlights the remarkable computational power

of quantum computing.

2.2.2 Quantum Gates

The state vector of a qubit system can be altered using

quantum gates, which are outlined below. For a more

comprehensive explanation, please refer to (Barenco

et al., 1995).

Rotation Gates. Rotation gates, (such as the R

gate), adjust the amplitudes of a qubit by rotat-

ing the associated complex coefﬁcient by an angle θ

around the speciﬁed axis in the complex plane. This

allows us to encode classical probabilities P(V

) of a

binary random variable V

into the angle θ of a qubit

θ = 2 ·tan

−1

P(V

= 1)

P(V

= 0)

. (2)

Conditional Gates. At times it is necessary to con-

dition an operation of one qubit on the values of an-

other qubit(s). The Controlled-NOT (CNOT or CX)

gate is a two-qubit quantum gate that toggles the state

of the second qubit (target qubit) when the ﬁrst qubit

(control qubit) is in state

⟩

. If the control qubit is in

state

⟩

, the target qubit remains unchanged.

Multi-Qubit Gates. Multi-qubit gates implement

conditioning the operation on one target qubit on

several control qubits. For example, an R

rotation

gate which is controlled by n qubits is denoted as

gate. Similarly, a CNOT gate conditioned on

n qubits is denoted as C

NOT gate. Although many

quantum computing frameworks such as Qiskit (Re-

search, 2024) already have implemented such gates,

they have to be decomposed (transpiled) internally

into elementary gates in order to be executed on a

quantum device.

Quantum Algorithms. Quantum algorithms are

sequences of quantum gates arranged in circuits and

applied to qubits to perform state changes. Because

of the probabilistic nature of quantum mechanics, the

results of a quantum algorithm are non-deterministic.

When measuring the qubits at the end of a quan-

tum circuit, the results will inherently vary each time,

even when ran with identical inputs. To solve this is-

IQSOFT 2025 - 1st International Conference on Quantum Software

sue, quantum computing requires the use of multiple

shots.

A shot refers to a single execution of a quantum

algorithm. After executing the algorithm, the qubit

states are measured, and the results are documented.

To achieve reliable and statistically signiﬁcant out-

comes from a quantum algorithm, the circuit is usu-

ally run multiple times. The results from these shots

are then combined to identify the most probable out-

come and to estimate the probabilities of various re-

sults. Generally, a higher number of shots can lead to

longer training times for models and increased costs;

however, there are methods available to determine

the optimal number of shots with minimal impact on

model performance (Phalak and Ghosh, 2023) (Gu

et al., 2021).

2.3 Quantum Computing Frameworks

2.3.1 Qiskit

Qiskit is an open-source software development frame-

work for quantum computing created by IBM. The

currently available software version v2.0.0 enables

users to develop, execute and analyse quantum algo-

rithms on quantum computers and simulators. Qiskit

has been designed for a modular structure with differ-

ent components focusing on various aspects of quan-

tum computing. A foundational layer of Qiskit, pro-

viding the tools for the creation of quantum circuits

at a low level. It is capable of undertaking tasks such

as circuit generation, compilation and optimisation.

Users can create quantum circuits, run simulations,

and manage the compilation of these circuits for ex-

ecution on various quantum devices. An additional

layer is implemented for simulation of quantum cir-

cuits. The software enables users to execute and de-

bug their quantum algorithms on classical comput-

ers by simulating quantum operations. It offers high-

performance simulators that can replicate the behav-

ior of quantum hardware, allowing users to test and

optimise their quantum algorithms before executing

them on real quantum devices. Quantum error cor-

rection and mitigation is a signiﬁcant challenge that

is also addressed in Qiskit. The framework provides

necessary tools to characterise the noise present in

quantum devices and to implement the requisite error-

correction techniques. The user can perform experi-

ments aimed at understanding and minimising the ef-

fects of noise, which is crucial for the reliable compu-

tation of quantum data. Qiskit provides tutorials, doc-

umentation, and online courses and access to tangible

quantum hardware via the IBM Quantum platform

Formerly known as Quantum Experience platform

2.3.2 Qrisp

Qrisp v0.5.10, developed by Fraunhofer

FOKUS (FOKUS, 2024b), is a framework de-

signed to bridge the gap between the high-level

programming paradigms that characterise modern

software engineering and the physical realities of

current quantum hardware. The goal of the frame-

work is to provide a uniﬁed high-level programming

interface as an abstraction to a low-level backend for

different hardware platforms. Qrisp is lightweight.

The Python framework has user-friendly program-

ming in focus and continues the evolution from pure

gate-based quantum programming towards functional

programming. With the abstraction of classical data

types, e.g. ﬂoat, bool, string, . . . , and programming

features such as array-handling and encapsulation,

this framework offers a common high-level program-

ming environment with a well-known Python syntax.

Qrisp contributes to a more human-readable code

with efﬁcient implementations while gate-based code

will be hidden underneath.

2.4 Similarity Search Using Quantum

Computing

A quantum similarity matching approach for images

is proposed in (Liu et al., 2019). It requires a quantum

representation of images that cannot be applied to ex-

isting descriptors. In another work, a quantum vari-

ational autoencoder is used as a feature embedding

for satellite imagery in order to perform approximate

k-NN search using Hamming distance (Gao et al.,

2020), demonstrating signiﬁcant speedup that can be

traded-off against accuracy. A similarity matching ap-

proach for proteins models the 20 amino acids de-

scribed in 5 qubits (Chagneau et al., 2024), and the

applied quantum versions of the Needleman–Wunsch

and Smith–Waterman algorithms.

An approach for matching a string against a set

of sets using the probabilistic quantum memory data

structure has been proposed in (Khan and Miranskyy,

2021). For the related problem of edit distance (in

particular, edit distance bounded by a maximum value

k) a quantum version with complexity

√

nk + k

)

has been proposed

, and the authors show that this is

optimal.

We follow the convention of denoting computational

complexity on quantum systems with

O in order to discrim-

inate it from the complexity O on conventional computers.

Exploring Image Search on Quantum Computing Systems

⟩

†

⟩

Figure 3: Quantum building block in Qiskit for the Ham-

ming distance estimation with QKE.

2.5 Supercomputing Hardware

As of the latest Top 500 list, the fastest supercomputer

is El Capitan, located at the Lawrence Livermore Na-

tional Laboratory in California, United States. The

hardware uses combined 11, 039, 616 CPU and GPU

cores consisting of 43, 808 AMD 4

Gen EPYC 24C

”Genoa” 24 core @1.8 GHz CPUs (1, 051, 392 cores)

and 43, 808 AMD Instinct MI300A GPUs (9, 988, 224

cores). A single MI300A unit consists of 24 Zen4

based CPU cores, and a CDNA3 based GPU, along

with 128 GB of HBM3 memory (Smith, 2025).

The CPUs are capable of processing 512-bit code

via the AMD AVX512 command extension, which

enhances its performance for data-intensive appli-

cations. With a peak performance of more than

2 Exaﬂops, at a power consumption rate of about

30MW, El Capitan has set new records in various

benchmarks, including the High-Performance Lin-

pack (HPL) test (Top500, 2025).

3 METHODS

Under the precondition to work only with real-world

data, our quantum algorithm implementations are not

yet runnable on real quantum hardware, due to the

lack of resources – either the number of available

qubits or the limited circuit depth. Therefore we ver-

ify our implementations via Qiskit QASM simulation

(suitable for less than 32 qubits, i.e. algorithm 1) and

– with restricted functionality, as to the best of our

knowledge the simulation of 10k+ qubits is only pos-

sible with constraints – with the Qrisp default backend

simulation (for algorithm 2). We do this on a classical

workstation with a 2.1GHz CPU, offering 20 logical

cores and 64GB of RAM.

3.1 Algorithm 1: Similarity Search

Based on Quantum Kernel

Estimation in Qiskit

Based on (Liu et al., 2021), we map a binary n-bit

descriptor x

onto a quantum feature map φ

7→

φ(x

)

⟩

(3)

•

Hal f adder

Adder

Hal f adder

Figure 4: Quantum building block in Qrisp for the Ham-

ming distance with CX gates and adders. The result is avail-

able at qubit x

by encoding the n bits of the descriptor into m qubits

via

φ(x

)

⟩

= U(x

)

⟩

(4)

with m = ⌈ld(x

)⌉. Then, the similarity between 2 de-

scriptors x

and x

can be estimated by applying an in-

verted version of x

, U

†

) and estimate the similar-

ity probability |

⟨

†

)U(x

)

⟩

by measuring

the frequency of the 0

output. A general circuit lay-

out is depicted at Fig. 3.

3.2 Algorithm 2: Calculate Similarity as

Sum of Differences in Qrisp

Based on (Orts et al., 2024), we calculate the simi-

larity between 2 n-bit descriptors as the sum of dif-

ferences. Furthermore, in contrast to algorithm 1, we

assume that hardware scaling issues have been solved

and the number of available qubits is by several or-

ders of magnitude higher than at present. Hence, we

can map a descriptor bit onto a qubit and use the

type system of Qrisp (QuantumBool, QuantumArray,)

along with the Quantum adder modules – especially

the Gidney quantum adder to calculate the Hamming

distance (sum of differences) between two binary de-

scriptors, x

and x

. We build a quantum circuit like

in Fig. 4 but with a ’function-centred’ approach rather

than a ’circuit-centred’ approach.

Support for pythonic programming paradigms like

in the following code snippet facilitates development.

# Example for initialising an array

# of QuantumBool from bitstring

a = QuantumArray(QuantumBool(),shape=8)

a[:] = np.fromiter(

[int(bit) for bit in ’01010011’], bool)

4 EXPERIMENTAL SETUP

We use CDVA (ISO/IEC15938, 2019) descriptors for

our experiment, which are extracted from images of

the WAVL dataset (Neuschmied and Bailer, 2024)

IQSOFT 2025 - 1st International Conference on Quantum Software

proposed for landmark retrieval (see Fig. 1). The de-

scriptors consist only of a binary-learned descriptor

component, forming a 512-bit vector per image. Real-

world data of this size is currently not yet applicable

on real quantum hardware. It even poses a remark-

able challenge to quantum simulators. Therefore, for

experiments with larger descriptors, we brieﬂy outline

a way to create these descriptor sizes by concatenat-

ing multiple image descriptors. We can think of this

as forming a descriptor for a video segment from con-

catenating subsequent key frame descriptors.

The default similarity metric between a pair of de-

scriptors is the Hamming distance, which can be efﬁ-

ciently implemented on AVX512-capable CPUs like

the 4t

gen AMD EPYC 24C by counting the set bits

(using ASM OpCode VPOPCNTQ) in the result of an

VXOR operation between the inputs.

We obtain a set of similarity scores from matching

a single binary image descriptor against a database

containing 100 descriptors. In order to obtain more

reliable results, we repeat each experiment for 100

randomly sampled descriptors and report the mean of

the results (see Tab. 2). We evaluate the implemen-

tations by comparing the similarities of a set of de-

scriptors returned by the quantum algorithms to those

of the CPU implementation. We do not require the

similarity scores to be exactly the same (in particu-

lar, in experiments simulating noisy quantum com-

puting operations), but we require the ranking to be

the same. Thus we use Spearman’s rank correlation ρ

as the metric for comparing the outputs of two algo-

rithms. We ignore differences in similarity values, if

the absolute difference is smaller than ±0.5, as in the

exact implementation any descriptor difference below

1 would be exactly 0.

We run experiments varying the following condi-

tions:

• Implementation of two fundamentally different

similarity search algorithms: algorithm 1, small

but deep, and algorithm 2, wide but shallow

• Varying the number of shots. Currently, with an

amount of qubits m ≥ 32 the simulation imple-

mentation does not allow to adjust the number of

shots (for algorithm 2)

• Varying descriptor length, down to 64-bit in order

to get the transpiled CX depth, i.e. the number of

layers hosting CX gates (not to be confused with

the number of CX gates)

As a consequence of current simulation restrictions,

varying the descriptor length beyond 512 bit is

planned for future tests, with updated quantum sim-

ulators.

5 RESULTS AND DISCUSSION

From (AI, 2024b) we obtain the most important key

specs of the Willow Quantum Processing Unit, which

consists of two chip units: the ﬁrst unit is responsible

for error correction, while the second unit performs

the random circuit sampling benchmark. Since the

characteristic values for both chips are distinct, we

choose the average of both chip-characteristic values.

These are for the decoherence time t

83µs. We

calculate the gate runtimes as an average value from

the cycle times of the ISWAP gates with 1.1µs and the

gate runtimes of 63kHz for a circuit depth of 40, re-

sulting in an average value of 0.75µs, and for the qubit

error rates, we also calculate the average of single-

and 2-qubit error rates to be 0.14%

For the runtime calculation on the El Capitan

CPU, we calculate 1 clock cycle each for the XOR

operation of the two descriptors to be compared and

also 1 clock cycle for counting the different bit values

(VPOPCNTQ) based on the use of the AVX512 unit,

which results in a computing time of 1.1 ×10

−10

s for

determining the Hamming distance of two 512-bit de-

scriptors at a CPU clock frequency of 1.8GHz.

The results related to number of qubits and CX

depth show the trade-off between both implementa-

tions. Since the CX depth is mainly responsible for

execution speed

, the 1321 extra CX layer for algo-

rithm 1 might slow it down by more than 280% com-

pared to algorithm 2 (see Figure 5). Note that cur-

rently, we were not able to evaluate the Qrisp based

algorithm on the Qiskit QASM simulator backend (as

we did in the Qiskit algorithm case), because the sim-

ulator has its maximum qubit number limited to 31

qubits. Therefore, the Qrisp numbers are the results

achieved on the Qrisp default backend – which does

not apply a noise model and hence retrieves the ex-

pected optimal ranking score of 1.0 regardless of the

number of shots. In any case, shallow circuit depths

promise shorter computing times and thus enable a

high number of shots, so that good ranking scores can

be expected. Looking at the numbers of shot counts,

the value of 5000 shots seems to be a good compro-

mise between speed and ranking quality.

With all assumptions, we calculate that in or-

der to meet the classical calculation requirement of

1.1 ×10

−10

s per 512-bit descriptor pair, we need for

algorithm 1 using a CX depth of 2042 an average gate

runtime lower than 5.39 ×10

−14

s and for algorithm

2 with 721 CX gate depth an average gate runtime

lower than 1.52 ×10

−13

s to become faster than the

fastest classical supercomputer.

Credits to R. Seidel from Fraunhofer FOKUS for

pointing this out.

Exploring Image Search on Quantum Computing Systems

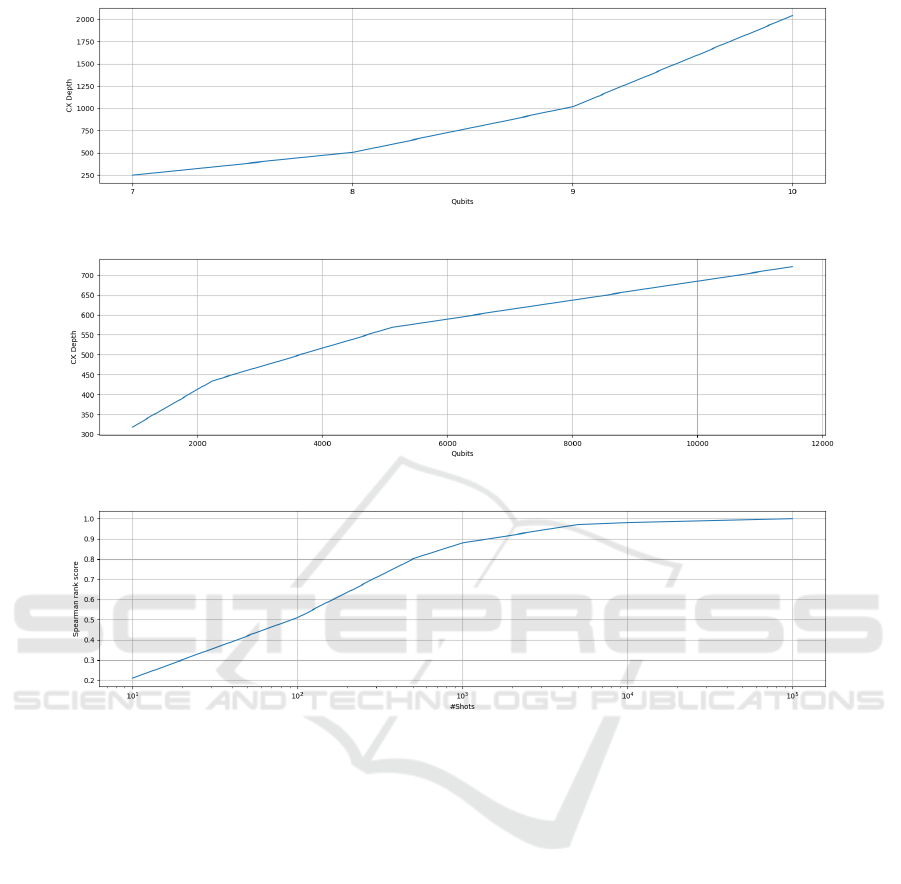
Figure 5: Qiskit algorithm 1: CX circuit depth depending on the number of qubits.

Figure 6: Qrisp algorithm 2: CX circuit depth depending on the number of qubits.

Figure 7: Qiskit algorithm 1: increasing Spearman rank correlation depending on the number of shots.

According to Google’s quantum road map (AI,

2024a), the next development goal is to reach 1000

physical qubits. Also in IBM’s quantum road map

(IBM, 2024), a modular quantum processing unit is

expected around 2025, capable to control 7500 gates,

which is promising, but the general request for more

circuit depth still remains (Chia et al., 2023).

6 CONCLUSION

In conclusion, this paper has explored the potential of

similarity searching via descriptor matching on quan-

tum computing systems. We developed two distinct

quantum algorithms: one characterised by a limited

number of qubits but a deep circuit depth, and the

other featuring a larger number of qubits with a shal-

low circuit depth. Given that the requirements of

these algorithms surpass the current capabilities of

quantum hardware, we conducted simulations to eval-

uate matching results on a database of 100 descrip-

tors. These evaluations showed that depending on the

number of shots, the baseline results created on clas-

sical CPUs are identical.

By making our source code available to the pub-

lic, we encourage researchers to take this as a starting

point for further exploration in this exciting ﬁeld.

ACKNOWLEDGEMENTS

The research leading to these results has been funded

partially by the Federal Ministry of the Republic of

Austria, responsible for Climate Action, Environ-

ment, Energy, Mobility, Innovation and Technology,

and by the European Union’s Horizon Europe pro-

gram under grant agreement n

◦

101070250 XRECO

(https://xreco.eu/).

IQSOFT 2025 - 1st International Conference on Quantum Software

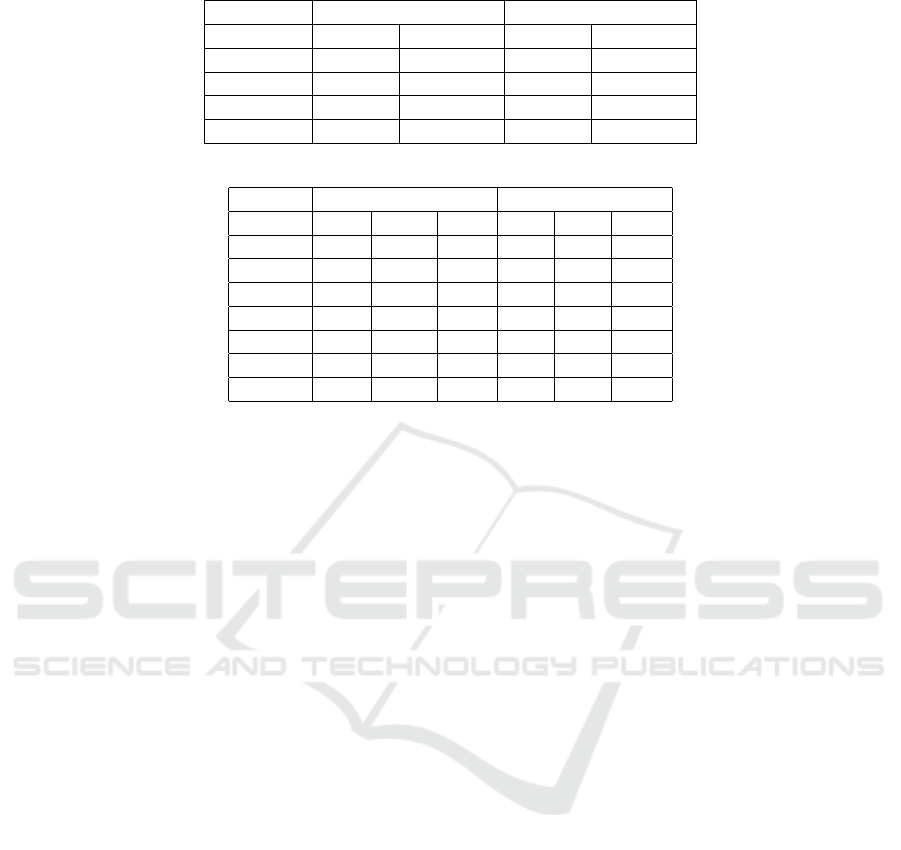
Table 1: Comparison of the implemented similarity search algorithms.

Qiskit Qrisp

Descriptor #Qubits CX Depth #Qubits CX Depth

64 7 250 961 319

128 8 506 2241 435

256 9 1018 5121 569

512 10 2042 11521 721

Table 2: Comparison: Spearman rank correlation over 100 512-bit descriptors depending on number of shots.

Qiskit Qrisp

#Shots Avg Min Max Avg Min Max

10 0.21 -0.07 0.51 1.0 1.0 1.0

100 0.51 0.28 0.69 1.0 1.0 1.0

500 0.80 0.66 0.90 1.0 1.0 1.0

1000 0.88 0.77 0.94 1.0 1.0 1.0

5000 0.97 0.93 0.99 1.0 1.0 1.0

10000 0.98 0.96 0.99 1.0 1.0 1.0

100000 1.00 0.99 1.00 1.0 1.0 1.0

REFERENCES

Adnan, S. M., Irtaza, A., Aziz, S., Ullah, M. O., Javed, A.,

and Mahmood, M. T. (2018). Fall detection through

acoustic local ternary patterns. Applied Acoustics,

140:296–300.

AI, Q. (2024a). Our quantum computing journey. https:

//quantumai.google/learn/map.

AI, Q. (2024b). Willow Spec Sheet. https://quantumai.go

ogle/static/site-assets/downloads/willow-spec-sheet

.pdf.

Barenco, A., Bennett, C. H., Cleve, R., DiVincenzo, D. P.,

Margolus, N., Shor, P., Sleator, T., Smolin, J. A., and

Weinfurter, H. (1995). Elementary gates for quantum

computation. Physical Review A, 52(5):3457–3467.

Publisher: American Physical Society.

Calonder, M., Lepetit, V., Ozuysal, M., Trzcinski, T.,

Strecha, C., and Fua, P. (2011). Brief: Computing

a local binary descriptor very fast. IEEE transac-

tions on pattern analysis and machine intelligence,

34(7):1281–1298.

Chagneau, A., Massaoudi, Y., Derbali, I., and Yahiaoui,

L. (2024). Quantum algorithm for bioinformatics to

compute the similarity between proteins. IET Quan-

tum Communication.

Chia, N.-H., Chung, K.-M., and Lai, C.-Y. (2023). On the

Need for Large Quantum Depth. J. ACM, 70(1):6:1–

6:38.

Duan, L.-Y., Lin, J., Chen, J., Huang, T., and Gao, W.

(2014). Compact descriptors for visual search. IEEE

MultiMedia, 21(3):30–40.

FOKUS, F. (2024a). Eclipse Qrisp. https://www.qrisp.eu/.

FOKUS, F. (2024b). Fraunhofer FOKUS | WIR VERNET-

ZEN ALLES. https://www.fokus.fraunhofer.de/.

urntratt, H., Schnabl, P., Krebs, F., Unterberger, R., and

Zeiner, H. (2024). Towards Higher Abstraction Levels

in Quantum Computing. In Service-Oriented Comput-

ing – ICSOC 2023 Workshops, pages 162–173, Singa-

pore. Springer Nature.

Gao, N., Wilson, M., Vandal, T., Vinci, W., Nemani, R.,

and Rieffel, E. (2020). High-dimensional similar-

ity search with quantum-assisted variational autoen-

coder. In Proceedings of the 26th ACM SIGKDD inter-

national conference on knowledge discovery & data

mining, pages 956–964.

Gao, Y., Qiao, Y., Li, Z., and Xu, C. (2013). Ltd: lo-

cal ternary descriptor for image matching. In 2013

IEEE International Conference on Information and

Automation (ICIA), pages 1375–1380. IEEE.

Greenberger, D., Hentschel, K., and Weinert, F., editors

(2009). Compendium of Quantum Physics. Springer,

Berlin, Heidelberg.

Gu, A., Lowe, A., Dub, P. A., Coles, P. J., and Arrasmith, A.

(2021). Adaptive shot allocation for fast convergence

in variational quantum algorithms. arXiv preprint

arXiv:2108.10434.

IBM (2024). Quantum roadmap. https://www.ibm.com/ro

admaps/quantum/www.ibm.com/roadmaps/quantum.

ISO/IEC15938 (2019). ISO/IEC 15938-15:2019 Informa-

tion technology-—-Multimedia content description

interface—Part 15: Compact descriptors for video

analysis.

Khan, M. and Miranskyy, A. (2021). String comparison on

a quantum computer using hamming distance. arXiv

preprint arXiv:2106.16173.

Laboratory, L. L. N. (2025). Using El Capitan Systems:

Hardware Overview | HPC @ LLNL. https://hpc.llnl

.gov/documentation/user-guides/using-el-capitan-sys

tems/hardware-overview.

Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).

Brisk: Binary robust invariant scalable keypoints. In

Exploring Image Search on Quantum Computing Systems

2011 International conference on computer vision,

pages 2548–2555. Ieee.

Liu, X., Zhou, R.-G., El-Rafei, A., Li, F.-X., and Xu, R.-

Q. (2019). Similarity assessment of quantum images.

Quantum Information Processing, 18:1–19.

Liu, Y., Arunachalam, S., and Temme, K. (2021). A rigor-

ous and robust quantum speed-up in supervised ma-

chine learning. Nature Physics, 17(9):1013–1017.

Publisher: Nature Publishing Group.

Morere, O., Lin, J., Veillard, A., Duan, L.-Y., Chan-

drasekhar, V., and Poggio, T. (2017). Nested invari-

ance pooling and rbm hashing for image instance re-

trieval. In Proceedings of the 2017 ACM on Inter-

national Conference on Multimedia Retrieval, pages

260–268.

Neuschmied, H. and Bailer, W. (2024). Mining landmark

images for scene reconstruction from weakly anno-

tated video collections. In International Conference

on Multimedia Modeling, pages 161–174. Springer.

Orts, F., Ortega, G., Combarro, E. F., R

ua, I. F., and Garz

on,

E. M. (2024). Quantum circuits for computing Ham-

ming distance requiring fewer T gates. The Journal of

Supercomputing, 80(9):12527–12542.

Phalak, K. and Ghosh, S. (2023). Shot optimization in quan-

tum machine learning architectures to accelerate train-

ing. IEEE Access, 11:41514–41523.

Portugal, R. (2018). Quantum Walks and Search Algo-

rithms. Quantum Science and Technology. Springer

International Publishing, Cham.

Research, I. (2024). IBM Quantum Documentation. https:

//docs.quantum.ibm.com/.

Rieffel, E. and Polak, W. (2000). An introduction to quan-

tum computing for non-physicists. ACM Computing

Surveys (CSUR), 32(3):300–335.

Simonyan, K. and Zisserman, A. (2015). Very deep con-

volutional networks for large-scale image recognition.

In 3rd International Conference on Learning Repre-

sentations (ICLR 2015). Computational and Biologi-

cal Learning Society.

Smith, R. (2025). El Capitan Supercomputer Detailed:

AMD CPUs & GPUs To Drive 2 Exaﬂops of Com-

pute. https://www.anandtech.com/show/15581/el-cap

itan-supercomputer-detailed-amd-cpus-gpus-2-exa

ﬂops.

Top500 (2025). El Capitan achieves top spot, Frontier and

Aurora follow behind | TOP500. https://www.top500

.org/news/el-capitan-achieves-top-spot-frontier-and

-aurora-follow-behind/.

Xiao, B., Hu, Y., Liu, B., Bi, X., Li, W., and Gao, X.

(2023). Dlbd: A self-supervised direct-learned bi-

nary descriptor. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 15846–15855.

Ye, J., Zhang, S., Huang, T., and Rui, Y. (2019).

CDbin: Compact discriminative binary descriptor

learned with efﬁcient neural network. IEEE Transac-

tions on Circuits and Systems for Video Technology,

30(3):862–874.

IQSOFT 2025 - 1st International Conference on Quantum Software