Mutation-Based Quantum Software Testing

Macario Polo-Usaola

, Manuel A. Serrano

and Ignacio García-Rodríguez de Guzmán

Universidad de Castilla – La Mancha, Spain

Keywords: Quantum Computing, Mutation Testing, Quantum Software Testing.

Abstract: Quantum technology is rapidly improving the capacity of quantum computers, increasing the number of cubits

and fostering the development of quantum software capable of solving complex problems that, until now,

were beyond the reach of the most powerful classical computers. Unfortunately, quantum computational

capacity is growing faster than Quantum Software Engineering, which is necessary to avoid a new (quantum)

software crisis. In this article, we focus on quantum software testing, with the specific goal of ensuring the

quality of quantum software. For this purpose, we propose to apply the mutation-based software testing

technique, applied to the context of quantum computing, since mutation has proven to be one of the most

powerful tools to improve the quality of test suites. A set of quantum mutation operators have been developed

to improve quantum test suites, and reduce the number of test cases required, which is important due to the

cost of using quantum computers (and the need to run each circuit multiple times to obtain reliable results due

to their stochastic nature). A tool for automating the generation of quantum mutants from original quantum

circuits is also presented.

1 INTRODUCTION

In 1982, Richard Feynman posed the question: “What

kind of computer are we going to use to simulate

physics?” This inquiry marked the beginning of the

“second quantum revolution.” Since then, quantum

computing has advanced significantly (Maslov et al.,

2018). Based on principles such as superposition and

entanglement, it enables faster and more efficient

computations, with applications in various domains

(Lopez & Da Silva, 2019), including economics,

healthcare, logistics, and energy.

Expectations surrounding quantum computing

have driven a global effort toward its development

(Humble & DeBenedictis, 2019). Companies such as

Google, IBM, and Microsoft are exploring its

applications in business, while countries like China

and the United States are heavily investing in the

technology. Notable initiatives include the U.S.

National Quantum Initiative Act and the Quantum

Manifesto in the European Union.

Currently, several quantum platforms exist, such

as IBM Q, IonQ, and Rigetti, along with multiple

https://orcid.org/0000-0001-6519-6196

https://orcid.org/0000-0003-0962-5659

https://orcid.org/0000-0002-0038-0942

programming languages (Qiskit, Q#) (Garhwal et al.,

2021) and development tools (Forest, Cirq,

Orquestra) (LaRose, 2019). A comprehensive review

of quantum computing and its software and hardware

ecosystem is provided in (Gill et al., 2022).

The Quantum Software Manifesto emphasizes the

urgency of strengthening quantum software

development due to hardware advancements,

highlighting the need for Quantum Software

Engineering (QSE) to ensure quality and productivity

(Piattini et al., 2020).

The predominant approach in quantum computing

is the gate-based model, which decomposes

algorithms into fundamental operations. Quantum

circuits are central to this paradigm and are used in

simulators such as Quirk and QCEngine, as well as in

platforms like Qiskit. Their transformation into

quantum code is straightforward and provides an

agnostic representation of the algorithm.

Given the current state of quantum software and

the challenges outlined in the Quantum Software

Manifesto, this paper focuses on strengthening

Quantum Software Engineering. It proposes the

development of processes and tools for software

138

Polo-Usaola, M., Serrano, M. A., García-Rodríguez de Guzmán and I.

Mutation-Based Quantum Software Testing.

DOI: 10.5220/0013561000004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 138-145

ISBN: 978-989-758-761-0

verification at the quantum circuit level, facilitating

testing across multiple platforms. This approach

contributes to the establishment of an agnostic testing

theory within Quantum Software Engineering, which

is considered a priority in (Piattini, 2021).

Furthermore, a high-level representation is crucial

due to the diverse topologies of gate-based quantum

computers (Pattel & Tiwari, 2020).

Before addressing the objectives of this study, it

is necessary to differentiate between “verification”

and “error identification.” Most studies attribute

quantum errors to their stochastic nature (Patel et al.,

2020), arising from variations in hardware

implementations (Pattel & Tiwari, 2020) and testing

in quantum environments (Smelyanskiy et al., 2016).

However, as highlighted in (Miranskyy & Zhang,

2019), it is essential to transfer software engineering

practices to quantum computing. This work aims to

develop a technique that, in addition to being useful

in classical software testing, enables the detection and

correction of faults in quantum circuits. In (Murillo et

al., 2024), a set of challenges in Quantum Software

Engineering is identified, among which several

critical issues related to quantum software testing are

emphasized, underscoring the need for further

development in this area.

Focusing on this paper, software mutation is an

effective testing technique in Software Engineering.

Empirical studies (Just et al., 2014) highlight its

potential for the automatic generation of test suites

and resource optimization in costly quantum

environments. This technique introduces artificial

faults into the system under test (SUT), based on the

“competent programmer hypothesis” (DeMillo et al.,

1978) and the “coupling effect,” allowing the

detection of both simple and complex errors. In the

context of quantum software, the SUT is referred to

as the CUT (Circuit Under Test).

This study identifies common errors in the

development of quantum circuits and proposes

mutant operators to simulate them. Following (Just at

al., 2014), these mutants can enhance the quality of

quantum test suites. Several studies (Murillo et al.,

2024) (Honarvar, 2020) (Garcia de la Barrera-Amo,

et al., 2024) (Garcia de la Barrera-Amo, et al., 2022)

have employed quantum mutation; however, they

have neither formalized nor classified the mutants,

leaving room for further exploration of their

application in quantum software development.

The remainder of this paper is structured as

follows: Section 2 presents a brief state-of-the-art

review, summarizing key aspects of quantum

https://n9.cl/aituw6

computing, quantum circuits, and quantum software

testing. Section 3 provides an overview of the testing

and mutation process, while Section 4 discusses the

application of this process using the QuMu tool,

which automates it, and includes a small validation

through an example. Finally, Section 5 presents the

conclusions of this study.

2 STATE OF THE ART

2.1 Quantum Software: Quantum

Circuits

A quantum circuit is both a visual representation of

the steps required to perform a quantum computation

and a high-level abstraction of a quantum program. In

fact, a quantum circuit can be translated into a

quantum program and vice versa. The circuit consists

of a set of horizontal lines, each representing a qubit

that is manipulated by the quantum gates placed on

that line. Thus, quantum gates affecting a qubit are

drawn on its corresponding line.

Figure 1 presents an excerpt from the

teleportation test circuit. It consists of five qubits,

each affected by the gates placed on their respective

lines. For example, the first qubit is manipulated by a

Hadamard gate on the first line, followed by a CNOT

gate applied to qubits 1 and 5.

A quantum circuit visually represents the steps of

a quantum computation and can be translated into a

quantum program and vice versa. It comprises

horizontal lines representing qubits, on which

quantum gates are applied.

Figure 1 illustrates an excerpt from the

teleportation circuit with five qubits. Each qubit is

affected by gates on its respective line, such as the

first qubit, which is subject to a Hadamard gate

followed by a CNOT gate applied along with qubit 5.

Figure 1: Quantum Circuit Fragment

In addition to operational gates, the circuit

includes measurement gates, which collapse the qubit

and allow its state to be read as a classical bit.

Mutation-Based Quantum Software Testing

139

Measurement is irreversible, preventing the qubit

from returning to its previous state.

Even without measurement, the qubit is always in

a state, represented as a particle at a specific position

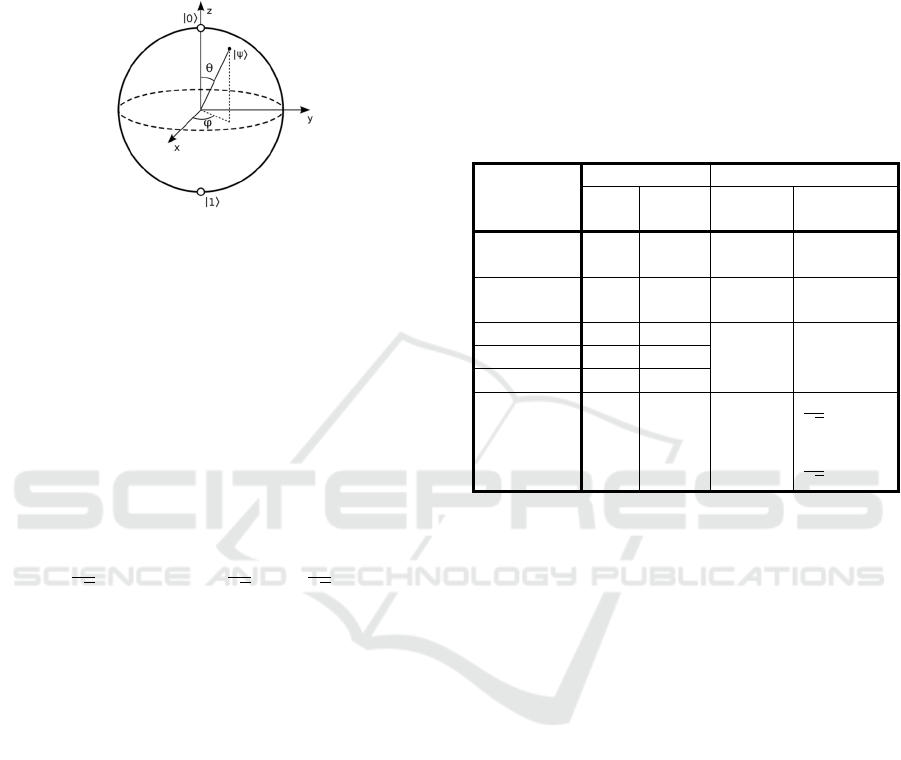
on the Bloch Sphere (Figure 2).

Figure 2: Representation of a qubit with a Blotch sphere.

Thus, a particle located at the north pole of the

sphere is in the state |0⟩. When rotating it along the Z-

axis, it moves to the south pole, which corresponds to

the state |1⟩. State changes are performed by quantum

gates, which can be represented as matrices. The

process of applying a gate to a qubit consists of

calculating the product of the matrix representing the

input qubit (or qubits) by the gate matrix. As an

example, Figure 3 describes the application of the

Hadamard gate to a qubit in state |0⟩. H rotates the

qubit particle π radians about X and π/2 radians over

𝐻|0 

√



11







√







√

|0  |1



Figure 3: H Gate applied to state |𝟎

⟩

There is a set of primitive quantum gates that

allow relatively simple operations to be performed

with cubits. All gates modify the state of the cubit by

changing the position of its associated particle on the

Bloch Sphere.

Just as it is possible to call a subroutine in

classical computing, it is also possible to integrate a

predefined quantum circuit into another, thus

handling it as if it were a primitive gate.

Table 1 summarizes the five most commonly used

gates acting on a single cubit. These gates rotate the

cubit particle about one or more axes of the Bloch

Sphere at a fixed angle.

The CNOT (aka Controlled NOT) gate performs

an X gate on one qubit (target) if the state of the other

qubit (control) is |1⟩. This gate is used, along with a

Hadamard gate, in the qubit entanglement

mechanism. Controlled-Z and Controlled-Phase

gates apply a Z-gate or an S-gate to a target qubit

whenever the controlling qubit is in the |1⟩ state.

The Toffoli gate is a three-qubit gate. It uses two

control qubits and a single target. If both control

qubits are in the |1⟩ state, an X gate is applied to the

target qubit, thus behaving like a classical AND gate.

The Fredkin gate (aka Controlled swap) performs

a swap between the two target qubits when the control

qubit is in the |1⟩ state. Finally, the Swap gate

swaps the state of two qubits.

Table 1: Quantum Gates for 1 qubit.

Gate

Rotation Example

Axis Angle

Initial

state

Final state

X (NOT) X

|0

|1

|0

Y Y

|0

|1

i·|1

-i·|0

Z (FLIP) Z

|0

|1

|0

|1

S Z

π/2

T Z

π/4

(Hadamard)

π/2

|0

|1

√

|

⟩



⟩



√

|

⟩



⟩



2.2 Mutation-Based Testing in

Quantum Software

Mutation testing has improved the quality of test

suites from structured programming (Agrawal et al.,

2006) to object-oriented development (Polo et al.,

2009) (Deng, L., Offutt, 2018) and other software

domains (Deng et al., 2017). These tests generate

mutants using automated tools that introduce

syntactic changes, simulating errors that a competent

programmer (DeMillo et al., 1978) might make,

which is more common in classical computer science

programmers (Li et al., 2020).

Mutation tools mimic simple human errors based

on the coupling effect, ensuring that a test suite

sensitive to simple bugs also detects more complex

bugs (Offutt, 1992).

In (Honarvar, 2020), it is used in metamorphic

testing of quantum software in Q#, but only as

validation. In (Boncalo et al., 2007), an innovative

fault injection technique based on quantum mutants,

replacing specific gates, is presented. In the review

presented in (Murillo et al., 2024), some more

proposals on the topic are identified, although their

scope is still very narrow.

IQSOFT 2025 - 1st International Conference on Quantum Software

140

2.3 Fault Models for Quantum

Software

Bug models are key to defining mutation operators,

as they should reflect real bugs from programmers.

Zhao et al. collected 36 bugs in Qiskit programs from

GitHub and forums, creating the Bug4Q repository

(Zhao et al., 2023). However, many bugs are more

related to Python than to Qiskit, so this repository is

not entirely representative for quantum bug models.

Huang and Martonosi (2018) analyzed bugs in

three applications: quantum chemistry, Shor's

algorithm, and Grover's algorithm. They identified

several types of faults, such as (i) incorrect classical

input parameters, (ii) incorrect operations and

transformations, or (iii) incorrect cubit deassignment.

Some of these, e.g. errors in classical input

parameters, composition of operations by iteration or

recursion, and incorrect cubit deassignment, originate

in the classical part of the program and are therefore

not relevant for pure quantum computation.

Among valid quantum bugs, incorrect initial

values stand out, although most programs start with

cubits at ∣0⟩| and then apply gates to modify them.

Also mentioned are errors in operations and

transformations, incorrect use of mirroring when

reverting changes, and failures in gate composition.

Biamonte et al. (2010) identify errors in quantum

circuits, distinguishing between quantum noise and

design faults, such as initialization errors, phase

errors and control gate faults. Lukac et al. (2017)

collect faults in reversible circuits, including

omission or incorrect use of gates and connection

errors between qubits.

3 MUTATION-BASED TESTING

PROCESS

The proposal made in this paper is based on (i) a

proposed process for performing mutation-based

quantum software testing, and (ii) a tool called

QuMu

that implements this process.

QuMu is a web tool for quantum software testing

based on the mutation technique. QuMu takes as input

a quantum circuit designed with Quirk

and generates

mutant circuits in this same notation. However, to

execute the mutants, QuMu translates the circuits into

Qiskit code and executes each circuit a customizable

number of times (known as shots). To determine

whether a mutant is alive or dead, the difference

https://alarcosj.esi.uclm.es/qumu/

between the probability distribution obtained by the

CUT and the mutant is compared.

QuMu consists of a single web page where all the

steps necessary to perform the mutation tests are

executed. The following subsections describe these

steps and the functionalities of the tool.

As shown in Figure 4, the process is divided into

two sub-processes: (i) CUT testing, and (ii) mutation

process.

Figure 4: Mutation process based on testing.

In the following section, the process illustrated in

Figure 4 will be explained, illustrated with a simple

example developed in QuMu.

4 QUMU - AUTOMATION OF

THE TESTING AND

MUTATION PROCESS

4.1 Fault Models for Quantum

Software

For the testing of the CUT (Figure 4), the CUT itself

and the test suite that has been designed to test it

(Figure 4, 2) are taken as input. The definition of the

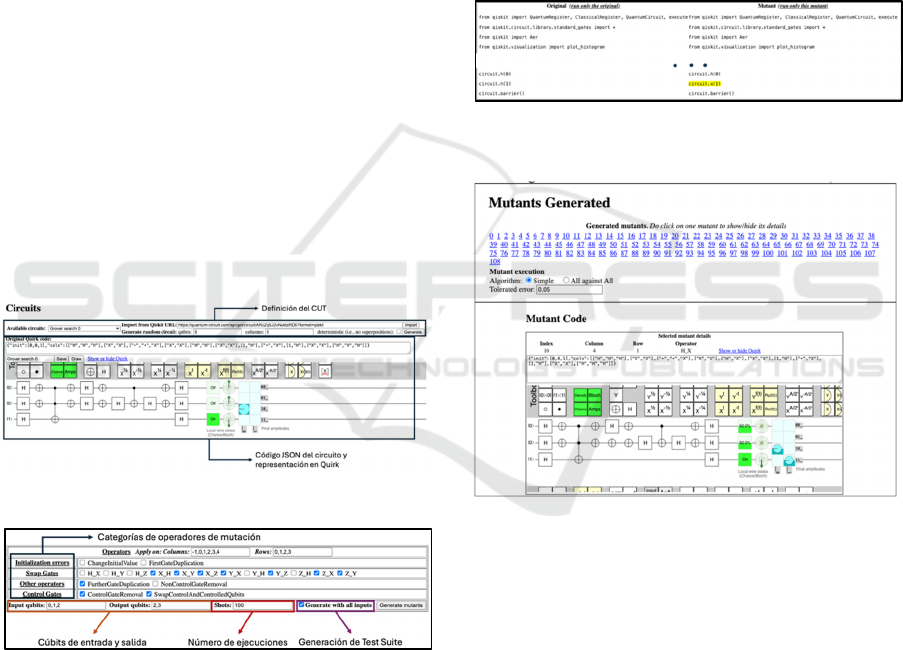
CUT can be done (see Figure 5): (i) by entering the

URL of the Quirk editor where a quantum circuit has

already been edited, (ii) by writing the JSON code of

the circuit in Quirk format in the “Original Quirk

code” area, or (iii) by selecting a previously defined

CUT in “Available circuits”. Once the CUT is

selected, QuMu loads the circuit into a Quirk-based

editor so that any modifications to the circuit can be

carried out if necessary.

https://algassert.com/quirk

Mutation-Based Quantum Software Testing

141

The testing subprocess is agnostic to the type of

testing technique applied or the type of circuit

(stochastic (Garcia de la Barrera-Amo, et al., 2024) or

deterministic (Garcia de la Barrera-Amo, et al.,

2022)). As can be seen, the first step consists of

executing the test cases against the CUT. The number

of runs of each test case (as occurs in quantum

circuits) should be calculated based on the number of

cubits and depth of the circuit, so that the resulting

probability distribution is sufficiently reliable to give

the result as correct. In the event that a test case

reveals a failure, the CUT will be corrected until all

test cases are satisfactory. After that, the CUT will be

mutated.

The QuMu prototype executes the testing and

mutation subprocesses sequentially, for which, the

selection of the mutation operators to be applied to

the CUT is required. Figure 5 details how to select

which cubits represent the input of the circuit (there

are cubits, called “ancilla”, which, due to their

auxiliary nature, are not considered a valid input of

information for the circuit) and the output cubits

(which will contain the relevant information to be

measured at the end of the execution). In addition, the

number of shots or runs of both the CUT and each of

the mutants generated from the CUT will also be

defined ( Figure 5).

Figure 5: Example CUT for mutation process.

Figure 6: Configuration of the testing and mutation process.

As Figure 6 shows, there are four types of

mutation operator categories (although thanks to

QuMu's extensible architecture, more advanced

quantum software mutation operators are already in

the works):

- Initialization errors, where the initialization

values of the cubits are mutated, or the first gate

in the circuit is repeated.

- Gate swapping, where a common error is the

confusion between the Pauli gates (X, Y and Z).

- Control gates, where typical errors arising from

CNOT and CCNOT/Toffoli gates are induced.

- Other operators, where the duplication and

elimination of quantum gates is simulated.

Once the configuration process has been carried

out, we proceed with the generation of mutants

(Figure 6). Depending on the number of cubits, the

number of quantum gates of the CUT, and the number

of mutation operators, the number of mutants

generated may vary. Thus, for the example shown, the

generation of mutants would be as shown in Figure 8,

obtaining a total of 143 mutants.

Figure 7: Fragment of the Qiskit code generated for the

mutant from the CUT with a specific operator.

Figure 8: (top) Collections of mutants generated with the

selected configuration, and (bottom) details of a specific

mutant.

Figure 8 (top) also shows, in its lower part, the

way in which the mutants will be “executed”. This

refers to the input values that will be used to perform

the execution of the CUT and the mutants and thus

compare the behavior of the latter with respect to the

former, determining whether the mutants “die” or

“survive”. Due to the “noise” generated in the

execution of the quantum software, a tolerance error

is defined to determine whether a mutant lives or dies,

whose probability distribution is slightly different

from the one obtained by the CUT.

The tester can know the details of a mutant by

selecting it: Figure 8 (bottom) shows the column, row

and operator applied to mutant number 10, as well as

IQSOFT 2025 - 1st International Conference on Quantum Software

142

its Quirk representation, so that the error introduced

by the mutation operator can be observed. In addition,

the tool also shows the Qiskit code of the mutant,

highlighting the mutated sentence (Figure 7).

Although QuMu is a prototype, it offers the

possibility to choose the execution strategy of the

CUT and the mutants (see Figure 6 and Figure 8 (top),

“Mutant execution”):

“As is” strategy (Figure 8(top)), where both the

CUT and mutants are executed with the initial values

of the CUT cubits. For the CUT in Figure 5, 100

executions are performed for the CUT and for each of

the mutants, amounting to a total of 14,500

executions (100 for the CUT, 14,400 for the mutants).

The “All against all” strategy (Figure 6), starts by

running the original circuit with all possible input

combinations (assuming 3 cubits, vary the input from

|000⟩ to |111⟩) and then each mutant also with every

possible input combination. For the example circuit

(which has three cubits with input data), both the

original and each mutant are executed 8 x 100 times

(100 shots). Thus, QuMu launches 8x100x145 (144

mutants plus the CUT), making a total of 116,000

runs.

“Run de circuit with specific inputs” (Figure 7,

top). In this strategy, assuming that the CUT has been

previously tested, and its operation is correct and

expected, specific inputs (test cases) can be

configured to perform the execution of the CUT and

mutants with those inputs.

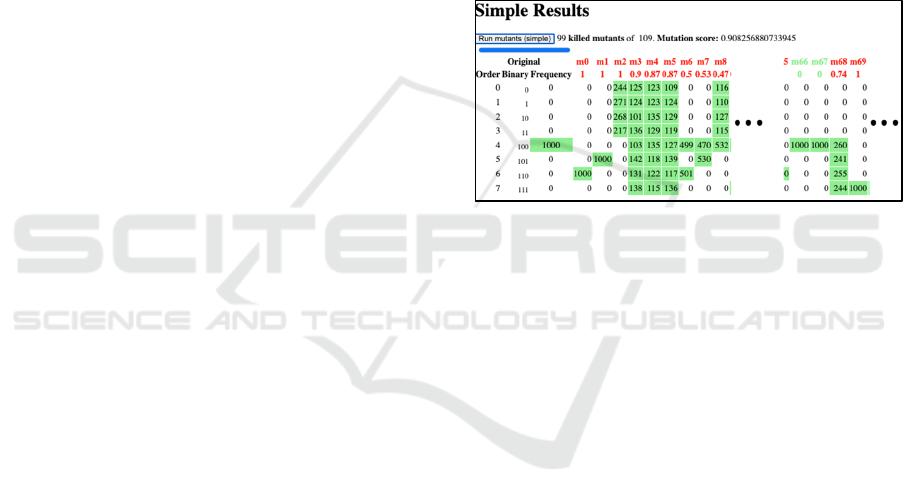
4.2 Results Analysis

When a quantum circuit is executed in Qiskit (Figure

7), a file is generated with the results where the output

frequency distribution is recorded, which is compared

with the CUT results file. During the execution of the

mutants, a table with the results, called “Killing

table”, is progressively filled in.

Suppose the tester has selected to run the circuit

in Figure 5 with the following configuration:

1) Consider all cubits of the CUT as input.

2) 1000 shots per circuit for the execution.

3) Tolerate an error of 0.05.

4) Simple execution strategy (“As is”) (i.e.,

consider only the initial input values).

Figure 9 shows the results of this execution: the

first three columns show the decimal and binary

outputs (from |000> to |111>) and their respective

frequencies in the original circuit (in this case, the

output is always 1002). The other columns show the

frequencies obtained in each mutant: mutant m7, for

example, concentrates all the outputs in the values

01002 and 01012 (with the respective frequencies 470

and 530).

The “dead” mutants appear in red, while the live

mutants appear in green. For example, since the

distribution of mutant m7 is very different from that

of the original, it is considered dead; m66 and m77,

which have exactly the same output distributions as

the original circuit, are considered “alive”.

Under each mutant name (m0, m1, etc.) is shown

the error committed in the execution of that mutant.

If this error is greater than the tolerance margin, the

mutant is eliminated. The error of a mutant is

calculated as the sum of the absolute values of the

differences between the frequencies obtained in the

original circuit and in the mutant, divided by twice the

number of shots.

Figure 9: Partial view of "Deads table" for the mutant

execution of the CUT.

Table 2 shows the outputs of both the CUT and

the m3 mutant: the total deviation of the frequencies

is 1.794. Since the number of shots is 1,000, the total

error is obtained as 1,794/2,000 = 0.897.

The reason for using this formula to calculate the

error ratio is that the maximum possible error occurs

when none of the mutant outputs match the outputs of

the original circuit. An example of this is the case of

mutant m0: its 1,000 shots fall on 1102, completely

outside of the original circuit's 1002 output. Thus, the

total error of m0 is 2,000, which when divided by

twice the number of shots results in 2,000/2,000 = 1.

It is important to note that the decision of whether a

mutant is removed or remains active is completely

different from that used in classical mutation testing.

Quantum computing requires the system under test to

be run multiple times (shots). Therefore, the quantum

computer returns a set of solutions with a given

probability distribution, which makes it unlikely that

two different runs of the same problem will generate

exactly the same set of solutions after, say, 1,000

shots.

For this reason, a mutant should be considered to

be eliminated when the probability distributions of

the CUT and the mutant are statistically different.

Mutation-Based Quantum Software Testing

143

Table 2. Error calculation of mutant "m3".

Output Original m3 Error

000 0 125 125

001 0 124 124

010 0 101 101

011 0 136 136

100 1000 103 897

101 0 142 142

110 0 131 131

111 0 138 138

1794

5 CONCLUSIONS AND FUTURE

WORK

This paper addresses software mutation as a

technique for improving the quality of test suites. This

technique has proven to be a powerful and effective

tool, which is why we propose to update and reinvent

it for its application to quantum software testing.

Thus, a process is proposed that contemplates (i) the

testing of the circuit under test (or CUT), and (ii) the

generation and execution of quantum mutants from

the CUT by applying a family of specific mutation

operators for quantum software.

Along with this process, we present QuMu, a

prototype that supports this process and by which to

carry out the generation, execution and evaluation of

quantum mutants generated from a CUT, thus

detecting opportunities for improvement in quantum

test suites, and contributing to the improvement of the

quality of quantum software.

As for future work, we present several lines

related to: (i) the identification of equivalent mutants,

(ii) the study of the usefulness or not of certain

mutation operators, (iii) identification of new

mutation operators based on the typical errors of

quantum software development, (iv) evaluation of the

real applicability of the mutation, because although

the initial results are promising, it is necessary to

perform validations according to the types of circuit,

thus being able to identify contexts where the

mutation has a greater or lesser applicability.

ACKNOWLEDGEMENTS

This work has been partially funded by Q-SERV-

Q&T (Quantum Services Engineering: Quality and

Testing of Quantum Software, PID2021-124054OB-

C32) of the Spanish Ministry of Economy, Industry

and Competitiveness and FEDER funds, QU-ASAP

(Quantum Software Modernization Prototype,

PDC2022-133051-I00) of the Spanish Ministry of

Science and Innovation and NextGenerationEU

funds, and UNION (2022-GRIN-34110), financial

support for the execution of applied research projects

within the framework of the UCLM Research Plan,

85% of which is co-financed by the European

Regional Development Fund (ERDF).

REFERENCES

Maslov, D., Nam, Y., & Kim, J. (2018). An outlook for

quantum computing [point of view]. Proceedings of the

IEEE, 107(1), 5-10.

López, M. A., & Da Silva, M. M. (2019). Quantum

technologies: Digital transformation, social impact, and

cross-sector disruption.

Humble, T. S., & DeBenedictis, E. P. (2019). Quantum

realism. Computer, 52(6), 13-17.

Garhwal, S., Ghorani, M., & Ahmad, A. (2021). Quantum

programming language: A systematic review of

research topic and top cited languages. Archives of

Computational Methods in Engineering, 28, 289-310.

LaRose, R. (2019). Overview and comparison of gate level

quantum software platforms. Quantum, 3, 130.

Gill, S. S., Kumar, A., Singh, H., Singh, M., Kaur, K.,

Usman, M., & Buyya, R. (2022). Quantum computing:

A taxonomy, systematic review and future directions.

Software: Practice and Experience, 52(1), 66-114.

Piattini, M., Peterssen, G., Pérez-Castillo, R., Hevia, J. L.,

Serrano, M. A., Hernández, G., ... & Rodríguez, M.

(2020). The Talavera Manifesto for quantum software

engineering and programming. In QANSWER (pp. 1-5).

Piattini, M., Serrano, M., Perez-Castillo, R., Petersen, G.,

& Hevia, J. L. (2021). Toward a quantum software

engineering. IT Professional, 23(1), 62-66.

Patel, T., & Tiwari, D. (2020). Veritas: accurately

estimating the correct output on noisy intermediate-

scale quantum computers. In SC20: International

Conference for High Performance Computing,

Networking, Storage and Analysis (pp. 1-16). IEEE.

Patel, T., Potharaju, A., Li, B., Roy, R. B., & Tiwari, D.

(2020). Experimental evaluation of nisq quantum

computers: Error measurement, characterization, and

implications. In SC20: International conference for

high performance computing, networking, storage and

analysis (pp. 1-15). IEEE.

Smelyanskiy, M., Sawaya, N. P., & Aspuru-Guzik, A.

(2016). qHiPSTER: The quantum high performance

software testing environment. arXiv preprint

arXiv:1601.07195.

Miranskyy, A., & Zhang, L. (2019). On testing quantum

programs. In 2019 IEEE/ACM 41st International

Conference on Software Engineering: New Ideas and

Emerging Results (ICSE-NIER) (pp. 57-60). IEEE.

Murillo, J. M., Garcia-Alonso, J., Moguel, E., Barzen, J.,

Leymann, F., Ali, S., ... & Wimmer, M. (2024).

Quantum Software Engineering: Roadmap and

Challenges Ahead. arXiv preprint arXiv:2404.06825.

IQSOFT 2025 - 1st International Conference on Quantum Software

144

Just, R., Jalali, D., Inozemtseva, L., Ernst, M. D., Holmes,

R., & Fraser, G. (2014). Are mutants a valid substitute

for real faults in software testing? In Proceedings of the

22nd ACM SIGSOFT International Symposium on

Foundations of Software Engineering (pp. 654-665).

DeMillo, R. A., Lipton, R. J., & Sayward, F. G. (1978).

Hints on test data selection: Help for the practicing

programmer. Computer, 11(4), 34-41.

Honarvar, S., Mousavi, M. R., & Nagarajan, R. (2020).

Property-based testing of quantum programs in Q#. In

Proceedings of the IEEE/ACM 42nd International

Conference on Software Engineering Workshops (pp.

430-435).

García de la Barrera-Amo, A., Serrano, M.A., García-

Rodríguez de Guzmán, I., Polo, M. & Piattini, M.

(2024) Automatic generation of property-based tests for

the verification of quantum algorithms. In Proceedings

of Services and Quantum Software 2024.

García de la Barrera-Amo, A., Serrano, M.A., García-

Rodríguez de Guzmán, I., Polo, M. & Piattini, M.

(2022) Automatic generation of test circuits for the

verification of Quantum deterministic algorithms. In

Proceedings of the 1st International Workshop on

Quantum Programming for Software Engineering.

Agrawal, H., DeMillo, R. A., Hathaway, B., Hsu, W., Hsu,

W., Krauser, E. W., ... & Spafford, E. (2006). Design of

Mutant Operators for the C Programming Language.

Polo, M., Piattini, M., & García‐Rodríguez, I. (2009).

Decreasing the cost of mutation testing with second‐

order mutants. Software Testing, Verification and

Reliability, 19(2), 111-131.

Deng, L., & Offutt, J. (2018). Reducing the Cost of Android

Mutation Testing. In SEKE (pp. 542-541).

Deng, L., Offutt, J., & Samudio, D. (2017). Is mutation

analysis effective at testing android apps? In 2017 IEEE

International Conference on Software Quality,

Reliability and Security (QRS) (pp. 86-93). IEEE.

Li, G., Zhou, L., Yu, N., Ding, Y., Ying, M., & Xie, Y.

(2020). Projection-based runtime assertions for testing

and debugging quantum programs. Proceedings of the

ACM on Programming Languages, 4(OOPSLA), 1-29.

Offutt, A. J. (1992). Investigations of the software testing

coupling effect. ACM Transactions on Software

Engineering and Methodology (TOSEM), 1(1), 5-20.

Boncalo, O., Udrescu, M., Prodan, L., Vladutiu, M., &

Amaricai, A. (2007, August). Assessing quantum

circuits reliability with mutant-based simulated fault

injection. In 2007 18th European Conference on

Circuit Theory and Design (pp. 942-945). IEEE.

Zhao, P., Miao, Z., Lan, S., & Zhao, J. (2023). Bugs4Q: A

benchmark of existing bugs to enable controlled testing

and debugging studies for quantum programs. Journal

of Systems and Software, 205, 111805.

Huang, Y., & Martonosi, M. (2018). QDB: from quantum

algorithms towards correct quantum programs. arXiv

preprint arXiv:1811.05447

Biamonte, J. D., Allen, J. S., & Perkowski, M. A. (2010).

Fault models for quantum mechanical switching

networks. Journal of Electronic Testing, 26, 499-511.

Lukac, M., Kameyama, M., Perkowski, M., Kerntopf, P., &

Moraga, C. (2017). Fault models in reversible and

quantum circuits. Advances in Unconventional

Computing: Volume 1: Theory, 475-493.

Mutation-Based Quantum Software Testing

145