ClustSize: An Algorithmic Framework for Size-Constrained

Clustering

Diego Vallejo-Huanga

1,2 a

and C

esar Ferri

and Fernando Mart

ınez-Plumed

IDEIAGEOCA Research Group, Universidad Polit

ecnica Salesiana, Quito, Ecuador

VRAIN, Universitat Polit

ecnica de Val

encia, Valencia, Spain

Keywords:

Size-Constrained Clustering, K-MedoidsSC, CSCLP, Interactive Web Application, R Shiny, User Experience.

Abstract:

Size-constrained clustering addresses a fundamental need in many real-world applications by ensuring that

clusters adhere to user-speciﬁed size limits, whether to balance groups or to satisfy domain-speciﬁc require-

ments. In this paper, we present ClustSize, an interactive web platform that implements two advanced

algorithms: K-MedoidsSC and CSCLP, to perform real-time clustering of tabular data under strict size con-

straints. Developed in R Studio using the Shiny framework and deployed on Shinyapps.io, ClustSize not

only enforces precise cluster cardinalities, but also facilitates dynamic parameter tuning and visualisation for

enhanced user exploration. We comprehensive validate its performance through comprehensive benchmark-

ing, also evaluating runtime, RAM usage, load, and stress conditions, and gather usability insights via user

surveys. Post-deployment evaluations conﬁrm that both algorithms consistently produce clusters that exactly

meet the speciﬁed size limits, and that the system reliably supports up to 50 concurrent users and maintains

functionality under stress, processing approximately 90 requests in 5 seconds. These results highlight the

potential of integrating advanced size-constrained clustering into interactive web platforms for practical data

analysis.

1 INTRODUCTION

Clustering techniques (Celebi and Aydin, 2016; Sax-

ena et al., 2017) are a cornerstone of unsupervised

learning, widely employed to uncover hidden struc-

tures in complex datasets across diverse domains such

as healthcare, ﬁnance, and natural sciences (Jain,

2010). In traditional clustering, however, little at-

tention is paid to a crucial practical constraint: en-

suring that clusters adhere to predetermined size lim-

its. In many real-world scenarios, balancing the num-

ber of elements in each cluster is crucial, not only

to improve the interpretability of results but also to

prevent imbalanced partitions that can skew subse-

quent analyses. Motivated by these concerns, size-

constrained clustering methods (Wagstaff et al., 2001)

have recently emerged as a promising solution, en-

abling more robust and representative groupings.

In this paper, we adapt and extend two state-

of-the-art size-constrained clustering algorithms,

K-MedoidsSC and CSCLP (Vallejo-Huanga et al.,

2017), originally developed for clustering documents,

https://orcid.org/0000-0002-2704-3858

to robustly and accurately handle structured tabular

data. To underpin these extensions, we introduce a

formal mathematical notation that rigorously deﬁnes

our problem—partitioning a dataset into clusters that

must satisfy exact size requirements—and the asso-

ciated algorithms. We aim that our methods are not

only theoretically sound, but also reproducible.

Equally importantly, we implement the extended

algorithms efﬁciently and effectively within a user-

friendly web application for real-time data explo-

ration and visualization: ClustSize aiming to

bridge the gap between algorithmic innovation and

usability. Developed in R (R Core Team, 2024) and

deployed via the Shiny framework (Beeley, 2016),

this application provides an interface where users

can upload datasets, conﬁgure clustering parameters,

and instantly visualize results. Our implementation

emphasizes efﬁcient resource management and fast

execution, which is particularly important for real-

time data exploration in resource-constrained envi-

ronments such as Shinyapps.io

The decision to develop both clustering algo-

https://www.shinyapps.io/

Vallejo-Huanga, D., Ferri, C., Martínez-Plumed and F.

ClustSize: An Algorithmic Framework for Size-Constrained Clustering.

DOI: 10.5220/0013558900003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 481-490

ISBN: 978-989-758-758-0; ISSN: 2184-285X

481

rithms is driven by their complementary strengths.

K-MedoidsSC, an extension of the conventional

K-Medoids method, is designed for speed and re-

source efﬁciency, making it well-suited for larger

datasets and interactive applications. In contrast,

CSCLP employs a linear programming formulation

that enforces size constraints even under complex data

distributions. By incorporating both methods, our

platform offers users a choice based on dataset char-

acteristics and performance requirements, also en-

abling side-by-side comparisons of the tradeoffs in-

herent in each approach.

To validate both the algorithms and the web ap-

plication, we conducted comprehensive evaluations

on 15 representative datasets from OpenML (Van-

schoren et al., 2014), spanning small to large vol-

umes and various domains. We analyzed execution

time and memory consumption, and performed load

and stress tests to determine system resilience under

increasing user concurrency. Complementing these

technical analyses, we also perform usability evalua-

tions via structured surveys to conﬁrm that our plat-

form is intuitive and accessible to both experts and

non-experts. Notably, our experiments reveal that the

K-MedoidsSC algorithm not only executes faster and

uses less memory than CSCLP, but it also supports

larger datasets—an important consideration given the

limitations of resource-constrained environments like

Shinyapps.io’s free tier.

The primary contributions of this work are as fol-

lows:

• We extend and rigorously formalize two state-of-

the-art size-constrained clustering algorithms for

structured tabular data, ensuring compliance with

explicit cluster size limits.

• We design and implement an efﬁcient, interactive

web platform (ClustSize) that seamlessly inte-

grates these algorithms to provide real-time clus-

tering with dynamic parameter tuning and visual-

ization.

• We present a comprehensive evaluation of al-

gorithmic performance—including performance,

runtime, memory usage, and scalability under

load—and complement this with practical usabil-

ity assessments.

• We offer valuable insights into integrating ad-

vanced clustering methodologies within web en-

vironments, addressing challenges related to re-

source limitations and multi-user access.

The rest of the paper is organized as follows. Sec-

tion2 reviews related work in size-constrained clus-

tering. Sections 3 and 4 describe our methodology

and details the development of the web platform, in-

cluding adaptations to the K-MedoidsSC and CSCLP

algorithms. Section 5 presents our experimental re-

sults, and Section 6 concludes the paper and outlines

future work.

2 RELATED WORKS

Over the past decade, researchers have increasingly

recognized that traditional clustering techniques often

fall short when practical constraints—especially those

related to cluster size—are imposed by real-world ap-

plications. This realization has spurred a range of

studies aimed at integrating size restrictions into clus-

tering algorithms while preserving or even enhancing

clustering quality.

For instance, (Zhu et al., 2010) highlights the im-

portance of incorporating size constraints into tra-

ditional clustering algorithms to improve clustering

accuracy and avoid the formation of outlier clus-

ters. They propose a heuristic algorithm that converts

size-constrained clustering problems into integer lin-

ear programming problems, offering an approach to

handle approximate size range constraints instead of

exact cluster size constraints. Building on similar

ideas, (Zhang et al., 2014) proposed a uniﬁed frame-

work that simultaneously incorporates size and pair-

wise constraints. Their method minimizes the dis-

crepancy between the ground truth distribution and

the clustering output, a strategy that has been vali-

dated across both balanced and imbalanced datasets

using metrics such as Normalized Mutual Informa-

tion (NMI) (Strehl and Ghosh, 2002) and a new mea-

sure called Alignment Score (AS). Also, (Tang et al.,

2019) proposed the Balanced Clustering Algorithm

(BCA). This method uses Integer Linear Program-

ming (ILP) to achieve balanced clustering. Compared

to other methods, experimental tests were performed

using synthetic and real datasets to evaluate the al-

gorithm’s performance. The results of the proposed

method show better performance in terms of MSE and

runtime compared with two other balanced clustering

algorithms (Malinen and Fr

anti, 2014) (Zhu et al.,

2010).

Parallel to these ILP-based and heuristic ap-

proaches, researchers have also explored direct mod-

iﬁcations to classical algorithms. (Ganganath et al.,

2014) modiﬁed the K-Means algorithm itself by inte-

grating explicit size constraints in the clustering pro-

cess. Their empirical studies with multidimensional

datasets modiﬁed the K-Means algorithm itself by

integrating explicit size constraints in the clustering

process.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

482

In addition to these centralized formulations, re-

cent work has expanded the scope of size-constrained

clustering to distributed systems. (Bassil et al., 2023),

for example, presented the SC-Clust algorithm—a de-

centralized approach designed for modular robotics.

By leveraging local information from individual mod-

ules, their distributed framework efﬁciently manages

large-scale clustering tasks while respecting size con-

straints, highlighting the beneﬁts of applying these

techniques in resource-constrained, distributed envi-

ronments.

Most pertinent to our work, (Vallejo-Huanga

et al., 2017) introduced two semi-supervised

clustering algorithms—K-MedoidsSC and CSCLP

(Clustering with Size Constraints with Linear

Programming)—that integrate size constraints within

the clustering process. Originally applied to cluster

scientiﬁc papers using natural language processing

techniques and textual embeddings, these algorithms

demonstrated how domain-speciﬁc information

could be harnessed to guide clustering outcomes in

a manner that respects predeﬁned size limits. This

approach underscored the potential of combining

traditional clustering paradigms with domain-relevant

constraints and has provided a strong foundation

for further extensions, including the adaptation to

structured tabular data as explored in our current

study.

Together, these lines of work offer a broad per-

spective on how size constraints can be effectively

incorporated into clustering methods. They moti-

vate our research objective: to extend and adapt the

K-MedoidsSC and CSCLP algorithms so that they can

process structured tabular data in a real-time, web-

based environment.

3 METHODS

We implemented a systematic methodology that en-

compasses dataset selection, algorithm development,

web application design, and multi-faceted perfor-

mance evaluation. Our approach, summarized in Fig-

ure 1, follows a waterfall model (Royce, 1987) in se-

quential and interlinked phases.

3.1 Data Selection and Preprocessing

A diverse collection of a subset of 15 tabular datasets

from OpenML (Vanschoren et al., 2014) (study

100 (Bischl et al., 2017)), was chosen to evaluate the

effect of cluster size constraints across various do-

mains. These datasets, as detailed in Table 1, were

chosen to span different scales (small: up to 2120 in-

stances, medium: from 2121 to 4000 instances, and

large: from 4001 to 6500 instances), variable counts,

and subject areas ranging from natural sciences to so-

cial sciences.

Table 1: Metadata for the 15 structured test datasets used

in our evaluations: identiﬁer (ID), dataset name, the total

number of instances, the number of variables, the relevant

ﬁeld of knowledge, and the empirical taxonomy categoriz-

ing the dataset by size.

ID Name #Instances #Variables Knowledge Field Taxonomy

1 Iris 150 3 Natural Sciences Small

2 Heart Disease 1025 14 Health Sciences Small

3 Obesity Levels 2111 17 Health Sciences Small

4 Glass Identiﬁcation 214 9 Natural Sciences Small

5 Breast Cancer Wisconsin 568 30 Health Sciences Small

6 Engineering Graduate Salary 2998 34 Finance Medium

7 Water Probability 3276 10 Natural Sciences Medium

8 Cure The Princess 2338 14 Multimedia Medium

9 AIDS Clinical 2139 24 Health Sciences Medium

10 Migration from Mexico to USA 2443 10 Social Sciences Medium

11 Bank Loan Approval 5000 14 Finance Large

12 Wine Quality 6497 13 Enology Large

13 Clustering of cycling 4435 11 Sports Analysis Large

14 Turkiye-student-evaluation 5820 33 Mathematical Sci. Large

15 Abalone 4177 8 Natural Sciences Large

In addition to the dataset metadata such as the

number of instances and variables, each dataset was

further characterized by its ground truth grouping and

cardinalities (see Table 2), thus serving as baselines

for both algorithm validation and comparative analy-

sis.

Table 2: Group sizes (cardinality) for each dataset in Ta-

ble 1.

ID #Groups

Cluster Size

1 2 3 4 5 6 7 8 9

1 3 50 50 50 – – – – – –

2 2 499 526 – – – – – – –

3 7 272 287 351 297 324 290 290 – –

4 6 70 76 17 13 9 29 – – –

5 2 356 212 – – – – – – –

6 2 226 2772 – – – – – – –

7 2 1998 1278 – – – – – – –

8 2 1177 1161 – – – – – – –

9 2 1618 521 – – – – – – –

10 6 330 593 392 93 162 873 – – –

11 2 4520 480 – – – – – – –

12 7 1599 4898 — – – – – – –

13 9 1399 312 467 356 290 549 503 185 374

14 3 775 1444 3601 – – – – – –

15 3 1307 1342 1528 – – – – – –

3.2 Algorithmic Implementation

Two semi-supervised clustering algorithms were

implemented in the R programming language:

K-MedoidsSC and CSCLP (Clustering with Size Con-

straints and Linear Programming) (Vallejo-Huanga

et al., 2017). Both algorithms are adapted to enforce

explicit size constraints while partitioning tabular

data. Also, both algorithms rely on distance metrics-

Cosine and Euclidean measures-computed over dis-

similarity matrices. These metrics directly inform the

ClustSize: An Algorithmic Framework for Size-Constrained Clustering

483

Figure 1: Diagram of the methodological process for implementing and deploying clustering algorithms with size restrictions

in the web application.

instance allocation procedures, ensuring that the ﬁ-

nal clustering solutions are consistent with both the

proximity-based grouping criteria and the external

size restrictions.

In our work, we consider a dataset D =

, x

, . . . , x

} where each x

is an observation. We

wish to partition D into k disjoint clusters while im-

posing an exact size constraint on each cluster. The

desired cluster sizes are speciﬁed by the vector E =

, E

, . . . , E

], so that for each cluster C

, it holds

that |C

| = E

. In addition, we deﬁne a distance func-

tion d(x, c) to quantify the dissimilarity between any

instance x ∈ D and a centroid c.

3.2.1 K-MedoidsSC

K-MedoidsSC extends the conventional K-Medoids

framework by pre-assigning instances to clusters

based on predeﬁned size requirements. Its procedure

involves an initial medoid selection, a distance-based

instance sorting, and a two-stage assignment process

that guarantees each cluster meets its cardinality con-

straint.

The K-MedoidsSC algorithm operates as fol-

lows. If no initial medoids are provided, a set

C = {c

, c

, . . . , c

} ⊂ D is randomly selected. Next,

the algorithm computes the distance d(x, c

) between

each instance x and every medoid c

. The dataset D is

then sorted in ascending order based on the minimum

distance min

1≤i≤k

d(x, c

). For each cluster index

i = 1, 2, . . . , k, the algorithm assigns the ﬁrst E

unas-

signed, closest instances to cluster C

. Finally, any

remaining instances are assigned to the cluster that

minimizes d(x, c

), i.e., Assign x to C

where j =

argmin

1≤i≤k

d(x, c

). This procedure guarantees that

the size constraints |C

| = E

are fulﬁlled exactly. The

detailed pseudocode for SC-Medoids is presented in

Algorithm 1.

Algorithm 1: K-MedoidsSC Clustering Algorithm.

Require: Data set D = {x

, x

, . . . , x

}, num-

ber of clusters k, desired cluster sizes

E = [E

, E

, . . . , E

1: (optional) initial medoids C =

, c

, . . . , c

} ⊂ D

Ensure: Partition {C

, C

, . . . , C

} of D satisfying

| = E

for i = 1, . . . , k

2: if C not provided then

3: Randomly select k distinct instances from D

as medoids; set C = {c

, . . . , c

}

4: end if

5: Compute the distance matrix: for every x ∈ D and

each medoid c

, calculate d(x, c

)

6: Sort D in ascending order according to

min

1≤i≤k

d(x, c

)

7: for i = 1, . . . , k do

8: Assign the ﬁrst E

(closest and unassigned) in-

stances from the sorted list to cluster C

9: end for

10: for each remaining instance x ∈ D do

11: Assign x to cluster C

where

j = arg min

1≤i≤k

d(x, c

12: end for

13: return Clusters {C

, C

, . . . , C

}

3.2.2 CSCLP

CSCLP integrates linear programming into the cluster-

ing process. Beginning with an initial partition de-

rived from K-Means clustering, the algorithm checks

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

484

whether the resultant clusters satisfy the imposed size

constraints. In cases where the constraints are vio-

lated, the algorithm reformulates the clustering task as

a binary linear programming problem. Here, the ob-

jective function minimizes cluster dissimilarity sub-

ject to equality constraints that enforce the desired

cluster sizes. Regarding their operation, we again

consider the dataset D and the desired cluster-size

vector E = [E

, E

, . . . , E

]. An initial clustering—

obtained, for instance, via K-Means—yields tenta-

tive clusters C

, C

, . . . , C

with corresponding cen-

troids c

, c

, . . . , c

. If these clusters already satisfy

| = E

for all i, the current assignment is returned.

Otherwise, we reformulate the clustering task as a bi-

nary linear programming (BLP) problem. For each

instance x

∈ D and cluster i, we introduce a binary

decision variable

i j

(

1, if x

is assigned to cluster i,

0, otherwise.

(1)

The objective is to minimize the overall assignment

cost:

min

∑

i=1

∑

j=1

d(x

, c

i j

, (2)

subject to the constraints

∑

i=1

i j

= 1, ∀ j = 1, 2, . . . , n, (3)

∑

j=1

i j

= E

, ∀i = 1, 2, . . . , k, (4)

i j

∈ {0, 1}, ∀i, j. (5)

After solving this binary LP, the optimal assignment

matrix Z

∗

is obtained. The ﬁnal cluster labeling is

then given by setting

R(x

) = i if Z

∗

i j

= 1, j = 1, . . . , n.

A complete pseudocode for CSCLP is provided in Al-

gorithm 2.

4 WEB APPLICATION

Following local validation of the clustering algo-

rithms, a robust web application was developed using

the R Shiny framework

to serve as an interactive

platform for real-time clustering analyses. The design

and implementation of ClustSize were driven

by the need to combine computational efﬁciency

with an intuitive user experience, ensuring that both

https://www.shinyapps.io/

Algorithm 2: CSCLP Clustering Algorithm.

Require: Data set D = {x

, . . . , x

}, desired number

of clusters k, desired cluster sizes E = [E

, . . . , E

]

Ensure: Cluster assignment R : D → {1, 2, . . . , k}

with |{x : R(x) = i}| = E

1: Perform an initial clustering (e.g., using k-means)

to obtain tentative clusters {C

, . . . , C

} with cen-

troids {c

, . . . , c

}

2: if for all i, |C

| = E

then

3: return current cluster assignment R

4: else

5: Deﬁne binary variables Z = [Z

i j

] following

Eq. 1

6: Formulate a binary linear programming

problem, minimizing Eq. 2 with the constraints 3

7: Solve the above LP to obtain the optimal as-

signment matrix Z

∗

8: for j = 1, . . . , n do

9: Set R(x

) = i such that Z

∗

i j

= 1

10: end for

11: return the updated cluster assignment R

12: end if

expert and non-expert users can easily deploy size-

constrained clustering on their datasets. ClustSize

is publicly accessible, and its services can be used at:

https://clustering-algorithms-with-size-constraints.

shinyapps.io/shinyapps/

4.1 Modular and Reactive Architecture

ClustSize is built on a modular, reactive archi-

tecture that separates user interface (UI) components

from server-side computations. This design lever-

ages Shiny’s reactive programming paradigm to en-

sure that any input parameter change triggers imme-

diate output updates. By encapsulating key function-

alities (such as data upload, parameter conﬁguration,

clustering execution, and visualization) within dis-

crete modules, the application maintains high code

reusability and ease of maintenance. In this client-

server setup, heavy computations (e.g., running the

clustering algorithms and performing principal com-

ponent analysis) are handled server-side, while the

client interface facilitates a seamless, interactive ex-

perience.

Furthermore, to overcome resource constraints

on platforms like Shinyapps.io, the application opti-

mizes computational performance and resource man-

agement by caching results and ﬁne-tuning reactive

expressions to avoid unnecessary recalculations. The

code architecture supports smooth interactivity under

high load by ofﬂoading data-heavy tasks to the server

and efﬁciently managing user sessions.

ClustSize: An Algorithmic Framework for Size-Constrained Clustering

485

4.2 User Interface and Interaction

ClustSize operates as a single-page interface or-

ganized into clearly deﬁned panels. As shown in Fig-

ure 2, the left-hand sidebar is dedicated to user inputs.

Here, users can upload their datasets (with common

formats such as CSV or Excel), specify clustering pa-

rameters (including the number of clusters, size con-

straints, and choice of distance metrics), and preview

dataset summaries. Tooltips and contextual help links

are embedded throughout the sidebar, providing addi-

tional guidance to ensure that conﬁguring a clustering

run is straightforward and efﬁcient.

Figure 2: Selecting parameters and displaying the dataset in

the UI.

Once the user has conﬁgured the desired param-

eters, ClustSize automatically initiates clustering

operations. The results are displayed on a separate

tab designated for output visualization. Figure 3 illus-

trates this results tab, which is subdivided into mul-

tiple sections. The primary visualization is a dy-

namic principal component analysis (PCA) plot that

maps clustered data into a two-dimensional space,

with clusters distinguished by color-coding and inter-

active elements such as hover-over tooltips that dis-

play detailed information regarding cluster member-

ship. In addition to the graphical output, a data ta-

ble presents the clustering results alongside the corre-

sponding ground truth labels, facilitating quantitative

assessments and further exploration of the clustering

quality.

5 EVALUATION AND TESTING

After verifying the functionality and performance of

the clustering algorithms in a controlled, local envi-

ronment, the complete web application was deployed

on Shinyapps.io. This cloud-based hosting platform

ensures immediate and broad access while provid-

ing an integrated environment for R Shiny applica-

tions. However, the inherent resource limitations (no-

tably, a 1GB RAM cap) necessitated further testing

to validate the system’s robustness under realistic us-

Figure 3: Results tab in the UI after a clustering process.

age conditions. Our testing methodology is organized

into multiple components, including clustering per-

formance, time and memory benchmarking, load test-

ing, stress testing, and usability evaluation.

5.1 Clustering Evaluation

To comprehensively assess our proposed

size-constrained clustering methods, we com-

pared CSCLP and K-MedoidsSC against conventional

clustering algorithms that do not explicitly enforce

size restrictions gainst the datasets in Table 1, focus-

ing on cluster sizes, external and internal validation

measures.

For the ﬁrst evaluation, Table 3 (column ”Clus-

ter Sizes”) compares the cluster sizes obtained by

applying algorithms without explicit size restric-

tions, namely, Agglomerative Hierarchical Cluster-

ing with complete linkage (AHC) (Johnson, 1967)

and standard K-Medoids (Park and Jun, 2009), with

our proposals that enforce cluster sizes (CSCLP and

K-MedoidsSC). We use the same initial cluster points

randomly, keeping the seed. As expected, both the

AHC and standard K-Medoids algorithms fail to meet

the expected cluster sizes since they do not incor-

porate any size restrictions, whereas the proposed

CSCLP and K-MedoidsSC methods perfectly match

the ground truth cluster sizes for all the datasets.

For a broader validation, our focus was to com-

pare the clustering quality and adherence to size con-

straints (Hubert and Arabie, 1985) achieved by the

four methods analyseds. To this end, we computed

several external validation metrics—such as the Ad-

justed Rand Index (ARI), Adjusted Mutual Infor-

mation (AMI), and Normalized Mutual Information

(NMI)—as well as the silhouette coefﬁcient S(i) to

assess internal cohesion and separation. Table 3

also summarizes these validation measures for each

dataset. The results indicate that while both methods

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

486

rigorously enforce the prescribed cluster sizes, there

is variability in clustering quality across datasets. In

several cases, CSCLP exhibits higher external valida-

tion scores (with values closer to 1), suggesting better

alignment with the ground truth partitioning. Con-

versely, for a few datasets, K-MedoidsSC attains com-

petitive or even superior internal cohesion as reﬂected

in the silhouette coefﬁcient.

Table 3: External and internal clustering validation indices

for OpenML datasets (column ID, see Table1). External in-

dices (ARI, AMI, and NMI) and the Silhouette Coefﬁcient

S(i) are reported for four different clustering algorithms.

Best results in bold.

ID Algorithm #Groups

Cluster Sizes

ARI AMI NMI S(i)

1 2 3 4 5 6 7 8 9

AHC 3 50 74 26 0.644 0.714 0.717 0.601

K-Medoids 3 50 62 38 0.730 0.748 0.751 0.540

CSCLP 3 50 50 50 0.813 0.769 0.772 0.631

K-MedoidsSC 3 50 50 50 0.015 0.013 0.025 -0.076

AHC 2 801 224 0.028 0.025 0.026 0.509

K-Medoids 2 501 524 0.020 0.014 0.015 0.462

CSCLP 2 499 526 0.149 0.110 0.111 0.325

K-MedoidsSC 2 499 526 0.024 0.018 0.019 0.107

AHC 7 1145 301 248 40 366 2 9 0.067 0.146 0.149 0.479

K-Medoids 7 343 332 440 317 179 340160 0.312 0.470 0.472 -0.035

CSCLP 7 272 287 351 297 324 290290 0.133 0.238 0.242 0.269

K-MedoidsSC 7 272 287 351 297 324 290290 0.085 0.134 0.138 -0.206

AHC 6 151 25 6 27 3 2 0.285 0.353 0.378 0.718

K-Medoids 6 39 65 60 20 28 2 0.199 0.305 0.332 0.279

CSCLP 6 70 76 17 13 9 29 0.206 0.270 0.302 0.196

K-MedoidsSC 6 70 76 17 13 9 29 0.080 0.135 0.172 -0.147

AHC 2 44 524 0.126 0.123 0.124 0.689

K-Medoids 2 139 429 0.533 0.458 0.459 0.556

CSCLP 2 356 212 0.609 0.484 0.484 0.619

K-MedoidsSC 2 356 212 0.066 0.034 0.035 0.230

AHC 2 2938 60 -0.029 0.005 0.006 0.869

K-Medoids 2 1664 1334 -0.009 0.026 0.027 0.275

CSCLP 2 226 2772 0.179 0.052 0.053 -0.345

K-MedoidsSC 2 226 2772 -0.036 0.004 0.004 -0.559

AHC 2 3274 2 1.23e-04 -2.87e-04 2.26e-05 0.998

K-Medoids 2 1826 1450 0.001 1.25e-04 3.47e-04 0.057

CSCLP 2 1998 1278 0.004 0.001 0.001 -0.022

K-MedoidsSC 2 1998 1278 0.004 6.30e-04 8.58e-04 0.291

AHC 2 1868 470 0.023 0.028 0.028 0.072

K-Medoids 2 970 1368 0.004 0.003 0.003 0.075

CSCLP 2 1177 1161 0.049 0.036 0.036 0.187

K-MedoidsSC 2 1177 1161 0.010 0.007 0.008 0.049

AHC 2 1952 187 0.083 0.018 0.018 0.479

K-Medoids 2 1433 706 0.044 0.011 0.011 0.513

CSCLP 2 1618 521 -0.067 0.065 0.065 0.210

K-MedoidsSC 2 1618 521 0.097 0.029 0.029 0.285

AHC 6 2032 90 110 78 93 40 0.002 0.003 0.007 0.842

K-Medoids 6 48 738 316 1231 11 99 -0.012 0.018 0.022 -0.594

CSCLP 6 330 593 392 93 162 873 0.022 0.033 0.036 -0.067

K-MedoidsSC 6 330 593 392 93 162 873 1.22e-04 0.016 0.020 -0.275

AHC 2 4756 244 0.172 0.045 0.045 0.822

K-Medoids 2 2448 2552 -9.59e-05 -1.43e-04 1.35e-06 0.002

CSCLP 2 4520 480 0.294 0.121 0.121 -0.024

K-MedoidsSC 2 4520 480 0.161 0.043 0.044 0.815

AHC 2 5743 754 0.445 0.303 0.303 0.846

K-Medoids 2 4175 2322 0.472 0.355 0.355 0.473

CSCLP 2 1599 4898 -0.070 0.116 0.116 -0.156

K-MedoidsSC 2 1599 4898 -0.066 0.068 0.068 -0.216

AHC 9 30 7 5 11 42 16 14 4288 22 0.012 0.029 0.033 0.931

K-Medoids 9 567 658 647 615 379 394522 371 282 0.361 0.525 0.527 -0.056

CSCLP 9 1399 312 467 356 290549 503 185 374 0.418 0.438 0.440 0.041

K-MedoidsSC 9 1399 312 467 356 290549 503 185 374 0.095 0.161 0.164 -0.201

AHC 3 4242 528 1050 -0.032 0.005 0.005 0.607

K-Medoids 3 2201 25271092 -0.004 0.008 0.009 0.124

CSCLP 3 775 14443601 -0.014 0.002 0.002 0.477

K-MedoidsSC 3 775 14443601 0.041 0.017 0.017 -0.353

AHC 3 3087 1088 2 0.125 0.114 0.114 0.775

K-Medoids 3 1373 14991305 0.153 0.164 0.164 0.501

CSCLP 3 1307 13421528 0.166 0.168 0.169 0.522

K-MedoidsSC 3 1307 13421528 0.037 0.034 0.034 -0.095

5.2 Performance Analysis

A series of experiments were performed to com-

pare the computational efﬁciency of SC-Medoids and

CSCLP across the datasets in Table 1. Using both Co-

sine and Euclidean distance metrics, execution times

and peak RAM consumption were recorded (see Ta-

ble 4). In general, SC-Medoids consistently out-

performed CSCLP, particularly for medium to large

datasets. For example, while SC-Medoids processed

certain datasets in under a second, CSCLP required

several orders of magnitude more time for equivalent

tasks and, in some cases, exceeded the 1GB RAM

threshold imposed by the hosting platform. This dis-

parity underscores the suitability of SC-Medoids for

resource-limited, interactive web applications.

Table 4: Comparison of execution times and peak RAM be-

tween K-MedoidsSC and CSCLP algorithms. The “–” sym-

bol indicates tests that could not be completed due to re-

source constraints or data issues.

ID Distance Time [s] RAM Peak [MB]

K-MedoidsSC CSCLP K-MedoidsSC CSCLP

Cosine 0.023 0.011 233.2 239.4

Euclidean 0.028 0.018 235.4 244.5

Cosine 0.055 0.492 256.6 272.6

Euclidean 0.256 0.719 256.6 364.4

Cosine 0.642 2.04 365.8 1022.1

Euclidean 0.438 1.624 954.4 1030.9

Cosine 0.026 0.046 758.1 767.8

Euclidean 0.003 0.307 759.7 760.1

Cosine 0.049 0.077 761.1 761.5

Euclidean 0.048 0.120 774.2 762.1

Cosine 1.398 2.366 652.4 2084.5

Euclidean 1.425 2.386 588.4 2079.8

Cosine 0.644 – 535.3 –

Euclidean 0.863 – 674.6 –

Cosine 0.317 1.281 374.8 1126.6

Euclidean 0.320 1.220 877.3 1105.2

Cosine 0.350 0.945 657.2 1042.7

Euclidean 0.292 0.984 690.7 1068.8

Cosine 0.315 4431 914.3 1187.2

Euclidean 0.326 4606 914.5 1187.3

Cosine 1604 6056 1053.6 2521.8

Euclidean 1.220 6249 1044.9 2513.9

Cosine 2988 – 3083.1 –

Euclidean 2152 – 1857.5 –

Cosine 1254 32319 2048.2 2935.7

Euclidean 0.976 36437 1118.8 2932.0

Cosine 3.330 16729 3257.9 5688.0

Euclidean 2.956 15091 1960.6 5777.4

Cosine 0.851 6695 4111.9 6911.5

Euclidean 0.821 6391 4112.8 6913.3

5.3 System Load Testing

Load testing is essential to ensure that the sys-

tem works optimally under actual conditions of use

with several users connected simultaneously (Dra-

heim et al., 2006). By simulating different load sce-

narios, such as user peaks or increases in data volume,

we can identify how our system responds and where

performance problems could arise.

Using Apache JMeter, we simulated various lev-

els of concurrent user activity. Three controlled sce-

narios were conﬁgured, with 30, 50, and 70 threads

(each representing a simultaneous user) launched

with a ramp-up time of 0 seconds to generate an in-

stantaneous peak load. In each scenario, every thread

executed a single iteration—submitting a clustering

ClustSize: An Algorithmic Framework for Size-Constrained Clustering

487

request—so that the system’s response, throughput,

and error rate could be accurately recorded.

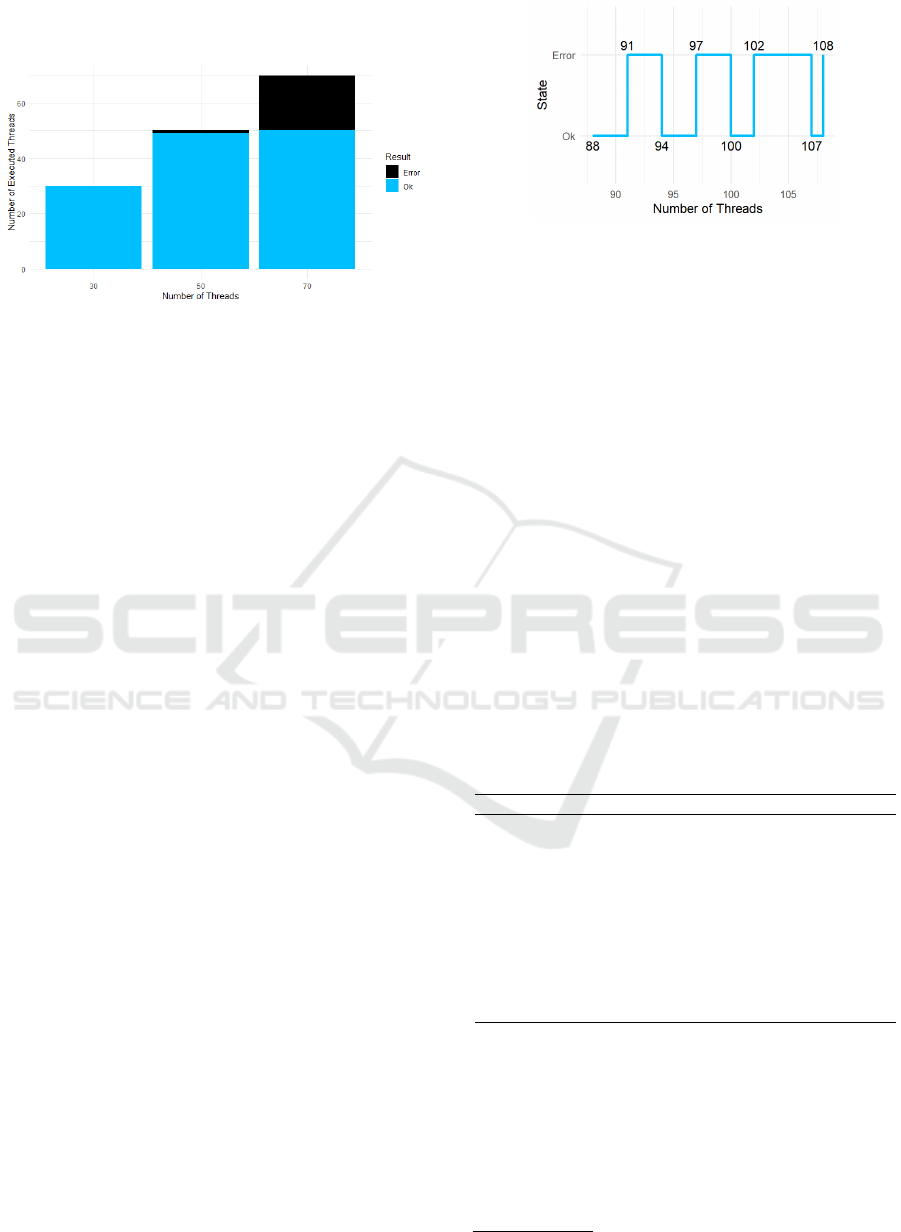
Figure 4: Load test results with different numbers of threads

(simulated concurrent users), showing accepted and failed

HTTP requests.

Figure 4 illustrates the load test results as simu-

lated by JMeter. Under a moderate load of 30 con-

current threads, the application maintained a through-

put of roughly 9.9 requests per second without any

errors. The performance improved when the load

was increased to 50 threads, reaching a throughput

of about 20.7 requests per second with only a mini-

mal error occurrence (approximately 2%). However,

when subjected to a heavier load of 70 threads, the

system’s reliability deteriorated considerably, with an

error rate climbing to 28.6%. This increase in errors

coupled with higher throughput indicates that, despite

good performance under moderate conditions, the ap-

plication approaches its stability limit under high con-

currency.

5.4 Stress Testing

Complementary to load testing, stress tests were de-

signed to evaluate the application’s resilience when

subjected to gradually increasing and sustained de-

mands (

Cih

ak, 2007). Utilizing also JMeter with

an initial conﬁguration of 10 threads and a ramp-up

period of 5 seconds, the test was executed continu-

ously in an “endless loop” mode. As thread count

increased over the course of testing (reaching up to

132 threads), the system began exhibiting instability.

We observed that the system became unstable beyond

approximately 90 concurrent threads (see Figure 5).

From this point on, persistent “503 Service Unavail-

able” errors were recorded. Even so, the system

showed acceptable tolerance up to that point. This

threshold thus represents the practical upper limit of

the application’s capacity on the Shinyapps.io free

tier.

Figure 5: Stress test results in the range of threads (88 to

111) where transitions between accepted and rejected re-

quests were found.

5.5 Usability Evaluation

In parallel with performance testing, we focus on

users’ experience (UX) and feedback when using

ClustSize. These tests record users’ behavior and

cognitive processes to understand their comfort in the

application (Aziz et al., 2021). In our case, UX was

assessed through a structured usability survey admin-

istered via Google Forms

to a sample of 25 users

(university students). The survey captured demo-

graphic data—including gender, age, and education

level—but, as well as detailed feedback on core us-

ability attributes, such as ease of understanding the

app, navigation efﬁciency, interface intuitiveness, re-

sponse time, clarity of the clustering results, and over-

all satisfaction (see Table 5). In general, the results

from the survey provided qualitative insights critical

for reﬁning the user interface and interaction ﬂows.

Table 5: Questions asked to measure the website’s usability

based on surveys.

ID Question

1 Select your gender.

2 Select your age.

3 Level of formal education.

4 How easy was it to understand how to use the app?

5 How would you rate the ease of navigation of the app?

6 Do you find the user interface intuitive?

7 Which of the following app features did you find confusing or

difficult to use?

8 How fast was the app’s loading time and the interface’s responses?

9 Did you experience any performance issues while using the app?

10 Was the presentation of the clustering results clear and

understandable?

11 How would you rate your overall satisfaction with the application?

12 Would you recommend this application to other users interested in

data analysis and clustering?

Figures 6, 7 and 8 present a summary of the user

responses. Figures 6 displays the demographic break-

down (gender and age), conﬁrming a diverse group

of respondents with adequate technical proﬁciency.

Figures 7 shows a stacked bar chart correlating re-

spondents’ formal education with perceived ease of

use; users with higher educational backgrounds gen-

erally reported the interface as intuitive and straight-

https://forms.gle/14Kb1d92e4ZRNVK28

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

488

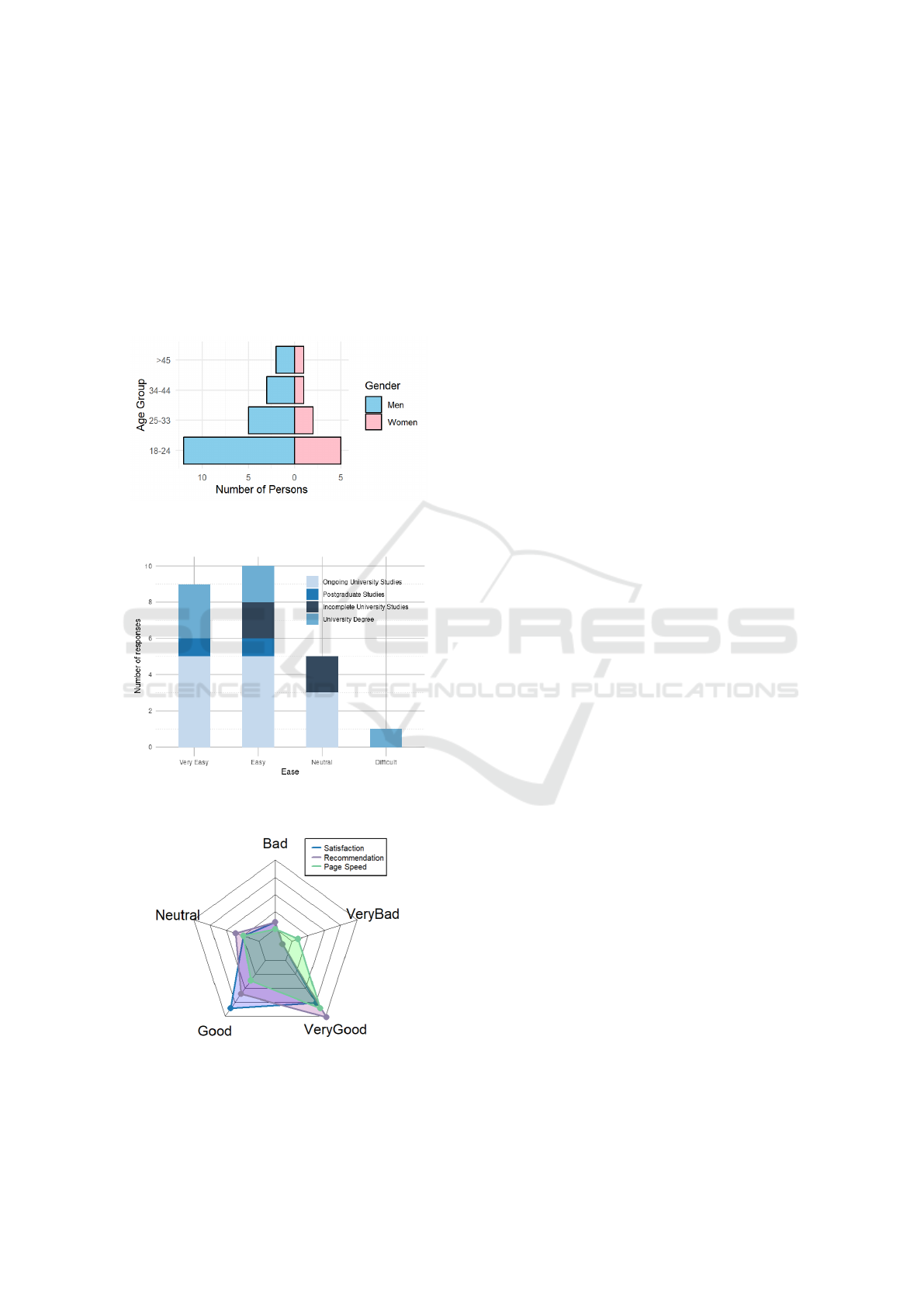
forward. Finally, Figure 8 summarizes key aspects

such as overall satisfaction, perceived response speed,

and willingness to recommend the application. The

majority of responses were positive, with most users

rating the application’s usability as “Good” or “Very

Good.” These results indicate that, despite some per-

formance limitations under extreme load conditions,

the overall user experience is robust and aligns with

the design goals of creating an accessible and interac-

tive data-analysis tool.

Figure 6: Demographic distribution of respondents by gen-

der and age range.

Figure 7: Stacked bar chart comparing respondents’ formal

education and perceived ease of use.

Figure 8: Spider graph of user perception regarding satis-

faction level, recommendation, and page speed.

6 CONCLUSIONS

In this paper, we have shown the practical viabil-

ity of integrating advanced size-constrained cluster-

ing algorithms—K-MedoidsSC and CSCLP—into a

user-friendly web application, ClustSize, built on

R Studio and the Shiny framework. The application

allows users to dynamically adjust parameters and

offers clustering visualizations, including interactive

PCA plots and detailed data tables. This empowers

users to explore complex datasets in real time while

ensuring clusters meet size requirements. Extensive

experimental evaluations conﬁrm that K-MedoidsSC

performs more efﬁciently than CSCLP in terms of

execution time and memory usage, particularly on

larger datasets, making it more suitable for interac-

tive applications on resource-limited platforms such

as Shinyapps.io.

Through targeted load and stress testing, we estab-

lished that the deployed application reliably supports

up to 50 concurrent users, with performance degrada-

tion and increased error rates observed at higher con-

currency levels due primarily to the inherent limita-

tions of the hosting environment. Furthermore, us-

ability evaluations (collected via structured surveys)

highlighted robust user satisfaction regarding inter-

face clarity, navigation, and response time.

Despite these positive outcomes, several chal-

lenges remain. The 1GB RAM cap on the free

Shinyapps.io tier restricts the processing of larger

datasets, and the CSCLP algorithm, in particular, strug-

gles to operate efﬁciently within these constraints.

These observations underscore the necessity for fur-

ther improvements in system scalability and resource

management. Exploring solutions like server-side op-

timization, cloud-based scaling, or containerization

might alleviate these constraints in future work. Ex-

tending the tool to handle unstructured data would

further enhance its applicability across various do-

mains.

ACKNOWLEDGEMENTS

This work was supported by IDEIAGEOCA Research

Group of Universidad Polit

ecnica Salesiana in Quito,

Ecuador.

REFERENCES

Aziz, N. S., Sulaiman, N. S., Hassan, W. N. I. T. M., Za-

karia, N. L., and Yaacob, A. (2021). A review of web-

site measurement for website usability evaluation. In

ClustSize: An Algorithmic Framework for Size-Constrained Clustering

489

Journal of Physics: Conference Series, volume 1874,

page 012045. IOP Publishing.

Bassil, J., Makhoul, A., Piranda, B., and Bourgeois, J.

(2023). Distributed size-constrained clustering algo-

rithm for modular robot-based programmable matter.

ACM Transactions on Autonomous and Adaptive Sys-

tems, 18(1):1–21.

Beeley, C. (2016). Web application development with R us-

ing Shiny. Packt Publishing Ltd.

Bischl, B., Casalicchio, G., Feurer, M., Hutter, F., Lang,

M., Mantovani, R. G., Van Rijn, J. N., and Van-

schoren, J. (2017). Openml benchmarking suites and

the OpenML100. stat, 1050:11.

Celebi, M. E. and Aydin, K. (2016). Unsupervised learning

algorithms, volume 9. Springer.

Cih

ak, M. (2007). Introduction to applied stress testing.

IMF Working Paper.

Draheim, D., Grundy, J., Hosking, J., Lutteroth, C., and We-

ber, G. (2006). Realistic load testing of web applica-

tions. In Conference on Software Maintenance and

Reengineering (CSMR’06), pages 11–pp. IEEE.

Ganganath, N., Cheng, C.-T., and Chi, K. T. (2014). Data

clustering with cluster size constraints using a mod-

iﬁed k-means algorithm. In 2014 International Con-

ference on Cyber-Enabled Distributed Computing and

Knowledge Discovery, pages 158–161. IEEE.

Hubert, L. and Arabie, P. (1985). Comparing partitions.

Journal of classiﬁcation, 2:193–218.

Jain, A. K. (2010). Data clustering: 50 years beyond k-

means. Pattern recognition letters, 31(8):651–666.

Johnson, S. C. (1967). Hierarchical clustering schemes.

Psychometrika, 32(3):241–254.

Malinen, M. I. and Fr

anti, P. (2014). Balanced k-means

for clustering. In Structural, Syntactic, and Statistical

Pattern Recognition: Joint IAPR International Work-

shop, S+ SSPR 2014, Joensuu, Finland, August 20-22,

2014. Proceedings, pages 32–41. Springer.

Park, H.-S. and Jun, C.-H. (2009). A simple and fast algo-

rithm for k-medoids clustering. Expert systems with

applications, 36(2):3336–3341.

R Core Team (2024). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria.

Royce, W. W. (1987). Managing the development of large

software systems: concepts and techniques. In Pro-

ceedings of the 9th international conference on Soft-

ware Engineering, pages 328–338.

Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P.,

Tiwari, A., Er, M. J., Ding, W., and Lin, C.-T. (2017).

A review of clustering techniques and developments.

Neurocomputing, 267:664–681.

Strehl, A. and Ghosh, J. (2002). Cluster ensembles—

a knowledge reuse framework for combining multi-

ple partitions. Journal of machine learning research,

3(Dec):583–617.

Tang, W., Yang, Y., Zeng, L., and Zhan, Y. (2019). Optimiz-

ing mse for clustering with balanced size constraints.

Symmetry, 11(3):338.

Vallejo-Huanga, D., Morillo, P., and Ferri, C. (2017). Semi-

supervised clustering algorithms for grouping scien-

tiﬁc articles. Procedia Computer Science, 108:325–

334.

Vanschoren, J., Van Rijn, J. N., Bischl, B., and Torgo,

L. (2014). OpenML: networked science in machine

learning. ACM SIGKDD Explorations Newsletter,

15(2):49–60.

Wagstaff, K., Cardie, C., Rogers, S., Schr

odl, S., et al.

(2001). Constrained k-means clustering with back-

ground knowledge. In Icml, volume 1, pages 577–584.

Zhang, S., Wong, H.-S., and Xie, D. (2014). Semi-

supervised clustering with pairwise and size con-

straints. In 2014 International Joint Conference on

Neural Networks (IJCNN), pages 2450–2457. IEEE.

Zhu, S., Wang, D., and Li, T. (2010). Data cluster-

ing with size constraints. Knowledge-Based Systems,

23(8):883–889.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

490