Fundamental Patterns for Composing Quantum Algorithms

Lavinia Stiliadou

, Johanna Barzen

, Martin Beisel

, Frank Leymann

and Benjamin Weder

University of Stuttgart, Institute of Architecture of Application Systems, Universit

atsstr. 38, 70569 Stuttgart, Germany

Keywords:

Quantum Computing, Pattern Languages, Quantum Algorithms.

Abstract:

Designing and implementing quantum algorithms is a time-consuming, complex, and error-prone task. As new

quantum algorithms are often published as scientiﬁc papers without sufﬁcient documentation and no available

software implementations, algorithm designers and software developers have to ﬁgure out the missing details

or redevelop parts of the quantum algorithm. Similar to classical programs, various quantum algorithms share

the same subroutines as building blocks to realize the required functionality. Therefore, these building blocks

have to be documented in a structured and easily understandable manner to foster their reuse and speed up

development. Patterns are a well-established concept for documenting proven solutions to recurring problems

and educating new developers. Hence, a pattern language capturing important concepts in the quantum com-

puting domain was established. It already contains an initial set of patterns documenting common building

blocks of quantum algorithms. In this paper, we extend the quantum computing pattern language by introduc-

ing ﬁve novel patterns, documenting fundamental building blocks to realize quantum algorithms.

1 INTRODUCTION

Quantum devices promise advancements in various

domains, such as ﬁnance, optimization, and cryp-

tography, by leveraging their ability to solve cer-

tain problems faster, with greater precision, or lower

energy consumption compared to classical comput-

ers (Nielsen and Chuang, 2010; Preskill, 2018). Due

to the high complexity of quantum computing, real-

izing quantum algorithms requires a thorough under-

standing of different topics, such as the encoding of

data for the quantum devices or the subroutines used

in quantum algorithms (Leymann and Barzen, 2020).

Moreover, there is also a lack of documentation

that provides quantum application developers with

the knowledge to understand existing quantum algo-

rithms, their building blocks, and corresponding im-

plementations. Thus, the required building blocks for

realizing quantum algorithms must be documented

in a comprehensive manner (Gilliam et al., 2019).

An established way to capture proven solutions

for recurring problems is patterns (Alexander et al.,

1977). Patterns abstractly document solution strate-

https://orcid.org/0009-0001-0957-6108

https://orcid.org/0000-0001-8397-7973

https://orcid.org/0000-0003-2617-751X

https://orcid.org/0000-0002-9123-259X

https://orcid.org/0000-0002-6761-6243

gies for problems occurring in a speciﬁc context.

Thereby, patterns provide a technology and problem-

independent description for solving problems that

can be applied generally. Additionally, they explain

why a problem is difﬁcult to solve and what conse-

quences might result from applying a pattern. To doc-

ument fundamental concepts in the quantum comput-

ing domain, Leymann (2019) introduced a pattern lan-

guage for quantum algorithms. Similar to other pat-

tern languages, the quantum computing pattern lan-

guage can be used to automatically generate soft-

ware artifacts utilizing suitable pattern implementa-

tions (Vietz et al., 2025).

Since pattern languages continuously evolve, it is

important to regularly update and expand the pattern

language to reﬂect the latest advances. Therefore, in

this paper, we extend the quantum computing pattern

language with ﬁve new patterns that capture funda-

mental building blocks for quantum algorithms.

The remainder of this paper is as follows: In Sec-

tion 2, fundamentals about quantum algorithms and

the used pattern format are introduced. Section 3

documents the newly introduced patterns for build-

ing quantum algorithms and Section 4 discusses their

usage and potential limitations. In Section 5 related

work is presented, and Section 6 concludes the paper.

Stiliadou, L., Barzen, J., Beisel, M., Leymann, F. and Weder, B.

Fundamental Patterns for Composing Quantum Algorithms.

DOI: 10.5220/0013555600004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 61-69

ISBN: 978-989-758-761-0

2 FUNDAMENTALS

This section brieﬂy introduces the fundamentals of

gate-based quantum computing and discusses the pat-

tern format and the applied pattern authoring process.

2.1 Gate-Based Quantum Computing

The currently predominant paradigm for realizing

quantum devices is gate-based quantum comput-

ing (Nimbe et al., 2021; Pfaendler et al., 2024). To

execute quantum algorithms on gate-based quantum

devices, they need to be implemented as so-called

quantum circuits (Nielsen and Chuang, 2010). These

circuits deﬁne a sequence of operations, called gates,

that manipulate the qubits and thereby modify the

state of the quantum system. To extract classical infor-

mation about a quantum system the state of its qubits

must be measured (Nielsen and Chuang, 2010). Mea-

suring a qubit causes its quantum state to collapse,

making it an irreversible operation that prevents fur-

ther computations using the measured qubit’s state.

2.2 Pattern Format & Authoring

Method

To facilitate the understanding of patterns within a

pattern language, typically a uniform pattern format

is used (Alexander et al., 1977; Fehling et al., 2014).

In this paper, we adopt the pattern format previously

used for documenting the quantum computing pat-

terns, which is organized as follows:

Each pattern is identiﬁed by a unique name within

the pattern language. Additionally, each pattern is as-

sociated with a mnemonic icon to aid in visual recog-

nition. The problem addressed by the pattern is de-

scribed in the problem statement, followed by an out-

line of the context in which the problem occurs. Af-

terward, the forces that complicate solving the prob-

lem are discussed. The solution section presents a

proven strategy for solving the problem, accompanied

by a corresponding solution sketch that visualizes the

essence of the solution. In the result section, the con-

sequences of applying the solution are discussed and

potential next steps for handling them are suggested.

To facilitate the navigation through the pattern lan-

guage, each pattern is semantically linked to related

patterns, e.g., to patterns that are commonly used in

combination. Lastly, the known uses section discusses

several real-world applications of the pattern.

In this paper, we focus on patterns related to build-

ing blocks for quantum algorithms. They were identi-

ﬁed by examining implementations and analyzing the

literature for building blocks that were utilized to im-

plement different quantum algorithms. These build-

ing blocks were then ﬁltered, documented, and iter-

atively reﬁned to extract a set of novel patterns that

can be used to understand and build quantum algo-

rithms. While different methods for identifying and

documenting patterns exist, we follow the approach

presented by Fehling et al. (2014). Their approach

comprises a pattern identiﬁcation, authoring, and ap-

plication phase, which emphasizes the incremental re-

ﬁnement of patterns.

3 PATTERNS FOR BUILDING

QUANTUM ALGORITHMS

In this section, we provide an overview of the existing

quantum computing pattern language and introduce

ﬁve novel patterns documenting fundamental building

blocks for realizing quantum algorithms.

3.1 Overview of the Quantum

Computing Pattern Language

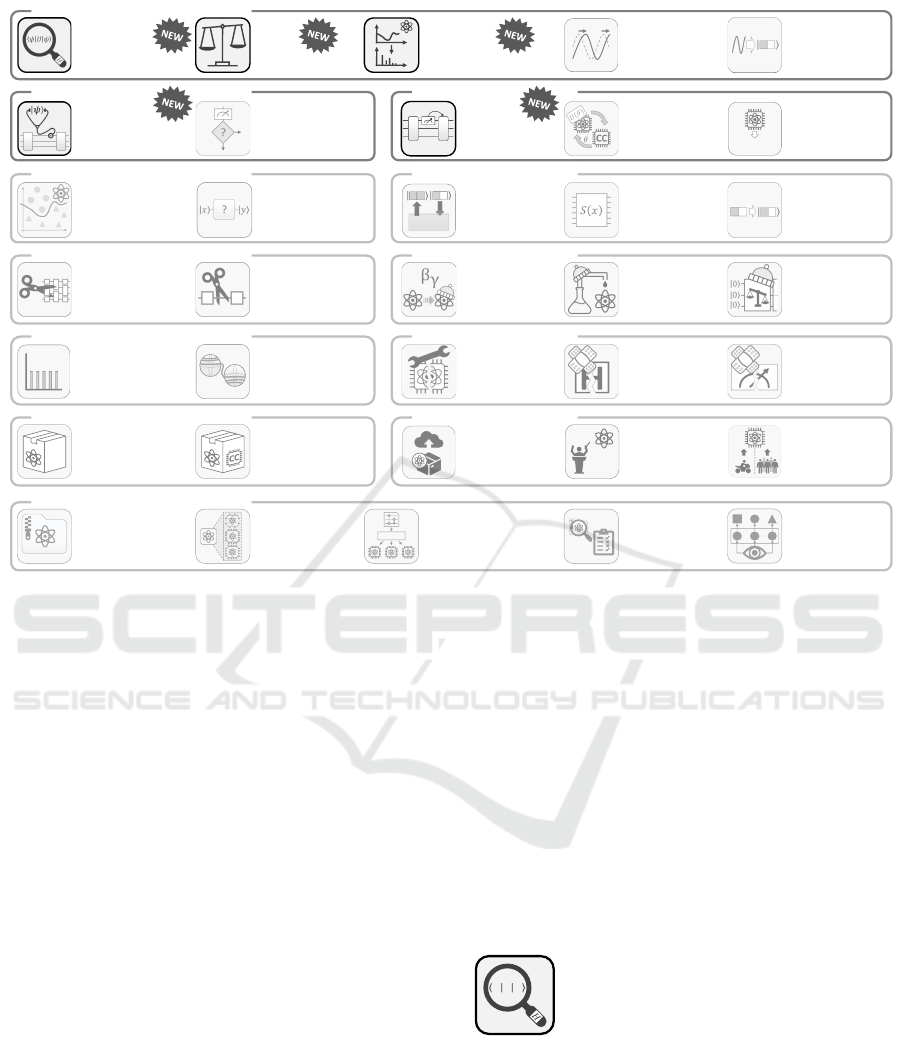
Figure 1 gives an overview of the quantum computing

pattern language, showcasing both existing patterns

as well as the novel patterns presented in this paper.

Each pattern is assigned to one category depending

on the related phase in the quantum software develop-

ment lifecycle (Weder et al., 2022). In the following,

the different pattern categories are presented:

First, the unitary transformations (Weigold et al.,

2021a) patterns document subroutines that can be

used as building blocks for realizing different quan-

tum algorithms. The measurement patterns (Weigold

et al., 2021a) describe techniques for extracting

classical data from quantum states, ensuring that

results from quantum computations can be inter-

preted and used effectively. Strategies for distributing

computations across quantum and classical hardware

are discussed by the program ﬂow patterns (Weigold

et al., 2021b). The quantum machine learning

patterns (Stiliadou et al., 2025) provide insights

into the development of quantum algorithms that

leverage quantum mechanics to enhance machine

learning tasks. To encode classical data into quantum

circuits, the data encodings patterns (Weigold et al.,

2021a) detail state preparation routines essential for

embedding classical information into quantum states.

Techniques to partition large quantum circuits into

smaller ones, which can be executed with higher pre-

cision on current quantum devices, are documented

in the circuit cutting patterns (Bechtold et al., 2023).

IQSOFT 2025 - 1st International Conference on Quantum Software

Biased

Initial

State

Development

...

Hybrid

Module

Quantum

Module

Readout

Error

Mitigation

Execution

Error Handling

Warm-Starting

...

Pre-

deployed

Execution

Prioritized

Execution

Quantum States

Circuit Cutting

Quantum Machine Learning





 





Quantum

Kernel

Estimator

Measurement

...

Variational

Parameter

Transfer

Orchestrated

Execution

Data Encodings

Basis

Encoding

Quantum

Classification

Quantum

Neural

Network

Variational

Quantum

Algorithm

Pre-Trained

Feature

Extractor

Operations

Quantum

Application

Archive

Quantum

Application

Testing

Quantum

Hardware

Selection

Unified

Observability

Unified

Execution

Mid-Circuit

Measurement

Circuit

Cutting

Dynamic

Circuit

Creating

Entanglement

Post-Selective

Measurement

QRAM

Encoding



QRAM

Schmidt

Decom-

position

Error

Correction

Gate Error

Mitigation

Wire

Cut

Uniform

Superposition

Program Flow

Quantum

Phase

Estimation

Quantum

Fourier

Transform

...

Unitary Transformations

Phase

Shift

Hadamard

Test

SWAP

Test

 



 



Figure 1: Overview of the quantum computing pattern language with some existing patterns (light gray) and the new patterns

introduced in this paper (dark gray).

The warm-starting patterns (Truger et al., 2024)

showcase techniques to improve the performance of

quantum algorithms by initializing them with favor-

able starting points. To realize quantum algorithms,

an understanding of quantum states (Leymann,

2019) is necessary. Approaches to mitigate noise in

today’s quantum devices are summarized in the error

handling patterns (Beisel et al., 2022). This category

describes how they can be created and potential

application areas. The development patterns (B

uhler

et al., 2023) summarize best practices for developing

hybrid quantum applications. An important aspect

of developing such applications is understanding

how quantum circuits are executed. These methods

are documented in the execution patterns (Georg

et al., 2023). Further, the operations patterns (Beisel

et al., 2025b) document how to execute, monitor, and

manage quantum applications.

In this work, we introduce ﬁve novel patterns

describing fundamental building blocks for realizing

various quantum algorithms: The HADAMARD TEST

pattern focuses on estimating the real and imaginary

parts of the expectation value of a unitary operator

with respect to a quantum state. Further, the SWAP

TEST pattern describes the computation of the

similarity of two quantum states. The QUANTUM

FOURIER TRANSFORM pattern addresses the chal-

lenge of efﬁciently transforming quantum states from

the computational basis to the Fourier basis. The

MID-CIRCUIT MEASUREMENT pattern documents

an approach for extracting partial information from

a quantum device while a circuit execution is still

running. Finally, the DYNAMIC CIRCUIT pattern de-

scribes how quantum computations can be modiﬁed

during runtime based on intermediate information

about a part of the quantum state.

3.2 Hadamard Test

𝝍 𝑼 𝝍

Problem: How to calculate the expec-

tation value of a unitary operator for a

given quantum state?

Context: Given a unitary operator U acting on n

qubits, and let |ψ⟩ be a n-qubit quantum state. Then,

the expectation value ⟨ψ|U |ψ⟩ should be estimated.

Forces: Determining the expectation value classically

is computationally expensive and scales exponentially

with the number of qubits (Bravyi and Gosset, 2016).

Quantum devices enable solving this problem more

efﬁciently (Aharonov et al., 2006). However, using to-

day’s quantum devices also leads to additional chal-

Fundamental Patterns for Composing Quantum Algorithms

𝑈

𝐻

Retrieve Re( 𝜓 𝑈 𝜓 )

ȁ ۧ

𝜓

ȁ ۧ

Retrieve Im( 𝜓 𝑈 𝜓 )

ȁ ۧ

𝜓

ȁ ۧ

𝑆

†

𝐻

𝑈

𝐻

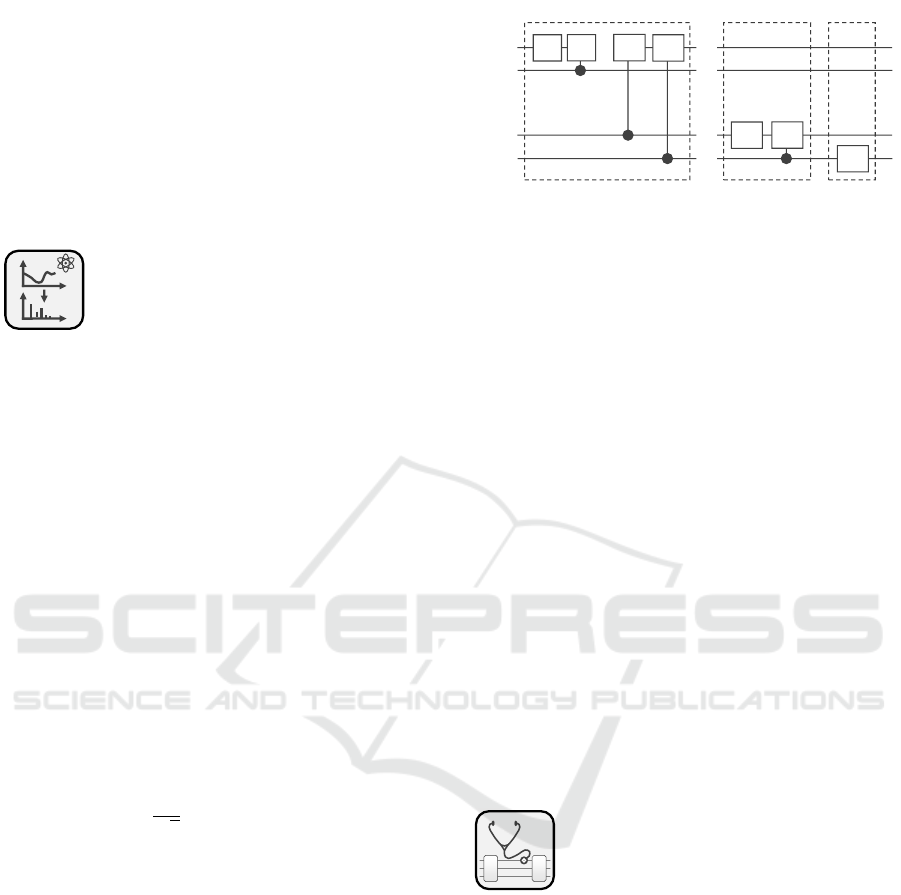
Figure 2: Solution sketch for the HADAMARD TEST pattern.

lenges. For example, large quantum circuits can not

be executed successfully, and results are prone to er-

rors (Preskill, 2018).

Solution: Figure 2 gives an overview of the structure

of the quantum circuit, which is required to perform

a Hadamard test. The quantum circuit requires one

ancilla qubit on which a Hadamard gate is applied

to bring it into an equal superposition. Subsequently,

depending on whether the real (see a) or imaginary

part (see b) of ⟨ψ|U |ψ⟩ should be retrieved, a S

†

gate

is added. Next, the unitary operator U is applied in

a controlled manner by using the ancilla qubit as the

control qubit. Due to a so-called phase-kickback, the

information is transferred from the target register to

the control qubit when entangling the qubits with the

controlled U gate (Ossorio-Castillo et al., 2023). Fi-

nally, another Hadamard gate is applied to the ancilla

qubit enabling the retrieval of the expectation value

⟨ψ|U |ψ⟩ by measuring the ancilla qubit.

Result: The real or imaginary part of the expectation

value ⟨ψ|U |ψ⟩ is the output after measuring the an-

cilla qubit. Depending on the required upper bound

of the absolute error, the number of samples must be

increased.

Related Patterns: The HADAMARD TEST can be

implemented using the QUANTUM MODULE pat-

tern (B

uhler et al., 2023), i.e., separating the inputs

from the code generation logic required to create the

quantum circuit realizing the Hadamard test. For sep-

arable input quantum states |ψ⟩, the SWAP TEST pat-

tern can be emulated by (i) separating the input state

into two separate quantum states and by (ii) utilizing

the SWAP gate as the unitary operator U within the

HADAMARD TEST.

Known Uses: The Hadamard test is utilized within

the Aharonov–Jones–Landau algorithm to compute

the Jones polynomial (Aharonov et al., 2006). Fur-

thermore, the Hadamard test can also be used for vari-

ational quantum algorithms to determine the gradient

of the objective function (Harrow and Napp, 2021).

Arad and Landau (2010) utilize the Hadamard test in

the context of tensor networks. Xu et al. (2022) em-

ploy the Hadamard test as the measuring method for

a variational quantum support vector machine.

ȁ ۧ

𝜑

ȁ ۧ

𝜑

ȁ ۧ

𝜑

𝑛

…

ȁ ۧ

𝜓

ȁ ۧ

𝜓

ȁ ۧ

𝜓

𝑛

…

𝐻 𝐻

Figure 3: Solution sketch for the SWAP TEST pattern.

3.3 SWAP Test

ȁ ۧ

𝝋

ȁ ۧ

𝝍

Problem: How to evaluate how simi-

lar two given quantum states are to each

other?

Context: Given two n-qubit quantum states |ϕ⟩ and

|ψ⟩. Then, the similarity between these states should

be calculated.

Forces: The similarity of two quantum states may

inﬂuence the processing of a quantum algorithm.

Performing classical measurements is unsuitable for

comparing quantum states as the states are destroyed

and can not be used for further computations.

Solution: Perform the SWAP test to determine

the similarity of the two given quantum states

|ϕ⟩ and |ψ⟩. The structure of the quantum circuit,

which is required to perform a SWAP test, is de-

picted in Figure 3. It requires one ancilla qubit

on which a Hadamard gate is applied. Next, a

sequence of controlled SWAP operators is applied

to each qubit of the two states using the ancilla

qubit as the control qubit. For example, the ﬁrst

controlled SWAP operation is performed between

|ϕ

⟩ and |ψ

⟩. Finally, another Hadamard gate is

applied to the ancilla qubit, leading to the state:

|0⟩(|φ⟩|ψ⟩+ |ψ⟩|φ⟩) +

|1⟩(|φ⟩|ψ⟩−|ψ⟩|φ⟩).

Result: After the measurement of the ancilla qubit,

the outcome determines the similarity between the

states |φ⟩ and |ψ⟩. If the states are identical, the mea-

surement of the ancilla bit results in 0 with probability

1. In contrast, if the states are orthogonal, the mea-

surement results in 0 or 1 with an equal probability of

0.5.

Related Patterns: The QUANTUM CLASSIFICATION

pattern (Stiliadou et al., 2025) can utilize the SWAP

TEST to estimate the distances between two points.

The SWAP TEST can be realized as a QUANTUM

MODULE, and its functionality can be provided via a

CLASSICAL-QUANTUM INTERFACE to ease its inte-

gration with additional classical functionality (B

uhler

et al., 2023).

Known Uses: The SWAP test was initially introduced

by Buhrman et al. (2001). Gitiaux et al. (2022) show

IQSOFT 2025 - 1st International Conference on Quantum Software

how to generalize the SWAP test for an arbitrary num-

ber m of states to compare using O(log(m)) ancilla

qubits. Foulds et al. (2021) adapt the SWAP test to en-

able checking the presence of entanglement and show

how it can be used to distinguish different entangle-

ment classes. Zhao et al. (2019) discuss how quantum

neural networks can be built using the SWAP test.

3.4 Quantum Fourier Transform (QFT)

Problem: How to extract frequencies

from a function using a quantum device?

Context: Frequencies need to be extracted from func-

tion values, which are given at N distinct points to

identify characteristics such as periodicity and distri-

bution of the frequencies.

Forces: The best known classical implementation of

a Fourier transform, the so-called Fast Fourier Trans-

form (FFT) is computationally expensive as it re-

quires O(N log N) operations for a vector that con-

tains N data points of a function (Camps et al., 2020).

While quantum computing enables solving this prob-

lem more efﬁciently, the number of operations ex-

ecutable in sequence on current quantum devices is

limited due to high error rates and short decoherence

times (Preskill, 2018).

Solution: The QFT extracts frequencies from a n-

qubit quantum register |x⟩ = |x

n−1

,. .. ,x

⟩, where

n = logN. x is interpreted as a decimal number and

∈{0, 1} are the binary digits of x. In the QFT, each

qubit |x

⟩ is transformed as follows:

⟩ 7→

√



|0⟩+ e

2πix/2

|1⟩



The required stages are illustrated in Figure 4. QFT

involves n stages, one for each qubit in the quantum

, operations are performed solely

on qubit x

n−j

, which involves a Hadamard gate, fol-

lowed by controlled R

,. .. ,R

n+1−j

gates, except in

stage S

, where only the Hadamard gate is applied.

The R

gate is controlled by qubit x

n+1−j−k

to realize

the phase e

2πi/2

. The gate R

has the form:



1 0

0 e

2πi/2



, for 2 ≤ k ≤n

This circuit requires O(n

) = O((log N)

) operations,

as each stage S

involves a single Hadamard operation

and n −1 + j controlled rotations.

Result: The QFT provides an exponential speedup

compared to the FFT. After applying the QFT, the

quantum state is transformed into the Fourier basis. If

ȁ ۧ

𝑥

𝑛−1

ȁ ۧ

𝑥

𝑛−2

…

ȁ ۧ

𝑥

ȁ ۧ

𝑥

…

𝑅

𝑛−1

𝑅

𝑛

𝐻

𝑅

𝐻

…

𝑆

𝑛−1

𝑆

𝑛

𝐻

…

Figure 4: Solution sketch for the QUANTUM FOURIER

TRANSFORM pattern.

the QFT is applied to a quantum state encoding a pe-

riodic function with period p, the resulting state has

a high probability of measuring y, where y is a mul-

tiple of N/p (Barzen and Leymann, 2022; Dixit and

Jian, 2022). Due to the controlled phase gates, QFT

requires a high connectivity between the qubits.

Related Patterns: The PHASE SHIFT pattern (Ley-

mann, 2019) is used to implement the modiﬁcation

of the phase. To reduce the depth of the quantum cir-

cuit implementing the QFT, the DYNAMIC CIRCUIT

pattern can be utilized (B

aumer et al., 2024a). The

QUANTUM PHASE ESTIMATION pattern (Weigold

et al., 2021a) uses QFT to estimate the eigenvalues

of a unitary operator.

Known Uses: Shor’s Algorithm extracts the period of

a modular exponentiation function using QFT (Shor,

1994). Dixit and Jian (2022) use QFT to estimate fre-

quencies from driving cycles of vehicles, i.e., graphs

visualizing the speed of the vehicle over time (Dixit

and Jian, 2022). Roncallo et al. (2023) use QFT to

compress digital images.

3.5 Mid-Circuit Measurement

ȁ ۧ

𝝍

Problem: How to extract partial infor-

mation from a quantum device while a

circuit execution is still running?

Context: During the execution of a quantum circuit,

intermediate results, i.e., information about the state

of one or multiple qubits, should be extracted before

the circuit execution ﬁnally terminates.

Forces: As quantum devices only provide a limited

number of qubits, these qubits must be utilized ef-

ﬁciently, e.g., by reusing ancilla qubits that are no

longer required. When measuring a qubit that is en-

tangled with other qubits, the measurement does not

only collapse the state of the measured qubit but also

irreversibly impacts the quantum states of the entan-

gled qubits.

Solution: Incorporate so-called mid-circuit measure-

ments into the quantum circuit, i.e., measurements be-

fore the quantum circuit execution terminates. As il-

Fundamental Patterns for Composing Quantum Algorithms

…

Figure 5: Overview of the solution sketch for the MID-

CIRCUIT MEASUREMENT pattern.

lustrated in Figure 5 various quantum operations are

performed on different qubits initialized in the |0⟩

state, resulting in an intermediate quantum state. A

subset of m qubits is then measured, yielding a mea-

surement outcome s ∈ {0, 1}

⊗m

, extracting classical

information about a part of this intermediate quantum

state. Afterwards, the execution of the quantum cir-

cuit continues. For example, in Figure 5 a mid-circuit

measurement is performed on the last qubit, measur-

ing a classical 0 and collapsing the state of the qubit

into the |0⟩ state.

Result: Mid-circuit measurements provide informa-

tion about the intermediate states of the measured

qubits. Each measured qubit collapses into the state

|0⟩ or |1⟩, which can, e.g., be used to reset them by

applying a controlled X operation after the measure-

ment (Xu et al., 2023). After resetting the qubits, they

can be reused for further computations. By perform-

ing mid-circuit measurements on a qubit, the states of

qubits that are entangled with the measured qubit are

inﬂuenced. The states of qubits that are not entangled

with the measured qubits are preserved.

Related Patterns: The DYNAMIC CIRCUIT pat-

tern uses the MID-CIRCUIT MEASUREMENT pattern

to retrieve intermediate information for dynamically

modifying quantum computations during runtime.

Known Uses: Mid-circuit measurements can be used

to reset a qubit conditionally (Koh et al., 2024). Govia

et al. (2023) analyze how mid-circuit measurements

affect the states of topologically connected qubits.

Smith et al. (2024) present a constant-depth state

preparation of matrix product states using mid-circuit

measurements and feedforward operations.

3.6 Dynamic Circuit

Problem: How to modify a quantum

computation during runtime based on

intermediate information about a part of

the quantum state?

Context: A quantum circuit must be modiﬁed based

on intermediate information about a part of the quan-

tum state.

Forces: Measuring a qubit causes its state to collapse

and breaks the entanglement between the measured

qubit and the entangled qubits. Operations between

…

𝑈

…

𝑈

…

Figure 6: Overview of the solution sketch for the DYNAMIC

CIRCUIT pattern.

qubits that are far apart from each other require a

lot of intermediate SWAP operations, increasing the

depth of the circuit. The low decoherence times of

current quantum devices limit the maximum execu-

tion time of quantum circuits.

Solution: To modify a quantum computation during

runtime based on intermediate information about a

part of the quantum state, deﬁne a dynamic quantum

circuit that utilizes mid-circuit measurements as well

as classical processing. Classical processing can ei-

ther be a feedforward of the measurement results or

a more complex computation that utilizes the mea-

surement results to adaptively apply or skip speciﬁc

quantum operations. Figure 6 exemplarily showcases

a dynamic circuit using feedforward: First, the quan-

tum circuit performs a sequence of operations. Then,

a mid-circuit measurement is performed on the ﬁrst

qubit and the measurement result is used for classi-

cal processing. Based on the outcome of the classical

processing, it is determined if the gate U

or U

shall

be applied. If the outcome of the classical processing

is 1, then U

is applied; if it is 0, then U

is applied.

Result: Dynamic circuits enable the development of

algorithms and optimization routines that require in-

termediate information about a part of the quantum

state. The classical processing performed after the

mid-circuit measurement must be faster than the de-

coherence time of the quantum device so that the

quantum state is not lost before the quantum compu-

tation can be modiﬁed and completed. Additionally,

feedforward of measurement results leads to constant

latency for executing conditional operations, while

more complex real-time computations introduce ad-

ditional variable delays depending on their complex-

ity (Gupta et al., 2024).

Related Patterns: The MID-CIRCUIT MEASURE-

MENT pattern is used to extract intermediate infor-

mation about the quantum states during runtime. Dy-

namic circuits can be utilized with the INITIALIZA-

TION pattern (Leymann, 2019) to reduce the depth

of the quantum circuits. Combining the CIRCUIT

CUTTING pattern (Bechtold et al., 2023) and the

DYNAMIC CIRCUIT pattern can reduce the number

of cuts required to split a quantum circuit (Pawar

et al., 2023). Further, dynamic circuits can be used

IQSOFT 2025 - 1st International Conference on Quantum Software

as ansatzes for the VARIATIONAL QUANTUM ALGO-

RITHM pattern (Weigold et al., 2021b) as they are free

of barren plateaus (Deshpande et al., 2024).

Known Uses: Dynamic circuits can be incorporated

into error correction techniques to reduce errors accu-

mulated during the quantum computation (Niu et al.,

2024). Another application area is to reduce the depth

of QFT circuits by utilizing dynamic circuits (B

aumer

et al., 2024a). Distant qubits can be entangled using

dynamic circuits, drastically reducing the number of

required SWAP operations and, therefore, the depth

of the quantum circuit (B

aumer et al., 2024b).

4 DISCUSSION

Patterns are commonly applied to solve real-world

problems. Due to the interdisciplinary nature of quan-

tum computing, establishing common knowledge be-

tween the different stakeholders is especially impor-

tant. As stated above, transferring this knowledge

into executable quantum applications is a complex,

time-consuming, and error-prone task. To facilitate

the development of quantum applications, various ap-

proaches to automate this process have been intro-

duced: Vietz et al. (2025) present an approach to auto-

mate the identiﬁcation of suitable patterns for a given

problem description. These patterns can be used to

generate a quantum application to solve this prob-

lem. Thus, in this work, we extend the set of usable

patterns, enhancing the capabilities of the framework.

Beisel et al. (2025a) uses the quantum computing pat-

terns to automatically generate quantum workﬂows.

While mid-circuit measurements can provide dif-

ferent beneﬁts, such as reducing circuit depth, they are

currently not supported by all quantum devices. This

limits the general applicability of the MID-CIRCUIT

MEASUREMENT pattern. Similar limitations apply to

the DYNAMIC CIRCUIT pattern, as it relies on the

availability of mid-circuit measurements and real-

time classical processing. While dynamic circuits are

a promising concept, they are currently only sup-

ported by a small number of quantum programming

frameworks, such as Qiskit or Pennylane.

5 RELATED WORK

This work introduces patterns for building quantum

algorithms that extend the existing quantum comput-

ing pattern language as discussed in Section 3.1. Var-

ious works have explored different aspects of quan-

tum computing, but they do not follow the pattern for-

mat established by Alexander et al. (1977): Baczyk

et al. (2024) document patterns that assist in architec-

tural decision-making for quantum applications. Sim-

ilarly, Khan et al. (2023) identify a range of architec-

ture design patterns for quantum applications through

a systematic literature survey. A variety of patterns for

building quantum circuits were introduced: Gilliam

et al. (2019) present a dictionary for building quantum

algorithms, which aims to avoid linear algebra and

quantum mechanics. While they include QFT in their

dictionary, they do not describe it as a pattern and

only mention it as an alternative to classical Fourier

transform. Huang and Martonosi (2019) apply quan-

tum programming patterns to ﬁnd bugs in quantum

circuits. Additionally, Guo et al. (2024) present a set

of patterns tailored for deﬁning ans

atze in variational

quantum algorithms. However, they do not include

mid-circuit measurements, which are necessary to re-

alize dynamic circuits that have been proven to be bar-

ren plateau-free (Deshpande et al., 2024). To evalu-

ate the real-world adoption of the quantum computing

pattern language, P

erez-Castillo et al. (2024) investi-

gate quantum software repositories, searching for in-

stances of pattern usage. However, their analysis is

limited to only ﬁve patterns.

To reduce the manual effort needed to implement

the abstractly documented solutions described by pat-

terns, Falkenthal et al. (2017) introduced the concept

of so-called concrete solutions. Concrete solutions

implement the solution strategy provided by patterns

for a speciﬁc use case utilizing a certain technology.

These concrete solutions can be employed as reusable

building blocks for realizing applications.

6 CONCLUSION AND OUTLOOK

Quantum algorithms are often composed utilizing

reusable building blocks. However, these building

blocks typically lack suitable documentation and

proper implementations that can be reused. To over-

come these issues, in this paper, we document ﬁve

novel patterns summarizing fundamental building

blocks for quantum algorithms. The patterns are in-

corporated into the quantum computing pattern lan-

guage, which is publicly available in the Pattern

Atlas (Kipu Quantum, 2025), a tool for author-

ing and sharing patterns from different pattern lan-

guages (Leymann and Barzen, 2021).

New quantum algorithms and corresponding soft-

ware tools are developed by researchers in industry

and academia. Thus, in future work, we plan to ana-

lyze new developments to identify best practices that

can be documented as patterns and included in the

quantum computing pattern language.

Fundamental Patterns for Composing Quantum Algorithms

ACKNOWLEDGEMENTS

This work was partially funded by the BMWK

projects EniQmA (01MQ22007B) and SeQuenC

(01MQ22009B).

REFERENCES

Aharonov, D., Jones, V., and Landau, Z. (2006). A Poly-

nomial Quantum Algorithm for Approximating the

Jones Polynomial. In Proceedings of the 38

annual

ACM symposium on Theory of Computing, pages 427–

436.

Alexander, C., Ishikawa, S., and Silverstein, M. (1977).

A Pattern Language: Towns, Buildings, Construction.

Oxford University Press.

Arad, I. and Landau, Z. (2010). Quantum computation and

the evaluation of tensor networks. SIAM Journal on

Computing, 39(7):3089–3121.

Baczyk, M., P

erez-Castillo, R., and Piattini, M. (2024).

Towards a Framework of Architectural Patterns for

Quantum Software Engineering. In Proceedings of the

International Workshop on Quantum Software En-

gineering and Technology (Q-SET), volume 2, pages

228–233.

Barzen, J. and Leymann, F. (2022). Continued Fractions

and Probability Estimations in Shor’s Algorithm: A

Detailed and Self-Contained Treatise. AppliedMath,

2(3):393–432.

aumer, E., Tripathi, V., Seif, A., Lidar, D., and Wang, D. S.

(2024a). Quantum Fourier transform using dynamic

circuits. Physical review letters, 133(15):150602.

aumer, E., Tripathi, V., Wang, D. S., Rall, P., Chen, E. H.,

Majumder, S., Seif, A., and Minev, Z. K. (2024b).

Efﬁcient long-range entanglement using dynamic cir-

cuits. PRX Quantum, 5(3).

Bechtold, M., Barzen, J., Beisel, M., Leymann, F., and

Weder, B. (2023). Patterns for Quantum Circuit Cut-

ting. In Proceedings of the 30

Conference on Pattern

Languages of Programs (PLoP). HILLSIDE.

Beisel, M., Barzen, J., Leymann, F., Stiliadou, L., Vietz, D.,

and Weder, B. (2025a). Pattern-based Generation and

Adaptation of Quantum Workﬂows. In Proceedings

of the 47

International Conference on Software En-

gineering (ICSE). Springer.

Beisel, M., Barzen, J., Leymann, F., Truger, F., Weder, B.,

and Yussupov, V. (2022). Patterns for Quantum Error

Handling. In Proceedings of the 14

International

Conference on Pervasive Patterns and Applications

(PATTERNS), pages 22–30. Xpert Publishing Services

(XPS).

Beisel, M., Barzen, J., Leymann, F., and Weder, B. (2025b).

Operations Patterns for Hybrid Quantum Applica-

tions. In Proceedings of the 15

International Con-

ference on Cloud Computing and Services Science

(CLOSER). SciTePress.

Bravyi, S. and Gosset, D. (2016). Improved Classical Sim-

ulation of Quantum Circuits Dominated by Clifford

Gates. Physical review letters, 116(25):250501.

uhler, F., Barzen, J., Beisel, M., Georg, D., Leymann, F.,

and Wild, K. (2023). Patterns for Quantum Software

Development. In Proceedings of the 15

Interna-

tional Conference on Pervasive Patterns and Appli-

cations (PATTERNS), pages 30–39. Xpert Publishing

Services (XPS).

Buhrman, H., Cleve, R., Watrous, J., and De Wolf, R.

(2001). Quantum Fingerprinting. Physical review let-

ters, 87(16):167902.

Camps, D., Van Beeumen, R., and Yang, C. (2020). Quan-

tum Fourier transform revisited. Numerical Linear Al-

gebra with Applications, 28(1).

Deshpande, A., Hinsche, M., Najaﬁ, S., Sharma, K., Sweke,

R., and Zoufal, C. (2024). Dynamic parameterized

quantum circuits: expressive and barren-plateau free.

arXiv:2411.05760.

Dixit, V. and Jian, S. (2022). Quantum Fourier transform to

estimate drive cycles. Scientiﬁc Reports, 12(1):654.

Falkenthal, M., Barzen, J., Breitenb

ucher, U., and Leymann,

F. (2017). Solution Languages: Easing Pattern Com-

position in Different Domains. International Journal

on Advances in Software, 10(3):263–274.

Fehling, C., Barzen, J., Breitenb

ucher, U., and Leymann,

F. (2014). A Process for Pattern Identiﬁcation, Au-

thoring, and Application. In Proceedings of the 19

European Conference on Pattern Languages of Pro-

grams (EuroPLoP). ACM.

Foulds, S., Kendon, V., and Spiller, T. (2021). The

controlled SWAP test for determining quantum en-

tanglement. Quantum Science and Technology,

6(3):035002.

Georg, D., Barzen, J., Beisel, M., Leymann, F., Obst, J., Vi-

etz, D., Weder, B., and Yussupov, V. (2023). Execution

Patterns for Quantum Applications. In Proceedings of

the 18

International Conference on Software Tech-

nologies (ICSOFT), pages 258–268. SciTePress.

Gilliam, A., Venci, C., Muralidharan, S., Dorum, V., May,

E., Narasimhan, R., and Gonciulea, C. (2019). Foun-

dational Patterns for Efﬁcient Quantum Computing.

arXiv:1907.11513.

Gitiaux, X., Morris, I., Emelianenko, M., and Tian, M.

(2022). Swap test for an arbitrary number of quantum

states. Quantum Information Processing, 21(10):344.

Govia, L. C. G., Jurcevic, P., Wood, C. J., Kanazawa, N.,

Merkel, S. T., and McKay, D. C. (2023). A ran-

domized benchmarking suite for mid-circuit measure-

ments. New Journal of Physics, 25(12):123016.

Guo, X., Muta, T., and Zhao, J. (2024). Quantum Circuit

Ansatz: Patterns of Abstraction and Reuse of Quan-

tum Algorithm Design. arXiv:2405.05021.

Gupta, R. S., Sundaresan, N., Alexander, T., Wood, C. J.,

Merkel, S. T., Healy, M. B., Hillenbrand, M., Jochym-

O’Connor, T., Wootton, J. R., Yoder, T. J., Cross,

A. W., Takita, M., and Brown, B. J. (2024). Encoding

a magic state with beyond break-even ﬁdelity. Nature,

625(7994):259–263.

IQSOFT 2025 - 1st International Conference on Quantum Software

Harrow, A. W. and Napp, J. C. (2021). Low-Depth Gradi-

ent Measurements Can Improve Convergence in Vari-

ational Hybrid Quantum-Classical Algorithms. Phys-

ical review letters, 126(14):140502.

Huang, Y. and Martonosi, M. (2019). Statistical Assertions

for Validating Patterns and Finding Bugs in Quantum

Programs. In Proceedings of the 46

International

Symposium on Computer Architecture (ISCA), pages

541–553. ACM.

Khan, A. A., Ahmad, A., Waseem, M., Liang, P., Fahmideh,

M., Mikkonen, T., and Abrahamsson, P. (2023). Soft-

ware architecture for quantum computing systems —

A systematic review. Journal of Systems and Software,

201:111682.

Kipu Quantum (2025). PlanQK Pattern Atlas. https:

//patterns.platform.planqk.de/pattern-languages/

af7780d5-1f97-4536-8da7-4194b093ab1d.

Koh, J. M., Koh, D. E., and Thompson, J. (2024). Readout

Error Mitigation for Mid-Circuit Measurements and

Feedforward. arXiv:2406.07611.

Leymann, F. (2019). Towards a Pattern Language for Quan-

tum Algorithms. In Proceedings of the 1

Interna-

tional Workshop on Quantum Technology and Opti-

mization Problems (QTOP). Springer.

Leymann, F. and Barzen, J. (2020). The bitter truth

about gate-based quantum algorithms in the NISQ era.

Quantum Science and Technology, 5(4):1–28.

Leymann, F. and Barzen, J. (2021). Pattern Atlas. In Next-

Gen Digital Services. A Retrospective and Roadmap

for Service Computing of the Future, pages 67–76.

Springer.

Nielsen, M. A. and Chuang, I. L. (2010). Quantum Compu-

tation and Quantum Information. Cambridge Univer-

sity Press.

Nimbe, P., Weyori, B. A., and Adekoya, A. F. (2021). Mod-

els in quantum computing: a systematic review. Quan-

tum Information Processing, 20(2):80.

Niu, S., Kokcu, E., Mitra, A., Szasz, A., Hashim, A.,

Kalloor, J., de Jong, W. A., Iancu, C., and Younis, E.

(2024). AC/DC: Automated Compilation for Dynamic

Circuits. arXiv:2412.07969.

Ossorio-Castillo, J., Pastor-D

ıaz, U., and Tornero, J. M.

(2023). A generalisation of the Phase Kick-Back.

Quantum Information Processing, 22(3):143.

Pawar, A., Li, Y., Mo, Z., Guo, Y., Zhang, Y., Tang, X.,

and Yang, J. (2023). Integrated Qubit Reuse and Cir-

cuit Cutting for Large Quantum Circuit Evaluation.

arXiv:2312.10298.

erez-Castillo, R., Fern

andez-Osuna, M., Cruz-Lemus,

J. A., and Piattini, M. (2024). A preliminary study of

the usage of design patterns in quantum software. In

Proceedings of the 5

ACM/IEEE International Work-

shop on Quantum Software Engineering (QSE), pages

41–48.

Pfaendler, S. M.-L., Konson, K., and Greinert, F. (2024).

Advancements in Quantum Computing—Viewpoint:

Building Adoption and Competency in Industry.

Datenbank-Spektrum, 24(1):5–20.

Preskill, J. (2018). Quantum Computing in the NISQ era

and beyond. Quantum, 2:79.

Roncallo, S., Maccone, L., and Macchiavello, C. (2023).

Quantum JPEG. AVS Quantum Science, 5(4):043803.

Shor, P. W. (1994). Algorithms for quantum computation:

discrete logarithms and factoring. In Proceedings 35

Annual Symposium on Foundations of Computer Sci-

ence, pages 124–134. IEEE.

Smith, K. C., Khan, A., Clark, B. K., Girvin, S., and Wei,

T.-C. (2024). Constant-depth preparation of matrix

product states with adaptive quantum circuits. PRX

Quantum, 5:030344.

Stiliadou, L., Barzen, J., Beisel, M., Leymann, F., and

Weder, B. (2025). Patterns for Quantum Machine

Learning. In Proceedings of the 17

International

Conference on Pervasive Patterns and Applications

(PATTERNS), pages 7–14. Xpert Publishing Services

(XPS).

Truger, F., Barzen, J., Beisel, M., Leymann, F., and Yus-

supov, V. (2024). Warm-Starting Patterns for Quan-

tum Algorithms. In Proceedings of the 16

Interna-

tional Conference on Pervasive Patterns and Appli-

cations (PATTERNS), pages 25–31. Xpert Publishing

Services (XPS).

Vietz, D., Barzen, J., Beisel, M., Leymann, F., Stiliadou, L.,

and Weder, B. (2025). Harnessing Patterns to Support

the Development of Hybrid Quantum Applications. In

Proceedings of 14

International Conference on Soft-

ware and Computer Applications (ICSCA ’25). ACM.

Weder, B., Barzen, J., Leymann, F., and Vietz, D. (2022).

Quantum Software Development Lifecycle. In Quan-

tum Software Engineering, pages 61–83. Springer.

Weigold, M., Barzen, J., Leymann, F., and Salm, M.

(2021a). Encoding patterns for quantum algorithms.

IET Quantum Communication, 2(4):141–152.

Weigold, M., Barzen, J., Leymann, F., and Vietz, D.

(2021b). Patterns for Hybrid Quantum Algorithms.

In Proceedings of the 15

Symposium and Sum-

mer School on Service-Oriented Computing (Summer-

SOC), pages 34–51. Springer.

Xu, C., Chen, J., Mi, A., and Szefer, J. (2023). Securing

NISQ Quantum Computer Reset Operations Against

Higher Energy State Attacks. In Proceedings of the

Conference on Computer and Communications

Security (CCS), page 594–607. ACM.

Xu, L., Zhang, X.-Y., Liang, J.-M., Wang, J., Li, M., Jian,

L., and Shen, S.-q. (2022). Variational quantum sup-

port vector machine based on Hadamard test. Com-

munications in Theoretical Physics, 74(5):055106.

Zhao, J., Zhang, Y.-H., Shao, C.-P., Wu, Y.-C., Guo, G.-

C., and Guo, G.-P. (2019). Building quantum neural

networks based on a swap test. Physical Review A,

100(1):012334.

Fundamental Patterns for Composing Quantum Algorithms