Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

Danel Arias Alamo

, Sergio Hern

andez L

opez

and Javier L

azaro Gonz

alez

University of Deusto, Avda. de las Universidades, 24, Bilbao 48007, Spain

Keywords:

Data Reuploading, Variational Quantum Circuits, Quantum Machine Learning, Expressibility, Barren

Plateaus, Quantum Classiﬁcation, Quantum Embedding, Quantum Optimization, Quantum Computing.

Abstract:

Data Reuploading has been proposed as a generic embedding strategy in Variational Quantum Circuits

(VQCs), offering a systematic approach to encoding classical data without the need for problem-speciﬁc cir-

cuit design. Prior studies have suggested that increasing the number of reuploading layers enhances model

performance, particularly in terms of expressibility. In this paper, we present an experimental analysis of

Data Reuploading, systematically evaluating its impact on expressibility, trainability, and completeness in

classiﬁcation tasks. Our results indicate that while adding some reuploading layers can improve performance,

excessive layering does not lead to expressibility gains and introduces barren plateaus, signiﬁcantly hindering

trainability. Consequently, although Data Reuploading can be beneﬁcial in certain scenarios, it is not a ”cheat

code” for optimal quantum embeddings. Instead, the selection of an effective embedding remains an open

problem, requiring a careful balance between expressibility and trainability to achieve robust quantum learn-

ing models.

1 INTRODUCTION

Quantum computing has witnessed tremendous

growth in recent years and is rapidly being recognized

as the next frontier for optimization and, possibly,

machine learning (ML) applications. By leveraging

distinct quantum phenomena, such as superposition

and entanglement, potentially transformative speed-

ups and improvements over classical approaches are

anticipated (Zhou et al., 2020). Nonetheless, the ﬁeld

remains in its early stages, and realizing its full poten-

tial often requires a high level of specialized knowl-

edge, extensive parameter tuning, and careful error

mitigation (Khanal et al., 2024). Consequently, build-

ing and training quantum models that are both robust

and effective still poses signiﬁcant challenges.

In response, recent studies have emerged reporting

promising strategies for simplifying quantum-based

ML model construction (Schuld et al., 2021). One

such strategy is Data Reuploading, which has shown

potential for improving how classical information is

embedded into quantum circuits (P

erez-Salinas et al.,

2020). In this paper, we aim to provide an experimen-

tal analysis of Data Reuploading, exploring both its

https://orcid.org/0000-0002-6586-346X

https://orcid.org/0009-0001-1245-6238

https://orcid.org/0009-0008-2195-4301

capabilities and its limitations. Through systematic

experimentation, we seek to study the practical ben-

eﬁts of this technique, while highlighting key chal-

lenges that remain in this ﬁeld.

1.1 Quantum Variational Machine

Learning

A core approach to Quantum Machine Learning

(QML) involves the use of Variational Quantum

Circuits (VQCs) (Benedetti et al., 2019). In this

paradigm, a parametrized quantum circuit is trained

via classical optimization techniques (e.g., gradient

descent) to solve a variety of learning tasks. Al-

though QML methods can be broadly divided into

kernel-based and VQC-based approaches (Mengoni

and Di Pierro, 2019), the latter has gained special

prominence due to its potential ﬂexibility and expres-

sive power.

VQC-based models typically consist of tunable

gates that act on qubits, altering their initial quantum

state. This initial state is usually obtained by encoding

classical data using additional gates. Once these gates

are parametrised, a cost function is deﬁned to measure

performance on the task at hand (e.g., classiﬁcation

error or policy gradient in reinforcement learning). A

classical optimizer iteratively updates the circuit’s pa-

128

Alamo, D. A., López, S. H. and González, J. L.

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis.

DOI: 10.5220/0013555000004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 128-137

ISBN: 978-989-758-761-0

rameters to minimize this cost. Despite the promise of

VQC-based methods, key challenges persist. Issues

such as barren plateaus, where gradients vanish ex-

ponentially as circuit depth increases (McClean et al.,

2018; Sim et al., 2019), and the intrinsic noise of near-

term quantum devices continue to limit the scalability

and reliability of these approaches.

1.2 Data Reuploading

Among the techniques proposed to overcome some

of these limitations, Data Reuploading has garnered

signiﬁcant attention. Originally introduced by P

erez-

Salinas et al. (P

erez-Salinas et al., 2020), Data Re-

uploading involves encoding the same classical in-

put data multiple times throughout the VQC, rather

than just once at the beginning. This approach bears

resemblance to other VQC-related works such as

the Quantum Approximate Optimization Algorithm

(QAOA), which promises eventual convergence onto

the optimal result (Blekos et al., 2024).

A key theoretical justiﬁcation for why such re-

peated angle-rotation blocks remain expressive comes

from the work of Schuld et al. By injecting data

angles multiple times throughout the circuit, one ef-

fectively generates higher-order Fourier terms in the

model’s expansion, thereby enabling complex func-

tion approximation (Schuld et al., 2021). Hence, the

circuit can realize a rich variety of decision bound-

aries, even if each individual layer relies on a rela-

tively small number of parameters.

The method was originally created as part of a

Universal Quantum Classiﬁer for generic ML tasks.

However, subsequent works have highlighted its po-

tential to substantially simplify the classical data em-

bedding process into the quantum circuit, avoiding the

need to generate complex or tailored strategies, as it

is the case with other well-known techniques such as

the Variational Quantum Eigensolver (VQE) (Peruzzo

et al., 2014; Tilly et al., 2022).

Early empirical studies have shown promising re-

sults, indicating that repeated encoding can improve

performance in tasks such as classiﬁcation and rein-

forcement learning (Lan, 2021; Skolik et al., 2022;

olle et al., 2024), making the technique an attrac-

tive avenue of research for building more generaliz-

able quantum ML models.

Still, much remains to be understood about the

trade-offs associated with layering additional encod-

ing blocks. While these layers may bolster express-

ibility, they may also amplify trainability issues like

barren plateaus and noise sensitivity (Coelho et al.,

2024). Through the experimental analysis presented

in this paper, we aim to clarify how Data Reupload-

ing impacts the trainability, expressibility, and com-

pleteness of VQCs in realistic ML tasks. Our goal

is to identify scenarios where the repeated encoding

strategy provides clear beneﬁts, as well as the limita-

tions that must be addressed to achieve more robust

and scalable quantum ML models.

2 METHODOLOGY

In this section, we outline our methodological frame-

work for examining Data Reuploading in Variational

Quantum Circuits. Our study focuses on a binary

classiﬁcation task using a synthetic dataset, where we

test multiple conﬁgurations of Data Reuploading. We

evaluate the resulting circuits along three key dimen-

sions: trainability, expressibility, and completeness,

which will be discussed in more detail in Section 2.3.

By combining systematic experimentation with these

evaluative criteria, we aim to gain a clear understand-

ing of both the beneﬁts and limitations of Data Re-

uploading in a practical ML setting (Holmes et al.,

2022).

2.1 Generation of the Dataset

To investigate the performance of different Data Re-

uploading conﬁgurations, we generate a synthetic

dataset using the make classification() function

from scikit-learn (Pedregosa et al., 2011). Specif-

ically, we create a binary classiﬁcation dataset con-

sisting of 200 samples, with 5 informative features

and no redundant attributes, organised in 2 clusters

per class. Each feature is then scaled by a factor

of 10 before being passed through the transforma-

tion 2 ·arctan(x). This scaling ampliﬁes the separa-

tion between points in the feature space and mitigates

issues associated with mapping values near zero via

the arctan function, ultimately helping to improve the

distinctiveness of the embedded data in our VQC. A

random seed is set to ensure reproducibility in the re-

sults.

We chose 200 rows, following the general rule of

thumb that a classiﬁcation task requires at least as

many rows as ten times the number of features for

each class, and doubled that amount for additional

conﬁdence.

2.2 Experimental Setup

2.2.1 Data Reuploading Circuit

In the original Data Reuploading framework, classi-

cal data x are repeatedly introduced into a quantum

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

129

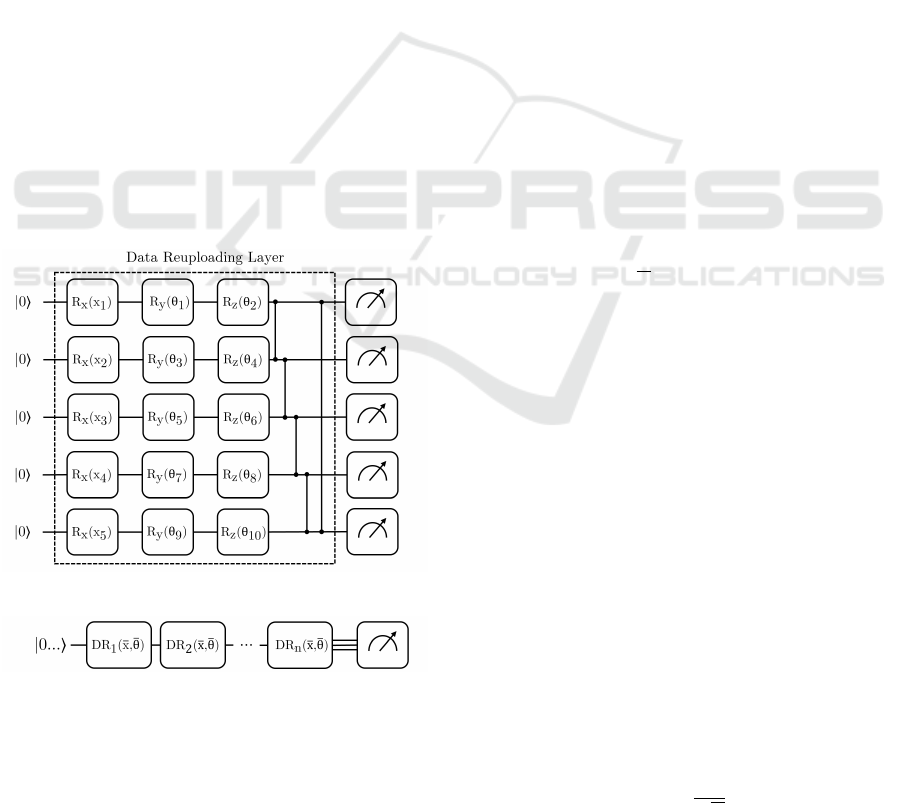
circuit through a data-encoding gate U(x), followed

by a trainable gate U(θ) (P

erez-Salinas et al., 2020).

L(i) ≡U (θ

)U(x

) (1)

By repeating N such layers, the classiﬁer gains ex-

pressive power akin to layered neural networks. Each

layer can be simpliﬁed into a single unitary gate that

includes both data encoding and trainable elements.

L(i) ≡U (θ

+ w

) (2)

This further highlighting its parallels with classi-

cal artiﬁcial neural networks by introducing the con-

cept of weights. Although these unitaries can, in prin-

ciple, be decomposed into elementary rotations cover-

ing the entire SU(2) space (R

or R

), the re-

sulting circuits can become quite deep and parameter-

heavy.

To address practical limitations of this fully gen-

eral SU(2) approach, Skolik et al. propose a more

hardware-friendly adaptation using multiple qubits

and a reduced gate set (Skolik et al., 2022). In par-

ticular, they insert the data through a R

rotation

whose angle is arctan(x ·w), with w being a trainable

weight, then introduce trainable parameters through

additional single-qubit gates R

and R

. After apply-

ing the rotation gates, the qubits are entangled with

their nearest neighbours using a circular entanglement

pattern.

Figure 1: Circuit structure using a single DR layer.

Figure 2: Generic circuit structure using N DR layers.

Building on this pattern, we deﬁne 7 circuits with

different numbers of repetitions that will allow us to

understand the effects of this technique. Speciﬁcally,

we deﬁne circuits with 1, 2, 3, 4, 5, 10 and 20 repe-

titions. The circuits have a width of 5 qubits because

this is a sufﬁcient number for our purposes and, given

that some of the circuits are relatively deep, a larger

width would have consumed a considerable amount of

time and computational resources. The resulting cir-

cuit is shown in Figure 1 with layered structure shown

in Figure2.

2.2.2 Quantum Variational Classiﬁer Model

It is worth noting that we are not training the model,

we are just exploring the results of random weights.

So the process is as follows:

1. Random data and weights are loaded into the cir-

cuit and the vector of states is measured to obtain

the exact probabilities of each state.

2. An interpretation function is used to transform

state probabilities into class probabilities. Speciﬁ-

cally, a modulus function is used, which in binary

classiﬁcation is equivalent to measuring only the

bit with the least weight, a location that has been

shown to avoid barren plateaus (Cerezo et al.,

2021). This is the reason why this function has

been chosen over others such as the number of

ones in the bit-string or half states for each class.

3. Finally, the cross-entropy function is used to cal-

culate the circuit’s loss function as shown in (3).

L = −

∑

j=1

∑

i=1

j,i

log ˆy

j,i

(3)

2.2.3 Monte Carlo Conﬁguration

We generate 4,000 random parameter sets following

a uniform distribution from −π to π, which is not

enough to explore all the possibilities of the circuits.

This particularly affects our expressibility metric. For

example, for an increment of, say, 0.1 π, we would

need just over 10

parameters. It is clear that a full

scan is not reasonable. We ran the same 4000 ran-

dom parameter sets for each data and number of rep-

etitions, for a total of 5.6 million circuits.

To calculate the metrics in Section 2.3, instead

of storing all the values, we calculate the means and

standard deviations of the 4000 circuits for each data.

As these statistical measures are subject to some er-

ror, we calculate conﬁdence intervals. (4) is the un-

certainty of the mean, (5) is the uncertainty of the

standard deviation and (6) is the propagation of this

uncertainty in the means of these measurements.

√

(4)

IQSOFT 2025 - 1st International Conference on Quantum Software

130

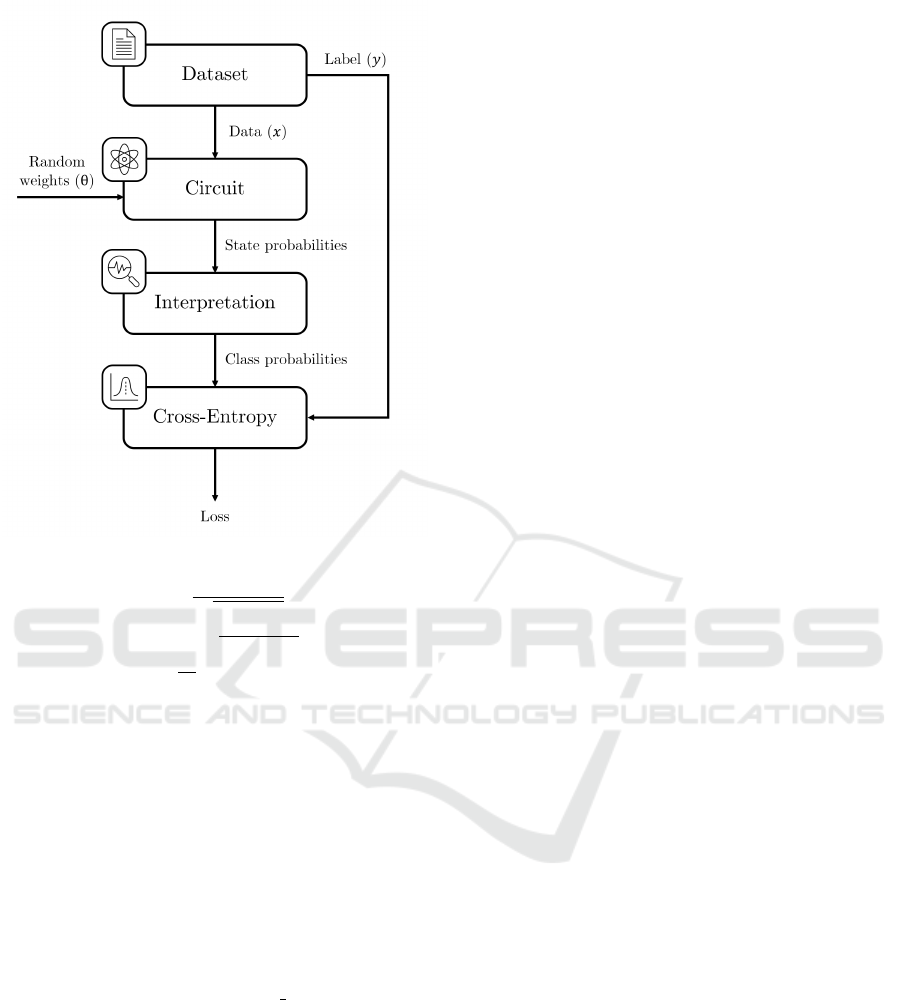
Figure 3: Data Reuploading evaluation process.

2(N −1)

(5)

∆ ¯x =

∑

j=1

(∆x

)

(6)

We also evaluated the minima and maxima; how-

ever, due to the intrinsic complexity in quantifying

their uncertainties and the limited interpretability of

these estimates, we chose not to compute them.

2.2.4 Implementation

We adopt Skolik’s variant of data reuploading, using

Qiskit’s TwoLocal class (Javadi-Abhari et al., 2024),

so that it has the same functionality as the standard

circuits used for QML, such as the EfﬁcientSU2.

We execute the VQCs in a simulator, using the

AerSimulator class from qiskit aer. We then ob-

tain the exact probabilities using its state vector. A

noisy simulation was discarded because it consumed

too many resources to get the exact probabilities and

these were more desirable than the quasiprobabilities

to better appreciate the effect of the technique.

2.3 Evaluation Metrics

The performance of a VQC is fundamentally deter-

mined by its ability to approximate an optimal solu-

tion within a given problem space. This capability

depends not only on the expressiveness of the circuit

but also on its optimization properties, which inﬂu-

ence how effectively the model can be trained. Specif-

ically, the literature identiﬁes three key characteristics

that govern the suitability of a variational model for

practical applications:

• Expressibility – The extent to which the circuit

can explore the entire search space, ensuring that

the chosen parametrised quantum states are sufﬁ-

ciently diverse to represent a wide range of solu-

tions.

• Trainability – The ability of the circuit to be ef-

ﬁciently optimized, which is closely tied to the

presence or absence of barren plateau—regions in

the parameter space where gradients vanish, hin-

dering learning.

• Completeness – The circuit’s capacity to reach the

global minimum of the optimization landscape,

indicating its ability to converge toward the most

optimal solution rather than getting trapped in lo-

cal minima.

These properties serve as fundamental evaluation

criteria for assessing the effectiveness of VQCs in ma-

chine learning tasks. In the following subsections, we

provide a detailed discussion of each characteristic,

along with the speciﬁc metrics used in this work to

quantify them.

2.3.1 Expressibility

The expressibility of a VQC is deﬁned as the pro-

portion of the Hilbert space it can cover through its

parametrised gates (Holmes et al., 2022; Nakaji and

Yamamoto, 2021; Sim et al., 2019). In other words,

a highly expressible VQC can, in principle, gener-

ate a wide range of quantum states, allowing for a

more expansive search over the solution space. This

characteristic typically depends on factors such as the

depth of the circuit, the variety of gate operations, and

the data encoding strategy, key elements in Data Reu-

ploading.

However, while high expressibility expands the

search space, it also tends to correlate with an in-

creased likelihood of encountering barren plateaus

(Larocca et al., 2024). The deeper and more complex

a circuit is the more parameters it has to optimize,

often leading to highly non-trivial energy landscapes

where gradients may vanish. Our methodology there-

fore quantiﬁes expressibility by computing the Kull-

back–Leibler (KL) divergence between the distribu-

tion of ﬁdelities generated by the VQC and that of

the Haar-random ensemble, following the approach

in (Sim et al., 2019).

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

131

Speciﬁcally, we estimate this ﬁdelity distribution

by sampling pairs of parameter vectors, computing

their corresponding state ﬁdelities, and treating these

ﬁdelities as random variables. We state ﬁdelities with

(7) (Jozsa, 1994), which can be simpliﬁed as the

square Bhattacharyya coefﬁcient Comparing the sam-

pled distribution to that of Haar-random states then

yields a KL divergence score. The closer this score is

to zero, the more expressible the VQC is. By vary-

ing the number of Data Reuploading layers, we can

characterize how they affect the circuit’s overall ex-

pressibility and, in turn, its subsequent trainability.

F(ρ

,ρ

) =

(

√

)

(7)

2.3.2 Loss Dispersion as a Trainability Indicator

Trainability in the context of gradient-based optimiza-

tion refers to the ability of a VQC to avoid barren

plateaus—regions in the parameter space where the

gradient of the cost function vanishes exponentially

with respect to the number of qubits or the circuit

depth (McClean et al., 2018; Cerezo et al., 2021;

Larocca et al., 2024). When a circuit experiences bar-

ren plateaus, learning becomes infeasible because the

parameter updates are effectively driven by inﬁnitesi-

mal gradients. As a result, the training converges ex-

tremely slowly or fails to converge altogether.

We focus on barren plateaus because they are the

most present problem in the existing literature on the

trainability of VQCs. Moreover, it has been shown

to occur together with other optimization challenges

such as the tightness of the minima of the cost func-

tion or the exponential concentration of costs over the

mean (Arrasmith et al., 2022). The latter is particu-

larly relevant, not only because it allows us to focus

on a single problem to address them all, but also be-

cause it allows us to identify barren plateaus through

costs instead of gradients, thus making it possible to

analyse the trainability of circuit without optimizing

it.

To evaluate trainability in our experiments, we ini-

tialize the variational parameters with random values

and analyse the statistical behaviour of the cost func-

tion. Speciﬁcally, we track loss dispersion, deﬁned as

the standard deviation of cost values across multiple

circuit instances. If this standard deviation decreases

signiﬁcantly as the system size increases, it may

indicate the presence of a barren plateau. A circuit is

considered trainable if it maintains a sufﬁciently large

standard deviation, ensuring that parameter updates

remain effective in practice. Conversely, a near-zero

standard deviation suggests an exceedingly ﬂat opti-

mization landscape, signalling the presence of a

barren plateau.

2.3.3 Completeness Estimation

A given VQC is considered complete if it is capable of

generating the optimal solution state within the man-

ifold of states it can represent (Holmes et al., 2022).

In the context of quantum optimization, this optimal

state corresponds to the ground state of a problem

Hamiltonian or, more generally, the state that mini-

mizes a given cost function.

While higher expressibility increases the probabil-

ity that the optimal state is included in the circuit’s

accessible state space, it does not guarantee its pres-

ence for every problem instance. Completeness there-

fore captures a fundamental aspect of solution feasi-

bility: even if a circuit is highly expressible, it may

still lack the ability to encode the optimal solution.

Additionally, achieving optimality requires more than

just completeness; trainability is essential to ensure

that the optimization process successfully converges

to the minimum. Without sufﬁcient trainability, even

a complete and expressive VQC may fail to reach its

optimal state in practice.

In this work, rather than training the circuit di-

rectly or computing the exact reachable minima, we

adopt an empirical approach to estimate complete-

ness. We uniformly sample a large number of param-

eter conﬁgurations and evaluate the loss function for

each data point in the dataset under these parameters.

For each data point, we record the lowest observed

loss, interpreting this as the minimum value the circuit

can feasibly attain. By averaging these minimum val-

ues across the dataset, we estimate the circuit’s appar-

ent global minimum. This method provides a practi-

cal indicator of whether the circuit is capable, in prin-

ciple, of representing solutions with sufﬁciently low

loss, thereby offering an empirical assessment of its

completeness.

2.3.4 Uniform Classiﬁer

To provide a meaningful reference for evaluating the

performance of our Data Reuploading circuits, we in-

troduce what we term the Uniform Classiﬁer. This

classiﬁer serves as a baseline by simulating a circuit

that applies a Hadamard gate to each qubit, effectively

preparing the qubits in an equal superposition of all

possible states. Sampling from this circuit results in a

uniform distribution over the possible outcomes, rep-

resenting a scenario where no learning or optimiza-

tion has taken place. By comparing the performance

of our Data Reuploading circuits against this uniform

baseline, we can better assess the impact of this strat-

IQSOFT 2025 - 1st International Conference on Quantum Software

132

egy on the model’s performance. The Uniform Clas-

siﬁer provides a clear benchmark for understanding

the advantages and limitations of Data Reuploading

in practical quantum machine learning tasks.

3 RESULTS

In this section, we present the experimental results of

our systematic evaluation on the impact of Data Reu-

ploading on the metrics. Through a combination of

quantitative analysis and visual representations, we

aim to offer a comprehensive understanding of the

trade-offs associated with this embedding strategy in

practical quantum machine learning tasks.

To summarize our ﬁndings, we provide Table 1

that presents the average values and corresponding

standard errors for all evaluated metrics across dif-

ferent numbers of reuploading layers. Additionally,

we include three plots (Figures 4, 5, and 6) that visu-

ally depict the trends in expressibility, loss dispersion,

and the cross-entropy loss, respectively, as the num-

ber of reuploading layers increases. These results col-

lectively illustrate the effects of the embedding tech-

nique on the performance and behaviour of VQCs.

3.1 Discussion

In this subsection, we discuss the implications of our

experimental results, focusing on the three charac-

teristics that permeate this document: expressibility,

trainability and completeness.

3.1.1 Expressibility

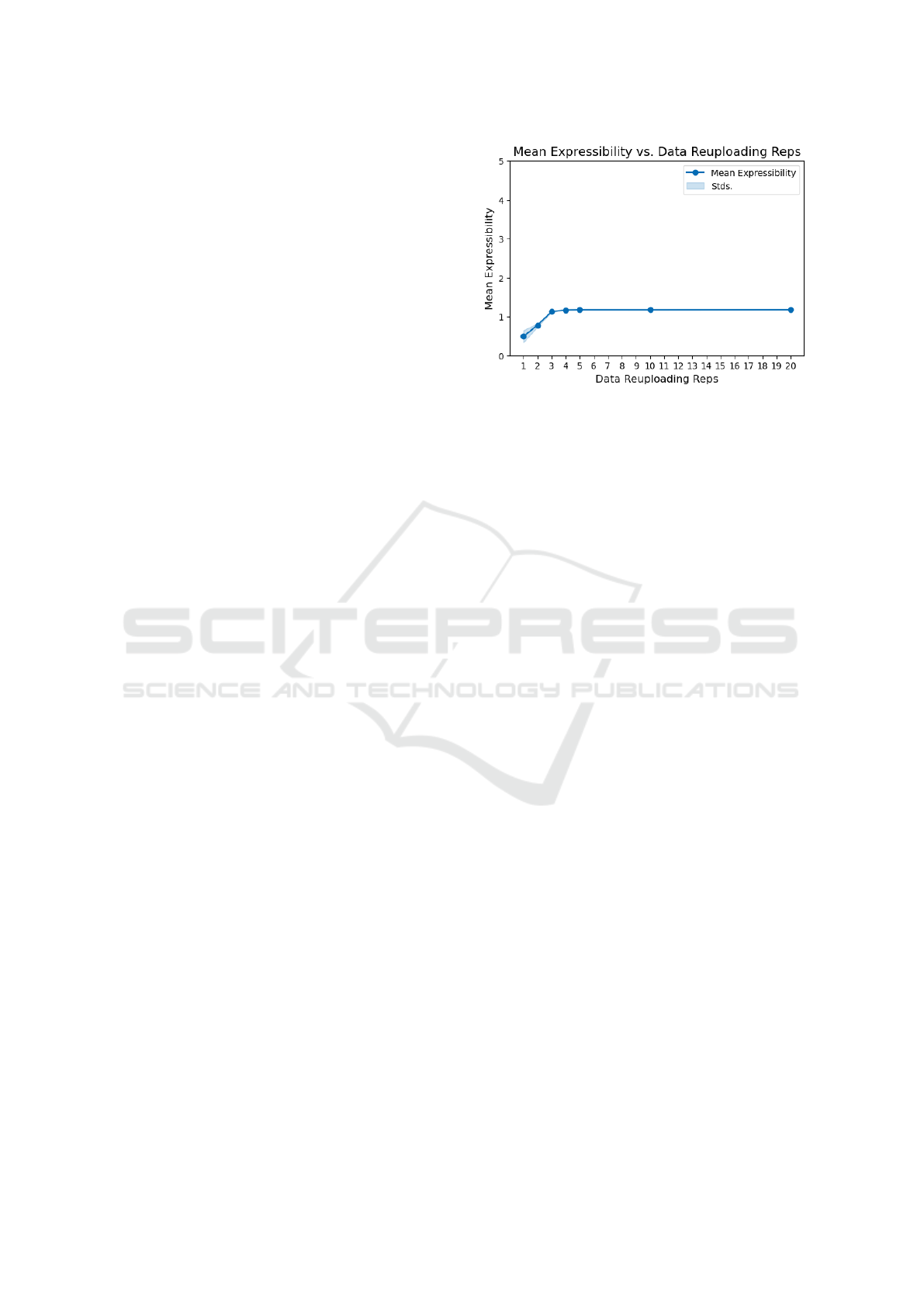
The expressibility results, as depicted in Figure 4, in-

dicate that increasing the number of reuploading lay-

ers degrades the circuit’s ability to explore a broader

portion of the Hilbert space. This is evidenced by

the increase in the expressibility metric from 0.4928

for a single layer to 1.1297 for three layers, suggest-

ing a decreased capacity to generate diverse quantum

states. This suggests that additional reuploading lay-

ers do not necessarily translate into greater state-space

coverage.

However, beyond this point, the trend changes.

From three layers onward, expressibility values ap-

pear to saturate, reaching 1.18 approximately for both

10 and 20 layers. This suggests that further layering

may introduce redundancies in parametrisation, ef-

fectively constraining the range of achievable states.

This phenomenon aligns with prior observations in

the literature, where excessive circuit depth has been

associated with the concentration of generated states

Figure 4: The evolution of the effect of data reuploading

layers on the average expressibility. In this case, only a

worsening of this metric is observed. With a small increase

after two repetitions, a larger increase after three repetitions

and a stagnation after the fourth repetition.

in speciﬁc subregions of the Hilbert space, thereby

limiting the overall diversity of the quantum model.

It is also worth noting that, while expressibility is

crucial for ensuring a sufﬁciently rich state space, ex-

cessive layering may lead to diminishing returns and

potentially adverse effects. This is reﬂected in our re-

sults, where the expressibility values plateau despite

increasing the number of reuploading layers. Such

behaviour suggests that, beyond a certain depth, the

circuit does not meaningfully expand its expressibil-

ity but instead exhibits structural limitations that con-

strain further improvements.

In comparison to the uniform classiﬁer (ln(150) ≈

5.0106), all conﬁgurations employing Data Reu-

ploading achieve signiﬁcantly lower expressibility

values (more expressive), conﬁrming that this ap-

proach enables more efﬁcient state-space exploration

than a purely random distribution of quantum states.

Nevertheless, the observed saturation highlights the

need for careful selection of the number of reupload-

ing layers to optimize expressibility without introduc-

ing unnecessary complexity.

3.1.2 Trainability

The trainability analysis, based on the loss dispersion

metric, reveals a clear trend: as the number of reu-

ploading layers increases, the dispersion of loss val-

ues systematically decreases (Figure 5). This reduc-

tion suggests that parameter updates become less ef-

fective as the circuit depth grows, ultimately leading

to a highly constrained optimization landscape.

For a single reuploading layer, the loss dispersion

is relatively high at 0.5950, indicating a sufﬁciently

diverse range of loss values across different parame-

ter initializations. This suggests that the optimization

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

133

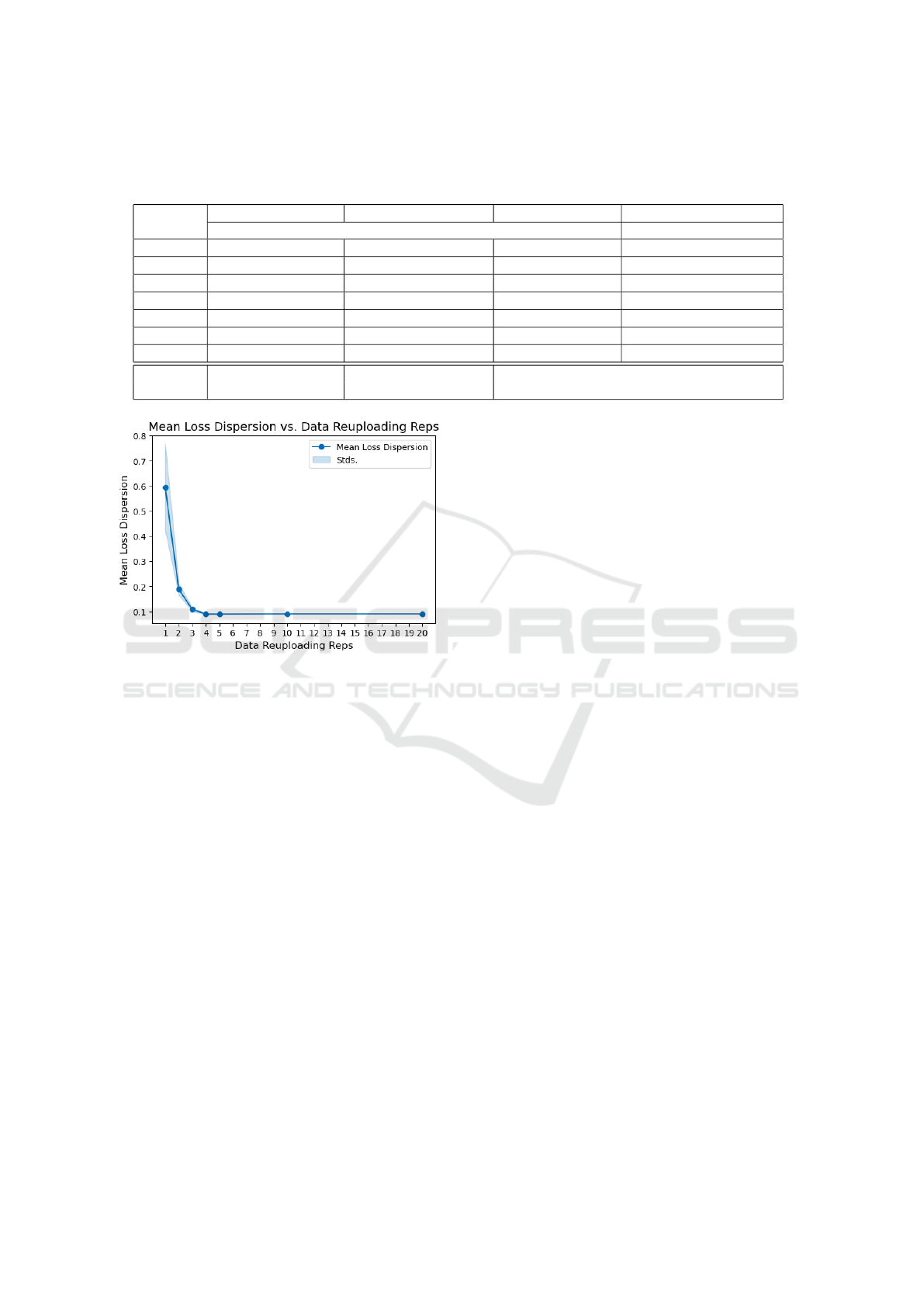
Table 1: Comparison of the effect of Reuploading Layers on Expressivity, Loss dispersion, and Loss metrics. Each of the

presented measurements is an average on the 200 rows of data parameters. Alongside the metrics is the standard error,

signalling the uncertainty associated to the statistical measures.

Reps

Avg. Expressibility Avg. Loss Dispersion Avg. Mean Loss Avg Min. & Max. Loss

Metrics Avg. (± Standard Error) (Min., Max.)

1 0.4928 (± 0.0111) 0.5949 (± 0.0005) 0.5738 (± 0.0007) (0.0231, 2.2449)

2 0.7828 (± 0.0030) 0.1884 (± 0.0002) 0.3792 (± 0.0002) (0.0558, 1.1299)

3 1.1297 (± 0.0009) 0.1079 (± 0.0001) 0.3581 (± 0.0001) (0.1062, 0.8389)

4 1.1747 (± 0.0003) 0.0901 (± 0.0001) 0.3548 (± 0.0001) (0.1167, 0.7763)

5 1.1791 (± 0.0002) 0.0898 (± 0.0001) 0.3544 (± 0.0001) (0.1205, 0.7811)

10 1.1783 (± 0.0002) 0.0905 (± 0.0001) 0.3544 (± 0.0001) (0.1183, 0.7889)

20 1.1803 (± 0.0003) 0.0905 (± 0.0001) 0.3546 (± 0.0001) (0.1182, 0.7934)

Uniform

ln(150) ≈ 5.0106 0.0 ln(2)/2 ≈ 0.3466

Classiﬁer

Figure 5: The evolution of the effect of data reuploading

layers on the average loss dispersion. This metric drops off

abruptly as layers are added. After 4 layers, the values are

so low that the circuit is practically untrainable.

landscape retains enough variability to allow effective

parameter updates. However, with the introduction

of additional layers, loss dispersion steadily declines,

dropping to 0.1884 for two layers and further decreas-

ing to 0.0898 by the ﬁfth layer. Beyond this point,

the metric plateaus, with values around 0.0905 for cir-

cuits with 10 or more layers.

This trend aligns with the onset of barren plateaus,

a well-documented issue in deep variational quan-

tum circuits. When the loss dispersion approaches

zero, it implies that most parameter conﬁgurations

yield nearly identical loss values, making it increas-

ingly difﬁcult for gradient-based optimization to dis-

tinguish between better and worse conﬁgurations. In

such cases, the gradient magnitude tends to vanish

exponentially with depth, rendering parameter up-

dates ineffective and signiﬁcantly hindering the train-

ing process.

The stagnation of loss dispersion beyond ﬁve re-

uploading layers suggests that, past a certain depth,

the circuit reaches a regime where barren plateaus

dominate, making further optimization impractical.

This is consistent with prior ﬁndings in the literature,

which indicate that while increased circuit depth may

sometimes enhance expressibility, it simultaneously

exacerbates trainability challenges due to gradient de-

cay. In our case, however, no signiﬁcant improvement

in expressibility is observed beyond two reuploading

layers. On the contrary, as discussed in Section 3.1.1,

further increases in depth appear to hinder even the

circuit’s ability to generate diverse quantum states.

This suggests that the trade-off between expressibility

and trainability is particularly unfavourable for deeper

reuploading circuits.

For comparison, the uniform classiﬁer yields

a perfectly uniform distribution over possible out-

comes, resulting in a loss dispersion of exactly 0.0.

This is not due to optimization difﬁculties but rather a

fundamental property of its construction: since it con-

sists solely of Hadamard gates applied to each qubit,

it always produces the same probability distribution,

regardless of input data. While all reuploading-based

circuits maintain non-zero dispersion, the observed

decline with increasing layers highlights a fundamen-

tal limitation: beyond a certain point, additional reu-

ploading layers do not enhance the circuit’s represen-

tation capacity and, instead, severely compromise its

trainability.

3.1.3 Completeness

The cross-entropy loss, depicted in Figure 6, pro-

vides insights into the completeness of the VQCs. As

expected, the average loss initially decreases as the

number of reuploading layers increases, indicating

an improvement in classiﬁcation performance. This

trend is particularly evident when transitioning from

one to two layers, where the average loss drops from

0.5738 to 0.3792, suggesting that the circuit gains

the ability to represent more accurate decision bound-

aries.

IQSOFT 2025 - 1st International Conference on Quantum Software

134

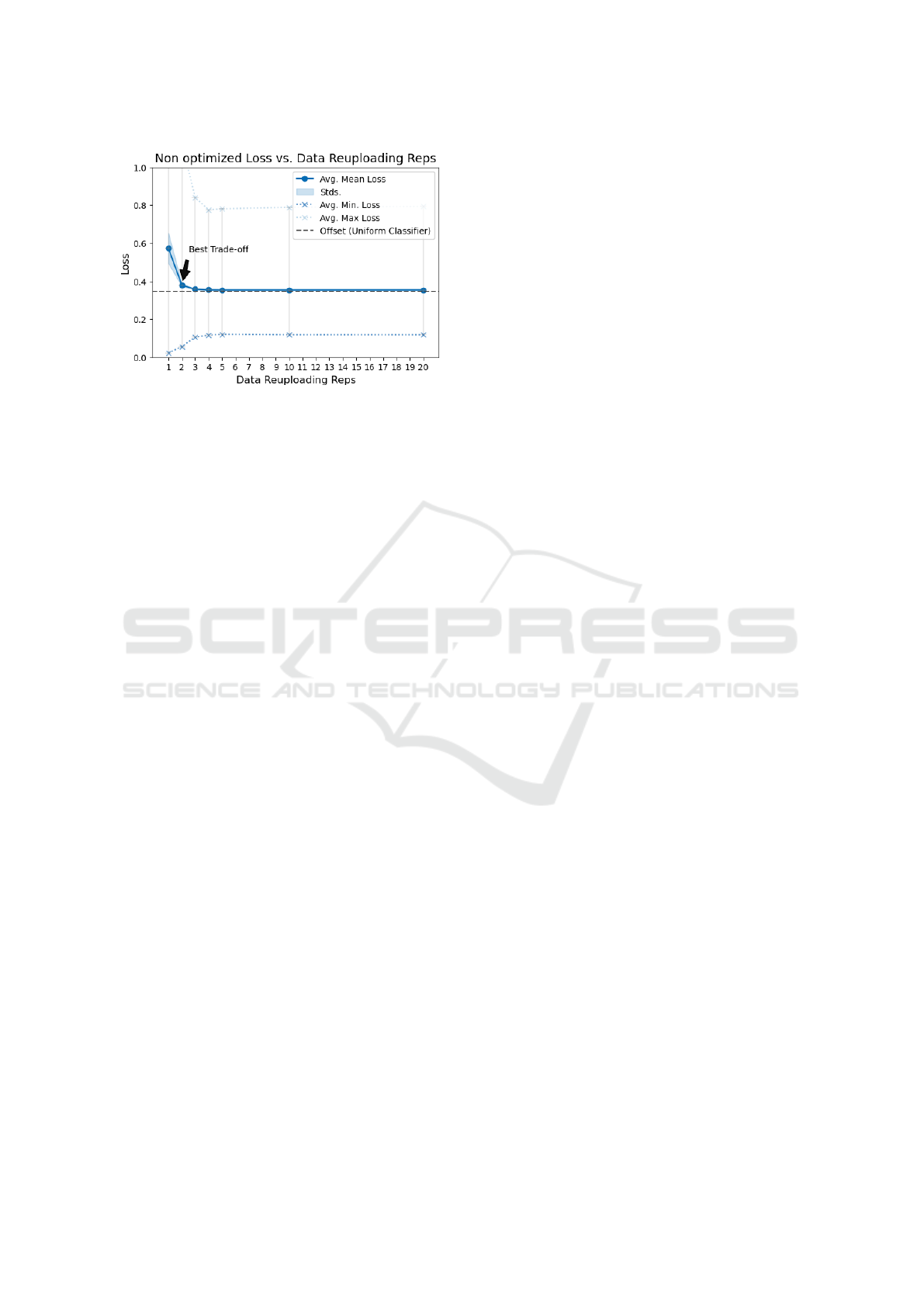
Figure 6: The evolution of the effect of data reuploading

layers on the loss. In the average of the mean loss, there is

an improvement that decreases until the ﬁfth layer, where

there is stagnation. However, the average of the minimums

only shows an improvement with two layers, after which

it worsens and also ends up stagnating on the ﬁfth layer.

Therefore, for our problem, we found the best performance

of this technique with two repetitions.

However, beyond two layers, the reduction in loss

slows down, and by four layers, it begins to plateau.

The difference between ﬁve, ten and twenty layers is

negligible (0.3544, 0.3544 and 0.3546). This stag-

nation suggests that additional reuploading layers do

not signiﬁcantly enhance the circuit’s ability to rep-

resent lower-loss conﬁgurations, reinforcing the ﬁnd-

ings from the expressibility and trainability analyses.

A crucial observation supporting this interpreta-

tion is the behavior of the minimum and maximum

loss values across different conﬁgurations. Unlike the

average loss, which consistently decreases up to two

layers, the minimum loss does not follow the same

trend. While the lowest observed loss for one layer is

0.0231, this value actually increases slightly for two

layers (0.0558) before continuing to rise at deeper

depths, reaching 0.1062 for three layers and 0.1205

for ﬁve layers. Beyond this point, the minimum loss

stabilizes around 0.118 for ten and twenty layers.

Similarly, the maximum loss, which is a measure of

the worst-case performance, decreases signiﬁcantly

between one and two layers (2.2449 to 1.1299), but

beyond this point, the decrease is much more moder-

ate, converging to a stable range (0.7763 to 0.7934).

These results suggest that while increasing the

number of reuploading layers initially provides a

more expressive circuit capable of better classiﬁca-

tion, excessive depth introduces diminishing returns.

The increase in minimum loss beyond two layers in-

dicates that, despite higher expressibility, the circuit is

less likely to encode optimal solutions. This is likely a

direct consequence of the barren plateaus observed in

Section 3.1.2, where deeper circuits suffer from van-

ishing gradients, concentrating most sampled loss val-

ues around the offset—the average loss of the uniform

classiﬁer (≈0.3466). As a result, fewer sampled con-

ﬁgurations reach low-loss regions, making optimiza-

tion increasingly difﬁcult.

Finally, while our Monte Carlo sampling approach

provides a practical means of estimating complete-

ness, it is important to recognize its limitations. The

minimum and maximum values are drawn from a ﬁ-

nite sample of 4,000 random parameter conﬁgurations

(see Section 2.2.3). Consequently, the absence of

lower minimum or higher maximum loss values may

partially be a result of sampling limitations. However,

the overall trend—where deeper circuits exhibit a nar-

rower range of loss values concentrated around the

offset—provides strong supporting evidence for the

onset of barren plateaus, making it increasingly difﬁ-

cult for the circuit to ﬁnd and exploit low-loss conﬁg-

urations.

3.1.4 Overall Implications

A key takeaway from our analysis is that the best

trade-off in this setting is achieved with two reupload-

ing layers. This conﬁguration achieves the lowest av-

erage loss while avoiding the excessive expressibility

that could introduce high variance in the optimization

landscape. The relatively low maximum loss at two

layers (1.1299) further supports this, as it suggests a

more controlled and stable learning process compared

to deeper circuits. Although the minimum loss at two

layers is slightly higher than for a single layer, the

fact that it remains relatively low while the average

loss is signiﬁcantly reduced indicates that this conﬁg-

uration is more likely to generalize well across differ-

ent parameter initializations. This suggests that the

circuit remains trainable while also beneﬁting from

an enhanced capacity to generate meaningful decision

boundaries.

Additionally, expressibility experiences only a

slight increase (less expressive) when moving from

one to two layers, indicating that the circuit at this

depth remains sufﬁciently expressive while also being

more structured and less prone to redundancy. Be-

yond two layers, expressibility stagnates, and train-

ability deteriorates, making further increases in depth

counterproductive.

4 CONCLUSION

Collectively, these results demonstrate that Data Reu-

ploading is a powerful but nuanced embedding strat-

egy. It is not guaranteed that increasing the number

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

135

of reuploading layers will make circuits more expres-

sive, but even if it does not, it can bias the circuit for

lower losses without losing too much trainability to

the point of being unable to optimise, thus improv-

ing classiﬁcation performance. However, excessive

layering introduces signiﬁcant trainability problems,

ultimately leading to barren plateaus.

Moreover, these results are in line with recent lit-

erature showing that hardware efﬁcient ansatzes us-

ing local costs functions are trainable with controlled

depths and suffer from barren plateaus if they are too

deep (Cerezo et al., 2021). The circuit used is based

on a hardware efﬁcient approach and the interpreta-

tion function is local (least signiﬁcant qubit) for two

classes. Thus, we note that the position of the bar-

ren plateaus can vary depending on the problem, and

factors such as the cost function can delay its appear-

ance.

These ﬁndings underscore the importance of care-

fully balancing the number of reuploading layers to

achieve robust and trainable quantum machine learn-

ing models. While Data Reuploading enhances the

representational power of Variational Quantum Cir-

cuits, our results highlight that more layers do not

necessarily translate into better performance. Instead,

an optimal number must be chosen to avoid barren

plateaus and preserve effective optimization dynam-

ics.

4.1 Future Work

This study highlights the potential and effect of Data

Reuploading in VQCs for quantum machine learn-

ing, yet several avenues remain open for investiga-

tion. First, it would be instructive to compare DR

based VQCs under different cost functions, datasets,

and learning tasks (including multi-class classiﬁca-

tion and regression) to identify how data character-

istics and performance metrics affect our ﬁndings.

Next, it would be valuable to extend the study to cir-

cuits with more qubits, to see if the observed trends

change with the width of the circuit.

Given that real quantum devices are prone to

noise, assessing the resilience of DR in noisy environ-

ments remains vital to determining its practical viabil-

ity. Finally, exploring alternative DR conﬁgurations,

such as variations in gate arrangements or parameter-

sharing strategies, could uncover novel approaches to

optimising performance and scalability.

ACKNOWLEDGEMENTS

Mr. Danel Arias thanks the Basque-Q strategy of

Basque Government for partially funding his doc-

toral research at the University of Deusto, within the

Deusto for Knowledge - D4K team on applied arti-

ﬁcial intelligence and quantum computing technolo-

gies.

REFERENCES

Arrasmith, A., Holmes, Z., Cerezo, M., and Coles, P. J.

(2022). Equivalence of quantum barren plateaus to

cost concentration and narrow gorges. Quantum Sci-

ence and Technology, 7(4):045015. arXiv:2104.05868

[quant-ph].

Benedetti, M., Lloyd, E., Sack, S., and Fiorentini, M.

(2019). Parameterized quantum circuits as machine

learning models. Quantum Sci. Technol., 4(4):043001.

Publisher: IOP Publishing.

Blekos, K., Brand, D., Ceschini, A., Chou, C.-H., Li, R.-

H., Pandya, K., and Summer, A. (2024). A review on

Quantum Approximate Optimization Algorithm and

its variants. Physics Reports, 1068:1–66.

Cerezo, M., Sone, A., Volkoff, T., Cincio, L., and Coles,

P. J. (2021). Cost function dependent barren plateaus

in shallow parametrized quantum circuits. Nat Com-

mun, 12(1):1791. Publisher: Nature Publishing

Group.

Coelho, R., Sequeira, A., and Paulo Santos, L. (2024).

VQC-based reinforcement learning with data re-

uploading: performance and trainability. Quantum

Mach. Intell., 6(2):53.

Holmes, Z., Sharma, K., Cerezo, M., and Coles, P. J.

(2022). Connecting Ansatz Expressibility to Gradi-

ent Magnitudes and Barren Plateaus. PRX Quantum,

3(1):010313. Publisher: American Physical Society.

Javadi-Abhari, A., Treinish, M., Krsulich, K., Wood, C. J.,

Lishman, J., Gacon, J., Martiel, S., Nation, P., Bishop,

L. S., Cross, A. W., Johnson, B. R., and Gambetta,

J. M. (2024). Quantum computing with qiskit.

Jozsa, R. (1994). Fidelity for Mixed Quantum

States. Journal of Modern Optics, 41(12):2315–

2323. Publisher: Taylor & Francis

eprint:

https://doi.org/10.1080/09500349414552171.

Khanal, B., Rivas, P., Sanjel, A., Sooksatra, K., Quevedo,

E., and Rodriguez, A. (2024). Generalization error

bound for quantum machine learning in NISQ era—a

survey. Quantum Machine Intelligence, 6(2):90.

olle, M., Witter, T., Rohe, T., Stenzel, G., Altmann, P.,

and Gabor, T. (2024). A Study on Optimization Tech-

niques for Variational Quantum Circuits in Reinforce-

ment Learning. arXiv:2405.12354.

Lan, Q. (2021). Variational Quantum Soft Actor-Critic.

ArXiv.

Larocca, M., Thanasilp, S., Wang, S., Sharma, K., Bia-

monte, J., Coles, P. J., Cincio, L., McClean, J. R.,

IQSOFT 2025 - 1st International Conference on Quantum Software

136

Holmes, Z., and Cerezo, M. (2024). A Review of Bar-

ren Plateaus in Variational Quantum Computing.

McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush,

R., and Neven, H. (2018). Barren plateaus in quan-

tum neural network training landscapes. Nat Com-

mun, 9(1):4812. Publisher: Nature Publishing Group.

Mengoni, R. and Di Pierro, A. (2019). Kernel methods in

Quantum Machine Learning. Quantum Mach. Intell.,

1(3):65–71.

Nakaji, K. and Yamamoto, N. (2021). Expressibility of the

alternating layered ansatz for quantum computation.

Quantum, 5:434. Publisher: Verein zur F

orderung

des Open Access Publizierens in den Quantenwis-

senschaften.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou,

X.-Q., Love, P. J., Aspuru-Guzik, A., and O’Brien,

J. L. (2014). A variational eigenvalue solver on a pho-

tonic quantum processor. Nature Communications,

5(1):4213.

erez-Salinas, A., Cervera-Lierta, A., Gil-Fuster, E., and

Latorre, J. I. (2020). Data re-uploading for a univer-

sal quantum classiﬁer. Quantum, 4:226. Publisher:

Verein zur F

orderung des Open Access Publizierens

in den Quantenwissenschaften.

Schuld, M., Sweke, R., and Meyer, J. J. (2021). Effect

of data encoding on the expressive power of varia-

tional quantum-machine-learning models. Phys. Rev.

A, 103(3):032430. Publisher: American Physical So-

ciety.

Sim, S., Johnson, P. D., and Aspuru-Guzik, A.

(2019). Expressibility and Entangling Capa-

bility of Parameterized Quantum Circuits for

Hybrid Quantum-Classical Algorithms. Advanced

Quantum Technologies, 2(12):1900070. eprint:

https://onlinelibrary.wiley.com/doi/pdf/10.1002/

qute.201900070.

Skolik, A., Jerbi, S., and Dunjko, V. (2022). Quantum

agents in the Gym: a variational quantum algorithm

for deep Q-learning. Quantum, 6:720. Publisher:

Verein zur F

orderung des Open Access Publizierens

in den Quantenwissenschaften.

Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y.,

Grant, E., Wossnig, L., Rungger, I., Booth, G. H.,

and Tennyson, J. (2022). The Variational Quantum

Eigensolver: A review of methods and best practices.

Physics Reports, 986:1–128.

Zhou, L., Wang, S.-T., Choi, S., Pichler, H., and Lukin,

M. D. (2020). Quantum Approximate Optimization

Algorithm: Performance, Mechanism, and Implemen-

tation on Near-Term Devices. Physical Review X,

10(2):021067.

APPENDIX

Code Availability

The code used to implement the algorithms and per-

form the analyses in this study is available at the

DRCC GitHub repository

. The repository includes

all relevant scripts, data processing methods, and ex-

ample datasets necessary to replicate the results pre-

sented in this paper. For questions regarding the code

or its application, please contact the corresponding

author at danel.a.a@deusto.es.

Repository available in https://github.com/

DeustoTech/research-quantum-conference-iqsoft-DRCC

Is Data-Reuploading Really a Cheat Code? An Experimental Analysis

137