AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

Javier Ibarra Veganzones

1 a

, Danel Arias Alamo

1 b

, Alfredo Cuzzocrea

2 c

and Pablo Garc

ıa Bringas

1 d

University of Deusto, Avda. Universidades 24, Bilbao, Spain

University of Calabria, Rende, Cosenza, Italy

Keywords:

Quantum Computing, Quantum Software Testing, Debugging, Swap Test, Circuit Assertions, Quantum

Veriﬁcation.

Abstract:

Quantum software debugging faces signiﬁcant challenges due to measurement-induced state collapse, deco-

herence, and gate noise. We introduce AssertsQ, a framework that integrates assertion-based debugging into

Qiskit, enabling automated veriﬁcation of quantum circuits. AssertsQ provides three key validation methods:

Swap Test-based state ﬁdelity checks, measurement-based Total Variation Distance (TVD) comparisons, and

noise-aware assertions adaptable to real hardware constraints. Our evaluation on benchmark circuits, including

GHZ, QFT, and Grover’s algorithm, demonstrates the framework’s ability to detect errors and quantify ﬁdelity

degradation under noise. By simplifying quantum circuit veriﬁcation, AssertsQ enhances the reliability of

quantum software in the NISQ era.

1 INTRODUCTION

Quantum computing has gained signiﬁcant momen-

tum in recent years due to its potential to outperform

classical computers in certain computational tasks,

including cryptographic analysis, optimization, and

simulation of quantum mechanical systems (Piattini

et al., 2021). However, the process of verifying the

correctness of quantum circuits remains a formidable

challenge (Arias et al., 2023). Unlike classical debug-

ging techniques, where the state of a program can be

inspected at any point without altering the outcome,

quantum states collapse upon measurement, and gate

errors or qubit decoherence can irreversibly disrupt an

entire computation (Metwalli, 2024). This intrinsic

fragility necessitates robust veriﬁcation tools tailored

to the probabilistic and non-local nature of quantum

phenomena.

In this paper, we introduce AssertsQ, a frame-

work that provides easy-to-use assertion methods

integrated into Qiskit (the IBM developed open-

source quantum programming language). By lever-

aging the Swap Test for state overlap checks and a

https://orcid.org/0009-0007-7382-1300

https://orcid.org/0000-0002-6586-346X

https://orcid.org/0000-0002-7104-6415

https://orcid.org/0000-0003-3594-9534

measurement-based approach for output distribution

veriﬁcation, AssertsQ aims to streamline the debug-

ging and validation pipeline for quantum software de-

velopers. The sections below detail the motivation be-

hind this work, the speciﬁc problems it addresses, the

novel contributions we present, and the layout of the

paper.

1.1 Motivation

As the ﬁeld of quantum computing transitions from

proof-of-concept experiments to the exploration of

real-world applications, reliable circuit validation

grows ever more critical (Arias et al., 2023). In clas-

sical computing, developers can inspect intermediate

variables and step through code execution. In quan-

tum computing, direct state inspections remain elu-

sive unless one resorts to full state tomography, which

becomes exponentially demanding with the number

of qubits (Hoag et al., 2019). Consequently, many de-

velopers rely on partial tests or repeated sampling that

provide incomplete insights into circuit correctness

(Li et al., 2019). Furthermore, quantum hardware re-

mains noisy, and the complex interplay of gate inﬁ-

delities and cross-talk can produce misleading results

if not properly accounted for in veriﬁcation (Mundada

et al., 2019). These concerns highlight the pressing

need for a user-friendly framework that can automate

Veganzones, J. I., Alamo, D. A., Cuzzocrea, A. and Bringas, P. G.

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging.

DOI: 10.5220/0013553300004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 49-60

ISBN: 978-989-758-761-0

routine checks of circuit ﬁdelity and identify discrep-

ancies early in the development cycle.

Verifying whether a quantum circuit performs as

intended typically involves comparing its ﬁnal state

or measurement distribution against an expected re-

sult(Kang et al., 2024). As circuits scale in complex-

ity, conventional debugging techniques do not readily

extend to quantum contexts. The problem is exac-

erbated by limited qubit counts and high error rates

in today’s quantum processors, making repeated sam-

pling or complicated protocols an inefﬁcient endeavor

(Arias et al., 2022). This exacerbates the necessity of

a supporting tool that seamlessly integrates with ex-

isting frameworks and provides accessible implemen-

tations of established techniques, such as the Swap

Test or statistical distance measures, to facilitate de-

bugging and validation.

1.2 Contribution

This paper addresses the challenges above by present-

ing AssertsQ, a modular toolkit that embeds quan-

tum circuit assertions directly into Qiskit-based work-

ﬂows. A key contribution is the implementation

of methods that allow developers to conﬁrm circuit

equivalence, validate ﬁdelity against a known tar-

get state, and compare measurement output distribu-

tions. By unifying these functionalities into a sin-

gle interface, we reduce the overhead of creating cus-

tom veriﬁcation schemes. Another important feature

is the seamless interoperability with IBM Quantum’s

cloud backends and local simulators, providing ﬂexi-

ble noise modeling and pass manager (transpiler) con-

ﬁguration. These capabilities allow researchers and

developers to iterate rapidly on quantum algorithms,

verifying correctness under both ideal and realistic

hardware conditions. Moreover, the introduction of

adjustable tolerances ensures that the tool can accom-

modate noisy intermediate-scale quantum (NISQ) de-

vices, making it a practical resource in the current

quantum computing landscape. In this way, the tool

presented in this work emerges as a tool that di-

rectly addresses the need for an integrated and efﬁ-

cient quantum circuit veriﬁcation framework, bridg-

ing the gap between theoretical validation and practi-

cal implementation.

The remainder of the paper is organized as fol-

lows. Section 2 discusses the state of the art in

quantum circuit veriﬁcation, highlighting why tradi-

tional classical debugging methods might fall short

for quantum software development, and introduces

the theoretical underpinnings of the techniques used

in this work. Section 3 details the methodology be-

hind AssertsQ, explaining how the toolkit composes

and executes specialized veriﬁcation circuits. Section

4 delves into the implementation aspects, including

class design, key methods, and workﬂow integration

within Qiskit. In Section 5, we describe experimental

results showcasing circuit veriﬁcation in both simu-

lated environments with noise simulation and perfect

simulation, followed by a discussion of the practical

advantages and limitations of the approach. Finally,

in Section 6 we conclude with an overview of future

directions, potential optimizations, and the broader

signiﬁcance of automated circuit assertions in quan-

tum computing.

2 STATE OF THE ART

In recent years, quantum computing has advanced

rapidly, promising computational advantages in ar-

eas such as optimization, cryptographic analysis, and

quantum simulation (Piattini et al., 2021). However,

verifying the correctness of quantum computations

poses new challenges that classical methods cannot

readily address (Arias et al., 2023). Gate noise, qubit

decoherence, and the collapse of quantum states upon

measurement all contribute to the difﬁculty of de-

bugging quantum programs (Metwalli, 2024). Even

straightforward techniques like inspecting intermedi-

ate states become prohibitive, since measurements ir-

revocably alter quantum superpositions (Hoag et al.,

2019).

Much of the existing literature highlights two

main strategies for quantum circuit veriﬁcation:

measurement-intensive approaches and direct ﬁdelity

or overlap checks. Measurement-intensive methods

can involve state tomography or repeated sampling,

but they tend to be resource-heavy and scale poorly

with increasing qubit numbers (Guo and Yang, 2024).

Partial tests have been introduced to mitigate com-

plexity, yet these may fail to capture subtle deviations.

By contrast, overlap checks through protocols like the

Swap Test estimate how closely two states (or two cir-

cuits’ outputs) coincide without requiring a full recon-

struction of the state (Foulds et al., 2021).

While the Swap Test is a standard method for es-

timating state overlap, recent works have explored al-

ternative approaches to reduce circuit depth and im-

prove efﬁciency on near-term quantum devices. For

instance, (Cincio et al., 2018) used machine learn-

ing to discover algorithms with shorter depths than

the Swap Test for computing state overlap, including

methods that use CNOT gates and achieve constant

depth. Similarly, (Garc

ıa de la Barrera Amo et al.,

2022)presented a method for automatic generation of

test circuits that verify quantum deterministic algo-

IQSOFT 2025 - 1st International Conference on Quantum Software

rithms using a CNOT-based test for state compari-

son. Our framework, AssertsQ, complements these

efforts by providing a user-friendly interface for inte-

grating various assertion methods, including the Swap

Test and measurement-based validations, directly into

Qiskit workﬂows

Despite these efforts, no consensus exists on a

universal debugging protocol for quantum software.

Some investigators explore specialized frameworks

that unify entanglement checks, circuit optimization

passes, and classical post-processing, but many re-

main narrowly focused on either ﬁnal-state ﬁdelity

(Ramalho et al., 2024) or distribution comparison in

the computational basis (Hashim et al., 2023). The

latter often involves metrics such as Total Variation

Distance (TVD) (Dahlhauser and Humble, 2024),

which can reveal discrepancies in measurement out-

comes but generally overlook phase-sensitive infor-

mation. Meanwhile, advanced noise modeling is in-

creasingly recognized as crucial for capturing the per-

formance of near-term quantum devices (Mundada

et al., 2019), yet many veriﬁcation proposals treat

hardware imperfections only superﬁcially or not at

all.

Recent approaches have begun to incorporate

quantum assertions, that is, specialized checkpoints

within algorithms, into standard development work-

ﬂows (Memon et al., 2024). These assertions aim to

detect anomalies early by targeting either the ampli-

tude overlap with an expected state or the probability

distribution of measurement outcomes. Nevertheless,

the difﬁculties posed by state collapse and limited

qubit availability mean that robust frameworks for au-

tomated veriﬁcation are still emerging. Tools must

balance direct ﬁdelity checks with measurement-

based methods and accommodate the realistic noise

models of modern quantum processors. Overcoming

these constraints is pivotal to ensuring that quantum

algorithms remain correct and resilient to hardware

imperfections.

Besides assertion-based methods, other testing

techniques have been adapted for quantum software.

Metamorphic testing, which leverages relations be-

tween multiple program executions to verify correct-

ness without an oracle, has been applied to quan-

tum programs. For instance, MorphQ (Paltenghi and

Pradel, 2023) uses metamorphic relationships to test

the Qiskit platform, uncovering numerous bugs. More

recently, (Pontolillo and Mousavi, 2024) introduced

an automated debugging technique based on delta de-

bugging and property-based testing for quantum pro-

grams, which identiﬁes changes causing regression

test failures. Similarly, (Abreu et al., 2022) propose

metamorphic testing for oracle quantum programs to

overcome the measurement problem. On the other

hand, mutation testing, which assesses test suite qual-

ity by introducing artiﬁcial faults, has also been ex-

plored.(Fortunato et al., 2022) introduce QMutPy, a

mutation testing tool for Qiskit, demonstrating its

effectiveness on real quantum programs. Addition-

ally, (Wang et al., 2022) present a multi-objective

search approach for generating mutation-based tests

for quantum programs. A recent empirical evaluation

by (Usandizaga et al., 2023) on quantum circuit mu-

tations provides insights into which mutants are most

effective for testing quantum software. A comprehen-

sive survey by (Paltenghi and Pradel, 2024) provides

an overview of various testing and analysis techniques

for quantum software, highlighting the growing inter-

est and diversity in this ﬁeld.

3 METHODOLOGY

Quantum circuits exhibit unique challenges absent in

classical computing: measurement collapses super-

positions, gate errors compound as circuits deepen,

and interference can mask intermediate states. To

address these concerns in a principled manner, we

propose a methodology leveraging three main com-

ponents: the Swap Test for circuit or state over-

lap, amplitude-based state initialization to compare

against a known reference, and a measurement-based

approach using the TVD metric. Collectively, these

strategies tackle typical NISQ-era constraints such as

limited qubits, high noise levels, and restricted oppor-

tunities for measurement, offering a ﬂexible veriﬁca-

tion suite applicable to various quantum algorithms.

3.1 Circuit Assertion Using Swap Tests

The Swap Test has emerged as a powerful means

to evaluate how closely two quantum states resem-

ble each other without performing a full, resource-

intensive state tomography. Conceptually, one ap-

pends an ancilla qubit to the two states under com-

parison and performs a conditional swap followed by

a ﬁnal measurement. The probability of measuring

the ancilla in the |0⟩ state corresponds directly to the

squared overlap (or similarity) of the two states(see

Appendix):

Similarity = 2 ×P(|0⟩) −1.

For circuit assertions, one can think of each quan-

tum circuit as producing an output state. By treating

these outputs as the two states in question, the Swap

Test reveals whether the circuits behave equivalently

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

within a chosen ﬁdelity threshold. This approach cir-

cumvents the need to measure and compare each qubit

individually, thus minimizing both the measurement

overhead and the risk of disturbing fragile superposi-

tions. As a result, the Swap Test serves as a concise,

powerful gauge for circuit-to-circuit or circuit-to-state

equivalences.

3.1.1 Reconstructing and Comparing States

Beyond comparing two circuits, AssertsQ also evalu-

ates a circuit’s output against a known reference state

vector. In such cases, one must prepare the target (ref-

erence) state vector as a second quantum system. In-

ternally, Qiskit’s amplitude-based approach as intro-

duced in its initialize method(Iten et al., 2016) can

create a circuit that produces the target state vector

from |0⟩. This target system is then brought into the

Swap Test framework. Measuring how often the an-

cilla remains in |0⟩ indicates whether the ﬁnal circuit

output matches the reference state’s amplitudes. Cru-

cially, this method does not necessitate direct tomog-

raphy, making it more scalable to multi-qubit states.

3.2 Measurement-Based Validation:

Total Variation Distance (TVD)

While the Swap Test reveals quantum overlaps, many

practical algorithms are ultimately concerned with

measurement outcomes. Moreover, in large multi-

qubit circuits, duplicating circuit size might not be

able due to the hardware capabilities.For these sce-

narios, AssertsQ provides a measurement-based val-

idation that compares classical probability distribu-

tions through the TVD. Each circuit is executed to

produce a bitstring distribution in the computational

basis. Given two distributions P and Q, the TVD is

deﬁned as

TVD(P,Q) =

∑



P(ω) −Q(ω)



where ω ranges over all possible bitstrings. A TVD

near zero signiﬁes that both circuits produce near-

identical distributions, whereas a larger TVD indi-

cates signiﬁcant discrepancies in measurement out-

comes (Hashim et al., 2023). This approach excels

in scenarios where the classical output is the main ﬁg-

ure of merit, such as sampling-based or combinational

quantum algorithms (Madsen et al., 2022).

3.3 Noise Handling and Tolerance

Near-term quantum devices—commonly referred to

as Noisy Intermediate-Scale Quantum (NISQ) hard-

ware—exhibit gate, readout, and decoherence errors

that can obscure correct circuit behavior(Khan et al.,

2024). Consequently, AssertsQ introduces tolerance

thresholds in both the Swap Test and TVD calcula-

tions, providing a buffer against minor ﬂuctuations. If

the computed overlap (or distribution similarity) re-

mains within the speciﬁed tolerance, the circuits or

states are considered “equivalent” for practical pur-

poses. At the same time, developers can opt for

stricter thresholds when using higher-ﬁdelity simula-

tors or hardware calibrations.

Additionally, the tool accounts for three primary

execution environments:

• Noiseless Simulation: Provides an ideal baseline,

ignoring all hardware imperfections.

• Noisy Simulation: Incorporates realistic error

models, thus approximating a real device’s per-

formance.

• Real Hardware: Executes the assertion on an ac-

tual quantum processor for deﬁnitive, real-world

veriﬁcation.

In all cases, careful transpilation ensures that the log-

ical gates are mapped effectively to the device’s phys-

ical qubits, factoring in connectivity constraints and

gate availability. This interplay of error modeling, tol-

erance tuning, and backend selection yields a compre-

hensive strategy that mitigates noise while remaining

ﬂexible enough to handle evolving hardware condi-

tions.

3.4 Experimental Setup for Tool

Validation

To validate AssertsQ, we designed a set of ex-

periments targeting canonical quantum algorithms

of varying complexity: Greenberger-Horne-Zeilinger

state (GHZ), quantum Fourier transform (QFT) and

Grover search. Each algorithm was tested at two

scales (5 and 10 qubits) to observe how circuit depth

inﬂuences veriﬁcation outcomes (see Section 5).

In both perfect and noisy simulation modes, GHZ

circuits generate a maximally entangled state through

a single Hadamard followed by a chain of CNOTs,

while QFT circuits apply phase shifts and Hadamard

gates in a pattern crucial for phase-estimation tasks.

Grover’s algorithm, meanwhile, demonstrates ampli-

tude ampliﬁcation and oracle-based state marking.

For the noisy simulations, we employed a noise model

generated from the calibrations of ibm

sherbrooke

mimicking realistic two-qubit gate error rates (e.g.,

≈3.51×10

−3

) as well as single-qubit and readout er-

ror parameters. Such a model allows us to emulate the

This calibrations where retrieved from 3 Feb 2025 to 6

Feb 2025.

IQSOFT 2025 - 1st International Conference on Quantum Software

performance constraints of this 127-qubit device, cap-

turing the inﬂuences of gate inﬁdelity and crosstalk

without requiring direct hardware access.

By comparing outcomes from noiseless vs. noisy

simulations, and evaluating metrics such as ﬁdelity

(from the Swap Test) and TVD (from measurement-

based checks), we benchmark both the robustness and

granularity of our assertion methods. This layered ex-

perimental design reveals how AssertsQ behaves un-

der increasing levels of circuit complexity and noise,

highlighting its capacity to catch meaningful errors

and degrade gracefully in the face of hardware im-

perfections. Lastly, these experiments are transpiled

using the qiskit pass manager with a default optimiza-

tion level of 3 and launched with 1024 shots.

4 IMPLEMENTATION

This section provides details on how AssertsQ is

structured at the code level, illustrates typical us-

age scenarios, and demonstrates how developers can

incorporate its capabilities into their existing Qiskit

workﬂows. The implementation comprises a set of

classes and functions that collectively offer circuit as-

sertion functionalities based on both the Swap Test

and measurement-based comparisons.

4.1 Code Overview

The core functionality of AssertsQ resides in

the Assertions class. This class includes

three primary methods for circuit validation:

assert equals, assert equals state, and

assert equals measure. Each method addresses

a different aspect of quantum circuit veriﬁcation.

The ﬁrst two employ the Swap Test to measure

circuit or state similarity, while the third applies a

measurement-based approach, computing the TVD

to determine equivalence of output distributions. All

methods share a similar structure: they accept the

circuits (or a circuit and target state), a tolerance

parameter, and an AssertionOptions object that

encapsulates backend selection, noise conﬁguration,

and custom transpilation pass managers. By default,

the code sets up specialized quantum registers

(including an ancilla qubit for the Swap Test) and

composes a dedicated circuit to execute the test

logic. Once the circuit is transpiled and submitted

to a chosen backend via SamplerV2, the returned

measurement data is interpreted to produce a ﬁdelity

metric or a distribution-based comparison result.

An auxiliary class, AssertionOptions which

validates user-speciﬁed settings such as whether to

run on simulated or real quantum hardware, whether

noise modeling should be enabled, and which pass

manager to invoke. If the user supplies invalid creden-

tials or an incompatible conﬁguration, the class raises

appropriate errors or warnings. When the user does

not specify a backend, it can attempt to automatically

select an available device. This design ensures a clear

separation between the high-level assertion logic and

lower-level infrastructure concerns, including authen-

tication and hardware interaction.

4.2 Simulation, Noise Modeling, and

Hardware Execution

AssertsQ manages both ideal and noisy simulations

through Qiskit Aer, providing a seamless way to test

quantum circuits under realistic error conditions. In

the default noiseless mode, it employs the standard

Aer simulator to generate perfect results, establishing

a baseline for ﬁdelity and distribution checks. When

noisy simulation is requested, AssertsQ loads an er-

ror model derived from calibration data (for example,

gate and readout inﬁdelities) using Qiskit Aer’s noise

modeling features. This allows developers to gauge

algorithm performance under conditions that approx-

imate actual hardware runs.

If real device execution is required, AssertsQ

makes use of QiskitRuntimeService to authenticate

with IBM Quantum backends. By switching its con-

ﬁguration to a non-simulator setting, AssertsQ re-

trieves the speciﬁed hardware or automatically se-

lects one based on availability. The same transpila-

tion routines and assertion methods apply: the code

compiles the circuit for the chosen quantum device,

submits a job via Qiskit’s runtime, and interprets the

measurement outcomes to yield ﬁdelity metrics or to-

tal variation distance comparisons. This uniﬁed ap-

proach enables developers to validate circuits consis-

tently across simulation and real-device runs, directly

from the same assertion framework.

4.3 Sample Usage

In this subsection, we illustrate how AssertsQ can be

seamlessly integrated into a typical Qiskit workﬂow

to validate quantum circuit correctness using a Bell

state as example see Figure 1.

•

c :



Figure 1: Bell state circuit.

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

To begin, a developer imports the re-

quired classes—namely, Assertions and

AssertionOptions—and constructs one or more

quantum circuits using Qiskit’s standard API. For

example, two Bell state circuits can be generated,

and subsequently compared via AssertsQ’s built-

in methods. When invoking the assert equals

method , the framework automatically composes

an ancillary circuit that embeds the swap test. This

process involves appending an ancilla qubit, applying

Hadamard gates, and executing controlled-swap op-

erations on the qubits of the circuits under evaluation.

The resulting measurement of the ancilla, combined

with a user-deﬁned tolerance parameter, produces a

similarity score that conﬁrms whether the circuits are

functionally equivalent,as seen in Figure 2.

circuit a

•

circuit a

circuit b

•

circuit b

ancilla :

• •

result :



Figure 2: Bell state Assert Equals.

In another scenario , a circuit’s ﬁnal state is com-

pared against a known target state vector through the

assert equals state method. In this case, As-

sertsQ augments the original circuit by initializing a

separate register to represent the reference state prior

to performing the swap test. This approach enables a

precise quantiﬁcation of the overlap between the cir-

cuit’s output and the intended state, yielding a ﬁdelity

measure that asserts correctness, as seen in Figure 3.

•

target

|ψ⟩(0.7071,0,0,0.7071)

target

ancilla :

• •

result :



Figure 3: Bell state Assert Equals State.

For instances where the primary focus

is on the ﬁnal measurement outcomes, the

assert equals measure method is employed.

Here, see ﬁgure 4 , AssertsQ appends measurement

operations to both distinct input circuits, collects the

resultant bitstring counts, and computes the TVD

between the corresponding probability distributions.

Throughout these examples, the user beneﬁts from

the option to enable verbose ﬂag output, which prints

•

c :



(−π/2)

•

(−π/2)

c :



Figure 4: Comparing two distinct circuits with Assert

Equals Measure.

intermediate metrics and ﬁnal similarity scores. This

feature proves invaluable for debugging purposes, as

it provides immediate insight into the performance of

the circuit assertions and facilitates iterative reﬁne-

ment.

4.4 Workﬂow Integration

Developers can seamlessly integrate AssertsQ into

their standard Qiskit-based workﬂows. After build-

ing or modifying a quantum circuit, they invoke

the desired assertion method, passing in the relevant

AssertionOptions conﬁguration. Under the hood,

the code composes and transpiles an augmented cir-

cuit that embeds the Swap Test or measurement in-

structions. By leveraging Qiskit’s SamplerV2, it sup-

ports both local simulators and remote quantum de-

vices. The execution results are returned in a struc-

tured form, which AssertsQ analyzes to produce a

deﬁnitive pass/fail statement along with a numerical

similarity or distance metric. If an assertion fails due

to exceeding the speciﬁed tolerance, developers im-

mediately receive an exception with a detailed mes-

sage describing the discrepancy, enabling rapid feed-

back loops for circuit debugging.

This integrated process reduces the burden of writ-

ing custom veriﬁcation scripts and leverages estab-

lished quantum programming paradigms. By au-

tomating tasks such as circuit compilation, backend

orchestration, and result interpretation, AssertsQ en-

sures that development teams can focus on algorithm

design and performance optimization, conﬁdent that

any functional regressions or unintended circuit trans-

formations will be detected promptly.

5 TOOL VALIDATION

5.1 Results

This section presents the main ﬁndings from running

AssertsQ on three representative quantum algorithms

(GHZ, QFT, and Grover) at different qubit scales (5

and 10) as presented in Section 3 As explained in the

methodology, each circuit was tested in both noise-

less and noisy simulation modes (ibm sherbrooke-

inspired model).

IQSOFT 2025 - 1st International Conference on Quantum Software

Table 1: Results for assert equals with GHZ, QFT, and

Grover Circuits.

Circuit Qubits Noiseless Fidelity Noisy Fidelity

GHZ 5 1.0 0.4785

GHZ 10 1.0 0.1406

QFT 5 1.0 0.3633

QFT 10 1.0 0.04297

Grover 5 1.0 0.1269

Grover 10 1.0 0.0039

Table 1 reports the ﬁdelity of GHZ, QFT, and

Grover circuits when tested with assert equals.

The ideal (noiseless) scenario yields ﬁdelity 1.0

across all circuits, conﬁrming perfect overlap. Un-

der simulated noise however, ﬁdelity degrades sig-

niﬁcantly, especially for circuits with deeper gate se-

quences such as Grover of 10 qubits and QFT of 10

qubits.

Table 2: Results for assert equals measure with GHZ,

QFT, and Grover Circuits.

Circuit Qubits Noiseless TVD Noisy TVD

GHZ 5 0.0185 0.0361

GHZ 10 0.0263 0.0830

QFT 5 0.0996 0.1035

QFT 10 0.5332 0.5313

Grover 5 0.1201 0.0664

Grover 10 0.5292 0.5244

A measurement-based comparison via

TVD (AssertsQ) was performed with the

assert equals measure method. Table 2 shows

how GHZ, QFT, and Grover circuits produce output

distributions that remain close under ideal conditions

but diverge in the presence of noise. For higher qubit

counts, deeper gate depths lead to larger TVD values.

Table 3: Results for assert equals state with GHZ,

QFT, and Grover Circuits.

Circuit Qubits Noiseless Fidelity Noisy Fidelity

GHZ 5 1.0 0.3184

GHZ 10 1.0 Incomplete

QFT 5 1.0 0.2461

QFT 10 1.0 0.0039

Grover 5 1.0 0.2051

Grover 10 1.0 0.0332

Lastly, assert equals state was used to check

whether a circuit’s ﬁnal state matched a known ref-

erence state. Table 3 reveals that noiseless ﬁdelity

remains at 1.0, whereas, as expected, noisy ﬁdelity

deteriorates sharply as the number of qubits and cir-

cuit depth increase (for instance, QFT with 10 qubits

drops near 0.0039). The assert equals state

noisy simulated experiment for GHZ with 10 qubits

was not fully executed due to our local hardware lim-

itations due to the large depth of the proper experi-

ment, more info about the hardware conducted for the

experiments see 6.

Table 4: Circuit depths before and after transpilation for all

the techniques presented in this paper. (a) assert equals,

(b) assert equals state, (c) assert equals measure.

Circuit Qubits Before After (a) After (b) After (c)

GHZ 5 5 223 454 25

GHZ 10 10 491 7095 33

Grover 5 13 893 770 493

Grover 10 13 7748 7689 6895

QFT 5 34 409 395 109

QFT 10 74 902 6543 423

To highlight the relationship between circuit

depth and noise impact Table 4 track both the

original depth (before embedding the swap test

or measurement blocks) and the transpiled depth.

For techniques requiring extra gates (for example,

assert equals state needs reference-state initial-

ization plus controlled swaps), the depth can multiply

exponentially.

Figures 5, 6, and 7 provide a deeper look at how

ﬁdelity and total variation distance (TVD) vary with

circuit depth and qubit count. In Figure 5, we ob-

serve that GHZ maintains comparatively higher ﬁ-

delity than QFT and Grover when the circuit involves

fewer qubits, but all three sharply decline at 10 qubits

under noisy conditions. Figure 6 captures the signiﬁ-

cant jump in transpiled circuit depth (shown on a log

scale) once additional gates for state assertion or mea-

surement are introduced. GHZ, for instance, shows

a notable increase in depth when asserting its state

vector against a reference state vector, whereas direct

measurement remains less expansive in gate count.

Finally, Figure 7 illustrates how each technique’s ﬁ-

delity (top two plots) drops as circuit size grows, par-

ticularly for QFT and Grover at 10 qubits, and how

the measurement-based TVD (bottom plot) escalates

above 0.5 for larger circuits. Collectively, these plots

mirror the tabulated results: circuits that are deeper or

have more qubits become more susceptible to noise,

and the choice of veriﬁcation method (swap test, state

assertion, or direct measurement) can greatly affect

both circuit overhead and accuracy.

5.2 Discussion

The experimental results obtained from validating As-

sertsQ across the GHZ, QFT, and Grover algorithms

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

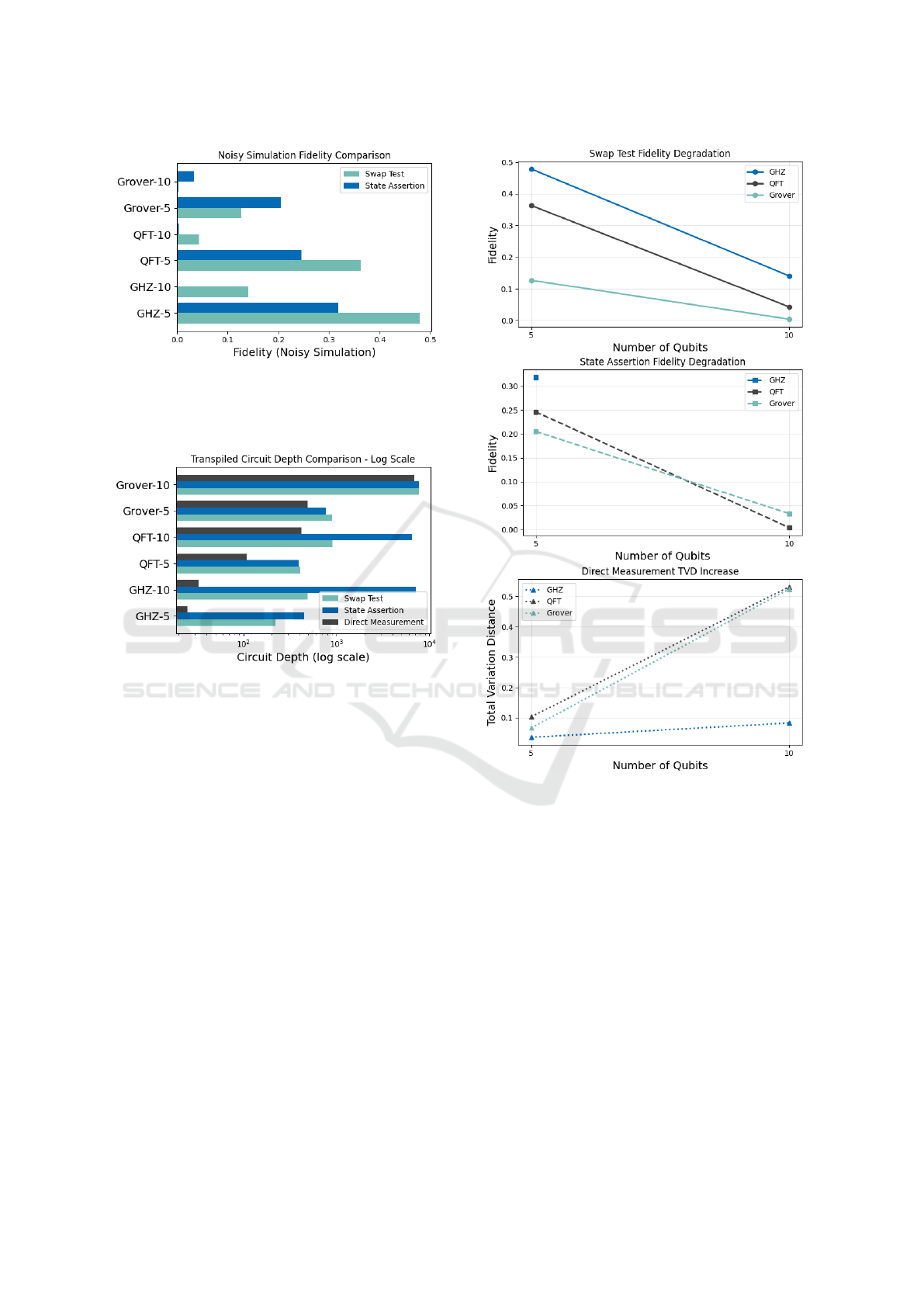
Figure 5: Fidelity Degradation with qubit count under noisy

conditions for Swap Test vs. State Assertion Methods. The

notation works as follows: ”algorithm-number of qubits

tested” (e.g. GHZ-10 means GHZ for 10 qubits).

Figure 6: Transpiled Circuit Depth Comparison for the

3 studied methods: Direct Measurement, Swap Test, and

State-Assertion Method. The notation works as follows:

”algorithm-number of qubits tested” (e.g. GHZ-10 means

GHZ for 10 qubits).

under both noiseless and noisy conditions reveal crit-

ical insights into the framework’s performance and

its susceptibility to key quantum circuit parameters:

circuit depth and the number of qubits. These ﬁnd-

ings, as summarized in Tables1, 2, 3, and 4, along-

side Figures5, 6, and 7, underscore the interplay be-

tween quantum circuit complexity, noise effects, and

the choice of assertion method. Below, we provide a

detailed analysis of the results and explain the under-

lying reasons for their observed trends.

In the noiseless simulation environment, all as-

sertion methods consistently achieve perfect ﬁdelity

(1.0) or near-zero TVD across all tested algorithms

and qubit scales. This is evident in Tables 1, 3, and

2 for the ideal cases. The perfect ﬁdelity reﬂects the

absence of noise, allowing the quantum states or out-

put distributions to align precisely with their expected

counterparts.

Under noisy conditions, the performace of As-

sertsQ degrades signiﬁcantly, with ﬁdelity decreasing

Figure 7: Fidelity and TVD Trends vs. Qubit Count.

and TVD increasing as circuit depth grows. This trend

is most pronounced in algorithms with inherently

deeper circuits, such as QFT and Grover, compared

to the relatively shallow GHZ circuit. The primary

reason for this degradation is the accumulation of er-

rors for deeper cicuits. Each quantum gate introduces

a small probability error, such as gate inﬁdelity or de-

coherence in noisy environments. As circuit depth

increases, the number of gates grows, amplyﬁng the

cumulative error. For example, QFT involves a series

of Hadamard and controlled-phase gates scaling with

O(n

), while Grover‘s algorithm applies multiple iter-

ations of the Grover operator, each adding gates pro-

portional to the qubit count. In contrast, GHZ’s depth

scales linearly with n due to its single Hadamard fol-

lowed by a CNOT chain, resulting in fewer opportuni-

ties for error accumulation. This depth-dependent er-

IQSOFT 2025 - 1st International Conference on Quantum Software

ror propagation explains why GHZ maintains higher

ﬁdelity under noise compared to QFT and Grover, as

visualized in Figure 5.

The number of qubits further exacerbates

performance degradation under noise. For

swap test-based methods (assert equals and

assert equals state), requires 2n + 1 qubits,

where n is the number of qubits in the original circuit,

plus one ancilla qubit. This doubling arises because,

as stated before, the swap test compares two n-qubit

states using controlled swap operations mediated by

the ancilla. As n increases from 5 to 10, the total

system size grows from 11 to 21 qubits, respectively.

As for assert equals measure avoids the swap

test, using only n qubits and appending measure-

ments, resulting in shallower circuits (e.g. 34 for

10-qubit GHZ), relying solely on classical post-

processing. However, its TVD metric (Table2)

captures only classical output distributions, missing

quantum state details and yielding higher TVD values

(e.g. 0.62 for 10-qubit QFT) under noise. Quantifying

the precise level of improvement offered by a new tool

within the evolving ﬁeld of Quantum Software Engi-

neering (QSE) is inherently complex, as noted by re-

viewers. However, the assertion framework presented

here introduces tangible beneﬁts to the development

and veriﬁcation workﬂow for quantum circuits.

We propose a tiered strategy for quantum cir-

cuit veriﬁcation that accommodates varying hard-

ware constraints, debugging goals, and developmen-

tal phases. Measurement-based veriﬁcation (‘as-

sert equals measure‘) serves as a practical starting

point for rapid prototyping on NISQ devices or when

usage quotas are limited, as demonstrated by the 34-

gate requirement for verifying a 10-qubit QFT com-

pared to the 1297 gates needed for swap-test-based

approaches. Although this method is less sensitive

to the full quantum state, it enables quick iterations

for early-stage development. By contrast, the swap-

test-based approach (‘assert equals‘) strikes a mid-

dle ground, detecting subtler phase-sensitive errors

such as those arising in QAOA and VQE while re-

quiring 2n+1 qubits. This increased resource cost is

justiﬁed by its ability to uncover mistakes that the

measurement-based method might overlook. For ap-

plications needing the highest possible ﬁdelity, ex-

act state veriﬁcation (‘assert equals state‘) delivers

the strictest validation and is invaluable for ﬁnal cir-

cuit conﬁrmation and error-correcting code develop-

ment. However, due to its steep computational ex-

pense, it is most appropriate for circuits with up to

around ten qubits. By beginning with measurement-

based checks, then adopting the swap test for phase-

sensitive debugging, and ultimately employing exact

state veriﬁcation for ﬁnal or mission-critical analyses,

developers can balance resource expenditure with ver-

iﬁcation accuracy throughout the lifecycle of quantum

application design.

Beyond its core validation capabilities, AssertsQ

delivers critical advances to quantum software en-

gineering by automating veriﬁcation tasks—such as

swap tests or custom comparison circuits—that would

otherwise require ad hoc approaches, thereby sub-

stantially reducing veriﬁcation time. Additionally,

its standardized assertion interface fosters consistency

and reusability across diverse algorithms (e.g., GHZ,

QFT, Grover’s), enabling a more systematic, test-

driven workﬂow that integrates seamlessly with con-

tinuous integration pipelines. Finally, the frame-

work’s conﬁgurable tolerance thresholds align with

NISQ-era hardware realities, allowing developers

to incrementally adjust these thresholds based on

hardware-speciﬁc noise and thus facilitate nuanced

error analysis beyond binary pass/fail outcomes. This

capability is especially beneﬁcial when moving algo-

rithms from ideal simulations to noisy devices, re-

moving the need for separate noise analysis tools.

In addition to this, as discussed while noise

does affect the ﬁdelity of the assertions, particularly

for deeper circuits, AssertsQ provides mechanisms

such as adjustable tolerances and multiple veriﬁcation

methods to accommodate these challenges. In indus-

trial settings, where quantum software development

often involves iterative testing on simulators before

hardware deployment, AssertsQ can play a crucial

role in verifying circuit correctness at various stages.

Furthermore, for smaller-scale circuits or those with

manageable depths, the tool maintains sufﬁcient ﬁ-

delity to detect errors effectively. Thus, we contend

that AssertsQ with slight improvements has indeed

potential to be industrially applicable, offering a prac-

tical solution for quantum software debugging in the

current NISQ era.

AssertsQ provides distinctive contributions to

quantum circuit validation compared to existing

frameworks AssertsQ offers a resource-efﬁcient and

integrated solution for quantum circuit validation. By

using the swap test, it validates circuits with only

2n+1 qubits—far more scalable than measurement-

intensive tomography (Yuen, 2023). Unlike frame-

works limited to either state ﬁdelity (Vadali et al.,

2024) or distribution checks (Maciejewski et al.,

2023), AssertsQ uniﬁes both, crucial for detecting

phase errors that TVD-based methods alone would

miss. Its noise-aware design features conﬁgurable

thresholds, balancing theoretical rigor with NISQ-

era feasibility. Furthermore, direct integration with

Qiskit’s transpilation pipeline lowers the adoption

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

barrier, making AssertsQ a practical and scalable

toolkit for quantum software veriﬁcation.

In conclusion, AssertsQ effectively veriﬁes quan-

tum circuits in ideal conditions but reveals the chal-

lenges of noise, circuit depth, and qubit scaling in re-

alistic settings. Its swap test-based methods, requiring

2n + 1 qubits,offer a compact alternative to tomog-

raphy, yet their efﬁcacy diminishes for large, deep

circuits on NISQ devices whereas the measurement-

based assertion offers a lighter alternative for verify-

ing output distributions, though it sacriﬁces quantum

state speciﬁcity.

These insights inform quantum software develop-

ment by highlighting trade-offs between veriﬁcation

accuracy and practical feasibility, paving the way for

future reﬁnements in quantum debugging tools.

6 CONCLUSION

The development of AssertsQ demonstrates that au-

tomated, swap-test-based quantum assertions can be

both practical and adaptable for a wide range of

circuit veriﬁcation tasks. By seamlessly integrat-

ing with Qiskit and supporting multiple veriﬁca-

tion modes—including direct circuit-to-circuit com-

parison, state overlap checks, and measurement-

based distribution comparisons—AssertsQ simpliﬁes

the process of diagnosing and correcting circuit-level

errors. The framework’s reliance on either real or sim-

ulated backends, coupled with adjustable tolerance

thresholds, accommodates both noisy intermediate-

scale quantum devices and idealized simulation envi-

ronments. Thus, aiding the circuit veriﬁcation process

and accelerating the development of new and accurate

quantum software.

Experimental results show that each veriﬁcation

approach has distinct trade-offs in terms of circuit

depth, susceptibility to noise, and granularity of

the diagnostic information provided. Measurement-

based checks via TVD are comparatively simpler but

can overlook subtle state overlaps, while swap-test-

based assertions offer deeper insight at the expense of

additional qubits and gates. These extra resources be-

come especially signiﬁcant for multi-qubit or highly

entangled circuits, where transpilation and noise ac-

cumulation pose notable challenges. Nonetheless, the

ability of AssertsQ to capture discrepancies in both

simulated and real-world conditions underscores its

potential value in current and forthcoming quantum

applications.

Although AssertsQ currently relies heavily on

simulations, rigorous testing on real quantum hard-

ware (e.g., IBM Quantum) is essential to conﬁrm

its noise resilience and empirically align simulation

results with physical behavior. Extending cross-

platform support to frameworks like Cirq and Ama-

zon Braket will further broaden its applicability by

accommodating different circuit representations and

backends. Robust diagnostics also motivate the cre-

ation of assertion coverage metrics—akin to classi-

cal code coverage—to guide where and how often

quantum assertions should be placed for maximum

effect and therefore being capable of knowing how

much these assertions could improve quantum com-

puting software development. Coupling these metrics

with IDE integration (e.g., VS Code) would enable

live ﬁdelity visualization, assertion breakpoints, and

automated diagnostics within a familiar development

workﬂow.

Since many assertions depend on ancillary qubits,

minimizing their overhead and vulnerability to noise

is critical; strategies such as probabilistic error cancel-

lation (PEC), extrapolation, advanced transpiler opti-

mizations, and careful qubit mapping can help pre-

serve circuit ﬁdelity. Finally, scaling to larger cir-

cuits (beyond 50 qubits) calls for approaches like par-

tial tomography, circuit cutting, and adaptive proto-

cols informed by calibration data or machine learn-

ing. These collective enhancements will strengthen

AssertsQ as a robust debugging platform for near-

term quantum systems and establish a foundation for

enduring veriﬁcation methodologies.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the partial

ﬁnancial support by Ministry of Science (project

QSERV-UD, PID2021-124054OB-C33). Addition-

ally, Mr. Danel Arias thanks the Basque-Q strategy

of Basque Government for partially funding his doc-

toral research at the University of Deusto, within the

Deusto for Knowledge - D4K team on applied arti-

ﬁcial intelligence and quantum computing technolo-

gies.

REFERENCES

Abreu, R., Fernandes, J. P., Llana, L., and Tavares, G.

(2022). Metamorphic testing of oracle quantum pro-

grams. In Proceedings of the 3rd International Work-

shop on Quantum Software Engineering, pages 16–

23.

Arias, D., Garc

ıa Rodr

ıguez de Guzm

an, I., Rodr

ıguez, M.,

Terres, E. B., Sanz, B., Gaviria de la Puerta, J., Pastor,

I., Zubillaga, A., and Garc

ıa Bringas, P. (2023). Let’s

do it right the ﬁrst time: Survey on security concerns

IQSOFT 2025 - 1st International Conference on Quantum Software

in the way to quantum software engineering. Neuro-

computing, 538:126199.

Arias, D., Sanz, B., de la Puerta, J. G., Pastor, I., and

Bringas, P. G. (2022). A repeated mistake is a choice:

Considering security issues and risks in quantum com-

puting from scratch. In 14th International Confer-

ence on Computational Intelligence in Security for In-

formation Systems and 12th International Conference

on European Transnational Educational (CISIS 2021

and ICEUTE 2021) 14, pages 156–166. Springer.

Cincio, L., Subas¸ı, Y., Sornborger, A. T., and Coles, P. J.

(2018). Learning the quantum algorithm for state

overlap. New Journal of Physics, 20(11):113022.

Dahlhauser, M. L. and Humble, T. S. (2024). Benchmarking

characterization methods for noisy quantum circuits.

Physical Review A, 109(4):042620.

Fortunato, D., Campos, J., and Abreu, R. (2022). Muta-

tion testing of quantum programs: A case study with

qiskit. IEEE Transactions on Quantum Engineering,

3:1–17.

Foulds, S., Kendon, V., and Spiller, T. (2021). The

controlled swap test for determining quantum en-

tanglement. Quantum Science and Technology,

6(3):035002.

Garc

ıa de la Barrera Amo, A., Serrano, M. A., Garc

ıa

Rodr

ıguez de Guzm

an, I., Polo, M., and Piattini,

M. (2022). Automatic generation of test circuits

for the veriﬁcation of quantum deterministic algo-

rithms. In Proceedings of the 1st International Work-

shop on Quantum Programming for Software Engi-

neering, pages 1–6.

Garcia-Escartin, J. C. and Chamorro-Posada, P. (2013).

Swap test and hong-ou-mandel effect are equivalent.

Physical Review A—Atomic, Molecular, and Optical

Physics, 87(5):052330.

Guo, Y. and Yang, S. (2024). Scalable quantum state tomog-

raphy with locally puriﬁed density operators and local

measurements. arXiv preprint arXiv:2307.16381.

Hashim, A., Seritan, S., Proctor, T., Rudinger, K., Goss, N.,

Naik, R. K., Kreikebaum, J. M., Santiago, D. I., and

Siddiqi, I. (2023). Benchmarking quantum logic op-

erations relative to thresholds for fault tolerance. npj

Quantum Information, 9(1):109.

Hoag, E., Zhu, M., and Decker, S. (2019). qdb: Inserted

tomography for breakpoint debugging in.

Iten, R., Colbeck, R., Kukuljan, I., Home, J., and Chri-

standl, M. (2016). Quantum circuits for isometries.

Physical Review A, 93(3):032318.

Kang, C. G., Lee, J., and Oh, H. (2024). Statistical testing

of quantum programs via ﬁxed-point amplitude am-

pliﬁcation. Proceedings of the ACM on Programming

Languages, 8(OOPSLA2):140–164.

Khan, M. U., Kamran, M. A., Khan, W. R., Ibrahim, M. M.,

Ali, M. U., and Lee, S. W. (2024). Error mitigation in

the nisq era: Applying measurement error mitigation

techniques to enhance quantum circuit performance.

Mathematics, 12(14):2235.

Li, G., Zhou, L., Yu, N., Ding, Y., Ying, M., and Xie, Y.

(2019). Proq: Projection-based runtime assertions for

debugging on a quantum computer. arXiv preprint

arXiv:1911.12855.

Maciejewski, F. B., Puchała, Z., and Oszmaniec, M. (2023).

Operational quantum average-case distances. Quan-

tum, 7:1106.

Madsen, L. S., Laudenbach, F., Askarani, M. F., Rortais,

F., Vincent, T., Bulmer, J. F., Miatto, F. M., Neuhaus,

L., Helt, L. G., Collins, M. J., et al. (2022). Quantum

computational advantage with a programmable pho-

tonic processor. Nature, 606(7912):75–81.

Memon, Q. A., Al Ahmad, M., and Pecht, M. (2024). Quan-

tum computing: navigating the future of computation,

challenges, and technological breakthroughs. Quan-

tum Reports, 6(4):627–663.

Metwalli, S. A. F. M. (2024). A suite for testing and debug-

ging quantum programs.

Mundada, P., Zhang, G., Hazard, T., and Houck, A. (2019).

Suppression of qubit crosstalk in a tunable coupling

superconducting circuit. Physical Review Applied,

12(5):054023.

Paltenghi, M. and Pradel, M. (2023). Morphq: Metamor-

phic testing of the qiskit quantum computing plat-

form. In 2023 IEEE/ACM 45th International Confer-

ence on Software Engineering (ICSE), pages 2413–

2424. IEEE.

Paltenghi, M. and Pradel, M. (2024). A survey on test-

ing and analysis of quantum software. arXiv preprint

arXiv:2410.00650.

Piattini, M., Peterssen, G., and P

erez-Castillo, R. (2021).

Quantum computing: A new software engineering

golden age. ACM SIGSOFT Software Engineering

Notes, 45(3):12–14.

Pontolillo, G. J. and Mousavi, M. R. (2024). Delta debug-

ging for property-based regression testing of quantum

programs. In Proceedings of the 5th ACM/IEEE Inter-

national Workshop on Quantum Software Engineer-

ing, pages 1–8.

Ramalho, N. C., Amario de Souza, H., and Lordello Chaim,

M. (2024). Testing and debugging quantum programs:

The road to 2030. ACM Transactions on Software En-

gineering and Methodology.

Usandizaga, E. M., Yue, T., Arcaini, P., and Ali, S. (2023).

Which quantum circuit mutants shall be used? an em-

pirical evaluation of quantum circuit mutations. arXiv

preprint arXiv:2311.16913.

Vadali, A., Kshirsagar, R., Shyamsundar, P., and Perdue,

G. N. (2024). Quantum circuit ﬁdelity estimation us-

ing machine learning. Quantum Machine Intelligence,

6(1):1.

Wang, X., Yu, T., Arcaini, P., Yue, T., and Ali, S. (2022).

Mutation-based test generation for quantum programs

with multi-objective search. In Proceedings of the ge-

netic and evolutionary computation conference, pages

1345–1353.

Yuen, H. (2023). An improved sample complexity lower

bound for (ﬁdelity) quantum state tomography. Quan-

tum, 7:890.

AssertsQ: A Quantum Assertion Tool for Quantum Software Debugging

APPENDIX

Mathematical Derivation of the Swap

Test Similarity

In this subsection the derivation that underpins the

functionality of methods like assert equals and

assert equals state in AssertsQ is presented. The

measured probability P

(see below) is translated to

a numerical similarity or ﬁdelity metric, thereby en-

abling automated veriﬁcation of circuit or state equiv-

alence. The following derivation is based on the state

of art (Garcia-Escartin and Chamorro-Posada, 2013)

and (Foulds et al., 2021).

Deﬁnition 1 (Quantum States). Let |ψ⟩ and |φ⟩

be two quantum states deﬁned on an n-qubit Hilbert

space, and let the ancilla qubit be initialized in the

state |0⟩.

Problem Statement. The objective of the Swap Test

is to estimate the squared overlap (or similarity) be-

tween these two states (|ψ⟩ and |φ⟩) by measuring a

single ancilla qubit:



⟨ψ | φ⟩



Proposition 1 (Swap Test Fidelity). After applying a

sequence of operations to the system, the probability

of measuring the ancilla in state |0⟩is related to the

squared overlap of |ψ⟩ and |φ⟩ by:



⟨ψ | φ⟩



= 2P

−1.

Proof. We apply the Swap Test circuit and track the

system step by step.

1. Initial state

|0⟩

ancilla

⊗ |ψ⟩ ⊗ |φ⟩.

2. Hadamard on the Ancilla.

The Hadamard transform acts as follows:

H|0⟩

ancilla

√



|0⟩

ancilla

+ |1⟩

ancilla



The system state becomes:

√



|0⟩

ancilla

+ |1⟩

ancilla



⊗ |ψ⟩ ⊗ |φ⟩.

3. Controlled-SWAP Operation.

The controlled-SWAP swaps |ψ⟩ and |φ⟩ only if

the ancilla is in |1⟩, producing:

√

|0⟩

ancilla

|ψ⟩|φ⟩+ |1⟩

ancilla

|φ⟩|ψ⟩

4. Second Hadamard on the Ancilla.

Applying H again:

H|0⟩=

√



|0⟩+ |1⟩



, H|1⟩=

√



|0⟩−|1⟩



Expanding this transformation:

|0⟩

ancilla

(|ψ⟩|φ⟩+ |φ⟩|ψ⟩) + |1⟩

ancilla

(|ψ⟩|φ⟩−|φ⟩|ψ⟩)

5. Measurement of the Ancilla.

The probability of measuring |0⟩

ancilla

is given by

the squared norm of its coefﬁcient:



|ψ⟩|φ⟩+ |φ⟩|ψ⟩



Using the identity:

∥|x⟩+ |y⟩∥

= ⟨x | x⟩+ ⟨y |y⟩+ 2Re⟨x |y⟩.

Note that:

⟨ψ | ψ⟩ = ⟨φ | φ⟩ = 1.

Thus:



2 + 2 Re⟨ψ | φ⟩



1 + Re(⟨ψ | φ⟩)

6. Final Expression.

For pure states, it holds that:



1 +



⟨ψ | φ⟩





Solving for



⟨ψ | φ⟩



⟨ψ | φ⟩



= 2P

−1.

□

Hardware Used for the Experiments

All the experiments described in this paper were car-

ried out on a system running Microsoft Windows 10

Pro. The system was an HP ZBook Fireﬂy 16 inch

G10 Mobile Workstation PC, equipped with a 13th

Gen Intel(R) Core(TM) i7-1365U processor at 1.8

GHz, featuring 10 physical cores and 12 logical pro-

cessor and 32.0 GB of RAM.

Code Availability

The code used to implement the tool in this work

is available at the AssertsQ GitHub repository

The repository includes all relevant scripts neces-

sary to replicate the results presented in this pa-

per. For questions regarding the code or its appli-

cation, please contact the corresponding author at

javi.ibarra@deusto.es.

Repository available in https://github.com/

DeustoTech/AssertsQ.

IQSOFT 2025 - 1st International Conference on Quantum Software