Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit

Simulation on Multicore CPUs and GPUs

Alfred M. Pastor

1 a

, Maribel Castillo

2 b

and Jose M. Badia

2 c

Dpt. of Computer Science, Universitat de Val

encia, Avinguda de la Universitat, s/n, 46100 Burjassot, Spain

Dpt. of Computer Science and Engineering, Universitat Jaume I, Av. Vicent Sos Baynat, s/n, 12071 Castell

on de la Plana,

Spain

Keywords:

Quantum Circuit Simulation, Tensor Network Contraction, Parallel Computing, Multicore CPUs, GPUs.

Abstract:

Quantum computing has the potential to transform ﬁelds such as cryptography, optimisation and materials

science. However, the limited scalability and high error rates of current and near-term quantum hardware

require efﬁcient classical simulation of quantum circuits for validation and benchmarking. One of the most

effective approaches to this problem is to represent quantum circuits as tensor networks, where simulation is

equivalent to contracting the network. Given the computational cost of tensor network contraction, exploiting

parallelism on modern high performance computing architectures is key to accelerating these simulations. In

this work, we evaluate the performance of ﬁrst-level parallelism in contracting individual tensor pairs during

tensor network contraction on both multi-core CPUs and many-core GPUs. We compare the efﬁciency of three

Julia packages, two optimised for CPU-based execution and the other for GPU acceleration. Our experiments,

conducted with two parallel contraction strategies on highly entangled quantum circuits such as Quantum

Fourier Transform (QFT) and Random Quantum Circuits (RQC), demonstrate the beneﬁts of exploiting this

level of parallelism on large circuits, in particular the superior performance gains achieved on GPUs.

1 INTRODUCTION

Quantum computing has the potential to solve

problems that are infeasible for classical comput-

ers (Nielsen and Chuang, 2010). However, cur-

rent quantum hardware remains limited by low qubit

counts and high error rates, leading to considerable in-

terest in simulating quantum circuits on classical sys-

tems. Such simulations provide critical insight into

algorithm performance and offer a practical means of

testing and benchmarking quantum algorithms.

This article explores advanced methods for sim-

ulating quantum circuits, with an emphasis on ten-

sor networks and parallelism to improve scalability

and efﬁciency. Tensor networks represent quantum

states and operations as interconnected tensors, al-

lowing signiﬁcant compression of the state space and

reducing the computational overhead of simulations.

By exploiting the structural properties of quantum cir-

cuits, tensor networks can simulate larger and more

https://orcid.org/0000-0002-7740-6354

https://orcid.org/0000-0002-2826-3086

https://orcid.org/0000-0002-5927-0449

complex systems (Markov and Shi, 2008).

Recent advances in tensor network simulations

include optimisation techniques for GPUs, such

as transforming Einstein summation operations into

GEMM operations and using mixed precision to bal-

ance speed and accuracy. Improved algorithms for

determining optimal tensor contraction paths have

further reduced computational times, demonstrating

signiﬁcant gains in performance and accuracy (Gray

and Kourtis, 2021). Parallelism complements these

advances by distributing computational workloads

across multiple processors, enabling the simulation

of larger circuits than would be feasible on a single

processor. By integrating tensor networks and paral-

lelism, classical simulations can approach the practi-

cal limits of quantum circuit emulation.

Parallel simulation algorithms can be classiﬁed by

the levels of parallelism they exploit and the types of

parallel architectures they target. At a ﬁne-grained

level, parallelism is applied to pairwise tensor con-

tractions, often reformulated as matrix multiplications

for compatibility with highly optimised linear alge-

bra libraries. A higher level of parallelism involves

the simultaneous contraction of groups of tensors, de-

120

Pastor, A. M., Castillo, M. and Badia, J. M.

Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit Simulation on Multicore CPUs and GPUs.

DOI: 10.5220/0013551400004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 120-127

ISBN: 978-989-758-761-0

termined by techniques such as community detection

in tensor network graphs or hypergraph partitioning.

Slicing, which splits indices to create subcircuits, fur-

ther increases parallelism by dividing the original ten-

sor network into smaller, independently contractible

components (Huang et al., 2021). Finally, multi-

ple output state amplitudes can be computed in par-

allel by contracting the same tensor network multi-

ple times while keeping both the input and output

indices closed. This is particularly useful for tasks

such as random circuit sampling, which was used by

Google in 2019 in an attempt to demonstrate quantum

supremacy (Arute et al., 2019).

The choice of parallel architecture also plays a

key role in simulation performance. Distributed mem-

ory systems are ideal for large-scale simulations due

to their large memory capacity, enabling the simula-

tion of high-qubit circuits where tensor sizes grow ex-

ponentially. Multicore processors, commonly found

in modern servers, facilitate shared memory commu-

nication and support multiple levels of parallelism.

GPUs excel at tensor contraction tasks due to their

massive data parallelism capabilities, although their

limited memory can limit the size of tensors they can

handle. Hybrid approaches that combine these archi-

tectures, such as using GPUs for matrix multiplica-

tion within a distributed memory framework, can mit-

igate individual limitations and improve overall per-

formance.

In this study, we evaluate the ﬁrst level of paral-

lelism using multicore processors and GPUs within

two different algorithms: one that applies this par-

allelism throughout the contraction process, and an-

other that combines both levels of parallelism in a

multi-stage algorithm, applying the ﬁrst level in the ﬁ-

nal stage. We have evaluated and compared the paral-

lel performance of three Julia packages, two that per-

form pairwise tensor contractions on multicore CPUs,

and one that performs them on the GPU. We used two

types of complex and highly entangled circuits as test

beds: Quantum Fourier Transform (QFT) and Ran-

dom Quantum Circuits (RQC). This work is carried

out in the QXTools environment, a Julia-based frame-

work for simulating quantum circuits via tensor net-

works (Brennan et al., 2022).

The main contributions of this work can be sum-

marised as follows:

• We evaluate the impact of ﬁrst-level parallelism

in tensor network contraction for quantum circuit

simulation on high-performance architectures.

• We compare the efﬁciency of two CPU-based and

one GPU-based Julia packages and analyse their

performance on different quantum circuit types.

• We evaluate the inﬂuence of circuit struc-

ture and contraction strategy on parallel perfor-

mance, distinguishing between full-network and

community-based tensor contraction.

• Our experimental results provide a quantitative

analysis of the scalability of multicore CPUs and

GPUs to contracts tensor networks in parallel.

The paper is structured as follows: Section 2 re-

views related work, while Section 3 provides back-

ground on tensor networks. Section 4 outlines tensor

contraction strategies, and Section 5 details the eval-

uation methodology. Section 6 presents experimental

results, followed by conclusions in Section 7.

2 RELATED WORK

A variety of libraries, frameworks and simulators

have been developed for tensor network contraction

to address the high computational and memory cost

of this process (Quantiki, 2023). Many of these tools

implement different levels of parallelism to improve

the efﬁciency of contraction and to enable the simula-

tion of larger quantum circuits.

One of the most notable frameworks for tensor

network-based quantum circuit simulation on CPU

is qFlex (Villalonga et al., 2019). This framework,

as many simulators, uses slicing techniques to parti-

tion tensor networks across nodes in a cluster, while

using a multithreaded BLAS library to perform pair-

wise tensor contractions on each node’s CPU. TAL-SH

was designed for GPU-based simulations and later

evolved into the qExaTN simulator (Lyakh et al.,

2022), which integrates the ﬁrst and second levels of

parallelism.

Other approaches optimise tensor network con-

traction using task-based execution models. The

Jet simulator combines slicing techniques and asyn-

chronous tasks to minimise redundant computation

and improve execution time on shared memory mul-

tiprocessors and GPUs (Vincent et al., 2022). The

AC-QDP simulator

has been applied to RQC circuits,

employing tensor network contraction optimisations

that have also been incorporated into the widely used

CoTenGra library

. Some of the latest implemen-

tations exploit GPU-based parallelism by optimising

tensor index reordering, adjusting data precision, and

using the cuTensor library to improve contraction ef-

ﬁciency (Pan et al., 2024).

NVIDIA’s cuQuantum SDK provides tools

for exact and approximate tensor contraction on

GPUs (Bayraktar et al., 2023). The framework

https://github.com/alibaba/acqdp

https://github.com/jcmgray/cotengra

Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit Simulation on Multicore CPUs and GPUs

121

provides the cuTensorNet library, which computes

contraction plans on the CPU and implements pair-

wise tensor contractions using single or multi-GPU

conﬁgurations. These methods combine the ﬁrst and

second levels of parallelism using both intra-node

and inter-node optimisations.

3 BACKGROUND

Tensors naturally generalise the concepts of vectors

and matrices to higher dimensions. A rank-r tensor

is an element of the space C

×···×d

, where d

, . . . , d

denote its dimensions. For example, a vector with d

complex components belongs to the space C

and is

classiﬁed as a rank-1 tensor (v ∈ C

), while a matrix

with dimensions n × m resides in the space C

n×m

and

is classiﬁed as a rank-2 tensor (M ∈ C

n×m

Quantum circuits can naturally be represented as

tensor networks, where the gates are represented as

tensors and the indices correspond to the qubits con-

necting these gates. In this representation, all indices

have a dimension of 2, reﬂecting the two possible base

states of a qubit, |0⟩ and |1⟩, which form the compu-

tational basis. The basic operation used with tensor

matrices is contraction, which corresponds to a tensor

product of two tensors followed by a trace over the

indices they share.

The use of tensor networks for the simulation of

quantum circuits was introduced in (Markov and Shi,

2008). The approach involves contracting tensors in

pairs until only a single tensor remains. However,

ﬁnding the optimal tensor contraction order, which

signiﬁcantly affects the time and space cost, is NP-

hard, leading to the development of various heuris-

tics (Gray and Kourtis, 2021).

Partitioning the tensor network into smaller sub-

networks is a widely used strategy to reduce the com-

plexity of the contraction process and enable paral-

lel execution. A particularly promising approach to

achieve this is community detection, a method from

graph theory that identiﬁes highly connected regions

within a network. In our previous work, we proposed

a multi-stage parallel algorithm that uses community

detection to partition tensor networks (Pastor et al.,

2025). We employed the Girvan-Newman (GN) al-

gorithm that uses edge betweenness centrality to iter-

atively remove high-centrality edges, isolating com-

munities within the network (Girvan and Newman,

2002). In tensor network contraction, it minimizes

inter-community connections, reducing tensor ranks

in later stages.

4 STRATEGIES FOR TENSOR

CONTRACTION

Due to its high computational and memory require-

ments, several strategies have been developed to opti-

mise the execution of tensor contractions on modern

hardware, especially on multicore CPUs and GPUs.

The three main approaches to tensor contraction are:

(1) direct execution as matrix multiplication, know as

GEMM (GEneral Matrix-Matrix), (2) explicit mem-

ory reordering to enable GEMM execution, known

as TTGT (Transpose-Transpose-GEMM-Transpose),

and (3) memory access optimisations that avoid ex-

plicit transpositions. This section discusses these

strategies, highlighting their advantages, limitations,

and implementations in widely used libraries.

The ﬁrst approach to tensor contraction is direct

matrix multiplication using optimized GEMM rou-

tines like multithreaded BLAS (CPUs) or cuBLAS

(GPUs) (NVIDIA, 2023). This method maximizes ef-

ﬁciency but is only feasible when tensor indices can

be grouped without transposition, which is uncom-

mon in general tensor network contractions for quan-

tum circuits.

When a tensor contraction does not map directly

to a matrix multiplication, a common alternative is

to explicitly reorder the tensor indices in memory to

transform the contraction into a GEMM operation.

This strategy is known as the TTGT approach, and is

widely used in GPU-based tensor contraction libraries

such as cuTensor (NVIDIA, 2024), which performs

optimised transpositions using CUDA kernels before

performing the GEMM operation.

Other advanced techniques have been developed

to optimise tensor contractions while avoiding data

reordering in memory. These include the GEMM-like

Tensor-Tensor Contraction (GETT) strategy or the

Block-Scatter-Matrix Tensor Contraction (BSMTC).

The GETT approach improves memory access efﬁ-

ciency by using cache-aware partitioning and hierar-

chical tensor contraction loops, reducing the need for

explicit reordering (Springer and Bientinesi, 2018).

BSMTC uses block-scatter vector layouts to dynam-

ically compute memory addresses, allowing data to

be accessed in its natural order without transposition.

It was introduced in the TBLIS library (Matthews,

2018).

The ﬁrst level of parallelism can be applied in the

three strategies just described. Optimised versions

of BLAS such as Intel MKL or OpenBLAS can be

used in multi-core CPUs and cuBLAS in GPUs to

perform parallel matrix multiplications. Data trans-

positions can be performed in parallel using spe-

cialised libraries. Finally, optimised multithreading

IQSOFT 2025 - 1st International Conference on Quantum Software

122

can also be applied in the BSMTC method by paral-

lelizing multiple loops around a microkernel, optimis-

ing memory access and minimising synchronisation

overhead (Matthews, 2018).

5 TENSOR NETWORK

CONTRACTION

5.1 QXTools Tensor Network

Contraction Framework

Our work involves the development and evaluation

of parallel algorithms within the QXTools simulation

framework (Brennan et al., 2021), a core component

of the QuantEx project. Implemented in Julia, QX-

Tools uses several external packages to manage ten-

sor operations, optimise contraction sequences, deter-

mine efﬁcient slicing strategies, and run large-scale

simulations on GPUs or high performance computing

clusters

. The framework supports all three levels of

parallelism described earlier.

For the ﬁrst level of parallelism, the framework

relies on QXContext, which relies on CUDA.jl to per-

form contractions on GPU, while CPU-based con-

tractions are performed using the OMEinsum and

ITensors packages

With respect to the second level of parallelism,

QXTools enables slicing to divide the tensor network

into multiple smaller subtensor networks, facilitating

the contraction of larger networks. In addition, QX-

Tools supports the use of MPI processes to perform

parallel contractions of the subtensor networks gener-

ated by slicing, both in shared memory multiproces-

sor servers and in distributed memory clusters.

Regarding the third level of parallelism, QXTools

allows the distribution of the output state amplitude

sampling across multiple MPI processes running in

parallel.

We used QXTools to implement and evaluate a

novel multi-stage parallel algorithm for tensor net-

work contraction and compared it with other paral-

lelization strategies (Pastor et al., 2025). This al-

gorithm integrates the ﬁrst two levels of parallelism.

Speciﬁcally, it uses the Girvan-Newman community

detection algorithm to partition the tensor network.

Then, multiple threads are used to contract the tensor

network associated with each detected community in

parallel. Finally, the ﬁrst level of parallelism is used

to contract each pair of tensors in the resulting net-

work on a GPU.

https://juliaqx.github.io/QXTools.jl

https://github.com/under-Peter/OMEinsum.jl

5.2 Parallel Tensor Network

Contraction Algorithms

In this paper we compare the performance of three Ju-

lia packages that exploit the ﬁrst level of parallelism

described in the introduction to contract tensor net-

works. Two of them run on multi-core CPUs, while

the third runs on GPUs. The tools used are OMEinsum

(OME): a Julia package used in QXTools to perform

pairwise tensor contractions within the network on a

CPU; BliContractor (BLI): a Julia package that

implements a wrapper for the TBLIS library to con-

tract tensor pairs on a CPU

; and CUDA.jl: a Julia

package used by QXTools to perform pairwise tensor

contractions on NVIDIA GPUs.

Our experiments analyse the performance of

these three packages using two different algorithms:

single-stage to carry out the contractions of all the

tensor pairs during the execution of a tensor network

contraction plan, and multi-stage to contract the

tensor pairs in the ﬁnal stage of the parallel multi-

stage method introduced in (Pastor et al., 2025).

The ﬁrst level of parallelism behaves differently

in the two algorithms. The ﬁrst contracts hundreds or

thousands of tensors with varying ranks, from small

single-qubit tensors to high-rank ones, involving sin-

gle or multiple indices. The second contracts fewer

but high-rank tensors, often sharing many qubits.

When both input and output are closed, the ﬁnal con-

traction reduces to a scalar.

OMEinsum.jl performs tensor contractions using

Einstein summation notation, providing an efﬁcient

and ﬂexible approach to tensor operations. If a tensor

contraction can be reformulated as a matrix multipli-

cation, OMEinsum.jl internally calls BLAS routines

(such as BLAS.gemm!), allowing multi-threaded exe-

cution and optimised performance.

The Julia package BliContractor.jl is based in

the TBLIS library, which optimizes tensor contrac-

tions using the BSMTC technique and parallelized its

execution on multi-core arquitectures.

To test the performance of BliContractor we

modiﬁed the method executed by QXTools to per-

form pairwise tensor contractions. Speciﬁcally, we

replaced the call to EinCode from OMEInsum with a

call to contract from BliContractor.

Finally, QXTools uses QXContexts for tensor

contraction on distributed machines, including GPUs.

QXContexts relies on CUDA.jl, which provides a

high-level interface to NVIDIA’s CUDA ecosystem,

enabling seamless execution of GPU kernels in Julia.

https://github.com/xrq-phys/BliContractor.jl

Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit Simulation on Multicore CPUs and GPUs

123

6 EXPERIMENTAL RESULTS

AND DISCUSSION

6.1 Experimental Environment

The experiments were conducted on a high perfor-

mance computing server equipped with two AMD

EPYC 7282 processors, each with 16 cores and run-

ning at a base frequency of 2.8GHz. The system is

conﬁgured with a total of 256 GiB of DDR4 RAM

and beneﬁts from 64 MiB of L3 cache. For GPU ac-

celeration, the server is equipped with an NVIDIA

RTX A6000 graphics card based on the Ampere ar-

chitecture (Compute Capability 8.6). This GPU has

10,752 CUDA cores and 336 Tensor cores and is man-

ufactured using 8nm process technology. It also in-

cludes 48 GiB of GDDR6 memory.

6.2 Pairwise Tensor Contraction

This section presents a comparative analysis of two

Julia packages, OMEinsum and BliContractor, for

sequential and parallel contraction of a pair of tensors

using a multi-core CPU. The experiments were per-

formed by contracting two tensors of different ranks

(10 and 22) that share a subset of their indices.

First, we evaluate the sequential performance of

both packages when the two tensors share only the

contracted index. We then analyse the impact on per-

formance of varying this index.

1 2 3 4 5 6 7 8 9 10

Package

OME

BLI

Time (s)

Contracted index

Figure 1: Comparison of the sequential contraction time of

OMEinsum and BliContractor to contract one index. Ten-

sors with ranks 10 and 22.

Figure 1 shows that OMEinsum consistently out-

performs BliContractor in sequential execution,

achieving approximately four times the speedup

across all indices tested.

Next, we examine the parallel performance of

both packages when contracting tensors over a single

index.

0.5

1.5

2.5

3.5

4.5

2 4 8 12 16 20 24 28 32

Package

OME−i1

OME−i5

BLI−i1

BLI−i5

BLIvsOME−i1

BLIvsOME−i5

Speedup

Number of threads

Figure 2: Comparison of the speedups of OMEinsum and

BliContractor to contract indices 1 and 5. BLIvsOME

lines show the speedup of BLIContractor with respect

to the fastest sequential version (OMEinsum). Tensors with

ranks 10 and 22.

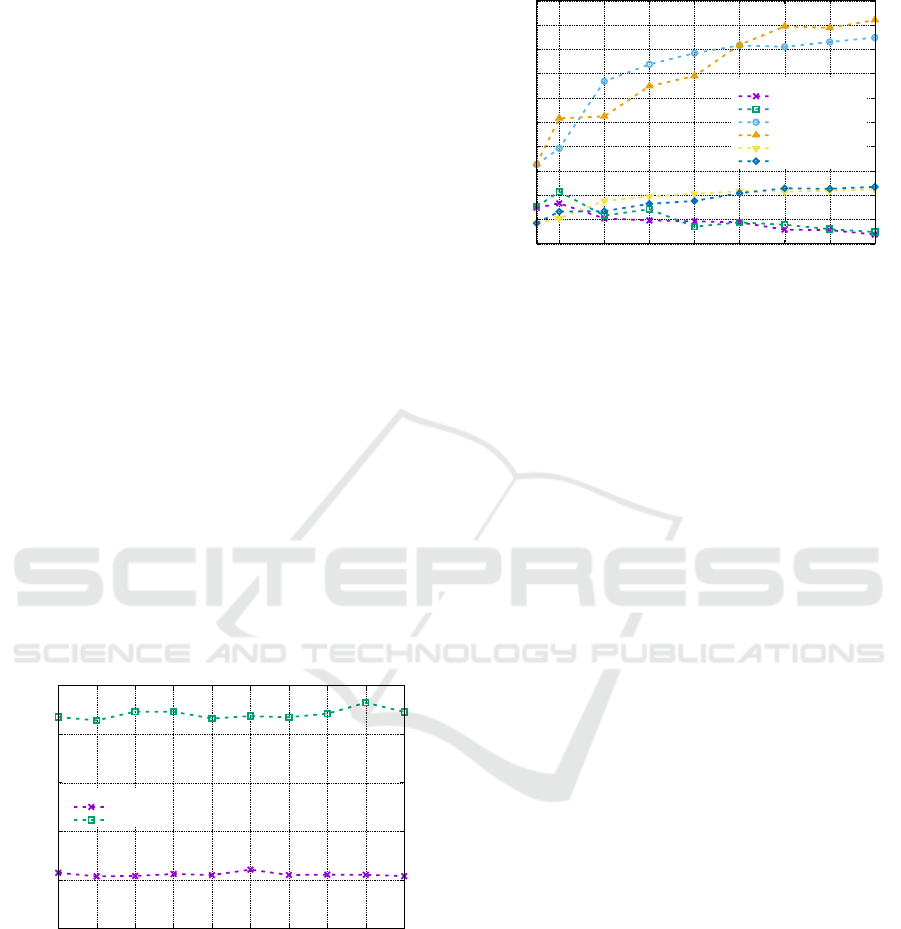
Figure 2 highlights a fundamental difference be-

tween the two packages: BliContractor allows

parallel contraction over a single index (1 and 5),

whereas OMEinsum does not. The conclusion from

these experiments is that OMEinsum was not de-

signed to take advantage of the parallelism offered

by modern multi-core processors, but rather to ef-

ﬁciently perform sequential pairwise tensor contrac-

tions. OMEinsum only uses multithreaded implemen-

tations of matrix multiplication in very few cases.

Conversely, BliContractor uses the C-based TBLIS

package, which is designed not only to minimise data

movement in memory, but also to efﬁciently perform

parallel pairwise tensor contractions.

Despite BliContractor’s ability to exploit par-

allelism, its sequential performance remains signiﬁ-

cantly lower than OMEinsum. As a result, when we

calculate the speedups of BliContractor with re-

spect to the fastest sequential algorithm, OMEinsum,

we only get small speedups when using more than 20

threads.

Finally, we compare the parallel performance of

both packages when the tensors share several indices

and are contracted over all of them. The speedup evo-

lution is analysed when contracting between 1 and the

10 indices of the lower-rank tensor. To eliminate po-

tential bias due to index selection, the indices were

chosen randomly and the reported results are the av-

erage of ﬁve different index sets.

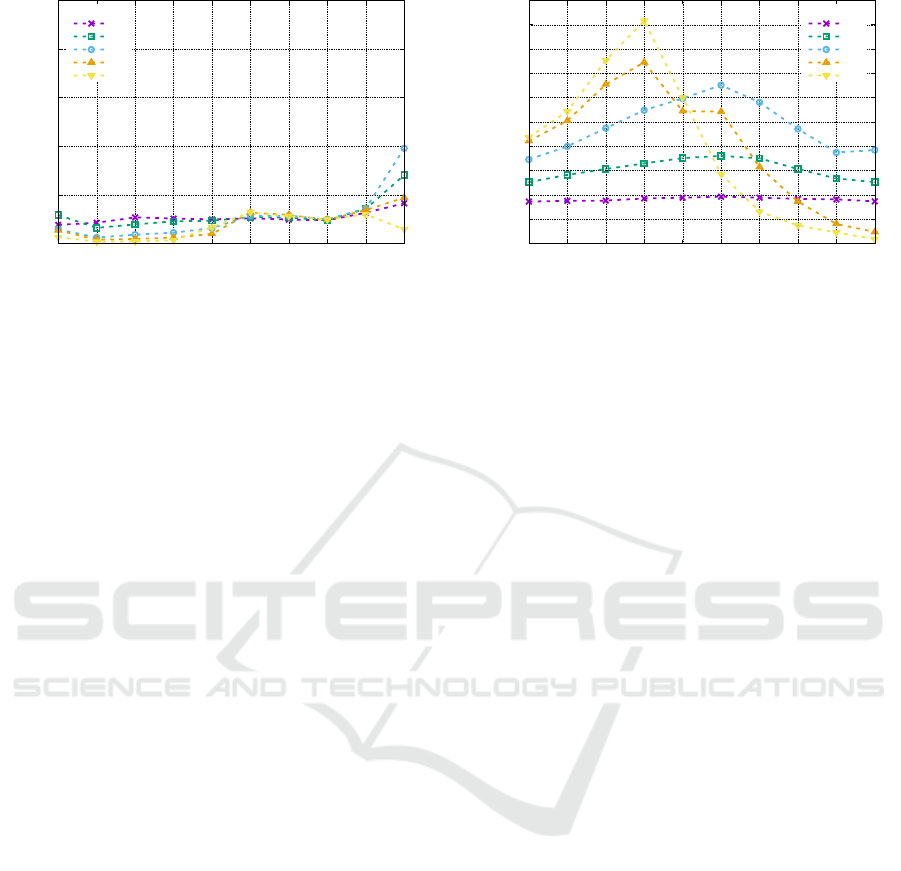
The ﬁgures 3a and 3b show different behaviour

of both packages. OMEinsum only achieves speedup

when the 10 indices of the lower-rank tensor are

contracted, and even then the acceleration is mod-

est (below 4). Furthermore, using more than eight

IQSOFT 2025 - 1st International Conference on Quantum Software

124

1 2 3 4 5 6 7 8 9 10

#Threads

Speedup

Number of indexes

(a) OMEinsum

1 2 3 4 5 6 7 8 9 10

#Threads

Speedup

Number of indexes

(b) BliContractor

Figure 3: Comparison of the speedups of OMEinsum and BliContractor to contract between 1 and 10 indices. Tensors with

ranks 10 and 22.

threads reduces the observed speedup. In contrast,

BliContractor shows a more regular speedup pat-

tern. For two threads, it achieves a near-optimal

speedup for any number of contracted indices. For

4 and 8 threads, the speedup increases progressively

for up to 6 indices and then decreases. Using more

than 8 threads reinforces this trend, with a rapid in-

crease up to 4 contracted indices, followed by an even

steeper decline beyond that point.

Additional experiments conﬁrm that the highest

parallel efﬁciency in both packages occurs when con-

tracting all indices of two tensors of equal rank,

and this efﬁciency tends to increase with rank. For

example, contracting all indices of two tensors of

rank 30 gives a speedup of 18.3 using 28 threads

with BliContractor and 6.9 using 20 threads with

OMEinsum. Both speedups are with respect to the se-

quential time using the same package.

The general conclusion from the experiments pre-

sented in this section is that OMEinsum is signiﬁcantly

more efﬁcient for sequential pairwise tensor contrac-

tions. However, BliContractor takes much better

advantage of the multi-core architecture of modern

processors, which can speed up contractions for both

single and multiple indices.

6.3 Parallel Tensor Network

Contraction

This section evaluates the performance of the three

packages introduced in section 5.2 for exploiting ﬁrst-

level parallelism in tensor network contraction on

both multicore CPUs and manycore GPUs. To quan-

tify the efﬁciency of the parallel algorithms, we use

two well-established types of quantum circuits: RQCs

and QFT. In both cases, contraction is performed by

summing over all input and output indices of the cir-

cuit, effectively computing the probability amplitude

of a given quantum state.

We ﬁrst analyse the scalability of BliContractor

in parallel execution as the contracted circuit size in-

creases. To this end, we evaluate QFT circuits of

different qubit sizes using the single-stage contrac-

tion algorithm, where BliContractor is used to con-

tract all tensor pairs deﬁned by a contraction plan de-

rived from the Girvan-Newman algorithm. Figure 4

illustrates the speedup achieved by the single-stage

method when using 2 to 32 threads for QFT circuits

of various sizes. The speedup is calculated relative to

the sequential execution time obtained with the same

package.

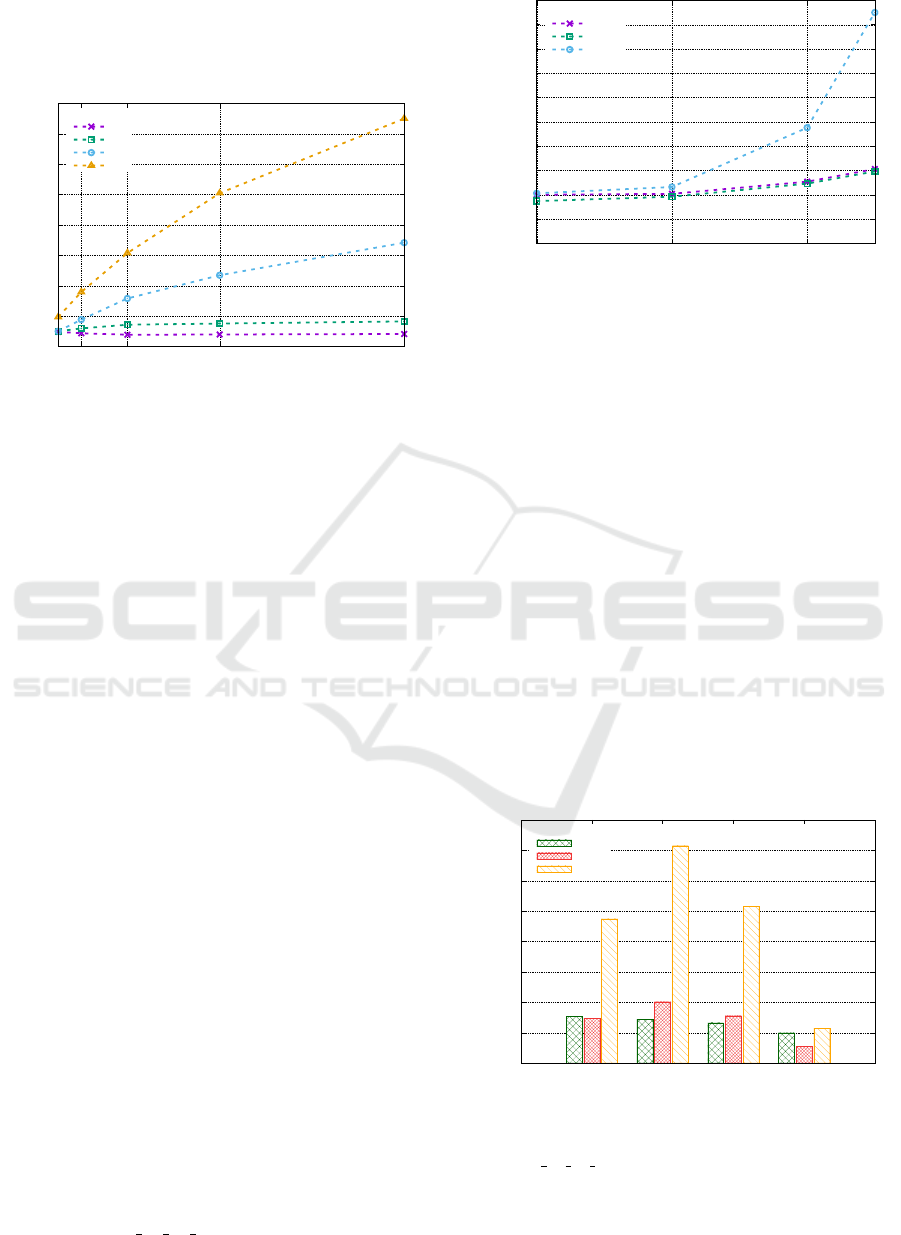
The results in Figure 4 show that the beneﬁts of

parallelism become more pronounced as the circuit

size increases, especially as the number of qubits in-

creases. This trend occurs because the computational

cost and tensor dimensions scale signiﬁcantly with the

number of qubits, resulting in a higher workload that

allows more efﬁcient thread utilisation in the contrac-

tion process.

For the smallest circuit (QFT25), parallel execu-

tion on multiple CPU threads does not speed up the

contraction; instead, it slightly increases the execu-

tion time compared to the sequential approach. For

the QFT29 circuit, only modest speedups (< 1.5) are

observed, with little improvement as more threads

are added. However, for the QFT33 circuit and be-

yond, speedups become signiﬁcant, peaking at 15×

for the QFT35 circuit. It is expected that even greater

speedups can be achieved for larger circuits, provided

that sufﬁcient memory is available.

As discussed in the previous section, the efﬁciency

of parallel execution in these contractions depends

heavily on the tensor ranks and the indices involved.

Higher-ranked tensors and a greater number of con-

Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit Simulation on Multicore CPUs and GPUs

125

tracted indices allow better exploitation of ﬁrst-level

parallelism in BliContractor. This explains the in-

creasing beneﬁts of parallelism with increasing circuit

size.

2 4 8 16 32

#Qubits

Speedup

Number of threads

Figure 4: Speedup evolution of the parallel algorithm us-

ing BliContractor for QFT circuits of different sizes

(#Qubits).

Next, we compare the performance of the three

Julia packages when contracting QFT-type circuits of

different sizes using the single-stage algorithm. To do

this, we compute the speedup achieved by OMEinsum,

BliContractor and CUDA (for GPU-accelerated con-

traction) relative to the sequential execution time of

the fastest method provided by OMEinsum. Figure 5

shows the speedup evolution for the three packages

as the circuit size increases. The results for the CPU-

based packages correspond to the fastest execution us-

ing 32 threads.

Results show that GPU-based contraction with

CUDA consistently outperforms CPU-based methods,

while the two CPU-based packages achieve similar

performance regardless of circuit size. In particu-

lar, for the smallest circuits (25 and 29 qubits), all

three packages yield modest speedups. In fact, par-

allel BliContractor shows longer execution times

than the sequential version of OMEinsum. As the

circuit size increases, all three methods improve,

although CPU-based packages show only marginal

gains, while the GPU-based package exploits its

many-core architecture to achieve signiﬁcant and

growing speedups, reaching up to 4.75× for the

QFT35 circuit. These results suggest that even greater

improvements can be achieved for larger circuits, pro-

vided sufﬁcient memory is available.

Finally, we compare the performance of the three

packages for two contraction algorithms: single-stage

and multi-stage. Figure 6 presents the speedups

achieved by the three packages relative to the best se-

quential algorithm for two circuit types: a QFT35 cir-

cuit and an RQC 12 12 14 circuit. The latter consists

0.5

1.5

2.5

3.5

4.5

25 29 33 35

Package

OME

BLI

CUDA

Speedup

Number of qubits

Figure 5: Speedup evolution using different packages for

QFT circuits of varying sizes for single-state algorithm.

of a 12 × 12 qubit array with 14 layers. The reported

speedups reﬂect only the portions of contraction that

leverage ﬁrst-level parallelism. Speciﬁcally, for the

single-stage method, speedups account for total con-

traction time, while for the multi-stage method, they

correspond to speedups achieved in the third stage.

These results conﬁrm that GPU execution con-

sistently delivers superior performance, while the

two CPU-based packages show similar behaviour.

In addition, the performance of all three packages

is comparable for both circuit types in the single-

stage approach. However, the multi-stage algorithm

achieves signiﬁcantly better performance for QFT cir-

cuits compared to RQC circuits. These results high-

light the impact of circuit structure on parallelism

beneﬁts. In particular, there is a distinction between

contracting all tensor pairs (single-stage) and con-

tracting only a much smaller set of tensors with high

ranks and numerous indices (multi-stage).

QFT-single QFT-multi RQC-single RQC-multi

Package

OME

BLI

CUDA

Speedup

Circuit-Method

Figure 6: Parallel performance of the three Julia packages

for the single- and multi-stage methods. Results for QFT35

and RQC 12 12 14 circuits.

IQSOFT 2025 - 1st International Conference on Quantum Software

126

7 CONCLUSIONS

In this work, we have evaluated the beneﬁts of par-

allelizing pairwise tensor contractions on both multi-

core CPUs and GPUs. Our experimental results, ob-

tained using three Julia packages, show that exploit-

ing this level of parallelism can signiﬁcantly accel-

erate the tensor network contraction process. In par-

ticular, we observed that the massive data parallelism

provided by GPUs signiﬁcantly outperforms the per-

formance of multicore CPUs.

For our experiments we used the QXTools pack-

age, which relies on OMEinsum for pairwise tensor

contraction on the CPU. Our results indicate that

OMEinsum gets limited speedups from parallel exe-

cution in most cases. In contrast, BliContractor

achieves a more effective use of ﬁrst-level paral-

lelism. However, since BliContractor is consid-

erably slower in sequential contraction, its overall

performance only slightly exceeds that of OMEinsum

when using parallel execution.

Finally, we observed that parallel performance is

strongly inﬂuenced by the structure of the circuit and

by whether ﬁrst-level parallelism is applied to the

contraction of all tensor pairs or is restricted to the

contraction of the reduced network formed by the

communities detected in the initial tensor network.

These results highlight the importance of choosing an

appropriate contraction strategy based on the circuit

properties to maximise computational efﬁciency.

ACKNOWLEDGEMENTS

This research was funded by the project

PID2023-146569NB-C22 supported by MI-

CIU/AEI/10.13039/501100011033 and ERDF/UE.

REFERENCES

Arute, F., Arya, K., Babbush, R., et al. (2019). Quan-

tum supremacy using a programmable superconduct-

ing processor. Nature, 574(7779):505–510.

Bayraktar, H., Charara, A., Clark, D., Cohen, S., Costa,

T., Fang, Y.-L. L., Gao, Y., Guan, J., Gunnels, J.,

Haidar, A., et al. (2023). cuQuantum SDK: A high-

performance library for accelerating quantum science.

In 2023 IEEE International Conference on Quantum

Computing and Engineering (QCE), volume 1, pages

1050–1061. IEEE.

Brennan, J., Allalen, M., Brayford, D., Hanley, K.,

Iapichino, L., O’Riordan, L. J., Doyle, M., and Moran,

N. (2021). Tensor network circuit simulation at exas-

cale. In 2021 IEEE/ACM Second International Work-

shop on Quantum Computing Software (QCS), pages

20–26. IEEE.

Brennan, J., O’Riordan, L., Hanley, K., Doyle, M., Allalen,

M., Brayford, D., Iapichino, L., and Moran, N. (2022).

Qxtools: A julia framework for distributed quantum

circuit simulation. Journal of Open Source Software,

7(70):3711.

Girvan, M. and Newman, M. E. (2002). Community struc-

ture in social and biological networks. Proceedings of

the national academy of sciences, 99(12):7821–7826.

Gray, J. and Kourtis, S. (2021). Hyper-optimized tensor

network contraction. Quantum, 5:410.

Huang, C., Zhang, F., Newman, M., Ni, X., Ding, D., Cai,

J., Gao, X., Wang, T., Wu, F., Zhang, G., et al. (2021).

Efﬁcient parallelization of tensor network contraction

for simulating quantum computation. Nature Compu-

tational Science, 1(9):578–587.

Lyakh, D. I., Nguyen, T., Claudino, D., Dumitrescu, E.,

and McCaskey, A. J. (2022). ExaTN: Scalable GPU-

accelerated high-performance processing of general

tensor networks at exascale. Frontiers in Applied

Mathematics and Statistics, 8:838601.

Markov, I. L. and Shi, Y. (2008). Simulating quantum com-

putation by contracting tensor networks. SIAM Jour-

nal on Computing, 38(3):963–981.

Matthews, D. A. (2018). High-performance tensor contrac-

tion without transposition. SIAM Journal on Scientiﬁc

Computing, 40(1):C1–C24.

Nielsen, M. A. and Chuang, I. L. (2010). Quantum compu-

tation and quantum information. Cambridge univer-

sity press, New York.

NVIDIA (2023). cuBLAS Library User Guide.

https://docs.nvidia.com/cuda/cublas/index.html.

NVIDIA (2024). cuTENSOR: A High-Performance CUDA

Library For Tensor Primitives. https://docs.nvidia.

com/cuda/cutensor.

Pan, F., Gu, H., Kuang, L., Liu, B., and Zhang, P. (2024).

Efﬁcient quantum circuit simulation by tensor net-

work methods on modern gpus. ACM Transactions

on Quantum Computing, 5(4):1–26.

Pastor, A. M., Badia, J. M., and Castillo, M. (2025). A com-

munity detection-based parallel algorithm for quan-

tum circuit simulation using tensor networks. The

Journal of Supercomputing, 81. Art. no. 450.

Quantiki (2023). List of QC simulators. https://quantiki.

org/wiki/list-qc-simulators.

Springer, P. and Bientinesi, P. (2018). Design of a high-

performance GEMM-like tensor–tensor multiplica-

tion. ACM Transactions on Mathematical Software

(TOMS), 44(3):1–29.

Villalonga, B., Boixo, S., Nelson, B., Henze, C., Rieffel, E.,

Biswas, R., and Mandr

a, S. (2019). A ﬂexible high-

performance simulator for verifying and benchmark-

ing quantum circuits implemented on real hardware.

npj Quantum Information, 5(1):86.

Vincent, T., O’Riordan, L. J., Andrenkov, M., Brown, J.,

Killoran, N., Qi, H., and Dhand, I. (2022). Jet: Fast

quantum circuit simulations with parallel task-based

tensor-network contraction. Quantum, 6:709.

Parallel Tensor Network Contraction for Efﬁcient Quantum Circuit Simulation on Multicore CPUs and GPUs

127