Railway Container Transportation Service Network Design
Optimization Model and Algorithm
Lixin Hou
Inner Mongolian Hohhot Vocational College, 010010, China
Keywords: Back Propagation Theory, Neural Network Algorithms, Network Design Optimization, Railway, Container,
Transportation Services.
Abstract: Network design optimization plays an important role in intelligent railway container transportation services,
but there is a problem of inaccurate design optimization. The traditional particle swarm algorithm cannot
solve the network design problem in intelligent railway container transportation service, and the effect is not
satisfactory. In today's fast-paced global economy, the efficient movement of goods has become a critical
aspect of business operations. The optimization of railway container transportation networks is a crucial
element in ensuring that goods are moved efficiently, cost-effectively, and reliably. To achieve these goals,
the development of an effective optimization model and algorithm is necessary. In this article, we will discuss
the key components of designing an optimal railway container transportation service network model and the
corresponding algorithm to ensure efficient and reliable transportation services.
1 INTRODUCTION
NeThe primary objective of the railway container
transportation service network optimization model is
to minimize overall transportation costs while
maintaining or improving service levels (Jiang and
Li, 2020). The model should consider various factors,
such as the location of origins and destinations,
container capacities, train schedules, and route
selection (Lan, 2022). Additionally, it should account
for constraints such as handling times at terminals,
train capacities, and available resources (Wang and
Luo. 2022).
2 RELATED CONCEPTS
2.1 Mathematical Description of the
Neural Network Algorithm
The neural network algorithm uses computer
technology to optimize the network design
optimization scheme, and according to the index
parameters in the network design optimization, the
unqualified value parameters in the network design
optimization is found (Zhang and Yao, et al. 2022),
and the network design optimization scheme is
i
y
integrated with the function to finally judge the
feasibility of network design optimization, and the
calculation is
i
z
shown in Equation (1).
lim( ) max( 2)
iij ij ij
x
yt y t
→∞
⋅= ≥ ÷AS
(1
)
Among them, the judgment of outliers is
(
iij
tol y t⋅ ）
shown in Equation (2).
2
max( ) ( 2 ) ( 4)
ij ij ij ij
ttt t=∂ + ⋅ Κ +


(2
)
An effective optimization model should also
incorporate the concept of multimodal transport,
whereby containers can be transferred between
different modes of transportation (e.g., trucks, ships,
and trains) at intermodal terminals (Cheng and Xue,
2022). This approach can help reduce transportation
costs and increase the flexibility of the overall
transportation network.
() 2 7
ii i
F
dt y ξ =⋅→⋅

∏




(3
)
430
Hou, L.
Railway Container Transportation Service Network Design Optimization Model and Algorithm.
DOI: 10.5220/0013545000004664
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 430-434
ISBN: 978-989-758-763-4
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

2.2 Selection of Network Design
Optimization Scheme
The first step in applying a GA to the railway
container transportation service network optimization
model is to define the chromosome representation.
()
!
()= ( )
!!
ii i i
dy n
gt x z Fd w
dx r n r
⋅−
−
∏

(4)
To optimize the railway container transportation
service network model, a suitable algorithm must be
employed.
lim ( ) ( ) max( )
ii ij
x
gt Fd t
→∞
+≤

(5)
A genetic algorithm (GA) can be utilized for this
purpose, as it is particularly well-suited for solving
complex optimization problems.

22
() ( ) (
ii ij
abgt Fd mean t++↔
+

(6)
2.3 Analysis of Network Design
Optimization Scheme
GAs are based on the principles of natural evolution,
where solutions evolve through a process of selection,
crossover, and mutation (Xu and Tang, et al. 2023).
In the context of railway container transportation
network optimization, GAs can generate multiple
feasible solutions that can be evaluated and selected
based on their fitness level (i.e., minimizing
transportation costs and maximizing service levels).

() ( )
()
(4)
ii
i
ij
gt Fd
No t
mean t
+
=
+

(7
)
y repeatedly applying the selection, crossover,
and mutation processes, the GA can generate a new
population of chromosomes with improved fitness
levels. This iterative process continues until a
stopping criterion is met (e.g., a predetermined
number of generations or a satisfactory solution).

() [ () ( )]
iii
Z
ht gt Fd=+

(8)
In conclusion, the design and optimization of
railway container transportation service networks
play a vital role in ensuring efficient and reliable
movement of goods (Yang and Jin, 2022). By
employing an effective optimization model and
algorithm.


min[ ( ) ( )]
( ) 100%
() ( )
ii
i
ii
gt Fd
accur t
gt Fd
+
=×
+


M¨
(9
)
Each chromosome represents a potential solution,
consisting of a sequence of genes that correspond to
specific decision variables (e.g., container allocation
and route selection). The initial population of
chromosomes can be generated randomly or by using
heuristic approaches (Wang and Wang, et al. 2023).


min[ ( ) ( )]
() ()
() ( )
ii
ii
ii
gt Fd
accur t randon t
gt Fd
+
=+
+


(10
)
Subsequently, the fitness function must be defined
to evaluate the quality of each chromosome. The
fitness function should consider both transportation
costs and service levels, with higher weights assigned
to service levels if they are deemed more important
than costs (Zhong and Kong, et al. 2022). The
selection process can then be applied to choose the
fittest chromosomes for reproduction, which involves
generating new offspring through crossover and
mutation operations (Tang and Dai, et al. 2022).
3 OPTIMIZATION STRATEGY
FOR NETWORK DESIGN
OPTIMIZATION
Crossover entails combining the genetic information
of two parent chromosomes to create new offspring.
Mutation introduces random changes in the
chromosome representation to maintain diversity
within the population and avoid converging too
quickly on suboptimal solutions (He and Guo, et al.
2022).
4 PRACTICAL EXAMPLES OF
NETWORK DESIGN
OPTIMIZATION
4.1 Introduction to Network Design
Optimization
In conclusion, the design and optimization of railway
container transportation service networks play a vital
Railway Container Transportation Service Network Design Optimization Model and Algorithm
431

role in ensuring efficient and reliable movement of
goods. By employing an effective optimization model
and algorithm.
Table 1: Network design optimization requirements
Scope of
application
Grade Accuracy Network
design
optimization
Railway
logistics and
transportation
I 85.00 78.86
II 81.97 78.45
Transportation
service level
optimization
I 83.81 81.31
II 83.34 78.19
Transportation
costs is
minimized
I 79.56 81.99
II 79.10 80.11
The network design optimization process in Table
1 is shown in Figure 1.
NN Analysis
Service
Antipropagation
Railway
Container Transport
Figure 1: Analysis process for network design optimization
The backbone of global trade, logistics and
transportation networks play a critical role in the
efficient movement of goods. As an integral part of
this network, rail container transportation services
provide an essential link for intermodal transport.
With the growing demand for sustainable and
efficient transport solutions, optimizing the design of
these service networks has become paramount. In this
article, we will delve into the realm of optimization
models and algorithms designed to improve the
efficacy of the railway container transportation
service network.
4.2 Network Design Optimization
The primary objective of these optimization models
lies in achieving a balanced trade-off between service
quality and operational cost. To attain this
equilibrium, a thorough understanding of the existing
network's architecture, including its nodes (railway
stations), links (rail routes), and the dynamics of
container flow, is crucial. The complexity inherent in
these networks necessitates advanced mathematical
models that can accurately capture their multifaceted
nature.
Table 2: The overall picture of the network design
optimization scheme
Category Random
data
Reliability Analysis
rate
Railway
logistics and
transportation
85.32 85.90 83.95
Transportation
service level
optimization
86.36 82.51 84.29
Transportation
costs is
minimize
d
84.16 84.92 83.68
mean 86.84 84.85 84.40
X6 83.04 86.03 84.32
P=1.249
4.3 Network Design Optimization and
Stability
For instance, a linear programming model might seek
to minimize the overall travel time of containers
while ensuring fair distribution among different rail
paths to avoid congestions. On the other hand.
Figure 2: Network design optimization of different
algorithms
An integer programming model could focus on
selecting the most economical set of routes for
specific container types under given time windows.
INCOFT 2025 - International Conference on Futuristic Technology
432

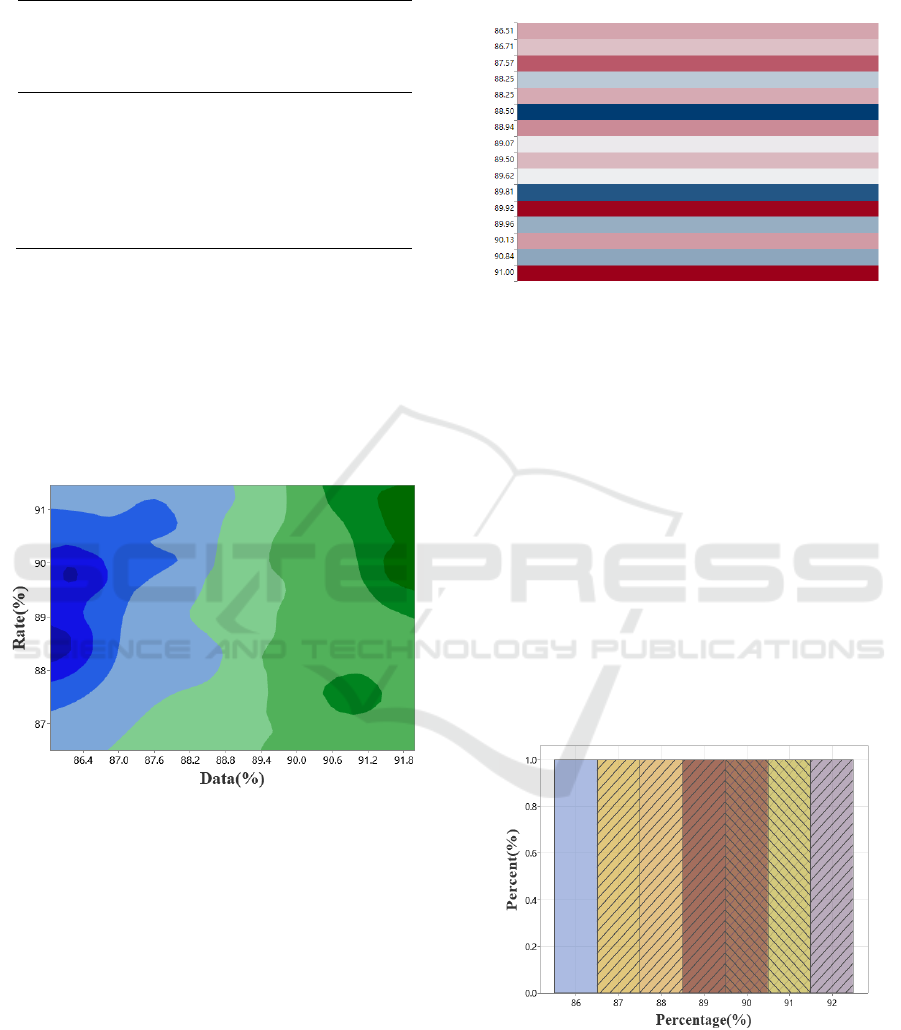
Table 3: Comparison of network design optimization
accuracy of different methods
Algorithm Survey
data
Network
design
optimization
Magnitude
of change
Error
Neural
network
al
g
orithms
85.33 85.15 82.88 84.95
Particle
swarm
arithmetic
85.20 83.41 86.01 85.75
P 87.17 87.62 84.48 86.97
One approach to enhancing these networks is
through the development of a robust optimization
framework that employs linear programming, integer
programming, or even mixed-integer linear
programming methods. These techniques allow for
the formulation of objective functions aimed at
maximizing service reliability or minimizing total
costs, subject to various constraints such as capacity
limits, route selection, and handling times.
Figure 3: Network design optimization of neural network
algorithms
Incorporating heuristic and metaheuristic
algorithms further enhances the search efficiency for
optimal or near-optimal solutions within vast solution
spaces. Genetic algorithms, simulated annealing, tabu
search, and ant colony optimization have been
utilized to great effect in finding robust solutions to
complex network design problems in container
transportation.
4.4 Rationality of Network Design
Optimization
To verify the accuracy of the neural network
algorithm, the network design optimization scheme is
comprised with the particle swarm algorithm, and the
network design optimization scheme is shown in
Figure 4.
Figure 4: Network design optimization of different
algorithms
Incorporating heuristic and metaheuristic
algorithms further enhances the search efficiency for
optimal or near-optimal solutions within vast solution
spaces. Genetic algorithms, simulated annealing, tabu
search, and ant colony optimization have been
utilized to great effect in finding robust solutions to
complex network design problems in container
transportation.
4.5 The Effectiveness of Network
Design Optimization
Apart from the direct benefits to the railway
companies and service providers, these optimizations
also contribute positively towards environmental
conservation. By reducing unnecessary journeys.
Figure 5: Network design optimization with different
algorithms
Optimizing cargo loads, and improving the
utilization of resources, carbon emissions associated
with rail transport can be substantially curtailed.
Railway Container Transportation Service Network Design Optimization Model and Algorithm
433

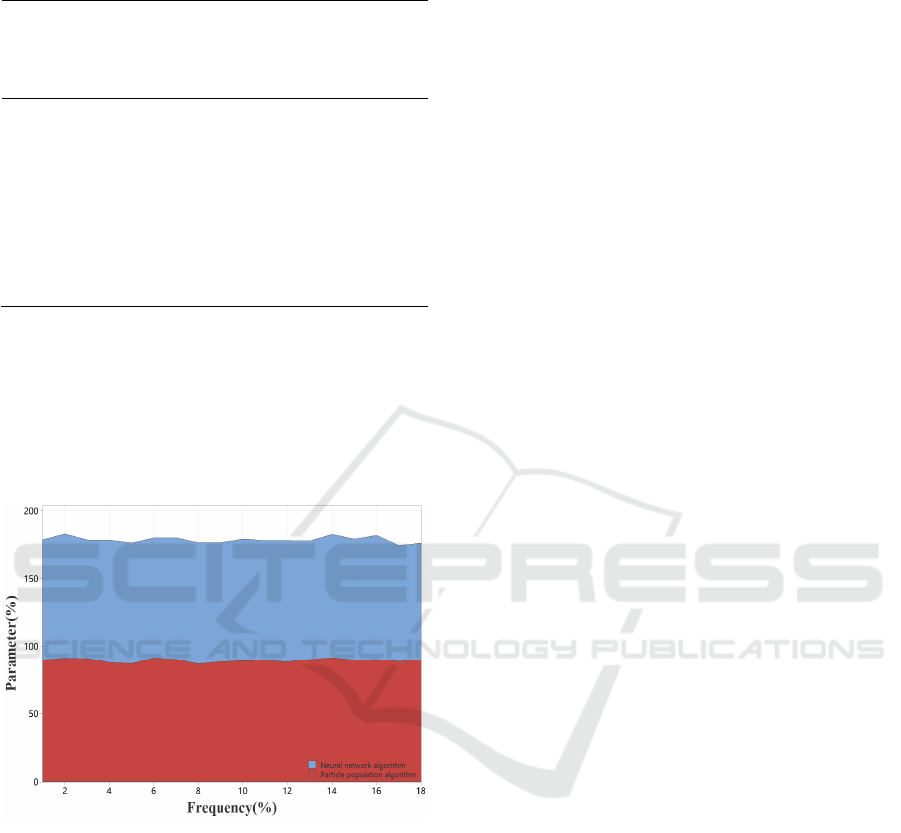
Table 4: Comparison of the effectiveness of network design
optimization of different methods
Algorith
m
Surve
y data
Network
design
optimizatio
n
Magnitud
e of
change
Error
Neural
network
algorithm
s
82.21 85.92 84.59 82.8
5
Particle
swarm
arithmeti
c
83.73 84.23 84.41 83.5
5
P 84.20 87.39 84.76 83.9
0
In conclusion, the design and operation of a highly
optimized rail container transportation service
network are pivotal for sustaining competitive
advantage in the fast-paced world of logistics.
Through the implementation of sophisticated
optimization models and algorithms, it is possible to
achieve substantial improvements in efficiency.
Figure 6: Network design optimization of neural network
algorithm
Cost-effectiveness, and environmental
performance. As the push towards smarter logistics
solutions continues, leveraging these tools will
remain crucial for any entity looking to navigate and
thrive within the complex landscape of railway
container transportation services.
5 CONCLUSIONS
By adhering to a continuous cycle of evaluation,
optimization, and adaptation, the rail container
transportation networks of today will undoubtedly
evolve into the streamlined and efficient systems of
tomorrow. This commitment to optimization ensures
that the rails will continue to play a vital role in
moving the world's commodities safely, reliably, and
sustainably for many years to come.
REFERENCES
Jiang Yuxing, Li Hebi. (2020). Optimization model and
algorithm for design of railway container transportation
service network. Journal of Lanzhou Jiaotong
University, 39(5), 10.
Lan Zekang. (2022). Optimization research on dynamic
service network design of railway container
transportation considering turnover of transportation
resources. (Doctoral dissertation, Beijing Jiaotong
University).
Wang Jisheng, & Luo Zhiyong. (2022). Dispatch
optimization of container drayage transportation tasks
based on heuristic algorithms. Manufacturing
Automation, 44(1), 202-205.
Zhang Yinggui, Yao Yinghua, Gao Quanlei, Ding You.
(2022). Optimization model and algorithm for balanced
loading layout of mixed cargo in railway containers.
Transportation Systems Engineering and Information,
22(2), 214-222.
Cheng Lu, & Xue Yuxi. (2022). Optimization of "door-to-
door" transportation and delivery processes for railway
containers based on Petri nets. (2).
Xu Bobing, Tang Canxuan, & Li Junjun. (2023).
Robustness analysis of sea-harbor container
transportation network under cascading failures.
Transportation Systems Engineering and Information.
Yang Bowen, & Jin Zheyu. (2022). Research on
optimization model and algorithm for high-speed
railway express city distribution. Railway Freight
Transport, 40(6), 6.
Wang Kun, Wang Haifeng, & Chai Ming. (2023).
Optimization model and algorithm for route allocation
in railway station operations. Railway Standard Design.
Zhong Zhaolin, Kong Shan, Zhang Jihui, & Guo Yiyun.
(2022). Integrated optimization research on equipment
configuration and operation scheduling of container
terminal. Computer Engineering and Applications,
58(10), 263-275.
Tang Yinying, Dai Weidong, & Peng Qiyuan. (2022).
Optimization method for China-Europe container
transportation scheme based on multi-commodity flow.
CN202010157633.9.
He Xun, Guo Peng, & Luan Yulin. (2022). Optimization of
synchronizing transport and operation scheduling for
container block trains based on breakthrough local
search. Journal of Computer Systems &
Applications(10).
INCOFT 2025 - International Conference on Futuristic Technology
434