Empirical Research on Dynamic Asset Allocation Based on Index
Hierarchical Structure Algorithm
Fuxiang Yu
Business School, Hangzhou City University, No. 48 Huzhou Street, Hangzhou, 310015, China
Keywords: Social Network Analysis Theory, Exponential Hierarchy Algorithm, Configure Empirical Studies, Dynamic,
Assets.
Abstract: Empirical research on allocation plays an important role in dynamic asset allocation, but there is the problem
of inaccurate empirical positioning. The traditional ant colony algorithm cannot solve the asset research
problem in dynamic asset allocation, and the effect is not satisfactory. With the continuous development of
the financial market and the diversification of investment needs, how to achieve the optimal allocation of
assets in different market environments has become the focus of investors' attention. Traditional asset
allocation methods tend to conduct static analysis based on historical data, ignoring the immediate changes in
the market and the uncertainty of future trends. To solve this problem, the index hierarchical structure
algorithm was developed, which dynamically adjusts the asset portfolio to adapt to market changes and pursue
optimal returns. This paper will deeply explore the application of the exponential hierarchical structure
algorithm in dynamic asset allocation, and verify its effectiveness through empirical analysis.
1 INTRODUCTION
First of all, we need to clarify what an exponential
hierarchical structure algorithm is. In simple terms, it
is a method of classifying and allocating assets
according to the different levels of market indices
(Tan, 2023). This algorithm is usually based on multi-
dimensional indicators such as volatility, market
capitalization, and growth of the index, so as to
identify asset classes with different risk and return
characteristics (Wu, 2022). In dynamic asset
allocation, the index hierarchical structure algorithm
can monitor market changes in real time (Wang Ping,
2022) and automatically adjust the weighting of
various assets to ensure that the portfolio always
matches the risk appetite and market conditions of
investors (Geng and Zhang, 2022).
2 RELATED CONCEPTS
2.1 Mathematical Description of the
Exponential Hierarchical Structure
Algorithm
In order to test the practical effect of the exponential
hierarchical structure algorithm (Liu, 2022), we
conducted an empirical analysis of a series of
historical data (Zhang and Liang, et al. 2023). We
have selected a variety of indices including large-cap
indices, small- and mid-cap indices, bond indices, and
commodity indices for our research, and used
historical data from the past decade to simulate
different market conditions (Li and Hao, et al. 2022).
By stratifying the historical performance of these
indices, we find that there are significant differences
and regularities in the performance of assets at each
level.
2
4
lim( ) max( 2)
2
iij ij ij
x
bb ac
yt y t
a
→∞
−± −
⋅= ≥ ÷
(1)
366
Yu, F.
Empirical Research on Dynamic Asset Allocation Based on Index Hierarchical Structure Algorithm.
DOI: 10.5220/0013543700004664
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 366-372
ISBN: 978-989-758-763-4
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

In the dynamic simulation, we set up different
market scenarios, including bull market, bear market,
volatile market, etc.
2
max( ) ( 2 ) ( 4)
ij ij ij ij
ttt t=∂ + ⋅ +

 M
(2)
Applied the index hierarchical structure algorithm
to optimize the asset allocation under these scenarios.
The results show that, compared with the traditional
static allocation strategy, the asset portfolio using the
index hierarchical structure algorithm shows higher
adaptability and return under different market
scenarios. Especially in periods of large market
fluctuations or transitions, the algorithm can adjust
the asset ratio in time, reduce unnecessary losses, and
even achieve excess returns in some cases..
2
() 4 2 7
iii
F
dbact y ξ =− ⋅→⋅




(3)
2.2 Selection of Configuration
Empirical Research Protocols
In addition, we also note that the index hierarchical
structure algorithm not only helps to improve
investment returns, but also reduces investment risks
to a certain extent. By analyzing the volatility and
correlation of assets at different levels
1
()= ( )
2
ii i i
dy
gt x z Fd w
dx
⋅−Γ
∏

(4)
The algorithm can effectively identify and
diversify specific risks, thereby improving the overall
stability of the portfolio. This finding is particularly
important for investors looking for a solid return on
their investment.
lim ( ) ( ) max( )
ii ij
x
gt Fd t
→∞
+≤

(5)
Although the results of the empirical analysis
support the application of exponential hierarchical
algorithms in dynamic asset allocation, we also
recognize that no model or algorithm can fully predict
the complexity and volatility of the market.

22
() ( ) ( 4)
ii ij
abgt Fd mean t++↔ +

(6)
2.3 Analysis of the Configuration of the
Empirical Research Protocol
Therefore, investors should still maintain flexibility
and prudence when using the algorithm based on their
own investment philosophy and market judgment.

2
() ( )
() 4
(4)
ii
i
ij
gt Fd
No t b ac
mean t
+
=−
+

(7)
In summary, the index hierarchical algorithm
provides us with a new tool to address asset allocation
challenges in dynamic markets (Xu, 2022). Through
the empirical analysis of this paper, we can see that
the algorithm can not only enhance the adaptability of
asset portfolios (Zhan and Zeng, et al. 2022), but also
help investors obtain more stable and considerable
returns in the ever-changing market. With the
advancement of financial technology and the
deepening of data analysis, we have reason to believe
that the index hierarchical structure algorithm will
play a more important role in asset management
practice in the future.

() [ () ( )]
iii
Z
ht gt F d=+


(8)
In the field of investment management, dynamic
asset allocation is one of the key strategies to achieve
portfolio optimization and risk control. With the
continuous development of financial technology, the
index hierarchical structure algorithm, as an advanced
technical means, is changing the traditional asset
allocation model and providing investors with more
accurate and efficient investment solutions.


min[ ( ) ( )]
()
() ( )
ii
i
ii
gt Fd
accur t
gt Fd
+
=
+


MA
(9)
The index hierarchical algorithm, in short, is a
technique that classifies assets according to their
characteristics and implements dynamic adjustments
based on them. This algorithm analyzes market data
in real-time to identify correlations between different
assets and trends that evolve over time, guiding
investors to make more flexible asset allocation
decisions (Liu and Gang, et al. 2022). At its core, it
uses complex mathematical models and big data
analysis techniques to conduct in-depth analysis of
the historical performance and future expectations of
Empirical Research on Dynamic Asset Allocation Based on Index Hierarchical Structure Algorithm
367

various assets, which can be used as the basis for
allocating the proportion of assets.


min[ ( ) ( )]
() ()
() ( )
ii
ii
ii
gt Fd
accur t randon t
gt Fd
+
=+
+


(10)
In practical applications, the index hierarchical
structure algorithm first needs to stratify various types
of assets according to their risk and return
characteristics.
3 CONFIGURE THE
OPTIMIZATION STRATEGY
OF EMPIRICAL RESEARCH
This includes, but is not limited to, stocks, bonds,
commodities and other financial derivatives. Each tier
of assets is given a specific weight based on their
historical performance and current market conditions.
These weights are not fixed, but are adjusted in real-
time in response to market changes in order to achieve
optimal portfolio performance.
3.1 Introduction to the Configuration
of Empirical Research
For example, if the stock market enters a bull market,
the traditional 60/40 allocation to stocks and bonds
may no longer be the best option. At this time, the
index hierarchical structure algorithm will capture the
growth signal of the stock market and dynamically
increase the weight of equity assets according to the
predicted market direction, while reducing the
allocation of bonds accordingly. Conversely, in
anticipation of increased market volatility or
recession, the algorithm protects the portfolio from
extreme market volatility by reducing the proportion
of risky assets and increasing holdings of bonds or
other low-risk assets.
Table 1: Configure empirical research requirements
Scope of
application
Grade Accuracy Configure
empirical
studies
Economic
Research
I 85.00 78.86
II 81.97 78.45
Institutional
investors
I 83.81 81.31
II 83.34 78.19
Individual
investors
I 79.56 81.99
II 79.10 80.11
In addition, the algorithm is able to handle the
problem of correlation between multiple asset classes.
In a diversified portfolio, there may be some
correlation between different assets, such as the price
of certain stocks and bonds that tend to be influenced
by the same macroeconomic factors. With the index
hierarchical algorithm, investors can better
understand these correlations and avoid over-
focusing on a specific risk factor when building
portfolios, thus effectively diversifying risk.
Index
stratification
Social
network
Analyse
Configuration
of empirical
Trends
Structural
algorithm
Distance
measure
Figure 1: Configure the analytical process for empirical
research
3.2 Configure Empirical Studies
At the operational level, the use of the index
hierarchical structure algorithm requires investors to
have the corresponding technical platform and
analytical tools. This often involves a series of
complex processes such as the acquisition, cleaning,
and processing of high-frequency data, as well as the
establishment and testing of models. Therefore, it
may be difficult for the average investor to apply
directly. However, they can indirectly enjoy the
benefits of this technology by purchasing fund
products or services that use such algorithms.
Table 2: Configure the overall picture of the empirical
research protocol
Category Random
data
Reliability Analysis
rate
Economic
Research
85.32 85.90 83.95
Institutional
investors
86.36 82.51 84.29
Individual
investors
84.16 84.92 83.68
Mean 86.84 84.85 84.40
X6 83.04 86.03 84.32
P=1.249
INCOFT 2025 - International Conference on Futuristic Technology
368

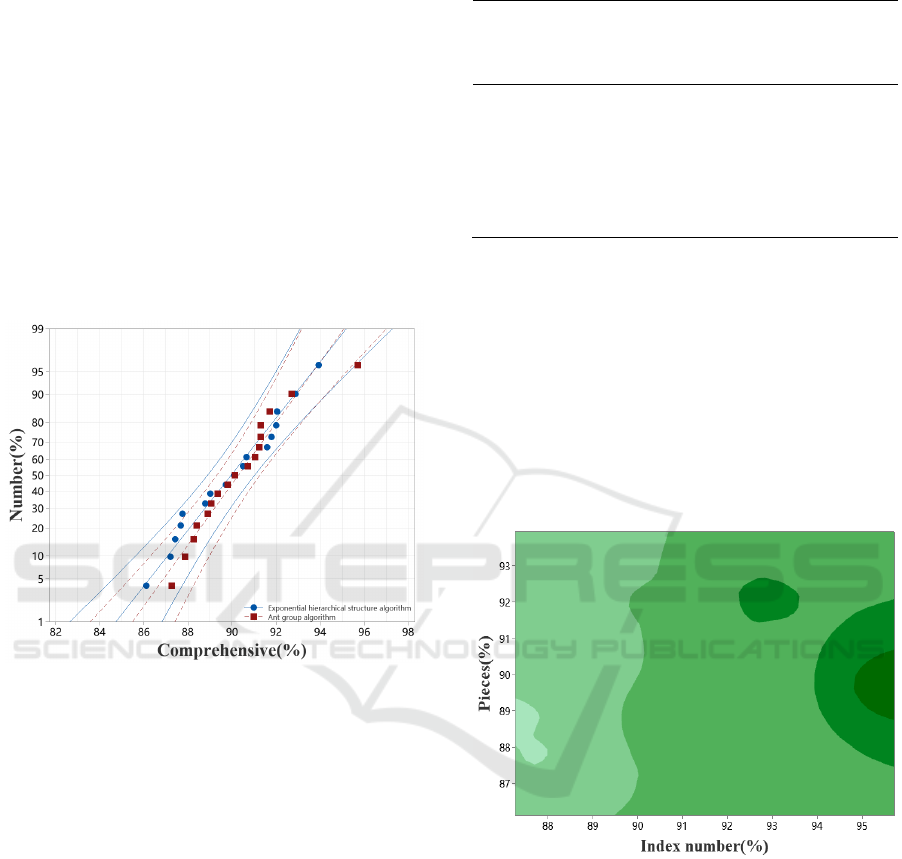
3.3 Configuration Empirical Research
and Stability
In summary, the index hierarchical structure
algorithm provides a scientific and refined approach
for dynamic asset allocation. It can not only adjust the
asset allocation in real time according to market
conditions, but also help investors grasp the
relationship between multiple asset classes, so as to
better diversify risks and pursue long-term stable
investment returns. In the modern financial
environment, mastering and applying such advanced
algorithms will undoubtedly become an important
magic weapon for investment success.
Figure 2: Empirical study on the configuration of different
algorithms
In the volatile waves of financial markets, asset
managers always seek to optimize their portfolios to
achieve the best risk-reward ratio. As one of the core
strategies of investment management, dynamic asset
allocation adjusts the weighting of asset classes at
different points in time to adapt to market changes
and capture investment opportunities. In this process,
the use of hierarchical structures plays a crucial role,
which not only improves the flexibility and efficiency
of asset allocation, but also provides a solid
foundation for risk management and long-term value-
added. This article will explore in detail the role of
hierarchical structures in dynamic asset allocation,
revealing their indispensable value in achieving asset
allocation goals.
Table 3: Comparison of the accuracy of empirical studies
on configuration of different methods
Algorithm Surve
y data
Configur
e
empirical
studies
Magnitud
e of
change
Error
Exponentia
l hierarchy
al
g
orith
m
85.33 85.15 82.88 84.9
5
Ant colony
algorithm
85.20 83.41 86.01 85.7
5
P 87.17 87.62 84.48 86.9
7
Hierarchical structure refers to the management
and configuration of assets into different tiers
according to different criteria. These criteria typically
include the asset's risk profile, expected return,
liquidity requirements, and correlation with other
assets, among other things. Through stratification,
asset managers can monitor the performance of
various assets in more detail and make timely
adjustments to ensure that the risk and expected
return of the entire portfolio are always within a
reasonable range.
Figure 3: An empirical study on the configuration of
exponential hierarchical structure algorithm
Dynamic asset allocation requires managers to
continuously adjust their portfolios based on market
volatility and forecasts, and the hierarchical structure
provides a clear operating framework. First, it helps
managers quickly identify the performance of assets
at various levels so as to make targeted adjustments;
secondly, it also helps to balance risks and returns in
different market environments, especially under
extreme market conditions, which can effectively
limit losses; thirdly, the hierarchical structure makes
asset allocation decisions more scientific and
Empirical Research on Dynamic Asset Allocation Based on Index Hierarchical Structure Algorithm
369

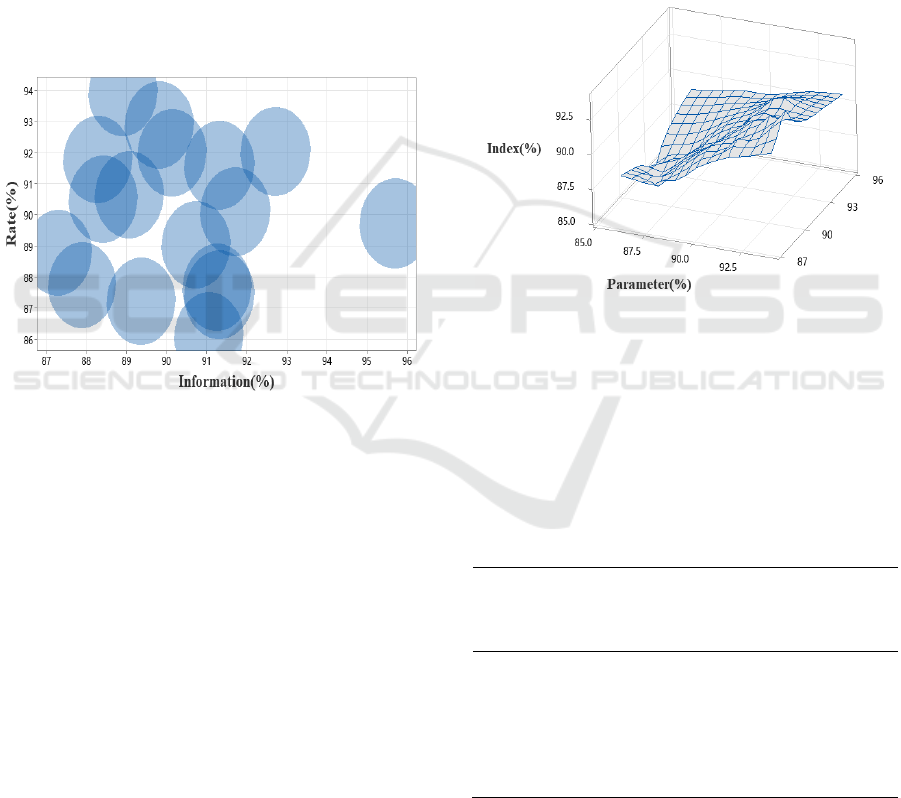
systematic, avoiding the excessive impact of a single
event.
3.4 Rationality of Configuring
Empirical Research
Risk management is a key component of dynamic
asset allocation. The hierarchical structure allows for
more precise quantification and control of risk, as
each layer of assets has its own specific risk tolerance
boundaries. For example, a conservative asset tier can
provide a stable income base and risk buffer for the
portfolio, while an aggressive asset tier may provide
additional growth momentum when the market is up.
By fine-tuning the risk exposure between these levels,
asset managers can better grasp the overall risk level
and develop effective risk response strategies.
Figure 4: Empirical study on the configuration of different
algorithms
For investors looking for long-term growth, a
hierarchical structure can help build a portfolio that
evolves over time. As market conditions change and
individual investment goals adjust, asset managers
can gradually adapt to changes by rebalancing the
ratios between different tiers, thereby maintaining the
growth momentum and stability of the portfolio. In
addition, a hierarchical structure can help managers
grasp the best time to reallocate assets, such as
moving a particular asset to another tier or category
when it reaches a predetermined return target, so as to
lock in earnings and reallocate funds.
3.5 Configure the Validity of Empirical
Research
In summary, the hierarchical structure plays a
multifaceted role in dynamic asset allocation, which
not only enhances the flexibility and systematization
of management, but also significantly improves the
effectiveness of risk control. Through meticulous
hierarchical division and scientific adjustment
mechanism, asset managers can navigate steadily in
the changing market environment and escort
investors' long-term asset appreciation. Therefore,
understanding and applying hierarchical structures as
an integral part of modern dynamic asset allocation is
a critical step on the road to successful investing.
At the operational level, the use of the index
hierarchical structure algorithm requires investors to
have the corresponding technical platform and
analytical tools. This often involves a series of
complex processes such as the acquisition, cleaning,
and processing of high-frequency data, as well as the
Figure 5: Empirical study on configuration of different
algorithms
establishment and testing of models. Therefore, it
may be difficult for the average investor to apply
directly. However, they can indirectly enjoy the
benefits of this technology by purchasing fund
products or services that use such algorithms.
Table 4: Comparison of the effectiveness of empirical
studies on the configuration of different methods
Algorithm Surve
y data
Configur
e
empirical
studies
Magnitud
e of
change
Error
Exponentia
l hierarchy
algorith
m
82.21 85.92 84.59 82.8
5
Ant colony
algorith
m
83.73 84.23 84.41 83.5
5
P 84.20 87.39 84.76 83.9
0
In the volatile waves of financial markets, asset
managers always seek to optimize their portfolios to
achieve the best risk-reward ratio. As one of the core
strategies of investment management, dynamic asset
INCOFT 2025 - International Conference on Futuristic Technology
370

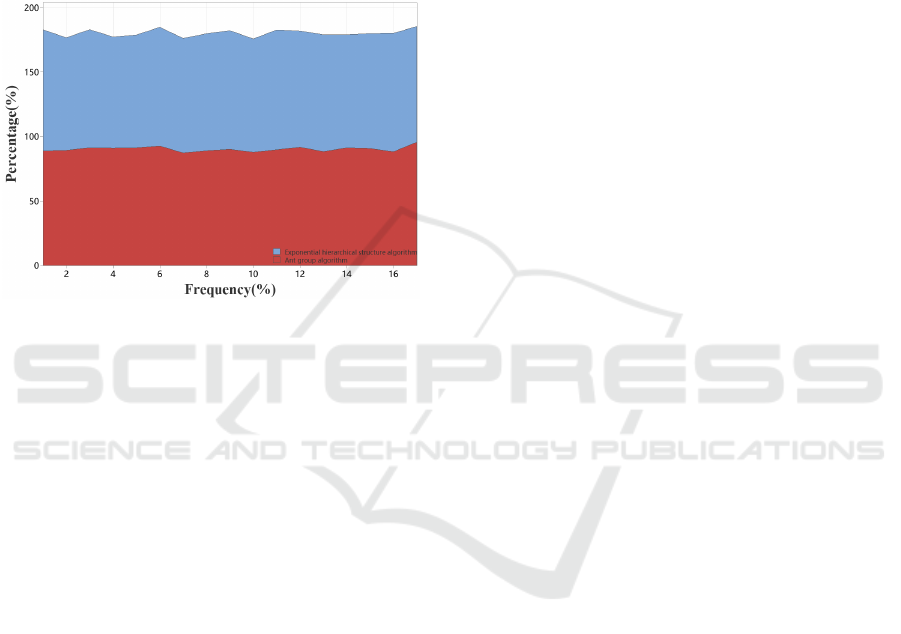
allocation adjusts the weighting of asset classes at
different points in time to adapt to market changes
and capture investment opportunities. In this process,
the use of hierarchical structures plays a crucial role,
which not only improves the flexibility and efficiency
of asset allocation, but also provides a solid
foundation for risk management and long-term value-
added. This article will explore in detail the role of
hierarchical structures in dynamic asset allocation,
revealing their indispensable value in achieving asset
allocation goals.
Figure 6: An empirical study on the allocation of
exponential hierarchical structure algorithm
For investors looking for long-term growth, a
hierarchical structure can help build a portfolio that
evolves over time. As market conditions change and
individual investment goals adjust, asset managers
can gradually adapt to changes by rebalancing the
ratios between different tiers, thereby maintaining the
growth momentum and stability of the portfolio. In
addition, a hierarchical structure can help managers
grasp the best time to reallocate assets, such as
moving a particular asset to another tier or category
when it reaches a predetermined return target, so as to
lock in earnings and reallocate funds.
4 CONCLUSIONS
In addition, the algorithm is able to handle the
problem of correlation between multiple asset classes.
In a diversified portfolio, there may be some
correlation between different assets, such as the price
of certain stocks and bonds that tend to be influenced
by the same macroeconomic factors. With the index
hierarchical algorithm, investors can better
understand these correlations and avoid over-
focusing on a specific risk factor when building
portfolios, thus effectively diversifying risk.
At the operational level, the use of the index
hierarchical structure algorithm requires investors to
have the corresponding technical platform and
analytical tools. This often involves a series of
complex processes such as the acquisition, cleaning,
and processing of high-frequency data, as well as the
establishment and testing of models. Therefore, it
may be difficult for the average investor to apply
directly. However, they can indirectly enjoy the
benefits of this technology by purchasing fund
products or services that use such algorithms.
REFERENCES
Tan Wei (2023) Research on the prediction model of
dynamic rebound modulus of fine-grained soil in
roadbed based on physical properties indicators Sino
foreign highways
Wu Jiaxian (2022) Tail risk and asset pricing in the A-share
market: an empirical study based on MEES indicators
(Doctoral dissertation, Southwest University of Finance
and Economics)
Wang Ping (2022) An Empirical Study on the Efficiency of
Investment and Allocation of Higher Education Funds
in Hebei Province - Based on the DEA and Malmquist
Index Models Research on Education Finance and
Accounting, 33 (5), 3-9
Geng Wenhui,&Zhang Zhifeng (2022) The Dynamic
Evaluation of Green Total Factor Productivity of the
Shanghai Cooperation Organization: An Empirical
Study Based on the DEA Malmquist Index Chinese
Business Theory (8), 4
Liu Mengting (2022) The Operational Efficiency of Basic
Pension Insurance for Urban and Rural Residents in
China: An Empirical Study Based on the DEA Model
and Malmquist Index Technology and Market, 29 (7),
5
Zhang Jiangfeng, Liang Longxue, Li Yao, Wu Xiaosuo,
Wang Jiawei,&Sun Chenglong (2023) Research on
micro ring resonators assisted by one-dimensional
photonic crystal nanobeam cavities Journal of Optics,
43 (22)
Li Jianping, Hao Jun,&Yuan Jiaxin (2022) A dynamic
optimization ensemble prediction method for price
index based on spectral clustering CN202211388148.8
Xu Zhenhua (2022) The Impact of ETFs on the Volatility
of Component Stock Returns: An Empirical Study
Based on the Chinese A-share Market (Doctoral
dissertation, Southwest University of Finance and
Economics)
Zhan Lin, Zeng Xianhui,&Dai Kaixuan (2022) A user
behavior anomaly detection algorithm based on
dynamic time span and clustering difference index
Microcomputers and Applications (004), 041
Liu Huanhuan, Gang Chengcheng, Wen Zhongming, Chen
Tongde, Liu Yue,&Chen Yin (2022) Spatial and
temporal dynamic analysis of soil erosion in the Yanhe
Empirical Research on Dynamic Asset Allocation Based on Index Hierarchical Structure Algorithm
371

River Basin based on structured vegetation index
Research on Soil and Water Conservation (005), 029
INCOFT 2025 - International Conference on Futuristic Technology
372