Toward Design and Implementation of a Quantum-Classical Hybrid

Computing System

Shota Arakaki

, Masao Hirokawa

and Hiroki Watanabe

Joint Graduate School of Mathematics for Innovation, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, Japan

Faculty of Information Science and Electrical Engineering, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, Japan

Keywords:

Quantum-Classical Hybrid Computation, High-Level Quantum Programming Language, Transpiler.

Abstract:

We propose the paradigm of our quantum-classical hybrid (QCH) computing system. The combination of

the quantum and classical parts i s realized by a kind of distributed computation with the help of the classical

channel such as used in the tr usted node of quantum network. In the programming at the front-end of the QCH

computing system, the description of quantum circuits is hidden as possible, and then, the intrinsic functions

corresponding to the individual quantum circuits is used instead. We show the example of a QCH computation

and the results of some of the experiments. We generalize the notion of the QCH computation based on those

results, and aim to establish the concept of our paradigm.

1 INTRODUCTION

Since the quantum supremacy was set as a quantum

computing milestone, quantum c omputer ha s been

the focus of attention in the last decade (Harrow and

Montanaro, 2017; Preskill, 2018; Arute et al., 2019).

Its social implementation is based o n nothing but the

establishment of a computing system with q uantum

computation. According to the current state of quan-

tum technology, it is the arithmetic unit of the pro-

cessor that reaps beneﬁts from quantum me c hanics.

Today’s quantum computer is among computin g sys-

tems with the quantum arithmetic unit; the system

needs the help of classical technologies for other units

in the computer architecture as well as the language

processor. Thus, researches on the problem of the

construction of the quantu m-classical hybrid (QCH)

computing systems have increased signiﬁcantly (Kim

et al., 2023; Tran et al., 2023). It, however, is hard

to reconcile classical and quantum worlds and make

both coexist since the physical theory combining clas-

sical mechanics and quan tum mechanics has not been

completed yet, and the classical logic and the quan-

tum logic are different from each other. The barriers

between the two worlds compound the problem of ex-

ploitation.

Another problem arises. A programmer p repares

a computer program with a high-level programming

https://orcid.org/0000-0001-9020-3992

languag e and feeds it into a compu ting system . T his

programmer’s job is the very beginning process at the

front-e nd of the computing system. In this sense,

we refer to the programmer as a fr ont-end program-

mer throughout this paper. For conventional com-

puting systems, the isolation between the language

system and th e circuit sy stem is almost established:

the language processor and the comp uter architecture.

Usually, therefore, the front-end programmers do not

have to write any logical circuit in their programs

for the conventional (hereinafter “classical”) compu-

tation. On the other hand, f or cu rrent quantum com-

puting systems, such the isolation ha s not bee n estab-

lished yet; ther efore, the front-end programmers have

to write som e quantum circuits in their programs.

This means that they have chances to operate some

quantum circuits. Regardless of whether it is inten-

tional or not, they can wr ite a circuit producing trou-

blesome noises and break a quantu m computation.

We propose a paradigm of the QCH computing

system so that the trou blesome and irksome tasks for

the front-end programme rs can be pushed away to the

low layers consisting of the language proc e ssor and

computer architecture. In our QCH computing sys-

tem, the front-end programmers have two options:

writing quantum circuits or not. In the latter ca se,

the front-end programmers use intrinsic functions for

quantum computation, just like as they use built-in

functions of the four arithm e tic operations. Thus, the

quantum computation is invoked as a subroutine in

112

Arakaki, S., Hirokawa, M. and Watanabe, H.

Toward Design and Implementation of a Quantum-Classical Hybrid Computing System.

DOI: 10.5220/0013542300004525

In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 112-119

ISBN: 978-989-758-761-0

the low-layer processes. To the best of authors knowl-

edge, such a paradigm for the QCH computing system

has not been proposed.

In our paradigm of the QCH computing system,

we consider the limit of the ability against noises

for individual quan tum processors. As the depth of

a quantum computation makes the proc e ssor go be-

yond the limit of its ability, the QCH transpiler warns

the front-end programme rs, and e nables them to use a

kind of distributed c omputation for the original quan-

tum com putation. For this computation, we employ

the classical channel such as used in the trusted node

of quantum network ( Salvail et al., 2010; Huttner

et al., 2022; Lemons et al., 2023). In order to obtain

the ability limit, we use a noise generation quan tum

circuit (NGQC) (Hirokawa, 2021) which is among

quantum circuits generating noises in the zero- noise

extrapolation (He et al., 2020; Majumdar et al., 2023).

Our goa l is that the QCH computing system makes the

front-e nd programmers avoid writing quantum cir-

cuits in their pr ogramming if at all possible. In this

paper, we report some results of the example of a

QCH computation. Based on these results, we estab-

lish the notion of the QCH c omputing system includ-

ing the high-level programming language.

Throu ghout this paper, the gate-level netlist means

the description of the design of a quantum circuit as

well as of a classical circuit after the logical syn-

thesis in classical computer architecture. Thus, the

gate-level netlist is ph ysically executable by a quan-

tum processor. The term, transpiler, is used for the

transformation from a source program written by a

front-e nd programmer to its gate-level netlist, while

the term, compiler, is used for the transformation from

the source prog ram to its object pro gram in the lan-

guage processing.

2 PROPOSAL OF NEW CONCEPT

OF QCH COMPUTATION

SYSTEM

In the ﬁrst part of this section, we propo se the con -

cept of an architecture design for the QCH computa-

tion, and formalize some of the m in brief. A class

of problems which the Q CH c omputation can apply

is restricted so that the speciﬁcation of the problem

in the class can be written in the classical logic, and

moreover, a proper quantum computation can be used

for the problem.

Our idea of the QCH computation is mo tivated

from the solution method for the fo llowing problem.

Give any sequence, a

, a

, ···, a

, of N bits. Assume

that all the elem ents a

are 1 other than a

∗

= 0 for

an index i

∗

. Then, consider the binary search for the

sequence to seek th e solution a

∗

. For simplicity, we

assume that there is just one solution in the sequence.

One of advantages of the cla ssical computation is

that the call by value method can be rep eated in an it-

eration statement over and over again. This cannot be

performed by quantum computation in general due to

the reduction of wave packet and no-cloning theorem.

The binary search is based on this advantage, and its

time complexity is O(ln

N). It basically consists of

the two operations.

O1. Determine a division point a

⋆

(i.e. i = ⋆) and split

the sequence at a

⋆

into the two exploration inte rvals

so that one interval includes a

for 1 ≤ i ≤ ⋆, while

another includes a

for ⋆ < i ≤N.

O2. Choose the interval with the solution, and screen

out the other interval.

If each e le ment a

were an in teger and the se-

quence were sorted, the standard method of the

classical c omputation would work for O2 since

it is easy to make a judgment function for O2

by comparing the values of the division point a

⋆

and the solution a

∗

. Unfortu nately, however, o ur

sequence is of N bits, and therefore, it is n ot

sorted. A qu a ntum computation can play the role

of the judgment for O2; the judgment function is

deﬁned by using the (m + 1 )- qubit Toffoli gate,

AND ··· AND x

)XOR x

m+1

, where x

,··· ,x

are f or the control qubits and x

m+1

is f or a target qubit.

The judgment function judgment(x

,··· ,x

) is

concretely deﬁne d by (x

AND ··· AND x

)XOR 1.

Therefore, if the sequence a

, ···, a

includes the

solution, then judgment(a

,··· ,a

) = 1. On the

other hand, if it does not include the solution, then

judgment(a

,··· ,a

) = 0. The front-end program-

mers can use this judgment function as if it were

an intrinsic function. Onc e the front-end program-

mers use the judgment function in their source pro-

grams, the QCH tra nspiler makes the subroutine call

for judgment and executes the q uantum computation.

If nece ssary, the QCH transpiler or the front-end

programmer divide the sequence of N bits into some

subsequen ces so that th e number of bits of each sub-

sequence can be less th a n 2M for a proper integer

M given below. For each quantum computer pro-

cessor (QP), a proper value N

∗

= N

∗

(hereinafter

“critical value”) of judgment is determined by the

total number o f CNOT gates used in the gate-level

netlist of judgment. We here assume that we use

one QP for one judgment function. The above in-

teger M is deﬁn ed by M := min

∗

, wh e re min

means the minimum running over all the QPs used

for judgment.

Toward Design and Implementation of a Quantum-Classical Hybrid Computing System

113

For an arbitrary subsequence, we denote by m

∗

the

number of bits making the subsequence. The divi-

sion points a

⋆

are set a s ⋆ = ⌊m

∗

/2⌋+ 1 = ⌈m

∗

/2⌉,

where ⌊ ⌋ and ⌈ ⌉ are respectively the ﬂoor func-

tion and ceiling function. We make the (m + 1)-

qubits Toffoli gate by using some standard Toffoli

gates for m ≤ m

∗

. The QCH transpiler reads o ut the

result of judgment(a

,··· ,a

⋆

). According to the re-

sult, it executes the judgment function for the sur-

vivor, tha t is, surviving subsequence. These pro-

cedures need a help of a classical chann e l between

the QP for judgment(a

,··· ,a

⋆

) and the QP for

judgment(the ﬁrst half sequen ce of survivor). Here,

we have two remarks. One is that we need an I/O

transformation between bits and qu bits in the chan-

nel. The other is that the result of judgment func tion

is obtained through quantum-state estimation.

We have implemented the judgment function, a nd

determined the critical value N

∗

for each proces-

sor. Then, some results of the benchmark f or N

∗

are given (Watanabe, 2022). For one judgment fun c-

tion, we use just one IBM Q processor: ibmqx2,

ibmq

quito, ibmq belem, ibmq lima, ibmq manila,

ibmq

santiago, ibmq bogota, ibmq athens (which are

5-qubits processor s) , and ibmq 16 m elbourne (which

is 15-qubits processors). O ur experimental results

say the following. In their individual netlists of the

judgment function for the subsequence w ith m

∗

= 9,

ibmqx2 with the cruciform topology uses about 20

CNOT gates. Meanwhile, ibmq

quito, ibmq belem,

and ibmq lima with the T-shaped topology use about

40 CNOT gates, a nd ibmq

manila, ibmq santiago,

ibmq bogota, ibmq athens with the linear-type topol-

ogy use about 50 CNOT gates. In the netlists of

the judgment function for the subsequence with m

∗

29, ibmq

16 melbourne uses about 230 CNOT gates.

Here, we note that the IBM Q processor requir es the

so-called nea rest-neighb or interaction, a nd therefore,

extra SWAP gates are used to ac hieve this interaction.

We recall that one SWAP gate consists of three CNOT

gates. The accur acy rate here is given by a statisti-

cal quantum-state estimation, that is, the number of

success divided by the total number of trials, in the

case for m

∗

= 9. The accu racy rates of ibmqx2 and

ibmq

bogota are almost 100%. Meanwhile, it is be-

tween 55% and 100% fo r ibmq belem, and between

77% and 10 0% for ibmq

lima. Therefore, deﬁning

the critical value of judgment by the maximum of the

number of variables so that judgment can work well,

we can set it as 9 f or these QP. However, our exper-

iments reveal that ibm q

16 melbourne works for the

subsequen ces only with m

∗

< 6.

We refer to the binary search described a bove as

“QCH binary search” from now on. Generalizing

this, we con sid er the QCH computation whose

computation procedures are in P1-P3 below. In

order to handle the QCH computation, we make the

concept of our QCH compu ting system. The concept

comprise C1-C3.

C1. The QCH transpiler h ides the description of

some quantum circuits in the front-end programming

as possible. The hidden d escription should be

processed as a subroutine call in the QCH transpiling

process.

C2. The QCH transpiler can handle a multi-thread

processing. Concretely, it divides a quantum compu -

tation written in a source program into several parts

so that the divided quantum computation of each part

is not broken. Therefore, the quantum transpiler uses

QP like a multi-core p rocessor, and assigns th e task

of each part to a proper core.

C3. The QCH transpiler works as a multi-pass

compiler. Thus, at least 2 languages for the inter-

mediate codes should be pre pared. Th ese codes are

respectively for the language and the quantum circuit,

and then, the optimizations of langua ge and qu a ntum

circuits are separated.

C4. In the error-recovery proce ss (Ullman, 1976) of

the Q CH transp iler, the error warnings are alerted if

it meets some problems concerning quantum circuits

as well as problems concerning the lexical, syntactic,

and semantic analysis in the languag e proce ssing.

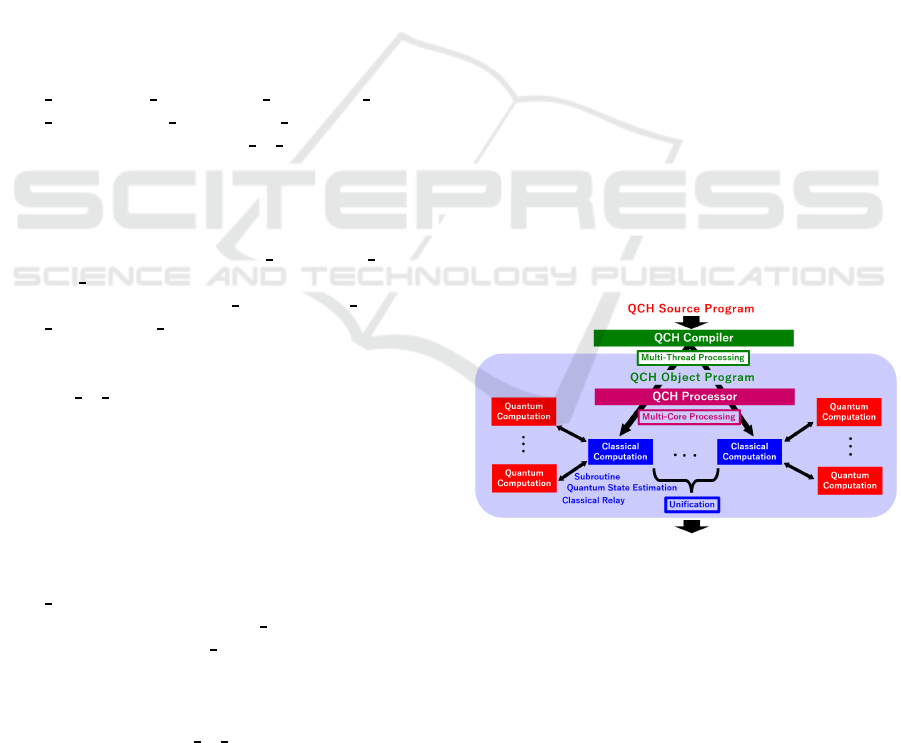
The ﬂow of the QCH computing system in Fig.1

is in the following. The QCH com puting system re-

Figure 1: The schematic picture of the QCH computing sys-

tem.

ceives a sourc e program input from the front-end.

The QCH transpiler classiﬁes the source program into

the classical and quantum parts. The QCH tran-

spiler makes the obje c t program o f the classical part,

and transfers it to the classical computer processor

through the optimization phase of the classical lan-

guage processor. In the source program, the quantum

part is written with some intrinsic functions or quan-

tum circuits by a front-end programmer. If QCH tran-

spiler gets the intrinsic function, it makes a subroutine

IQSOFT 2025 - 1st International Conference on Quantum Software

114

call for the correspond ing quantum computatio n, and

asks a QP to give its answer. If the quantum computa-

tion is not so deep, the QCH transpiler optim iz e s the

quantum circuit and executes it with a proper QP. Oth -

erwise, the QCH transpiler executes the multi-thread

processing with good use of a multi-core processor. In

this multi-thread processing , since the quantum mem-

ory for movement of the halfway computatio n from

an exhausted core to another fresh core has n ot been

invented yet, we adopt a notion of classical chan-

nel, as is often used in the tr usted node of quantum

network (Salvail et al., 2010; Huttner et al., 2022;

Lemons et al., 2023). The result of the halfway quan-

tum compu ta tion by the exhausted core is measured

and converted to the classical data. The converted

data are converted to quantum data, and handled in

the next fresh core. Since measurements destroy the

quantum states such as superposition, the QCH tran-

spiler uses the quantum-state estimation and the help

of classical re la ys. The QCH computing system uni-

ﬁes the results of the divided quantum computation if

necessary, and outputs the answer to the front-end.

One of the examples for C1 is the QCH binary

search. As explained in Sec.3, the f ront-end program-

mers can write the circuit destroying a quantum com-

putation in their programs whether they willingly or

unwillingly do it. Th us, we think it is important to

hide som e vital operatio ns in the low-layer from the

front-e nd. We can learn such importance from the

history of the exploitation of the classical comput-

ing system, for instance, the history of th e disappear-

ance of the go- to statemen t in high-level program-

ming languages. The recursiveness is vital for the

classical computability in accordance with the recur-

sive function theory (Cutland, 198 0), and therefore,

its notion is indispen sable for classical computation

(Roberts, 198 6). Nowdays, we use the iteration state-

ment (i.e., loop statement) to de scribe th e recursion

without using the go-to statement. The recursion is

handled by th e GOTO function in the syntactic analy-

sis (i.e., parsing) of compiler (Aho and Ullman, 1977;

Aho et al., 2006). The recursiveness is realized on

the circuits w ith the help of the jump instruction in

the instruction set of the computer architecture (Dan-

damudi, 1998). Thus, the go-to operation is important

for the compiler and instruction-set architectur e. Nev-

ertheless, the go-to statement is hidden in the struc-

tured programming (Dijkstra, 1970; Dahl et al., 1972;

Ullman, 1976) based on th e structured program the-

orem (B¨ohm and Jacopini, 1966 ). It is because the

go-to statement c a uses the so-called spaghetti code

(Dijkstra, 19 68; Knuth, 1974 ) and the software crisis

(Naur and Randell, 1969; Dijkstra, 1978).

We prepare an alternative for the front-end pro-

grammers so that the QCH comp uting system can

hide some quantum circuits from the m. In other

words, in the case wher e the f ront-end progr a mmers

need only the speciﬁcation of a quantm computation,

the only thing they have to do is to write the intrin-

sic function (e.g., judgment) satisfying the sp eciﬁca-

tion, not to write the quantum circuit. Then, the quan-

tum comp utation is handled as a subroutine inside the

QCH transpiler.

We can come up with an example of the scheme

for C2 in the QCH binary search. A quantum cir-

cuit destroying quantum computation with noises is

given by, for instance , NGQC (Hirokawa, 2021) as in

Sec.3. The quantum computation by QP is broken if

its depth exceeds the critical value. Referring to the

critical value, the QCH transpiler divides the original

quantum computatio n into some sm all quantum com-

putations so that the depth of each divided quantum

computation can be less than critical value. The QCH

transpiler ha s to refer to all the results of the divided

quantum computations, and then, it can obtain a solu-

tion of the original qu antum computation by gather-

ing and processing them with the help of the cla ssical

computation. For the re sult of each divided quantum

computation, it estimates the individual correct an-

swer. Thus, the no tion of cla ssical channel explained

above is adopted in the QCH computing system. De-

scribing repeate dly, the QCH transpiler employs the

quantum-state estimation and the classical relays to

connect the small quan tum computations. Therefo re,

the procedur e s of our QCH computation a re as fol-

lows:

P1. D ivide the target quantum computation into some

quantum computation so that the depths of all the di-

vided quantum co mputations can be less than the crit-

ical value.

P2. Label divided quantum computations with num-

bers. The labeled quantum computations are handled

in the order of labels. Read out each result and store

it in the individual classical register.

P3. Output the solution if all the computations are

completed and the data make th e solution of the or ig-

inal quan tum computation. If another qua ntum com-

putation is nee ded using the data in the classical regis-

ter, input them and execute a new QCH computation.

P4. Use the iteratio n process as a classical computa-

tion in the case where so me r e petitions are required

for P1–P3.

The high-level programming language to write

programs for the QCH computation consists of a stan-

dard programming language and a quantum-circuit

description language. The two types of languages are

mathematically different. We need to m ake the both

coexist in a hig h-level programming language. We

Toward Design and Implementation of a Quantum-Classical Hybrid Computing System

115

design the high-level programm ing lan guage for the

QCH computation so that it ca n be processed by the

QCH transpiler.

We have been studying its design and implementa-

tion of the prototype of the high-level QCH program-

ming language according to C3 and C4 (Arakaki,

2023). We have tried to write a program for the QCH

binary search with the language, and to execute it on

a qu antum-co mputation simulator. The design direc-

tions for our high-level QCH programming language

is as follows.

D1. We make the hig h-level QCH programming lan-

guage free from the properties of quantum hardware.

D2. We consider and add some special rewriting rule s

(i.e., production rules) for the error-recovery process

(Ullman, 1976) in the language processing so that the

front-e nd programmers can be alarmed to the possi-

bility that th e q uantum computation has some noise-

induced error s.

D3. We adopt the lambda-calculu s for quantum com-

putation (van Tonder, 2004; Selinger and Varilon,

2005).

D4. We introduce the type theory (Fu et al., 2020) and

multi-stage calculus (or multi-stage prog ramming)

(Taha and Sheard, 2000) into our QCH computing

system.

D1 means the ideal separation of software and

hardware. More precisely, we consider the com-

pletely executable description of quantum circuit so

that the QCH program can be f ree from the character-

istic of physics of the device for QP. In particular, the

QCH program should be freed from how to use the

classical and quantum registers. Recall the recursive

program in the C programming language. In the case

the computation is so deep, we often meet ‘Segmenta-

tion Fault’ due to the stack overﬂow. Actually, NGQC

in Sec.3 is made by taking advantage of how to use of

quantum registers. In order to gain its freedom, the

roles of the compiler p art and the instruction-set ar-

chitecture part of the QCH transpiler are important.

For D2, the QCH transpiler must learn the err or

rates of the quantum gates and the critical values of in-

trinsic functions for quantum computation. The QCH

transpiler should activate the special rewriting rules

if it detects the possibility of errors as well as other

linguistic errors in the langua ge processing.

We set D3 and D4 because several preceding stud-

ies show that qua ntum computation can be repre-

sented with the typed lambda calculu s (Selinger and

Varilon, 2005; Varilon, 2011; Kawata and Igarashi,

2019). In particular, it enables us to manipulate c la s-

sical and quantum both data. In the multi-stage cal-

culus, the process of the target program is divided

into several stages, and it is eva luated at the individ-

ual stages. Therefore, we believe that the method of

the typed lam bda calc ulus meets ou r QCH compu ta -

tion, and moreover, that it is useful for the multi-pass

compiler. We think we can pre pare the individual

codes f or language and quantum circuit following the

types. For our QCH programming language, there-

fore, we adopt the ML-like syn tax with the extended

let-bindin g (such as let val bindings of ML, or let/let*

bindings of Common Lisp) for stage progression in

order to facilitate the handling of both classical and

quantum data.

3 NOISE CREEPING IN

QUANTUM CIRCUIT

The pass manager carries th e qua ntum-circuit opti-

mization in IBM Q transpiler. We, in fact, can w rite

several quantum circuits producing noises and chea t-

ing the pass manager’s ability. We are interested in

the noises caused chieﬂy by CNOT gates (He et al.,

2020; Hirokawa, 2021; Majumdar et al., 20 23). How

to cheat is to use the fact that the technology of op-

timization in the language processing of the compiler

and that in the circuit processing o f the logical synthe-

sis ar e different. The in dividual optimizations meet

so tough pr oblems. Th e combin ation of the language

processing a nd the m ic roarchitectu re compounds the

difﬁculties of the problem. For instance, the optimiza-

tion prob le m of the instruction scheduling combined

with the register allocation is NP-hard even for classi-

cal computer processors. In particular, the optimiza-

tion of the q uantum circuits means that of the individ-

ually correspondin g quantum Hamiltonian (Kandala

et al., 2019).

We co nsider NGQC which g e nerates some noises

in a QP during the computation. The simplest NGQC

is the quantum circuit for the skip statement. We de-

note this program speciﬁcation merely by skip. In

mathematical terms, skip plays the role of the iden-

tity in quantum computatio n. Therefore, the best op-

timization of skip is to do nothing. NGQC can de-

ceive the IBM Q’s transpiler into believing NGQC is

for a meaningful oper ation, not just an identity oper-

ation, and it can slip through the individual optimiza-

tion processes in the transpiler.

Let A and B be unitary op erators in a Hilbert

space. We now assume AB = I, where I is the iden-

tity operator. Then, we realize that B is uniquely

determined; we obtain B = A

∗

, the adjoint operator

of A, in mathematics. In the individual optim iz a tion

processes, therefore, the compiler should employ the

NOP instruction, a nd then, the logical synthesis only

has to avoid the executions of A and A

∗

. Thus, as the

IQSOFT 2025 - 1st International Conference on Quantum Software

116

transpiler ﬁnds AA

∗

, it should not output any quantum

circuit in the gate-level netlist. The computation in

the low layers a re sometimes beyond a mathematical

grasp. By think ing out how to use some quantum reg-

isters, we can make a circ uit of th e qua ntum operation

for B so that it is different from that of the quantum

operation for A

∗

though AB = I holds. The most fun-

damental operation with a use of register in classical

computation is for the assignment statement, x := a,

restoring the value of a in the register of the variable x.

The classical SWAP statement is written by the three

assignment statements, and then, skip is obtain by ex-

ecuting the SWAP statements twice in succession. In

the individual optimization processes even o f classi-

cal computer s, it is difﬁcult remove skip ···skip, the

serial executions of skip. We can realize this difﬁ-

culty, for instance, by using the optimization options

of GCC, the GNU Compiler Collection. We can set

up a similar trick using the quantum register of the

CNOT gate, and make a SWAP gate with the three

CNOT gates. The skip gate is obtained by repeating

the two SWAP gates continuously. Th e n, the trick en-

ables us to make various NGQCs in Qiskit of IBM

Q so that the transpiler seldom grasps all of them

and cannot reduce them to the best optimization. Be-

cause our NGQC is made by using the CNOT gate s,

the noise of NGQC o riginates from tha t of the CNOT

gate. The total number of the CNOT gates in the gate-

level netlist is at least 6 per one fun damental module

of NGQC. We denote by U

the unitary operator for

our NGQC. Thus, U

is U

···U

, the n times prod-

ucts of U

We consider quantum circuits for the two-qubits

skip opera tion given by

|11i = |11i. (1)

This unitary operator is implemented by using SWAP

gates as described above. We use ibmq

santiago for

the examination s in Fig.2. The left graph of Fig.2

is one of the results for Eq.(1) with n = 0. Follow-

ing the majority d ecision, we can realize that |11i is

the solution of the quantum computation, U

|11i, for

n = 0. O nce turning NGQC on, the a spects of the re-

sults change completely. The right graph of Fig.2 is

one of the results for n = 30. In the case n = 30, the

majority decision cannot tell us that |11i is the solu-

tion of the quantum co mputation, U

|11i. The to-

tal number N

of the CNOT gates in the netlist is

equal to or more than 180 for n = 30. In this way,

we can statistically obtain an approximate upper limit

of N

. We note that the value of N

is dependent

on the topolo gy of QP and the ability of th e IBM Q

transpiler.

Actually, the value of N

also depends o n a kind

of quantum state. For the unitary operator U of any

quantum computation, we can leave U

in the quan-

tum computation by, for instance, U

U and UU

The resu lts of U, U

U, and UU

are same. How-

ever, the noise induced by NGQC creeps in the latter

two unitar y opera tions. The larger n grows, the more

the noise effect increases. Let us take U

, the unitary

operator of making an entangled state, for the unitary

operation U . For example, it is given by

|00i =

√

(|00i+ |11i). (2)

to produce a Bell state now. Then, we realize that the

noise produc e d by NGQC easily destroys the quan-

tum entanglement. We use ibmq

athens for the tests

in Fig.3. The left graph of Fig.3 is for n = 0, and the

right graph of Fig.3 is for n = 10.

Figure 2: U

|11i = |11i. Test results for n = 0 (left) and

n = 30 (right).

Figure 3: U

|00i = (|00i+ |11i)/

√

2. Test results

for n = 0 (left) and n = 10 (right).

4 CONCLUSION

We have described the conception of our quantum-

classical hybrid (QCH) computing system as well as

we have explained the background that led up to it.

We have introduced the broad outline of our concept

of the QCH tra nspiler for the system and tha t of our

scheme for the design of the high-level QCH pro-

gramming language. We have reported implementa-

tion of QCH computing system in progr ess.

In the light of the security for the compu ting sys-

tem, it should be restricted that the front-en d program-

mers write quantum circuits in the ir p rogram b ecause

there is a possibility that NGQC makes a quantum

computer virus.

In order to achieve our paradigm, we must clarify

what kinds of quantum computations can be hidden

Toward Design and Implementation of a Quantum-Classical Hybrid Computing System

117

from the front-end programmers, and estab lish how

we can divide quantum computation into some parts

which are computable in the QCH computing system.

We have been studying these pr oblems.

ACKNOWLEDGMENTS

The authors wish to thank the referees for the ir use-

ful comments. They acknowledge the support from

MEXT Quantum Leap Flagship Program (MEXT Q-

LEAP) Grant Number JPMXS0120351339.

REFERENCES

Aho, A. V., Lam, M. S. , Sethi, R ., and Ullman, J. D. (2006).

Compilers: Principles, Techniques, &Tools. Addison-

Wesley, Boston, 2nd edition.

Aho, A. V. and Ullman, J. D. (1977). Principles of Compiler

Design. Addison-Wesley, Boston, 1st edition.

Arakaki, S. (2023). A Research on Classical-Quantum

Hybrid Programming Language And Its Implementa-

tion (in Japanese). Master thesis, Kyushu University,

Fukuoka.

Arute, F., Arya, K., Babbush, R. , Bacon, D., Bardin, J. C.,

Barends, R., Biswas, R., Boixo, S., Brandao, F. G.

S. L., Buell, D. A., Burkett, B., Chen, Y., Chen, Z. ,

Chiaro, B., Coll ins, R., Courtney, W., Dunsworth, A.,

Farhi, E., Foxen, B., Fowler, A., Gidney, C., Giustina,

M., Graff, R., Guerin, K., Habegger, S., Harrigan,

M. P., Hartmann, M. J., Ho, A., Hoffmann, M., Huang,

T. , Humble, T. S. , Isakov, S. V., Jeffrey, E., Jiang,

Z., Kafri, D., Kechedzhi, K., Kelly, J., Klimov, P. V.,

Knysh, S., Korotkov, A., Kostritsa, F., Landhuis, D.,

Lindmark, M., Lucero, E., Lyakh, D., Mandr`a, S.,

McClean, J. R., McEwen, M., Megrant, A., Mi, X.,

Michielsen, K., Mohseni, M., Mutus, J., Naaman, O.,

Neeley, M., Neill, C ., Niu, M. Y., Ostby, E. , Petukhov,

A., Platt, J. C. , Quintana, C., Rieffel, E. G., Roushan,

P., Rubin, N. C., Sank, D., Satzinger, K. J., Smelyan-

skiy, V., Sung, K. J., Trevithick, M. D., Vainsencher,

A., Villalonga, B., White, T., Yao, Z. J., Yeh, P., Zal-

cman, A., Neven1, H., and Martinis, J. M. (2019).

Quantum supremacy using a programmable supercon-

ducting processor. Nature, 574:505–510.

B¨ohm, C. and Jacopini, G. (1966). Flow diagrams, tur-

ing machines and languages with only two formation

rules. Communications of the ACM, 9:366–371.

Cutland, N. (1980). Computability: An Introduction to

Recursive Function Theory. Cambridge University

Press, Cambridge, 1st edition.

Dahl, O.-J. , Dijkstra, E. W., and Hoare, C. A. R. (1972).

Structured Programming. Academic Press, London.

Dandamudi, S. P. (1998). Introduction to Assembly Lan-

guage Programming. Springer, Berlin, 1st edition.

Dijkstra, E. W. (1968). Go to statement considered harmful.

Communications of the ACM, 11(3):147–148.

Dijkstra, E. W. (1970). Structured programming. In Ran-

dell, B. and Buxton, J., editors, Software Engineering

Techniques, pages 84–88. NATO Scientiﬁc Affairs Di-

vision.

Dijkstra, E. W. (1978). The humble programmer. In Gries,

D., editor, Programming Methodology. A Collection

of Articles by Members of IFIP WG2.3, pages 84–88.

Springer.

Fu, P., Ki shida, K., and Selinger, P. (2020). Linear de-

pendent type theory for quantum programming lan-

guages. In Proceedings of the 35th Annual ACM/IEEE

Symposium on Logic in Computer Science, pages

440–453. ACM.

Harrow, A. W. and Montanaro, A. (2017). Quantum com-

putational supremacy. Nature, 135:203–209.

He, A., Nachman, B., de Jong, W. A., and Bauer, C. W.

(2020). Zero-noise extrapolation for quantum-gate er-

ror mitigation with identity insertions. Phys. Rev. A,

102:012426.

Hirokawa, M. (2021). Can we make the noise ﬁltering

theory for nisq computer? In Proceedings of the

Joint Workshop of 14th Superconducting SFQ VLSI

Workshop and 3rd Workshop on Quantum and Classi-

cal Cryogenic Devices, Circuits, and Systems. Nagoya

University.

Huttner, B., All´eaume, R., Diamanti, E., Fr¨owis, F., Grang-

ier, P., H¨ubel, H., Martin, V., Poppe, A., Slater, J. A.,

Spiller, T., Tittel, W. , Tranier, B., Wonfor, A., and

Zbinden, H. (2022). Long-range qkd without trusted

nodes is not possible with current technology. npj

Quantum Information, 8:108.

Kandala, A., Temme, K., C´orcoles, A. D., Mezzacapo, A .,

Chow, J. M., and Gambetta, J. M. (2019). Error mit-

igation extends the computational r eaqch of a nboisy

quantum processor. Nature, 108:491–495.

Kawata, A. and Igarashi, A. (2019). A dependently typed

multi-stage calculus. In Programming Languages and

Systems. Springer.

Kim, D., Noh, P., Lee, H.-Y. , and Moon, E.-G. (2023).

Advancing hybrid quantum-classical algorithms via

mean operators. Phys. Rev. A, 108:L010401.

Knuth, D. E. (1974). Structured programming with go to

statements. ACM Computing Surveys, 6(4):261–301.

Lemons, N., Gelfand, B., Lawrence, N., Thresher, A.,

Tripp, J. L., Gammel, W. P., Nadiga, A., Meier, K.,

and Newell, R. (2023). E xtending quantum key distri-

bution through proxy re-encryption. J. Opt. Commun.

Netw., 15:457–465.

Majumdar, R., Rivero, P., Metz, F., Hasan, A., and Wang,

D. S. (2023). Mitigation with digital zero-noise ex-

trapolation. In 2023 IEEE International Conference

on Quantum Computing and Engineering (QCE), vol-

ume 1, pages 881–887. IEEE.

Naur, P. and Randell, B. (1969). Software Engineering.

NATO Scientiﬁ c Affairs Division, Brussels,.

Preskill, J. (2018). Quantum computing in the NISQ era

and beyond. Quantum, 2:79.

Roberts, E. (1986). Thinking Recursively. John Wiley &

Sons, New York, 1st edition.

IQSOFT 2025 - 1st International Conference on Quantum Software

118

Salvail, L., Peev, M., Diamanti, E., All´eaume, R.,

L¨utkenhaus, N., and L¨anger, T. (2010). Security of

trusted repeater quantum key distribution networks. J.

Comput. Secur., 18:61–87.

Selinger, P. and Varilon, B. (2005). A lambda calculus for

quantum computation with classical control. In Urzy-

czyn, P., editor, Typed Lambda Calculi and Applica-

tions, pages 354–368. Springer Berlin Heidelberg.

Taha, W. and Sheard, T. (2000). Metaml and multi-stage

programming with explicit annotations. Theor. Com-

put. Sci., 248:211–242.

Tran, Q. H., Ghosh, S., and Nakajima, K. (2023). Quantum-

classical hybrid information processing via a single

quantum system. Phys. Rev. Research, 5:043127.

Ullman, J. D. (1976). Fundamental Concepts of Program-

ming Systems. Addison-Wesley, Boston, 1st edition.

van Tonder, A. (2004). A lambda calculus for quantum

computation. SIAM Journal on Computing, 33:1109–

1135.

Varilon, B. (2011). On quantum and probabilistic linear

lambda-calculi (extended abstract). Electronic Notes

in Theor. Comp. Sci., 270(1):121–128.

Watanabe, H. (2022). A Research Toward Classical-

Quantum Hybrid Distributed Computation (in

Japanese). Master thesis, Hir oshima Universit y,

Higashi-Hiroshima.

Toward Design and Implementation of a Quantum-Classical Hybrid Computing System

119