Portfolio Algorithm Based on Correlation of Accounting Information

Systems

Yanhui Zhang, Ruolin Song and Qingchang Liu

Weifang Engineering Vocational College, 262500, China

Keywords: Accounting Information System, Correlation, Portfolio Algorithms.

Abstract: This paper analyzes the corporate investment portfolio based on the correlation of accounting information

system, and proposes a portfolio algorithm to facilitate the analysis results. In the process of research, this

paper gradually implements a system based on various steps such as system architecture, modeling, model

optimization and training, and then implements a portfolio algorithm based on the correlation of accounting

information system, and puts it into application. Experimental results show that after applying the algorithm,

the annual return of the optimized portfolio increases by 10% and the overall volatility decreases, which

proves that the method is effective. The final conclusion shows that the portfolio algorithm based on the

correlation of accounting information system,It can significantly improve the balance between return and risk,

and provide a sufficient and powerful basis for the company to formulate long-term investment strategies.

1 INTRODUCTION

In recent years, the market environment faced by

various companies has become increasingly complex,

and how to maximize investment returns while

controlling risks has become a hot topic in the field of

investment management. Some researchers use

traditional portfolio theories, such as the Markowitz

mean-variance model, to optimize asset allocation,

but this method is slower to respond to market

fluctuations and more difficult to adapt to complex

and volatile financial market environments. Some

researchers have proposed a portfolio optimization

method based on genetic algorithm, which is effective

in some scenarios, but still shows the problems of

overfitting and inefficient calculation. Some

researchers have proposed that investment portfolios

can be optimized by using artificial neural networks,

but this method relies on a large amount of historical

data and is easily affected by data quality in practical

applications. This paper is based on the correlation of

accounting information systems combined with

intelligent algorithms to improve the balance of return

and risk of investment portfolios. This approach is

based on dynamically adjusting investment ratios,

which can effectively respond to market volatility and

improve the overall performance of the portfolio.

Based on this research, this paper hopes to verify the

advantages of the portfolio algorithm based on the

correlation of accounting information systems, so as

to provide effective support for the company's

investment decision-making.

2 RELATED WORKS

2.1 Factor Analysis Theory

Factor analysis theory is a statistical method that is

based on extracting a set of potential common factors

to explain the intercorrelation between multiple

variables. In financial and investment analysis (Hu,

Tang, et al. 2024), factor analysis is used to extract

various key financial factors that affect investment

returns, such as earnings growth rate, asset-liability

ratio, etc. (Kuroki, 2024). It reduces redundant

information and simplifies complex financial data

sets, while improving the explanatory power and

predictive power of algorithmic models. In portfolio

optimization, based on the correlation between

analytical factors and market performance, investors

can identify the key variables that affect returns, so as

to make more accurate asset allocation, and achieve a

balance between risk control and return enhancement

(Laichuk, Maksym, et al. 2023).

Zhang, Y., Song, R. and Liu, Q.

Portfolio Algorithm Based on Correlation of Accounting Information Systems.

DOI: 10.5220/0013540100004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 1, pages 289-294

ISBN: 978-989-758-763-4

289

2.2 Portfolio Theory

Portfolio theory is the core theory used in finance to

optimize asset allocation, and its goal is to maximize

returns at a given level of risk (Long, 2024). The

classical portfolio theory was proposed by Harry ·

Markowitz, the mean-variance model. Based on the

calculation of the expected return and risk of the

asset, and the covariance between each asset, the

theory emphasizes that the optimal portfolio can be

constructed. From the current practice, modern

portfolio theory has introduced multi-factor models

and behavioral finance research results (Moreira,

Araujo, et al. 2023), which can play a role in

improving the methods of asset pricing and risk

management. The portfolio theory is based on

diversification to effectively reduce unsystematic

risks, which provides a more scientific and reasonable

basis for investors to formulate reasonable investment

strategies in a complex market environment (Ning,

2023).

3 METHODS

3.1 Introduction to the Base Portfolio

Algorithm

Specifically, the core task of the data collection

module is to obtain investment portfolio-related

accounting and market data based on various external

data sources, including financial statements,

macroeconomic indicators, market conditions, etc.,

and update them regularly based on automated

processes. The data is accessed based on external

APIs to ensure the integrity and consistency of the

collected data, and the cleaned data needs to be

converted to a format, so that the model can obtain

high-quality data in real time (Penman, 2024). The

function of the data processing and preprocessing

module is to standardize the data imported by the data

collection module, process the data in different

formats based on unified rules, and ensure that the

data quality meets the standards. All processed data is

stored in a structured database for efficient access and

recall for subsequent steps. The Factor Analysis

module extracts key financial factors, such as return

on equity and debt-to-asset ratio, based on statistical

methods and machine learning techniques to predict

portfolio performance. Based on correlation and

regression analysis, the accounting information is

converted into factor inputs to the model. Factor

weights are dynamically adjusted with market

changes to ensure that the model can accurately and

timely reflect new market signals. At the same time,

the module also supports a variety of statistical tools

for factor screening and regression analysis to ensure

the accuracy of the analysis results. Based on the

results provided by the factor analysis module, the

portfolio construction module combines with the

classical portfolio algorithm to automatically

calculate the weight distribution of various assets, and

carries out personalized adjustments according to

investors' preferences and risk tolerance. The model

balances returns and risks based on an optimization

algorithm to ensure the stability of the portfolio in the

face of market fluctuations. This module requires

periodic dynamic adjustment of asset weights

(Purwanti, 92023) to keep the portfolio in step with

market conditions. The risk management and

monitoring module is mainly used to monitor the risk

status of the portfolio in real time, such as the risk

caused by market fluctuations and the abnormal

fluctuations of individual assets. By setting risk

thresholds and using a risk budget model, potential

investment risk signals can be automatically

identified. Moreover, the system will issue timely

warnings based on different market scenarios and

automatically adjust the risk exposure of the

portfolio. In addition, the algorithm in the module can

adjust the allocation of the portfolio based on

historical data and market trends, so that investors can

get real-time risk management tips when the market

fluctuates violently. The backtesting and performance

evaluation module is responsible for simulating the

performance of investment strategies in historical

market data to verify the reliability and stability of the

model. Evaluate the performance of data from

different economic cycles in various market

environments based on the input of data from

different economic cycles. In addition, the module

needs to provide feedback content for the factor

analysis and risk management module based on the

backtest results to help optimize parameter settings

and algorithm adjustments. The evaluation results

also provide a reference for the optimization of the

investment portfolio and ensure the long-term stable

return performance of the model.

3.2 Portfolio Algorithm Design

The collection of data is the basis of the model

construction, which mainly includes comprehensive

accounting information system data related to the

investment portfolio, such as balance sheet, income

statement, cash flow statement, etc., as well as

macroeconomic data in the market, such as GDP

INCOFT 2025 - International Conference on Futuristic Technology

290

growth rate, inflation rate, etc., to ensure the diversity

and comprehensiveness of the data. These raw data,

when unprocessed, often contain missing values,

outliers, and even different units for different

accounts, so they need to be standardized to eliminate

dimensional differences between data and eliminate

abnormal data points. The purpose of this step is to

ensure the uniformity of data quality and the training

effect of the model. See Eq. (1) for details.

−





(1)

In this formula, the

is original accounting data,

such as net assets per share, operating income, etc., is

the



is mean of the data set, the



is standard

deviation of the data set, and

is the normalized

data for subsequent model training.

Correlation analysis based on accounting

information system is the core link of the whole

model construction. At this stage, based on statistical

analysis methods such as factor analysis and principal

component analysis, the key factors that can

significantly affect the return of the portfolio are

selected, such as the asset-liability ratio, return on

equity, operating profit margin, etc., which are

relatively common accounting and financial

indicators. At the same time, macroeconomic

variables, such as interest rate level and market

volatility, can be introduced to effectively ensure the

robustness and accuracy of the model. Multiple

regression analysis is then used to quantify these

factors and analyze their impact on the expected

return of the portfolio. See Eq. (2) for details.

0 1 1 2 2 n n

Y=β + β X+β X +L+ β X

(2)

In this formula, the

is expected rate of return

representing the portfolio ,

X ,X , ,X



is the

screened accounting information system factors, such

as asset-liability ratio, gross profit margin, etc.,

, , ,

   

is the regression coefficient of each

factor, that is, the weight of its contribution to the

portfolio return, which



is the constant term of the

model, which is reflected in the basic return of the

portfolio when the factors are zero.

After selecting the investment factors, it is

necessary to construct the objective function and

constraints of the portfolio. The objective function is

usually to maximize the return of the portfolio and

minimize its risk. This can be achieved based on

maximizing the Sharpe ratio, based on Markowitz's

mean-variance model, which allows the portfolio to

balance risk and return. Because it is necessary to

truly meet the market demand in actual operation, it

is necessary to introduce constraints, such as the asset

allocation ratio cannot exceed a certain upper limit,

industry concentration, etc., to ensure the rationality

and safety of investment. See Eq. (3) for details.

E[R ] R

Maximize

−



(3)

In this constraint,

 

E R _ p

is represents the

expected return of the portfolio,

is the risk-free

rate,



is the standard deviation of the portfolio and

reflects the volatility of the portfolio. It is used to

measure excess returns per unit of risk, optimizing the

return-to-risk ratio of a portfolio based on

maximizing the Sharpe ratio.

3.3 Portfolio Algorithm System

Training for Relevance

The training process of the model usually relies on the

backtesting of historical accounting information and

market data, and the data segmentation training is

carried out based on the method of rolling window,

and the parameters of the model are dynamically

updated and optimized. In this step, different

optimization algorithms can be used to adjust the

weight coefficients in the model to ensure that the

prediction effect is the best. In order to improve the

generalization ability of the model, cross-validation

and other problems can be used to prevent overfitting,

so that the portfolio algorithm can have high

adaptability in different market environments.

To optimize the model, it is necessary to select the

appropriate optimization algorithm, such as gradient

descent method, L-BFGS, genetic algorithm, etc., to

iteratively optimize the key parameters in the model,

so that the value of the objective function is gradually

close to the optimal solution. Based on the backtest of

the historical data of the accounting information

system,

In this paper, we choose to apply the gradient

descent algorithm to repeatedly update the weight

coefficient of the model, and adjust the optimization

path according to the feedback of errors, so that the

Portfolio Algorithm Based on Correlation of Accounting Information Systems

291

desired convergence effect can be achieved in a small

number of iterations. For details, see Eq. (4).

t t t

J( )

 =  − 

(4)

In this formula,



is the set of parameters

representing the model, such as factor weights,



the learning rate, and the main task is to control the

step size of parameter updates,

J( )

representing the gradient value of the objective

function at the current iteration, and its value reflects

the direction and magnitude of the error of the model

at that point.

Based on the correlation analysis of the

accounting information system, the risk management

of the investment portfolio can be optimized, and the

risk of each asset in the portfolio can be quantitatively

analyzed by using Markowitz's mean-variance theory

and other risk models. In addition, a risk budget

model can be introduced to set risk limits for each

asset, thereby ensuring the volatility of a single asset

without affecting the overall portfolio. For this, see

Eq. (5) for details.

min











(5)

In this optimization formula,



is the weight of

the first

asset in the portfolio



is the standard

deviation of the asset, that is, its risk level, and the

balance between risk and return can be achieved by

minimizing the total risk of the portfolio.

In actual investment, transaction costs and

liquidity will directly affect the performance of the

portfolio. Therefore, the optimization process also

needs to take into account the minimization of

transaction costs, which can be achieved based on the

cost function of introducing transaction fees into the

buying and selling decisions to maximize the net

return of the portfolio. In addition, liquidity issues

also need to be taken into account, so it is necessary

to maintain sufficient liquidity to cope with sudden

market changes, and then ensure that the investment

strategy of the portfolio is adjusted without affecting

market liquidity. See Eq. (6) for details.

C T c

=



(6)

In this formula,

is the total transaction cost,

is the trading volume of the first

is asset, and

is its

unit transaction cost, and this step is used to calculate

the transaction fee that the portfolio will pay for each

adjustment, ensuring that the transaction cost

minimization strategy balances the benefits and costs.

3.4 Portfolio Algorithm System

Optimization

System integration requires the integration of

individual modules through seamless integration. The

data collection module uses APIs and data interfaces

to transmit real-time data to its data processing

module (Sabac, and Tian, 2023)10 and after the data

processing module is cleaned and standardized, the

data will be passed to the factor analysis module for

further processing. Subsequently, the investment

factor generated by the factor will pass the investment

factor to the portfolio building module, and the

optimization algorithm will be used to generate the

optimal investment plan. Next, the risk management

module is responsible for continuously monitoring

market conditions and portfolio risks, and is

connected to the backtesting module based on the

feedback mechanism to finally complete the closed-

loop management process of the system (Zhong,

Ren, et al. 2023).

4 RESULTS AND DISCUSSION

4.1 Introduction to Portfolio Algorithm

Cases

A large company plans to optimize its existing

investment portfolio to enhance overall investment

returns and reduce investment risk. The company's

current portfolio spans a variety of asset classes such

as equities, bonds, and cash, and in order to better

manage risk and return, this paper uses a portfolio

based on:

Accounting Information System Correlation

Portfolio Analysis System (EAS) is a portfolio

analysis system designed to maximize investment

performance based on balancing returns and

volatility. A total of 30 million US dollars were

invested in this investment case, 4 types of assets

were invested, held for 4 years, and 300 people

participated.

INCOFT 2025 - International Conference on Futuristic Technology

292

Table 1 shows the percentage of the company's

current portfolio by asset allocation. The initial

results of information investment are shown in Figure

Table 1: Analysis of the current situation and returns of the

portfolio

Asset

class

Investmen

t Ratio

(%)

Current

Market

Cap

(USD

millions

)

Expecte

d Rate

Return

(%)

Historica

Volatilit

y (%)

Stock

200

8.0

Bonds

120

4.5

Cash

2.0

Figure 1: The initial result of information investment.

4.2 Correlation Analysis of Accounting

Information

Table 2: Portfolio Optimization Scenarios and Profitability

Analysis

Asset class

Adjusted

Investment

Ratio (%)

Adjusted

Expected

Rate of

Return (%)

Adjusted

expected

annual

earnings

(US$

millions)

Stocks

7.5

240 * 7.5%

= 18.0

Bonds

5.0

210 * 5.0%

= 10.5

Cash

2.0

90 * 2.0%

= 1.8

Real Estate

6.5

60 * 6.5%

= 3.9

Table 2 shows the portfolio rebalancing based on

optimization Correlation analysis of accounting

investments, the specific results are shown in Figure

Figure 2: Correlation analysis of these investments

4.3 The Investment Portfolio Results of

Accounting Information

As can be seen from the above examples, the

optimized portfolio has increased the overall

expected annual return to US$34.2 million, which is

about 10% higher than the annual return of the

original portfolio. Based on the reduction of the

proportion of equity assets and the increase of bonds

and real estate assets, the company has achieved a

better risk-return balance, and the overall volatility

and risk have been significantly reduced.

Table 3: Risk and Reward Balance Analysis

Asset

class

Adjusted

Standard

Deviation

(%)

Adjusted

Sharpe

ratio

Maximum

Drawdown

(%)

Stocks

0.65

-15

Bonds

0.60

-7

Cash

0.50

-1

Real

Estate

0.62

-10

Table 3 shows the balance between risk and return

of the optimized portfolio. The adjusted Sharpe ratio

has increased significantly, from 0.60 to 0.65 for

equity assets and slightly for bond assets, making the

overall portfolio more balanced. Based on risk

reduction, the portfolio's performance in market

volatility is more stable and the maximum drawdown

is reduced. The numerical combination result is

shown in Figure 3.

Based on 3 years of simulated historical data, the

optimised portfolio is more robust in different market

conditions, with a 5% increase in total return.

Especially in the economic downturn, the optimized

portfolio shows stronger risk resistance, showing the

Portfolio Algorithm Based on Correlation of Accounting Information Systems

293

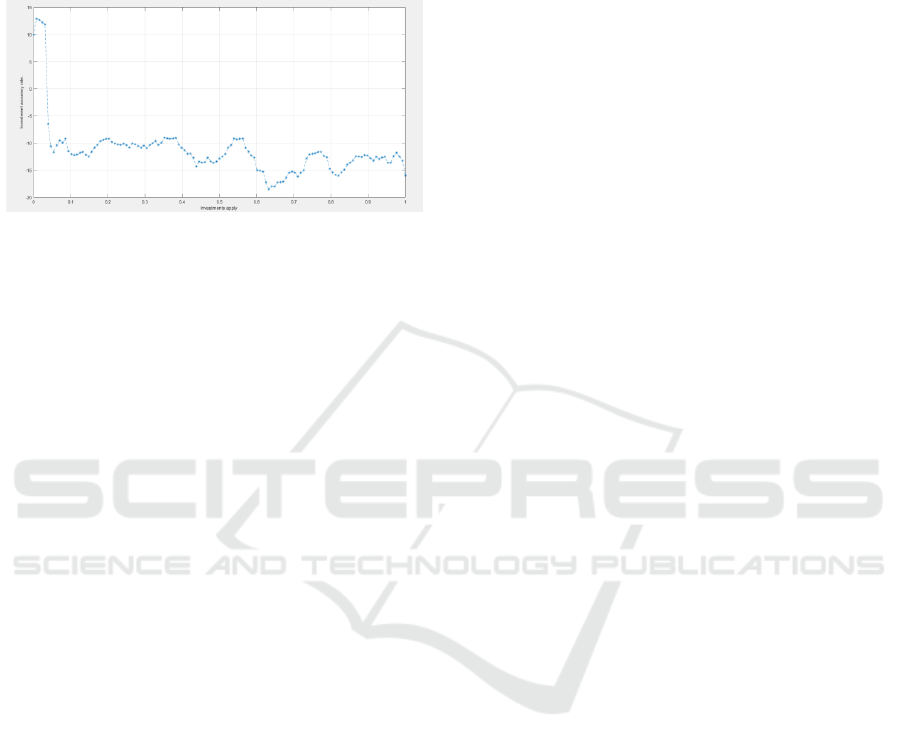
effectiveness and feasibility of the strategy. Based on

the optimized portfolio, the company achieves an

increase in returns while controlling risk. The

addition of real estate assets provides good risk

diversification for the portfolio while optimizing the

overall rate of return.

Figure 3: Judgment of accounting investment portfolio

results.

5 CONCLUSIONS

This paper studies the portfolio algorithm based on

the correlation of accounting information system, and

builds a complete system, integrates the algorithm,

and then implements the application. Judging from

the data results, the optimization method used in this

time has significant results. Based on the correlation

of accounting information systems, combined with

intelligent algorithms, such as factor analysis and

gradient descent methods, this paper successfully

identifies the key financial factors that have an impact

on investment returns, and then balances returns and

risks in asset allocation. Through the effective

application of this system, the optimized portfolio has

a very strong anti-risk performance, and at the same

time, the overall return is good. This proves that the

portfolio algorithm based on the correlation of

accounting information system is effective and can

provide reliable decision support for the long-term

investment strategy of enterprises. In short, the

research in this paper will provide a good foundation

for improving the financial management efficiency

and investment decision-making ability of

enterprises. Although the data collection in this paper

is very complete, its data coverage is still very

limited, so there are still many deficiencies in this

paper, which need to be further optimized.

REFERENCES

Hu, J. F., Y. Y. Tang, N. Yin, and X. Guo. (2024).

Institutional Investor Information Competition and

Accounting Information Transparency. Implications

for Financial Markets and Corporate Governance in

China. Journal of the Knowledge Economy, 15(2),

9629-9666.

Kuroki, M. (2024). Voter rationality, the use of accounting

information and voting behavior. evidence from a

referendum. Pacific Accounting Review, 36(1), 1-20.

Laichuk, S., Y. Maksym, L. Koval, O. Dovzhyk, and S.

Harkusha. (2023). ENSURING CYBERSECURITY

IN ACCOUNTING IN THE DIGITAL ECONOMY

ERA. Financial and Credit Activity-Problems of

Theory and Practice, 6(53), 145-157.

Long, V. T. (2024). THE IMPACT OF ACCOUNTING

INFORMATION ON CORPORATE GOVERNANCE

WITHIN VIETNAMESE COMPANIES. Revista

Gestao & Tecnologia-Journal of Management and

Technology, 24(2), 31-44.

Moreira, R. D., A. C. R. Araujo, and B. M. Bacharel.

(2023). DECISION MAKING PROCESS ON

INVESTING IN FINTECHS. INVESTOR

SPECIALIZATION AND POSITIVE AND

NEGATIVE INFORMATION BIAS. Revista Gestao

& Tecnologia-Journal of Management and Technology,

23(1), 245-275.

Ning, Y. (2023). Research on the extraction of accounting

multi-relationship information based on cloud

computing and multimedia. International Journal of

Grid and Utility Computing, 14(5), 505-515.

Penman, S. (2024). Accounting for Uncertainty.

Accounting Economics and Law-a Convivium, 14(3),

309-327.

Purwanti, D. (2023). Does Government Accounting

Information Matter to Gain Votes? Evidence from

Local Elections in Indonesia. Gadjah Mada

International Journal of Business, 25(3), 355-383.

Sabac, F., and J. J. Tian. (2023). Unintentional Bias and

Managerial Reporting. Journal of Management

Accounting Research, 35(2), 169-187.

Zhong, X., L. Y. Ren, and G. Ren. (2023). Does

performance persistence below aspirations affect firms'

accounting information disclosure strategies? An

empirical study based on reliability and comparability.

Business Ethics the Environment & Responsibility,

32(3), 1060-1077.

INCOFT 2025 - International Conference on Futuristic Technology

294