
Adaptive Market-Based Dynamic Task Allocation Under Environmental
Uncertainty
Hasan Berke Ozturk
a
, Nezih Bora Yavas
b
and Zafer Bingul
c
Department of Mechatronics Engineering, Kocaeli University, Turkey
Keywords:
Multi-Agent Systems, Uncertainty Theory, Swarm and Collective Intelligence, Decentralized Algorithms.
Abstract:
This paper presents a novel consensus-based adaptive genetic-optimized auction (CAGA) algorithm to solve
the dynamic t ask allocation (DTA) problem for a fleet of autonomous vehicles. The algorithm employs an
auction routine for task assignment and a genetic algorithm (GA) to optimize task prices subject to the price
update rule. The proposed algorithm is devised to achieve superior solutions in real-world applications. Hence,
uncertainty theory was adopted to model uncertainties in task positions to create a realistic environment. In
addition, Monte Carlo (MC) simulations are performed to effectively determine the degree of uncertainty.
Several test scenarios have been carried out using other market-based methods, and the results illustrate the
effectiveness of the algorithm.
1 INTRODUCTION
Autonomous vehicles (AUVs) have been extensively
researched and used in numerous fields over the past
decade due to their adaptable nature. Potential appli-
cations include mapping, reconnaissance, distributed
sensor networks, hazardous metal handling, search
and rescue operations, etc. Although their individ-
ual effectiveness has been proven, the deployment of
multiple AUVs provides even more potent and appro-
priate so lutions. Hence, the term multi-a gent systems
(MAS) has become a major topic as the significance
of the problem continues to grow.
The primary objective of MAS is to ensure that
agents in the fleet exhibit cooperative behaviors to
effectively perform tasks. Also, from a task as-
signment perspective, it means multiple robots are
tasked with achieving optimal assignments under cer-
tain constraints and maximizing their overall score.
To establish a struc ture where a fleet of autonomous
agents constantly perceives their surroundings and
takes actions with regard to their benefit, coordination
and cooperatio n amo ng agents must be maintained.
Several research studies have been carried out in this
area, a nd th e key points have been elaborated.
The centralized planners (Chen et al., 2024),
(Hwang et al., 2022) assume a single computational
a
https://orcid.org/0009-0006-5730-4904
b
https://orcid.org/0009-0008-9315-8494
c
https://orcid.org/0000-0002-9777-9203
unit that co ntrols and coordinates e ach agent in the
fleet b y computing their cost and providing a com-
munication network throughout a fixed location. Due
to this ce ntralized processing structur e , the computa-
tional burden on a gents is reduced, and they become
simpler to build. However, coordinating agents from
a stationary location restricts the workspace of the
entire fleet, which further limits th e potential tasks
that the agents can handle and creates a single poin t
of failure in the system.
Decentralized methods (Peng et al., 202 4),
(Zhang et al., 2024), (Ozturk et al., 2024b) have
been proposed to solve the problems of centralized
task allocation . This approach distributes the to-
tal computational load among agents rather than
gathering it in a single unit. Thus, agents p erform
tasks based on their knowledge sets. Discarding
the central structure that forces the system to fixate
on a limited workspace has led to more robust and
scalable agent cooperation. Conversely, to converge
on an exact solution, agents should be able to sh a re
their status and information set amon g themselves
through a particular network topology, which can
result in intensive communicatio n overhead and local
optimality.
Market-based strategies are another well-known
approa c h researched in the task allocation problem
context (Ozturk et al., 2024a), (Wang et al., 2024).
The auction algorithm mimics the auction environ-
ment, specifically by simulating bidders and auction-
70
Ozturk, H. B., Yavas, N. B., Bingul and Z.
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty.
DOI: 10.5220/0013522600003970
In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 70-80
ISBN: 978-989-758-759-7; ISSN: 2184-2841
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

eers. First, bidders bid on the tasks they want to be
assigned and calculate their maximum payoff. Af te r-
ward, auctioneers collect these bids and announce the
highest bid as the contest winner.
Depending on how the problem is handled ,
market-based methods can be divided into single-
item and combinatorial auctioning. Single-item auc-
tions perform ta sk-wise operations at each iter a tion.
In contrast, combinatorial auctions p resent tasks as
bundles (task sets), and agents bid on these bun-
dles to minimize the path cost from their initial lo-
cation. Researchers have developed variants of these
approa c hes, includin g parallel single-item (PSI) and
sequential single-item (SSI) auctions. Un like single-
item auction procedures, PSI performs auctions in a
parallelized manner, in which agents are allocated to
tasks via simultaneously performed auctions. Thus, it
accelerates the assignment process but leads to subop-
timal solutions. The SSI method, on the other hand, is
a strategy that combines both combinatorial and PSI
auctions to leverage their advantages. The method is
based on a ser ies of single-item auctions, assuming
each agent is initially unallocated. To a llocate tasks,
agents place bids reflecting the increase in their small-
est path cost that arises from win ning the target they
bid on. The agent offering the overall smallest bid
is assigned to the corresponding target. Once agents
determine the winner by observing the bids from the
environment, the unassigned agents re-bid for the re-
maining tasks until all agents are assigned. Partic-
ularly in dynamic environments, SSI-based task up-
dates are highly motivated since environmental quan-
tities cha nge drastically. Nonetheless, these auction
methods neither provide a framework for resolving
conflicting assignments nor guarantee optimal solu -
tions in specific scenarios. Therefore, an agreement
among the fleet should be consistently m aintained to
overcome th ese issues.
Consensus-based algorithms (Herty et al., 20 24),
(Bonandin and Herty, 2 024) have thus gained promi-
nence in addressing multi-agent co ordination chal-
lenges. However, the se approaches often face diffi-
culties in achieving a commo n situational awareness
(SA) among agents, that is, agreement that the per-
ceived environment is the same for all of them. Al-
though it is applicable across various network topolo-
gies, their impleme ntation demands significant com-
putational resources, and the co nvergence process can
be notably time-intensive.
To resolve these problems, the consensus-based
auction algorithm (CBAA) and, for multitask as-
signments, the consensus-based bundle alg orithm
(CBBA) have been introduced by (Choi et al., 2009).
Both algorithms guarantee convergence on an agreed
SA while ensuring conflict-fr ee assignments. In con-
trast to traditional consensus approaches, these al-
gorithms leverage a decentralized auction scheme in
decision-making. Also, instead of agents’ SA, they
struggle to achieve an agreement on winning bid lists.
Unfortu nately, all of the methods discussed above
converge on a solution under the assumption of con-
stant states and neglect unce rtainty. This shortcoming
implies they are unsuitable for real-world applications
where the environment and its dynamics vary contin-
uously.
This paper proposes a novel consensus-based
adaptive gene tic-optimized auctio n (CAGA) algo-
rithm for dynamic task allocation of a multi-robot sys-
tem. Th e algorithm can also consider the uncertainty
in the environmen t and enable agents to make deci-
sions based on the scenario characteristics. Th erefore,
the utilization of genetic algorithms (GA) is motivated
by their ab ility to handle complex, multi-dimensional
optimization problems where analytical solutions are
infeasible to implement. In this context, the incre-
mental constant (ε) serves as a critica l parameter to
regulate the pace of optimization, ensuring both con-
vergence efficiency and computational feasib ility.
The remainder of this paper is organ iz e d as fol-
lows: Section 2 investigates the related works pro-
posed by other authors. Section 3 introduces the prob-
lem definition and preliminaries. Section 4 pre sents
the proposed algorithm and its partitions. Section 5
illustrates the conducted simulations and provides test
results, while Section 6 discusses the outcomes sub-
ject to th e scenarios. Finally, Section 7 concludes the
paper and gives valuable insights for futu re works.
2 RELATED WORKS
DTA has b een investigated in detail, and various ef-
forts have been made to solve this problem because
of its importance. The proposed meth ods can be clas-
sified into two types: exact solutions and heuristics.
For heuristic methods, evolution a ry-based ap-
proach e s have mostly been utilized to solve the DTA.
(Yan and Di, 2023) investigated the multi-robot task
allocation prob le m and classified tasks as compul-
sory ( must be co mpleted) and functional (optional
but beneficial). They aimed to op timize task as-
signments to minimize time c osts by focusing on a
novel hyper-heuristic algorithm. For this reason, re-
searchers introduced an d enlarged low-level heuris-
tic (LLH) and high-level strategy (HLS) algorithms.
LLH scores functional tasks based on an influence
diffusion model, while HLS optimize s LLH param-
eters using a particle swarm optimization (PSO) al-
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty
71

gorithm. The proposed algorithm was compared
against classical greedy, metaheuristic, and SSI-based
approa c hes. It was shown that the proposed algorithm
is flexible and scalab le . Nevertheless, it relies heav-
ily on parameter tuning and struggles with extremely
large or small rob ot groups, where simpler meth ods
may suffice. Furthermore, adding one m ore layer in-
creases the complexity of the implementatio n.
(Li et al., 2024) investigates task allocation chal-
lenges for h e te rogeneous unmanned aerial vehicles
(UAVs), pa rticularly in re source con stra ints and dy-
namic task demands. The authors proposed a heuris-
tic allocation method grounded in the overlapping
coalition formation game framework (OCF) to en -
hance resource utilization and task u tility. This frame-
work allows UAVs to operate under multiple condi-
tions simultaneously, while the heuristic allocation
method avoids repetitive and inefficient resourc e al-
locations. Moreover, the proposed task exit mecha-
nism allows UAVs to exit coalition s w hen their util-
ity contribution decreases. Although the algorithm
demonstra te s flexibility and dyn a mically responds to
changes, the reliance o n heuristic strategies results
in high c omputational demands and a dependency on
overly simplistic models, limiting its applicability in
real-world scenar ios.
In (Bischoff et al., 2024), re-optimization meth-
ods a re introduced to tackle time-extended multi-
robot task allocation problems involving task dele-
tion and insertion in dynamic environments. The pro-
posed optimization framework offers mechanisms to
adapt to situations where new tasks are added or exist-
ing tasks are removed. As a heuristic approach, they
present the cheapest ma ximum insertion cost heuristic
(CMI) for task insertion by balancing comp lexity and
performance. The intr oduced optimization heuristics
are both scalable and efficient. This method estab-
lishes upper bounds o n solution quality while ensur-
ing predictability and reliability in dynamic systems.
However, CMI heuristics can overestimate insertion
costs, rendering the resulting bounds limited applica-
bility and potentially inadequate in reflecting actua l
resource r e quirements.
Regarding exact solutions, these methods of DTA
tend to achieve better convergence. One of the most
commonly r e cognized strategies for solving DTA
problems is the market-based approach, which op-
erates main ly through auction routines. The study
presented b y (Hossain et al. , 2023) o ffers a parallel
task allocation framework using a multi-stage iter-
ative combina torial auction mechanism, introducing
uncertainties in multi-robot environments. The pa-
per aims to improve the task alloc ation process by ex-
ploiting different metrics, including task preferences,
path collision avoidance, task prioritization, and ex-
ecution deadlines. The prop osed method offers two
stages. In the initial stage, multiple round s of bidding
occur, and the temporary winner is determined. After
that, a single roun d in which robots submit their fi-
nal bids based on updated task values is executed for
the final stage. The proposed mechanism is scalable
and comprehensive, but it relies on a centr alized en-
tity, leading to a single po int of failure in the system.
Furthermore, the practical implementation of uncer-
tain environments requir es extensive fine- tuning.
3 PROBLEM DEFINITION
3.1 Task Allocation
In multi-robot task allocation (MRTA), the re a re m
agents and n tasks, which can be defined as
A , {a
1
,a
2
,... ,a
m
}
T , {t
1
,t
2
,. .. ,t
n
}
(1)
where A and T represent th e sets of agents and
tasks, respectively. The goal is for agents to find
conflict-fre e assignments that maximize their payoff.
Conflict-free means each agent is assigned only one
task. The task assignment p rocedure continues until
all agents are allocated to the tasks.
The overall score function for a conventional auc-
tion procedu re is introduced. It can be expressed as
max
m
∑
i=1
n
∑
j=1
(c
i j
− p
i j
)x
i j
!
subject to
m
∑
i=1
x
i j
= 1, ∀j ∈T
n
∑
j=1
x
i j
= 1, ∀i ∈ A
x
i j
∈ {0,1}, ∀(i, j) ∈ A ×T
(2)
where c
i j
is the benefit of agent a
i
if it is assigned ta sk
t
j
and p
i j
is the price of ta sk t
j
for agent a
i
. The x
i j
is
a binary decision variable, ind ic a ting that agent a
i
is
assigned task t
j
if x
i j
= 1 and 0 otherwise.
3.2 Auction Routine
Auction-based strategies are widely employed to
solve task assignment problems. These routines pro-
mote competition among bidders, which significantly
impacts the procedure’s completion time.
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
72

Conventional auction sche mes assume that agent
a
i
receives the maximum profit of c
i j
for task t
j
, where
c
i j
depicts the benefit of agent a
i
if it bids for task t
j
.
It can be c oncluded that agent a
i
will not bid for a task
if it does not benefit from it.
Suppose tha t agent a
i
pays the price p
j
for task t
j
;
then, the payoff can be calculated as c
i j
−p
j
. Thereby,
payoff functions of the agent and sy stem ca n be at-
tained in Eqs.(3) an d (4) as follows:
θ
i
= ma x
t
j
∈T
(c
i j
− p
j
), (3)
Θ =
m
∑
i=1
θ
i
(4)
Here, T denotes the task set. In decentralized auc-
tion routines, if Eq.( 3) is ensured for each agent in the
fleet, then the agents are satisfied with their decision,
and the global optimum is achieved. Th e system pay-
off Θ can be depicted as in Eq.(4).
If this is not the case, agents proceed to the next
round, whe re the price update rule is executed.
An agent can raise the price offered by another
agent to the extent that it becomes indifferent between
its op timal and suboptimal payoffs. In light of this
strategy, agents calculate their payoff for each task
and bid on the task to m a ximize their benefit.
The optimal payoff is calculate d as in Eq.(5).
Where θ
i
is the o ptimal pa yoff for the agent a
i
and
j
∗
is the task number corresponding to the optimal
payoff.
θ
i
= g
i j
∗
= ma x
t
j
∈T
(c
i j
− p
j
) t
j
∗
∈ T , (5)
After that, calculate the suboptimal payoff g
i j
∗
1
for
agent a
i
:
g
i j
∗
1
= ma x
t
j
(c
i j
− p
j
) t
j
∗
∈ T t
j
∗
1
6= t
j
∗
, (6)
where j
∗
1
is the task corresponding to the subop-
timal pa yoff. By exploiting these equ ations, the next
round offer of agent a
i
can be introduced as
p
i j
∗
= d
j
∗
+ g
i j
∗
−g
i j
∗
1
+ ε (7)
where d
j
∗
is the highest bid for task j
∗
offered
in the previous round, and ε denotes the incremen-
tal constant, which significantly impa cts th e auction’s
course. I n fact, it allows the system to converge on op-
timal solutions and overcom e deadlocks (infinite iter-
ations), whereas poor ε selection leads to higher com-
putational resource consumption. Thus, it ne eds to be
adjusted according to the specific scenario. Section 4
further elucidates how this value is optimized through
a genetic algorithm (GA).
3.3 Communication Topology
The graph G = (N ,V ) is adopted to estab lish
a network topology between decentralized agents.
Namely, N is the set of nodes, and V is the set of
vertices. If there is a d irect communication lin k be-
tween two agents, that is, (δ,η) ⊆ V , then these two
agents are adjacent. The number of a gents in the net-
work is N , and the adjacency matrix C of G can be
defined as in Eq.(8).
c
δ,η
=
(
1, if (δ,η) ⊆ V
0, if (δ,η) * V
(8)
c
δ,η
is the eleme nt of the adjacency matrix C, a
binary decision variable tha t denotes w hether a link
exists between two nodes δ and η. When d ealing
with uncertainties and executing the algorithm, it is
assumed that the gr aph is undirected and fully con-
nected.
3.4 Uncertainty Theory
When allocating tasks to ag ents, the severity of the
uncertainty directly affects the dec isio n-makin g pro-
cess and, hence , how fast and effectively agents oper-
ate (ElGibreen and Youcef-Toumi, 2019).
Most conventional approaches do not c onsider
uncertainty and its possible effects on the assignment
proced ure. Conversely, in cases where the environ-
ment is highly dynamic, task positions are not deter-
ministic, and mea surements vary over time . In this
paper, uncertainty is introduced based on changes in
the environment and is used to determine the accuracy
of the agents’ sensor measurements.
Uncertainty can be introduced with an uncertainty
space (Liu and Liu, 2010), represented as (Γ,L,M )
where Γ is a n on-empty set, L is σ −algeb ra over a
non-empty set Γ, and M {∧} is an uncertainty mea-
sure which indicates the level of belief that an event
∧ will occur. This space has a measurable function
defined as ξ that maps th e quantities from uncertainty
space to real n umbers.
The lognormal distribution is implemented to
model the uncertainty. Henc e, ξ ∼ LOGN (e,σ) and
the uncertainty distribution is measured by M {ξ ≤x }
for x ≥ 0 in Eq.(9).
Φ(x) =
1 + exp
π(e −ln(x))
√
3σ
−1
(9)
On the other hand, finding the uncertainty
distribution is not helpful since determining the un-
known value of x is not possible in a dynamic environ-
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty
73

ment. Thus, the distribution must be reconstructe d us-
ing the un c ertainty theory’s ope rational prope rties. In
this case, the inverse uncertainty distribution Φ
−1
(α)
is obtained, and its uncertainty variable ξ has a regu -
lar distribution Φ(x), where α ∈[0,1] is a confidence
constant. For ξ ∼ LOGN (e,σ), inverse uncertainty
distribution can be derived as
Φ
−1
(α) = exp(e)
α
1 −α
√
3σ/π
(10)
Utilizing the Eqs.(9) and (10), the overall score
function can be f ormulated as
max
m
∑
i=1
n
∑
j=1
1/Φ
−1
(α)
i j
− p
i j
x
i j
!
(11)
where Φ
−1
(α) is the inverse uncertainty distribution,
and it represents the uncertainty of ta sk position s.
Eq.(11) is used when calculating payoffs.
4 METHODOLOGY
In th is section, the proposed algorithm and its
modules are introduce d. Additionally, their working
principles are elaborated.
4.1 Algorithm Framework
The proposed algorithm comprises two phases: First,
a predefined number of CBAA operations are exe-
cuted by agents in parallel, that is, each agent simul-
taneously performs a sp ecific number of CBAA and
aims to maximize its own score. The properties of
locally executed CBAAs (level of possible task com-
binations, the a mount of CBAA opera tions) ar e de-
termined by GA’s evolutionary parameters, including
population size, crossover, and mutation. For each
CBAA execution, agents randomly initialize different
ε values ranging from
5.10
−6
,5.10
−4
and find the
best possible ε value by determining the overall max-
imum payoff (d e rived in Eq.(11)) among calculated
CBAA procedures. Ultimately, the final CBAA is car-
ried ou t with the best obtained ε values and allocates
tasks to agents.
As a toy example of the proposed algorithm, as-
sume that there are room s where potential bidders are
interested in the products being auctioned. The prod-
ucts are offered for sale to bidders in accordance with
specific auction ru le s. Bidders submit bids on the
most desirable item, thereby maintaining the momen-
tum of the auction. The auctions are conducted in par-
allel sessions, with the same products b eing offered
at varying levels o f aggressiveness in each session.
It is expected that the bidders maxim iz e their profit,
and if this criterion is not met, the auction extends
for a predetermined number of days. At each au ction,
Bidders prioritize maximizing their own interests, and
if the auction does not yield the desired profit, they
must re-bid on a subsequent day. Moreover, prior to
each auction, bidders conduct an internal assessment
of the upcoming session, analyzing past results to re-
fine th e ir b idding strategies and optimize their offers
accordin gly. Subsequently, the most profitable auc-
tion combinations are identified, and buyers are en-
courag e d to submit o ptimized bids for the correspond-
ing products. Thus, by conducting multiple auctions,
the profits of the bidders will be optimized, and the
system will reach a state of equilibrium.
4.2 Monte Carlo Simulation
The Monte Carlo (MC) approach is adopted to deter-
mine the un certain positions of the tasks and increase
adaptability in a dynamic environme nt. Primarily,
random distances betwee n (0,150) were calculate d,
and by using Eq.( 9), severa l distance points were col-
lected to determine the LOGN (e,σ) uncertainty pat-
tern. Spec ifica lly, e and σ values are obtained over
1000 iterations, and the lognorma l uncertainty distri-
bution is acquired.
When locating task s to place bids, task positions
can be predicted by using the un c ertainty theory.
Uncertainty space can be reconstructed as {T , D,ξ},
where T is the tasks, D is the distances, and ξ is
the agent’s benefit fun c tion. The goal is to find the
uncertainty distribution of each task, in othe r word s,
ξ
n
∼ LOGN (e,σ).
Subject to the task position a mbiguity prob-
lem, suppose ξ
1
,ξ
2
,. .. ,ξ
n
are independent uncer-
tain variables with a regular uncertainty distribution.
Φ
1
(x),Φ
2
(x),... , Φ
n
(x) and the inverse uncertainty
distribution for ξ = f (ξ
1
,ξ
2
.. .ξ
n
), where f : ℜ
n
→
ℜ is strictly increasing function denoted in Eq.(12).
Thereby, agents have valuable insights and awareness
regarding their benefits befo re assigning tasks in a dy-
namic environment.
Ψ
−1
(α) = f (Φ
−1
1
(α),Φ
−1
2
(α),.. . ,Φ
−1
n
(α)) (12)
4.3 CAGA Algorithm
The CAGA algo rithm is proposed to solve the de-
centralized dynamic task allocation problem of the
MAS. The algorithm is divided into two phases: the
optimization phase and the assignment phase. Ini-
tially, with random ε combinations, agents conduct
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
74

parallel CBAA processes and compute their payoffs.
Further, GA optimizes the whole procedure by adjust-
ing the ε values.
input : ag ents A
i
, population size P
output: assignment matrix H
initialize y
t
, generations P
g
for each agent a
i
do
initialize populations
end
for each generation do
for each solution P do
calculate fitn ess
share fitne ss values
end
while new population < P do
select fir st parent from P
select second parent from P
crossover fir st and second parent
mutate c rossover-ed populations
add new solutions to the P
end
end
for each agent a
i
do
calculate global best solution
end
for each agent a
i
do
update p a rameters
end
Algorithm 1: Optimization Phase of CAGA Algorithm.
In the optimization phase, each agent initial-
izes parameters, including popu la tion size, crossover,
and mutation rate. Particularly, between the pop-
ulation members ( each CBAA performed by each
agent), combinations with the best payoffs are stored,
and the remainder sizes are filled with the arith-
metic crossover of former populations. In addition,
by leveraging Gaussian distribution, populations ex-
Table 1: Symbol description of CAGA algorithm.
Symbol Description
z
i
The task list of agent i
w
i
The winning bid list of agent i
v
i
The valid task list for agent i
q
i,J
i
The agent that currently assigned task J
i
P(·)
It i s the indicator function that is unity
if t he argument is true and zero otherwise
G The communication topology
k Agent k is the neighbor of agent i
posed to crossover are m utated, and new epsilon com-
binations are obtained. After these operations, each
combination is reserved, and agen ts proceed to the as-
signment phase.
In th e assignment phase, after determining the ε
that provides the highest system payoff, agents carry
out the original CBAA and assign themselves to tasks.
input : The agent set A the task set T , the
communication topology G and the
initial price p
i j
output: system payoff
while iteration < max iteration do
for each agent a
i
do
z
i
(t) = z
i
(t −1)
w
i
(t) = w
i
(t −1)
if
∑
j
z
i j
= 0 then
v
i j
= P(c
i j
> w
i j
(t)),∀j ∈ T
if v
i
6= 0 then
J
i
= argma x
j
v
i j
·c
i j
z
i,J
i
(t) = 1
w
i,J
i
(t) = c
i,J
i
update the price p
i j
end
end
send w
i
to k with g
ik
(τ) = 1
receive w
k
from k with g
ik
(τ) = 1
w
i j
(t) = m ax
k
g
ik
(τ) ·w
k j
(t),∀j ∈ T
q
i,J
i
= argma x
k
g
ik
(τ) ·w
k,J
i
(t)
if q
i,J
i
6= i then
z
i,J
i
(t) = 0
end
end
end
Algorithm 2: Assignment Phase of CAGA Algorithm.
In addition, the MC simulations help them effec-
tively detect the exposed uncertainty and make deci-
sions acco rdingly.
5 SIMULATION RESULTS
This section provides a detailed description of the cru-
cial aspects of the simulation process and presents
various test scenarios. In fact, small-, medium-, an d
large-scale applications are conducted, and the re-
sults are visualized to illustrate the adaptability of the
CAGA alg orithm.
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty
75
5.1 Experimental Setup
The simulation setup introduces the preliminaries, in-
cluding initial configura tions, M C operations, and
the evaluation metrics used for analysis. Initially,
agents and task positions are set, and then agents ex-
ecute the CAGA algorithm to determine assignments.
Once targets are identified, the simulation begins to
demonstra te scenarios at predefined scales. Due to
environmental uncertainty, agents must periodically
update their measurements fo r accurate task execu-
tion. Also, these updates should be synchron ized to
ensure feasible b id assessment and task re-allocation
when necessary.
During simulations, the uncertainty degree is as-
sumed to increase proportionally with distance and
follow a lognorma l distribution. The simulation en-
vironm ent adjusts the fleet’s measurem e nt frequency
to improve assignment efficiency, co nsidering the dis-
tance of the farthest agent from the task, as this agent
experiences the highest level of uncertainty. In con-
trast, the time step is adjusted inversely to the de -
gree of unc ertainty, ensuring ad a ptive responsiveness.
This relationship can be expressed as
∆t =
C
max(γ) + κ
(13)
where ∆t represents time step, C signifies constant
scale factor defined as 1, γ denotes the set of uncer-
tainty degre e ( γ ∈ [0,1]) experienced by each agent
and κ depicts the increment to avoid d ivision by zero.
For the purposes of illu stra tion, consider a sce-
nario in which three agents (a
1
,a
2
,a
3
) ar e involved
in a given problem, with the agents positioned 10,
20, and 30 meters away from their de signated tasks,
respectively. Accor ding to the simulation, the agent
positioned 30 meters away exhibits the highe st de-
gree of uncertainty. To determine the furthest one,
agents share their degree of uncertainty with them-
selves. Late r, they define the highest bid and use it to
calculate Eq.(1 3) while updating their status. As the
agents appro ach their assigned tasks, the uncertainty
decreases, thereby enhancing the agents’ confidence
in their me asurements and decreasing the me asure-
ment frequency. Conversely, in a scenario where the
agents are distant from the task s, the uncertainty is
elevated, and the measuremen ts are rec eived at more
frequent intervals.
The CAGA algo rithm introduces an MC simu-
lation to capture uncertainty characteristics at var-
ious levels of uncertainty. This way, agents will
have more informatio n about their workspace. Be-
fore performing assignments, agents are informed of
the p resented uncertainty (LOGN (3.6,0.6)) with the
historical data collected from MC operations in a
100 ×100 workspace.
0 50 100 150
Distance (m)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Level of Uncertainty (x)
Relationship Between Distance and Uncertainty Degree
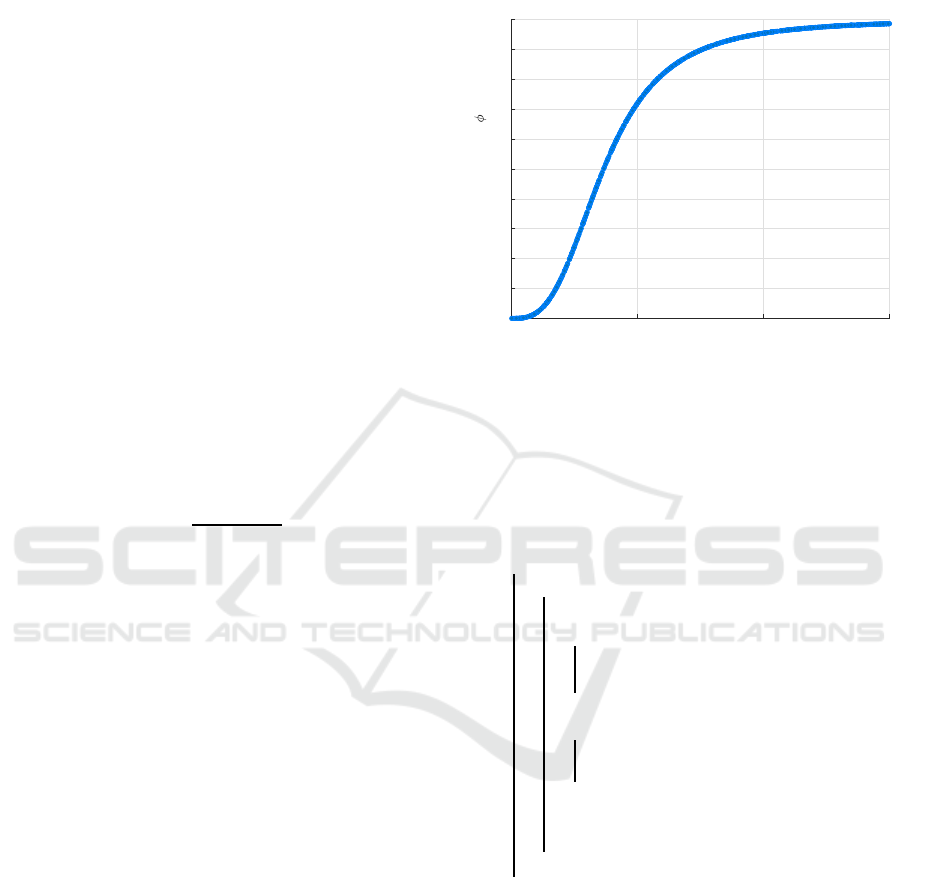
Figure 1: Lognormal uncertainty distribution function.
Figure 1 visualize s the uncertainty distribution
adopted in this pa per. By using this knowledge,
agents have the capability to analyze the environment
and make decisions more accurately.
Carry out MC simulations
while system progress < t do
for current positions do
calculate E uclidean distance D
i j
if D
i j
< 10
−6
then
nullify the uncertainty
coeff = 0
end
else
calculate measured distan ce
calculate measur e d target
end
calculate new positions
calculate ∆
t
value
end
end
Algorithm 3: Simulation steps.
5.2 Results
Simulations for scales of 3 × 3, 5 × 5, and 10 × 10
were carried out, and the task assignments performed
by the CAGA algor ithm have been visualized. The
proposed algorithm’s performance metr ic s w e re col-
lected using the same mode l created in Py thon.
For the simulations, the initial agent and task po-
sitions for sma ll-, medium-, and large-scale appli-
cations were randomly defined within a 1 00 × 100
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
76
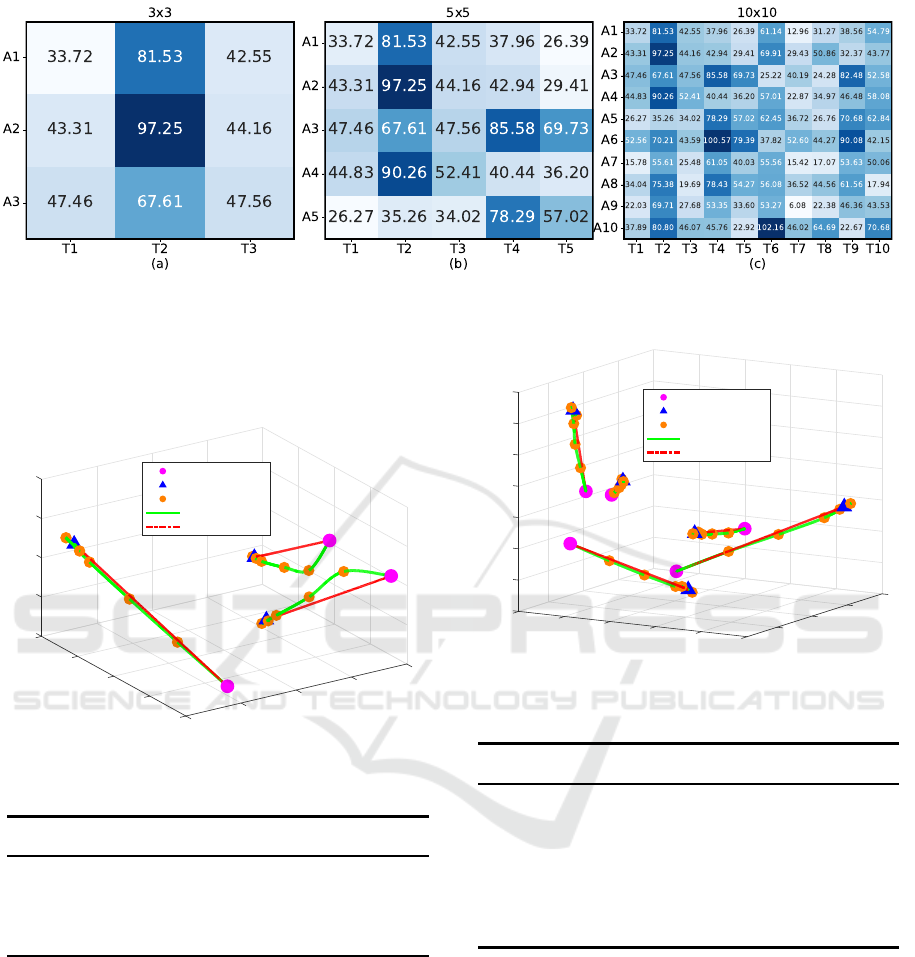
Figure 2: Initial payoff matrices for conducted scenarios.
workspace. The initial payoff matrices, which are
shown in Figure 2, were derived by calculating the
Euclidean distance b e tween the a gent-task pairs and
30
100
40
T3
80
50
Z (m)
80
60
Y (m)
60
CAGA Algorithm Task Assignment - 3 X 3 Scenario
60
T1
T2
70
X (m)
40
40
A2
A3
20
20
0
A1
Agents
Tasks
Checkpoints
Assignments
Initial Assignments
Figure 3: The CAGA algorithm performance for 3 × 3.
Table 2: Positions on XYZ (in meters) for 3 × 3 Scenario.
Agent Positions Task Positions Sensor Outputs
[54 23 65] [47 54 54] [32.1 72.2 40.51]
[75 21 53] [52 55 37] [38.5 76.1 41.4]
[17 23 34] [2 85 57] [42.2 58.6 42.8]
adding a LOGN (3.6,0.6) uncertainty noise to these
values. After that, at e ach checkp oint of th e simu-
lation, sensor outputs wer e obta ined from the corre-
sponding positions of the agen ts (To improve read-
ability, only the first senso r measurement output is
provided for each agent) . These values are presented
in Tables 2, 3, and 4, respectively.
The simulation mechan ism devised for the scenar-
ios is as follows: Agents and task locations are ini-
tialized for each procedure, and tasks are allocated by
leveraging the CAGA algorithm subject to the payoff
matrices in Figure 2. The simulation is divided into
A3
0
T2
A5
20
A4
CAGA Algorithm Task Assignment - 5 X 5 Scenario
A1
30
40
T1
T3
50
0
60
X (m)
70
Z (m)
40
80
A2
20
90
100
Y (m)
40
T5
T4
60
60
80
100
Agents
Tasks
Checkpoints
Assignments
Initial Assignments
Figure 4: The CAGA algorithm performance for 5 × 5.
Table 3: Positions on XYZ (in meters) for 5 × 5 Scenario.
Agent Positions Task Positions Sensor Outputs
[54 23 65] [71 41 74] [70.3 40.2 73.6]
[75 21 53] [52 55 37] [53.6 52.6 38.1]
[17 23 34] [2 85 57] [4.27 75.6 53.5]
[53 11 65] [76 23 96] [74.3 22.1 93.8]
[21 56 51] [47 54 54] [45.8 54.9 53.8]
five time intervals, each containing a checkpoint. This
structure allows agents to simultaneously up date their
measurements, refine their positions, and potentially
reallocate tasks. At each checkpoint, they recalcu-
late their payoffs to each task and, if a high e r payoff
exists, reallocate to another task by re-executing the
CAGA algorithm. Since age nts synchrono usly reach
checkpoints and ad just their progression rates accord-
ing to the agent most affected by the uncertainty, task
conflicts will not arise.
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty
77
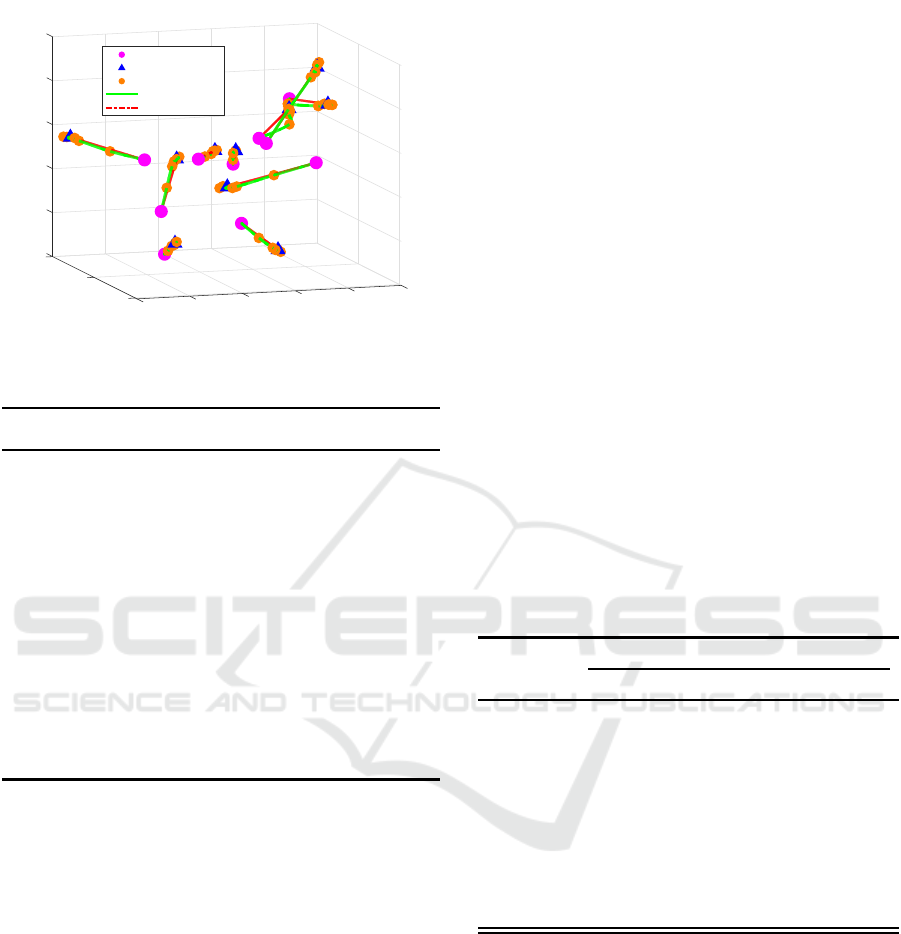
0
20
40
60
100
80
100
Z (m)
T2
A10
T3
T1
CAGA Algorithm Task Assignment - 10 X 10 Scenario
T9
A8
A5
T10
Y (m)
50
T5
A7
A6
A9
T7
A2
T4
A1
T8
A3
100
X (m)
A4
80
60
T6
40
0
20
0
Agents
Tasks
Checkpoints
Assignments
Initial Assignments
Figure 5: The CAGA algorithm performance for 10 × 10.
Table 4: Positions on XYZ (in meters) for 10 × 10 Scenario.
Agent Positions Task Positions Sensor Outputs
[54 23 65] [71 41 74] [84.2 40.9 74.4]
[75 21 53] [52 55 37] [54.2 51.6 38.5]
[17 23 34] [25 30 56] [24.6 29.6 55]
[53 11 65] [76 23 96] [74.6 22.2 94.1]
[21 56 51] [2 85 57] [3.69 82.4 56.4]
[22 35 12] [15 0 24] [15.4 1.98 23.3]
[37 42 53] [47 54 54] [46.7 53.7 53.9]
[53 41 23] [64 32 12] [63.5 32.3 12.4]
[47 32 52] [48 32 58] [47.9 32 57.8]
[78 63 74] [86 42 75] [71.2 41.8 74]
A sm a ll-scale app lication was initially conducted,
with results visualized in Figure 3. Due to uncertainty
and sensor errors, agents deviated fr om their trajecto-
ries. A t each checkpoint, they reassessed their po-
sitions and, if necessary, reallocated tasks. Notably,
at the secon d and third checkpoints, agents 2 and 3
switched tasks, but by the final checkpoint, updated
payoffs led them to reallocate to their initial tasks.
This behavior distinctly illustrates the proposed algo-
rithm’s resilience to uncertainty.
In med ium-scale applications, as depicted in Fig-
ure 4, agents effectively navigated environmental un-
certainty while mainta ining their initial alloca tion
paths, in contrast to the deviations o bserved in small-
scale scenarios.
Ultimately, the CAGA a lgorithm was tested in a
10 × 10 scenario , with results presented in Figure 5
and Table 4. The simulation outcomes demonstrate
that agents suc cessfully ma intained their initial task
assignments while effectively adapting to uncertain-
ties. Througho ut the execution, they remained within
their designated m easurement corridors, ensuring sta-
ble an d reliable task completion.
Interestingly, during the execution of the simula-
tion scenarios, the uncertainty inhe rent in the envi-
ronment does not significantly divert the agents from
their trajectories. In contrast, results clearly show
that the MC approac h introduces adaptability to the
CAGA algorithm, allowing agents to manage unc e r-
tainty effectively within d ynamic environments.
6 DISCUSSION
The CAGA algorithm was comp ared with CBAA
and other market-based approaches across differ-
ent scenarios both in terms of computationa l time
and total payoff. Particularly, the proposed optimal
market-based (OMB) (Liu and Shell, 20 13) and im-
proved market-based (IDMB) (Trigui et al., 2014) ap-
proach e s were performed, and re sults are shown in
Ta ble 5 and 6. A ll simulatio ns were imple mented in
Python 3.12.7 and tested on a system with a 4-core
4.2 GHz i7-7700K CPU and 16 GB of memory.
Table 5: The payoff comparison of the algorithms. The
boldface values are the best average for each algorithm.
Scenarios Algorithms
CAGA CBAA OMB IDMB
3 × 3 6.71 6.71 6.71 6.71
5 × 5 13.82 13.82 13.2 13.80
7 × 7 29.13 28.37 25.5 22.61
10 × 10 50.59 49.82 49.6 43.22
15 × 15 75.689 74.74 71.87 72.81
20 × 20 125.86 111.4 106.5 109.72
25 × 25 182.32 143.8 126.4 127.4
30 × 30 209.09 169.1 157.8 148.07
35 × 35 248.06 247.7 227.7 209.8
40 × 40 279.42 281.6 265.8 244.5
In the proposed algorithm, the assignments are de-
rived from the last checkpoint of the simulations. On
the other hand, since other algorithms do not utilize
checkpoints, assignments are made dire ctly based on
the initial cost matrix. After that, cost matrices with
uncertainties have been used to perform all assign-
ments. Finally, cost m atrices without uncertainty h ave
been used to calculate payoffs to ensure a consistent
evaluation of p ayoffs.
The payoff and runtime perf ormances of the algo-
rithms, as presented in Tables 5 and 6, were tested in
25 trials, and the arithmetic mean of the results was
used f or comparison. The resu lts are calculated using
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
78

100 λ
−1
, where λ denotes the cost matrix. The ma-
trix elemen ts are derived based on the Euclidean dis-
tance between the positions of the agents and tasks.
To prevent extremely small values and enhance the
accuracy o f the results, the inverse of the cost ma-
trix is scaled by a factor of 100. Acco rding to the re-
sults, the proposed algorithm demonstrates superior-
ity for small- and medium-scale applications regard-
ing system payoff in an uncertain environment. It ex-
pands the search space and identifies possible solu-
tions available to agents.
Table 6: The computational time comparison of the algo-
rithms (in milliseconds). The boldface values are the best
average for each algorithm.
Scenarios Algorithms
CAGA CBAA OMB IDMB
3 × 3 8.89 0.97 0.09 0.03
5 × 5 9.76 0.99 0.17 0.24
7 × 7 11.95 1.89 0.42 0.30
10 × 10 13.16 1.99 0.4 4 0.38
15 × 15 18.02 4.98 0.7 9 0.71
20 × 20 22.92 8.97 0.86 0.92
25 × 25 30.78 17.9 7 1.15 1.65
30 × 30 40.84 35.9 0 2.06 2.80
35 × 35 66.41 55.8 2 3.36 3.69
40 × 40 83.79 73.8 0 3.84 4.32
However, as the operational scale increases, the
CAGA algorithm struggles with the growing num-
ber of uncertain conditions in the system, which ul-
timately leads to computational overhe a d. Table 6 il-
lustrates the computational times of e a ch algo rithm
across various applications. The resu lts highlight the
efficiency of the OMB algorithm, where a s th e CAGA
algorithm demonstrates relatively poor performanc e.
Nevertheless, the CAGA algorithm accounts for un-
certainty and c an be easily adjusted for ap plication
scenarios where optim ality pre cedes time sensitivity.
7 CONCLUSION
In this paper, the decentralized dynamic task
allocation problem o f MAS was introduced and
solved with the proposed CAGA algorithm. The pro-
posed alg orithm was compared with several market-
based methods and the well-known consensus-based
decentralized task assignm ent alg orithm CBAA, and
the results are discussed. Accordin g to the sim-
ulations conducted in different operational sizes, it
has been demon strated that the proposed algorithm
provides valuable outputs in terms of system pay-
off in an uncertain environment, although it sacri-
fices computational time to find more optimal solu-
tions. Unlike CBAA or other conventional task al-
location algorithms, the CAGA algorithm introduces
adaptability and fea sibility for real-world applica-
tions. In future works, plans ar e to use un certainty
synergistically while tackling the formation flight and
task allocation problems and cre a ting realistic en-
vironm ents much more analogous to real-world ap-
plications. Beyond the current uncertainty handling
framework of the algorithm, incorporating additional
checkpoints could enable more precise task assign-
ments for agents. This enhancement can potentially
improve efficiency, particularly in environments with
high levels of uncertainty. Moreover, the failures
that may arise due to the high communication bur-
den of the system can be investigated, and the lim-
ited communication problem can be used jointly in
the task assignment scenario. Also, an algorithm with
higher efficiency and performance can be created by
adapting the genetic parameters used in the proposed
algorithm to the specific problem. Future research
could explo re trajectory planning problems for agents
under uncertainty in conjunction with task assign-
ments. Enhancing agents’ adaptability and sensitiv-
ity in rea c hing tasks may lead to more efficient and
robust decision-making in dynamic environments.
REFERENCES
Bischoff, E., Kohn, S., Hahn, D., Braun, C., Rothfuß, S.,
and Hohmann, S. (2024). Heuristic reoptimization of
time-extended multi-robot task allocation problems.
Networks, 84(1):64–83.
Bonandin, S. and Herty, M. (2024). Consensus-based al-
gorithms for stochastic optimization problems. arXiv
preprint arXiv:2404.10372.
Chen, Y., Zhang, Y., Zhang, G., and Gu, Y. (2024). A drone
swarm-based wildfire search and rescue method with
autonomous behavior modeling and centralized task
assignment. In 2024 IEEE 4th International Confer-
ence on Power, Electronics and Computer Applica-
tions (ICPECA), pages 341–345. IEEE.
Choi, H.-L., Brunet, L., and How, J. P. (2009). Consensus-
based decentralized auctions for robust task alloca-
tion. IEEE transactions on robotics, 25(4):912–926.
ElGibreen, H. and Youcef-Toumi, K. (2019). Dynamic task
allocation in an uncertain environment with heteroge-
neous multi-agents. Autonomous Robots, 43:1639–
1664.
Herty, M., Huang, Y., Kalise, D., and Kouhkouh, H . (2024).
A multiscale consensus-based algorithm for multi-
level optimization. arXiv preprint arXiv:2407.09257.
Hossain, M. S., Ibrahim, I., and Fukuta, N. (2023). Par-
allel task allocation in multi-robot environment un-
der uncertainty based on auction mechanism. In 2023
Adaptive Market-Based Dynamic Task Allocation Under Environmental Uncertainty
79

15th International Congress on Advanced Applied In-
formatics Winter (IIAI-AAI-Wi nter), pages 97–100.
IEEE.
Hwang, N. E., Kim, H. J., and Kim, J. G. (2022). Cen-
tralized task allocation and alignment based on con-
straint table and alignment rules. Applied Sciences,
12(13):6780.
Li, Y., Z hang, Z., He, Z., and S un, Q. (2024). A heuristic
task allocation method based on overlapping coalition
formation game for heterogeneous uavs. IEE E Inter-
net of Things Journal.
Liu, B. and Liu, B. (2010). Uncertainty theory. Springer.
Liu, L. and Shell, D. A. (2013). Optimal market-based
multi-robot task allocation via strategic pricing. In
Robotics: Science and Systems, volume 9, pages 33–
40.
Ozturk, H. B., Ozturk, U., Yavas, N. B., and Bingul, Z.
(2024a). Development of optimal task allocation al-
gorithm for unmanned aerial vehicle swarms. In Pro-
ceedings of the Cognitive Models and A rtificial Intel-
ligence Conference, pages 341–348.
Ozturk, H. B., Yavas, N. B., Ozturk, U., and Bingul, Z.
(2024b). Game theory based decentralized multi-task
allocation algorithm for multi-agent systems. In 2024
International Congress on Human-Computer Interac-
tion, Optimization and Robotic Applications (HORA),
pages 1–9. IEEE.
Peng, J., Viswanath, H., and Bera, A. (2024). Graph-based
decentralized task allocation for multi-robot target lo-
calization. IEEE Robotics and Automation Letters.
Trigui, S., Koubaa, A., Cheikhrouhou, O., Youssef, H., Ben-
naceur, H., Sriti, M.-F., and Javed, Y. (2014). A dis-
tributed market-based algorithm for the multi-robot
assignment problem. Procedia Computer Science,
32:1108–1114.
Wang, G., Wang, F., Wang, J., Li, M., Gai, L., and Xu,
D. (2024). Collaborative target assignment problem
for large-scale uav swarm based on t wo-stage greedy
auction algorithm. Aerospace Science and Technol-
ogy, 149:109146.
Yan, F. and Di, K. ( 2023). Solving the multi-robot task allo-
cation wi th functional tasks based on a hyper-heuristic
algorithm. Applied Soft Computing, 146:110628.
Zhang, Z., Jiang, J., Haiyan, X., and Zhang, W.- A . (2024).
Distributed dynamic task allocation for unmanned
aerial vehicle swarm systems: A networked evolu-
tionary game-theoretic approach. Chinese Journal of
Aeronautics, 37(6):182–204.
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
80
