
Trajectory Planning for a Knuckle Boom Crane Using Differential
Dynamic Programming
Chair of Materials Handling, Material Flow, Logistics, Technical University of Munich, Boltzmannstraße 15, 85748
Garching bei M
¨
unchen, Germany
Keywords:
Knuckle Boom Crane, Trajectory Planning, Differential Dynamic Programming, Kinematic Constraints.
Abstract:
Knuckle boom cranes are widely used in numerous applications, making effective obstacle avoidance trajec-
tory planning critical for automation. However, the cranes’ inherent kinematic constraints pose significant
challenges to designing and optimizing such trajectory planning problems. In this study, we develop a tra-
jectory planning method that addresses obstacle avoidance under these kinematic constraints by employing
Differential Dynamic Programming (DDP). We first derive an explicit Euler-based dynamic model of the
crane, integrating Baumgarte stabilization to suppress kinematic constraint violations within the DDP frame-
work. Additionally, a relaxed log-barrier function is introduced to handle both states and obstacle-avoidance
constraints during trajectory planning. Comparative numerical simulations with the Ipopt solver demonstrate
the effectiveness of the proposed approach in achieving obstacle avoidance and constraints suppression.
1 INTRODUCTION
The knuckle boom crane is a representative type of
engineering equipment with a wide range of appli-
cations, including logistics, construction, and indus-
trial manufacturing. Among the areas, knuckle boom
cranes are required to efficiently transport heavy pay-
loads in complex working environments. However,
as a typical underactuated mechanical system, rapid
crane movements involving large acceleration or de-
celeration often lead to undesirable payload oscilla-
tions, posing significant challenges for manual crane
operation. To address this issue, the development
of efficient and safe trajectory planning methods for
knuckle boom cranes has attracted growing attentions
from both industry and academia.
In recent years, numerous studies have made sig-
nificant progress in crane trajectory planning. For the
typical underactuated overhead crane system, (Zhang
et al., 2021) employed the principle of differential
flatness to generate a time-optimal trajectory for a
planner double-pendulum overhead crane, thereby
improving the transportation efficiency. In (Thi et al.,
2024), the differential flatness-based trajectory plan-
ning method was extended to a three-dimensional
overhead crane. Furthermore, (Li et al., 2022) an-
alyzed minimum-time, minimum-energy, and com-
bined optimal time-energy trajectory planning for an
overhead crane with pendulum-sloshing dynamics by
formulating the problem under a quasi-convex op-
timization framework. Another typical crane sys-
tem was investigated in (Farrage et al., 2023), which
proposed a three-dimensional rotary crane trajectory
planning method using the A* algorithm to gener-
ate an obstacle-avoidance path, followed by a time-
optimal trajectory solution under crane dynamics and
load-sway constraints. Besides, a neural network-
based time-optimal trajectory planning method for
rotary cranes was further developed in (Zhu et al.,
2023). However, compared to overhead or rotary
cranes, knuckle boom cranes typically feature a more
complex mechanical structure with higher dimension-
ality and greater flexibility, which complicates the
process of trajectory planning.
As an efficient indirect trajectory planning method
characterized by its rapid convergence and relatively
low computational cost, Differential Dynamic Pro-
gramming (DDP) has been utilized in many fields,
including quadruped robots (Li and Wensing, 2020;
Kim et al., 2022; Mastalli et al., 2020), autonomous
driving (Chen et al., 2019; Huang et al., 2023; Lee
et al., 2022), and robotic manipulators (Zimmermann
et al., 2021; Wang et al., 2023). The theoretical
foundation of DDP, as presented in (Zheng et al.,
2021), is based on the Bellman optimality principle
and second-order Taylor expansions, effectively split
Zhiwei Wang, Lingchong Gao, Michael Kleeberger and Johannes Fottner
62
Wang, Z., Gao, L., Kleeberger, M., Fottner and J.
Trajectory Planning for a Knuckle Boom Crane Using Differential Dynamic Programming.
DOI: 10.5220/0013522000003970
In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 62-69
ISBN: 978-989-758-759-7; ISSN: 2184-2841
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

2 CRANE DYNAMICS
Referring to (Martin and Irani, 2021), a simplified
knuckle boom crane is illustrated in Fig. 1, in this
model, the crane system is modelled as a rigid multi-
body system, where the distributed mass payload is
attached to the tip of the crane boom via a rigid, mass-
less cable.
To describe the motion of the crane system, a set
of generalized coordinates is defined:
𝑞
𝑞
𝑞 =
(
𝜃
1
, 𝜃
2
, 𝜃
3
, 𝑑
4
, 𝜃
5
, 𝑑
6
, 𝜃
7
, 𝑑
8
, 𝜙
1
, 𝜙
2
)
⊤
, (1)
where 𝜃
1
denotes the rotation angle of the column, 𝜃
2
denotes the relative rotation of the inner boom with re-
spect to the column. Correspondingly, the inner boom
hydraulic actuator consists of a cylinder rotates an an-
gle 𝜃
5
and a rob translates a distance 𝑑
6
. Similar with
the inner boom, the relative rotation of the outer boom
is represented by 𝜃
3
, the rotation and the translation of
the outer boom hydraulic actuator are represented by
𝜃
7
and 𝑑
8
, respectively. In addition, the translation of
the extension boom is expressed by 𝑑
4
, while 𝜙
1
and
𝜙
2
are utilized to describe the oscillation angles of the
payload.
Without loss of generality, the dynamic equations
that govern the motion of the crane system can be
expressed as:
𝑀
𝑀
𝑀
(
𝑞
𝑞
𝑞
)
¥
𝑞
𝑞
𝑞 + 𝚽
⊤
𝑞
𝑞
𝑞
𝜆
𝜆
𝜆 = 𝐹
𝐹
𝐹
(
𝑞
𝑞
𝑞,
¤
𝑞
𝑞
𝑞
)
+ 𝐵
𝐵
𝐵𝑢
𝑢
𝑢, (2)
𝚽
(
𝑞
𝑞
𝑞
)
= 0
0
0, (3)
where 𝑀
𝑀
𝑀 ∈ R
10×10
denotes the generalized mass ma-
trix, 𝐹
𝐹
𝐹 ∈ R
10
represents the generalized force vector,
which includes Coriolis and gravity terms. The con-
trol vector is given by 𝑢
𝑢
𝑢 ∈ R
4
, while 𝐵
𝐵
𝐵 ∈ R
10×4
isthe
transformation matrix of the control vector, 𝚽 ∈ R
4
represents the kinematic constraints, 𝚽
𝑞
𝑞
𝑞
∈ R
10×4
is
the Jacobian matrix of the kinematic constraints, and
𝜆
𝜆
𝜆 ∈ R
4
represents the corresponding Lagrange multi-
pliers.
3 CRANE TRAJECTORY
PLANNING
In this section, the dynamic equations of the con-
strained crane system described in Section 2 are trans-
formed into an explicit Euler dynamic model, fa-
cilitating its incorporation into the DDP framework.
Then, the optimal trajectory planning problem for the
knuckle boom crane is formulated.
3.1 Kinematic Constraints Elimination
To address the kinematic constraints in the knuckle
boom crane system, the constraints at the velocity and
the trajectory planning task into smaller subproblems
at each time step. However, despite its high effec-
tiveness for unconstrained problems, DDP encounters
difficulties in handling constraints. In (Kazdadi et al.,
2021), an augmented Lagrangian method was intro-
duced to handle equality-constrained DDP trajectory
planning. In (Jallet et al., 2022), a more generic
primal-dual augmented Lagrangian strategy for deal-
ing with equality and inequality constraints in non-
linear DDP problems was proposed, while (Aoyama
et al., 2021) investigated penalty methods and active-
set methods to tackle constrained DDP trajectory
planning problems.
In contrast to the dynamic system featuring ex-
ternal constraints, knuckle boom cranes feature a set
of inherent kinematic equality constraints originating
from their mechanical structure, commonly known as
closed-loop constraints. It is often necessary to intro-
duce constraint forces or include Lagrange multipli-
ers in the construction of dynamic equations, form-
ing differential-algebraic equations (DAEs), to ensure
that the closed-loop kinematic relations are satisfied.
This complicates the design and reduces the optimiza-
tion efficiency of DDP-based trajectory planning for
knuckle boom cranes.
Motivated by the aforementioned analysis, the
main contributions of this paper are as follows:
• The standard Lagrange multiplier method is com-
bined with Baumgarte stabilization to embed con-
straint equations into the crane system dynamics,
thereby converting DAEs into a more convenient
ODE form for DDP algorithm design.
• Additionally, a relaxed log-barrier function-based
DDP algorithm is employed to handle state con-
straints and obstacle avoidance constraints during
knuckle boom crane trajectory planning.
• The effectiveness and constraint violation sup-
pression of the proposed method are demonstrated
through several numerical simulations.
The paper is organized as follows. In Section 2,
the dynamic equations for the knuckle boom crane
are presented. In Section 3, the standard Lagrange
method is combined with Baumgarte stabilization to
transform the crane dynamics with kinematic con-
straints into a general ODE form. Additionally, a re-
laxed log-barrier function is introduced to handle state
constraints and obstacle avoidance during trajectory
planning. The effectiveness of the proposed method
is validated through numerical cases in Section 4. Fi-
nally, Section 5 presents conclusions and outlines po-
tential directions for future research.
Trajectory Planning for a Knuckle Boom Crane Using Differential Dynamic Programming
63
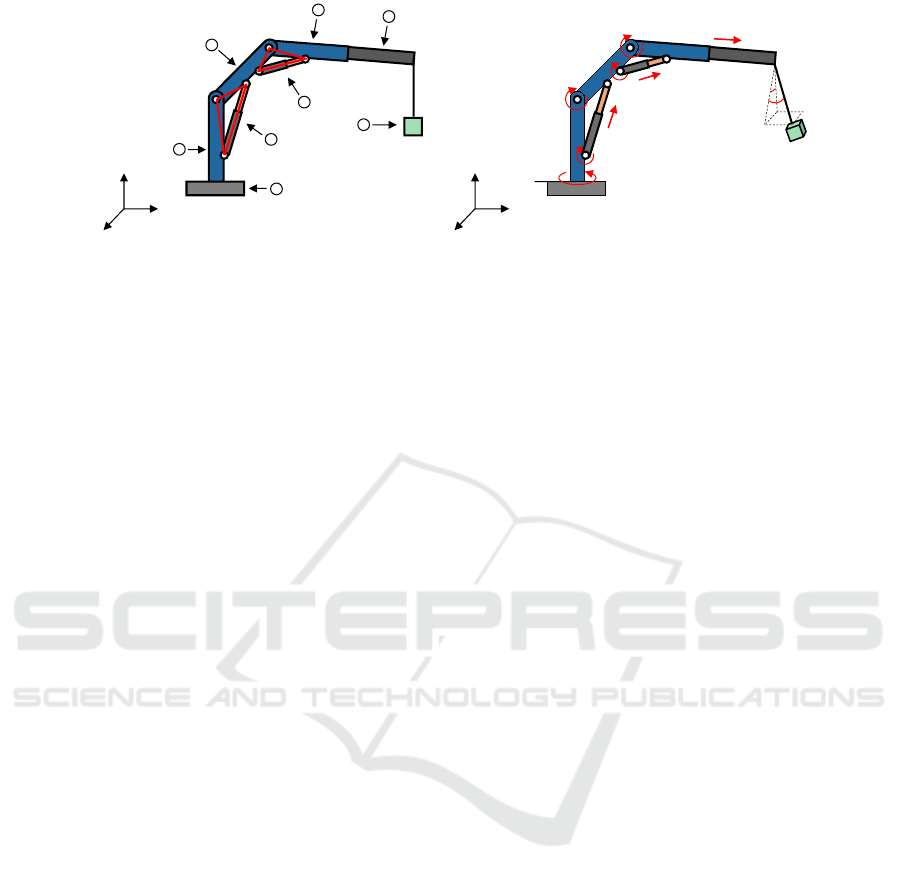
𝒙
𝒚
𝒛
𝜃
1
𝜃
2
𝜃
3
𝑑
4
𝜃
5
𝑑
6
𝜃
7
𝑑
8
𝜙
1
𝜙
2
𝒙
𝒚
𝒛
𝑜
1
2
3
4
8
𝑜
5
6
7
Figure 1: Knuckle boom crane: (a) Crane components: 1. Column; 2. Inner boom; 3. Outer boom; 4. Extension boom; 5.
Base; 6. Inner boom hydraulic actuator; 7. Outer boom hydraulic actuator; 8. Payload; (b) Kinematics depiction.
acceleration levels in the crane system derived from
Eq. (3) can be further expressed as:
𝚽
𝑞
𝑞
𝑞
¤
𝑞
𝑞
𝑞 = 0
0
0, (4)
𝚽
𝑞
𝑞
𝑞
¥
𝑞
𝑞
𝑞 +
¤
𝚽
𝑞
𝑞
𝑞
¤
𝑞
𝑞
𝑞 = 0
0
0. (5)
The acceleration constraints formulated in Eq. (5)
introduce auxiliary equations equal in number to the
Lagrange multipliers.
By integrating these constraints with the system
dynamic equations Eq. (2) with the Baumgarte sta-
bilization method, the constrained dynamic system is
reformulated as:
𝑀
𝑀
𝑀 𝚽
⊤
𝑞
𝑞
𝑞
𝚽
𝑞
𝑞
𝑞
0
0
0
¥
𝑞
𝑞
𝑞
𝜆
𝜆
𝜆
=
𝐹
𝐹
𝐹 + 𝐵
𝐵
𝐵𝑢
𝑢
𝑢
−
¤
𝚽
𝑞
𝑞
𝑞
¤
𝑞
𝑞
𝑞 − 2𝜉
1
¤
𝚽 −
−
− 𝜉
2
𝚽
, (6)
where 𝜉
1
is the damping coefficient and 𝜉
2
is a positive
stiffness coefficient.
Eliminating the acceleration vector
¥
𝑞
𝑞
𝑞 in Eq. (6),
the Lagrange multiplier 𝜆
𝜆
𝜆 can be explicitly expressed
as:
𝜆
𝜆
𝜆 =
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
−1
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
(
𝐹
𝐹
𝐹 + 𝐵
𝐵
𝐵𝑢
𝑢
𝑢
)
+
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
−1
¤
𝚽
𝑞
𝑞
𝑞
¤
𝑞
𝑞
𝑞 + 2𝜉
1
¤
𝚽 + 𝜉
2
𝚽
,
(7)
Substituting Eq. (7) into Eq. (6) yields the con-
strained system acceleration:
¥
𝑞
𝑞
𝑞 =
𝑀
𝑀
𝑀
−1
− 𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
−1
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
!
(
𝐹
𝐹
𝐹 + 𝐵
𝐵
𝐵𝑢
𝑢
𝑢
)
− 𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
𝚽
𝑞
𝑞
𝑞
𝑀
𝑀
𝑀
−1
𝚽
⊤
𝑞
𝑞
𝑞
−1
¤
𝚽
𝑞
𝑞
𝑞
¤
𝑞
𝑞
𝑞 + 2𝜉
1
¤
𝚽 + 𝜉
2
𝚽
.
(8)
Note that this transformation for solving the dy-
namic equations is often referred to as the standard
Lagrange multipliers method (Marques et al., 2017).
Over a small time interval Δ𝑡 = 𝑡
𝑘+1
− 𝑡
𝑘
, the sys-
tem dynamics are discretized using the Explicit Euler
method, resulting in:
𝑥
𝑥
𝑥
𝑘+1
= 𝑓
𝑓
𝑓
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
= 𝑥
𝑥
𝑥
𝑘
+
¤
𝑥
𝑥
𝑥
𝑘
Δ𝑡, (9)
where 𝑘 is the time step, 𝑥
𝑥
𝑥
⊤
𝑘
=
[
𝑞
𝑞
𝑞
⊤
(𝑡
𝑘
),
¤
𝑞
𝑞
𝑞
⊤
(𝑡
𝑘
)
]
=
𝑞
𝑞
𝑞
⊤
𝑘
,
¤
𝑞
𝑞
𝑞
⊤
𝑘
denotes the state vector, and the control in-
puts 𝑢
𝑢
𝑢
𝑘
is assumed to remain constant throughout each
interval.
3.2 Optimization Problem Formulation
Trajectory planning for the knuckle boom crane aims
to determine an optimal trajectory for payload trans-
portation, ensuring safety, smoothness, and precision.
Consequently, the optimization problem is formulated
as follows:
min
𝑢
𝑢
𝑢
0:𝑁 −1
(
𝑥
𝑥
𝑥
𝑁
− 𝑥
𝑥
𝑥
d
)
⊤
𝑄
𝑄
𝑄
f
(
𝑥
𝑥
𝑥
𝑁
− 𝑥
𝑥
𝑥
d
)
+
𝑛−1
𝑘=0
(
𝑥
𝑥
𝑥
𝑘
− 𝑥
𝑥
𝑥
d
)
⊤
𝑄
𝑄
𝑄
(
𝑥
𝑥
𝑥
𝑘
− 𝑥
𝑥
𝑥
d
)
+ 𝑢
𝑢
𝑢
⊤
𝑘
𝑅
𝑅
𝑅𝑢
𝑢
𝑢
𝑘
,
(10)
where 𝑄
𝑄
𝑄 ∈ R
20×20
, 𝑅
𝑅
𝑅 ∈ R
20×20
and 𝑄
𝑄
𝑄
f
∈ R
20×20
are
weighting matrices, with 𝑄
𝑄
𝑄 and 𝑄
𝑄
𝑄
f
being positive
semi-definite and 𝑅
𝑅
𝑅 being positive definite. 𝑥
𝑥
𝑥
d
∈ R
20
represents the target state of the crane.
The knuckle boom crane is typically subject to
several inequality constraints imposed by mechanical
and actuator limitations, including hydraulic cylinder
extensions, forces, and payload oscillations, which can
be expressed as:
𝑥
𝑥
𝑥
min
≤ 𝑥
𝑥
𝑥
𝑘
≤ 𝑥
𝑥
𝑥
max
, (11)
𝑢
𝑢
𝑢
min
≤ 𝑢
𝑢
𝑢
𝑘
≤ 𝑢
𝑢
𝑢
max
, (12)
where 𝑥
𝑥
𝑥
min
and 𝑥
𝑥
𝑥
max
represent the lower and upper
bounds of the states, respectively, while 𝑢
𝑢
𝑢
min
and 𝑢
𝑢
𝑢
max
denote the lower and upper bounds of the control in-
puts, respectively.
Furthermore, the payload must be constrained
within a predefined safe region to ensure collision
avoidance with obstacles, thereby guaranteeing the
safety and feasibility of the planned trajectory, this
can be formulated as:
𝑑
𝑥
𝑥
𝑥
𝑘
, 𝑝
𝑝
𝑝
𝛾
≥ 𝑑
safe
, 𝛾 = 0, . . . , 𝐵, (13)
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
64

where 𝑑
𝑥
𝑥
𝑥
𝑘
, 𝑝
𝑝
𝑝
𝛾
represents the Euclidean distance
between the payload and the surface of the 𝛾
th
obsta-
cle, 𝑝
𝑝
𝑝
𝛾
denotes the position of the 𝛾
th
obstacle, 𝑑
safe
represents the predefined safety margin, and 𝐵 is the
total number of obstacles.
Considering the crane dynamics described in Eq.
(9), the cost function in Eq. (10), and inequality con-
straints described from Eq. (11) to Eq. (13), the
trajectory planning of the crane can be formulated in
an optimization problem as follows:
min
𝑈
𝑈
𝑈
𝐽
(
𝑋
𝑋
𝑋,𝑈
𝑈
𝑈
)
= min
𝑈
𝑈
𝑈
𝑙
𝑁
(
𝑥
𝑥
𝑥
𝑁
)
+
Í
𝑁 −1
𝑘=0
𝑙
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
,
(14a)
𝑥
𝑥
𝑥
𝑘+1
= 𝑓
𝑓
𝑓
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
, 𝑘 = 0, . . . , 𝑁 − 1, (14b)
𝑔
𝑔
𝑔
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
> 0, (14c)
where 𝑙
𝑘
and 𝑙
𝑁
represent the stage and terminal cost
terms of Eq. (10),
{
𝑋
𝑋
𝑋,𝑈
𝑈
𝑈
}
is a sequence of sys-
tem states 𝑋
𝑋
𝑋 :=
{
𝑥
𝑥
𝑥
0
, 𝑥
𝑥
𝑥
1
, . . . , 𝑥
𝑥
𝑥
𝑁
}
and control inputs
𝑈
𝑈
𝑈 :=
{
𝑢
𝑢
𝑢
0
, 𝑢
𝑢
𝑢
1
, . . . , 𝑢
𝑢
𝑢
𝑁 −1
}
, besides, 𝑔
𝑔
𝑔
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
∈ R
𝑚
represents a general formulation of inequality con-
straints, incorporating both state constraints and ob-
stacle avoidance constraints.
3.3 Inequality-Constrained Differential
Dynamic Programming
For the inequality-constrained optimization problem
described in Eq. (14a), a well-established relaxed
log-barrier function method (Grandia et al., 2019) is
employed to transform the problem into an uncon-
strained optimization framework. Consequently, the
cost function in Eq. (10) is modified as:
min
𝑢
𝑢
𝑢
0:𝑁 −1
𝐽
(
𝑋
𝑋
𝑋,𝑈
𝑈
𝑈
)
= 𝑙
𝑁
(
𝑥
𝑥
𝑥
𝑁
, 𝑢
𝑢
𝑢
𝑁
)
+
𝑁 −1
𝑘=0
h
𝑙
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
+ 𝑏
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
i
,
(15)
where barrier function 𝑏
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
is introduced:
𝑏
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
=
−𝜔
Í
𝑚
𝑗=1
ln
𝑔
𝑔
𝑔
𝑘, 𝑗
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
, 𝑔
𝑔
𝑔
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
≥ 𝛿,
Í
𝑚
𝑗=1
𝛽
𝑔
𝑔
𝑔
𝑘, 𝑗
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
, 𝛿
, 𝑔
𝑔
𝑔
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
< 𝛿,
(16)
where 𝜔 > 0 and 𝛿 > 0 are penalty parameters, and
function 𝛽
𝑔
𝑔
𝑔
𝑘, 𝑗
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
, 𝛿
is defined as:
𝛽
𝑔
𝑔
𝑔
𝑘, 𝑗
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
, 𝛿
=
𝜔
2
𝑔
𝑔
𝑔
𝑘, 𝑗
(
𝑥
𝑥
𝑥
𝑘
,𝑢
𝑢
𝑢
𝑘
)
−2𝛿
𝛿
2
− 1
− 𝜔 ln(𝛿).
(17)
To evaluate the cost function in Eq. (15) cumula-
tively, the cost-to-go function is defined:
𝐽
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
= 𝑙
𝑁
(
𝑥
𝑥
𝑥
𝑁
,𝜆
𝜆
𝜆
𝑁
)
+
𝑁 −1
𝑗=𝑘+1
𝑙
𝑗
𝑥
𝑥
𝑥
𝑗
, 𝑢
𝑢
𝑢
𝑗
. (18)
Thus, the value function, which represents the op-
timal cost-to-go, is given by:
𝑉
𝑘
(
𝑥
𝑥
𝑥
𝑘
)
= min
𝑢
𝑢
𝑢
𝑘
𝐽
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
. (19)
According to the Bellman optimality principle, the
recurrence relationship of the value function in back-
ward pass of DDP can be expressed as:
𝑉
𝑁
(
𝑥
𝑥
𝑥
𝑁
)
= 𝑙
𝑁
(
𝑥
𝑥
𝑥
𝑁
)
, (20)
𝑉
𝑘
(
𝑥
𝑥
𝑥
𝑘
)
= min
𝑢
𝑢
𝑢
𝑘
[
𝑙
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
+𝑉
𝑘+1
(
𝑥
𝑥
𝑥
𝑖+1
)]
. (21)
To evaluate the contribution of a specific control
action to the overall cost, the action-value function is
further employed:
𝑄
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
= 𝑙
𝑘
(
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
)
+𝑉
𝑘+1
(
𝑥
𝑥
𝑥
𝑘+1
)
. (22)
Instead of solving the optimization problem glob-
ally, DDP performances a local second-order Taylor
series approximation of value function 𝑉
𝑘
, that is
𝛿𝑉
𝑘
≈ 𝑉
⊤
𝑥
𝑥
𝑥,𝑘
𝛿𝑥
𝑥
𝑥
𝑘
+
1
2
𝛿𝑥
𝑥
𝑥
⊤
𝑘
𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
𝛿𝑥
𝑥
𝑥
𝑘
, (23)
where 𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
and 𝑉
𝑥
𝑥
𝑥,𝑘
are the Hessian and gradient
of the cost-to-go function at time step 𝑘, respectively.
Following Eq. (20), the second order expansion of the
value function at the terminal time are 𝑉
𝑥
𝑥
𝑥, 𝑁
= 𝑙
𝑥
𝑥
𝑥,
,
,𝑁
,
and 𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥, 𝑁
= 𝑙
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,
,
,𝑁
.
Likewise, the second-order Taylor approximation
of the action-value function about the current nominal
trajectory is:
𝑄
𝑘
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
≈ 𝑄
𝑘
𝑥
𝑥
𝑥
𝑘
, 𝑢
𝑢
𝑢
𝑘
+ 𝑄
⊤
𝑥
𝑥
𝑥,𝑘
𝛿𝑥
𝑥
𝑥
𝑘
+ 𝑄
⊤
𝑢
𝑢
𝑢, 𝑘
𝛿𝑢
𝑢
𝑢
𝑘
+
1
2
𝛿𝑥
𝑥
𝑥
𝑘
𝛿𝑢
𝑢
𝑢
𝑘
⊤
𝑄
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
𝑄
𝑥
𝑥
𝑥𝑢
𝑢
𝑢, 𝑘
𝑄
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
𝛿𝑥
𝑥
𝑥
𝑘
𝛿𝑢
𝑢
𝑢
𝑘
,
(24)
where 𝑥
𝑥
𝑥
𝑘
and 𝑢
𝑢
𝑢
𝑘
represent the nominal state trajectory
and control trajectory, the partial derivatives terms of
𝑄
𝑘
are given by:
𝑄
𝑥
𝑥
𝑥,𝑘
= 𝑙
𝑥
𝑥
𝑥,𝑘
+ 𝑓
𝑓
𝑓
⊤
𝑥
𝑥
𝑥,𝑘
𝑉
𝑥
𝑥
𝑥,𝑘+1
, (25)
𝑄
𝑢
𝑢
𝑢, 𝑘
= 𝑙
𝑢
𝑢
𝑢, 𝑘
+ 𝑓
𝑓
𝑓
⊤
𝑢
𝑢
𝑢, 𝑘
𝑉
𝑥
𝑥
𝑥,𝑘+1
, (26)
𝑄
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
= 𝑙
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
+ 𝑓
𝑓
𝑓
⊤
𝑥
𝑥
𝑥,𝑘
𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑥
𝑥
𝑥,𝑘
+𝑉
𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘
,
(27)
𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
= 𝑙
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
+ 𝑓
𝑓
𝑓
⊤
𝑢
𝑢
𝑢, 𝑘
𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑢
𝑢
𝑢, 𝑘
+𝑉
𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
,
(28)
𝑄
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
= 𝑙
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
+ 𝑓
𝑓
𝑓
⊤
𝑢
𝑢
𝑢, 𝑘
𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑥
𝑥
𝑥,𝑘
+𝑉
𝑥
𝑥
𝑥,𝑘+1
𝑓
𝑓
𝑓
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
.
(29)
Trajectory Planning for a Knuckle Boom Crane Using Differential Dynamic Programming
65

Minimizing Eq. (24) with respect to 𝛿𝑢
𝑢
𝑢
𝑘
yields
the locally optimal control deviation:
𝛿𝑢
𝑢
𝑢
∗
𝑘
= 𝐾
𝐾
𝐾
𝑘
𝛿𝑥
𝑥
𝑥
𝑘
+ 𝑑
𝑑
𝑑
𝑘
, (30)
where the feedback term and feedforward term are:
𝐾
𝐾
𝐾
𝑘
= −𝑄
−1
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
𝑄
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
, and 𝑑
𝑑
𝑑
𝑘
= −𝑄
−1
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
𝑄
𝑢
𝑢
𝑢, 𝑘
. (31)
Substituting 𝛿𝑢
𝑢
𝑢
∗
𝑘
into Eq. (24), the second order
approximation the value function at time step 𝑘 is
obtained as:
𝑉
𝑥
𝑥
𝑥,𝑘
= 𝑄
𝑥
𝑥
𝑥,𝑖
+ 𝐾
𝐾
𝐾
⊤
𝑘
𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
𝑑
𝑑
𝑑
𝑘
+ 𝐾
𝐾
𝐾
⊤
𝑘
𝑄
𝑢
𝑢
𝑢, 𝑘
+ 𝑄
𝑥
𝑥
𝑥𝑢
𝑢
𝑢, 𝑘
𝑑
𝑑
𝑑
𝑘
,
(32)
𝑉
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑖
= 𝑄
𝑥
𝑥
𝑥𝑥
𝑥
𝑥,𝑖
+ 𝐾
𝐾
𝐾
⊤
𝑘
𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
𝐾
𝐾
𝐾
𝑘
+ 𝐾
𝐾
𝐾
⊤
𝑘
𝑄
𝑢
𝑢
𝑢𝑥
𝑥
𝑥,𝑘
+ 𝑄
𝑥
𝑥
𝑥𝑢
𝑢
𝑢, 𝑘
𝐾
𝐾
𝐾
𝑘
.
(33)
To ensure that the Hessian matrix 𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
remains
positive definite, we add a small regularization term
𝜖 𝐼
𝐼
𝐼 to 𝑄
𝑢
𝑢
𝑢𝑢
𝑢
𝑢, 𝑘
whenever its positive definiteness is not
guaranteed. Additionally, during the forward pass, a
line search is performed on the optimal control update,
𝑢
𝑢
𝑢
∗
𝑘
= 𝐾
𝐾
𝐾
𝑘
𝛿𝑥
𝑥
𝑥
𝑘
+𝛼 𝑑
𝑑
𝑑
𝑘
, to evaluate its effect on the overall
cost. Note that in this paper we use a Gauss–Newton
approximation in DDP, which is computationally effi-
cient and facilitates computation.
4 SIMULATION RESULTS AND
DISCUSSION
This section validates the performance of the DDP as
applied to the transformed knuckle boom crane dy-
namics for trajectory planning.
4.1 Simulation Setting
In this section, simulations were conducted using
MATLAB 2022b on a computer platform equipped
with an Intel Core E5-1620 3.6 GHz processor. The
CasADi framework (Andersson et al., 2019) was uti-
lized to leverage its efficient symbolic computation
and automatic differentiation capabilities.
The state constraints for the knuckle boom crane
system are set as follows:
0 ≤ 𝑑
4
≤ 5m, 0 ≤ 𝑑
6
≤ 2m, 0 ≤ 𝑑
8
≤ 1.6m,
−10
◦
≤ 𝜙
1
≤ 10
◦
, −10
◦
≤ 𝜙
2
≤ 10
◦
,
𝑢
min
= −10
6
N, 𝑢
max
= 10
6
N.
The initial payload position is set to 𝑝
𝑝
𝑝
init
=
(−4.7321, 8.1962, 3) in Cartesian space, and
the target payload position is defined as 𝑝
𝑝
𝑝
goal
=
(4.7321, 8.1962, 3). The corresponding crane config-
urations for both initial and target states can be derived
through inverse kinematics.
The simulation parameters for the DDP method
are set as follows: the state weighting matrix is de-
fined as 𝑄
𝑄
𝑄 = diag(1, . . . , 1) and the control weight-
ing matrix as 𝑅
𝑅
𝑅 = diag
10
−5
, 10
−5
, 10
−5
, 10
−5
, with
the terminal cost weighting matrix given by 𝑄
𝑄
𝑄
f
=
diag
10
3
, . . . , 10
3
. In addition, the damping co-
efficient is set to 𝜉
1
= 10 and the stiffness coeffi-
cient to 𝜉
2
= 20. The penalty parameters for the re-
laxed log-barrier function are chosen as 𝜔 = 0.1 and
𝛿 = 0.01. The regularization term is 𝜖 = 1𝑒 − 5. Fi-
nally, the line search parameter 𝛼 is selected from the
set (1, 0.05, 0.0025).
4.2 Static Obstacle Avoidance
This case evaluates the performance of the DDP
method to handle multiple obstacle avoidance task.
Three spherical obstacles with radius of 0.9 m, 0.7
m, and 0.7 m are positioned at 𝑝
𝑝
𝑝
1
= (0, 10, 3),
𝑝
𝑝
𝑝
2
= (−2, 8.5, 3) and 𝑝
𝑝
𝑝
3
= (2, 9.3, 4), respectively.
The simulation is configured with a time horizon of
5s and a discrete time step of 0.1s. The DDP algo-
rithm is executed with a maximum of 2000 iterations
to optimize the trajectory planning process.
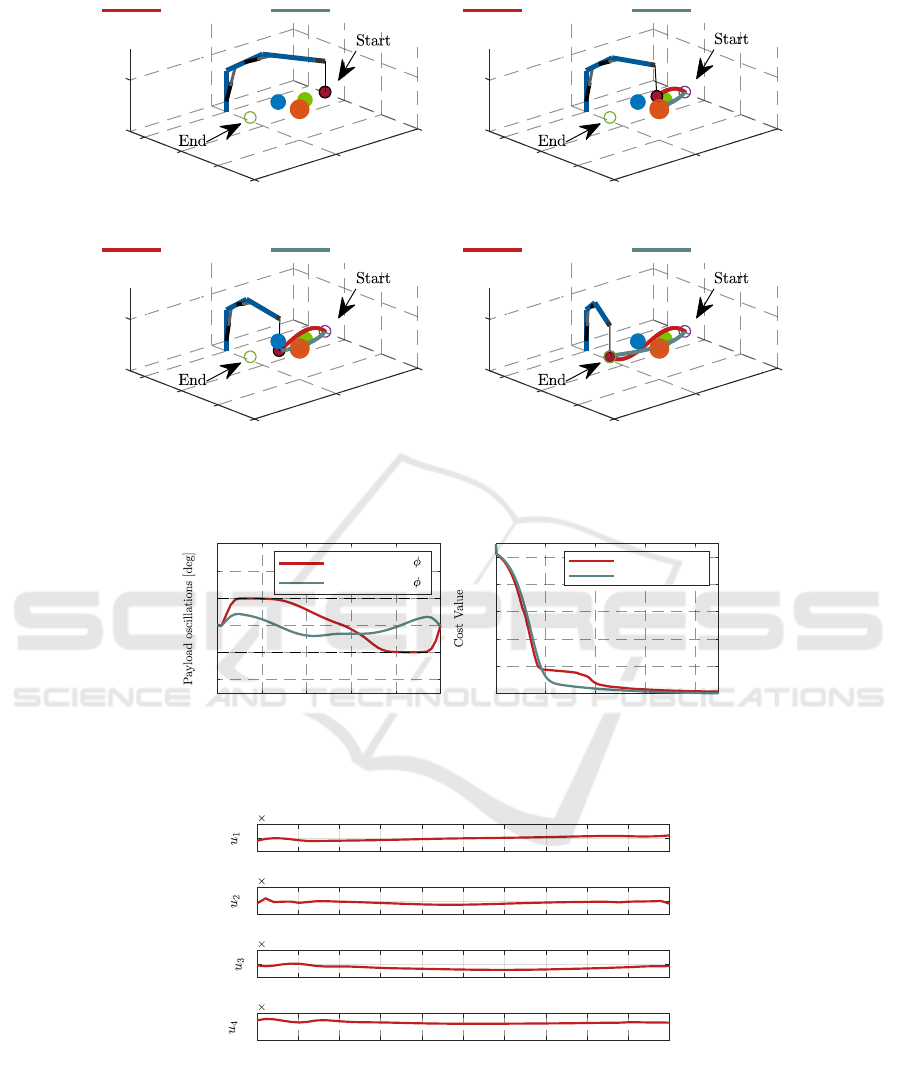
Fig. 2 illustrates the trajectory comparison, where
the green line represents the trajectory without obsta-
cle avoidance and the red line denotes the optimized
trajectory with obstacle avoidance, both trajectories
are generated by DDP method. The crane’s trajectory
without obstacles avoidance collides with the orange
obstacle during its operation. In contrast, the red tra-
jectory, optimized with a relaxed log-barrier function,
successfully generates a feasible trajectory that avoids
all obstacles. This highlights the capability of the DDP
method to effectively plan a collision-free trajectory
in a complex obstacle environment.
Fig. 3 illustrates the payload oscillations during
obstacle avoidance and the corresponding cost opti-
mization over iterations. Fig. 3(a) shows that the
proposed DDP method successfully regulates the pay-
load oscillations in the obstacle avoidance trajectory,
ensuring that they remain within acceptable limits
throughout the entire time horizon and stabilize at
the end. Fig. 3(b) presents the cost evolution for both
scenarios, with and without obstacles. Notably, the
trajectory with obstacles maintains a higher cost due
to the obstacle penalty term, particularly during the
early optimization stages. Ultimately, both scenarios
are converged, demonstrating the effectiveness of the
DDP method in handling obstacle avoidance.
Fig. 4 shows the time evolution of control inputs
from 𝑢
1
to 𝑢
4
during the obstacle avoidance process.
The results indicate that the control inputs remain
smooth and within bounds throughout the trajectory.
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
66
0
-10
(a)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
With obstacles Without obstacles
0
-10
(b)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
With obstacles Without obstacles
0
-10
(c)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
With obstacles Without obstacles
0
-10
(d)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
With obstacles Without obstacles
t=0s t=2.7s
t=3.4s t=5s
Figure 2: Trajectory comparison: (a) trajectories at initial instant; (b) trajectories at 2.7s; (c) trajectories at 3.4s; (d) trajectories
at 5s.
0 1 2 3 4 5
Time [s]
-20
-10
0
10
20
30
(a)
Oscillation angle
1
Oscillation angle
2
0 500 1000 1500 2000
Iteration
0
200
400
600
800
1000
(b)
With obstacles
Without obstacles
Figure 3: Payload oscillations and cost optimization: (a) payload oscillations during obstacle avoidance; (b) cost evolution
over iterations.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
-5
0
5
10
5
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
-1
0
1
10
4
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
7
8
9
10
5
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [s]
9
10
10
5
Figure 4: Control inputs during obstacle avoidance: (a) 𝑢
1
; (b) 𝑢
2
; (c) 𝑢
3
; (d) 𝑢
4
.
4.3 Comparison of Kinematic
Constraint Violation Suppression
To evaluate the performance of the DDP method in
suppressing kinematic constraint violations, which is
achieved by applying a Baumgarte stabilization ap-
proach within the transformed dynamics, this section
compares its results with those of the Ipopt solver that
directly solves the dynamics described in Eq. (2).
This case involves a spherical obstacle with a radius
Trajectory Planning for a Knuckle Boom Crane Using Differential Dynamic Programming
67
0
-10
(a)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
DDP Ipopt
0
-10
(b)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
DDP Ipopt
0
-10
(c)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
DDP Ipopt
0
-10
(d)
5
Z[m]
0
5
X[m]
Y[m]
0
10
15
10
DDP Ipopt
t=0s t=2.7s
t=3.4s t=5s
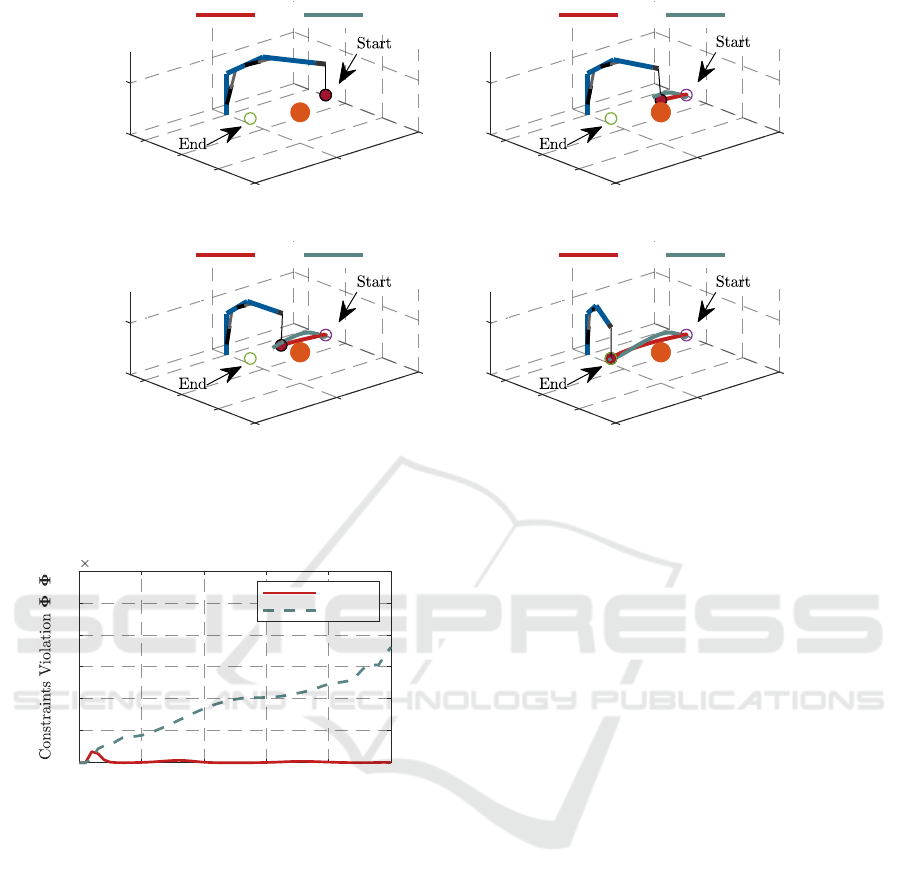
Figure 5: Trajectory comparison of the two solvers: (a) trajectories at initial instant; (b) trajectories at 2.7s; (c) trajectories at
3.4s; (d) trajectories at 5s.
0 1 2 3 4 5
Time [s]
0
0.5
1
1.5
2
2.5
3
T
10
-7
Proposed
Ipopt
Figure 6: Kinematic constraints violation comparison.
of 1m, positioned at 𝑝
𝑝
𝑝
4
= (0, 10, 3). All other param-
eters remain the same as in Subsection 4.2. To balance
convergence speed and accuracy, Ipopt’s convergence
tolerance is set to 1 × 10
−6
. In this case, the violation
error 𝚽
⊤
𝚽 is used to evaluate each method’s perfor-
mance in suppressing kinematic constraint violations.
Fig. 5 presents the optimization results obtained
by the two solvers. The results indicate that both the
proposed method and Ipopt generate feasible obstacle
avoidance trajectories.
Fig. 6 compares the constraint violation suppres-
sion performance between the DDP method with the
transformed crane dynamics and the Ipopt solver. The
results show that the constraint violation for the Ipopt
solver increases over time. In contrast, the DDP
method with the transformed crane dynamics main-
tains a low and stable constraint violation throughout
the entire time horizon. This difference indicates that
Baumgarte stabilization effectively prevents the accu-
mulation of constraint errors in the dynamic system.
5 CONCLUSIONS
In this paper, we investigated an obstacle avoidance
trajectory planning method for knuckle boom cranes.
The standard Lagrange multiplier method, combined
with Baumgarte stabilization, was employed to de-
rive the crane’s dynamic equations, which were then
expressed in an explicit Euler form to facilitate the
design of the DDP method. In addition, we adopted a
relaxed log-barrier function to handle state constraints
and obstacle avoidance during crane operation. The
effectiveness of the proposed approach was validated
through simulations in MATLAB, where the kine-
matic constraint suppression performance was com-
pared with the Ipopt solver. The results demonstrated
the advantages of the proposed method for trajectory
planning in kinematically constrained mechanical sys-
tems.
ACKNOWLEDGEMENTS
This research was funded by the China Scholarship
Council (Grant No. 202109150003).
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
68

REFERENCES
Andersson, J. A. E., Gillis, J., Horn, G., Rawlings, J. B., and
Diehl, M. (2019). CasADi – A software framework
for nonlinear optimization and optimal control. Math-
ematical Programming Computation, 11(1):1–36.
Aoyama, Y., Boutselis, G., Patel, A., and et al. (2021). Con-
strained differential dynamic programming revisited.
In 2021 IEEE International Conference on Robotics
and Automation (ICRA), pages 9738–9744. IEEE.
Chen, J., Zhan, W., and Tomizuka, M. (2019). Autonomous
driving motion planning with constrained iterative lqr.
IEEE Transactions on Intelligent Vehicles, 4(2):244–
254.
Farrage, A., Takahashi, H., Terauchi, K., and et al. (2023).
Trajectory generation of rotary cranes based on a* al-
gorithm and time-optimization for obstacle avoidance
and load-sway suppression. Mechatronics, 94:103025.
Grandia, R., Farshidian, F., Ranftl, R., and et al. (2019).
Feedback mpc for torque-controlled legged robots. In
2019 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS), pages 4730–4737.
IEEE.
Huang, Z., Shen, S., and Ma, J. (2023). Decentralized
ilqr for cooperative trajectory planning of connected
autonomous vehicles via dual consensus admm. IEEE
Transactions on Intelligent Transportation Systems.
Jallet, W., Bambade, A., Mansard, N., and et al. (2022).
Constrained differential dynamic programming: A
primal-dual augmented lagrangian approach. In
2022 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS), pages 13371–13378.
IEEE.
Kazdadi, S. E., Carpentier, J., and Ponce, J. (2021). Equal-
ity constrained differential dynamic programming. In
2021 IEEE International Conference on Robotics and
Automation (ICRA), pages 8053–8059. IEEE.
Kim, G., Kang, D., Kim, J. H., and et al. (2022). Contact-
implicit differential dynamic programming for model
predictive control with relaxed complementarity con-
straints. In 2022 IEEE/RSJ International Confer-
ence on Intelligent Robots and Systems (IROS), pages
11978–11985. IEEE.
Lee, Y., Cho, M., and Kim, K. S. (2022). Gpu-parallelized
iterative lqr with input constraints for fast collision
avoidance of autonomous vehicles. In 2022 IEEE/RSJ
International Conference on Intelligent Robots and
Systems (IROS), pages 4797–4804. IEEE.
Li, G., Ma, X., Li, Z., and et al. (2022). Optimal tra-
jectory planning strategy for underactuated overhead
crane with pendulum-sloshing dynamics and full-state
constraints. Nonlinear Dynamics, 109(2):815–835.
Li, H. and Wensing, P. M. (2020). Hybrid systems differ-
ential dynamic programming for whole-body motion
planning of legged robots. IEEE Robotics and Au-
tomation Letters, 5(4):5448–5455.
Marques, F., Souto, A. P., and Flores, P. (2017). On the
constraints violation in forward dynamics of multibody
systems. Multibody System Dynamics, 39:385–419.
Martin, I. A. and Irani, R. A. (2021). Dynamic modeling
and self-tuning anti-sway control of a seven degree of
freedom shipboard knuckle boom crane. Mechanical
Systems and Signal Processing, 153:107441.
Mastalli, C., Budhiraja, R., Merkt, W., and et al. (2020).
Crocoddyl: An efficient and versatile framework for
multi-contact optimal control. In 2020 IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 2536–2542. IEEE.
Thi, H. L., Vu, M. N., Khanh, H. B. T., and et al. (2024).
Flatness-based motion planning and control strategy
for payload positioning of an overhead crane.
Wang, Y., Li, H., Zhao, Y., and et al. (2023). A fast co-
ordinated motion planning method for dual-arm robot
based on parallel constrained ddp. IEEE/ASME Trans-
actions on Mechatronics.
Zhang, W., Chen, H., Chen, H., and et al. (2021). A time op-
timal trajectory planning method for double-pendulum
crane systems with obstacle avoidance. IEEE Access,
9:13022–13030.
Zheng, X., He, S., and Lin, D. (2021). Constrained tra-
jectory optimization with flexible final time for au-
tonomous vehicles. IEEE Transactions on Aerospace
and Electronic Systems, 58(3):1818–1829.
Zhu, H., Ouyang, H., and Xi, H. (2023). Neural network-
based time optimal trajectory planning method for ro-
tary cranes with obstacle avoidance. Mechanical Sys-
tems and Signal Processing, 185:109777.
Zimmermann, S., Poranne, R., and Coros, S. (2021). Dy-
namic manipulation of deformable objects with im-
plicit integration. IEEE Robotics and Automation Let-
ters, 6(2):4209–4216.
Trajectory Planning for a Knuckle Boom Crane Using Differential Dynamic Programming
69
