Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model

for RFID

Ferucio Laurent¸iu T¸ iplea

Faculty of Computer Science, “Alexandru Ioan Cuza” University of Ias¸i, Romania

Keywords:

RFID Protocol, Privacy, Indistinguishability.

Abstract:

RFID schemes that provide weak privacy or similar privacy forms are useful in any domain where the adver-

sary cannot mount a corruption attack. In addition, these schemes can be constructed using only symmetric

cryptography and can provide time-efﬁcient identiﬁcation. This paper focuses on RFID schemes that provide

weak privacy in the Hermans-Pashalidis-Vercauteren-Preneel (HPVP) model based on tag indistinguishabil-

ity. We ﬁrst show that no adversary can have a non-negligible advantage in distinguishing between keys of a

pseudo-random function. We then use this result to highlight RFID schemes that provide weak, weak-insider,

and randomized weak privacy in the model above.

1 INTRODUCTION

Applying radio frequency identiﬁcation (RFID) tech-

nology requires ensuring security and privacy prop-

erties appropriate to the scope. Security in this con-

text means unilateral or mutual authentication, while

privacy can encompass a wide range of properties

such as unlinkability, untraceability, anonymity, etc.

The environment in which the RFID technology is

deployed plays an important role because it dictates

the type of adversary that must be considered when

studying the security and privacy properties. For ex-

ample, an RFID scheme implemented in a hypermar-

ket does not face a strong adversary. In contrast, an

RFID scheme for identifying and authenticating per-

sonal identity documents may be subject to attacks

by very strong adversaries. As a result, the levels of

privacy provided by an RFID scheme must be ranked

according to the adversary’s power.

In this context, the RFID security and privacy

model proposed in (Hermans et al., 2011; Hermans

et al., 2014), inspired by Vaudenay’s model and here-

inafter referred to as the HPVP model, proposes the

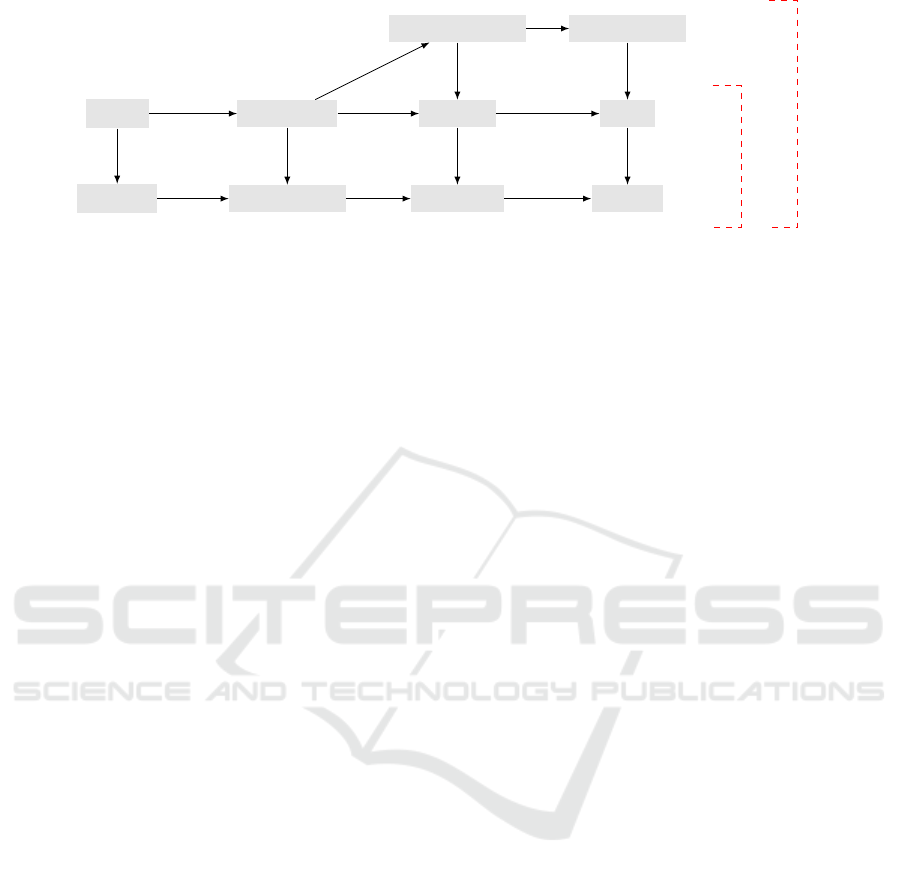
hierarchy of privacy levels in Figure 1. However,

while Vaudeay’s model studies privacy by referring

to a simulator (blinder), the HPVP model proposes a

study based on the indistinguishability between tags.

The method is appealing and in line with the study of

encryption schemes by indistinguishability.

https://orcid.org/0000-0001-6143-3641

The diagram in Figure 1 shows that weak privacy

is among the lowest privacy levels in the HPVP hier-

archy. The difference between this privacy level and

those above it is that it cannot be used in an environ-

ment where adversaries can corrupt tags. However,

there are many other practical situations in which this

level of privacy is sufﬁcient, such as:

1. The RFID scheme is implemented in a populated

and video-monitored environment where the ad-

versary cannot mount a corruption attack;

2. The adversary needs specialized equipment to

mount a corruption attack, and the environment

that implements the RFID scheme does not allow

intervention with such equipment;

3. The RFID tags identify disposable or low-value

objects that do not justify a costly corruption at-

tack.

RFID schemes dedicated to achieving weak pri-

vacy can have signiﬁcant beneﬁts compared to

schemes that achieve more than weak privacy. First,

RFID schemes for weak privacy generally use sym-

metric cryptography, while schemes for higher lev-

els of privacy need public-key cryptography. Sec-

ond, RFID schemes based on symmetric cryptogra-

phy may provide an efﬁcient identiﬁcation time (log-

arithmic and not linear).

Unfortunately, to our knowledge, studies on RFID

schemes dedicated to weak privacy are lacking. Even

the papers introducing the HPVP model focus only

156

ciplea, F. L.

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID.

DOI: 10.5220/0013521100003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 156-167

ISBN: 978-989-758-760-3; ISSN: 2184-7711

forward-insider weak-insider

strong

destructive forward weak

n-strong

n-destructive n-forward n-weak

Vaudenay’s model

HPVP model

Figure 1: Privacy levels in Vaudenay’s and the HPVP model: “n-p” means “narrow p” and an arrow means “implication”.

on schemes offering higher privacy levels, based on

public-key cryptography.

Contribution. In the context described above, our

paper focuses on the weak and weak-insider privacy

levels in the HPVP model, and introduces two new

levels, weak-winsider and randomized weak privacy.

Speciﬁcally:

– We introduce the problem of distinguishing keys

of a pseudo-random function (PRF) and show that

no adversary has more than a negligible advantage

over it;

– We present a PRF-based RFID scheme that is

weak private in the HPVP model. The proof heav-

ily relies on the PRF key indistinguishability (dis-

cussed previously);

– We discuss weak-insider privacy for RFID

schemes based on symmetric cryptography and

show that this is equivalent to a weaker form of

privacy, called weak-winsider privacy;

– We introduce randomized weak privacy and

present a PRF-based RFID scheme that achieves

this type of privacy. The proof is also based on the

PRF key indistinguishability.

Our study highlights that the PRF key indistin-

guishability is a basic tool for studying privacy of

PRF-based RFID schemes in the HPVP model.

Paper Structure. The paper is structured into ﬁve

sections, the ﬁrst one being the introduction. In the

second section we recall basic concepts on RFID as

well as the HPVP security and privacy model. The

third section discusses the PRF key indistinguisha-

bility, as a central tool for studying privacy of PRF-

based RFID schemes in models based on indistin-

guishability. The fourth section presents a PRF-

based RFID scheme that achieves weak privacy in

the HPVP model, shows that weak-insider privacy of

RFID schemes based on symmetric cryptography is

equivalent to a weaker form of weak privacy, namely

weak-winsider privacy. This result allows us to prove

that the previous RFID scheme is even weak-insider

private. Then, we introduce randomized weak privacy

and present an RFID scheme that achieves it. The last

section concludes the paper.

2 RFID SCHEMES AND SYSTEMS

We begin by recalling and ﬁxing some standard

cryptography concepts and notations (for details, the

reader is referred to (Katz and Lindell, 2020)).

We use in our exposition probabilistic polynomial

time (PPT) algorithms A as deﬁned in (Sipser, 2012)

that can consult oracles. To specify that the algorithm

A can consult the oracles O

,...,O

we will write

,...,O

. For a set A, a ← A means that a is uniformly

at random chosen from A. If A is a probabilistic algo-

rithm, then a ← A means that a is an output of A for

some given input. The asymptotic approach to secu-

rity makes use of security parameters, denoted by λ in

our paper. A positive function f (λ) is called negligi-

ble if for any positive polynomial poly(λ) there exists

such that f (λ) < 1/poly(λ), for any λ ≥ n

. f (λ)

is called overwhelming if 1 − f (λ) is negligible.

RFID Scheme. An RFID scheme is typically com-

posed of three main entities: a reader, a set of tags,

and a radio frequency communication protocol be-

tween reader and tags. The reader is a powerful de-

vice not computationally restricted so it can perform

any cryptographic operation. It stores tag related in-

formation in a database to which it has secure access.

On the other side, tags are small devices that are con-

sidered to be resource constrained.

The memory of a tag is typically split into per-

manent (or internal) and temporary (or volatile). The

permanent memory stores the state values of the tag,

while the temporary memory can be viewed as a set

of temporary/volatile variables used to carry out the

calculations required by the communication protocol.

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

157

Let R be a reader identiﬁer and T be a set of tag

identiﬁers whose cardinal is polynomial in some secu-

rity parameter λ. An RFID scheme over (R ,T ) (Vau-

denay, 2007; Paise and Vaudenay, 2008) is a triple of

PPT algorithms Σ = (SetupR, SetupT, Ident), where:

1. SetupR(λ) sets up the reader. It inputs a secu-

rity parameter λ and outputs a triple (pk, sk, DB)

consisting of a key pair (pk, sk) and an empty

database DB. pk is public, while sk is kept secret

by reader;

2. SetupT (pk,ID) initializes the tag identiﬁed by

ID. It outputs an initial tag state S and a tag-

speciﬁc secret K. The identity ID together with K

is stored as a pair (ID,K) in the reader’s database;

3. Ident(pk; R (sk,DB); ID(S)) is an interactive

protocol between the reader identiﬁed by R (with

its private key sk and database DB) and a tag iden-

tiﬁed by ID (with its state S) in which the reader

ends with an output consisting of ID or ⊥. The

tag may end with no output (unilateral authenti-

cation), or it may end with an output consisting of

OK or ⊥ (mutual authentication).

The correctness of an RFID scheme refers to the

honest behavior of the reader and tag in a complete

protocol session. That is, regardless of how the sys-

tem is set up, after each complete and honest execu-

tion of the interactive protocol one of the two cases

holds with overwhelming probability:

• If the tag is legitimate, the reader outputs tag’s

identity (and the tag outputs OK, in case of mu-

tual authentication);

• If the tag is illegitimate, the reader outputs ⊥.

The communication protocol is an alternating se-

quence of reader-to-tag and tag-to-reader communi-

cation steps in which the ﬁrst step can be taken by

either of them. When the reader sends a message m

to the tag, we will often say that the reader queries

the tag on m. When the ﬁrst protocol step is taken by

the tag, we will say that the tag answers to the empty

query (this corresponds to the tag being powered by

the reader).

An instantiation of an RFID scheme is sometimes

called an RFID system. It is usually performed by a

trusted operator who establishes a reader identiﬁer R ,

a set T of tag identiﬁers, and run the RFID scheme

over (R ,T ).

RFID Security and Privacy Model An RFID se-

curity and privacy model establishes the type of ad-

versary to consider, how it interacts with the RFID

scheme, and how the security and privacy proper-

ties of RFID schemes are deﬁned. In this paper,

we will adopt the Hermans-Pashalidis-Vercauteren-

Preneel (HPVP) model (Hermans et al., 2011; Her-

mans et al., 2014), which is based on tag indistin-

guishability.

The adversary is a PPT algorithm. It inter-

acts with the RFID scheme through a set of oracles

that he can query, namely: CreateTag(), Launch(),

DrawTag(), Free(), SendTag(), SendReader(),

Result(), Corrupt(), CreateInsider(). The original

approach allows for the creation of multiple readers,

but for the discussion in this paper, it is sufﬁcient to

consider only a single reader R . The adversary’s in-

teraction with the oracles is described below:

1. T ←CreateTag(ID): On input a tag identiﬁer ID,

the oracle calls SetupT (pk,ID) to generate a pair

(S,K). It adds (ID,K) to DB and the tag is con-

sidered registered with the reader (and so it is a

legitimate tag). Moreover, a distinct reference T

to the tag is returned. The oracle does not reject

duplicate IDs;

2. π ← Launch(): Launches a new protocol instance

(session), assigns a unique identiﬁer π to it, and

outputs it;

3. vtag/⊥ ← DrawTag(T

): On input a pair of

tag references T

and T

, the oracle outputs a vir-

tual tag reference vtag as a monotonic counter

or ⊥. The virtual tag reference vtag, when out-

putted, refers to either T

or T

, depending on

the left or right indistinguishability game, respec-

tively, where the oracle is used. The oracle main-

tains a table Γ of triples (vtag

′

). All virtual

tag references point to the left or the right refer-

ence tag in such a table.

The output of this oracle must meet the following

requirements:

• If one of the tags T

or T

is in the list of insider

tags, then the output is ⊥;

• If the virtual tag references in Γ refer to the left

tag reference and (vtag

′

) ∈ Γ for some

vtag

′

and T

′

, then the output is ⊥;

• If the virtual tag references in Γ refer to the

right tag reference and (vtag

′

) ∈ Γ for

some vtag

′

and T

′

, then the output is ⊥;

• In all the other cases the output is vtag.

The triple (vtag,T

), when the output if vtag,

is added to Γ;

4. Free(vtag): This oracle retrieves the unique triple

(vtag,T

) from Γ, resets the tag that vtag

refers to, and removes (vtag,T

) from Γ (this

means that the tags T

and T

are freed). More-

over, the identiﬁer vtag will no longer be used.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

158

When a tag is reset, its temporary memory is

erased, while the permanent one is preserved;

5. m

′

/⊥ ← SendTag(m,vtag): Outputs the tag’s an-

swer m

′

to the query m sent to the tag referred to

by vtag, and ⊥ if vtag is not in any triple in Γ (we

draw attention that vtag when in Γ, refers to one

of two tags depending on the privacy game). We

will consider m

′

as the empty message, abusively

but suggestively denoted by

0, to specify that the

tag outputs nothing, thus marking the last step of

communication;

6. m

′

/⊥ ← SendReader(m,π): Outputs the reader’s

answer m

′

to the query m in the protocol instance

π, if π is an active instance, and ⊥ otherwise (π is

not active or does not even exist). When m is the

empty message, this oracle outputs the ﬁrst mes-

sage of the protocol instance π, assuming that the

reader takes the ﬁrst step in the protocol. When

′

is the empty message, we understand that the

reader does not output anything (this marks the

last communication step of the protocol);

7. 1/0/⊥ ← Result(π): Outputs ⊥ if in session π the

reader has not yet made a decision on tag authen-

tication (this also includes the case when the ses-

sion π does not exist), 1 if in session π the reader

authenticated the tag, and 0 otherwise. This oracle

is both for unilateral and mutual authentication;

8. S ← Corrupt(T ): Outputs the current permanent

and temporary state S of the tag T , when the tag

is not involved in any computation of any protocol

step (that is, the permanent state before or after a

protocol step);

9. T ,S ← CreateInsider(ID): This oracle creates a

new tag referenced by T and registers it with the

reader. Then, it outputs T and the tag’s full inter-

nal state S. The tag T is then included in a list I

of so-called insider tags and destroyed.

Depending on the oracles they can query, adver-

saries are classiﬁed into:

• Weak-insider adversaries: they do not have access

to the Corrupt oracle;

• Weak adversaries: these are weak-insider adver-

saries that do not have access to the CreateInsider

oracle;

• Forward-insider adversaries: if they access the

Corrupt oracle, then they can only access the

Corrupt oracle;

• Forward adversaries: these are forward-insider

adversaries that do not have access to the

CreateInsider oracle;

• Destructive adversaries: after the adversary has

queried Corrupt(T ) and obtained the correspond-

ing information, the tag refereed by T is de-

stroyed. The database DB will still keep the

record associated to this tag (the reader does not

know that the tag was destroyed);

• Strong adversaries: no restrictions on the use of

oracles.

Some authors (Hermans et al., 2014) refer to these

classes of adversaries as being wide in the sense that

the adversaries in these classes may consult the Result

oracle. When an adversary is not allowed to consult

the Result oracle, we will refer it as being narrow.

The narrow property can be combined with any of the

properties strong, destructive, forward, and weak in

order to get another four classes of adversaries, nar-

row weak/forward/destructive/strong.

Security in the HPVP model means that no strong

adversary has more than a negligible probability

to make the reader authenticate an uncorrupted le-

gitimate tag without having any tag authentication

matching conversation. When the RFID scheme is

with mutual authentication, besides the above require-

ment, it is asked that no strong adversary has more

than a negligible probability to make an uncorrupted

legitimate tag to authenticate the reader without hav-

ing any reader authentication matching conversation.

To deﬁne privacy in the HPVP model, we

consider the probability experiment (privacy game)

PRIV

A,Σ

(λ) described in the table in Figure 2, where

A is an adversary, O is the set of oracles A is allowed

to query, Σ is an RFID scheme, and the bit b ∈ {0,1}

shows when A interacts with the left-hand side tag

(b = 0) or with the right-hand side tag (b = 1) of the

pairs of tags drawn by him.

PRIV

A,Σ

(λ)

1 (pk, sk,DB) ← SetupReader(λ)

′

← A

(pk, λ);

3 Return b

′

Figure 2: Privacy game in the HPVP model.

An RFID scheme Σ achieves V privacy, where V

is a class of adversaries, if PRIV

A,Σ

(λ) is negligible,

for any adversary A ∈ V , where:

PRIV

A,Σ

(λ) = |P(PRIV

A,Σ

(λ) = 1)

−P(PRIV

A,Σ

(λ) = 1)|

According to the type of adversary considered

(class V above), the privacy classes (levels) in Figure

1 are obtained.

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

159

3 PRF KEY

INDISTINGUISHABILITY

This section will present a speciﬁc property of

pseudo-random functions, crucial in studying RFID

schemes’ privacy properties in models based on in-

distinguishability.

Let K be an at most countable set whose elements

we call keys. Suppose that we have deﬁned a measure

(length) of keys on this set, | · |, which takes values in

the set N of positive integers. We will refer to |K| as

the length of the key K ∈ K . For example, K may be

a set of binary strings, and | · |, their length.

Given a positive integer λ, we denote K

= {K ∈

K ||K| = λ}. A K -indexed family of functions is a

function F that associates to each key K ∈ K a func-

tion F

: D

→ R

, where λ = |K|, and D

and R

are

ﬁnite sets (the same for all keys of length λ). A conve-

nient way to deﬁne D

and R

is to use two polynomi-

als ℓ

and ℓ

speciﬁc to the family F, and then choos-

ing D

= {0.1}

ℓ

(λ)

and R

= {0.1}

ℓ

(λ)

. We usually

denote the family F by F = (F

)

K∈K

or F = (F

)

λ∈N

where F

= {F

||K| = λ}. The difference in notation

will be clear from the context.

We say that F is a pseudo-random function (PRF)

if the following two properties hold:

1. F is efﬁciently computable: there is a determinis-

tic algorithm of polynomial time complexity that

can compute every function F

deﬁned by F;

2. F is indistinguishable from truly random func-

tions: for each PPT algorithm A, its PRF-

advantage against F

PRF

A,F

(λ) = |P(1 ← A

(λ)|K ← K

)

−P(1 ← A

(λ)| f ← (D

))|,

is negligible as a function of λ.

The two probabilities in the deﬁnition above

are often associated with the probability experi-

ments (also called security games) PRF

A,F

(λ) and

PRF

A,F

(λ) from the table in Figure 3.

PRF

A,F

(λ) PRF

A,F

(λ)

1 K ← K

f ← (D

)

2 b ← A

(λ) b ← A

(λ)

3 Return b Return b

Figure 3: PRF security games.

As can be seen, the function PRF

A,F

(λ) calculates

the difference between the probabilities with which

the adversary outputs the same bit (for example, 1) in

both probability experiments. We can write equiva-

lently

PRF

A,F

(λ) = |P(PRF

A,F

(λ) = 1)

−P(PRF

A,F

(λ) = 1)|

In the above security games, the adversary queries

a single function. One can show by using a hybrid

argument (Mittelbach and Fischlin, 2021; Boneh and

Shoup, 2023) or directly that allowing the adversary

to query a polynomial number of functions in the two

probability experiments does not change the concept

of PRF function. In this case, the security games are

shown in the table in Figure 4 (ℓ is a parameter of

polynomial size with respect to λ that depends on A).

PRF

∗,0

A,F

(λ) PRF

∗,1

A,F

(λ)

1 ℓ(λ) ← A(λ) ℓ(λ) ← A(λ)

2 K

,. ..,K

ℓ

← K

,. .., f

ℓ

← (D

)

3 b ← A

,...,F

ℓ

(λ) b ← A

,..., f

ℓ

(λ)

4 Return b Return b

Figure 4: PRF

∗

security games.

Then, F is a PRF if and only if the PRF

∗

advantage of A against F,

PRF

∗

A,F

(λ) = |P(PRF

∗,0

A,F

(λ) = 1)

−P(PRF

∗,1

A,F

(λ) = 1)|,

is negligible.

A speciﬁc property of PRFs is that no adversary

can distinguish between two keys of a PRF based on

(having) a value computed with one of them, except

with negligible probability. To deﬁne this property

precisely, we consider the probability experiments in

the table in Figure 5, where F is a K -indexed family

of functions, A is a PPT algorithm, and ℓ is a param-

eter of polynomial size in λ that depends on A.

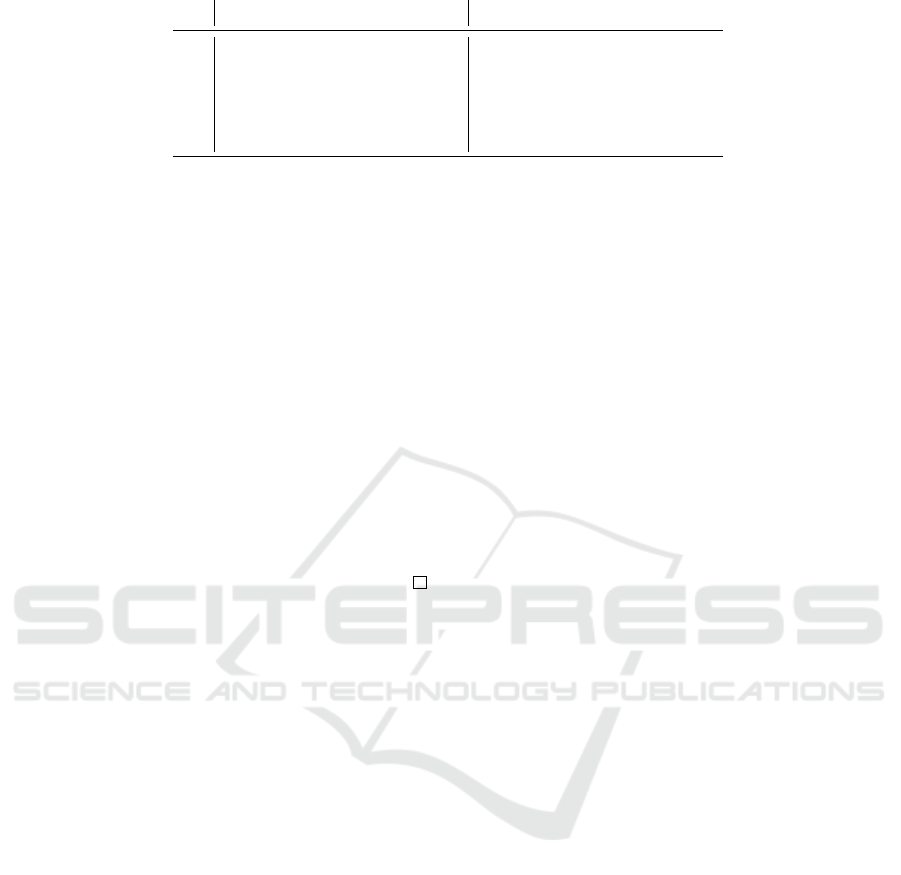
We deﬁne now the key distinguishing advantage

(KD-advantage) of A against F by

A,F

(λ) = |P(KD

A,F

(λ) = 1)−P(KD

A,F

(λ) = 1)|.

Theorem 3.1. Let F be a K -indexed family of func-

tions. If F is a PRF, then the KD-advantage of any

adversary A against F is negligible.

Proof. Let F be a PRF and A an adversary that re-

quests ℓ = ℓ(λ) key pairs to query in the KD security

games against F. We will shown that KD

A,F

(λ) is a

negligible function. The triangle inequality for abso-

lute values leads to:

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

160

A,F

(λ) KD

A,F

(λ)

1 ℓ(λ) ← A(λ) ℓ(λ) ← A(λ)

2 (K

),...,(K

ℓ

) ← K

),...,(K

ℓ

) ← K

3 b ← A

,...,F

ℓ

(λ) b ← A

,...,F

ℓ

(λ)

4 Return b Return b

Figure 5: KD security games.

A,F

(λ) =

= |P(1 ← A

,...,F

ℓ

(λ)|(K

) ←

ℓ

i=1

)−

P(1 ← A

,...,F

ℓ

(λ)|(K

) ←

ℓ

i=1

|P(1 ← A

,...,F

ℓ

(λ)|K

,. ..,K

ℓ

← K

)−

P(1 ← A

,...,F

ℓ

(λ)|K

,. ..,K

ℓ

← K

≤ |P(1 ← A

,...,F

ℓ

(λ)|K

,. ..,K

ℓ

← K

)−

P(1 ← A

,..., f

ℓ

(λ)| f

,. .., f

ℓ

← (D

))|+

|P(1 ← A

,..., f

ℓ

(λ)| f

,. .., f

ℓ

← (D

))−

P(1 ← A

,...,F

ℓ

(λ)|K

,. ..,K

ℓ

← K

Since F is a PRF, both absolute values in the last term

of the above inequality are negligible, which shows

that KD

A,F

(λ) is negligible.

In the key distinguishability security games for a

family of functions F (Figure 5), the challenger ran-

domly chooses several key pairs, and the adversary

interrogates (the functions indexed by) the ﬁrst or sec-

ond component of these pairs (depending on the secu-

rity game he is playing). If F is a PRF, the two se-

quences of values obtained by the adversary through

interrogation are indistinguishable (Theorem 3.1).

We now consider a stronger security game for

distinguishing keys of a family of functions F. In

this game, the challenger randomly generates several

keys, but the adversary is the one who pairs them as he

wishes to interrogate them. The signiﬁcant difference

from the previous game is that, by pairing the keys,

the adversary can create patterns by which he can dis-

tinguish between the two sequences of values he ob-

tains through interrogation (as we said above). Since

the keys are randomly generated and unknown to the

adversary, the pattern that the adversary can create is

based on repeating some keys on the ﬁrst or second

component of the pairs so that, upon querying, one

of the two sequences contains repetitions of the same

value.

For example, suppose the adversary requests to

query (K

) and (K

) on the same input x and

obtains the same value y. In that case, he knows with

overwhelming probability that he is querying the ﬁrst

component of the key pairs (if the values obtained by

querying are distinct, then he knows with overwhelm-

ing probability that he is querying the second compo-

nent of the key pairs). As a result, the adversary can

distinguish between the keys of the function family F.

If the adversary requests to query (K

) and

then again (K

) on the same input x, he will not

be able to draw any clear conclusion about the compo-

nent that was evaluated unless he knows, for instance,

(x) (the adversary can obtain this value by query-

ing the pair (K

)).

As a result, the pairs that leak information to the

adversary are of the form (K

) and (K

′

), where

= K

′

and K

̸= K

′

, or K

̸= K

′

and K

= K

′

. The

pair (K

) leaks information to the adversary only

if it is accompanied by another pair that has K

on the

ﬁrst or second component, while the other component

is different from K

; this case actually falls into the

ﬁrst case mentioned above.

The discussion above leads us to consider a

stronger probability experiment for key distinguisha-

bility in which the adversary can pair keys as he

wants. We denote this game by SKD

A,F

and deﬁne

it as in the table in Figure 6.

Similarly, using the second component of the key

pairs, the security game SKD

A,F

(λ) is deﬁned. We

deﬁne now the strong key distinguishing advantage

(SKD-advantage) of A against F by

SKD

A,F

(λ) = |P(SKD

A,F

(λ) = 1)

−P(SKD

A,F

(λ) = 1)|.

Theorem 3.2. Let F be a K -indexed family of func-

tions. If F is a PRF, then the SKD-advantage of any

adversary A against F is negligible.

Proof. Let F be a PRF and A an adversary. Accord-

ing to Theorem 3.1, there exists a negligible function

µ(λ) such that KD

A,F

(λ) ≤ µ(λ).

By a sequence of security games we will shown

that SKD

A,F

(λ) is a negligible function. For readabil-

ity, we denote by G

(λ) the security game SKD

A,F

(λ)

and assume the adversary requests ℓ(λ) queries (see

the security game in the table from Figure 6). For

0 < t ≤ ℓ(λ), we recursively deﬁne the security game

(λ) as obtained by modifying the security game

t−1

(λ) as follows:

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

161

SKD

A,F

(λ)

1 A asks the challenger to randomly generate p keys, where p is a polynomial

parameter in λ;

2 The challenger draws uniformly at random and independent of each other p

keys K

,. ..,K

, which he will identify by their index;

3 A repeats the following procedure ℓ times, where ℓ is a polynomial parameter

in λ:

3.1 A adaptively chooses a pair of indices (i, j) and an input x not previously

used before with different pairs of indices;

3.2 A sends (i, j) and x to the challenger and receives back F

(x);

4 A outputs a bit b;

5 Return b.

Figure 6: SKD

security game.

- at the t-th query made by A, the answer given by

the challenger contains the evaluation of the func-

tion deﬁned by the second component of the key

pair and not by the ﬁrst. The other queries remain

unchanged (as they are in the game G

t−1

(λ)).

Clearly, the requirement from (3.1) in Figure 6 re-

mains fulﬁlled.

According to Theorem 3.1, for any 0 < t ≤ ℓ(λ),

|P(G

(λ) = 1) − P(G

t−1

(λ) = 1)| ≤ µ(λ),

Moreover, G

ℓ(λ)

(λ) = SKD

A,F

(λ).

The triangle inequality for absolute values leads

then to:

SKD

A,F

(λ) =

= |P(SKD

A,F

(λ) = 1) − P(SKD

A,F

(λ) = 1)|

= |P(G

(λ) = 1) − P(G

ℓ(λ)

(λ) = 1)|

≤

∑

ℓ(λ)

t=1

|P(G

(λ) = 1) − P(G

t−1

(λ) = 1)|

≤ ℓ(λ)µ(λ).

As ℓ is a polynomial and µ is negligible, ℓ(λ)µ(λ)

is a negligible function.

Remark 3.1. We believe that the SKD security games

can further be strengthened relative to the values cho-

sen by the adversary for which he requests the eval-

uation of a function (item (3.1) in the security game

in Figure 6). However, for our purpose, the already

chosen variant is sufﬁcient.

4 WEAK, WEAK-INSIDER, AND

RANDOMIZED WEAK

PRIVACY

There are many practical situations in which the RFID

system is not subject to a corruption attack, such as:

1. The RFID system is implemented in a populated

and video-monitored environment;

2. The adversary needs specialized equipment to

mount the corruption attack, and the environment

that implements the RFID system does not allow

intervention with such equipment;

3. The RFID tags identify disposable or low-value

objects to justify a corruption attack.

In such situations, weak privacy is sufﬁcient for

the RFID system. Except for the fact that “weak

privacy” does not ensure privacy when the adver-

sary uses corruption, weak privacy is not really that

“weak”. In addition, protocols that ensure weak pri-

vacy can only use symmetric cryptography, and in

some cases can provide efﬁcient-time identiﬁcation.

In this section, we will discuss three forms of

weak privacy in the HPVP model. We explicitly

mention from the beginning that the literature on the

HPVP model does not present any protocol of this

type. Therefore, our paper is the ﬁrst to present pro-

tocols and proofs of their weak privacy in the HPVP

model.

To better understand what follows, we will brieﬂy

discuss the cryptographic ingredients used in con-

structing RFID schemes (protocols). Thus, RFID pro-

tocols can use symmetric cryptography, public key

cryptography, and, more recently, physically unclon-

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

162

able functions (PUFs) for security and privacy rea-

sons. Among these, symmetric cryptography is vi-

tal in constructing RFID protocols because it is much

more efﬁcient to implement than public key cryptog-

raphy. Physically unclonable functions have received

special attention recently and offer unique advantages

when combined with symmetric cryptography. In this

paper, we will only consider the case of symmetric

cryptography, which we will assume includes:

1. Invertible algorithms: algorithms O for which

there exists a deterministic polynomial time al-

gorithm O

−1

that inverts O in the sense that x =

−1

(K, y) for all y ← O(K, x);

2. One-way algorithms: algorithms O for which

there exists a deterministic polynomial time algo-

rithm O

that veriﬁes the output of O in the sense

that

(K, x,y) =

(

1, if y ← O(K,x)

0, otherwise;

3. Random number generators: algorithms G of

polynomial time complexity that might depend on

some secret key and are used to generate random

numbers.

Symmetric-key encryption and decryption algo-

rithms fall in the ﬁrst category, while hash functions,

message authentication codes (MACs), and pseudo-

random functions (PRFs) fall in the second category.

Pseudo-random generators (PRGs) may be thought as

deterministic random number generators that depend

on some secret key or seed. All the operations with in-

tegers, such as addition, multiplication, XOR and so

on, can also be viewed as being performed by algo-

rithms as those above (except that they do not depend

on any secret key).

What is the maximum level of privacy an RFID

protocol can achieve in the HPVP model using only

symmetric cryptography? For Vaudenay’s model,

(T¸ iplea, 2022b) proved this is “weak privacy”. A

similar result for the HPVP model is missing, but we

ﬁrmly believe that the above result also holds in this

case. The papers (Hermans et al., 2011; Hermans

et al., 2014) that introduce the HPVP model do not

discuss the case of RFID protocols based on symmet-

ric cryptography. We are unaware of any study ded-

icated to these protocols in the HPVP model. In this

context, we present below RFID protocols that ensure

different types of weak privacy in the HPVP model.

The key tool in our study is Theorem 3.2 obtained

in the previous section, which functions as a general

methodology for establishing privacy properties in the

HPVP model for PRF-based RFID protocols.

4.1 Weak Privacy

This section shows that the PRF-based RFID proto-

col in (Vaudenay, 2007), which is weak private in

Vaudenay’s model, is also weak private in the HPVP

model. Again, we mention that, to our knowledge,

there is no proof of this fact yet. One cannot adapt

the proof in Vaudenay’s model to the HPVP model

because it relies on constructing a blinder. In con-

trast, the privacy properties in the HPVP model rely

on tag indistinguishability. Moreover, tag indistin-

guishability cannot be directly related to the speciﬁc

property of pseudo-random functions. In other words,

the assumption that the RFID protocol does not pro-

vide tag indistinguishability does not directly contra-

dict the fact that it relies on a pseudo-random func-

tion. However, as we will see, it contradicts the key

indistinguishability property of PRFs.

Let us recall now the PRF-based RFID scheme

from (Vaudenay, 2007). The scheme, pictorially rep-

resented in Figure 7, is based on a PRF F = (F

)

where F

is a function from {0,1}

ℓ

(λ)

to {0,1}

ℓ

(λ)

for all K ∈ K

and some polynomials ℓ

(λ) and ℓ

(λ).

Each tag is equipped with a pair (ID,K), where ID is

the tag’s identity and K is a key for F, uniformly at

random chosen and independent from the other tags.

Theorem 4.1. The PRF-based RFID scheme assures

weak privacy in the HPVP model.

Proof. (sketch) Assume that the PRF-based RFID

scheme, denoted Σ, does not assure weak privacy in

the HPVP model. Then, there exists a weak adversary

A that has a non-negligible advantage against Σ.

Deﬁne a PRF adversary A

′

that breaks the strong

key indistinguishability property of F with non-

negligible probability. First, assume that C is a chal-

lenger for F that initiates the SKD

′

game of A

′

against F, where b ∈ {0,1}. The basic steps are as

follows:

1. A

′

simulates the scheme Σ for A:

(a) When A asks for tag creation with identity ID,

′

will ask C to generate a key and assign the

identity ID to it. A speciﬁcation T

is returned

to A;

(b) When A draws (T

) and sends x for in-

terrogation, A

′

generates a random y and sends

(ID

,ID

), x, and y to C. Then, C generates at

random y, computes z = F

(x,y), and returns

the result (y,z) to A

′

. In turn, A

′

returns (y, z)

to A;

within the protocol session π preserve the or-

der of the steps in the RFID scheme (possibly

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

163

Reader (F, DB) Tag (ID,K)

x ← {0,1}

ℓ

(λ)

−→

2 y,z

←−−

y ← {0,1}

ℓ

(λ)

, z = F

(x,y)

3 If ∃(ID, K) ∈ DB s.t. z = F

(x,y)

then output ID else output ⊥

Figure 7: PRF-based RFID scheme.

with a delay), and the messages have not been

changed by A, then A

′

will return 1. If the or-

der of the steps is preserved but the messages

have been changed by A, then A

′

will return 0.

In all the other cases, A

′

will return ⊥;

2. It is easy to check that

|P(PRIV

A,Σ

(λ) = 1) − P(SKD

′

(λ) = 1)|

is negligible for any b. As a conclusion,

|SKD

′

(λ) − PRIV

A,Σ

(λ)|

is negligible.

Therefore, if PRIV

A,Σ

(λ) is non-negligible, then

SKD

′

(λ) is non-negligible, contradicting Theorem

3.2.

4.2 Weak-Insider Privacy

From design to utilization in practice, an RFID system

goes through several stages, such as physical manu-

facturing, software implementation of the protocols,

deployment, and maintenance. Each party responsi-

ble for these stages can maliciously intervene in the

system, inserting tags into the database that the adver-

sary can control by knowing their internal state. Such

tags are called insider tags, and the HPVP model

takes them into consideration for studying the secu-

rity and privacy of RFID systems.

The use of insider tags by adversaries usually goes

along the following line (for examples, please see

(van Deursen and Radomirovi

c, 2012)):

1. The adversary queries let us say two pairs of tags,

gets the responses c and c

′

, and wants to ﬁnd out

if the responses satisfy a certain property φ (for

instance, if c and c

′

come from the same tag);

2. The adversary uses an insider tag, prepares a valid

message m for the reader, and “adds” φ(c,c

′

) to it

getting a new message m

′

. The trick is for the

reader to accept m

′

only if c and c

′

verify φ, ex-

cept with negligible probability. Then, by con-

sulting the oracle Result, the adversary will know

whether or not the property in question is satisﬁed

by c and c

′

The insider tag-based attack is relevant only for

the forward and weak privacy levels. Destructive (and

therefore strong) adversaries can simulate insider tags

by creating legitimate tags and then corrupting them.

What does a weak-insider private RFID scheme

look like? To our knowledge, no such scheme

has been proposed in the literature. Existing RFID

schemes resistant to insider tag attacks are based on

public-key cryptography and ensure forward-insider

privacy.

In this section, we will show that the PRF-based

RFID scheme discussed in the previous section is in-

deed weak-insider private. We will start with an im-

portant observation about SKC-based RFID schemes.

For such schemes, verifying a property between the

responses of two queries can be much simpler be-

cause this type of cryptography uses deterministic al-

gorithms. As a result, it is no longer necessary to

record the insider tag in the database in such a case.

From a practical point of view, this means that the

RFID system manufacturer can keep a few tags for

later use without them being recorded in the database.

To model this case, we introduce a new or-

acle, CreateW Insider, which creates a weak in-

sider (winsider) tag. Its creation means launching

SetupTag(pk, ID) to generate (S,K) and then give S

to the adversary. The tag will not be created and,

therefore, will not be registered. It will not be pos-

sible to draw it, so it will not be possible to com-

municate with it. The reader will never be able to

identify it, but its state can be used by the adversary,

possibly in combination with other states. As a re-

sult, a winsider tag is an insider tag that is not reg-

istered in the database. Replacing the CreateInsider

oracle with CreateW Insider we obtain the concept of

weak-winsider adversary and weak-winsider privacy

(see Section 2).

To make our result as general as possible, we will

assume that the RFID protocols in the theorem below

have at most three communication steps:

1. The reader sends a message m

to the tag;

2. On receiving the message m

, the tag computes

and sends back its answer m

;

3. On receiving the message m

, the reader runs the

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

164

identiﬁcation and/or authentication procedure and

sends back to the tag its answer m

The ﬁrst two steps are usually used in the case of uni-

lateral authentication. The third step is used to allow

the tag to authenticate the reader.

Theorem 4.2. Any weak-winsider private SKC-based

RFID scheme is also weak-insider private in the

HPVP model.

Proof. Assume that Σ is an weak-winsider private

SKC-based RFID scheme that is not weak-insider pri-

vate in the HPVP model. Let A be a weak-insider

adversary against Σ. We deﬁne a weak-winsider ad-

versary A

′

that has the same advantage against Σ as

A, leading thus to a contradiction (because Σ is weak

private).

The main idea is the next one. The adversary A

′

runs and monitors A to play with Σ:

• If A does not use any insider tag, then A

′

does not

do anything;

• If A queries CreateInsider, A

′

will create an win-

sider tag for A and gives him the internal state.

Moreover, A

′

will keep track of this tag (state up-

dates and involvements in the protocol sessions);

• Insider tags cannot be drawn and so they can-

not be queried by means of SendTag. However,

their internal states can be used by A to query

SendReader(m,π), where m is a valid message

built from an insider tag information and accord-

ing to the messages of the protocol session π. The

adversary A

′

can check is m fulﬁlls this property

because Σ uses only SKC and the winsider tags

were created by A

′

. Therefore, in such a case, A

′

will simulate the reader’s answer for A and also

know how to answer queries addressed to the ora-

cle Result.

In this way, A

′

will play with Σ as A does, but without

using any insider tag. In other words, A

′

is a weak-

winsider adversary. Moreover, its advantage against

Σ is exactly the advantage of A against Σ. Hence,

the assumption that A has a non-negligible advantage

against Σ contradicts the weak-winsider privacy of Σ.

Remark 4.1. If the adversary can create himself win-

sider tags in an RFID scheme, then the scheme is

weak private if and only if it is weak-winsider pri-

vate. The PRF-based scheme in the previous section

ﬁts this case because the function F is public, and so

is its keyspace; the adversary can create insider tags

himself.

Corollary 4.1. The PRF-based RFID scheme in Sec-

tion 4.1 is weak-insider private.

Proof. From Theorem 4.2 and Remark 4.1.

4.3 Randomized Weak Privacy

Randomized weak (r-weak) privacy was introduced in

(Hristea and T¸ iplea, 2020) as a weaker form of weak

privacy in Vaudenay’s model. It helps identify enti-

ties where tracing is unimportant or cannot be done

appropriately due to very high mobility or crowding

in which the entity is. For details, please see (Hristea

and T¸ iplea, 2020).

In the HPVP model, r-weak privacy can simply be

obtained by replacing the oracle Free(vtag) with the

oracle r-Free(vtag) deﬁned as follows:

r-Free(vtag): the freed tag is re-randomized.

By tag re-randomization, we mean that after the

tag is freed, some of the parameters that were set ran-

domly are replaced by others, also chosen randomly,

so that the tag’s response to a new communication

with the adversary is indistinguishable from the re-

sponses from previous communications. For exam-

ple, if the tag computes F

(x), where F is a PRF and

x is a random secret parameter, re-randomization can

be achieved by randomly choosing a new parameter x

or a new key K.

The RFID scheme in Figure 8, proposed in (Hris-

tea and T¸ iplea, 2020), is r-weak private in the Vau-

denay model. We will show that it is r-weak pri-

vate in the HPVP model as well. First, let us dis-

cuss the scheme a little. The tag, which takes the

ﬁrst step in the protocol, computes z = F

(0,0,x),

where F = (F

)

is a pseudo-random function, and

sends it to the reader. The reader checks its database

for a triple (ID, K,x) such that z = F

(0,0,x) or z =

(0,0,x + 1). The reason is that at most one step

of desynchronization may occur between reader and

tag. When the reader ﬁnds the right value, resynchro-

nizes with the tag and prepares the answer w. The

tag checks the value w received from reader, takes a

decision, updates x if necessary, and prepares the an-

swer for reader. On receiving the tag’s answer, the

reader checks it, takes a decision, and updates x. If

the reader does not update x (because it rejects the

tag), then it will do so in the second step of the next

protocol session (with the same tag). Therefore, the

desynchronization between reader and tag is at most

one step.

It is straightforward to check the correctness of the

scheme in Figure 8. We remark that it does not use

temporary variables, and the tag only needs to com-

pute F. Moreover,the scheme allows for a quite efﬁ-

cient search procedure in the reader’s database. Two

ordered sets of indices are used: the ﬁrst one with in-

dices of the form F

(0,0,x), and the second one with

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

165

Reader (DB,F) Tag (K, x)

1 z

←−

z = F

(0,0,x)

2 If ∃((ID, K,x) ∈ DB, i ∈ {0,1})

such that z = F

(0,0,x + i)

then x = x + i, w = F

(0,1,x + i)

else w ← {0,1}

ℓ

−→

3 w

′

= F

(0,1,x)

If w = w

′

then output OK, x = x + 1, w

′

= F

(1,1,x)

′

←−

else output ⊥, w

′

= F

(1,0,x)

4 If w

′

= F

(1,1,x + 1)

then output ID, x = x + 1 else output ⊥

Figure 8: Stateful PRF-based RFID scheme.

indices of the form F

(0,0,x + 1). Both F

(0,0,x)

and F

(0,0,x + 1) will point to the same database

record (ID,K,x). When z is received by reader, the

ﬁrst set of indices is searched for it; if not found, then

the second set is searched for it. Therefore, it takes

O(logn) time to search for a tag, where n is the size of

the databases. When the reader authenticates the tag,

x is updated both in the database and in the indices

sets. Moreover, the indices sets must be resorted. This

can be simply done in O(logn) time because the old

indices have to be removed and the new ones have to

be reinserted in the right position.

A more efﬁcient search can be performed by using

hash indices as in (Alomair et al., 2012), where con-

stant time is claimed for search. Moreover, the tech-

nique in (Alomair et al., 2012) applied to our scheme

works much better than for the scheme in (Alomair

et al., 2012). This is because the reader-tag desyn-

chronization in our scheme is at most one step, while

in (Alomair et al., 2012) it is bounded by some poly-

nomial c(λ) in the security parameter λ. This fact

leads to c(λ) sets of indices in (Alomair et al., 2012),

while in our case we have only two.

Of course, the scheme is not weak private in the

HPVP model because the tag identiﬁer (z) is not ran-

domized (T¸ iplea, 2022a). However, we have the fol-

lowing result.

Theorem 4.3. The RFID scheme in Figure 8 assures

r-weak privacy in the HPVP model.

Proof. (sketch) Assume that the PRF-based RFID

scheme, denoted Σ, does not assure r-weak privacy in

the HPVP model. Then, there exists a weak adversary

A that has a non-negligible advantage against Σ.

Deﬁne a PRF adversary A

′

that breaks the strong

key indistinguishability property of F with non-

negligible probability. First, assume that C is a chal-

lenger for F that initiates the SKD

′

game of A

′

against F, where b ∈ {0,1}. The basic steps are as

follows:

1. A

′

simulates the scheme Σ for A:

(a) When A asks for tag creation with identity ID,

′

will ask C to generate a key and assign

the identity ID to it. The internal state of the

tag must also contain a counter x that is incre-

mented after each completed session. However,

working in the randomized model, this counter

is randomized every time the tag is freed. As

a result, A

′

doesn’t need to generate a random

x to be recorded in the internal state of the tag

along with the key generated by C (please see

below the query process).

A speciﬁcation T

is returned to A;

(b) When A draws (T

) and asks for inter-

rogation, A

′

generates a random x and sends

(ID

,ID

) and x to C . Then, C computes

z = F

(0,0,x), and returns the result z to A

′

In turn, A

′

returns z to A;

′

either

generate a random value w or queries C with

the same pair of tags (ID

,ID

) and (0,1, x),

depending on the case (please see the above

item and the step 2 in the RFID scheme).

Similarly, to simulate the tag’s answer w

′

, A

′

queries C with the same pair of tags (ID

,ID

)

and (1, 1,x) or (1, 0,x), depending on the case

(please see the above item and the step 3 in the

RFID scheme);

(d) Result(π) is simulated similar to that in the

proof of Theorem 4.1.

2. It is easy to check that

|P(PRIV

A,Σ

(λ) = 1) − P(SKD

′

(λ) = 1)|

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

166

is negligible for any b. As a conclusion,

|SKD

′

(λ) − PRIV

A,Σ

(λ)|

is negligible.

Therefore, if PRIV

A,Σ

(λ) is non-negligible, then

SKD

′

(λ) is non-negligible, contradicting Theorem

3.2.

5 CONCLUSIONS

In recent years, many studies have been devoted to

RFID schemes that provide a high degree of privacy

in Vaudenay’s or the HPVP model, such as forward-

insider, destructive, or strong privacy. These schemes

are based on public-key cryptography or combina-

tions of symmetric cryptography with physically un-

clonable functions (PUFs). The use of public-key

cryptography is expensive. Even though PUFs are

considered light physical devices, their use in the con-

struction of RFID schemes requires error correction

methods, which makes their practical use difﬁcult.

In contrast, using symmetric cryptography, RFID

schemes that provide weak privacy or similar forms

can be built. It is true, however, that such schemes

cannot offer privacy against adversaries with the abil-

ity to corrupt tags (T¸ iplea, 2022b). However, there

are many practical situations in which it is not nec-

essary to use RFID schemes that are resistant to cor-

ruption attacks. This paper focuses on schemes that

provide various forms of weak privacy in the HPVP

model. In addition to highlighting such schemes, a

central objective of this paper is to establish a funda-

mental property of pseudo-random functions (PRFs)

through which one can show that a given RFID

scheme achieves weak privacy. Thus, we believe PRF

key indistinguishability is the deﬁning property for

PRF-based RFID schemes in the HPVP model (or any

other model based on tag indistinguishability).

REFERENCES

Alomair, B., Clark, A., Cu

ellar, J., and Poovendran, R.

(2012). Scalable RFID systems: A privacy-preserving

protocol with constant-time identiﬁcation. IEEE

Transactions on Parallel and Distributed Systems,

3(8):1536–1550.

Boneh, D. and Shoup, V. (2023). A Graduate Course in Ap-

plied Cryptography. Stanford University, California,

USA.

T¸ iplea, F. L. (2022b). Narrow privacy and desynchroniza-

tion in Vaudenay’s RFID model. International Jour-

nal of Information Security, 22:563–575.

Hermans, J., Pashalidis, A., Vercauteren, F., and Preneel,

B. (2011). A new RFID privacy model. In Atluri, V.

and Diaz, C., editors, Computer Security – ESORICS

2011, pages 568–587, Berlin, Heidelberg. Springer

Verlag.

Hermans, J., Peeters, R., and Preneel, B. (2014). Proper

RFID privacy: Model and protocols. IEEE Transac-

tions on Mobile Computing, 13(12):2888–2902.

Hristea, C. and T¸ iplea, F. L. (2020). Privacy of stateful

RFID systems with constant tag identiﬁers. IEEE

Transactions on Information Forensics and Security,

15:1920–1934.

Katz, J. and Lindell, Y. (2020). Introduction to Modern

Cryptography. Chapman & Hall/CRC, 3rd edition.

Mittelbach, A. and Fischlin, M. (2021). The Theory of

Hash Functions and Random Oracles - An Approach

to Modern Cryptography. Information Security and

Cryptography. Springer.

Paise, R.-I. and Vaudenay, S. (2008). Mutual authentication

in RFID: Security and privacy. In Proceedings of the

2008 ACM Symposium on Information, Computer and

Communications Security, ASIACCS ’08, pages 292–

299, New York, NY, USA. ACM.

Sipser, M. (2012). Introduction to the Theory of Computa-

tion. Cengage Learning.

van Deursen, T. and Radomirovi

c, S. (2012). Insider attacks

and privacy of RFID protocols. In Petkova-Nikova,

S., Pashalidis, A., and Pernul, G., editors, Public Key

Infrastructures, Services and Applications, pages 91–

105, Berlin, Heidelberg. Springer Berlin Heidelberg.

Vaudenay, S. (2007). On privacy models for RFID. In Pro-

ceedings of the Advances in Crypotology 13th Interna-

tional Conference on Theory and Application of Cryp-

tology and Information Security, ASIACRYPT’07,

pages 68–87, Berlin, Heidelberg. Springer-Verlag.

T¸ iplea, F. L. (2022a). Lessons to be learned for a good

design of private RFID schemes. IEEE Transactions

on Dependable and Secure Computing, 19(4):2384–

2395.

Weak, Weak-Insider, and Randomized Weak Privacy in the HPVP Model for RFID

167