MICODE: A Minimal Code Design for Secret Sharing Scheme

Belkacem Imine

1 a

, Rahul Saha

2,3

and Mauro Conti

LACOSI Laboratory, Faculty of Electrical Engineering,

University of Science and Technology of Oran Mohamed Boudiaf (USTO-MB), Oran, Algeria

Department of Mathematics, University of Padua, Padua, Italy

School of Computer Science and Engineering, Lovely Professional University, Punjab, India

Keywords:

Reed-Muller, Code, Secret, Sharing, Minimal.

Abstract:

Secret Sharing Schemes (SSS) in cryptography often utilize minimal linear codes for efﬁciency, with minimum

distance playing a crucial role. Determining minimal codewords in general linear codes presents a challenge

known as the linear code covering problem. To address this, we propose MInimal COde DEsign (MICODE),

a novel method for generating minimal codes from binary Reed-Muller (RM) codes using the Ashikhmin-Barg

lemma. Unlike existing approaches limited to small RM codes, MICODE extends to higher orders through

a systematic puncturing strategy. By recursively removing one-weight columns from the generator matrix,

we reduce the RM code’s maximum Hamming weight preserving its minimum distance. The RM generator

matrix’s structure, derived from the Kronecker product of lower-triangular binary matrices, facilitates this con-

struction. We conduct rigorous mathematical analysis of MICODE establishing parameters for a secure SSS.

While these minimal codes are unsuitable for error correction due to their reduced code rate, they are proven

highly effective for cryptographic applications, such as Massey SSS, where security depends on minimum

distance. Our analysis also explores trade-offs between code rate and error performance offering new insights

into their theoretical and practical implications.

1 INTRODUCTION

Conﬁdentiality is a fundamental service of cryptog-

raphy, achieved through symmetric and asymmetric

methods. However, the security of these methods re-

lies heavily on the protection of secret keys. Accord-

ing to Kerckhoff’s principle, the security of a cryp-

tosystem depends entirely on the secrecy of its en-

cryption key. Storing the key in a single device poses

a risk of system failure, while storing multiple copies

across devices increases the risk of exposure. To ad-

dress these challenges, Secret Sharing Schemes pro-

vide a robust cryptographic solution, ensuring both

the security and availability of secret keys by dis-

tributing them across multiple parties without com-

promising conﬁdentiality. Blakley (Blakley, 1979)

and Shamir (Shamir, 1979) schemes are the ﬁrst pro-

posed secret sharing schemes. Shamir’s SSS is a

(k, n)-threshold SSS with P as the dealer and n par-

ticipants P = {p

,..., p

}. Every participant p

keeps

one share and any group of k or more can ﬁgure out

https://orcid.org/0000-0002-2295-5145

the secret s. The number of authorized participants

who can recover the secret s in this scheme is at least

k. The set containing these authorized participants is

called an access set, whereas the set containing the

smallest number of authorized participants is called a

minimal access set and has a size of k. Shamir’s SSS

is much more popular because all minimal access sets

are of the same size, which makes the implementation

easier.

In (McEliece and Sarwate, 1981), the researchers

suggested employing Error Correction Codes (ECC

)

to construct a SSS, wherein a (k,n)-threshold scheme

is generalized using the Reed-Solomon code. Massey

has proposed an ECC-based SSS with different-sized

minimal access sets (Massey, 1993), where the ac-

cess structure is deﬁned by the minimal codewords

of the dual code. A nonzero codeword in a linear

code is considered minimal if its support is not a

proper superset of the support of any other nonzero

codeword. The general properties of minimal code-

words were discussed in (Agrell, 1996; Agrell, 1998).

The Massey’s secret sharing involves determining the

Imine, B., Saha, R. and Conti, M.

MICODE: A Minimal Code Design for Secret Sharing Scheme.

DOI: 10.5220/0013517300003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 381-391

ISBN: 978-989-758-760-3; ISSN: 2184-7711

381

minimal access sets by computing all the minimal

codewords in a linear code. However, we observe in

the literature that minimal codewords are difﬁcult to

determine (Covering problem) (Ding and Yuan, 2003;

Li et al., 2010); thus, Massey’s secret sharing is dif-

ﬁcult to implement. This invokes the search for a

class of codes in which determining minimal code-

words is easier, or in other words, in which solv-

ing the covering problem is simple. For speciﬁc

families of linear codes, minimal codewords have

been determined by leveraging their structural prop-

erties (Ding et al., 2000; Schillewaert et al., 2010;

Yuan and Ding, 2005). Reed-Muller codes are an

intriguing class of codes. Still, the covering prob-

lem has only been solved for second-order binary

Reed-Muller codes (Ashikhmin and Barg, 1998), or

only minimal low-weight codewords have been de-

termined in Reed-Muller codes(Schillewaert et al.,

2010). As a result, this leads to the search for a class

of codes in which all codewords are minimal to fa-

cilitate determining the access structure of the secret

sharing scheme. This class is called minimal linear

code.

Ashikhmin and Barg propose a sufﬁcient condi-

tion for determining whether or not a linear code is

minimal (Ashikhmin and Barg, 1998). Yun Song and

Zhihui Li have proposed a minimal linear code con-

struction based on irreducible cyclic codes and have

investigated the conditions under which a given irre-

ducible cyclic code is minimal (Song and Li, 2012).

In (Xu and Qu, 2019), the authors construct three

classes of minimal linear codes over ﬁnite ﬁelds.

Even if the Ashikhmin-Barg inequality is not satis-

ﬁed, another method allows for the construction of a

minimal code (Chang and Hyun, 2018; Ding et al.,

2018). On the other hand, Chang and Hyun have pre-

sented a method for constructing a class of minimal

binary linear codes that violate the Ashikhmin-Barg

inequality by using Boolean functions derived from

mathematical objects known as simplicial complexes.

Another necessary and sufﬁcient condition presented

in (Ding et al., 2018) allows for the generation of

three inﬁnite classes of minimal binary linear codes,

which are based on the Walsh-Hadamard transform of

a Boolean function. The work also demonstrates that

these three classes of minimal binary linear codes vi-

olate the Ashikhmin-Barg inequality.

1.1 Motivations and Contributions

Our proposed MICODE has the following contribu-

tions.

• Minimal Code Construction with a Large Min-

imum Distance: Our proposed minimal code

(MICODE) constructs a minimal linear code with

a large minimum distance, a property essential for

secret sharing schemes (SSS). Unlike Ding’s min-

imal code (Ding et al., 2018), MICODE achieves

a higher minimum distance, enhancing both the

security and robustness of SSS applications. Our

approach leverages the structured properties of

RM codes, where the minimum distance is well-

deﬁned. Given the generator matrix of an RM

code, we recursively reduce the maximum Ham-

ming weight by applying a puncturing scheme to

one-weight columns and their corresponding rows

until the Ashikhmin-Barg inequality is satisﬁed.

This ensures that the resulting code remains min-

imal while maintaining the same minimum dis-

tance as the original RM code

• Ideal and Perfect SSS: Our contribution presents

a perfect and ideal code-based secret sharing

scheme based on the dual of the generated min-

imal code. The scheme ensures that only au-

thorized participants can reconstruct the secret,

while unauthorized sets learn nothing. It is efﬁ-

cient and easy to implement, as all minimal ac-

cess sets have the same size, similar to Shamir’s

SSS (Shamir, 1979). However, our approach of-

fers signiﬁcant advantages over Shamir’s SSS,

including ﬁne-grained access control, enhanced

security, customizable access structures, and re-

silience to share compromise, making it partic-

ularly suitable for applications requiring speciﬁc

access rules and higher security.

1.2 Paper Organization

We organize the rest of the paper in the following

sections. Section 2 provides general deﬁnitions con-

cerning linear codes, how to construct a Reed-Muller

code, and minimal code characteristics. Section 3 in-

troduces MICODE and explains the steps of generat-

ing a minimal code from the Reed-Muller code. Sec-

tion 4 shows an application of MICODE in SSS. It

describes a perfect Massey’s secret sharing based on

the generated minimal code and the number of possi-

ble minimal access sets. The last section of the paper

concludes the paper.

2 AN OVERVIEW OF

REED-MULLER CODES AND

MINIMAL CODES

Let F

be a ﬁnite ﬁeld of q elements. An [n,k]

q−ary

code C is a k−dimensional subspace of the vector

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

382

space F

such that the sum of any two codewords

u,v ∈ C produces another codeword c = u + v ∈ C.

Deﬁnition 1 (Hamming weight). Let v =

,..., v

n−1

) ∈ F

be a vector, then the Ham-

ming weight w

(v) of v is the number of its non-zero

coordinates.

(v)

∆

= |{i | v

̸= 0}|. (1)

Deﬁnition 2 (Hamming distance). The Hamming dis-

tance d

between two vectors u,v ∈ F

is deﬁned by:

(u,v)

∆

= |{i | u

̸= v

}|. (2)

A [n,k,d] code C is a linear code in which the Ham-

ming distance between any two distinct codewords is

at least d.

Deﬁnition 3 (Support of a vector). The support of a

vector v ∈ F

is the set of indices of its nonzero coor-

dinates.

Supp(v)

∆

= {i | v

̸= 0, 0 ≤ i ≤ n − 1}. (3)

Let C be a linear code, we say that a codeword c ∈ C

covers a codeword c

′

∈ C if and only if Supp(c

′

) ⊆

Supp(c).

Deﬁnition 4 (Evaluation function). Consider

the polynomial ring F

= [x

,..., x

p−1

]/(x

−

,..., x

p−1

− x

p−1

) with p variables, and F

= {0,1}

is a binary ﬁeld. The elements of F

are ordered in

decreasing index order. Let n = 2

, the evaluation

function of a monomial g ∈ F

is the evaluation

function Eval(g) at all n vectors of F

Eval : g ∈ F

→ (g(v))

v∈F

. (4)

Example 1. Table 1 displays the evaluation of all the

monomials with 3 variables and degree less than or

equal to 2.

Table 1: The evaluation of all monomials with 3 variables

and degree less than or equal to 2 (Abbe et al., 2020).

Eval(1) 1 1 1 1 1 1 1 1

Eval(x

) 1 1 0 0 0 0 0 0

Eval(x

) 1 0 1 0 0 0 0 0

Eval(x

) 1 0 0 0 1 0 0 0

Eval(x

) 1 1 1 1 0 0 0 0

Eval(x

) 1 1 0 0 1 1 0 0

Eval(x

) 1 0 1 0 1 0 1 0

Deﬁnition 5 (Reed-Muller code). The r-th order bi-

nary Reed-Muller code RM(p,r) code is deﬁned by

evaluating all p−variate monomials with degree less

than or equal to r.

RM(p,r)

∆

= {Eval(g) | g ∈ F

, deg(g) ≤ r}. (5)

The code parameters of an RM(p,r) code are as

follows:

• Code length: 2

• Code dimension:

∑

i=0





• Minimum distance: 2

p−r

Example 2. The RM(3, 1) is deﬁned by the evalua-

tion of all 3−variate monomials of degree less than

or equal to 1 (Abbe et al., 2020).

RM(3,1)







Eval(x

)

Eval(x

)

Eval(x

)

Eval(1)













1 1 1 1 0 0 0 0

1 1 0 0 1 1 0 0

1 0 1 0 1 0 1 0

1 1 1 1 1 1 1 1







Deﬁnition 6 (Minimal codeword (Ding and Salomaa,

2006)). Let [n, k]

be a linear code over F

. A non-

zero codeword c ∈ C is minimal if it does not cover

any other codeword c

′

∈ C.

Deﬁnition 7 (Minimal code (Ding and Salomaa,

2006)). A code C is minimal if all of its non-zero

codewords are minimal.

Lemma 1 (Ashikhmin-Barg (Ashikhmin and Barg,

1998)). An [n,k,d]

code C is minimal if:

min

max

q − 1

. (6)

min

and W

max

denote the non-zero minimum-weight

codeword and the miximum-weight codeword in C, re-

spectively.

3 OUR PROPOSAL: MICODE

In this section, we introduce our algorithm for con-

structing a minimal code from the Reed-Muller code.

We use the upper bound described in (Ball and

Blokhuis, 2013) to compute the maximum weight

max

for a linear code such that the Hamming dis-

tance is preserved in the resulting minimal code.

Theorem 1. Let C be an [n,k,d]

code such that q

is prime, then the maximum weight W

max

fulﬁls (Ball

and Blokhuis, 2013)

max

≤ (n − d)q − e(q − 1), (7)

where e ∈ {0,1,..., k − 2} is the maximal integer sat-

isfying:



n − d



̸≡ 0 (mod q

k−1−e

). (8)

Our algorithm is a recursive algorithm that pro-

duces a minimal code from a binary RM code of

length n, dimension k, and minimum distance d. It

takes a generator matrix G at each instance and ver-

iﬁes the Ashikhmin-Barg condition to ensure mini-

mality, such that the Hamming distance remains un-

changed. At each instance for a given G, our algo-

rithm searches for all columns with Hamming weights

of one, then:

MICODE: A Minimal Code Design for Secret Sharing Scheme

383

• If the computed columns are all different: it

deletes one column and one row in such a way that

the deleted row has the greatest Hamming weight

and the intersection of the deleted row and column

is one.

• If at least two columns match: it deletes all match-

ing columns as well as the corresponding row,

which is indexed by the position of their non-zero

coordinates.

• This process is repeated until the generator matrix

satisﬁes the Ashikhmin-Barg condition for mini-

mality, speciﬁcally

max

Algorithm 1 describes in detail how to generate mini-

mal code from a RM code.

Example 3. Suppose the RM(4,2) code generated by

the generator matrix G

RM(4,2)







1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0

1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0

1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0

1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0

1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0

1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1







• Step 1: There is only one column of Hamming

weight 1, we remove the last column (column 15)

and the last row (row 10).







1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0

1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0

1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0

1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0

1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0

1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1







• Step 2: Following (Ball and Blokhuis, 2013), we

compute W

max

of the code generated by G

. Given

= 15,k

= 10, and d = 4, we obtain W

max

≤ 14

for e = 8.

• Step 3: We compute (

Min(n

max

)

) =

0.2857 <

. We proceed to the next step.

• Step 4: The columns {7,11,13, 14} have Ham-

ming weight 1, then I = {7,11,13, 14} and T =

{Supp(g

),Supp(g

)} =

Input: Generator matrix G of [n,k, d]-RM code C

Output: A generator matrix G

of a minimal

code

Function Puncture(G):

n ← Number of columns of G ;

k ← Number of rows of G ;

′

← n;

′

← k;

max

← n;

I ←

0 ;

T ←

0 ;

for j ← 0 to n − 1 do

if w

) = 1 then

I ← I ∪ { j} ;

end

for i ← 0 to k − 1 do

T ← {T ∪ i | G

i, j

= 1,∀ j ∈ I} ;

end

R(T ) ← The rows of G indexed by T ;

ℏ

ℓ

⊆ I ← {x

,. .., x

|Supp(g

) = · ·· =

Supp(g

) = ℓ, 0 ≤ x

< x

< ... ≤ m < n} ;

if |ℏ

ℓ

| > 1 then

Delete the row indexed by ℓ from G;

Delete the columns indexed by ℏ

ℓ

from

′

← n − |ℏ

ℓ

| ;

′

← k − 1 ;

max

← Max weight([n

′

,d]) (Ball and

Blokhuis, 2013) ;

else

max

← r ∈ R(T ) | w

(r) ≥ r

′

,∀r

′

∈ R(T )

;

for j ← 0 to n − 1 do

′

← {g

| r

max

∩ g

= 1, j ∈ I } ;

end

Delete the row r

max

from G;

Delete the column g

′

from G;

′

← n − 1;

′

← k − 1;

max

← Max weight([n

′

,d]) (Ball and

Blokhuis, 2013);

end

if (d/(Min(W

max

′

)) >

) then

return G

= G

else

Puncture(G)

end

End Function

Algorithm 1: Constructing Minimal code from RM(p, r).

{3,6, 8,9}. Since all the rows indexed by T have

the same Hamming weight, we can remove either

(row 3 and column 7), (row 6 and column 11),

(row 8 and column 13), or (row 9 and column 14).

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

384

Let us take the ﬁrst case.







1 1 1 1 0 0 0 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0 1 1 0 0 0 0 0

1 0 1 0 0 0 0 0 1 0 1 0 0 0 0

1 1 1 1 0 0 0 0 1 1 1 1 0 0 0

1 0 0 0 1 0 0 0 1 0 0 0 1 0 0

1 1 0 0 1 1 0 0 1 1 0 0 1 1 0

1 0 1 0 1 0 1 0 1 0 1 0 1 0 1







• Return to steps 2 and 3, W

max

≤ 14 for

= 14,k

= 9, and d = 4. We compute

(

Min(n

max

)

) =

= 0.2857 <

. We proceed to

the next step.

• Step 5: I = {10,12,13} and T =

{Supp(g

),Supp(g

)} = {5, 7,8}.

Since all the rows indexed by T have the same

Hamming weight, we can remove either (row 5

and column 10), (row 7 and column 12), or (row

8 and column 13). Let us take the ﬁrst case.







1 1 1 1 0 0 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0 0 0

1 1 0 0 0 0 0 1 1 0 0 0 0 0

1 0 1 0 0 0 0 1 0 1 0 0 0 0

1 1 1 1 0 0 0 1 1 1 1 0 0 0

1 0 0 0 1 0 0 1 0 0 0 1 0 0

1 1 0 0 1 1 0 1 1 0 0 1 1 0

1 0 1 0 1 0 1 1 0 1 0 1 0 1







• Return to steps 2 and 3, W

max

≤ 13 for

= 13,k

= 8, and d = 4. We compute

(

Min(n

max

)

) =

= 0.3077 <

. We proceed to

the next step.

• Step 6: I = {3, 11,12} and T =

{Supp(g

),Supp(g

)} = {0,6, 7}.

Since the row 0 has a weight 4 and rows {6,7}

have weights 8, we can remove either (row 6 and

column 11) or (row 7 and column 12). Let us

remove (row 6 and column 11).







1 1 1 1 0 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0 0

1 1 0 0 0 0 0 1 1 0 0 0 0

1 0 1 0 0 0 0 1 0 1 0 0 0

1 0 0 0 1 0 0 1 0 0 1 0 0

1 1 0 0 1 1 0 1 1 0 1 1 0

1 0 1 0 1 0 1 1 0 1 1 0 1







• Return to steps 2 and 3, W

max

≤ 12 for

= 12,k

= 7, and d = 4. We compute

(

Min(n

max

)

) =

= 0.3333 <

. We proceed to

the next step.

• Step 7: I = {3,5, 8,11} and T = {0,1, 3,6}. The

rows {0,1,3} have Hamming weight 4 and the

row 6 has Hamming weight 8. We must remove

(row 6 and column 11), we obtain:







1 1 1 1 0 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0 0

1 1 0 0 0 0 0 1 1 0 0 0

1 0 1 0 0 0 0 1 0 1 0 0

1 0 0 0 1 0 0 1 0 0 1 0

1 0 1 0 1 0 1 1 0 1 1 1







• Return to steps 2 and 3, W

max

≤ 10 for

= 11,k

= 6, and d = 4. We compute

(

Min(n

max

)

) =

= 0.4 <

. We proceed to the

next step.

• Step 8: I = {3,5,6, 8,9,10} and T =

{0,1, 2,3,4, 5}. All rows indexed to T have

Hamming weight 4. We can remove either (row

0 and column 3), (row 1 and column 5), (row 2

and column 6), (row 3 and column 8), (row 4

and column 9), or (row 5 and column 10). Let us

remove (row 0 and column 3), then we obtain:







1 1 1 1 0 0 0 0 0 0 0

1 1 0 0 1 1 0 0 0 0 0

1 0 1 0 1 0 1 0 0 0 0

1 1 0 0 0 0 0 1 1 0 0

1 0 1 0 0 0 0 1 0 1 0

1 0 0 0 1 0 0 1 0 0 1







• Return to steps 2 and 3, W

max

≤ 10 for

= 10,k

= 5, and d = 4. We compute

(

Min(n

max

)

) =

= 0.4 <

. We proceed to the

next step.

• Step 9: I = {4,5,7, 8,9} and T = {0, 1,2,3,4}.

All rows indexed to T have Hamming weight 4.

We can remove either (row 0 and column 4), (row

1 and column 5), (row 2 and column 7), (row 3

and column 8), or (row 4 and column 9). Let us

remove (row 0 and column 4), then we obtain:







1 1 0 1 1 0 0 0 0 0

1 0 1 1 0 1 0 0 0 0

1 1 0 0 0 0 1 1 0 0

1 0 1 0 0 0 1 0 1 0

1 0 0 1 0 0 1 0 0 1







• Return to steps 2 and 3, W

max

≤ 9 for n

= 9,k

4, and d = 4. We compute (

Min(n

max

)

) =

0.444 <

. We proceed to the next step.

MICODE: A Minimal Code Design for Secret Sharing Scheme

385

• Step 10: I = {1, 4,6,7,8} and T = {0,1,2, 3}.

Two columns are identical (1 and 6) and have 1 in

position 1, so ℏ

= {1,6}. We must remove (row

1, column 1 and column 6), then we obtain:







1 0 1 1 1 0 0 0 0

1 1 0 0 0 1 1 0 0

1 0 1 0 0 1 0 1 0

1 0 0 1 0 1 0 0 1







• Return to steps 2 and 3, W

max

≤ 5 for n

= 7,k

3, and d = 4. We compute (

Min(n

max

)

) =

0.8 >

. Therefore, G

is a valid generator matrix

of a minimal code of length n = 7, dimension k =

3, and minimum distance d = 4.

Proposition 1. For any RM(p,r) code of length n,

dimension k and minimum distance d there exists an

minimal code of length n

′

≤ n, dimension k

′

≤ k and

minimum distance d such that:

• If p = r, then n

′

= k

′

= 1.

• If r = 0 and p > 0, then k = k

′

= 1 and n

′

= n.

• If 0 < r < p, then k

′

≥ 2 and n

′

< n.

Proof. If p = r, the RM(p,r) code’s generator ma-

trix G is formed by the evaluation vectors of all the

p−variate monomials, i.e. n = k, implying the exis-

tence of the row (1,0,...,0) in the generator matrix G

and that its support is covered by all the other k − 1

rows. As a result, all of the remaining k − 1 rows

and n− 1 columns (g

,...g

n−1

) must be deleted. If

r = 0 and p > 0, then the RM(p,r) has only one non-

zero codeword which is minimal, so k = k

′

= 1 and

′

= n.

If 0 < r < p, then the RM(p, r) code contains at least

two codewords of weight d = 2

p−r

. Let G

(i)

be the

matrix produced by our algorithm at instance i, if the

removed row from G

(i)

has a weight d, then no code-

word of a weight greater than d exists. If G

(i)

has two

rows, they must have the same weight and have ”1” in

the ﬁrst position, this means

(i)

max

Proposition 2 (Maximum number of iterations). Let

C be an [n, k, d]

RM(p,r) code, 0 < r < p and C

′

the generated [n

′

,d]

minimal code. The maximum

number of iterations I

max

required to move from code

C to code C

′

is the smallest integer i that satisﬁes:

n −

′

− 2d < i, 0 ≤ i ≤ k − 2 (9)

Such that e

′

∈ {0,...,k −i −2} is the maximum integer

that satisﬁes:



n − i − d

′



̸≡ 0 (mod 2

k−i−1−e

′

). (10)

Proof. Let W

′

max

be the maximum Hamming weight

in C

′

. According to equations 6 and 7 we have:

′

max

≤ 2(n

′

− d) − e

′

< 2d

Such that e ∈ {0,...,k

′

− 2} is the maximum inte-

ger that satisﬁes



′

−d

′



̸≡ 0 (mod 2

′

−1−e

′

). In the

worst-case scenario, our algorithm allows us to delete

only one column and one row for each instance where

condition 6 is not met. Assume that the produced

code is minimal after i iterations, which means that

′

= (n −i) and k

′

= (k − i) resulting in the following:

2(n − i − d) − e

′

< 2d

2n − 2i − 4d − e

′

< 0

n − 2d −

′

< i

Because 0 < r < p, the dimension of the minimal code

produced must be at least two. As a result, the small-

est integer i that solves the preceding equation is the

maximum number of iterations.

Deﬁnition 8. A [n,k, d]-binary simplex code is a

linear code characterized by the following proper-

ties (Helleseth et al., 2004):

• The minimum distance d = 2

k−1

, where k is the

dimension the code.

• The code length n = 2

− 1 = 2d − 1.

• All of its nonzero codewords have Hamming

weights equal to d.

Proposition 3. By recursively puncturing a Reed-

Muller (RM) code’s generator matrix using the pro-

posed algorithm based on the Ashikhmin-Barg in-

equality, the resulting MICODE is equivalent to a bi-

nary simplex code.

Proposition 4. Any Reed-Muller code of minimum

distance d generates a MICODE of length n

′

= 2d −1

and dimension k

′

= log

(d) + 1.

Proof. Given a Reed-Muller code of minimum dis-

tance d, the minimal code generated by our algo-

rithm is equivalent to a simplex code. Since the min-

imum distance is preserved in the generated minimal

code, and the length and dimension of a simplex code

are determined by its minimum distance d, it fol-

lows that any RM code with minimum distance d,

irrespective of its original length and dimension, pro-

duces a minimal code with parameters n

′

= 2d −1 and

′

= log

(d) + 1 under our construction.

Table 2 displays the minimal code parameters de-

rived from a set of Reed-Muller codes, as well as the

number of iterations I required to move from C to C

′

The importance of the minimum distance of a code

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

386

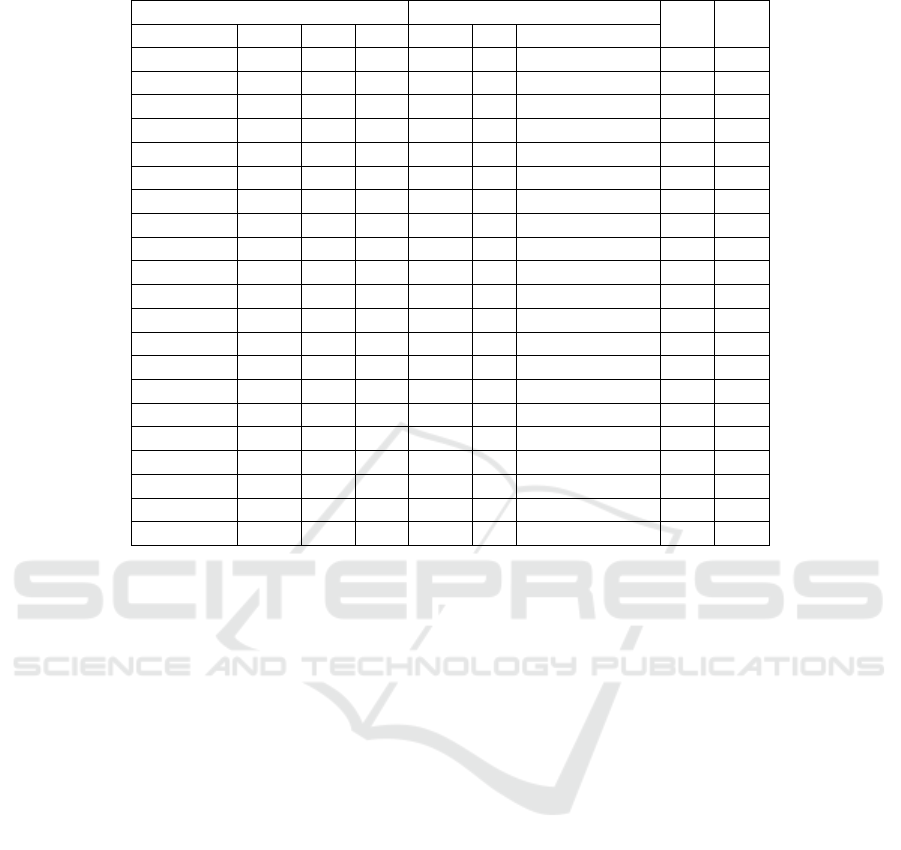
Table 2: The generated minimal code from the original Reed-Muller code.

The original Reed-Muller code The generated minimal code

I I

max

RM(m,r) n k d n

′

RM(3,1) 8 4 4 7 3 4 1 1

RM(3,2) 8 7 2 3 2 2 5 5

RM(4,1) 16 5 8 15 4 8 1 1

RM(4,2) 16 11 4 7 3 4 8 9

RM(5,1) 32 6 16 31 5 16 1 1

RM(5,2) 32 16 8 15 4 8 12 14

RM(5,3) 32 26 4 7 3 4 23 24

RM(5,4) 32 31 2 3 2 2 29 29

RM(6,1) 64 7 32 63 6 32 1 1

RM(6,2) 64 22 16 31 5 16 17 20

RM(6,3) 64 42 8 15 4 8 38 40

RM(7,1) 128 8 64 127 7 64 1 1

RM(7,2) 128 29 32 63 6 32 23 27

RM(7,3) 128 64 16 31 5 16 59 62

RM(7,4) 128 99 8 15 4 8 95 97

RM(8,2) 256 37 64 127 7 64 30 35

RM(8,3) 256 93 32 63 6 32 87 91

RM(8,6) 256 247 4 7 3 4 244 245

RM(10,2) 1024 56 256 511 9 256 47 54

RM(10,3) 1024 176 128 255 8 128 168 174

RM(11,2) 2048 67 512 1023 10 512 57 65

is widely recognized in the context of error correc-

tion and detection. A large minimum distance en-

hances the error-correcting capability of a code. How-

ever, the minimal codes derived in our work tend to

have a large minimum distance at the expense of a re-

duced code rate. This trade-off makes such minimal

codes less practical for real-time communication sys-

tems, where achieving a balance between error perfor-

mance and code rate is crucial. While our MICODE

may have limited practicality for real-time communi-

cation due to its poor code rate, offers a large mini-

mum distance, making it ideal for cryptographic ap-

plications, such as Massey’s secret sharing (Massey,

1993; Massey, 1995). We will show how MICODE

can enhance the security of such schemes.

4 PROPOSED MASSEY SCHEME

BASED ON MICODE

This section describes Massey’s secret sharing

scheme (Massey, 1993; Massey, 1995). We deﬁne the

minimal access structure of the secret sharing based

on the dual of the generated MICODE and the num-

ber of authorized minimal access sets.

4.1 Massey’s Secret Sharing

Consider P = {p

,..., p

n−1

} to be a set of n − 1 par-

ticipants, Γ ⊆ 2

to be the collection of all access

sets known as the access structure and Γ

⊂ Γ to

be the collection of all minimal access sets known

as the minimal access structure. The Massey’s se-

cret sharing works as follows: Let C be an [n,k]

lin-

ear code over F

and G = [g

,..., g

n−1

] its generator

matrix. Let s ∈ F

be the secret and m ∈ F

be the

message vector that satisﬁes s = mg

. In the secret

sharing based on C the dealer computes s = mG =

(s,s

,..., s

n−1

), and then each participant p

receives

the share s

, i = {1, ...,n − 1}.

A group of participants {p

, p

,..., p

} can re-

cover s if and only if g

is a linear combination of

,..., g

}, 0 < i

< ... < i

≤ n − 1, i.e. there

exists a codeword c

′

= (1, 0,..,c

′

,..., 0,...,c

′

,..., 0) ∈

⊥

provided c

′

̸= 0 for at least one j. If there exists

such a codeword, then the secret s can be computed

as follows (Ding and Yuan, 2003):

• Determine x = (x

,..., x

) by solving

∑

j=1

= g

. (11)

MICODE: A Minimal Code Design for Secret Sharing Scheme

387

• Then compute

s =

∑

j=1

. (12)

Theorem 2. Let C be a binary RM(p, r) code and C

′

the [n

′

,d] MICODE generated from C. There are

′

−1

minimal access sets in the SSS based on C

′

⊥

Proof. Assume G

′

is the generator matrix of the gen-

erated binary [n

′

,d] minimal code, and each row of

′

has one in the ﬁrst coordinate; there are 2

′

min-

imal codewords. According to (Massey, 1993) each

minimal codeword whose ﬁrst coordinate equal to one

is a minimal access set; thus, each information vector

m with an odd number of non-zero coordinates pro-

duces a minimal codeword with the ﬁrst coordinate

equal to one. Thus, there are 2

′

−1

minimal code-

words with the ﬁrst coordinate equal to one from all

possible 2

′

information vectors, implying 2

′

−1

min-

imal access sets.

Deﬁnition 9 (Dictatorial participant). Let P =

,..., p

n−1

} be a set of n − 1 participants. A par-

ticipant p

,0 < i < n is called dictatorial if it serves

in every minimal access set (Ding and Yuan, 2003).

Theorem 3. Let G = [g

,..., g

n−1

] be a generator ma-

trix of a [n,k]

minimal code, and P = {p

,..., p

n−1

}

is the set of participants. If g

,0 < i < n is a multiple

of g

, then the participant p

is dictatorial. Otherwise,

if g

is not a multiple of g

, the participant must be in

(q − 1)q

k−2

out of the q

k−1

possible minimal access

sets (Ding and Yuan, 2003).

Remark 1. In our proposal, the target code is a bi-

nary Reed-Muller C, and the generated minimal code

′

is also binary, which means that all the columns

of C

′

are distinct and no column is a multiple of the

other, implying that no dictatorial participant exists.

It is worth noting that each participant p

∈ P,0 < i <

n appears in 2

k−2

out of the 2

k−1

possible minimal ac-

cess sets.

Example 4. Suppose the generator matrix G

the [7, 3,4]-minimal code C

′

. In the SSS based on

′

⊥

, from the set of shares {s

,..., s

}, the 4 pos-

sible minimal access sets are: {1,2,3}, {1, 4,5},

{2,4, 6},{3,5,6}

Example 5. Table 3 shows the minimal access sets

corresponding to some of the generated MICODEs.

5 ANALYSIS AND EVALUATION

The security of Massey secret sharing based on a code

C depends signiﬁcantly on the minimum distance of

⊥

. A. Renvall and C. Ding have demonstrated the

following theorem in their publisher paper (Renvall

and Ding, 1996).

Theorem 4. If G is a generator matrix of a [n,k]

linear code over F

, then any coalition of d

⊥

− 2 or

fewer participants cannot determine the secret in the

secret sharing scheme based on C for Massey con-

struction, and there is at least a group of d

⊥

− 1 par-

ticipants that can recover the secret, where d

⊥

is the

minimum distance of the dual code of C.

Thus, the access structure and security of the

Massey secret sharing scheme are entirely dependent

on the structure of the dual code C

⊥

. As a result, the

access structure in our proposal is deﬁned by the gen-

erated [n

′

,d]-MICODE. For meaningful security, it

should consider the minimum distance d of the gen-

erated minimal code. An attacker should be unable to

reconstruct the secret if they possess fewer than d − 1

shares. Nevertheless, there is a scenario where the

attacker can ﬁnd a speciﬁc set of d − 1 shares that re-

veals the secret. By ﬁnding a solution x = (x

,..., x

)

that satisﬁes the equation 11 where w

(x) = d −1, the

attacker can successfully determine the secret through

d−1

possible guesses. As a result, a code with a

high minimum distance is preferable for secret shar-

ing because it ensures that the secret is secure even

if some of the shares are compromised. This asser-

tion strengthens the superiority of our proposed mini-

mal code over certain existing works, like the one pre-

sented in (Ding et al., 2018). For example, in (Ding

et al., 2018), the authors introduced a minimal code

with length 63 and minimum distance 14. In contrast,

our proposed minimal code achieves a minimum dis-

tance of 32 with the same code length. Table 4 pro-

vides a comparative analysis between our proposed

minimal code and the one presented in (Ding et al.,

2018) for various code lengths.

Proposition 5. In the SSS based on the dual of our

MICODE, all the minimal access sets have the same

size.

Proof. All nonzero codewords of a simplex code have

the same Hamming weight. Since our MICODE

is equivalent to a simplex code, it follows that in

the secret sharing scheme based on the dual of our

MICODE, all minimal access sets have the same

size.

5.1 Comparison of Our Secret Sharing

Scheme with Shamir’s Scheme

This section compares our secret sharing scheme with

Shamir’s Secret Sharing (Shamir, 1979), emphasiz-

ing key advantages. Although Shamir’s scheme is

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

388

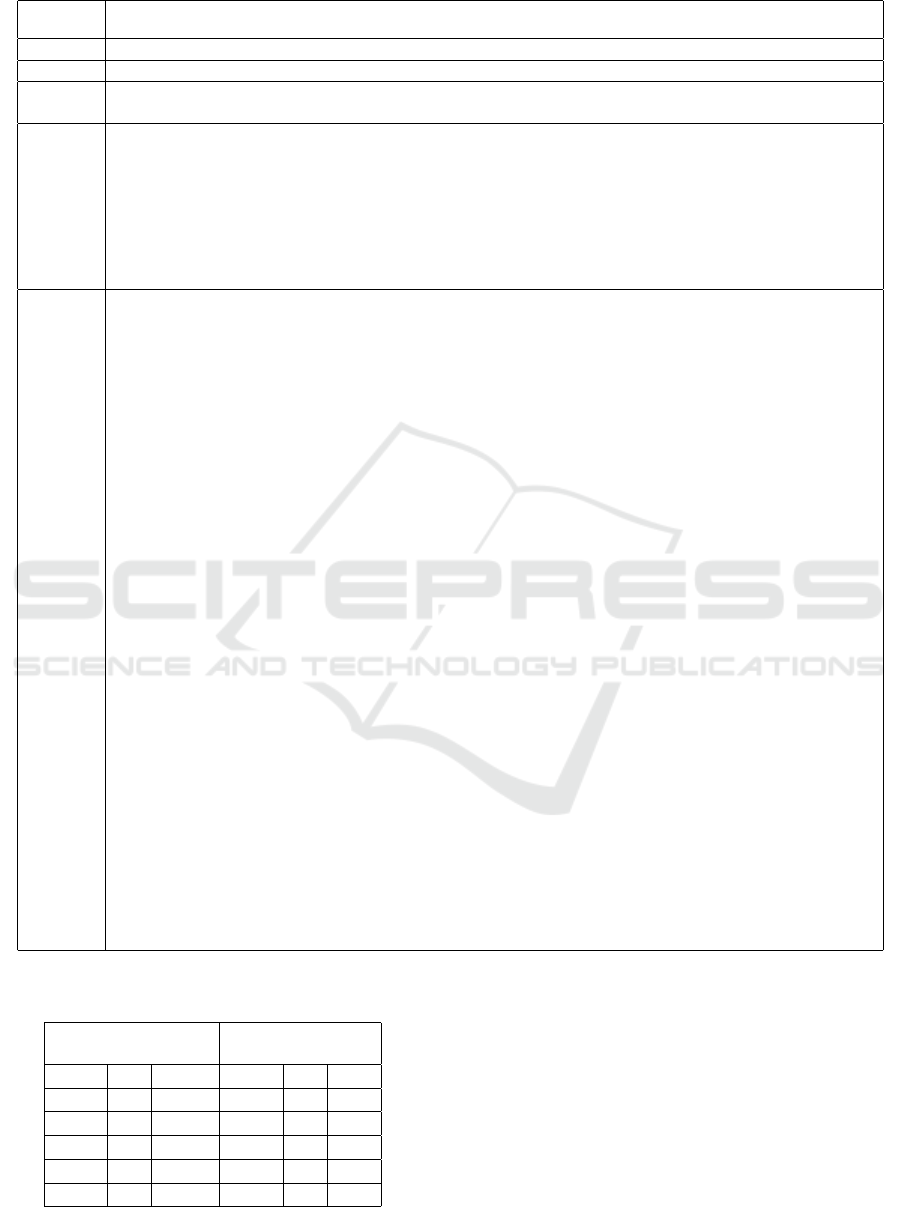
Table 3: The minimal access sets corresponding to some of the generated MICODEs.

MICODE

′

,d]

Minimal Access Sets

[3,2,2] {2}, {1}

[7,3,4] {2,4,6}, {1,4,5}, {1,2, 3}, {3,5,6}

[15,4,8] {2,4,6,8,10,12,14}, {1,4, 5,8,9, 12,13}, {1, 2,3,8, 9,10,11}, {3, 5,6,8, 11,13,14}, {1,2, 3,4,5, 6,7},

{3,4,7,9,10,13, 14}, {2,5,7, 9,11,12, 14}, {1,6,7, 10,11,12, 13}

[31,5,16] {2,4,6, 8,10,12, 14,16,18, 20,22,24, 26,28,30}, {1,4,5,8,9,12, 13,16,17, 20,21,24, 25,28,29},

{1,2,3,8,9,10, 11,16,17, 18,19,24, 25,26,27}, {3,5, 6,8,11,13,14,16,19,21,22,24, 27,29,30},

{1,2,3,4,5,6, 7,16,17, 18,19,20, 21,22,23}, {3,4,7, 9,10,13, 14,16,19, 20,23,25, 26,29,30},

{2,5,7,9,11,12, 14,16,18, 21,23,25, 27,28,30}, {1,6,7,10,11,12, 13,16,17, 22,23,26, 27,28,29},

{1,2,3,4,5,6, 7,8,9, 10,11,12, 13,14,15}, {3,4,7,8,11,12, 15,17,18, 21,22,25, 26,29,30},

{2,5,7,8,10,13, 15,17,19, 20,22,25, 27,28,30}, {1,6, 7,8,9,14,15,18,19,20,21,26, 27,28,29},

{2,4,6,9,11,13, 15,17,19, 21,23,24, 26,28,30}, {1,4,5,10,11,14, 15,18,19, 22,23,24, 25,28,29},

{1,2,3,12,13,14, 15,20,21, 22,23,24, 25,26,27}, {3, 5,6,9, 10,12,15, 17,18,20, 23,24,27, 29,30}

[63,6,32] {2,4,6, 8,10,12, 14,16,18, 20,22,24, 26,28,30, 32,34,36, 38,40,42, 44,46,48, 50,52,54, 56,58,60, 62},

{1,4,5,8,9,12, 13,16,17, 20,21,24, 25,28,29, 32,33,36, 37,40,41, 44,45,48, 49,52,53, 56,57,60, 61},

{1,2,3,8,9,10, 11,16,17, 18,19,24, 25,26,27, 32,33,34, 35,40,41, 42,43,48, 49,50,51, 56,57,58, 59},

{3,5,6,8,11,13, 14,16,19, 21,22,24, 27,29,30, 32,35,37, 38,40,43, 45,46,48, 51,53,54, 56,59,61, 62},

{1,2,3,4,5,6, 7,16,17, 18,19,20, 21,22,23, 32,33,34, 35,36,37, 38,39,48, 49,50,51, 52,53,54, 55},

{3,4,7,9,10,13, 14,16,19, 20,23,25, 26,29,30, 32,35,36, 39,41,42, 45,46,48, 51,52,55, 57,58,61, 62},

{2,5,7,9,11,12, 14,16,18, 21,23,25, 27,28,30, 32,34,37, 39,41,43, 44,46,48, 50,53,55, 57,59,60, 62},

{1,6,7,10,11,12, 13,16,17, 22,23,26, 27,28,29, 32,33,38, 39,42,43, 44,45,48, 49,54,55, 58,59,60, 61},

{1,2,3,4,5,6, 7,8,9, 10,11,12, 13,14,15, 32,33,34, 35,36,37, 38,39,40, 41,42,43, 44,45,46, 47},

{3,4,7,8,11,12, 15,17,18, 21,22,25, 26,29,30, 32,35,36, 39,40,43, 44,47,49, 50,53,54, 57,58,61, 62},

{2,5,7,8,10,13, 15,17,19, 20,22,25, 27,28,30, 32,34,37, 39,40,42, 45,47,49, 51,52,54, 57,59,60, 62},

{1,6,7,8,9,14, 15,18,19, 20,21,26, 27,28,29, 32,33,38, 39,40,41, 46,47,50, 51,52,53, 58,59,60, 61},

{2,4,6,9,11,13, 15,17,19, 21,23,24, 26,28,30, 32,34,36, 38,41,43, 45,47,49, 51,53,55, 56,58,60, 62},

{1,4,5,10,11,14, 15,18,19, 22,23,24, 25,28,29, 32,33,36, 37,42,43, 46,47,50, 51,54,55, 56,57,60, 61},

{1,2,3,12,13,14, 15,20,21, 22,23,24, 25,26,27, 32,33,34, 35,44,45, 46,47,52, 53,54,55, 56,57,58, 59},

{3,5,6,9,10,12, 15,17,18, 20,23,24, 27,29,30, 32,35,37, 38,41,42, 44,47,49, 50,52,55, 56,59,61, 62},

{1,2,3,4,5,6, 7,8,9, 10,11,12, 13,14,15, 16,17,18, 19,20,21, 22,23,24, 25,26,27, 28,29,30, 31},

{3,4,7,8,11,12, 15,16,19, 20,23,24, 27,28,31, 33,34,37, 38,41,42, 45,46,49, 50,53,54, 57,58,61, 62},

{2,5,7,8,10,13, 15,16,18, 21,23,24, 26,29,31, 33,35,36, 38,41,43, 44,46,49, 51,52,54, 57,59,60, 62},

{1,6,7,8,9,14, 15,16,17, 22,23,24, 25,30,31, 34,35,36, 37,42,43, 44,45,50, 51,52,53, 58,59,60, 61},

{2,4,6,9,11,13, 15,16,18, 20,22,25, 27,29,31, 33,35,37, 39,40,42, 44,46,49, 51,53,55, 56,58,60, 62},

{1,4,5,10,11,14, 15,16,17, 20,21,26, 27,30,31, 34,35,38, 39,40,41, 44,45,50, 51,54,55, 56,57,60, 61},

{1,2,3,12,13,14, 15,16,17, 18,19,28, 29,30,31, 36,37,38, 39,40,41, 42,43,52, 53,54,55, 56,57,58, 59},

{3,5,6,9,10,12, 15,16,19, 21,22,25, 26,28,31, 33,34,36, 39,40,43, 45,46,49, 50,52,55, 56,59,61, 62},

{2,4,6,8,10,12, 14,17,19, 21,23,25, 27,29,31, 33,35,37, 39,41,43, 45,47,48, 50,52,54, 56,58,60, 62},

{1,4,5,8,9,12, 13,18,19, 22,23,26, 27,30,31, 34,35,38, 39,42,43, 46,47,48, 49,52,53, 56,57,60, 61},

{1,2,3,8,9,10, 11,20,21, 22,23,28, 29,30,31, 36,37,38, 39,44,45, 46,47,48, 49,50,51, 56,57,58, 59},

{3,5,6,8,11,13, 14,17,18, 20,23,25, 26,28,31, 33,34,36, 39,41,42, 44,47,48, 51,53,54, 56,59,61, 62},

{1,2,3,4,5,6, 7,24,25, 26,27,28, 29,30,31, 40,41,42, 43,44,45, 46,47,48, 49,50,51, 52,53,54, 55},

{3,4,7,9,10,13, 14,17,18, 21,22,24, 27,28,31, 33,34,37, 38,40,43, 44,47,48, 51,52,55, 57,58,61, 62},

{2,5,7,9,11,12, 14,17,19, 20,22,24, 26,29,31, 33,35,36, 38,40,42, 45,47,48, 50,53,55, 57,59,60, 62},

{1,6,7,10,11,12, 13,18,19, 20,21,24, 25,30,31, 34,35,36, 37,40,41, 46,47,48, 49,54,55, 58,59,60, 61}

Table 4: Our MICODE vs. the minimal code presented

in (Ding et al., 2018).

The minimal code

(Ding et al., 2018)

Our MICODE

n k d n k d

63 7 14 63 6 32

127 8 52 127 7 64

255 9 60 255 8 128

511 10 224 511 9 256

1023 11 248 1023 10 512

commonly used for threshold-based secret sharing, it

lacks ﬂexibility in access structure design and does

not inherently provide enhanced security for appli-

cations requiring strict security and customizable ac-

cess policies. Furthermore, Shamir’s scheme requires

that the ﬁeld F

be larger than the number of shares

n. Consequently, each share must be represented us-

ing at least log

(n) bits, resulting in inefﬁciencies in

both communication and storage. Table 5 provides a

detailed comparison, highlighting key differences be-

tween the two schemes.

MICODE: A Minimal Code Design for Secret Sharing Scheme

389

Table 5: Our Secret Sharing vs. Shamir’s Secret Sharing (Shamir, 1979).

Scheme Our scheme Shamir’s scheme

Mathematical Basis Linear algebra and coding theory Polynomial interpolation over ﬁnite ﬁeld

Access Structure Flexible (based on [n,k, d] MICODE) Fixed threshold k (any k or more shares)

Share Size (Bits) 1 O(log n)

Secret Reconstruc-

tion

Requires exactly d − 1 out of n − 1 shares

(only those in the minimal access set)

Requires at least k out of n shares

Resilience to Share

Compromise

More resilient (secret remains secure un-

less speciﬁc shares are compromised)

Less resilient (secret can be reconstructed

if any k shares are compromised)

6 CONCLUSIONS

The main goals of this paper are to generate a min-

imal code from a Reed-Muller code with good and

ﬂexible parameters and then to derive a secret sharing

scheme from the generated minimal code. There are

some existing works to determine the minimal code-

words, i.e. (solving the covering problem), in a spe-

ciﬁc class of codes, such as the Reed-Muller code.

However, in the case of Reed-Muller code, this has

only been solved for the second-order binary Reed-

Muller code, and the problem for general code, in-

cluding Reed-Muller code, remains difﬁcult. In con-

trast, we have used the Ashikhmin-Barg inequality

to efﬁciently construct a minimal code (called MI-

CODE) from the Reed-Muller code while preserving

the minimum distance. While our MICODE exhibits

a reduced code rate, it offers substantial advantages

for cryptographic applications, particularly in secret

sharing schemes like Massey’s secret sharing, where

the emphasis is on enhancing security through a large

minimum distance, rather than optimizing for high-

rate communication.

This work opens up new possibilities for enhanc-

ing the security of SSS protocols by using codes with

large minimum distances. Future work could focus on

further improving the construction techniques to opti-

mize the code rate while maintaining a high minimum

distance. Additionally, exploring the application of

these minimal codes in other cryptographic contexts,

such as secure multiparty computation, would offer

valuable insights into their broader applicability.

ACKNOWLEDGEMENT

This work was supported by the European Commis-

sion under the Horizon Europe Programme, as part of

the project LAZARUS (https://lazarus-he.eu/) (Grant

Agreement no. 101070303). The content of this ar-

ticle does not reﬂect the ofﬁcial opinion of the Euro-

pean Union. Responsibility for the information and

views expressed therein lies entirely with the authors.

REFERENCES

Abbe, E., Shpilka, A., and Ye, M. (2020). Reed–muller

codes: Theory and algorithms. IEEE Transactions on

Information Theory, 67(6):3251–3277.

Agrell, E. (1996). Voronoi regions for binary linear block

codes. IEEE Transactions on Information Theory,

42(1):310–316.

Agrell, E. (1998). On the voronoi neighbor ratio for binary

linear block codes. IEEE Transactions on Information

Theory, 44(7):3064–3072.

Ashikhmin, A. and Barg, A. (1998). Minimal vectors in lin-

ear codes. IEEE Transactions on Information Theory,

44(5):2010–2017.

Ball, S. and Blokhuis, A. (2013). A bound for the maximum

weight of a linear code. SIAM Journal on Discrete

Mathematics, 27(1):575–583.

Blakley, G. R. (1979). Safeguarding cryptographic keys.

In Managing requirements knowledge, international

workshop on, pages 313–313. IEEE Computer Soci-

ety.

Chang, S. and Hyun, J. Y. (2018). Linear codes from sim-

plicial complexes. Designs, Codes and Cryptography,

86:2167–2181.

Ding, C., Heng, Z., and Zhou, Z. (2018). Minimal binary

linear codes. IEEE Transactions on Information The-

ory, 64(10):6536–6545.

Ding, C., Kohel, D. R., and Ling, S. (2000). Secret-sharing

with a class of ternary codes. Theoretical Computer

Science, 246(1-2):285–298.

Ding, C. and Salomaa, A. (2006). Secret sharing schemes

with nice access structures. Fundamenta Informati-

cae, 73(1-2):51–63.

Ding, C. and Yuan, J. (2003). Covering and secret sharing

with linear codes. In International Conference on Dis-

crete Mathematics and Theoretical Computer Science,

pages 11–25. Springer.

Helleseth, T., Klove, T., and Levenshtein, V. I. (2004). The

simplex codes and other even-weight binary linear

codes for error correction. IEEE transactions on in-

formation theory, 50(11):2818–2823.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

390

Li, Z., Xue, T., and Lai, H. (2010). Secret sharing

schemes from binary linear codes. Information Sci-

ences, 180(22):4412–4419.

Massey, J. L. (1993). Minimal codewords and secret shar-

ing. In Proceedings of the 6th joint Swedish-Russian

international workshop on information theory, pages

276–279.

Massey, J. L. (1995). Some applications of coding theory in

cryptography. Codes and Ciphers: Cryptography and

Coding IV, pages 33–47.

McEliece, R. J. and Sarwate, D. V. (1981). On sharing se-

crets and reed-solomon codes. Communications of the

ACM, 24(9):583–584.

Renvall, A. and Ding, C. (1996). The access structure

of some secret-sharing schemes. In Information Se-

curity and Privacy: First Australasian Conference,

ACISP’96 Wollongong, NSW, Australia, June 24–26,

1996 Proceedings 1, pages 67–78. Springer.

Schillewaert, J., Storme, L., and Thas, J. A. (2010). Mini-

mal codewords in reed–muller codes. Designs, Codes

and Cryptography, 54:273–286.

Shamir, A. (1979). How to share a secret. Communications

of the ACM, 22(11):612–613.

Song, Y. and Li, Z. (2012). Secret sharing with a

class of minimal linear codes. arXiv preprint

arXiv:1202.4058.

Xu, G. and Qu, L. (2019). Three classes of minimal linear

codes over the ﬁnite ﬁelds of odd characteristic. IEEE

Transactions on Information Theory, 65(11):7067–

7078.

Yuan, J. and Ding, C. (2005). Secret sharing schemes from

three classes of linear codes. IEEE transactions on

information theory, 52(1):206–212.

MICODE: A Minimal Code Design for Secret Sharing Scheme

391