Requirements Cube: Towards a Matrix-Based Model of Requirements
Benjamin Aziz
1 a
, Gareth Hewlett
2
, Ukamaka Oragwu
1 b
, Peter Richards
3
, Safa Tharib
1 c
and Erica Yang
3
1
School of Creative and Digital Industries, Buckinghamshire New University, High Wycombe, U.K.
2
Flying River Ltd., London, U.K.
3
Chilton Computing, Oxfordshire, U.K.
fl
Keywords:
Healthcare, Matrix Theory, Requirements Engineering, Scenarios, User Stories.
Abstract:
In critical and robust systems, requirements modeling and analysis is an essential step, called requirements en-
gineering, in the process of system development, which stems from the non-ambiguous identification of end-
users and stakeholders needs and goals. Despite the wide application of requirements engineering methodolo-
gies, such as KAOS, i
⋆
/Tropos, often this step is marred by either the lack of robustness or the lack of usability
on part of the analysts. In this paper, we present a 3-dimensional model of requirements, called the Require-
ments Cube, that is clear, usable and can be manipulated using general matrix algebra. Our model stands
on the three main components of requirements; goals, resources and infrastructure, and does not present any
complex concepts that may render it unusable. We consider the semantics of the Cube in three different value
domains: 2- and 3-valued logic values and probabilistic values. Finally, we demonstrate how this model can
be applied to healthcare monitoring scenarios.
1 INTRODUCTION
Despite the widespread use and adoption of require-
ments engineering methodologies and techniques for
the gathering and analysis of stakeholder and end-
user requirements, there is still a notable gap in the
use of mathematical modeling of such requirements
(Yang et al., 2014), except with discrete mathematics-
based and logic-based methods (better known as for-
mal modeling). Even so, such formal modeling is not
so popular in real-world projects, due to the complex-
ity and the steep learning curve associated with for-
mal methods-based approaches (Bruel et al., 2021).
We believe that addressing this integration barrier is
essential for advancing the field of requirements en-
gineering and enhancing the quality of software sys-
tems and services, in general.
In some critical fields, e.g. healthcare monitoring
and care at home for the vulnerable, the application
of requirements engineering, gathering and analysis
is pivotal for developing effective and user-centered
a
https://orcid.org/0000-0001-5089-2025
b
https://orcid.org/0009-0008-5213-9967
c
https://orcid.org/0000-0002-0088-3363
solutions. This process ensures that healthcare tech-
nologies are tailored to meet the specific needs of
vulnerable (e.g. elderly, disabled) users, thereby en-
hancing the safety, well-being and overall quality of
life for such users (McGee-Lennon, 2008). More-
over, involving end-users in the requirements gath-
ering phase ensures that the developed solutions are
user-friendly and address actual challenges to those
users. For example, recent research (Tajudeen et al.,
2022) has demonstrated that understanding require-
ments from users’ perspective is crucial for creating
senior-friendly mobile health applications that have
increased engagement and lead to better health.
In this paper, we introduce a new mathematical
approach, the Requirements Cube, for the capturing
and modeling of stakeholder requirements
1
and user
needs, which is based on matrix theory. We consider
that the three most fundamental components that un-
derlie the ability to express requirements in any sce-
nario are goals (requirements), resources and infras-
1
We shall use the terms “goal” and “requirement” in-
terchangeably, even though in requirements engineering lit-
erature (Van Lamsweerde and Letier, 2002), there is often
a distinction between the two, in that a requirement is re-
garded as a refinement of a (high-level) goal.
238
Aziz, B., Hewlett, G., Oragwu, U., Richards, P., Tharib, S. and Yang, E.
Requirements Cube: Towards a Matrix-Based Model of Requirements.
DOI: 10.5220/0013514600003964
In Proceedings of the 20th International Conference on Software Technologies (ICSOFT 2025), pages 238-245
ISBN: 978-989-758-757-3; ISSN: 2184-2833
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

tructure. Without any of these three components, ones
is unable to express fully the requirements of a sce-
nario and how those requirements can be met. There-
fore, we introduce a 3-dimensional model that cap-
tures these components. We demonstrate how the
model is used to express requirements in a case of
a healthcare monitoring scenario inspired from the
ADA project (ADA Project, 2025).
The paper is organised as follows. In Section 2,
we discuss some related works. In Section 3, we de-
fine the concept of scenarios and their use to extract
end-user goals. In Section 4, we present our model,
the Requirements Cube, and discuss the concept of
a requirements cube, as a three-dimensional matrix
that captures end-user goals, required resources and
required infrastructure to fulfill those goals. We also
consider three cases of how the values of the matrix
cells are defined and calculated. In Section 5, we
show how a requirements cube can be validated, and
whether a specific validation satisfies a predefined fit-
ness function. Finally, in Section 6, we conclude the
paper and discuss directions for future work.
2 RELATED WORK
Requirements engineering is a crucial phase in the
software development process that focuses on iden-
tifying, analysing, documenting and maintaining sys-
tem requirements (Pohl, 2010; Sommerville, 2011).
Various approaches to the gathering and analysis of
requirements have been developed to address the
challenges of capturing stakeholders’ needs and en-
suring system functionality aligns with business ob-
jectives. These include scenario-based requirements
engineering, goal-oriented requirements engineering,
viewpoint-based requirements engineering, model-
driven requirements engineering and others.
Scenario-based approaches use real-world scenar-
ios to capture and analyse requirements (Rolland
et al., 1998). Such scenarios would provide concrete
descriptions of system interactions in order to un-
derstand user needs, system behavior and edge cases
(Potts et al., 1994). Notable scenario-based method-
ologies include use case modeling in UML-based
software engineering (Cockburn, 2001), as well as
event-driven scenario analysis, which aids in defining
system responses to external stimuli (Sutcliffe, 2003).
The goal-oriented approach to requirements engi-
neering emphasises more the capturing of stakehold-
ers’ objectives and refining these to operational sys-
tem requirements (Van Lamsweerde, 2001) . The
framework provides a structured methodology for
decomposing high-level goals into sub-goals and
constraints, ensuring alignment between stakeholder
needs and system capabilities (Dardenne et al., 1993).
Popular goal-oriented methodologies include KAOS
(Dardenne et al., 1993), i
⋆
(Yu, 1997) and Tropos
(Giorgini et al., 2005).
Viewpoint-based requirements engineering ac-
knowledges the diverse perspectives of stakeholders
involved in systems development (Kotonya and Som-
merville, 1998). This approach structures require-
ments based on different viewpoints, allowing con-
flicting interests to be identified and resolved system-
atically. The VORD (Viewpoint-Oriented Require-
ments Definition) method (Sommerville et al., 1998)
is a well-known viewpoint-based approach that cat-
egorises viewpoints into direct users, indirect users,
and regulatory authorities. By integrating multiple
perspectives, this approach enhances completeness
and reduces inconsistencies in requirements.
In more recent years, the use of AI-driven tech-
niques has been deployed to many of the require-
ments engineering activities both in industry and in-
novation. For example, the authors in (Nadeem et al.,
2022) used AI techniques to compare requirements
gathering and requirement management tools for IoT-
Enabled Sustainable Cities. The research compared
various techniques for requirements gathering like,
context diagrams, functional decomposition, AS-IS
activity models, TO-BE activity models, user stories
and mind maps. Their conclusion was that no single
tool is universally optimal as each has its strengths
and weaknesses depending on the projects needs.
Within the healthcare sector, requirements engi-
neering and analysis has also been suggested as a ma-
jor phase when developing new systems. For exam-
ple, the authors in (McGregor et al., 2008) introduce
a structured approach to gathering requirements in
health information systems using the patient journey
modeling approach, or PaJMa models. Using a case
study for a local mental health centre, they showed
that the PaJMa model improved on requirements de-
tail of traditional methods by including details like
non-functional requirements and enhanced staff en-
gagement. This approach, increased interest and ac-
ceptance of changes in hospital information systems.
In (Avelino et al., 2014), the authors emphasise the
critical role of requirements gathering in customising
health information systems for small-scale healthcare
facilities. Using a university health service as their
case study, they showed that through a detailed un-
derstanding of the facility’s processes and user needs,
the system can be tailored to match the existing man-
ual workflows, ensuring high usability.
Requirements Cube: Towards a Matrix-Based Model of Requirements
239

3 SCENARIOS, USER STORIES
A scenario is a detailed description of what happens
in reality in regards to the problem at hand. In
our case, a scenario will describe the health care
process, environment and context. One of the current
popular forms of scenarios are user stories, which
are essentially user-centric scenarios usually of
short lengths. User stories are concise, narrative
descriptions of how users interact with a system,
focusing on their needs and goals. Written from
the perspective of the end user, these stories help
ensure that development efforts are aligned with user
expectations and requirements. They typically follow
a simple format:
“As a [type of user], I want [some goal/requirement]
for [some reason].”
This approach promotes user-centric design and facil-
itates iterative development, allowing teams to deliver
value incrementally and address real-world problems
effectively (Kannan et al., 2019; Turner et al., 2013).
Figure 1 below describes the story of a hypotheti-
cal elderly person (user), named Jane, with healthcare
requirements described as a story. In this case, we
have followed a free-text approach to the story, rather
than structured (controlled) text.
Table 1: A free-text example of a user story.
Jane is an old lady who is suffering from arthri-
tis, and rather frail. As an elderly person, Jane
wants to receive immediate assistance if she falls
down so that she can feel safe and secure at
home (including care homes). In addition to
that, Jane requires that her environment temper-
ature be maintained at 20
◦
C. In order to fulfill
the first goal, a special wearable device is needed
that alerts carers or family members when a fall
is detected. For the second goal, a heating de-
vice, e.g. a continuously functioning boiler or
electric heater, is required at her home.
From a visual analysis of the story’s text, one can
derive two sample goals for Jane:
G1: Jane needs help if she falls
G2: Jane’s environment temperature must be
maintained at 20
◦
C
For the case of G1, the resource required is a wear-
able device, which detects movement (or lack of) and
also has a big red panic button to summon help. At
the same time, the infrastructure needed to support
this resource is a radio communication network (e.g.
WiFi, 5G, 4G, 3G etc.) and a source of electricity
supply to work the radio network and recharge the
device’s battery. On the other hand, for G2, we find
that the resource needed is a central heating system
(consisting of a boiler, radiators, thermostat etc.) or
some electric heating device (e.g. underfloor heat-
ing, electric radiators, heat pumps etc.). At the same
time, the infrastructure needed to support this is either
a gas/electricity supply
2
or an electricity-only supply.
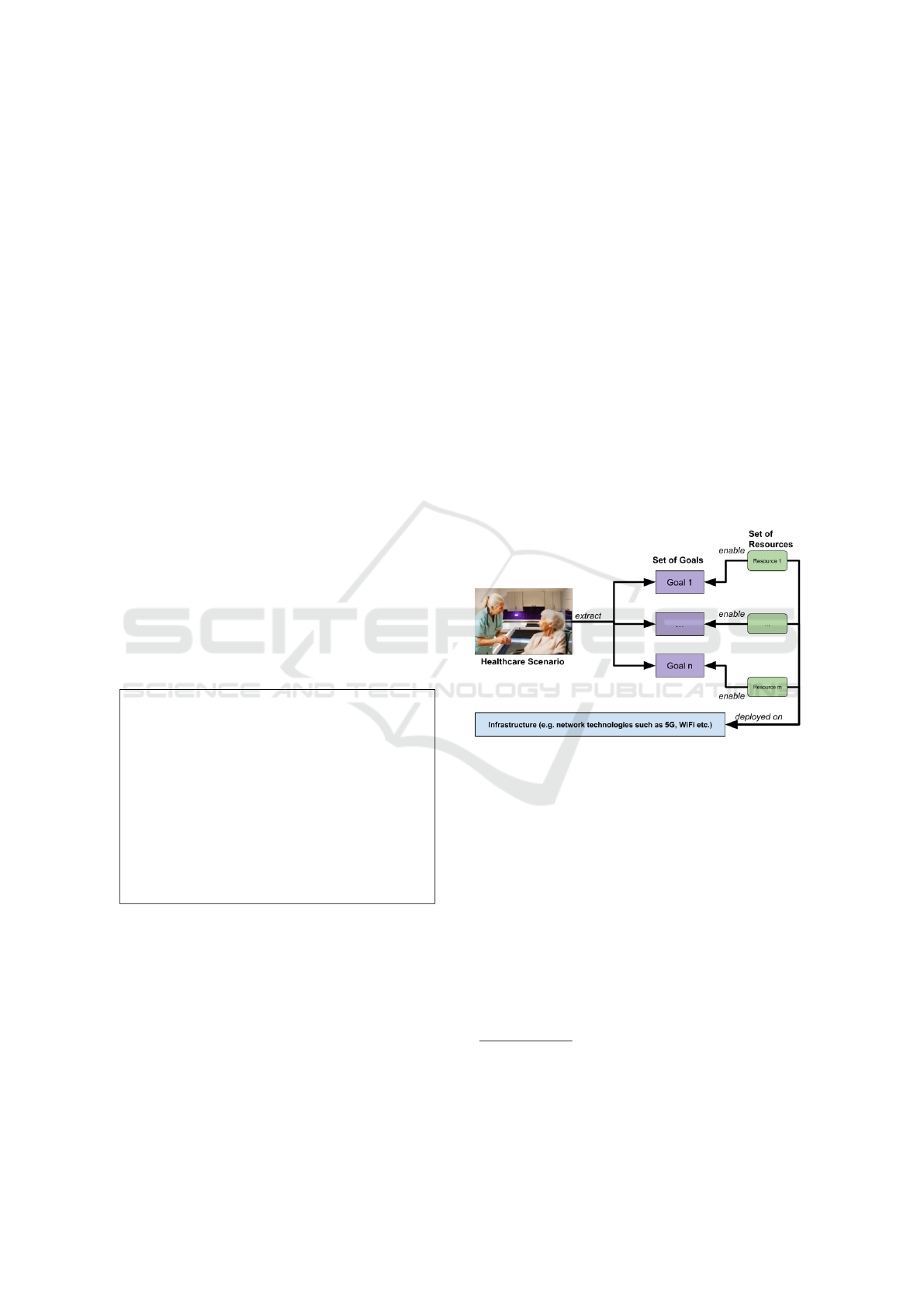
Once the set of goals underlying a user story or
scenario has been defined and formulated, we can
then define another set, which is the “set of resources”
that will provision those goals and enable them to be
achieved or maintained. For example, for the goal
of maintaining a constant room temperature for the
person requiring healthcare, it is necessary to have
a temperature-monitoring sensor and some kind of a
temperature control unit. These last two are defined
as resources that enable our temperature goal. Fi-
nally, such resources are deployed on top of “infras-
tructure”, for example, 5G, WiFi etc. Figure illus-
trates the model 1.
Figure 1: Resources deployment on infrastructure.
4 THE THEORETICAL MODEL
We start our model by identifying three non-
intersecting universal sets:
• G = {g
1
, g
2
, . . .}: the set of all possible goals de-
rived from a scenario, as we discussed in the pre-
vious section
• R = {r
1
, r
2
, . . .}: the set of all possible resources,
for example any hardware such as various sensors,
wearable devices etc., which play a role in the en-
abling of the goals derived from some scenario
2
Strictly speaking, a gas-based central heating sys-
tem also requires an electricity supply, in order to oper-
ate the pumps, thermostats etc. We shall refer to this set-
up as “gas/electricity” supply, to differentiate it from an
electricity-only heating system.
ICSOFT 2025 - 20th International Conference on Software Technologies
240

• I = {i
1
, i
2
, . . .}: the set of all possible infras-
tructure elements, for example energy and com-
munication infrastructure such as gas, electricity,
5G/4G/WiFi etc., which in turn, enable the func-
tioning of the resources required by the goals
4.1 Requirements Cube
A requirements cube is the following mathematical
structure, which expresses the relationship between
goals, resources and infrastructures.
Definition 1 (Requirements Cube). Define a require-
ments cube, A, as a 3-dimensional matrix structure,
A : G × R × I, with elements (g, r, i) ∈ A such that a
resource r ∈ R and an infrastructure element i ∈ I en-
able the fulfillment of a goal g ∈ G.
In other words, there is an association among el-
ements g, r and i in each cell of a requirements cube.
As we explain later in the following sections, the
value of the cell will determine the nature of this as-
sociation. As a matter of analogy, we can imagine the
requirements cube above as a loaf of Battenberg cake
(as in Figure 2), where each slice of the loaf represents
a 2-dimensional matrix corresponding to the specific
goal, g, at which the slice was taken. This analogy
brings us to the definition of a requirements slice.
Figure 2: The Battenberg Cake of Requirements.
Definition 2 (Requirements Slice). For a specific
goal, g, define a requirements slice, A
g
, as a 2-
dimensional matrix, A
g
: R × I, with elements (r, i) ∈
A
g
such that a resource r ∈ R and an infrastructure
element i ∈ I enable the fulfillment of the specific goal
g ∈ G, at which the slice is taken.
Therefore, a requirements cube is the stacking of
several requirements slices together, such that the re-
sulting cube represents the total number of require-
ments (goals) identified in the context of a specific
scenario. In this 2-dimensional matrix (i.e. slice), the
values of cells at the intersection of each row and col-
umn are calculated based on the specific values of the
intersecting rows and columns. We shall next expand
on cell values and what that means.
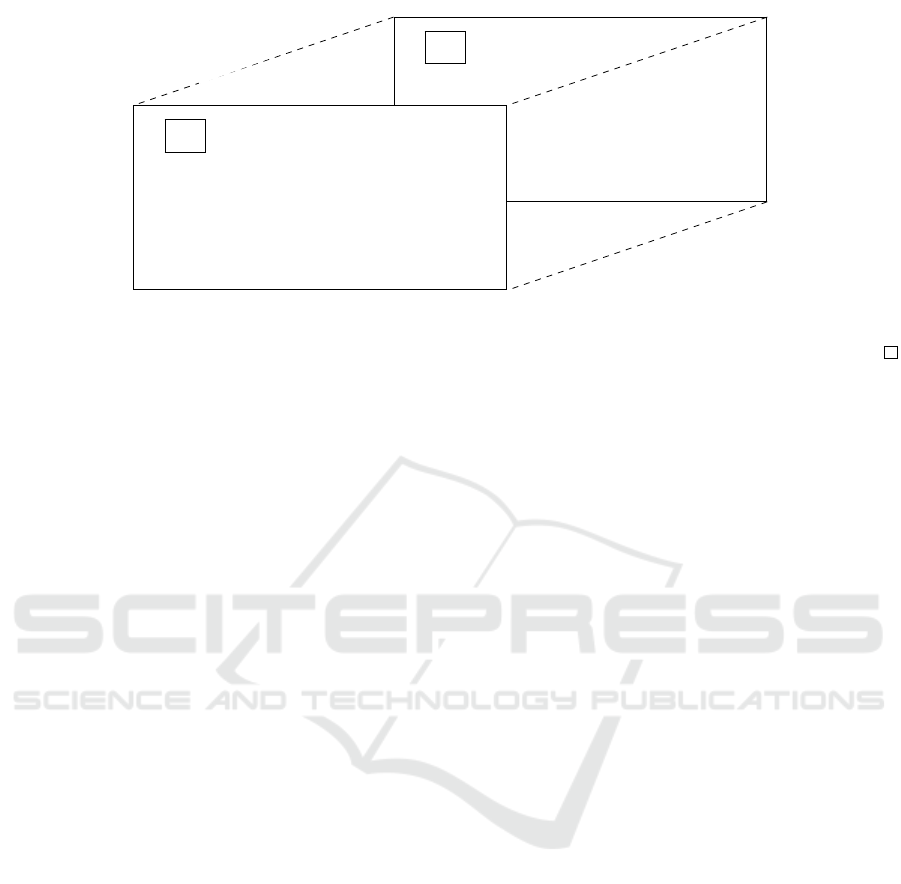
Figure 3 illustrates a generic k-size requirements
cube, which stacks together k number of require-
ments, each requirement slice is defined as an m × n
matrix, with m number of infrastructure elements, and
n number of resources. We assume that a cube repre-
sents the requirements of a single stakeholder or end-
user in whatever scenario is being considered.
4.2 2-valued Logic
In our first case, we assume a model based on 2-
valued (i.e. Boolean) logic, the value of a cell in a
2-dimensional slice matrix (i.e. the intersection of a
row representing a resource and a column represent-
ing some infrastructure) denotes the availability re-
quirement of the resource and infrastructure elements.
We assume that the availability value for a
resource or an infrastructure element is defined using
the following operation:
ν : (R ∪ I) → B
Informally, when ν(r) = T or ν(i) = T for some re-
source r and infrastructure i, then that means that r
and i are required to be available, in whatever goal
slice they fall within. This is different from the actual
availability at the environment itself, e.g that there is
currently a telephone device available in the patient’s
apartment (we discuss this difference later in Section
5). On the other hand, if ν(r) = F or ν(i) = F, then
this means that either of these two elements is not re-
quired to be available, for the current goal to succeed.
The value of a cell in a slice belonging to some
goal g, is then calculated as the logical conjunction
of the values of ν(r) and ν(i). More formally,
A
g
(r, i) = ν(r) ∧ ν(i)
Mathematically, this would become a cell in the ac-
tual cube by attaching to it the name of a specific goal:
A(g, r, i) = (g, ν(r) ∧ ν(i))
Informally, when A
g
(r, i) = T, this means that the goal
for which this slice of the loaf belongs requires both r
Requirements Cube: Towards a Matrix-Based Model of Requirements
241

A
g1
r
11
. . .
r
1n
i
11
.
.
.
i
1m
A
gk
r
k1
. . .
r
kn
i
k1
.
.
.
i
km
k Requirements
Figure 3: A generic k-size requirements cube.
and i to be available. But, if A
g
(r, i) = F, then the goal
does not depend on the combination of the specific
resource and infrastructure.
Example 1. for g
2
(from Section 3) that states that
“Room temperature must be maintained at 20
◦
C”,
and that r = Central Heating, i
1
= Gas/Electricity
and i
2
= WiFi, where ν(r) = T, ν(i
1
) = T and
ν(i
2
) = F, then we have the following matrix:
A
g
2
=






Central Heating . . . Falls Alarm
Gas/ T F
Elect.
.
.
.
WiFi F F






Since ν(r) ∧ ν(i
1
) = T but ν(r) ∧ ν(i
2
) = F. Infor-
mally, to maintain room temperature at 20
◦
C, we
need the combination of a central heating system (re-
source) and a gas/electricity (infrastructure) to be
both available. But the combination of a central heat-
ing system and WiFi (different infrastructure) would
not be useful for such goal regardless of their avail-
ability. Similarly, the combination of a falls alarm
device and either infrastructure element is false since
this device is not required for this specific goal.
On the other hand, consider the goal g
1
, which
states that “the person must be wearing a WiFi-
connected falls alarm device”, then the matrix for
this goal is the following:
A
g
1
=






Central Heating . . . Falls Alarm
Gas/ F F
Elect.
.
.
.
WiFi F T






where the falls alarm device now is required, in ad-
dition to the requirement for a WiFi connectivity el-
ement (e.g. an enabled access point). However, for
this goal, neither the central heating resource nor the
gas/electricity system are required. The full cube for
the above two matrices is as shown in Figure 4.
4.3 3-valued Logic
In the second model, we assume a 3-valued logic,
where the possible values are {T, F, ⊥}, and which
include the two Boolean values and an undefined el-
ement, ⊥. The latter expresses situations where the
availability requirement on a resource or an infras-
tructure is simply undefined or unknown. In other
words, we do not know if the resource of infrastruc-
ture are required for a specific goal. Such 3-valued
logic is useful in expressing incomplete requirements,
where certain values are left undefined in the case of
intermediate versions of the requirements cube, but
that later become fully defined in the final version.
We define undefined case as follows:
T ∧ ⊥ = ⊥, F ∧ ⊥ = F
For example, if at the stage of specifying the require-
ments, we are unable to determine the type of the falls
alarm’s connectivity (i.e. whether it operates over 5G,
4G, WiFi etc.), then it becomes unknown whether
WiFi is really required. Hence, ν(WiFi) = ⊥, and the
2-dimensional matrix for g
1
becomes as follows:
A
g
2
=






Central Heating . . . Falls Alarm
Gas/ F F
Elect.
.
.
.
WiFi F ⊥






This means that we are unable to confirm whether a
WiFi access point will be required or not at the pa-
tient’s or vulnerable person’s premise, therefore, this
requirement remains incomplete at this stage, until
further clarification is made on the type of the alarm.
ICSOFT 2025 - 20th International Conference on Software Technologies
242

A
g2
Central Heating
. . .
Falls Alarm
Gas/Electricity
T F
.
.
.
WiFi
F F
A
g1
Central Heating
. . .
Falls Alarm
Gas/Electricity
F F
.
.
.
WiFi
F T
Figure 4: Example of a requirements cube.
4.4 Probabilistic Availabilities
The third model we consider here is that of proba-
bilistic availability values instead of binary ones. For
this we assume a new definition of the ν operation,
which we call ν
P
:
ν
P
: (R × I) → [0, 1]
Unlike ν, ν
P
returns a value between 0 and 1, where 0
denotes the case where the requirement states that the
probability of a resource or infrastructure element, x,
being available need only be 0% (i.e. that the ele-
ment is not required to be available. This is similar to
saying ν(x) = F). On the other hand, a value of 1 de-
notes that the probability is 100%, or in other words,
that the element must be available as a requirement
(or that ν(x) = T).
Informally, ν
P
represents the minimum probabilis-
tic expectation of the availability of some resource
or infrastructure at the environment being considered.
For example, we may state that the WiFi coverage is
expected to be at least 0.8, which means that 80% of
time the WiFi signal must be available in some loca-
tion, or that the WiFi signal may be available in at
least 8 out of 10 locations at any point in time (the se-
mantics of this percentage maybe further refined con-
sidering various different scenarios). Similarly, it is
not uncommon for energy providers to advertise en-
ergy supply availability ratios usually the 6 9s golden
standard, i.e. 99.9999%, which allows only 31.5 sec-
onds of downtime per year. Again, this would express
the availability requirement (as a probability) needed
by various devices perhaps stemming from the nature
of equipment in those devices or the criticality of their
role in the business context.
Based on this probabilistic model, the value of a
cell can now be defined as follows:
A
g
(r, i) = ν
P
(r).ν
P
(i)
and this again can be transformed into a cube cell
value by including the name of the goal:
A(g, r, i) = (g, ν
P
(r).ν
P
(i))
Example 2. Let’s consider the same scenario
as discussed in Example 1, except this time, we
assign probabilistic values to the availability ex-
pectation for all the resources and infrastructure
elements. For example, ν
P
(Central Heating) = 0.85
and ν
P
(Gas) = 0.999999 for goal A
g
2
, whereas
ν
P
(Falls Alarm) = 0.7 and ν
P
(WiFi) = 0.9 for the
goal A
g
1
. As a result, we obtain the following two
requirement slices:
A
g
2
=






Central Heating . . . Falls Alarm
Gas/ 0.84999915 0
Elect.
.
.
.
WiFi 0 0






A
g
1
=






Central Heating . . . Falls Alarm
Gas/ 0 0
Elect.
.
.
.
WiFi 0 0.63






5 CUBE VALIDATION
A requirements cube, specified using some scenario,
can be validated in terms of the actual real-time
availability values for the resources and infrastructure
elements in some environment. This validation step
will clarify whether the requirement (slice) is being
me or not, and therefore, if we need to take further
mitigation steps to remedy the situation. Define
the following operation, which returns the actual
availability value for some resource or infrastructure,
Requirements Cube: Towards a Matrix-Based Model of Requirements
243

A
g2
Central Heating
. . .
Falls Alarm
Gas/Electricity
T F
.
.
.
WiFi
F F
A
g1
Central Heating
. . .
Falls Alarm
Gas/Electricity
F F
.
.
.
WiFi
F F
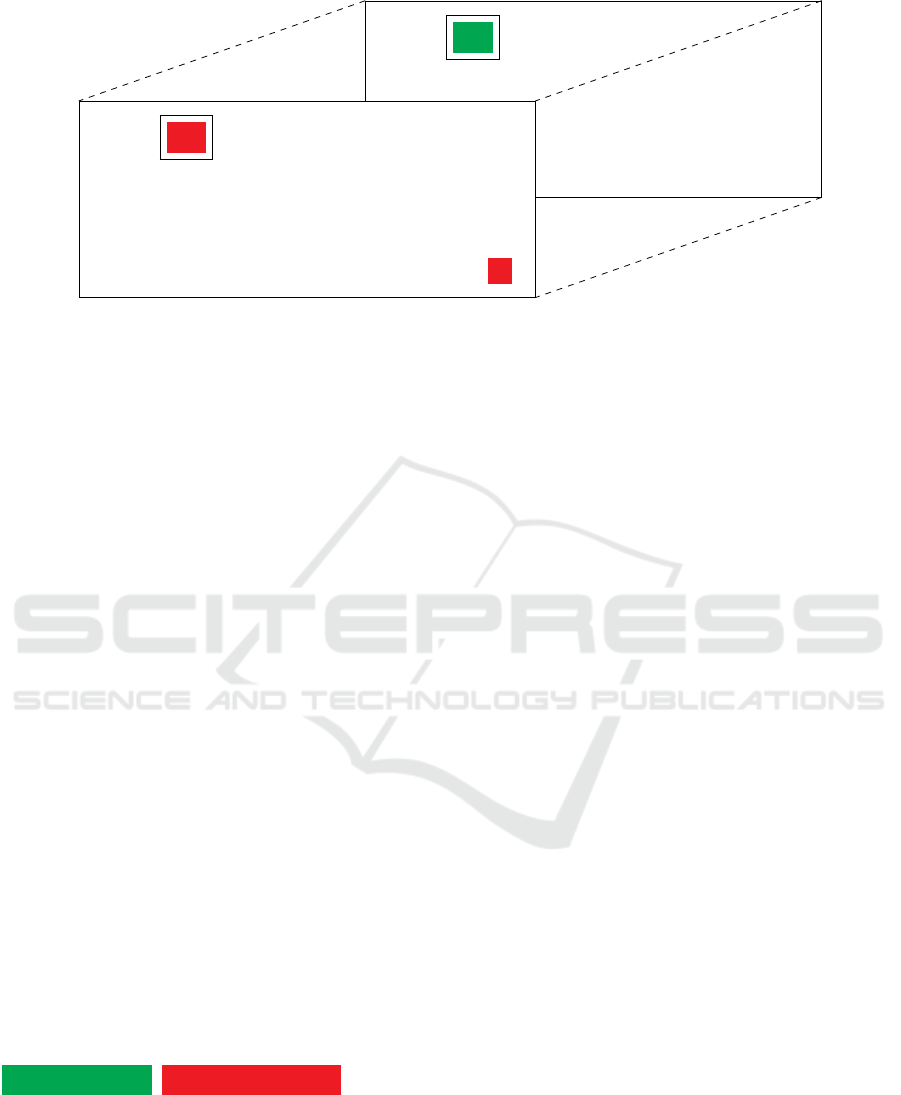
Figure 5: An example of a validated requirements cube.
at a certain point in time:
η : (R ∪ I) → B
Note that η is different from ν in that the latter ex-
presses the availability requirement whereas the for-
mer expresses the actual availability value.
Based on the above, we define a 2-valued fitness
function as one that compares the specified avail-
ability to the actual availability values, within the
2-valued logic we discussed in Section 4.2:
f : B × B → N
We define f as follows:
f (x, y) =

0 if x = T and y = F
1 otherwise
where ∀e ∈ (R × I) : x = ν(e) is the expected (re-
quired) availability value for some resource or infras-
tructure element, e. On the other hand, ∀e ∈ (R × I) :
y = η(e) is the actual availability value for that el-
ement e. The fitness function will return 0 only in
the case where the expected (required) value was true
(i.e. requiring an available element), whilst the actual
value was false (i.e. element was not available). A
0 value represents an unfit requirement, whereas a 1
value represents a fit requirement.
To simplify the visual representation of the fitness
function, We adopt the following colouring scheme:
A fit requirement An unfit requirement
For example, in our scenario, if the the WiFi
connectivity is found, on a certain day/time, to
be completely down at Jane’s home, whereas the
gas/electricity supply is running as normal and both
the falls alarm and the central heating resources are
functional, then her validated requirements cube be-
comes as in Figure 5, due to the fact that the fitness
of A
g
1
is 0 (unfit). We took the liberty to also colour
the specific cell, which is causing the fitness of the re-
quirement slice to be 0. In an actual situation, such
a visual scheme will indicate to the care provider that
a certain requirement is not being met at the patient’s
premise or environment.
6 CONCLUSION
We presented in this paper the sketch of a new model
of end-user requirements based on matrix theory. We
termed this model the Requirements Cube due to its
analogy with Battenberg cake loaves. We defined a
slice in this loaf to be a single requirement, with rows
and columns representing relevant resources and in-
frastructure elements. The intersection value of each
cell defines the semantics of whether the resource and
infrastructure elements are needed for the specific re-
quirement. The stacking of multiple requirements
then defines a full loaf (cube).
It would be interesting, in the future, to explore
further the current ideas in a digital twin and the cre-
ating of training data to support the validation of this
model. In particular, we plan to apply the model to
several scenarios observed within the current project
ADA (ADA Project, 2025). Additionally, there are
several other directions of research work , which we
plan to pursue in the future. These include the idea of
applying machine learning techniques to predict when
requirements might fail (i.e. become unfit) before the
conditions for their failure occur. We will use the
data collected in project ADA (ADA Project, 2025)
as ground truth to train our classification algorithms.
It is important for evaluating care actions and risks
to consider failure scenarios. In Example 2, we as-
signed a probabilistic availability expectation on the
WiFi connectivity to be ν
P
(WiFi) = 0.9. However,
ICSOFT 2025 - 20th International Conference on Software Technologies
244

suppose that the WiFi fails, i.e. η(Wifi) = 0, at a
given instant in time. Then Jane, Susan or anyone else
connected, will suddenly have a problem with their
WiFi-dependent requirement(s) identified simultane-
ously by one or more slices of the composite cube
matrix becoming unfit (i.e. turning red). Appropriate
care actions, therefore, can follow for all persons af-
fected. This requires an adequate risk mitigation plan
and an underlying risk analysis of the damage that a
requirement’s slice turning red can cause.
ACKNOWLEDGMENTS
The research work presented in this paper was funded
by Innovate-UK grant #10098971 under project name
ADA-UK: “Remote Healthcare Monitoring powered
by Network Intelligence and Automation”.
REFERENCES
ADA Project (2025). https://www.celticnext.eu/project-
ada/. Last accessed 1 February 2025.
Avelino, J. N. M., Hebron, C. T., Laranang, A. L. E., Paje, P.
N. G., Bautista, M. M. F., and Caro, J. D. (2014). Re-
quirements gathering as an essential process in cus-
tomizing health information systems for small scale
health care facilities. In IISA 2014, The 5th Interna-
tional Conference on Information, Intelligence, Sys-
tems and Applications, pages 184–189. IEEE.
Bruel, J.-M., Ebersold, S., Galinier, F., Mazzara, M., Naum-
chev, A., and Meyer, B. (2021). The role of formal-
ism in system requirements. ACM Computing Surveys
(CSUR), 54(5):1–36.
Cockburn, A. (2001). Writing Effective Use Cases.
Addison-Wesley.
Dardenne, A., van Lamsweerde, A., and Fickas, S. (1993).
Goal-directed requirements acquisition. Science of
Computer Programming, 20:3–50.
Giorgini, P., Mylopoulos, J., and Sebastiani, R. (2005).
Goal-oriented requirements analysis and reasoning in
the tropos methodology. Engineering Applications of
Artificial Intelligence, 18(2):159–171.
Kannan, V., Basit, M. A., Bajaj, P., Carrington, A. R., Don-
ahue, I. B., Flahaven, E. L., Medford, R., Melaku, T.,
Moran, B. A., Saldana, L. E., et al. (2019). User sto-
ries as lightweight requirements for agile clinical de-
cision support development. Journal of the American
Medical Informatics Association, 26(11):1344–1354.
Kotonya, G. and Sommerville, I. (1998). Requirements En-
gineering: Processes and Techniques. Wiley.
McGee-Lennon, M. R. (2008). Requirements engineer-
ing for home care technology. In Proceedings of the
SIGCHI Conference on Human Factors in Computing
Systems, pages 1439–1442.
McGregor, C., Percival, J., Curry, J., Foster, D., Anstey,
E., and Churchill, D. (2008). A structured approach
to requirements gathering creation using pajma mod-
els. In 2008 30th annual international conference of
the IEEE engineering in medicine and biology society,
pages 1506–1509. IEEE.
Nadeem, M. A., Lee, S. U.-J., and Younus, M. U. (2022).
A comparison of recent requirements gathering and
management tools in requirements engineering for iot-
enabled sustainable cities. Sustainability, 14(4):2427.
Pohl, K. (2010). Requirements Engineering: Fundamen-
tals, Principles, and Techniques. Springer.
Potts, C., Takahashi, K., and Anton, A. I. (1994). Inquiry-
based requirements analysis. In Proceedings of the
16th International Conference on Software Engineer-
ing, pages 58–76.
Rolland, C., Souveyet, C., and Achour, C. (1998). Guid-
ing goal modeling using scenarios. In Proceedings of
the IEEE International Symposium on Requirements
Engineering, pages 53–62.
Sommerville, I. (2011). Software Engineering. Addison-
Wesley.
Sommerville, I., Sawyer, P., and Viller, S. (1998). View-
points for requirements elicitation: A practical ap-
proach. In Proceedings of the International Confer-
ence on Software Engineering (ICSE), pages 74–81.
Sutcliffe, A. (2003). Scenario-based requirements engineer-
ing. Proceedings of the IEEE International Require-
ments Engineering Conference, pages 320–329.
Tajudeen, F. P., Bahar, N., Tan, M. P., Peer Mustafa, M. B.,
Saedon, N. I., and Jesudass, J. (2022). Understanding
user requirements for a senior-friendly mobile health
application. Geriatrics, 7(5):110.
Turner, A. M., Reeder, B., and Ramey, J. (2013). Scenarios,
personas and user stories: User-centered evidence-
based design representations of communicable dis-
ease investigations. Journal of biomedical informat-
ics, 46(4):575–584.
Van Lamsweerde, A. (2001). Goal-oriented requirements
engineering: A guided tour. In Proceedings fifth ieee
international symposium on requirements engineer-
ing, pages 249–262. IEEE.
Van Lamsweerde, A. and Letier, E. (2002). From object
orientation to goal orientation: A paradigm shift for
requirements engineering. In International Workshop
on Radical Innovations of Software and Systems En-
gineering in the Future, pages 325–340. Springer.
Yang, Z., Li, Z., Jin, Z., and Chen, Y. (2014). A systematic
literature review of requirements modeling and anal-
ysis for self-adaptive systems. In Requirements En-
gineering: Foundation for Software Quality: 20th In-
ternational Working Conference, REFSQ 2014, Essen,
Germany, April 7-10, 2014. Proceedings 20, pages
55–71. Springer.
Yu, E. S. (1997). Towards modelling and reasoning support
for early-phase requirements engineering. In Proceed-
ings of the 3rd IEEE International Symposium on Re-
quirements Engineering (RE’97), pages 226–235.
Requirements Cube: Towards a Matrix-Based Model of Requirements
245