Comparison of Tree-Based Learning Methods for Fraud Detection in

Motor Insurance

David Paul Suda

, Mark Anthony Caruana

and Lorin Grima

Department of Statistics and Operations Research, Faculty of Science, University of Malta, Msida, Malta

Keywords:

Insurance Fraud Detection, Random Forests, Gradient Boosting, Data Imbalance.

Abstract:

Fraud detection in motor insurance is investigated with the implementation and comparison of various tree-

based learning methods subject to different data balancing approaches. A dataset obtained from the insurance

industry will be used. The focus is on decision trees, random forests, gradient boosting machines, light gradient

boosting machines and XGBoost. Due to the highly imbalanced nature of our dataset, synthetic minority

oversampling and cost-sensitive learning approaches will be used to address this issue. A study aimed at

comparing the two data-balancing approaches is novel in literature, and this study concludes that cost-sensitive

learning is overall superior for this application. The light gradient boosting machine using cost-sensitive

learning is the most effective method, achieving a balanced accuracy of 81% and successfully identifying 83%

of fraudulent cases. For the most successful approach, the primary insights into the most important features

are provided. The ﬁndings derived from this study provide a useful evaluation into the suitability of tree-based

learners in the ﬁeld of insurance fraud detection, and also contribute to the current development of useful tools

for correct classiﬁcation and the important features to be addressed.

1 INTRODUCTION

Motor insurance is an essential component of the

automotive industry, as it offers ﬁnancial protection

to vehicle owners against potential losses stemming

from accidents, theft, or other unexpected incidents.

As the auto insurance market continues to expand, it

inevitably attracts fraudulent activities, leading to a

surge in the number of motor insurance fraud cases

(Hashmi et al., 2018). Insurance fraud is a deceptive

practice that often carries the false perception of be-

ing a victimless crime. In reality, it adversely affects

not only the insurance industry, but all policyholders.

When insurance companies incur losses due to fraud-

ulent claims, they often have to increase premiums

to compensate for the ﬁnancial impact. This results

in higher costs for all policyholders, including those

who have never engaged in fraudulent activities.

In recent years, motor insurance fraud has become

a signiﬁcant concern, with statistics demonstrating

the growing scale of the problem. According to the

Federal Bureau of Investigation, in the United States,

insurance fraud, excluding health insurance, amounts

https://orcid.org/0000-0003-0106-7947

https://orcid.org/0000-0002-9033-1481

to approximately $40 billion per year, increasing the

average family’s insurance premium by $400 to $700

annually, (Gomes et al., 2021). This highlights the

signiﬁcant impact of motor insurance fraud on the in-

dustry and policyholders, necessitating effective fraud

detection and prevention strategies to protect honest

policyholders and create a sustainable market (Harg-

reaves and Singhania, 2015).

Traditional fraud detection methods, which relied

heavily on extensive auditing and manual investiga-

tion, have been demonstrated to be both costly and

inefﬁcient (Nian et al., 2016). As a result, insurance

companies are increasingly adopting statistical and

data analysis techniques to enhance their fraud de-

tection capabilities (Kemp, 2010). Statistical learning

theory emerged in the 1960s, but practical algorithms

developed in the 1990s (Vapnik, 2000). These ad-

vanced methods offer innovative fraud detection solu-

tions, aiding insurers in mitigating losses and protect-

ing policyholders and offer promising solutions for

fraud detection, surpassing classical statistical meth-

ods like logistic regression. (Aslam et al., 2022),

(Al-Hashedi and Magalingam, 2021)), (Phua et al.,

2004) introduced a novel fraud detection method for

skewed data, employing NN, Na

ıve Bayes (NB) and

DT algorithms on minority oversampled data. The

390

Suda, D. P., Caruana, M. A., Grima and L.

Comparison of Tree-Based Learning Methods for Fraud Detection in Motor Insurance.

DOI: 10.5220/0013513900003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 390-397

ISBN: 978-989-758-758-0; ISSN: 2184-285X

approach combines stacking and bagging to enhance

cost savings, using a ﬁxed cost matrix. Stacking-

bagging techniques achieved marginally higher cost

savings compared to other widely used techniques.

(Bhattacharyya et al., 2011) used logistic regression,

support vector machines and random forests to detect

credit card fraud .

With the advent of big data, a number of reviews

demonstrate that classiﬁcation algorithms, particu-

larly supervised techniques, have been widely utilized

in motor insurance fraud detection. The review by

(Ngai et al., 2011) has shown that while logit and pro-

bit regression models remain popular, more complex

algorithmic methods like neural networks, tree-based

methods, and Bayesian belief networks are increas-

ingly being used. This trend is further corroborated by

the more recent review from (Al-Hashedi and Maga-

lingam, 2021), which highlights the growing promi-

nence of statistical learning techniques such as ran-

dom forest, na

ıve Bayes, support vector machines,

K-Nearest Neighbour (KNN) and Gradient Boosting

Machine (GBM) learners. Furthermore, the imbal-

ance problem is well described by (He and Garcia,

2009), who identiﬁed cost-sensitive learning and syn-

thetic minority oversampling methods as viable solu-

tions.

The main aim of this study is to focus on a number

of tree-based learning classiﬁcation methods to a data

set provided by an anonymous insurance company

which contains 159045 countrywide insurance claims

of which 3199 (2.01%) are fraudulent. The original

dataset has 95 variables (including the target variable)

which include, age and gender of claimant, date and

time of accident, and province of claim and policy

holder - however information such as the provenance

of this dataset and the associated misclassiﬁcation

costs cannot be published due to identiﬁability rea-

sons and commercial sensitivity. This dataset was col-

lected between 2011 and 2015. Tree-based methods

were found to be among the most popular techniques

in fraud-detection literature due to their superior clas-

siﬁcation abilities. In this study, apart from compar-

ing the tree-based classiﬁcation approaches, the aim

is to address data imbalance via both cost-sensitive

learning approaches and synthetic minority oversam-

pling, and ﬁnally provide a comparison to identify

which tree-based learner combined with which learn-

ing approach is most promising. Which of the men-

tioned approaches for data imbalance is more success-

ful will also be postulated.

The rest of this paper is structured as follows. In

Section 2, the core concepts and characteristics of de-

cision trees are discussed, together with the tree-based

learning techniques which will be used. In Section 3,

the results are presented, where a comparative study

of the techniques and learning approaches described

is presented, and a discussion of the more prominent

features of the most successful method included. Fi-

nally, in Section 4, a discussion of the results will

ensue with concluding remarks on the study and an

overview of limitations together with some recom-

mendations for future work.

2 METHODOLOGY

Statistical learning methods bring together a range of

techniques and algorithms, all designed to learn from

input data, with the goal of emulating human learning

and making predictions. In this paper we will primar-

ily focus on supervised learning techniques and thus

we deﬁne the input space X as a set of all possible in-

stances that need to be labelled from the output space

Y . In the context of motor insurance fraud detec-

tion, the instances are claims and have to be labelled

as ’fraud’ or ’not-fraud’. Let x

( j)

= (x

( j)

, . . . , x

( j)

)

be the vector of observed entries of the input space

of the j

observation with corresponding observation

( j)

from the output space. In our case, the output

space is a binary categorical variable taking values

from {0, 1}, where 0 implies that the claim is legit-

imate, while 1 implies that the claim is fraudulent. In

supervised learning, we split the given data set in two:

the training set and the test set. In the following pages,

the training set will be dented by D = {x

( j)

, y

( j)

}

j=1

where N represents the number of claims in the train-

ing set. The performance of the models with be tested

through the use of the confusion matrix and related

metrics on the test set. A 90-10 split ratio is taken ,

given the size of the dataset, 10%still yields a sufﬁ-

ciently large test set for evaluative purposes. Correct

predictions of no fraud will be considered as true neg-

ative (TN) while correct predictions of fraud will be

considered as true positive (TP). Incorrect predictions

of no fraud and incorrect predictions of fraud will be

considered false positive (FP) and false negative (FN)

respectively.

The rest of this section will be structured as fol-

lows. In Section 2.1 will discuss the data imbalance

issue, and how we can address it through synthetic

minority oversampling and cost-sensitive learning. In

Section 2.2 will introduce decision trees - the base

learner for all techniques which will be covered in

this paper. Finally, in Section 2.3, tree-based learning

techniques such as random forests and boosted trees

will be discussed.

Comparison of Tree-Based Learning Methods for Fraud Detection in Motor Insurance

391

2.1 Addressing Data Imbalance

Data imbalance will be an issue with our dataset

due to the fact that non-fraudulent claims compose

the overwhelming majority. SMOTE-NC by (Chawla

et al., 2002) is a synthetic minority oversampling

technique that aims to address the issue of imbalanced

datasets by generating synthetic samples from the mi-

nority class. SMOTE-NC is a variant of the SMOTE

technique with modiﬁcations to account for nominal

features. However, in the context of motor insurance

fraud, a crucial aspect of the model’s performance

evaluation is to consider the costs of different mis-

classiﬁcation errors. Speciﬁcally, FNs can have sub-

stantially higher consequences than FPs. In this case,

a standard loss function, such as the 0-1 loss func-

tion, may not accurately reﬂect the true risk of the

model’s predictions. To address this, a cost-sensitive

loss function could be used to take into account the

different costs of these errors. The focus of statistical

learning, under a cost-sensitive loss function, shifts to

minimizing the total cost. Let the subsets of fraudu-

lent and legitimate training samples be denoted as D

and D

−

respectively. Adjusting the 0-1 loss function

to cater for this cost factor, results in the following

empirical risk of some classiﬁer

f :

f ) =

∑

(i)

∈D

{f (x

(i)

)̸=

f (x

(i)

)}

∑

(i)

∈D

−

{f (x

(i)

)̸=

f (x

(i)

)}

(1)

where a indicates the cost-sensitive factor (He and

Garcia, 2009). If the cost-sensitive factor a > 1, it

os apparent that a false negative outcome will result

in a higher loss. On the other hand, if a < 1, a false

positive outcome will result in a greater loss. In the

insurance fraud context, a is taken to be a ratio of the

average fraudulent claim loss to the cost of investi-

gating a claim and will be greater than 1 in our con-

text. In Section 3, we will compare the results for var-

ious tree-based learners using both the cost-sensitive

loss function and the synthetic minority oversampling

technique SMOTE-NC.

2.2 Decision Trees

The concept behind decision trees is intuitive when

dealing with a classiﬁcation problem. The algorithm

uses a tree-like framework to make predictions by di-

viding the input data into smaller subsets, each corre-

sponding to a speciﬁc class. The process of dividing

the input space can be formalised as a recursive al-

gorithm that starts with the entire input space X and

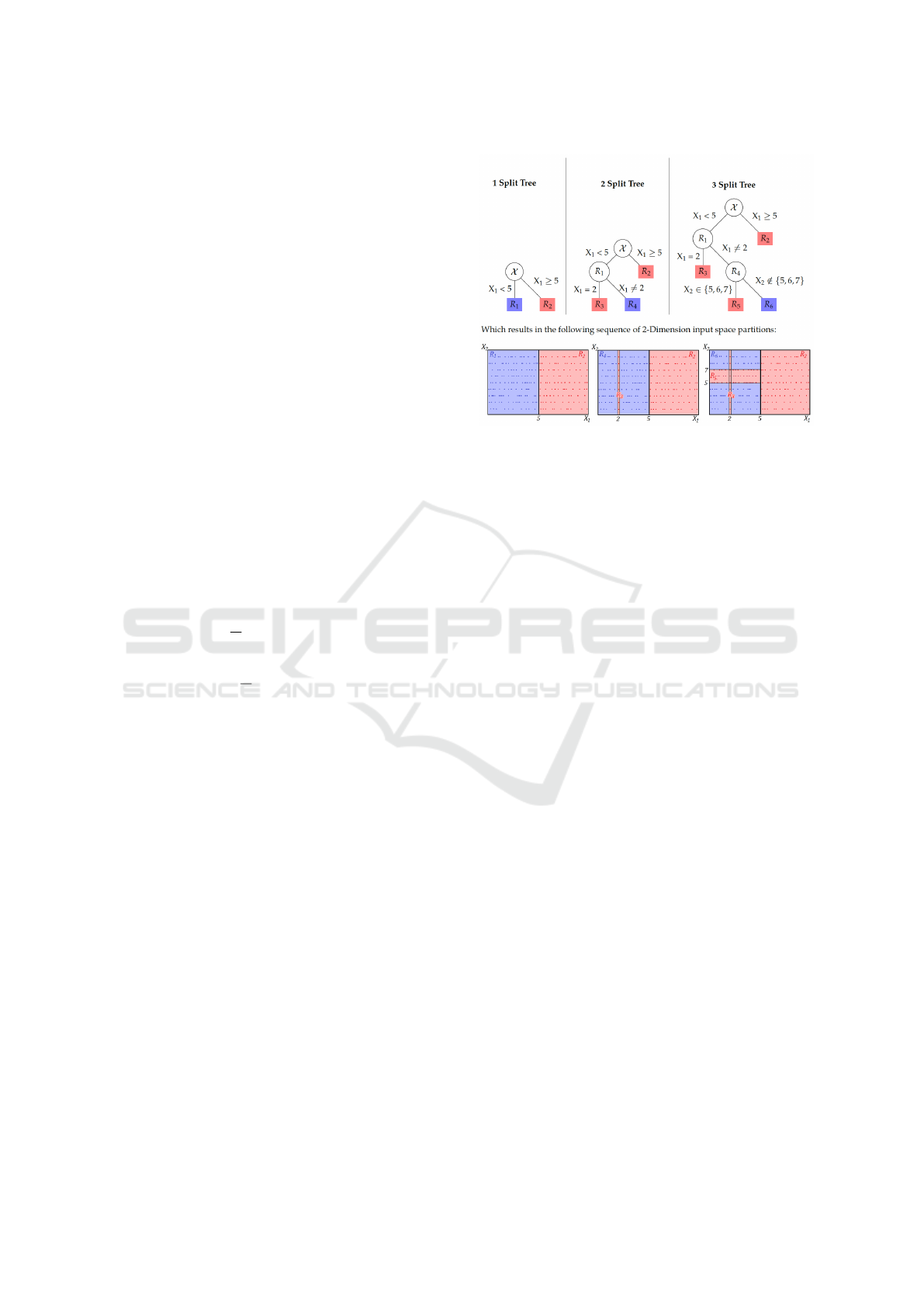
repeatedly splits it into smaller subsets. The splits in

Figure 1: Illustration of a decision tree model’s sequential

division of the input space.

the input space are based on the values of the pre-

dictors, resulting in the dataset becoming increasingly

homogeneous with each split. The ﬁnal result of this

process is a tree-like structure where each node repre-

sents a subset of the input data. The end nodes of the

tree, known as leaf nodes, are assigned a class based

on the distributions of the classes of the training cases.

This tree structure can be used to make predictions

for new data points by traversing the tree and arriv-

ing at a ﬁnal prediction based on the class assigned

to the leaf node that the data point belongs to. The

decision tree algorithm provides a visual and hence

intuitive representation of the relationships between

the predictors and the classes, making it a useful tool

for understanding and interpreting the data. Advances

in decision tree theory lead to various different algo-

rithms for constructing decision trees. In this paper

we will primarily use the CART algorithm (Breiman,

1984) to construct trees.

The algorithm is primarily divided into three parts:

selection of splits, pruning the tree and assigning the

leaf node labels. Figure 1 demonstrates the sequential

division of the input space X , using continuous pre-

dictor X

and discrete predictor X

. Each tree in the

diagram represents one partition of the input space, il-

lustrating how the model splits the data based on these

predictors. This depiction of decision trees takes a

top-down approach, starting from the root node (in-

put space) X , which is split into two nodes R

and

based on ranges of X

. Discrete variable X

then

splits the tree twice, ﬁrst splitting R

into R

and R

and then splitting R

into R

and R

. Each node rep-

resents a disjoint subset of X .

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

392

2.3 Tree-Based Learners

In this section we explore tree-based learners, which

comprise techniques that utilise multiple decision

trees to tackle a learning task. These form part of

the ensemble learning umbrella of techniques, where

the aim of ensemble learning is to construct a pre-

diction model by combining the strengths of a set of

simpler base models. This process can be divided into

two steps: creating a set of base learners and combin-

ing them to form a composite predictor. Tree-based

learners are often able to achieve stronger generalisa-

tion abilities than individual decision trees due to the

combination of multiple models. Tree-based learners

can be largely classiﬁed into two categories, depend-

ing on the approach used to generate the individual

learners:

1. Bagging and Random Forests: These meth-

ods generate individual learners independently.

Bagging (Bootstrap Aggregating) is a technique

where the same model is trained on different boot-

strapped samples of the data, and then their out-

puts are averaged to obtain a ﬁnal prediction. Ran-

dom forests is a variant of bagging that constructs

a collection of decision trees using random feature

subsets.

2. Boosting: Boosting methods generate learners

with strong correlations and create them in a se-

quence. The idea behind boosting is to sequen-

tially train models on weighted versions of the

data, where the weights are adjusted to emphasize

the instances that were misclassiﬁed by the pre-

vious models. In this study, we consider GBM,

XGBoost and LightGBM.

The main difference between these categories is

how the base learners are generated. Bagging and

random forests generate learners independently, while

boosting methods generate learners in sequence with

strong correlations. Despite this, both bagging and

boosting methods use similar techniques to combine

the multiple base learners. In Section 2.3.1 and Sec-

tion 2.3.2 we describe these two main approaches in

more detail.

2.3.1 Bagging and Random Forests

One approach to generating different base learners is

to divide the original training data into a number of

distinct subsets and use each subset to train a differ-

ent base model. To improve the quality of each base

model, it is often necessary to allow some overlap be-

tween the subsets, such that each one contains an ad-

equate number of training samples. Several random-

ization approaches have been proposed to build inde-

pendent base learners. Bootstrap aggregating, com-

monly known as bagging, is one example of a re-

sampling method for classiﬁer design as it utilizes the

bootstrap sampling method.

Given the training set D = {x

( j)

, y

( j)

}

j=1

, a boot-

strap sample would be a subset D

⊆ D of the full

learning set each created by randomly drawing N

′

≤

N instances from D with replacement. In bagging, the

ﬁnal prediction is obtained by combining the outputs

of all the base learners in the committee through an

aggregation method, such as taking their average in

case of regression or taking the mode in case of clas-

siﬁcation. Since each sample is drawn from the same

distribution, the base learners are considered to be

identically distributed. As a result, the expected value

of the average of multiple base learners is equivalent

to the expected value of a single learner. Therefore,

the bias of bagged base learners is identical to that of

individual learners. This means that bagging can only

improve performance by reducing the variance.

Bagging is known to be highly effective for low-

bias, high-variance methods like trees (Hastie et al.,

2009). Random forests, are a signiﬁcant modiﬁcation

of bagging proposed by (Breiman, 2001). They en-

hance the latter technique by building a large ensem-

ble of uncorrelated trees and ﬁnd the mode to obtain

the ﬁnal classiﬁcation. While in traditional decision

trees, the feature that is used to split a node is cho-

sen from the entire set of features, in a random forest

tree, a subset of K features is randomly selected from

the feature set at each node. This introduces a degree

of randomness, controlled by the parameter K, with

K = p resulting in the selection of features being the

same as traditional trees, and K = 1 resulting in a com-

pletely random selection. In order to achieve optimal

outcomes, it is a frequently adopted practice to use

K = log

p (Breiman, 1984) or K =

√

p (Hastie et al.,

2009). However, it should be noted that this approach

may not be universally applicable, and alternative val-

ues may be necessary in certain situations.

2.3.2 Boosting

Boosting is an ensemble technique that involves com-

bining the outputs of many weak classiﬁers in series

to create a strong committee. The key idea behind

boosting is to adjust the distribution of training sam-

ples based on the errors made by weak base learn-

ers. This adjustment of the distribution is what makes

boosting fundamentally different from other ensem-

ble methods. Boosting grows the base learners in an

adaptive way that removes bias by adjusting the distri-

bution of training samples. This approach means that

the base learners in boosting are not identically dis-

tributed (Hastie et al., 2009). By iteratively adapting

Comparison of Tree-Based Learning Methods for Fraud Detection in Motor Insurance

393

the distribution of training samples, boosting aims to

reduce both the bias and variance of the base learners.

This particular feature of boosting makes the method

especially useful for real-life application scenarios,

such as in predicting, detecting, and ultimately pre-

venting motor insurance fraud.

Boosting algorithms start by training a base

learner and adjusting the distribution (through re-

weighting) of training samples based on the base

learner’s output. Instances that were incorrectly clas-

siﬁed by the base learner are given more importance

by subsequent base learners. The following base

learner utilizes the modiﬁed training data, and this

cycle continues until a predetermined number, repre-

sented by M, of base learners are created. Finally,

this results in a sequence

(x), m = 1, 2, . . . , M of

base learners which in turn are combined to form

the ﬁnal classiﬁer

f (x). In this research a variety

of boosting algorithms were used. These include

GBMs (Hastie et al., 2009), XG Boosting (XGBoost)

(Chen and Guestrin, 2016) and Light Gradient Boost-

ing Machines (LightGBM) (Ke et al., 2017). GBMs

are learners that utilise gradient descent to minimise

the loss function. Moreover, XGBoost and Light-

GBM are both powerful Gradient Boosting frame-

works that leverage the second-order Taylor expan-

sion for approximating the objective function, opti-

mizing the performance of decision tree ensembles.

Despite their similarities, these frameworks employ

different strategies for growing trees. XGBoost grows

trees level-wise, ensuring balanced tree structures,

while LightGBM grows trees leaf-wise, prioritizing

the most signiﬁcant splits to achieve faster conver-

gence and higher accuracy. Furthermore, LightGBM

implements two algorithms to accelerate the train-

ing process: Gradient-Based One Sided Sampling

(GOSS) algorithm and Exclusive Feature Bundling

(EFB). The former selectively samples instances from

the dataset based on the absolute values of their gra-

dients, ensuring that instances with larger gradients,

which contribute more to the information gain, are in-

cluded, while the latter enables LightGBM to process

large datasets more efﬁciently. Regularization tech-

niques are crucial in preventing overﬁtting in Gradient

Boosting models. The Gradient Boosting techniques

employ the L1 and L2 regularization terms in their

loss functions. These are terms that can be added to

the loss function during training to prevent overﬁtting.

3 RESULTS

The description of the dataset under study has been

provided in Section 1. The insurance company

that provided the data did so under condition of

anonymity, hence no information regarding the coun-

try of origin of the claims as well as the name of

the company will be provided. The justiﬁcation for

the 90-10 split ratio has been given in Section 2.

Any model validation that occurs during the pre-

processing and building up to the optimal model is

performed solely on the training set. The test set is

reserved for a single use at the end with the aim of

determining the optimal model, to avoid introducing

any bias in the evaluation process.

Primarily, feature extraction was implemented.

This included extracting information from date vari-

ables, creating indicator variables for speciﬁc condi-

tions, and addressing high cardinality issues in nom-

inal variables. Furthermore, the dataset contained

missing data. A median imputation approach was im-

plemented, with the mean imputation and k-Nearest

Neighbors (KNN) imputation also attempted but not

affecting the results obtained. Feature selection was

required to improve the computational efﬁciency in

the training of the tree-based learners. To conduct

feature selection, a LightGBM model was used on

the unbalanced dataset to obtain feature importance

scores due to its speed and efﬁciency compared to

other approaches. A plot of the mean ROC AUC vs

the feature importance threshold was then obtained to

determine the ideal threshold. The Receiver Operat-

ing Characteristic curve, abbreviated as ROC curve,

is a tool for plotting the true positive rate TPR =

TP+FN

against the false positive rate FPR =

FP+TN

and AUC stands for area under the curve which quan-

tiﬁes model ability to discriminate between the two

categories.

To select the optimal subset of features, an iter-

ative process was then employed. The process be-

gan with a feature importance threshold of 0, progres-

sively increased by increments of 1, and at each step,

the model re-evaluated with the variables that met or

exceeded this threshold using 5-fold cross-validation.

Figure 2 was then used to determine a cut-off point

using the elbow method, with a threshold of 22.0 be-

ing identiﬁed. This resulted in a selection of 28 vari-

ables, as this is the threshold beyond which the mean

ROC AUC resulted in a sudden shift downwards. The

most important variables (together with their level of

importance) are shown in Figure 3 It can be seen that

the province in which the claim was made and the

province of the policy holder were the most impor-

tant features by a huge margin, but an interpretation

of feature importance values will be given later due

to the fact that SMOTE-NC or cost-sensitive learn-

ing have not yet been implemented and feature im-

portance scores can change once this is the case.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

394

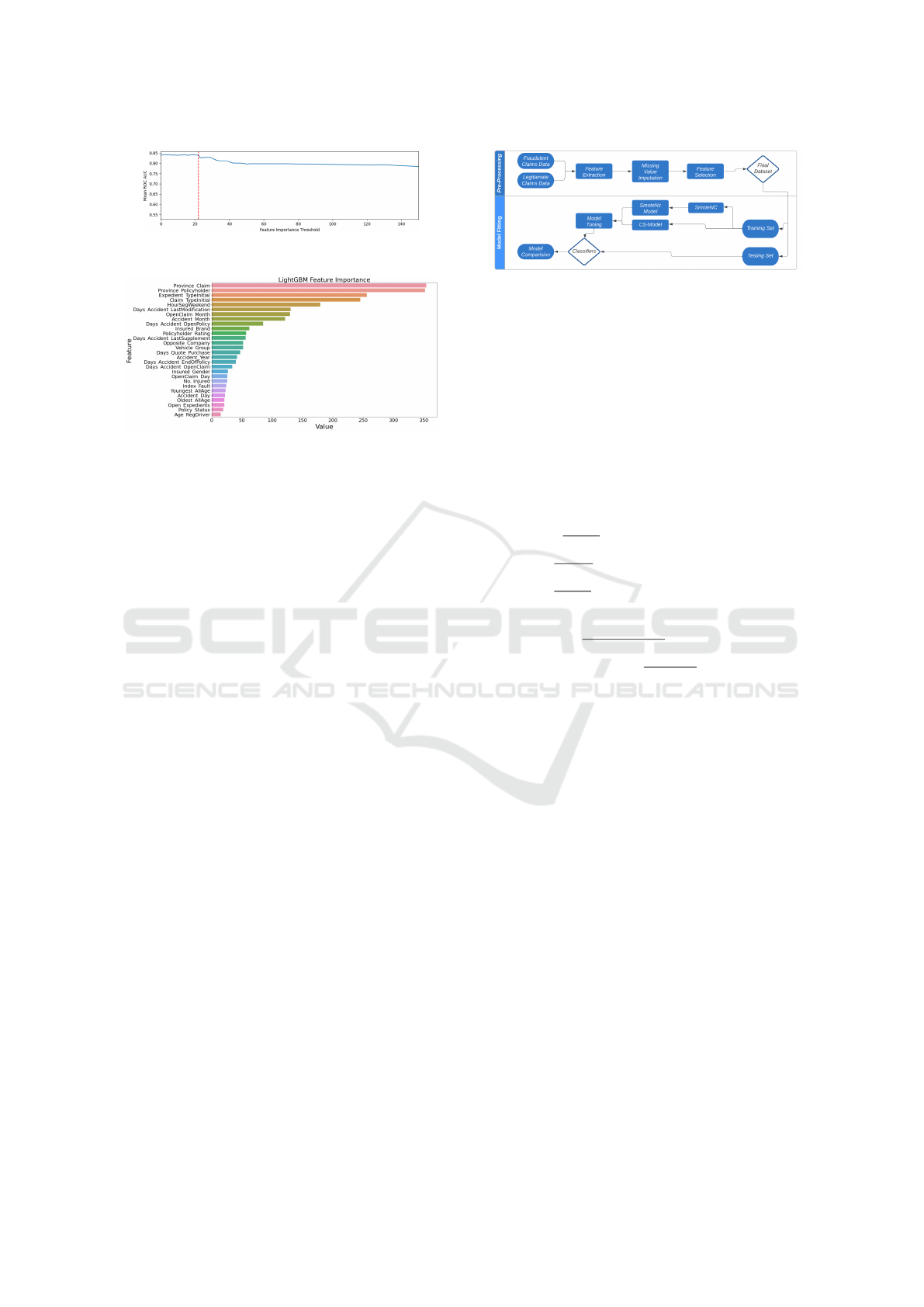
Figure 2: Mean ROC vs Feature Importance Threshold.

Figure 3: LightGBM feature importance scores of the se-

lected 28 variables.

Following feature extraction, missing data impu-

tation and feature selection, the ﬁnal dataset is cre-

ated and randomly divided into a training set and a

test set. Decision trees, random forests, GBM, Light-

GBM and CatBoost are implemented using both a

SMOTE-NC approach and cost-sensitive learning on

the training set. During the training phase, model pa-

rameter tuning also occurs via 5-fold cross-validation

on the training set. Finally, the ﬁtted models are

implemented on the test set for comparative pur-

poses. A ﬂowchart illustrating the entire model im-

plementation and evaluation process is presented in

Figure 4. The ﬁne tuned parameters for decision

trees were the maximum depth of the tree, the min-

imum number of rows to create a leaf node, and

the minimum relative improvement in impurity re-

duction for a split to happen. These were optimised

on ranges {3, 6, 9}, {3, 6, 9} and {0, 0.2, 0.4} respec-

tively. The ﬁne tuned parameters for random forests

were the proportion of rows to be randomly sam-

pled for each tree, the proportion of columns to ran-

domly select at each tree node split, and the number

of trees in the random forest model. These were op-

timised on ranges {0.5, 0.7, 0.9}, {0.5, 0.7, 0.9} and

{50, 100, 200, 500, 1000} respectively. The ﬁne tuned

parameters for the boosting methods were maximum

depth of the tree, the minimum sum of instances

weights are needed in a child node, the fraction of

data used for training each iteration and the frac-

tion of features used to build each tree during train-

ing. These were optimised on ranges {3, 5, 7, 9},

{1, 3, 5, 7}, {0.6, 0.7, 0.8, 0.9} and {0.6, 0.7, 0.8, 0.9}

respectively. Finally the L1 and L2 regularization

terms were found to progressively decrease the per-

formances when increased and were set to the default

of 0.

Figure 4: Flowchart illustrating the model implementation

and evaluation process.

In Table 1 and 2, the results obtained when ﬁt-

ting decision trees, random forests, GBM, XGBoost

and LightGBM are shown for both the SMOTE-NC

approach and the cost-sensitive learning approach.

For the SMOTE-NC approach, in Table 1 we de-

note these models by SNC-DT, SNC-RF, SNC-GBM,

SNC-XGB and SNC-LGBM. For the cost-sensitive

learning approach, in Table 2 we denote these mod-

els by CS-DT, CS-RF, CS-GBM, CS-XGB and CS-

LGBM respectively. The metrics we consider for

model evaluation are the following:

1. Recall =

TP+FN

2. NPV =

TN+FN

(negative predicted value)

3. TNR =

TN+FP

(true negative rate)

4. ROC AUC (deﬁned earlier)

5. Accuracy =

TP+TN

TP+TN+FP+FN

6. Balanced Accuracy =

TPR+TNR

In Table 1, when implementing synthetic minority

oversampling, it can be seen that random forests and

XGBoost have the best recall, with the other methods

performing poorly. Nonetheless, XGBoost also per-

forms worst in terms of accuracy and second worst

in terms of balanced accuracy. Only random forests

appear to provide consistently good metrics through-

out. In Table 2, on the other hand, when applying

cost-sensitive learning, the recall for decision trees

deteriorates while the recall for all the other meth-

ods improve throughout, as does the balanced accu-

racy (albeit only marginally for random forests). In-

deed one can see that recall is best for random forests

with LightGBM second best, while TNR, ROC AUC

and balanced accuracy are the best for LightGBM,

where random forests also yield the worst perfor-

mance for TNR. Random forests and LightGBM tie

when it comes to NPV while GBM is the best when it

comes to accuracy (with LightGBM also second best

here). Nonetheless, recall, TNR, accuracy and bal-

anced accuracy are all above 0.7 for random forests

and the boosting algorithms, while the the ROC AUC

is above 0.8 throughout. The NPV is also consistently

close to 1 or 1. Since LightGBM under cost-sensitive

Comparison of Tree-Based Learning Methods for Fraud Detection in Motor Insurance

395

Table 1: Comparison of different tree-based learners using

SMOTE-NC.

SNC-DT SNC-RF SNC-GBM SNC-XGB SNC-LGBM

Recall 0.66 0.82 0.53 0.91 0.55

NPV 0.99 1.00 0.99 0.99 0.99

TNR 0.83 0.73 0.86 0.27 0.87

ROC AUC 0.77 0.84 0.81 0.69 0.83

Accuracy 0.83 0.73 0.85 0.28 0.86

Balanced Accuracy 0.75 0.78 0.70 0.71 0.81

Table 2: Comparison of different tree-based learners using

cost-sensitive learning.

CS-DT CS-RF CS-GBM CS-XGB CS-LGBM

Recall 0.23 0.86 0.79 0.81 0.83

NPV 0.98 1.00 0.99 0.99 1.00

TNR 0.96 0.72 0.80 0.74 0.79

ROC AUC 0.84 0.85 0.86 0.83 0.87

Accuracy 0.95 0.72 0.80 0.74 0.79

Balanced Accuracy 0.6 0.79 0.79 0.77 0.81

learning is the best or second best throughout all con-

sidered metrics, this is considered to be the best model

overall when it comes to successfully detecting fraud-

ulent cases without compromising heavily TNR. Fur-

thermore, cost-sensitive learning has shown to be a

considerable improvement over SMOTE-NC for all

approaches except decision trees in increasing recall

and balanced accuracy.

To further illustrate the performance of the cost-

sensitive LightGBM model, an ROC curve and a

Precision-Recall (PR) curve are presented in Figure

5. The ROC curve demonstrates the model’s perfor-

mance on both the training and test sets, showcas-

ing how closely they align. This indicates a good

balance between complexity and performance, and

also signiﬁes the model’s generalizability to new data.

Furthermore, the PR curve indicates that to obtain a

good recall, a poor precision is unavoidable. Note

that Precision =

T P

T P+FP

which indicates that a large

percentage of false positive non-fraudulent claims

is required to have a good recall. Indeed, for the

LightGBM under cost-sensitive learning which has

achieved a recall of 0.83, the precision lies just at

0.08. This, however, is the drawback that comes with

detecting more fraudulent cases. Overall, metrics be-

tween training and tests sets were comparable, indi-

cating that overﬁtting was not an issue.

Figure 5: ROC and PR curves for the ﬁnal cost-sensitive

LightGBM model.

In Figure 6, the feature scores by order of impor-

tance for LightGBM using cost-sensitive learning are

given. It can be seen that claim type has been by

Figure 6: Feature importance scores of the selected vari-

ables for LightGBM with cost-sensitive learning.

far the most important feature in this case, superced-

ing the province in which the claim was made and

the province of the policy holder, which were origi-

nally the most important in the absence of any syn-

thetic minority oversampling or cost-sensitive learn-

ing. Through further investigation, it was found that

certain claim types such as injury claims were more

prone to fraud than others. Province-related variables

now place second and third in terms of importance.

The number of days between accident occurrence and

last insurance policy modiﬁcation was the fourth most

important feature, with shorter periods being more

likely to be associated with fraud. The variable re-

lated to claim processing (Expedient TypeInitial) was

the ﬁfth most important variable, with the MREC cat-

egory (standing for Maximum Reasonable Estimate

of Claim - related to providing a reasonable estimate

of damages rather than detailed assessment) being the

most likely associated with fraud. The sixth most im-

portant variable was the number of injured individu-

als, where there is evidence that claims with a higher

number of injured individuals were more likely to be

fraudulent.

4 DISCUSSION

In this study, it has been shown that the more complex

tree-based learners outperformed decision trees when

implementing cost-sensitive learning. These included

random forests, GBM, XGBoost and LightGBM. The

comparison with decision trees turned out to be more

of a mixed bag when applying SMOTE-NC. Nonethe-

less, the results obtained for the more complex tree-

based learners were best when implementing cost-

sensitive learning, with a stark improvement in the

poorly performing metrics related to the synthetic mi-

nority oversampling is applied. Indeed, only ran-

dom forests had an overall good performance under

SMOTE-NC, which still showed a slight improve-

ment under cost-sensitive learning, and which still

did not exceed the capabilities of LightGBM under

cost-sensitive learning. When compared to random

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

396

forests, LightGBM yielded more balanced results

and although random forests produced a marginally

higher recall, this came at the expense of a signiﬁ-

cantly increased number of FPs - a trade-off which

is deemed unfavourable, as high false positives can

lead to increased operational costs and potential cus-

tomer dissatisfaction. Hence, the LightGBM model

with cost-sensitive learning emerges as the preferred

choice due to its enhanced fraud capturing capabil-

ities and balanced performance. Furthermore, cost-

sensitive learning emerged as the superior way to ad-

dress data imbalancing on this dataset. Also, when

comparing feature importance under an imbalanced

dataset with feature importance when data imbalanc-

ing is addressed, one can see that variables related to

the claim type, claim processing and the number of

injuries became more promintent in the latter. In-

deed, injury-related claims have been found to be

more prone to fraud.

It is important to recognise the limitations of the

dataset, particularly with regard to the accuracy and

completeness of the fraud labels. As the data is

sourced from a single motor insurance company, it

is subject to the speciﬁc methods and procedures

used by that company to identify and report fraud-

ulent claims. Consequently, the dataset may not be

fully representative of the true incidence of fraudu-

lent claims within the wider motor insurance indus-

try. This could potentially impact the reliability and

generalisability of any results obtained from the data,

particularly if the sample is biased in any way towards

certain types of claims or customers. Nonetheless,

further research can be done to determine which clas-

siﬁcation techniques are useful for correctly identify-

ing fraud in a cost-effective manner, and whether cost-

sensitive learning is truly a more superior approach

to addressing data imbalance when compared to syn-

thetic minority oversampling. Furthermore, this re-

search can be further enhanced by possibly incorpo-

rating principal component analysis to reduce the di-

mensionality of the data set. This would allow us to

use information from all the features and improve pre-

dictability, however this could come at the expense of

interpretability of the features.

REFERENCES

Al-Hashedi, K. G. and Magalingam, P. (2021). Financial

fraud detection applying data mining techniques: A

comprehensive review from 418 2009 to 2019. Com-

put. Sci. Rev., 40, . 419:100–402.

Aslam, F., Hunjra, A. I., Ftiti, Z., Louhichi, W., and Shams,

T. (2022). Insurance fraud detection: Evidence from

artiﬁcial intelligence and 416 machine learning. Res.

Int. Bus. Financ., 62, . 417:101–744.

Bhattacharyya, S., Jha, S., Tharakunnel, K., and Westland,

J. C. (2011). Data mining for credit card fraud: A

comparative study. Decis. Support, 50(3):602–613.

424 Syst.,, . 425.

Breiman, L. (1984). Classiﬁcation and regression trees.

Chapman and Hall/CRC: New York, 431:18–58.

Breiman, L. (2001). Classiﬁcation and regression trees.

Mach. Learn, 45, . 434:5–32.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. J. Artif. Intell., 429 Res., 16, .

430:321–357.

Chen, T. and Guestrin, C. (2016). Xgboost: A scalable tree

boosting system. In Proceedings of the 22nd ACM

SIGKDD International 436 Conference on Knowledge

Discovery and Data Mining, San Francisco, USA, 13-

27 August 2016, pages 785–794.

Gomes, C., Jin, Z., and Yang, H. (2021). Insurance fraud

detection with unsupervised deep learning. J. Risk In-

sur., 88:591–624.

Hargreaves, C. A. and Singhania, V. (2015). Analytics for

insurance fraud detection: An empirical study. Am. J.

Mob. Syst. Appl. Serv., 1(410):3. 227–232. 411.

Hashmi, N., Shankaranarayanan, G., and Malone, T. W.

(2018). Is bigger better? a study of the effect of group

size on collective intelligence 407 in online groups.

Decis. Support Syst., 107:88–98.

Hastie, T., Tibshirani, R., and Friedman, J. H. (2009).

The elements of statistical learning: Data mining,

inference, and prediction. In 432, pages 261–288.

Springer-Verlag, New York, 2 edition.

He, H. and Garcia, E. A. (2009). Learning from imbalanced

data. IEEE Trans. Knowl. Data Eng., 21(9):1263–

1284.

Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Weidong,

M., Ye, Q., and Liu, T. Y. (2017). Lightgbm: A highly

efﬁcient gradient boosting 438 decision tree. In Pro-

ceedings of the 31st Conference of Neural Information

Processing Systems, Long Beach, USA, 4-9 December

439 2017, pages 3149–3157.

Kemp, G. (2010). Fighting public sector fraud in the 21st

century. Comput. Fraud Secur., 11, . 414:16–18.

Ngai, E. W. T., Hu, Y., Wong, Y. H., Chen, Y., and Sun, X.

(2011). The application of data mining techniques in

ﬁnancial fraud detection: A 426 classiﬁcation frame-

work and an academic review of literature. Decis.

Support Syst., 50(3):559–569.

Nian, K., Zhang, H., Tayal, A., Coleman, T., and Li, Y.

(2016). Auto insurance fraud detection using unsu-

pervised spectral ranking for anomaly. 412 J. Financ.

Data Sci., 2, . 413:58–75.

Phua, C., Alahakoon, D., and Lee, V. (2004). Minority re-

port in fraud detection: Classiﬁcation of skewed data.

ACM SIGKDD Explor., 6(420):1. pp. 50–59. 421.

Vapnik, V. (2000). The Nature of Statistical Learning The-

ory. New York, pp, Springer-Verlag, 2 edition. 1–16.

Comparison of Tree-Based Learning Methods for Fraud Detection in Motor Insurance

397