
Warm-Starting the VQE with Approximate Complex Amplitude
Encoding
Felix Truger
a
, Johanna Barzen
b
, Frank Leymann
c
and Julian Obst
d
Institute of Architecture of Application Systems, University of Stuttgart, Universit
¨
atsstraße 38, Stuttgart, Germany
Keywords:
Variational Quantum Algorithm, Eigenvalues, Warm-Start, Classical Shadows.
Abstract:
The Variational Quantum Eigensolver (VQE) is a Variational Quantum Algorithm (VQA) to determine the
ground state of quantum-mechanical systems. As a VQA, it makes use of a classical computer to optimize
parameter values for its quantum circuit. However, each iteration of the VQE requires a multitude of measure-
ments, and the optimization is subject to obstructions, such as barren plateaus, local minima, and subsequently
slow convergence. We propose a warm-starting technique, that utilizes an approximation to generate beneficial
initial parameter values for the VQE aiming to mitigate these effects. The warm-start is based on Approximate
Complex Amplitude Encoding, a VQA using fidelity estimations from classical shadows to encode complex
amplitude vectors into quantum states. Such warm-starts open the path to fruitful combinations of classical
approximation algorithms and quantum algorithms. In particular, the evaluation of our approach shows that
the warm-started VQE reaches higher quality solutions earlier than the original VQE.
1 INTRODUCTION
Quantum computers are expected to excel in tasks
directly related to the properties of quantum me-
chanical systems, e.g., in quantum chemistry and
condensed matter physics (Feynman, 1982; Preskill,
2018; Tilly et al., 2022; Peruzzo et al., 2014). The
Variational Quantum Eigensolver (VQE) is a hy-
brid quantum-classical algorithm to obtain the ground
state energy of a given Hamiltonian operator describ-
ing such a system. As a Variational Quantum Al-
gorithm (VQA), the VQE is suited for current Noisy
Intermediate-Scale Quantum (NISQ) devices with
limitations in the width and depth of executable quan-
tum circuits (Preskill, 2018; Leymann and Barzen,
2020). Therefore, the VQE makes use of param-
eterized quantum circuits executed on NISQ hard-
ware and optimization algorithms executed on clas-
sical computers. This hybrid quantum-classical ap-
proach is deemed promising in the current era, where
quantum computers are still error-prone and limited in
number of qubits. Despite the bright prospects for the
VQE, several potential obstacles remain (Tilly et al.,
2022): To evaluate the energy of a system, each opti-
a
https://orcid.org/0000-0001-6587-6431
b
https://orcid.org/0000-0001-8397-7973
c
https://orcid.org/0000-0002-9123-259X
d
https://orcid.org/0000-0002-1898-2167
mization step of the VQE requires a multitude of mea-
surements depending on the composition of the given
Hamiltonian. Moreover, the optimization landscape
may be hard to navigate due to adverse effects such
as barren plateaus and local optima, and the algorithm
may exhibit insufficient convergence properties.
Warm-starts are known for their capability to
mitigate some of these obstacles in quantum algo-
rithms (Truger et al., 2024). Warm-starting tech-
niques focus on the utilization of known or efficiently
generated results instead of starting an algorithm from
scratch, e.g., by making use of previous results or ef-
ficient approximation algorithms. Several kinds of
warm-starting techniques affect quantum algorithms
in different ways. For example, there are two major
entry points for warm-starts of VQAs: Initial states
and initial variational parameter values. On the one
hand, such warm-starts can be realized through the
encoding of prior knowledge into the initial state of
a quantum circuit (cf. Egger et al., 2021; Tate et al.,
2023). Thereby, the initial state is biased towards fa-
vorable solutions, as opposed to neutral initial states
frequently assumed in conventional quantum algo-
rithms. On the other hand, warm-starts for VQAs can
be realized by providing viable initial values for the
parameters of the quantum circuit instead of a random
parameter initialization, e.g., by transferring optimal
parameter values from related problem instances or
Truger, F., Barzen, J., Leymann, F., Obst and J.
Warm-Starting the VQE with Approximate Complex Amplitude Encoding.
DOI: 10.5220/0013513400004525
In Proceedings of the 1st International Conference on Quantum Software (IQSOFT 2025), pages 15-26
ISBN: 978-989-758-761-0
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
15

precomputing beneficial parameter initializations, (cf.
Galda et al., 2021; Mitarai et al., 2022; Sack and Ser-
byn, 2021; Shaydulin et al., 2023).
Encoding approximate eigenvectors via amplitude
encoding yields a simple biased initial state to warm-
start the VQE. However, this warm-start is imprac-
tical due to the inefficiency of the encoding and
current hardware limitations. Moreover, it imposes
certain restrictions on the Ansatz of the VQE, as
we further elaborate in Section 4. In this work,
we utilize Approximate Complex Amplitude Encoding
(ACAE) (Mitsuda et al., 2024) to convert this idea into
a warm-start via parameter initialization, that is more
suitable for current hardware. By means of a fidelity
estimation from so-called classical shadows (Huang
et al., 2020), the variational ACAE algorithm pro-
vides an efficient approximate amplitude encoding of
complex vectors into a quantum state. We evaluate the
performance benefits of the resulting warm-started
VQE (henceforth WS-VQE) over the standard VQE.
The underlying warm-starting technique employed in
WS-VQE can be used as a blueprint for other VQAs.
The remainder of this paper is organized as fol-
lows: In Section 2, we introduce the background and
fundamentals for this work. Section 3 discusses re-
lated work and Section 4 introduces WS-VQE, which
is evaluated and analyzed in Section 5. The results are
further discussed in Section 6 and the paper is con-
cluded with a summary and outlook in Section 7.
2 BACKGROUND AND
FUNDAMENTALS
We introduce VQE and ACAE in more detail to pro-
vide the background and fundamentals for WS-VQE.
2.1 Variational Quantum Eigensolver
The VQE follows the general construction of VQAs,
i.e., it is a hybrid quantum-classical algorithm based
on a parameterized quantum circuit, frequently re-
ferred to as Ansatz, and a classical optimizer (Peruzzo
et al., 2014; Cerezo et al., 2021). The Ansatz aims to
prepare a quantum state that represents a solution to
the problem instance at hand. The classical optimizer
iteratively adjusts the parameter values for the Ansatz,
which is in turn executed on a quantum device to as-
sess the current solution and navigate to an optimum.
Peruzzo et al. (2014) introduced the VQE to de-
termine eigenvalues of operators more efficiently than
possible with Quantum Phase Estimation. At its heart,
the VQE makes use of Quantum Expectation Estima-
tion (QEE), a subroutine that evaluates the expecta-
tion value of the given Hamiltonian for the state pre-
pared by the Ansatz. For the measurements on the
quantum computer, the Hamiltonian is decomposed
into a real-valued linear combination of tensor prod-
ucts of the identity I and the Pauli operators X, Y ,
and Z. The overall expectation value of the Hamilto-
nian H is computed as per Equation (1), i.e., as the
weighted sum of the expectation values of each Pauli
string P
i
in the linear combination, where x
i
are the
real-valued coefficients of H’s Pauli decomposition.
⟨H⟩ =
∑
i
x
i
⟨P
i
⟩ (1)
Therefore, the state prepared by the Ansatz needs
to be measured multiple times for different measure-
ment bases as prescribed by the Pauli decomposition.
These measurements require the preparation of mea-
surement circuits with appropriate rotations to adjust
the measurement basis for each qubit. However, there
are various strategies of grouping Pauli strings that
can be measured jointly, which can reduce the num-
ber of measurement circuits significantly (Tilly et al.,
2022). Nonetheless, the QEE subroutine typically re-
quires a multitude of measurement circuits to cover
all Pauli strings composing H. Each measurement on
a quantum computer typically needs to be repeated
multiple times to obtain results of a certain preci-
sion. These measurements are commonly referred
to as shots. Therefore, a hyperparameter N
shots
de-
termines the number of shots executed for measuring
each Pauli string. Thus, the total number of shots re-
quired for each call of the QEE subroutine amounts to
N
shots
× n
meas.circuits
, where n
meas.circuits
is the number
of measurement circuits, i.e., the number of groups of
jointly measurable Pauli strings.
The variational optimization of the VQE’s Ansatz
parameters aims to prepare a state that minimizes H’s
expectation value. Optimization typically starts from
a random initial parameterization or beneficial val-
ues determined through specific methods (Tilly et al.,
2022). Thereby, the VQE eventually prepares an
approximate ground state of H with the lowest ex-
pectation. Potential applications include determining
electronic ground state energies and molecular poten-
tial energy surfaces in quantum chemistry (Li et al.,
2019), strongly correlated systems in condensed mat-
ter physics (Head-Marsden et al., 2021), protein fold-
ing for drug discovery (Mustafa et al., 2022; Barkout-
sos et al., 2021), material design (Barkoutsos et al.,
2021), and chemical engineering (Bernal et al., 2022).
The remainder of this work focuses on the underlying
mathematical problem tackled with the VQE, namely
to determine the lowest eigenvalue and corresponding
eigenvector of Hermitian matrices.
IQSOFT 2025 - 1st International Conference on Quantum Software
16

2.2 Approximate Complex Amplitude
Encoding
Amplitude encoding refers to encoding a vector
⃗
x ∈ C
n
with
⃗
x = (x
0
,. . . , x
n−1
) of unit length into the
amplitudes of a quantum state
|
⃗
x
⟩
, as shown in Equa-
tion (2) (Schuld and Petruccione, 2018).
|
⃗
x
⟩
=
n−1
∑
i=0
x
i
|
i
⟩
(2)
Its main advantage is that storing data of length n re-
quires only log n qubits. However, exact amplitude
encoding is infeasible because a circuit depth of at
least
1
n
2
n
is required for the preparation of an arbi-
trary state on n qubits (Schuld and Petruccione, 2018;
Shende et al., 2006). Approximate amplitude encod-
ing (Nakaji et al., 2022) suggests a VQA that approxi-
mately encodes vectors into the amplitudes of a quan-
tum state by training a shallow Ansatz. However, it
only supports the encoding of real-valued data.
Recently, Mitsuda et al. (2024) proposed Approxi-
mate Complex Amplitude Encoding (ACAE) based on
classical shadows (Huang et al., 2020). A classical
shadow is an approximate classical description of a
quantum state that is generated with few measure-
ments. It can be used to estimate different properties
of the captured quantum state. In the case of ACAE,
classical shadows are employed to estimate the fi-
delity between a model state with the density operator
ρ
model
(θ) and a target state with the density operator
ρ
target
. Based on the estimated fidelity, an Ansatz can
be variationally optimized to approximately encode
the target state described by ρ
target
. Classical shadows
are created by applying random unitary transforma-
tions to the state before measurements. For the fi-
delity estimations in ACAE, the random unitaries are
taken from the n-qubit Clifford group. Results of mul-
tiple shots with different unitaries are averaged to ob-
tain an expectation value. The general idea is to clas-
sically undo these steps for each measurement result
ˆ
b
i
. The averaging operation is viewed as a quantum
channel M , that is reverted by the inverse M
−1
. To
undo the random Clifford unitary U, the inverse trans-
formation U
†
is applied. The result
ˆ
ρ
i
of undoing
these operations is called a snapshot:
ˆ
ρ
i
= M
−1
U
†
i
|
ˆ
b
i
⟩⟨
ˆ
b
i
|U
i
(3)
A classical shadow of the original state is a col-
lection of N
snaps
snapshots. From this approximate
classical description of the state, we can estimate cer-
tain properties. For instance, the expectation value of
an observable. Since the expectation value of an ob-
servable O in a state with the density operator ρ is
⟨O⟩ = Tr(Oρ), it is estimated by ⟨
ˆ
O⟩ in Equation (4).
⟨
ˆ
O⟩ =
1
N
snaps
N
snaps
∑
i=1
Tr(O
ˆ
ρ
i
) (4)
Setting O = ρ
target
allows us to estimate the fidelity
in ACAE. As shown in the supplementary material
provided by Huang et al. (2020), M
−1
boils down to
M
−1
(ρ) = (2
n
+ 1)ρ − I (5)
Thus, the fidelity can be estimated by
ˆ
f (θ):
ˆ
f (θ) =
1
N
snaps
N
snaps
∑
i=1
Tr(ρ
target
ˆ
ρ
i
)
=
1
N
snaps
N
snaps
∑
i=1
(2
n
+ 1)⟨
ˆ
b
i
|U
i
ρ
target
U
†
i
|
ˆ
b
i
⟩ − 1
(6)
Mitsuda et al. (2024) used ACAE to perform am-
plitude encoding of data for a quantum classifier.
3 RELATED WORK
Tilly et al. (2022) provide a comprehensive review of
the VQE as well as methods and best practices related
to it, however, not explicitly focusing on warm-starts
for the VQE. Truger et al. (2024) conducted a map-
ping study for research on warm-starting techniques
in the quantum computing domain, including warm-
starts applicable to the VQE: Zhang et al. (2021) pro-
pose an adaptive construction of Ansatz circuits that
takes information obtained from a classical approx-
imation into account. Grimsley et al. (2023) pro-
pose dynamically growing the Ansatz during the ex-
ecution of the VQE and recycling previous parame-
terizations. Moreover, the VQE is compatible with
meta-learning, i.e., classical machine learning mod-
els trained to take over the task of the optimizer in
VQAs (Verdon et al., 2019; Wilson et al., 2021), and
plugging together multiple optimization steps that uti-
lize optimized parameters from one step to initialize
the next (Tao et al., 2023). Most relevant to our work,
various techniques for the parameter initialization of
the VQE have been proposed. Machine learning en-
ables generating circuits and viable initial parameter
values for each problem instance, that can be further
optimized (Dborin et al., 2022; Rudolph et al., 2023).
Exploiting the classically feasible simulation of Clif-
ford circuits can yield viable parameter initializations
for the VQE (Ravi et al., 2022; Mitarai et al., 2022).
Other approaches try to obtain viable parameter ini-
tializations for a parameterized Hamiltonian, thus tak-
ing advantage of the continuity of the problem to
obtain initializations for any parameterization of the
Warm-Starting the VQE with Approximate Complex Amplitude Encoding
17
ȁ ۧ
Ԧ𝑣
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
VQE
Ansatz
Ԧ
𝑣
ACAE
Ansatz
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
Ԧ
𝑣
ACAE
Ansatz
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
VQE
Ansatz
𝜃
𝜃
𝐶
VQE
Ansatz
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
Ԧ
𝑣
VQE
Ansatz
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
𝜃
𝜃
𝐶
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
ȁ ۧ
0
ȁ ۧ
0
ȁ ۧ
0
VQE
Ansatz
≈ Ԧ𝑣
Ԧ
𝑣 𝜃
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝐶
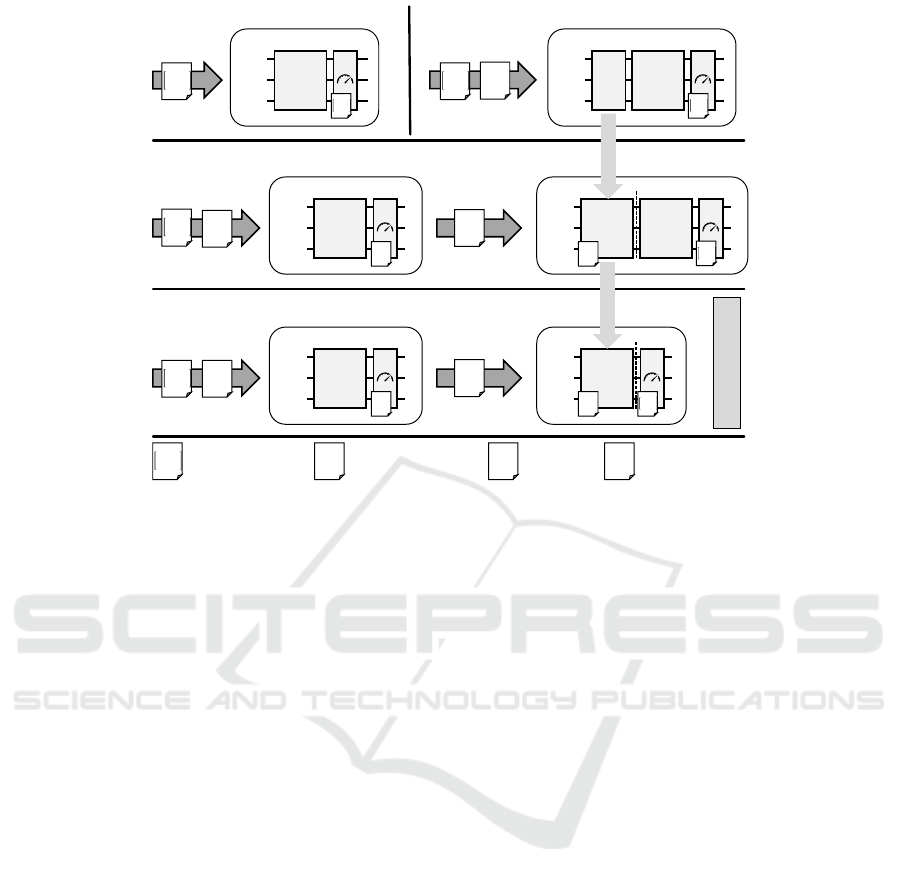
a) Standard VQE b) WS-VQE with Biased Initial State
c) WS-VQE with Biased Initial State via ACAE
d) WS-VQE with Parameter Initialization via ACAE
≈ Ԧ𝑣
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
𝟏 𝟎 𝟑
𝟎 𝟎 𝟏
𝟑 𝟏 𝟐
Problem Instance
(Hermitian Matrix)
Approximate Solution
(Eigenvector)
ACAE/VQE
Parameters
Random Clifford
Measurements
OUR
APPROACH
ACAE Pre-Training
ACAE/VQE Pre-Training
Figure 1: Shaping WS-VQE: a) The standard VQE without warm-start. b) A simple warm-start for the VQE using amplitude
encoding to prepend a biased initial state based on an approximate eigenvector ⃗v to the VQE Ansatz. c) A warm-start for the
VQE that prepends a pretrained ACAE Ansatz instead of amplitude encoding. d) Our approach, a warm-start for VQE based
on ACAE pretraining of the VQE Ansatz to approximately encode a given approximate eigenvector.
Hamiltonian (Cervera-Lierta et al., 2021; Harwood
et al., 2022). Similarly, the VQE has been shown to be
compatible with parameter transfers, where optimized
parameters from one instance are reused to initialize
the algorithm for a similar problem instance (Skogh
et al., 2023; Kanno and Tada, 2021).
Apart from these concrete techniques, the Quokka
ecosystem, which enables the utilization of workflow
technology for the service-based execution of VQAs,
includes a warm-starting service, that facilitates the
precomputation of parameter initializations and bi-
ased initial states in quantum workflows (Beisel et al.,
2023). Our approach for WS-VQE in this work is
different from the aforementioned warm-starts in that
it is compatible with any given approximation of the
problem and Ansatz for the VQE. Moreover, since it
does not require changes to the VQE, it is also com-
patible with adaptations of the VQE, including some
of the aforementioned methods.
Furthermore, the VQE’s measurements could be
implemented based on classical shadows (Tilly et al.,
2022). A derandomized variant of classical shadows
has shown potential in experiments (Huang et al.,
2021). However, the performance compared to the
grouping of Pauli strings and other grouping methods
is still unclear (Tilly et al., 2022). In any case, WS-
VQE is also compatible with VQE implementations
based on classical shadows.
4 WARM-STARTING THE VQE
In this section, we introduce our approach for warm-
started VQE with ACAE (WS-VQE). First, we dis-
cuss a simple warm-start for the VQE via a biased ini-
tial state. Then, we explain how ACAE helps in con-
verting the impractical biased initial state into a prac-
tically usable parameter initialization for the VQE,
hence shaping WS-VQE as illustrated in Figure 1.
4.1 Biased Initial State
Figure 1a) depicts the circuit of the standard VQE
consisting of the Ansatz and measurements that de-
pend on the problem instance, a Hermitian H. Given
an approximation⃗v for an eigenvector of H that corre-
sponds to H’s lowest eigenvalue, a simple warm-start
for VQE consists of prepending the amplitude encod-
ing of⃗v to the Ansatz as shown in Figure 1b) and start-
ing the optimization with the variational parameters
initialized to
⃗
0. Intuitively, this warm-start can be vi-
able since the optimized Ansatz of VQE encodes the
eigenvector corresponding to the lowest eigenvalue of
H. Therefore, the encoded approximate eigenvector
⃗v and associated solution quality are trivially retained
as long as the VQE’s Ansatz parameterization results
in the identity. In turn, the solution can be improved
IQSOFT 2025 - 1st International Conference on Quantum Software
18

from this state by optimizing the variational parame-
ters. However, the VQE Ansatz may therefore only
contain gates that cancel out through neutralizing pa-
rameter values, typically 0, or cancel out each other,
such as CNOT gates uncomputing each other. But
also other parameter initializations evaluating to the
identity are conceivable (Grant et al., 2019).
Amplitude encoding is impractical due to unfavor-
able scaling, as detailed in Section 2.2. As Figure 1c)
shows, approximately encoding ⃗v with ACAE yields
an alternative biased initial state. However, the re-
strictions for VQE’s Ansatz remain when a pretrained
ACAE Ansatz is prepended to it.
4.2 Parameter Initialization
The restrictions for the VQE’s Ansatz mentioned
above can be circumvented by utilizing ACAE’s ap-
proximate encoding to obtain a parameter initializa-
tion for the VQE instead of a biased initial state,
which is illustrated in Figure 1d). Since both the VQE
and ACAE are VQAs with a relatively free choice for
the Ansatz (see Section 2), the VQE’s Ansatz can be
pretrained using ACAE to encode ⃗v and thereby ob-
tain initial parameters for the VQE. Hence, the main
idea of WS-VQE is to use the same Ansatz for both
the VQE and ACAE, and conduct a two-step opti-
mization of the Ansatz: First, ACAE starts with a ran-
dom parameter initialization to determine parameters
for the Ansatz that approximately encode⃗v. Then, the
VQE is initialized with the parameters obtained for
the encoding of⃗v and continues optimizing the Ansatz
to improve the solution. The main advantage of us-
ing ACAE instead of starting the VQE training from
scratch is that ACAE can be expected to require fewer
measurements. Recall, that the VQE requires multi-
ple measurement circuits for different Pauli strings to
estimate the expectation value of H, each measure-
ment circuit consuming N
shots
shots in every iteration,
whereas ACAE utilizes classical shadows consuming
N
snaps
single-shot snapshots to estimate the fidelity.
Thus, depending on H’s composition, pretraining the
Ansatz with ACAE may be significantly cheaper than
training the VQE directly in terms of overall shots.
WS-VQE in the remainder of this paper refers to
the this parameter initialization from ACAE pretrain-
ing (Figure 1d)).
5 EVALUATION
This section first provides all necessary details on
the evaluation’s setup and configuration before com-
paring the results obtained for both VQE and WS-
VQE. Afterward, optimization landscapes of VQE
and ACAE are analyzed to provide deeper insights
into WS-VQE’s two-step optimization. Finally, we
examine the scalability prospects of WS-VQE.
5.1 Setup and Configurations
We describe the problem instances, approximations,
Ansatz, number of shots, and optimizer used for eval-
uation.
5.1.1 Problem Instances
For the evaluation of our approach, we generated 500
problem instances to examine VQE and WS-VQE
configurations. Each problem instance is a randomly
generated 8 × 8 Hermitian matrix. The matrices are
sparse, with 50% probability for each entry of being
either zero or a random complex number in the in-
terval [−5, 5] + [−5,5]i. Reference eigenvalues were
computed using the NumPyMinimumEigensolver
provided by Qiskit (Qiskit Contributors, 2023). Thus,
approximation ratios can be computed as r
appr
=
λ
λ
ref
,
where λ is an eigenvalue computed by VQE and λ
ref
the instance’s classically computed minimum eigen-
value. Hence, r
appr
= 1 corresponds to an optimum.
5.1.2 Classical Approximation
For WS-VQE, we utilize a simple classical approxi-
mation of an eigenvector corresponding to the lowest
eigenvalue based on the power method (Quarteroni
et al., 2006). First, we apply the Gershgorin cir-
cle theorem (Gershgorin, 1931) to determine a lower
bound for the eigenvalues of H. The theorem im-
plies that each eigenvalue of H is located within
either of the circles surrounding H
ii
with a radius
of R
i
=
∑
k̸=i
|H
ik
|. Based on the lower bound µ =
min
i
{H
ii
− R
i
}, the inverse power method allows us
to obtain an approximation of an eigenvector to the
eigenvalue closest to µ, i.e., an approximate eigen-
vector to the lowest eigenvalue of H. Starting with
a random initial vector q
(0)
, approximating the eigen-
vector boils down to Equation (7). We provide q
(3)
as
approximate eigenvector to WS-VQE.
M = (H − µI)
−1
z
(k)
= Mq
(k−1)
q
(k)
=
z
(k)
||z
(k)
||
2
(7)
5.1.3 Ansatz and VQE Implementation
We employ Qiskit’s hardware efficient SU(2) Ansatz
(EfficientSU2), a multipurpose Ansatz that has
Warm-Starting the VQE with Approximate Complex Amplitude Encoding
19

q
0
:
R
Y
(θ
0
) R
Z
(θ
3
)
•
R
Y
(θ
6
) R
Z
(θ
9
)
•
R
Y
(θ
12
) R
Z
(θ
15
)
q
1
:
R
Y
(θ
1
) R
Z
(θ
4
)
•
R
Y
(θ
7
) R
Z
(θ
10
)
•
R
Y
(θ
13
) R
Z
(θ
16
)
q
2
:
R
Y
(θ
2
) R
Z
(θ
5
) R
Y
(θ
8
) R
Z
(θ
11
) R
Y
(θ
14
) R
Z
(θ
17
)
Figure 2: Qiskit’s hardware efficient SU(2) Ansatz (EfficientSU2) with two repetitions as used in the evaluation.
been shown to be sufficiently expressive to prepare
arbitrary quantum states (Funcke et al., 2021). It con-
sists of alternating rotation and entanglement blocks
as depicted in Figure 2. Particularly, we generate
the Ansatz with two repetitions of the alternating lay-
ers and a final rotation layer, resulting in a total of
18 variational parameters. Two repetitions have been
shown to provide a maximally expressive Ansatz for 3
qubits (Funcke et al., 2021). Moreover, we utilize the
VQE implementation and a noiseless quantum simu-
lator provided by Qiskit for all executions of the VQE.
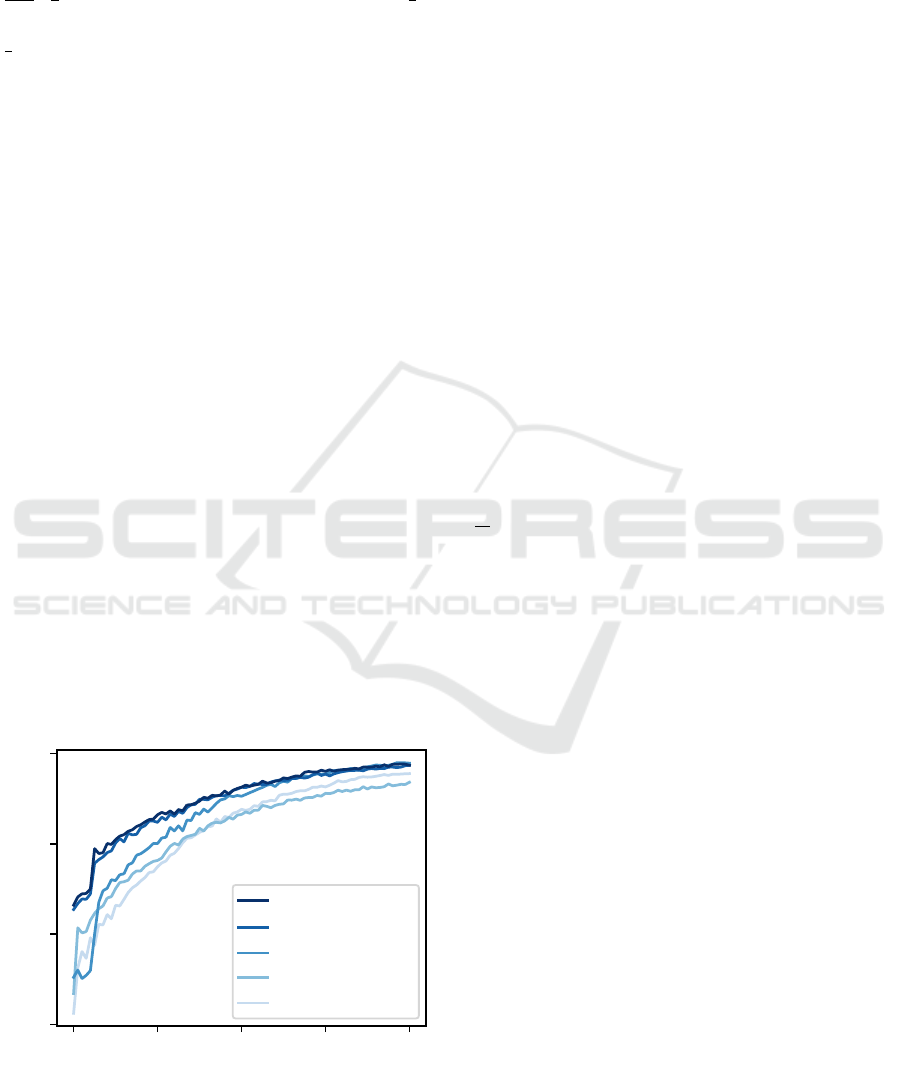
5.1.4 Shots and Snapshots
Following preliminary experiments summarized
in Figure 3 we estimated that N
shots
= 200 in VQE’s
circuit executions yields a reasonable cost-benefit
ratio. Moreover, we take N
snaps
= 400 snapshots,
i.e., N
snaps
single shots, for the fidelity estimation in
ACAE to attain sufficient accuracy. For simplicity,
we reduce the classical effort of the random Clifford
measurements in ACAE by using the same N
snaps
unitaries throughout the optimization instead of
generating new random Clifford unitaries in each it-
eration. The Clifford operators are sampled uniformly
at random using Qiskit’s implementation of Bravyi
and Maslov’s method (Bravyi and Maslov, 2021).
As mentioned above, computing the expectation
value in the VQE consumes N
shots
shots for multi-
50
100
150
200
250
300
350
400
450
500
Number of shots
0.2
0.4
0.6
0.8
1.0
Final approx. ratio
Figure 3: Median approximation ratio (horizontal markers)
reached after 80 iterations of VQE on 1 000 random prob-
lem instances per number of shots. Statistical sampling er-
rors cause some erroneous approximation ratios above 1.0,
which fade with the increasing number of shots.
ple measurement circuits, whereas ACAE consumes
only N
snaps
shots to estimate the fidelity. For the pre-
sentation of our evaluation results for WS-VQE, we
prepend ACAE iterations of the pretraining to the sub-
sequent VQE iterations. To account for the different
quantum computational effort, we rescale ACAE iter-
ations to an equivalent of VQE iterations with at least
the same total number of shots. For instance, assum-
ing one function evaluation per iteration, 20 iterations
of ACAE pretraining consume 400 shots each, i.e.,
8000 shots in total and would be counted as an equiv-
alent of 3 VQE iterations, where 15 measurement cir-
cuits consume 200 shots each, i.e., 9000 shots in total.
As this example illustrates, WS-VQE’s performance
is slightly underestimated in our evaluation to achieve
an easier comparison based on VQE iterations.
5.1.5 Parameter Initialization
All initial ACAE and VQE parameter values are
drawn uniformly at random from [−π,π].
5.1.6 Optimizer Configuration
We employ the gradient-free COBYLA (Powell, 1994)
as the classical optimizer in both ACAE and VQE.
COBYLA is known to perform reasonably well in noise-
free simulation of VQAs (Pellow-Jarman et al., 2021).
For the pretraining of ACAE, we allow up to 50 iter-
ations, whereas we execute up to 100 iterations for
each run of the VQE. Moreover, we set the initial step
size parameter rhobeg (ρ) of COBYLA to ρ
ACAE
=
1
4
π
for ACAE and ρ
VQE
=
3
8
π for the VQE following our
observations in preliminary experiments. For WS-
VQE, we assume that a reduction of ρ is beneficial
due to the head start provided by ACAE pretraining.
Therefore, we expect WS-VQE to start closer to an
optimum and require smaller changes to the parame-
ters. To confirm this assumption, we run WS-VQE
with both ρ
VQE
and ρ
static
WS-VQE
=
1
2
· ρ
VQE
. In addi-
tion, we consider a dynamic setting where ρ depends
on the final estimated fidelity f
final
achieved during
ACAE pretraining. A fidelity close to 1 indicates a
successful encoding of the approximated eigenvector,
and therefore smaller steps should be required during
the subsequent execution of the VQE. In contrast, a
fidelity close to 0 indicates less successful pretrain-
IQSOFT 2025 - 1st International Conference on Quantum Software
20
ing and therefore more leeway should be given to the
optimizer, since it may start farther from a global opti-
mum. This is taken into account by setting ρ
dynamic
WS-VQE
=
1
f
final
·
1
4
· ρ
VQE
. Therefore, ρ
dynamic
WS-VQE
ranges from
1
4
·
ρ
VQE
in case that f
final
is 1, i.e., perfect ACAE, over
1
2
·ρ
VQE
(= ρ
static
WS-VQE
) in the case f
final
= 0.5 and ρ
VQE
for f
final
= 0.25 to virtually ∞ in the worst case.
5.1.7 Reproducibility
Our WS-VQE implementation for the evaluation as
well as all detailed results can be found in the GitHub
repository associated with this work (Truger and
Obst, 2024).
5.2 Results
Figure 4 shows the progress of the optimization of
the VQE and WS-VQE with different optimizer con-
figurations as stipulated above. Evidently, utilizing
ACAE for the parameter initialization in WS-VQE
significantly improves the median approximation
ratio over standard VQE. While the median ap-
proximation ratio after 20 iterations reaches just
above 0.3 for the VQE, the WS-VQE variant can
reach a median approximation ratio well above 0.5,
depending on the optimizer configuration. The final
median approximation ratios obtained with WS-VQE
are also above those of the standard VQE. Moreover,
the different optimizer configurations for WS-VQE
discussed above significantly impact its performance.
As Figure 4 shows, WS-VQE optimized with ρ
VQE
reaches lower median approximation ratios than
standard VQE for a portion of the early iterations.
In contrast, WS-VQE/ρ
static
WS-VQE
, where COBYLA’s ρ
20 40 60 80 100
Iteration
0.3
0.5
0.7
0.9
Median approx. ratio
WS-VQE/%
dynamic
WS-VQE
WS-VQE/%
static
WS-VQE
WS-VQE/%
VQE
VQE/%
static
WS-VQE
VQE/%
VQE
Figure 4: Progress of the (WS-)VQE optimization: Median
approximation ratio after each iteration i ∈ {20,. . ., 100} for
the 500 problem instances (see Section 5.1.1) with different
initial step sizes ρ, as declared in Section 5.1.6.
parameter is halved, performs significantly better up
until just above 65 iterations where it starts to overlap
with WS-VQE/ρ
VQE
. Median approximation ratios
obtained with WS-VQE/ρ
dynamic
WS-VQE
are above those
of all other variants until they also start to overlap
with WS-VQE/ρ
static
WS-VQE
in the 50th iteration. These
results confirm our assumptions regarding different
optimizer settings for WS-VQE. However, the differ-
ences appear to fade as the optimization progresses.
Moreover, the results of VQE/ρ
static
WS-VQE
, which we
included for comparison, show that the advantages of
WS-VQE are not merely due to the optimizer setting.
5.3 Optimization Landscape Analysis
Next, we further analyze WS-VQE’s two-step opti-
mization by illustrating parts of the parameter space
for the variational optimization. The optimization
landscapes plotted in Figure 5 show expectation val-
ues and fidelities in a random two-dimensional slice
of the parameter space of the Ansatz depicted in Fig-
ure 2. Values for parameters not annotated on the axes
were selected uniformly at random for each problem
instance. Expectation values and fidelities, respec-
tively, were evaluated for each point of an equidistant
grid in the space [−π, π] × [−π,π] with a distance of
π
20
. The problem instances and approximate eigen-
vectors are identical to the first three instances from
the experiments above (cf. Figure 4). The approxi-
mation ratios are 0.99, 0.86, and 0.76, respectively.
For each problem instance (rows in Figure 5), four
different properties are shown in the respective slice
of the parameter space (columns in Figure 5): (i) the
expectation value for VQE as per Equation (1), (ii) the
estimated fidelity for ACAE as per Equation (6) of
the respective quantum state prepared by the Ansatz
to the approximate eigenvector ⃗v
appr.
, (iii) the actual
fidelity of the quantum state to ⃗v
appr.
, and (iv) the
actual fidelity of the quantum state to an optimal ref-
erence eigenvector⃗v
opt.
. As in the experiments above,
the VQE expectation values were computed from 200
shots per circuit, whereas the fidelity was estimated
based on 400 snapshots. The circuits were executed
on a noiseless simulator, actual fidelities were
determined based on state vector simulation in Qiskit.
Due to the construction of WS-VQE, the parame-
ters are optimized for the estimated fidelity of ACAE
(second column) first, before the optimization con-
tinues for the expectation value of VQE (first col-
umn). Therefore, it is essential for WS-VQE that a
high fidelity is observed in proximity to low expecta-
tion values. Figure 5 illustrates a proximity of the re-
spective extrema of both properties in the parameter
space, which depends on the quality of the approxi-
Warm-Starting the VQE with Approximate Complex Amplitude Encoding
21
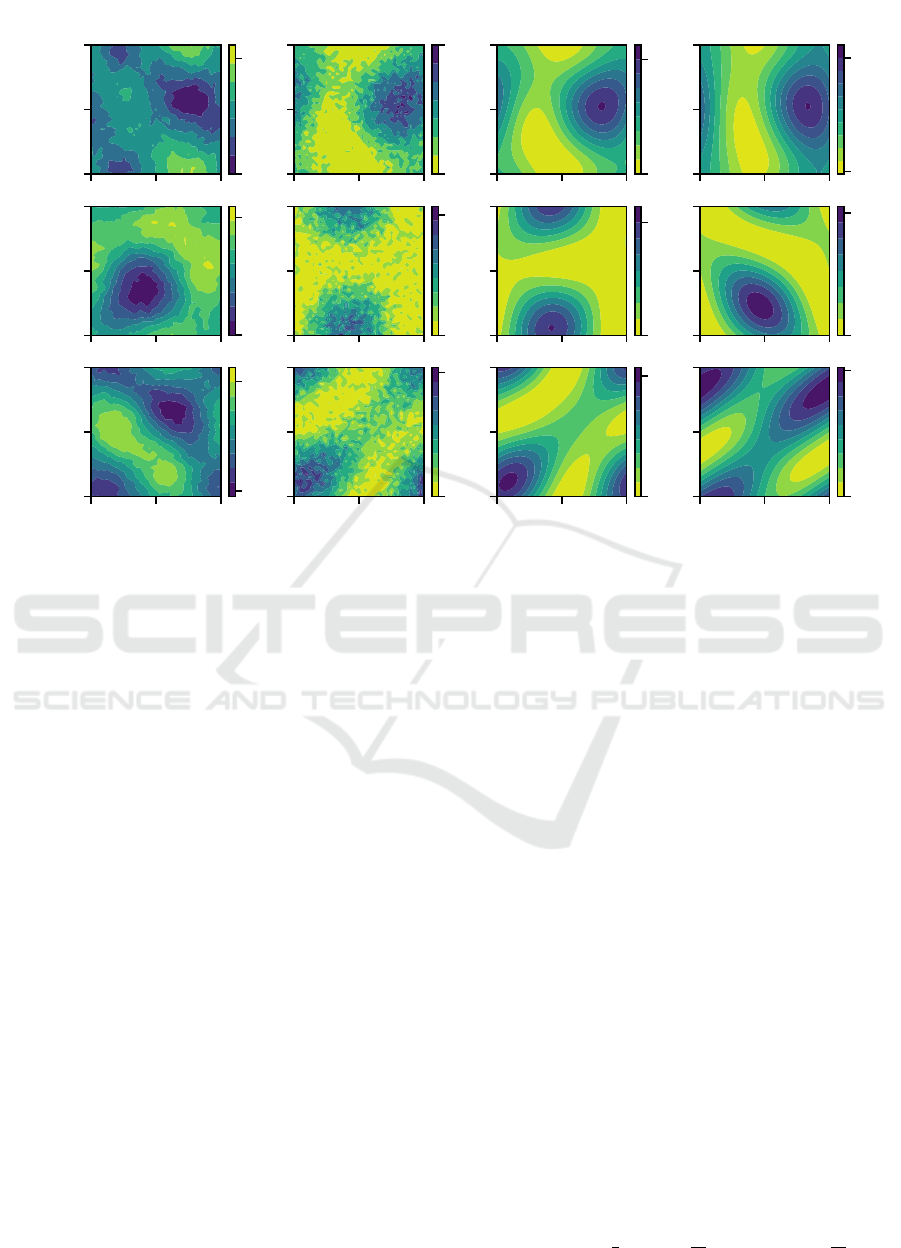
θ
11
−π
0
π
Problem 1
r
appr.
= 0.99
θ
14
Expectation Value
(VQE)
θ
11
Estimated Fidelity
to
~
v
appr.
(ACAE)
θ
11
Actual Fidelity
to
~
v
appr.
θ
11
Actual Fidelity
to
~
v
opt.
-6.0
3.41
0.56
0.0
0.48
0.0
0.45
0.01
θ
1
−π
0
π
Problem 2
r
appr.
= 0.86
θ
2
θ
1
θ
1
θ
1
-9.96
6.44
0.42
0.0
0.28
0.0
0.38
0.0
−π 0 π
θ
0
−π
0
π
Problem 3
r
appr.
= 0.76
θ
1
−π 0 π
θ
0
−π 0 π
θ
0
−π 0 π
θ
0
-9.18
6.05
0.52
0.0
0.42
0.0
0.22
0.0
Figure 5: Slices of the parameter space of VQE and ACAE (left) for three different problem instances as compared to the
actual fidelity of the quantum states prepared by the Ansatz to the approximate and an optimal eigenvector of the instance,
⃗v
approx.
and ⃗v
opt.
, (right). Each line corresponds to a problem instance as described in Section 5.1.1 for which a random
two-dimensional slice of the full 18-dimensional parameter space of the Ansatz depicted in Figure 2 is plotted. The other
parameters were chosen uniformly at random from [−π,π]. Labels on the color bars indicate minimal and maximal values.
mation. For example, the minimal expectation value
for problem 1 appears at parameter values very close
to those of the maximum estimated and actual fidelity
to the approximate eigenvector. Since the approxi-
mate eigenvectors for problems 2 and 3 are of lower
quality, the similarities appear to fade progressively.
Meanwhile, the actual fidelity to an optimal eigenvec-
tor (rightmost column) appears to still exhibit its max-
imum at a similar location for problem 2. However,
since only one single optimal eigenvector is consid-
ered in the illustration of the landscapes, the extrema
of the fidelity do not necessarily coincide with those
of VQE, as is the case for problem 3. We assume that
there are other optimal or near optimal eigenvectors
that make the minima of the expectation value appear
in a different position. In other words, the quantum
state of the fidelity maximum for the specific optimal
eigenvector of problem 3 may have less influence on
the expectation value than other solutions. This is also
consistent with the state fidelity to this eigenvector
reaching a maximum value of only 0.22, as compared
to higher values for the other problems.
One particularly noteworthy observation in Fig-
ure 5 is that all fidelities have only one clearly pro-
nounced maximum in the respective two-dimensional
space (for estimated fidelity: an area where high val-
ues concentrate). For this observation the periodicity
of the analyzed parameter space with a period of 2π,
due to the simple rotation gates of the ansatz, needs to
be taken into account. In contrast, the expectation val-
ues exhibit local minima. Together with a proximity
of fidelity maxima for good approximate eigenvectors
and expectation minima, this indicates that WS-VQE
might be able to avoid local optima due to initial
parameter optimization based on estimated fidelity.
5.4 Scalibility
To assess WS-VQE’s scalability, we repeated the ex-
periments of Section 5.2 for larger sizes of matrices
and with adjusted hyperparameters to account for the
larger problem instances. In particular, we generated
100 random 32 × 32 Hermitian matrices, i.e., matri-
ces with 1 024 entries each, with a sparsity of 90%,
increased N
snaps
to 800 and N
shots
to 400, and allowed
for 100 iterations in ACAE and 200 iterations in VQE
optimization. Also the circuit depth, i.e., repetitions
in the Ansatz, has been doubled from two to four.
In addition, the optimizer’s parameters have been up-
dated to ρ
′
VQE
=
1
2
ρ
VQE
=
3
16
π, ρ
′
static
WS-VQE
=
3
24
π, and
IQSOFT 2025 - 1st International Conference on Quantum Software
22

Table 1: Median final approximation ratio for 100 random
32 × 32 problem instances reached after a maximum of 200
VQE iterations, including ACAE pretraining for WS-VQE,
as described in Section 5.1.4.
X
X
X
X
X
X
X
X
Variant
Config.
ρ
′
VQE
ρ
′
static
WS-VQE
ρ
′
dynamic
WS-VQE
VQE 0.518 0.481 -
WS-VQE 0.530 0.507 0.548
ρ
′
dynamic
WS-VQE
=
3
64
π. The approximate eigenvector was
q
(12)
for the warm-start as per Equation (7).
The results are summarized by median final ap-
proximation ratios for each variant’s parameteriza-
tion presented in Table 1. These results indicate that
the advantage of the warm-start persists also with in-
creasing problem instances. In particular, WS-VQE
reached higher approximation ratios for both values
of the initial step size parameter ρ. Also the dynamic
initial step size persisted as the most beneficial regime
for setting this hyperparameter in WS-VQE. How-
ever, the results in Table 1 indicate that further ad-
justment of ρ may be needed, since the decrease from
ρ
′
VQE
to ρ
′
static
WS-VQE
lead to a reduced approximation
ratio in both cases and the overall performance de-
creased significantly compared to the results of Sec-
tion 5.2, although the resources have been increased.
6 DISCUSSION
The evaluation shows that WS-VQE can be worth-
while, but a few caveats remain to be discussed.
6.1 Quality of the Approximation
Clearly, the success of WS-VQE depends on the qual-
ity of the approximations fed to the algorithm. On av-
erage, the approximations corresponded to an approx-
imation ratio around 0.850 (σ = 0.126) in our evalu-
ation in Section 5.2 and 0.911 (σ = 0.052) in Sec-
tion 5.4. We utilized a simple, but not generally fea-
sible approximation for eigenvectors, as the inverse
power method requires matrix inversion or solving
linear systems of equations, which incur a cost of cu-
bic complexity similar to that of the eigenvalue prob-
lem itself (Pan and Chen, 1999). Therefore, it would
be desirable to utilize more efficient approximations.
These could be obtained, e.g., from previous solu-
tions of periodically recurring problems with only lit-
tle changes to the matrix, which are well-conditioned
according to the Bauer-Fike theorem (Bauer and Fike,
1960; Quarteroni et al., 2006). We emphasize that our
focus is on the warm-starting technique behind WS-
VQE; we do not intend to prove a quantum advantage.
6.2 Performance of ACAE
Another important factor in WS-VQE is the perfor-
mance of ACAE. In our evaluation, we observed
an average estimated fidelity of 0.625 (σ = 0.230)
achieved within the 50 ACAE iterations in Section 5.2
and 0.197 (σ = 0.097) within the 100 ACAE itera-
tions in Section 5.4. Although the approximations
obtained from the inverse power method were of rel-
atively high quality, the low average fidelity indi-
cates that ACAE was hardly able to retain this qual-
ity in its encoding. Despite the seemingly low fi-
delity, WS-VQE still surpassed the performance of
standard VQE. However, another allocation of quan-
tum resources for ACAE and WS-VQE, respectively,
in particular providing more resources for the opti-
mization of ACAE, could yield a higher fidelity and,
thus, better results. Moreover, further adjustment of
ACAE and its hyperparameters may be needed to im-
prove the quality of the encoding.
6.3 Expressivity of the Ansatz
An important prerequisite of the VQE is an Ansatz
that is tunable to prepare the desired optimal solu-
tion. This translates to the requirements of expressiv-
ity and trainability, i.e., the Ansatz needs to be expres-
sive enough to capture the optimal solution, but sim-
ple enough that its parameter space can be traversed
by the optimizer to reach an optimum (Funcke et al.,
2021; Du et al., 2022). Likewise, the ACAE requires
an expressive and trainable Ansatz for the encoding
of complex amplitudes. Although the Ans
¨
atze for the
VQE and ACAE in principle need not be identical,
WS-VQE implicitly assumes that an Ansatz for the
VQE is also suitable to encode an approximate eigen-
vector with ACAE. This assumption appears reason-
able, particularly since ACAE only aims for an ap-
proximate encoding. Provided that the VQE Ansatz
is expressive, i.e., able to capture the optimum, and
trainable, which entails the ability to reach states “sur-
rounding” the optimum during the optimization to-
ward it, and that the approximate solution ⃗v is suffi-
ciently close to the optimal solution, the same Ansatz
should also suffice to approximately encode⃗v.
6.4 Choice of Classical Optimizers
The choice of the classical optimizer in VQE has sig-
nificant impact on the efficiency and performance,
as it directly affects the number of measurements
and iterations required and can mitigate adverse ef-
fects (Tilly et al., 2022). Particularly, gradient-free
optimizers require significantly fewer function eval-
Warm-Starting the VQE with Approximate Complex Amplitude Encoding
23

uations, as they omit evaluating points in the param-
eter space to compute gradients. For the evaluation,
we used the same gradient-free optimizer for both
ACAE and (WS-)VQE. However, it may be more
beneficial to select different optimizers for each op-
timization, since the optimization landscapes of both
algorithms may exhibit different properties, as was il-
lustrated in Section 5.3. Moreover, some optimizers
are known to be more resilient to the noise on quan-
tum devices (Pellow-Jarman et al., 2021). Therefore,
different optimizers may be required when executing
(WS-)VQE on noisy quantum devices.
6.5 Mitigation of Adverse Effects
Parameter initializations have been shown to mitigate
adverse effects in the optimization of VQAs (Grant
et al., 2019; Lee et al., 2021). Particularly, barren
plateaus, i.e., areas with vanishing gradients in the pa-
rameter space of the cost function, and local minima
can be avoided with viable parameter initializations.
Thus, the convergence of VQAs may improve signif-
icantly when optimization is started closer to a global
optimum. We assume that the benefits of WS-VQE
are partially due to the avoidance of adverse effects
by means of a viable parameter initialization. This
is supported by our analysis in Section 5.3, but addi-
tional evaluation is needed to quantify the mitigation.
6.6 VQE and Classical Shadows
As mentioned in Section 3, the idea of implement-
ing the VQE based on classical shadows has emerged.
WS-VQE also combines the VQE with classical shad-
ows, albeit differently. Additionally, WS-VQE is
fully compatible and complementary to a VQE imple-
mentation with classical shadows. Recall that ACAE
requires only an estimated fidelity, that is obtained
with classical shadows from relatively few random
Clifford measurements. In contrast, the VQE may
still require a multitude of measurements even when
classical shadows are exploited, depending on the
Pauli composition of the operator (Tilly et al., 2022).
Hence, WS-VQE with ACAE pretraining could still
be more cost-efficient than starting a VQE implemen-
tation with classical shadows from scratch.
6.7 Reuse of Clifford Unitaries
As mentioned in Section 5.1.4, we reduced the clas-
sical effort of the Clifford measurements in ACAE
by reusing the unitaries for the classical snapshots
throughout an optimization. Using the same unitaries
for fidelity estimations throughout the optimization
could lead to overfitting, i.e., the model could learn
to accommodate the selected set of unitaries instead
of actually improving the state fidelity. On the other
hand, changing the unitaries in each iteration may in-
crease the perturbation of the fidelity estimation, mak-
ing the optimization more vulnerable. However, we
used relatively many snapshots, which mitigates both
potential problems to a certain extent. Moreover, our
results indicate that the fidelity and encoding achieved
by ACAE was sufficient to retain WS-VQE’s perfor-
mance benefit. As an alternative, the random Clifford
unitaries could be sampled from a reduced set that ef-
fectively preserves the original quantum channel in-
troduced in Section 2.2, thus reducing the sampling
and compilation costs (Zhang et al., 2024).
6.8 Iterations and Queuing Times
Despite potentially recuding the total number of shots
needed, WS-VQE increases the total number of iter-
ations due to the pretraining. Since quantum com-
puters are often available as shared resources through
cloud services (Leymann et al., 2020; Vietz et al.,
2021), queueing times for quantum circuit execution
could increase with the number of iterations. Appro-
priate execution patterns supported by quantum cloud
service providers mitigate this drawback by enabling
prioritized execution of VQAs, removing the need to
wait in queues for every iteration (Georg et al., 2023).
7 SUMMARY AND OUTLOOK
In this work, we proposed a warm-starting technique
for the VQE that utilizes classical shadows. In partic-
ular, the warm-start is based on an approximate am-
plitude encoding of an approximate solution for the
problem at hand. The proposed technique enables uti-
lizing any given approximation of the problem that
determines an (approximate) eigenvector to generate
a beneficial parameter initialization for the VQE. WS-
VQE is also compatible with different variants and
improvements of the VQE, as it does not require any
changes of the original algorithm or its quantum cir-
cuit. As shown in the evaluation, the VQE benefits
from the warm-start in terms of a reduced quantum
computational effort needed to reach a certain solu-
tion quality. In addition, the evaluation showed that
adjusting the optimizer used in WS-VQE can fur-
ther improve the performance. As an auxiliary result,
we outlined a way to derive a parameter initializa-
tion from a biased initial state, which may serve as
a blueprint for warm-starting other VQAs.
For future work, it remains to evaluate WS-VQE
IQSOFT 2025 - 1st International Conference on Quantum Software
24

in more detail and with real-world use cases to de-
termine which applications could benefit from it.
As Section 6 explained, changes in configuration
and implementation could further improve the warm-
starting technique. Moreover, we aim to analyze
which other VQAs could benefit from this technique
or adaptations. Furthermore, the Quokka ecosys-
tem (Beisel et al., 2023) could be extended to in-
tegrate WS-VQE-like warm-starts. The Quokka’s
warm-starting service currently facilitates the clas-
sical precomputation of parameter initializations and
biased initial states, which could be extended for WS-
VQE’s hybrid quantum-classical pretraining.
ACKNOWLEDGMENTS
This work was partially funded by the BMWK
projects SeQuenC (01MQ22009B) and EniQmA
(01MQ22007B).
REFERENCES
Barkoutsos, P. K., Gkritsis, F., Ollitrault, P. J., Sokolov,
I. O., Woerner, S., and Tavernelli, I. (2021). Quan-
tum algorithm for alchemical optimization in material
design. Chemical science, 12(12):4345–4352.
Bauer, F. L. and Fike, C. T. (1960). Norms and exclusion
theorems. Numer. Math., 2(1):137–141.
Beisel, M., Barzen, J., Garhofer, S., Leymann, F., Truger,
F., Weder, B., et al. (2023). Quokka: A Service
Ecosystem for Workflow-Based Execution of Vari-
ational Quantum Algorithms. In Service-Oriented
Computing – ICSOC 2022 Workshops. Springer.
Bernal, D. E., Ajagekar, A., Harwood, S. M., Stober, S. T.,
Trenev, D., and You, F. (2022). Perspectives of quan-
tum computing for chemical engineering. AIChE
Journal, 68(6).
Bravyi, S. and Maslov, D. (2021). Hadamard-free circuits
expose the structure of the clifford group. IEEE Trans-
actions on Information Theory, 67(7):4546–4563.
Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C.,
Endo, S., Fujii, K., et al. (2021). Variational quantum
algorithms. Nature Reviews Physics, 3(9):625–644.
Cervera-Lierta, A., Kottmann, J. S., and Aspuru-Guzik, A.
(2021). Meta-variational quantum eigensolver: Learn-
ing energy profiles of parameterized hamiltonians for
quantum simulation. PRX Quantum, 2(2).
Dborin, J., Barratt, F., Wimalaweera, V., Wright, L., and
Green, A. G. (2022). Matrix product state pre-training
for quantum machine learning. Quantum Science and
Technology, 7(3).
Du, Y., Tu, Z., Yuan, X., and Tao, D. (2022). Efficient mea-
sure for the expressivity of variational quantum algo-
rithms. Phys. Rev. Lett., 128.
Egger, D. J., Mare
ˇ
cek, J., and Woerner, S. (2021). Warm-
starting quantum optimization. Quantum, 5.
Feynman, R. P. (1982). Simulating physics with computers.
International Journal of Theoretical Physics, 21(6/7).
Funcke, L., Hartung, T., Jansen, K., K
¨
uhn, S., and Stornati,
P. (2021). Dimensional expressivity analysis of para-
metric quantum circuits. Quantum, 5.
Galda, A., Liu, X., Lykov, D., Alexeev, Y., and Safro,
I. (2021). Transferability of optimal QAOA pa-
rameters between random graphs. In International
Conference on Quantum Computing and Engineering
(QCE), pages 171–180. IEEE.
Georg, D., Barzen, J., Beisel, M., Leymann, F., Obst, J.,
Vietz, D., et al. (2023). Execution Patterns for Quan-
tum Applications. In Proceedings of the 18
th
Inter-
national Conference on Software Technologies (IC-
SOFT). SciTePress.
Gershgorin, S. A. (1931).
¨
Uber die Abgrenzung der Eigen-
werte einer Matrix. Bull. Acad. Sci. USSR, ser. VII,
7(6).
Grant, E., Wossnig, L., Ostaszewski, M., and Benedetti, M.
(2019). An initialization strategy for addressing bar-
ren plateaus in parametrized quantum circuits. Quan-
tum, 3.
Grimsley, H. R., Barron, G. S., Barnes, E., Economou, S. E.,
and Mayhall, N. J. (2023). Adaptive, problem-tailored
variational quantum eigensolver mitigates rough pa-
rameter landscapes and barren plateaus. npj Quantum
Information, 9(1).
Harwood, S. M., Trenev, D., Stober, S. T., Barkoutsos, P.,
Gujarati, T. P., Mostame, S., et al. (2022). Improving
the variational quantum eigensolver using variational
adiabatic quantum computing. ACM Transactions on
Quantum Computing, 3(1).
Head-Marsden, K., Flick, J., Ciccarino, C. J., and Narang,
P. (2021). Quantum information and algorithms
for correlated quantum matter. Chemical Reviews,
121(5):3061–3120.
Huang, H.-Y., Kueng, R., and Preskill, J. (2020). Predicting
many properties of a quantum system from very few
measurements. Nature Physics, 16(10):1050–1057.
Huang, H.-Y., Kueng, R., and Preskill, J. (2021). Efficient
estimation of pauli observables by derandomization.
Phys. Rev. Lett., 127.
Kanno, S. and Tada, T. (2021). Many-body calculations for
periodic materials via restricted boltzmann machine-
based VQE. Quantum Science and Technology, 6(2).
Lee, X., Saito, Y., Cai, D., and Asai, N. (2021). Parameters
fixing strategy for quantum approximate optimization
algorithm. In International Conference on Quantum
Computing and Engineering (QCE), pages 10–16.
Leymann, F. and Barzen, J. (2020). The bitter truth
about gate-based quantum algorithms in the NISQ era.
Quantum Science and Technology, pages 1–28.
Leymann, F., Barzen, J., Falkenthal, M., Vietz, D., Weder,
B., and Wild, K. (2020). Quantum in the Cloud: Ap-
plication Potentials and Research Opportunities. In
Proceedings of the 10
th
International Conference on
Cloud Computing and Services Science (CLOSER),
pages 9–24. SciTePress.
Warm-Starting the VQE with Approximate Complex Amplitude Encoding
25

Li, Y., Hu, J., Zhang, X.-M., Song, Z., and Yung, M.-H.
(2019). Variational quantum simulation for quantum
chemistry. Advanced Theory and Simulations, 2(4).
Mitarai, K., Suzuki, Y., Mizukami, W., Nakagawa, Y. O.,
and Fujii, K. (2022). Quadratic clifford expansion
for efficient benchmarking and initialization of vari-
ational quantum algorithms. Physical Review Re-
search, 4(3).
Mitsuda, N., Ichimura, T., Nakaji, K., Suzuki, Y., Tanaka,
T., Raymond, R., et al. (2024). Approximate complex
amplitude encoding algorithm and its application to
data classification problems. Phys. Rev. A, 109.
Mustafa, H., Morapakula, S. N., Jain, P., and Ganguly, S.
(2022). Variational quantum algorithms for chemical
simulation and drug discovery. In International Con-
ference on Trends in Quantum Computing and Emerg-
ing Business Technologies (TQCEBT), pages 1–8.
Nakaji, K., Uno, S., Suzuki, Y., Raymond, R., Onodera, T.,
Tanaka, T., et al. (2022). Approximate amplitude en-
coding in shallow parameterized quantum circuits and
its application to financial market indicators. Physical
Review Research, 4(2).
Pan, V. Y. and Chen, Z. Q. (1999). The complexity of
the matrix eigenproblem. In Proceedings of the 31
st
Annual ACM Symposium on Theory of Computing,
STOC ’99, page 507–516, New York, NY, USA.
ACM.
Pellow-Jarman, A., Sinayskiy, I., Pillay, A., and Petruc-
cione, F. (2021). A comparison of various classi-
cal optimizers for a variational quantum linear solver.
Quantum Information Processing, 20(6).
Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou,
X.-Q., Love, P. J., et al. (2014). A variational eigen-
value solver on a photonic quantum processor. Nature
communications, 5(1):4213.
Powell, M. J. D. (1994). A Direct Search Optimiza-
tion Method That Models the Objective and Con-
straint Functions by Linear Interpolation, pages 51–
67. Springer Netherlands.
Preskill, J. (2018). Quantum computing in the NISQ era
and beyond. Quantum, 2.
Qiskit Contributors (2023). Qiskit: An open-source frame-
work for quantum computing.
Quarteroni, A., Sacco, R., and Saleri, F. (2006). Numerical
mathematics, volume 37. Springer Science & Busi-
ness Media.
Ravi, G. S., Gokhale, P., Ding, Y., Kirby, W., Smith, K.,
Baker, J. M., et al. (2022). CAFQA: A classical sim-
ulation bootstrap for variational quantum algorithms.
In Proceedings of the 28th ACM International Con-
ference on Architectural Support for Programming
Languages and Operating Systems (ASPLOS), page
15–29. ACM.
Rudolph, M. S., Miller, J., Motlagh, D., Chen, J., Acharya,
A., and Perdomo-Ortiz, A. (2023). Synergistic pre-
training of parametrized quantum circuits via tensor
networks. Nature Communications, 14(1).
Sack, S. H. and Serbyn, M. (2021). Quantum annealing ini-
tialization of the quantum approximate optimization
algorithm. quantum, 5.
Schuld, M. and Petruccione, F. (2018). Supervised learning
with quantum computers, volume 17. Springer.
Shaydulin, R., Lotshaw, P. C., Larson, J., Ostrowski, J., and
Humble, T. S. (2023). Parameter transfer for quantum
approximate optimization of weighted maxcut. ACM
Transactions on Quantum Computing, 4(3).
Shende, V., Bullock, S., and Markov, I. (2006). Syn-
thesis of quantum-logic circuits. IEEE Transactions
on Computer-Aided Design of Integrated Circuits and
Systems, 25(6):1000–1010.
Skogh, M., Leinonen, O., Lolur, P., and Rahm, M. (2023).
Accelerating variational quantum eigensolver conver-
gence using parameter transfer. Electronic Structure,
5(3).
Tao, Z., Wu, J., Xia, Q., and Li, Q. (2023). LAWS:
Look around and warm-start natural gradient descent
for quantum neural networks. In International Con-
ference on Quantum Software (QSW), pages 76–82.
IEEE.
Tate, R., Farhadi, M., Herold, C., Mohler, G., and Gupta,
S. (2023). Bridging classical and quantum with sdp
initialized warm-starts for qaoa. ACM Transactions
on Quantum Computing, 4(2).
Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y.,
et al. (2022). The variational quantum eigensolver:
A review of methods and best practices. Physics Re-
ports, 986:1–128.
Truger, F., Barzen, J., Bechtold, M., Beisel, M., Leymann,
F., Mandl, A., et al. (2024). Warm-starting and quan-
tum computing: A systematic mapping study. ACM
Comput. Surv., 56(9).
Truger, F. and Obst, J. (2024). WS-VQE-prototype GitHub
Repository. https://github.com/UST-QuAntiL/
WS-VQE-prototype.
Verdon, G., Broughton, M., McClean, J. R., Sung, K. J.,
Babbush, R., Jiang, Z., et al. (2019). Learning to learn
with quantum neural networks via classical neural net-
works.
Vietz, D., Barzen, J., Leymann, F., Weder, B., and Yus-
supov, V. (2021). An Exploratory Study on the
Challenges of Engineering Quantum Applications in
the Cloud. In Proceedings of the 2
nd
Quantum
Software Engineering and Technology Workshop (Q-
SET). CEUR Workshop Proceedings.
Wilson, M., Stromswold, R., Wudarski, F., Hadfield, S.,
Tubman, N. M., and Rieffel, E. G. (2021). Optimiz-
ing quantum heuristics with meta-learning. Quantum
Machine Intelligence, 3:1–14.
Zhang, Q., Liu, Q., and Zhou, Y. (2024). Minimal-clifford
shadow estimation by mutually unbiased bases. Phys.
Rev. Appl., 21.
Zhang, Z.-J., Kyaw, T. H., Kottmann, J. S., Degroote, M.,
and Aspuru-Guzik, A. (2021). Mutual information-
assisted adaptive variational quantum eigensolver.
Quantum Science and Technology, 6(3).
IQSOFT 2025 - 1st International Conference on Quantum Software
26
