Advanced Predictive Process Control for Industrial Thickeners

Mouna El Hamrani

1,2

, Khalid Benjelloun

1,3

, Jean-Pierre Kenn

, Saad Maarouf

and Mohamed Elkhouakhi

Mohammadia School of Engineers, Mohammed V University, Rabat, Morocco

Technology Development Cell, Mohammed VI Polytechnic University, Benguerir, Morocco

Green Tech Institute, Mohammed VI Polytechnic University, Benguerir, Morocco

Mechanical Engineering Department,

Ecole de Technologie Sup

erieure, Canada

GREPCI Laboratory,Ecole de Technologie Superieure, Montreal, QC H3C 1K3, Canada

Keywords:

Advanced Process Control, Industrial Thickeners, Thickener Automation, Adaptive Model Predictive Control,

Real-Time Parameter Estimation.

Abstract:

Efﬁcient control of industrial thickeners is crucial for optimizing solid-liquid separation processes, especially

in ﬁelds like mining and wastewater treatment. Traditional model predictive control (MPC) strategies, even

though useful in most applications, can face trouble trying to maintain their performance when faced with

time-varying dynamics due to factors such as wear and tear of equipment or changes in feed properties. To

address these limitations, this paper highlights an adaptive model predictive control (AMPC) strategy that uses

real-time parameter identiﬁcation to update the prediction model of the usual MPC algorithm. The results show

that while AMPC improves the robustness of the controller signiﬁcantly, keeping critical process parameters

such as slurry density well within operational limits under changing conditions, it still faces a number of

challenges. AMPC struggles to compensate for unknown disturbances or to optimize ﬂocculant consumption,

resulting in economic problems. These results suggest that, despite the improvements offered by AMPC,

further research is required to develop advanced disturbance rejection mechanisms and incorporate ﬂocculant

optimization strategies for more efﬁcient and cost-effective performances.

1 INTRODUCTION

Thickeners are vital elements in industrial processes,

intended to enhance the effectiveness of solid-liquid

separation. These units are essential in several

industries, such as mining and wastewater treat-

ment, improving the solid concentration of slurries

to guarantee cleaner overﬂows and denser under-

ﬂows. (Adewuyi et al., 2024; Wang et al., 2024).

Thickeners utilize ﬂocculants to consolidate tiny par-

ticles, thus enhancing settling rates and clarifying

the overﬂow.(Farrow et al., 2000; Concha and Fer-

nando, 2014). Although this task is straightforward,

the variable nature of the input, which ﬂuctuates in

concentration, particle size, pH, and other parame-

ters, presents ongoing challenges to control systems.

(Betancourt et al., 2014; Juan and Aldo, 2019). In

modern contexts, improved process control is essen-

tial for negotiating the intricate interactions of chem-

istry and physics within thickeners, assuring max-

imum performance. (Ojeda et al., 2014; Kosonen

et al., 2017).The transition from manual to automated

control systems in thickening operations illustrates

this ongoing progress intended to address the difﬁcul-

ties through technological advances.(Xie et al., 2015).

Traditional Model Predictive Control (MPC) ef-

fectiveness accounts for its widespread use in many

industrial applications. However, it faces constraints

that necessitate the investigation of more adaptable

control strategies.

The paper presents an Adaptive Model Predictive

Control (AMPC) framework to improve the robust-

ness and adaptability of thickening operations, en-

suring process parameters remain within operational

norms under variable conditions. It also explores the

challenges faced by this method, particularly in ad-

dressing unknown dynamics and optimizing ﬂoccu-

lant consumption, which are crucial for operational

and economic efﬁciency in industrial thickening pro-

cesses.

262

El Hamrani, M., Benjelloun, K., Kenné, J.-P., Maarouf, S. and Elkhouakhi, M.

Advanced Predictive Process Control for Industrial Thickeners.

DOI: 10.5220/0013508000003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 262-269

ISBN: 978-989-758-759-7; ISSN: 2184-2841

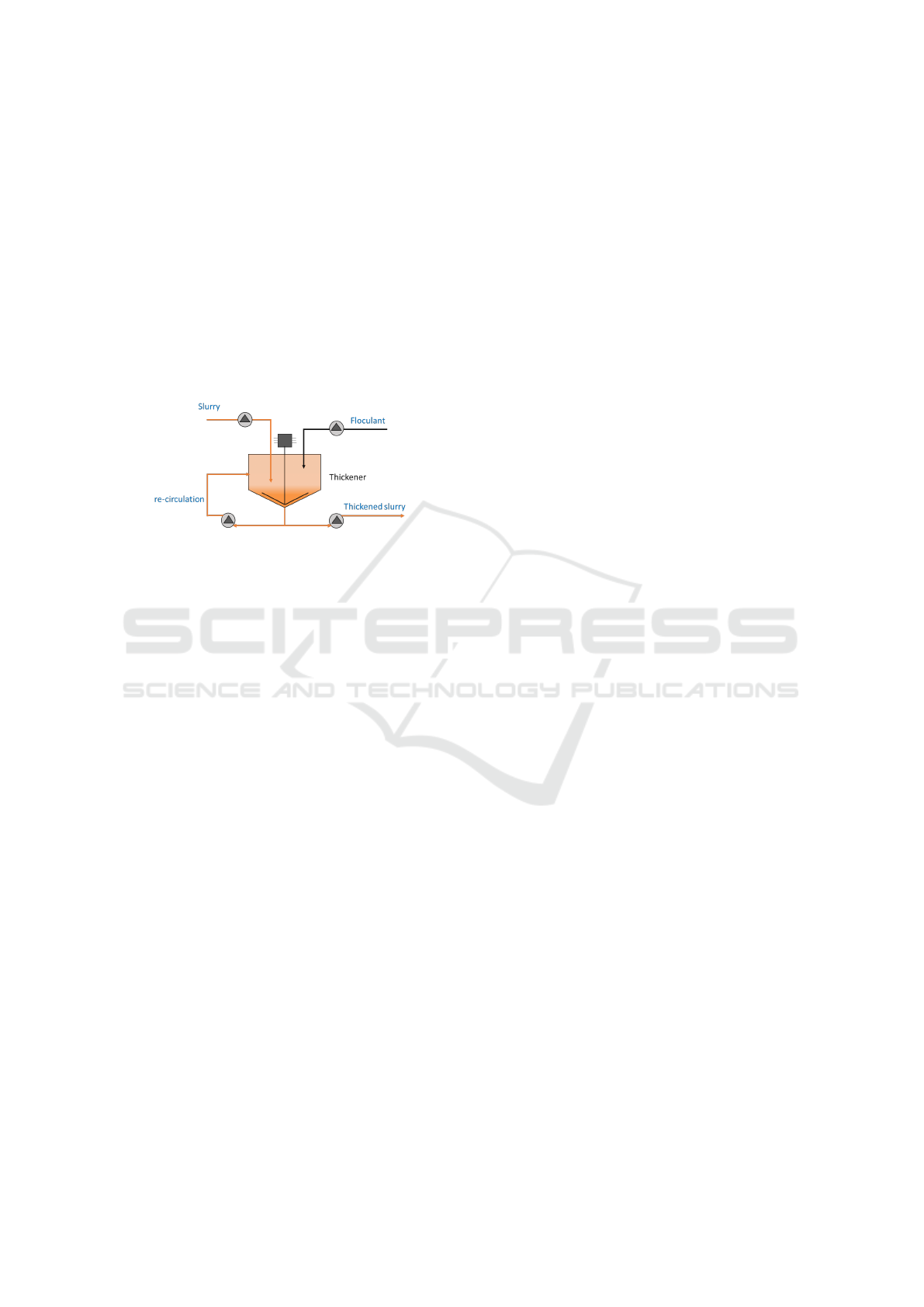
2 THICKENER OPERATION:

NAVIGATING THE

COMPLEXITIES

Thickening is considered the most implemented tech-

nology for producing high-solids slurries in the min-

ing industry.(Oulhiq et al., 2024; Wang et al., 2024).

Thickening provides two main purposes: clear water

recovery at the surface and thickened tailings by sed-

imentation.(Wang and Xiao, 2024). Flocculants and

coagulants are then widely used to increase the set-

tling velocity of the solids to provide fast clear-water

recovery.(Zaki et al., 2023). Figure 1 illustrates a typ-

Figure 1: Typical Thickener used in the mining industry.

ical thickener commonly used in many mining opera-

tions. Thickeners are complex systems, using several

components to achieve a suitably high density. (Na-

gai et al., 2018). Their mode of operation is based on

the coexistence of certain fundamental elements (Juan

and Aldo, 2019).

The operation of the thickener analyzed begins at

the entry point, where the pulp is introduced into the

thickener by a centrifugal pump with a density of be-

tween 1450 and 1530 kg/m³. The thickened sludge is

transferred to the center of the thickener by means of

slow-moving arms, also known as rake mechanisms,

which play a key role in consolidating the sedimented

particles, known as residues(Ojeda et al., 2014; Xu

et al., 2017).

The pulp fed to the thickener is mixed with a ﬂoc-

culant solution using another pump. These ﬂoccu-

lants, usually long-chain polymers, help to agglom-

erate small particles into large agglomerates, encour-

aging rapid settling and improving the separation of

the solid and liquid phases.

Effective control of the tailings and overﬂow

streams is essential to optimize the performance of the

thickener (Ruuska et al., 2020; Oulhiq et al., 2024).

Dense residues must be pumped out to avoid clog-

ging, while clariﬁed liquid is discharged from the top

of the thickener. A recycle pump is used to reintro-

duce the pulp into the circuit, improving the overall

process. This step is crucial for balancing the density

of the lower ﬂow and reducing the pressure around

the thickener cone, which is essential for maintain-

ing the mechanical integrity and operational stabil-

ity of the thickener. The ﬁnal stage of the thicken-

ing process produces a thickened slurry, ready to be

processed or disposed of according to speciﬁc indus-

trial needs (Serova et al., 2016; Oulhiq et al., 2021).

Thickeners face challenges related to the interaction

between operational variables and variable time con-

stants. Downstream thickeners thus control varia-

tions in the ﬂow characteristics of upstream opera-

tions, covering both physical and chemical aspects (Li

and Gupta, 2023). These ﬂuctuations, linked to feed

rate and solids concentration, result from variations in

upstream conditions (Pirouz et al., 2017). These de-

ﬁned problems result in inferior products, highlight-

ing the need to improve operational practices and im-

plement advanced process control systems.

3 ADVANCED PROCESS

CONTROL OF THICKENERS

The thickening process requires elaborate control sys-

tems to ensure optimal performance. While the man-

agement of non-linearities and operational complex-

ities is facilitated by intelligent control systems, no-

tably fuzzy logic controllers and expert systems, their

use is limited by the lack of historical or heuristic

data.Thus, this paper will review and evaluate two

predictive control solutions with the aim to assess

their effectiveness, discern their limitations, and high-

light opportunities for improvement.

3.1 Model Predictive Control (MPC)

A prominent advanced control strategy for thickening

processes is Model Predictive Control has (MPC). It

has been applied in a number of areas, including coal

mining, in order to tackle the difﬁculties of time vary-

ing dynamics and complexity of measured parame-

ters such as coal residue.(Tan et al., 2017) This pre-

dictive control strategy is based on an explicit dy-

namic model of the process to determine the con-

sequence of future changes in the manipulated vari-

ables on the output. The control signal is obtained by

minimizing a cost function and the controller perfor-

mance depends highly on the accuracy of the input-

output model.(Camacho and Bordons, 1999; Kouvar-

itakis and Cannon, 2016) The controlled variable of

the thickener process is the output slurry density D

out

also a state variable. Additional state variables in-

clude bed level L

, overﬂow turbidity T

, rake torque

, and cone pressure P

. Manipulated variables are

feed slurry ﬂow rate F

and ﬂocculant ﬂow rate F

ﬂoc

Measured disturbances are inlet slurry density D

Advanced Predictive Process Control for Industrial Thickeners

263

underﬂow slurry ﬂow rate F

out

, and circulation ﬂow

rate F

circ

To predict the output of the process at future times,

we use the state space model proposed by (Oulhiq

et al., 2024):

k|k−1

= AX

k−1

+ BU

k−1

+ KD

k−1

ˆy

k|k−1

= C

k|k−1

(1)

For a system with multiple delays, it is suggested

that an extended state-space formulation be used.

This approach amounts to rewriting the system in

terms of additional state variables, which results in

a standard delay-free system of increased order. The

augmented state vector is deﬁned as follows(Oulhiq

et al., 2024):





k−1





∈ R

, with n = n

+ ρ

Subsequently, an augmented state space representa-

tion of the system is obtained:

k|k−1

k−1

Bu(k − 1) +

Kd(k − 1)

k|k−1

(2)

The objective of the control is the thickener

outlet slurry density under measured disturbances

while considering the process constraints, namely,

the bed level, the overﬂow turbidity, the rake torque,

and the cone pressure. It also considers the process

disturbances including the feed slurry density, the

circulation ﬂowrate, and the outlet slurry ﬂowrates.

The MPC problem is then formulated as:

min

J(S) =

∑

i=1

Q( ˆx

− w

)

∑

i=1

Subject to:

for k ∈ [1, N]

ˆx(k + 1) = Ax(k) + Bu(k) + Kd(k)

ˆy(k + 1) = C ˆx(k + 1)

min

≤ ˆx(k + 1) ≤ x

max

min

≤ u(k) ≤ u

max

for i ∈ [M, N]

u(i) = 0.

(3)

Where w

is the underﬂow slurry density reference

at time step i, S = {u(1), . . . , u(M)} is the set of

optimized manipulated inputs, M is the control

horizon, N is the prediction horizon, R is the penalty

for the manipulated variables, Q is the penalty for the

quadratic error, x

max

and x

min

are the maximum and

minimum values, respectively, of the state vector x,

and u

max

and u

min

are the maximum and minimum

values of the manipulated inputs, respectively.

Model Predictive Control (MPC) is fundamentally

based on its capacity to resolve a time-dependent op-

timization problem during each iteration of the al-

gorithm. Following the completion of the optimiza-

tion, the system is transitioned to a new state through

the execution of a segment of the computed optimal

control sequence within the established application

horizon. Nonetheless, the accuracy of the prediction

model is a pivotal element in the efﬁcacy of MPC,

a feature that can be signiﬁcantly inﬂuenced by the

uncertainties and dynamic characteristics commonly

present in real-world situations.

The integration of adaptive control strategies into

the MPC framework presents a promising solution to

this challenge. The predictive model’s robustness and

reliability are enhanced by adaptive control, which al-

lows the system to respond dynamically to changing

conditions, even in the presence of ambiguous or ﬂuc-

tuating parameters.

3.2 Adaptive Model Predictive Control

Adaptive Model Predictive Control (AMPC) is a ver-

sion of Model Predictive Control (MPC) designed to

handle the challenges of systems with time-varying

dynamics. While traditional MPC relies on a de-

terminist model of the process, AMPC continu-

ously updates the model in real time based on new

data.(Landau et al., 2024; Sanchez, 1981) This allows

AMPC to compensate for changes in system behav-

ior due to external disturbances, equipment wear, or

changing process conditions, ensuring optimal perfor-

mance over time.

3.2.1 Real-Time Model Adaptation

The fundamental principle of AMPC is real-time

model adaptation. AMPC periodically updates

the process model as new data becomes avail-

able.(Landau et al., 2024). This is crucial in processes

where the system dynamics change over time, such

as in industrial thickeners, where slurry composition,

feed rates, or chemical properties often ﬂuctuate.

Real-time model adaptation typically involves the

following steps:

1. Model Identiﬁcation. The system parameters are

identiﬁed from process data using online estima-

tion techniques, such as Recursive Least Squares

(RLS) or Kalman Filtering. The identiﬁed param-

eters reﬂect the current operating conditions of the

process.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

264

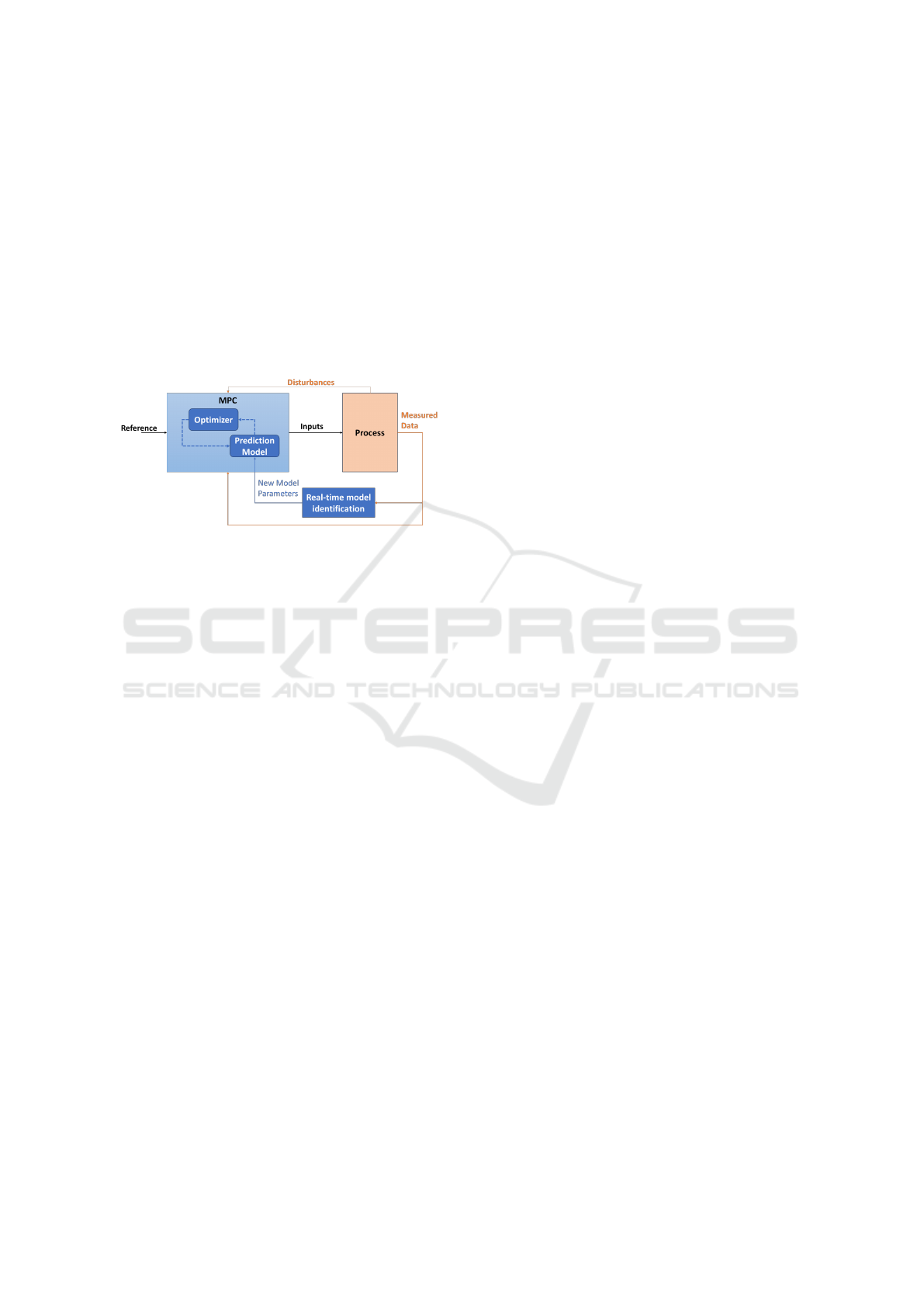
2. Model Update. The process model used in the

MPC optimization is updated at each control in-

terval using the latest parameter estimates.

3. MPC Optimization. The MPC algorithm solves

an optimization problem using the updated model

to compute the optimal control inputs.

4. Control Implementation. The ﬁrst control input

in the optimized sequence is applied to the pro-

cess.

these steps are represented in the framework illus-

trated in 2 This real-time adaptation allows AMPC

Figure 2: AMPC Framework.

to track changes in process dynamics and maintain

high-performance control, even in the presence of un-

certainties or disturbances.

3.2.2 Recursive Least Squares (RLS) for

Parameter Identiﬁcation

Recursive Least Squares (RLS) is a popular technique

for online parameter estimation in adaptive control

systems.(Mohseni et al., 2020; Salamati et al., 2017)

It is particularly suited for AMPC because of its abil-

ity to efﬁciently update parameter estimates in real-

time, with minimal computational overhead.(Nguyen

et al., 2020) RLS is used to minimize the prediction

error between the measured system output and the

output predicted by the current model.(Gholaminejad

et al., 2016) At each discrete time step, the RLS al-

gorithm updates the parameter estimates based on the

new input-output data, ensuring that the model accu-

rately reﬂects the current system behavior. (Ziemann,

2023; Jin and Ding, 2023) The updated parameters

are then used by the MPC to compute the control in-

puts for the next time step.

In the thickener control context, the system dy-

namics are governed by a set of state-space equations,

where the system matrix A and input matrix B can

change due to variations in feed characteristics, chem-

ical properties of the slurry, or environmental condi-

tions. The RLS algorithm is employed to update these

matrices in real time based on process measurements.

At each time step, the AMPC algorithm solves the

following optimization problem:

min

U(1),...,U(M)

∑

i=1

( ˆx(k + i|k) − x

ref

)

Q( ˆx(k + i|k) − x

ref

)

∑

i=1

U(i)

RU(i)

(4)

Subject to:

ˆx(k + i + 1|k) = A(k) ˆx(k + i|k)+ B(k)U(i),

ˆx(k) = x(k),

min

≤ U (i) ≤ U

max

Where:

• ˆx(k + i|k) is the predicted state at time k + i,

• x

ref

is the reference state (setpoint),

• Q and R are the weighting matrices for state devi-

ations and control effort, respectively,

• A(k) and B(k) are the updated system matrices ob-

tained using RLS.

The AMPC controller uses the updated model

A(k), B(k) at each time step to compute the optimal

control inputs that minimize the cost function while

satisfying the system constraints.

3.3 Practical Application

To compare the control strategies, we utilize a model

developed by (Oulhiq et al., 2024) using the Historical

Data-Driven System Identiﬁcation method. The state

space model developed by (Oulhiq et al., 2024) is as

follows:

ˆx

k|k−1

= A ˆx

k−1

+ BU

k−1

+ KD

k−1

ˆy

k|k−1

= C ˆx

k|k−1

(5)

Where:

• ˆx

k|k−1

is the state estimate at time k, given the in-

formation up to time k − 1,

• ˆy

k|k−1

is the output estimate at time k, given the

state estimate ˆx

k|k−1

• A is the state transition matrix,

• B is the input matrix,

• K is the gain matrix for the disturbance,

• C is the output matrix,

• U

k−1

is the control input at time k − 1,

• D

k−1

is the disturbance input vector at time k − 1,

•

k|k−1

is the prediction error for the state estimate.

The matrices are deﬁned by (Oulhiq et al., 2024).

Advanced Predictive Process Control for Industrial Thickeners

265

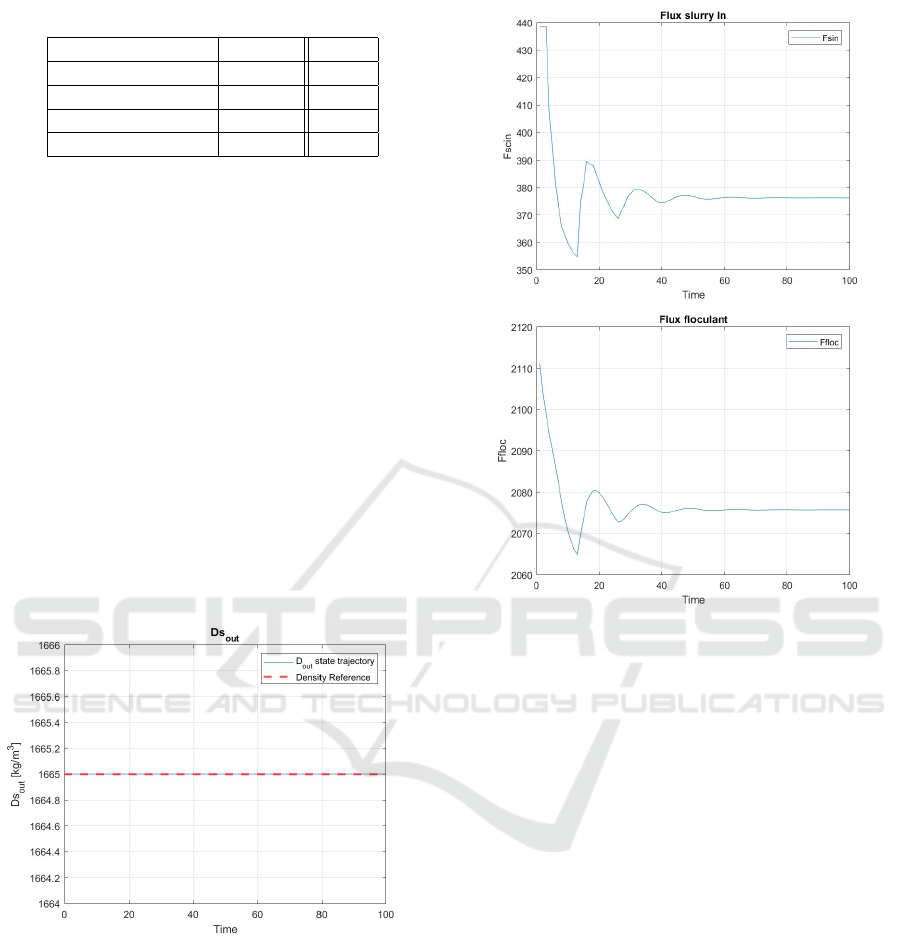
Table 1: MPC Parameters.

Parameter Symbol Value

Prediction horizon N 20

Control horizon M 2

Control weighting R 0.01

Error weighting Q 1

3.3.1 Application of MPC

Table 1 presents the MPC parameters used in our ap-

plication.

Initially, the MPC, the model parameters, and the

disturbance constraints speciﬁed by (Oulhiq et al.,

2024) are established. At each sampling instance k,

the current states x(k) and disturbances d(k) are mea-

sured, and the state prediction

is calculated utiliz-

ing the previous values of X, U, and D.

Subsequently, the MPC problem, as formulated in

Equation (11), is addressed using an optimizer. Once

the optimization concludes, the control inputs u

(k)

and u

(k) are derived from the solution and conveyed

to the processing system. At the termination of each

sampling period, the variables X

k−1

, u(k − 1), and

d(k − 1) are updated to inform the subsequent itera-

tion. The effectiveness of this approach is evidenced

by the simulation results presented in Figure 3

Figure 3: Underﬂow slurry density D

s,out

trajectory with

MPC.

As depicted in Figure 3 and Figure 4, the per-

formance of the Model Predictive Control (MPC) is

mainly assessed by the controlled process variable

and control inputs.

Figure3 illustrates the course of the underﬂow

slurry density, referred to as Dsout. The trajectory

closely corresponds with the reference(desired set

point) value. This demonstrates the controller’s pro-

ﬁciency in sustaining the slurry density near the in-

tended set point.

Figure 4: Control inputs.

Figure 4 illustrates the manipulated inputs: feed

slurry ﬂow rate (F

sin

) and ﬂocculant ﬂow rate (F

ﬂoc

Each plot tracks the respective ﬂow rate as a function

of time during the MPC operation.

The feed slurry ﬂow rate stabilizes within set lim-

its, with smooth and decisive control input avoiding

saturation. The rest of the parameters also transition

smoothly and remain within operational constraints.

This highlights the ability of the MPC to effectively

regulate inputs without exceeding physical limits or

causing reluctance in the command signal.

However, in real-world industrial applications, the

dynamics of the system are not always constant.

Gradual changes in parameters, such as those caused

by wear and tear of pumps or partial clogging of

pipes, can signiﬁcantly alter the behavior of the pro-

cess. These physical degradations manifest as shifts

in the system matrices A and B, affecting the perfor-

mance of the control strategy.

In our simulation, we introduced parameter varia-

tions to emulate these real-world challenges. Starting

from t = 30 minutes, the matrices A and B were

adjusted to simulate scenarios where equipment efﬁ-

ciency declines or ﬂow characteristics are adversely

affected. For instance, reduced pump efﬁciency can

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

266

alter the gain of the system, while a partially clogged

pipe may increase the resistance and impact ﬂuid

ﬂow rates. Despite the Model Predictive Control

(MPC) initially maintaining robust control, these

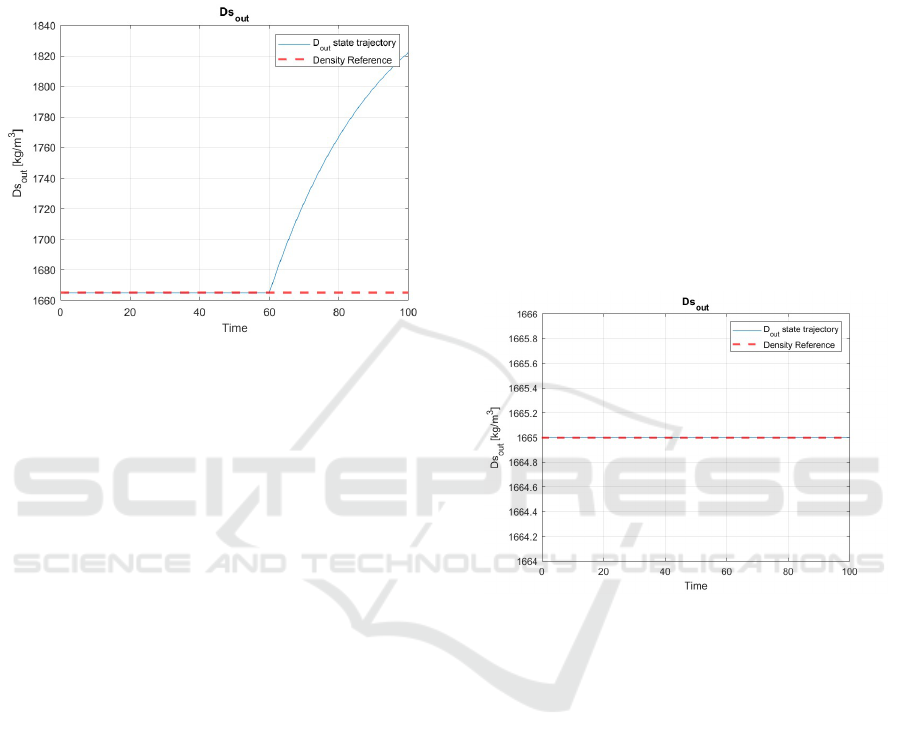
parameter changes exposed its limitations.

Figure 5: Results of MPC faced with a change in system

parameters.

As shown in Figure 5, the underﬂow slurry den-

sity D

s,out

begins to deviate signiﬁcantly from the ref-

erence trajectory when the system parameters shift

beyond a certain threshold. This occurs because the

MPC, relying on a static model, cannot fully compen-

sate for these evolving dynamics. Consequently, the

controller struggles to uphold performance, highlight-

ing the need for adaptive control strategies that can

adjust in real-time to changing process conditions.

3.3.2 Application of Adaptative MPC

To address the limitations of conventional Model Pre-

dictive Control (MPC) in handling time-varying sys-

tem dynamics, we implement an Adaptive Model Pre-

dictive Control (AMPC) strategy. In the previous ex-

ample of the thickener model, the physical degrada-

tions alter the dynamics of the thickening process, af-

fecting critical parameters in the system matrices A

and B. The adaptive approach involves identifying

these changes and updating the system model in real-

time. The identiﬁcation process focuses on detecting

variations in speciﬁc elements of the matrices A and

B. The simulation of change in the matrices concerns

the elements A

1,1

(k), A

3,3

(k), and A

4,4

(k) of matrix A

and B

1,13

(k), B

2,3

(k), and B

4,7

(k) of matrix B which

change from their initial value, reﬂecting the degrada-

tion or changes in the system dynamics.

The recursive update of the matrices parameters

estimates is performed using the RLS algorithm, pre-

viously explained.

In our simulations, parameter changes were intro-

duced between t = 30 min and t = 80min to emulate

the effects of equipment deterioration. The AMPC

framework was then applied to adapt the control strat-

egy in real time. Figures 6, 7, and 8 illustrate the per-

formance of the AMPC in managing the system under

these challenging conditions.

The trajectory of the underﬂow slurry density

s,out

is shown in Figure 6. Unlike the standard MPC,

the AMPC maintains the density close to the refer-

ence value despite the parameter variations, demon-

strating improved robustness and adaptability. Figure

7 and 8 depict the behavior of the feed slurry ﬂow rate

sin

and the ﬂocculant ﬂow rate F

ﬂoc

. The AMPC pro-

vides a smooth and responsive adjustment, stabilizing

the ﬂow rates within their operational limits. How-

ever, it is important to note that F

sin

is saturated at the

upper constraint limits.

Figure 6: Underﬂow slurry density D

s,out

trajectory with

AMPC.

The results demonstrate AMPC’s ability to adapt

to real-time parameter variations, ensuring thickener

performance, but reveals a critical issue where feed

slurry ﬂow rate becomes saturated at upper con-

straints. Once saturation occurs, the AMPC loses its

ability to respond effectively to further disturbances

or changes in the process, potentially compromising

stability and performance.

Additionally, it is important to note that the ﬂoc-

culant ﬂow rate F

ﬂoc

is not optimized in this control

approach. As a result, the consumption of ﬂoccu-

lant may become inefﬁcient and economically chal-

lenging. Excessive use of ﬂocculants increases oper-

ational costs and can lead to wastage, which is a sig-

niﬁcant concern in large-scale industrial processes.

Moreover While AMPC demonstrates robustness

in adapting to parameter variations, its effectiveness is

limited when faced with unknown disturbances. Fig-

ure 9 illustrates the response of the underﬂow slurry

density D

s,out

when subjected to an unknown distur-

Advanced Predictive Process Control for Industrial Thickeners

267

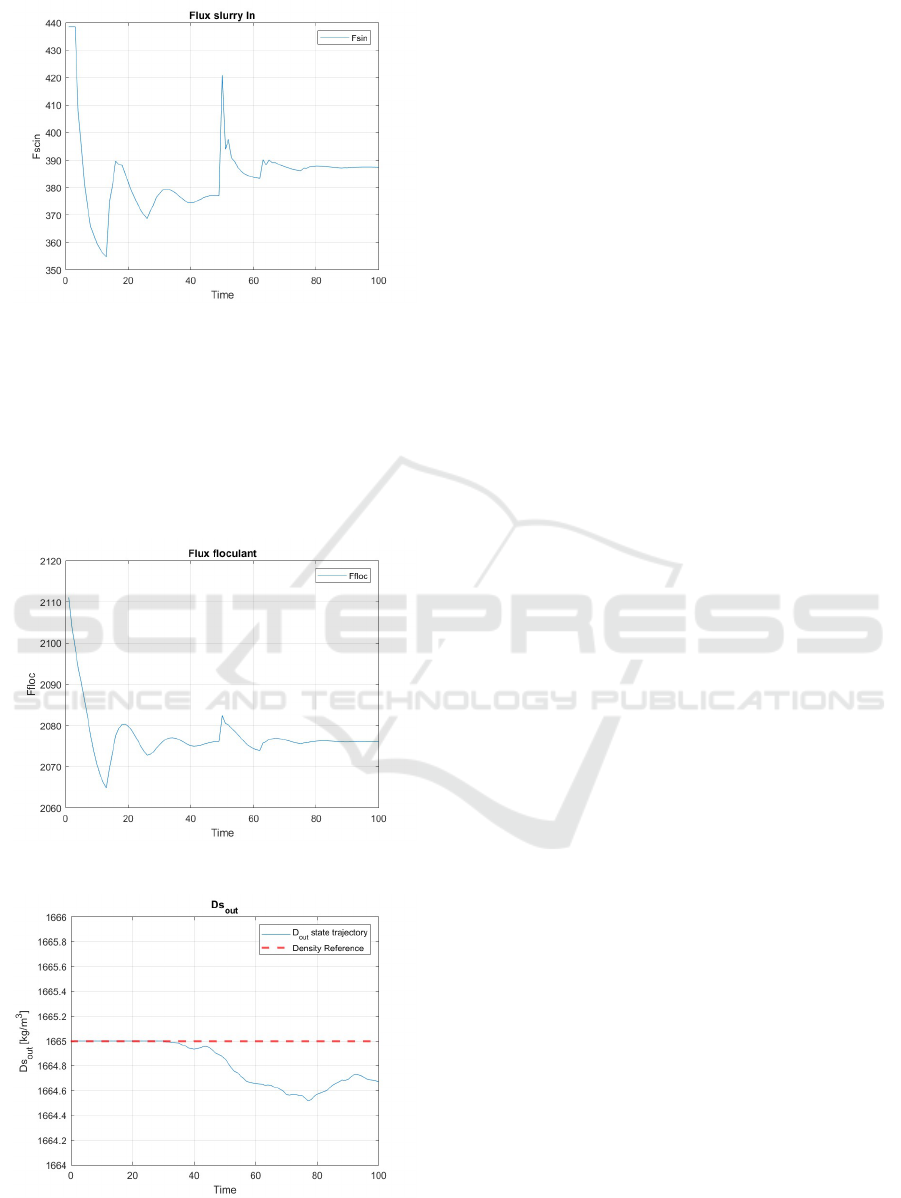
Figure 7: Feed slurry ﬂow rate F

sin

under AMPC.

bance modeled as white noise. The ﬁgure shows that

the AMPC cannot fully compensate for these random

variations, leading to deviations from the desired set-

point. This limitation underscores the inherent chal-

lenge of handling unpredictable physical phenomena,

which may require more advanced strategies, such as

disturbance observers or robust control techniques, to

mitigate.

Figure 8: Flocculant ﬂow rate F

ﬂoc

controlled by AMPC.

Figure 9: Underﬂow slurry density D

s,out

trajectory with

unknown dynamics.

4 CONCLUSION

This paper details the deployment and assessment of

Adaptive Model Predictive Control (AMPC) for in-

dustrial thickening operations. The AMPC frame-

work enhances control performance by the continu-

ous update of the system model via real-time param-

eter estimation methods. The ﬁndings indicate that

AMPC markedly enhances the resilience of thickener

operations, maintaining essential parameters within

speciﬁed operational thresholds despite varying sys-

tem conditions. The study underscores ongoing is-

sues, notably the AMPC framework’s failure to ad-

dress unforeseen disturbances like white noise and

the suboptimal use of ﬂocculants, resulting in eco-

nomic inefﬁciencies and elevated operational costs.

Consequently, subsequent research should concen-

trate on incorporating intelligent control methodolo-

gies to augment AMPC’s disturbance rejection proﬁ-

ciency, as well as implementing ﬂocculant optimiza-

tion methods to decrease operational costs and en-

hance thickening control efﬁciency.

ACKNOWLEDGEMENTS

The authors acknowledge having used artiﬁcial

intelligence-based authoring tools such as Quillbot,

ChatGPT, and Grammarly to reﬁne the language, im-

prove clarity, and increase the overall readability of

this document. Despite the contribution of these tools

to facilitating language improvements, it should be

emphasized that the intellectual content, analysis, and

conclusions set out in this document remain entirely

the authors’ responsibility.

REFERENCES

Adewuyi, S. O., Anani, A., and Luxbacher, K. (2024). Ad-

vancing sustainable and circular mining through solid-

liquid recovery of mine tailings. Process Safety and

Environmental Protection, 189:31–46.

Betancourt, F., B

urger, R., Diehl, S., and Far

as, S. (2014).

Modeling and controlling clariﬁer–thickeners fed by

suspensions with time-dependent properties. Minerals

Engineering, 62:91–101.

Camacho, E. F. and Bordons, C. (1999). Model Predictive

Control. Springer.

Concha, A. and Fernando (2014). Thickening. In Solid-

Liquid Separation in the Mining Industry, pages 173–

280. Springer International Publishing.

Farrow, J. B., Fawell, P. D., Johnston, R. R. M., Nguyen,

T. B., Rudman, M., Simic, K., and Swift, J. D. (2000).

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

268

Recent developments in techniques and methodolo-

gies for improving thickener performance. Chemical

Engineering Journal, 80(1):149–155.

Gholaminejad, T., Khaki-Sedigh, A., and Bagheri, P.

(2016). Adaptive tuning of model predictive control

based on analytical results. In 2016 4th International

Conference on Control, Instrumentation, and Automa-

tion (ICCIA), pages 226–232.

Jin, Y. and Ding, F. (2023). 1. a coupled recursive least

squares algorithm for multivariable systems and its

computational amount analysis by using the coupling

identiﬁcation concept. International Journal of Adap-

tive Control and Signal Processing.

Juan, I. and Aldo, C. (2019). Dynamic modeling and simu-

lation of tailing thickener units for the development of

control strategies. Minerals Engineering 131.

Kosonen, M., Kauvosaari, S., Gao, S., and Henriksson, B.

(2017). Performance optimization of paste thickening.

In Wu, A. and Jewell, R., editors, Paste 2017: Pro-

ceedings of the 20th International Seminar on Paste

and Thickened Tailings, pages 13–22, Beijing. Uni-

versity of Science and Technology Beijing.

Kouvaritakis, B. and Cannon, M. (2016). Model Predictive

Control. Springer International Publishing.

Landau, I. D., Lozano, R., Saad, M. M., and Karimi, A.

(2024). 2. adaptive control: Algorithms, analysis and

applications. arXiv.org.

Li, Z. and Gupta, R. (2023). 1. impacts of various hydraulic

and solid loading conditions on process capability of

sludge thickening with thickening centrifuges. Pro-

ceedings of the Water Environment Federation.

Mohseni, N., Nguyen, T. W., Ul Islam, S. A., Kolmanovsky,

I. V., and Bernstein, D. S. (2020). Active noise con-

trol for harmonic and broadband disturbances using

rls-based model predictive control. In 2020 American

Control Conference (ACC), pages 1393–1398.

Nagai, T., Tanaka, M., Oishi, T., and Kitazaki, T. (2018).

Thickener for obtaining high concentration slurry and

control method for same.

Nguyen, T. W., Islam, S. A. U., Bruce, A. L., Goel, A.,

Bernstein, D. S., and Kolmanovsky, I. (2020). Output-

feedback rls-based model predictive control *. pages

2395–2400. IEEE.

Ojeda, P., Bergh, L. G., and Torres, L. (2014). Intelligent

control of an industrial thickener. In 2014 13th Inter-

national Conference on Control Automation Robotics

& Vision (ICARCV), pages 505–510.

Oulhiq, R., Benjelloun, K., Kali, Y., and Saad, M. (2021).

Identiﬁcation and control of an industrial thickener

using historical data. In 2021 International Multi-

Conference on Systems, Signals & Devices (SSD).

Oulhiq, R., Benjelloun, K., Kali, Y., Saad, M., and Griguer,

H. (2024). Constrained model predictive control of

an industrial high-rate thickener. Journal of Process

Control, 133:103147.

Pirouz, B., Javadi, S., and Seddon, K. (2017). 5. thickener

performance variability: underﬂow solids concentra-

tion and ﬂowrate.

Ruuska, J., Nikula, R.-P., Ruhanen, E., Kauppi, J., Kau-

vosaari, S., and Kosonen, M. (2020). Data analysis of

a paste thickener. Open Engineering, 10(1):362–367.

Salamati, S. M., Salamati, S. A., Mahoor, M., and Salmasi,

F. R. (2017). Leveraging adaptive model predictive

controller for active cell balancing in li-ion battery.

In 2017 North American Power Symposium (NAPS),

pages 1–6.

Sanchez, J. M. (1981). 2. adaptive-predictive control sys-

tem.

Serova, N. V., Olyunina, T. V., Lysykh, M. P., Ermishkin,

V. A., and Smirnova, V. B. (2016). Thickening and

rheological properties of slurries as functions of the

oxidized nickel ore composition. Russian Metallurgy.

Tan, C. K., Bao, J., and Bickert, G. (2017). 5. a study on

model predictive control in paste thickeners with rake

torque constraint. Minerals Engineering.

Wang, L., Cheng, L., Yin, S., and Chen, J. (2024). Floccula-

tion, dewatering and sedimentation behaviour of mine

backﬁll slurry in deep cone thickener (dct). Journal of

Environmental Chemical Engineering, 12(2):112168.

Wang, Y. and Xiao, B. (2024). 3 - theory, experiment, and

equipment in tailings thickening process. In Wang, Y.

and Xiao, B., editors, Cemented Paste Backﬁll, pages

25–65. Elsevier.

Xie, D. D., Tong, X., Xie, X., Hou, K., and Li, J. Y.

(2015). Efﬁcient application of automation technol-

ogy in thickener process. In Advanced Materials

Research, volume 1094, pages 441–444. Trans Tech

Publications, Ltd.

Xu, J. N., Zhao, Z. B., and Wang, F. Q. (2017). Data

driven control of underﬂow slurry concentration in

deep cone thickener. In 2017 6th Data Driven Con-

trol and Learning Systems (DDCLS), pages 690–693.

Zaki, N., Hadoudi, N., Charki, A., Bensitel, N., Ouarghi,

H. E., Amhamdi, H., and Ahari, M. (2023). Ad-

vancements in the chemical treatment of potable

water and industrial wastewater using the coagula-

tion–ﬂocculation process. Separation Science and

Technology, 58(15–16):2619–2630.

Ziemann, V. (2023). 2. simulations of real-time system

identiﬁcation for superconducting cavities with a re-

cursive least-squares algorithm. Physical review ac-

celerators and beams.

Advanced Predictive Process Control for Industrial Thickeners

269