EDQKD: Enhanced-Dynamic Quantum Key Distributions with

Improved Security and Key Rate

Nikhil Kumar Parida

1 a

, Sarath Babu

2 b

, Neeraj Panwar

1 c

and Virendra Singh

1 d

Indian Institute of Technology Bombay, Mumbai, Maharashtra, India

National Institute of Technology Warangal, Warangal, Hanamkonda, Telangana, India

Keywords:

Quantum Key Distribution, BB84, Decoy State, Control Key, Beam Splitter Attack, Photon Number Splitting

Attack.

Abstract:

Widely adopted public key cryptography algorithms such as RSA and Elliptic Curve Cryptography (ECC)

are susceptible to Shor’s algorithm, necessitating the development of quantum-secure cryptographic solutions.

Quantum Key Distribution (QKD) has emerged as a potential approach for secure communication in the quan-

tum era. However, existing QKD protocols suffer from inefﬁciencies in key exchange rates and vulnerabilities

to attacks such as Photon Number Splitting (PNS) and Beam Splitter attacks. This paper proposes two dy-

namic QKD schemes that enhances security and efﬁciency by employing a dynamically changing control key.

The unpredictability of these control keys ensures stronger randomness and resistance against adversarial at-

tacks. The proposed scheme achieves a key exchange rate of 87.5%, signiﬁcantly surpassing the 50% rate of

the widely used BB84 protocol. These improvements demonstrate the potential of the proposed approach as a

secure and efﬁcient solution for quantum communication networks.

1 INTRODUCTION

Quantum-secure networks are essential due to the rise

of of quantum computers (Imran et al., 2024). The

traditional cryptographic protocols are computation-

ally infeasible to solve with current technology or

classical computers (Tom et al., 2023). However,

quantum computers are being a threat to many exist-

ing encryption methods such as RSA (Rivest et al.,

1978), ECC (Hankerson and Menezes, 2021), DHKE

(Difﬁe and Hellman, 2022), etc. One approach to

achieve quantum secure communication is Quantum

Key Distribution (QKD).

QKDs leverages the uncertainty principle (Nwaga

and Nwagwughiagwu, 2024), entanglement and the

no-cloning theorem to securely transmit the key. The-

oretically, QKDs are secure against eavesdropping,

even from adversaries with quantum computing ca-

pabilities. Typically QKD involves ﬁve phases : key

generation, transmission, measurement, key recon-

ciliation, and error checking. BB84 was the ﬁrst

https://orcid.org/0009-0007-3403-1074

https://orcid.org/0000-0003-3823-2213

https://orcid.org/0000-0002-6592-9254

https://orcid.org/0000-0002-7035-7844

ever QKD scheme, presented in 1984 by, Bennet

and Brassard. This scheme used polarized light for

communication (Bennett and Brassard, 2014) and

classical channel for key reconciliation. Later, in

1991, Arthur Ekert developed an entanglement-based

scheme called E91 (Ekert, 1991). These two proto-

cols become the foundation of many upcoming QKD

schemes. The independent measurement in QKDs in-

troduces randomness, making it difﬁcult for an eaves-

dropper to predict the basis or the ﬁnal key. Thereby

improving the secrecy of the shared data. However,

randomness inevitably leads to discarding a signiﬁ-

cant amount of data, resulting in only 50% (Hassan

and Abouelazm, 2024) of the transmitted bits being

usable (those with matching basis). Consequently, the

key generation rate reduces and increases the trans-

mission overhead leading to high system cost.

Numerous QKD algorithms, mostly extensions of

BB84 or E91, address security challenges, by relying

on randomness and base matching. In this paper, we

propose two dynamic QKD approaches those enhance

the key exchange rate and improves the efﬁciency

of quantum key distribution by using a dynamically

changing control key. The control keys do not exhibit

predictable patterns or correlations, ensuring the ran-

domness and security of the system. Furthermore, the

586

Parida, N. K., Babu, S., Panwar, N. and Singh, V.

EDQKD: Enhanced-Dynamic Quantum Key Distributions with Improved Security and Key Rate.

DOI: 10.5220/0013507900003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 586-591

ISBN: 978-989-758-760-3; ISSN: 2184-7711

proposed method ensures robustness against attacks

on QKD, including the (Wang, 2005) Photon Number

Splitting (PNS) attack and beam splitter attack (Du

sek

et al., 1999).

2 RELATED WORK

Over the years, researchers have discovered various

challenges in quantum key exchange, such as low

key generation rate, lack of hardware of efﬁcient im-

plementation of QKD, cost, limited transmission dis-

tance, etc. Most QKD protocols require public rec-

onciliation of measurement bases, exposing them to

eavesdropping. In 1998, (Hwang et al., 1998) pro-

posed to share the basis for measurement either by

courier or BB84 itself to counter this information loss.

However, it is impractical to exchange information by

courier. Moreover, initial exchange using BB84, re-

mained vulnerable to PNS and beam splitter attacks.

In 2009, C

alin Anghel (Anghel, 2009) intro-

duced base selection and synchronization to BB84,

improving key generation and fooling eavesdrop-

pers with fake photons. He extended this in 2011

with eavesdropper detection(Anghel, 2011). In 2010,

(Chong and Hwang, 2010) a scheme was proposed

where both parties contributed to key generation,

however the overall key generation efﬁciency was

50%. In 2017 (Ur Rehman et al., 2017) suggested

a QKD protocol with a control key. They used tradi-

tional BB84 to transfer a bit sequence is called control

keys. Both parties generate a random key K

using the

control key K

. Alice transfers original key K

to Bob

using K

. The scheme is secure against PNS, although

it increases complexity and overhead.

From the literature review, we realized that QKDs

are theoretically secure, however they can still leak in-

formation. Several improvements such as decoy state

protocols and synchronization techniques, were pro-

posed to enhance security and efﬁciency, though these

solutions often introduced complexity and overhead.

3 PROPOSED SCHEME

In the proposed QKD schemes, the key is transmit-

ted in ﬁxed sized segments (blocks) instead of trans-

mitting the key at once. The proposal contains two

QKD protocols: (i) Dynamic Quantum Key Distribu-

tion (DQKD), and (ii) Enhanced Quantum Key Dis-

tribution (EQKD).

3.1 Dynamic Quantum Key

Distribution (DQKD)

The proposed key exchange scheme includes two

phases: (i) Control key exchange and (ii) Dynamic

basis generation and key exchange.

3.1.1 Control Key Exchange

Two parties (Alice and Bob) want to exchange a se-

cret key of size n bits. They will transmit a portion

of the qubits (m bits) using the BB84 protocol, with

the initial bits representing a fraction of the actual key

size (m = n/4 bits). Only a fraction of those m qubits

will be successfully interpreted by Bob. The correctly

interpreted k bits are considered as the initial control

key. The control key exchange using BB84 is as fol-

lows:

1. Initial Qubit Preparation. Alice prepares and

sends m qubits to Bob over a quantum channel,

using either the rectilinear or diagonal basis.

2. Measurement by Bob. Bob measures the qubits

and records the measurement result.

3. Basis Exchange. After the transmission of m

qubits, both parties exchange the basis used for

measurement over a public classical channel..

4. Key Generation. The measured value corre-

sponding to matching basis are retained and the

non-matching bases and values are discarded.

Alice and Bob use the received k bits as the control

key. From the control key, they derive the informa-

tion needed for the dynamic basis generation and key

exchange, as shown in Figure 1.

3.1.2 Dynamic Basis Generation and Key

Exchange

The major processes of the dynamic basis generation

are base mapping and timing control. During the base

mapping, Alice and Bob select the basis (rectilinear

or diagonal) for the next segment.

A. Basis Mapping:

The control key, K

, is used to determine the basis

for further communication. Both parties compute

the parity of the control key to determine the ba-

sis, based on Table 1 and then decides the encod-

ing scheme. The control key bits (0s and 1s) are

transformed into the corresponding basis to gen-

erate the basis sequence. The generated basis se-

quence is used to transmit and measure the qubits

present in the partial key (next key segment). The

key preparation is depicted in Figure 2.

EDQKD: Enhanced-Dynamic Quantum Key Distributions with Improved Security and Key Rate

587

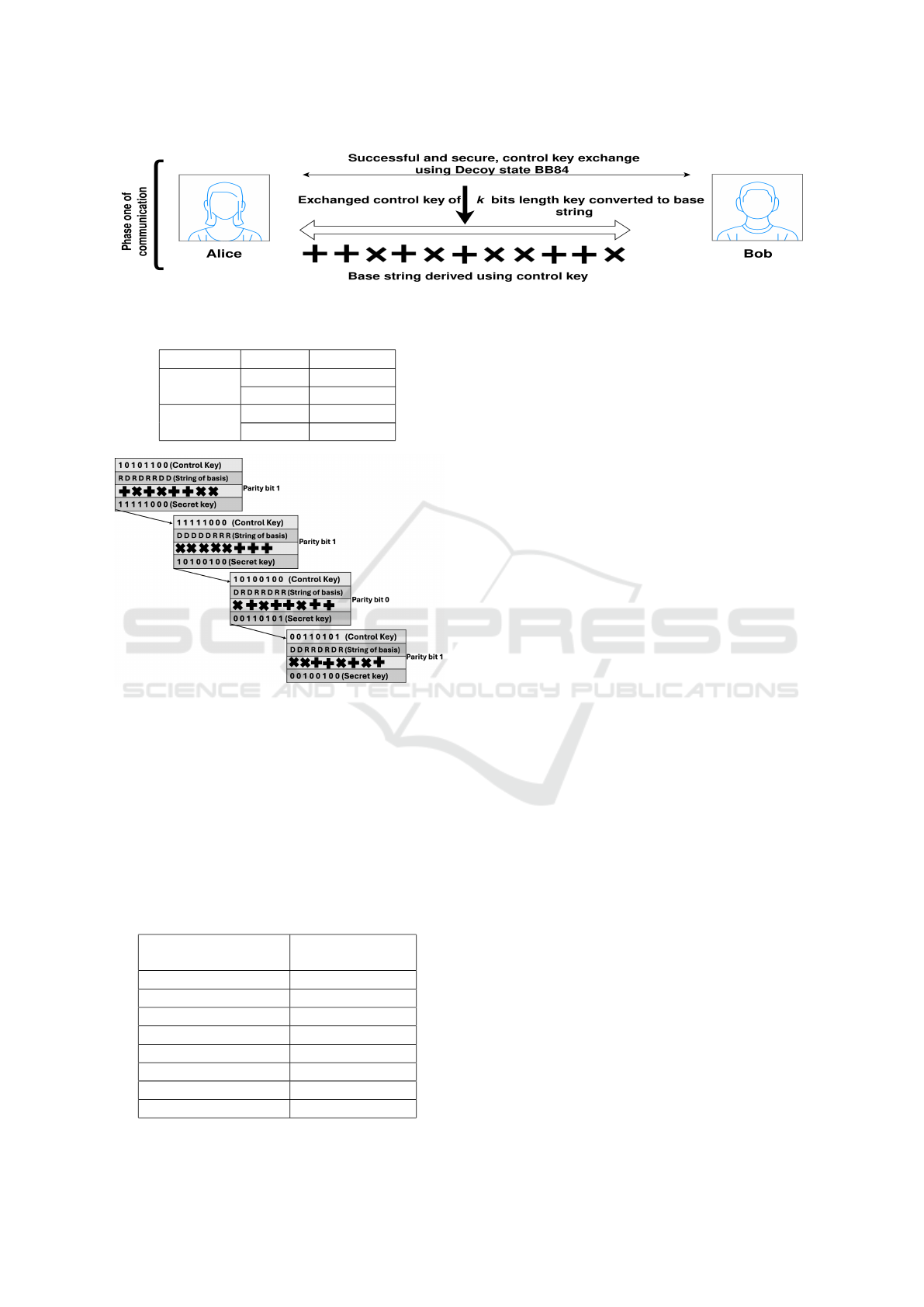
Figure 1: Control key exchange.

Table 1: Basis mapping for parity bit.

Parity bit Key Bit Basis

1 Diagonal

0 Rectilinear

1 Rectilinear

0 Diagonal

Figure 2: Key exchange and dynamic basis generation.

B. Timing Control:

For synchronization, the most signiﬁcant three

bits of the control key K are used to determine the

interval between consecutive qubit transmissions.

For example, the most signiﬁcant three bits of the

control key, “001”, will represent a 3-millisecond

gap, the timing signal selection is shown in Table

C. Qubit Encoding and Transmission:

Table 2: Timing control and synchronization.

Most signiﬁcant bits

(ﬁrst three bits)

Time interval

(in milliseconds)

000 2

001 3

010 4

011 5

100 6

101 7

110 8

111 9

Alice encodes the partial secret key according to

the bit string K and sends it to Bob via the quan-

tum channel.

D. Key Expansion:

Since Bob has already received the initial con-

trol key, he follows the same procedure as Alice

for time synchronization. Bob performs measure-

ments with respect to timing control and the cor-

rect base sequence. The resulting bit stream is

considered as the new partial secret key. This

ensures 100% measurement accuracy in an ideal

scenario.

Alice and Bob use the current partial secret key as

the new control key for encoding and timing control,

repeating the process iteratively (n/k times) until the

entire secret key is transmitted. The dynamic basis

generation and key exchange is depicted in Figure 3.

As traditional BB84 implementations using weak

coherent weak coherent pulses containing one or

more photons, are susceptible to PNS attack and beam

splitter attack. In order to make DQKD resilient to

Beam splitter and PNS attack we proposed Enhanced

Quantum Key Distribution (EQKD) scheme which is

secure against these attacks.

3.2 Enhanced Quantum Key

Distribution (EQKD)

We adopt the decoy-state BB84 protocol proposed by

(Wang, 2005) to mitigate shortcomings of DQKD. We

named this scheme as Enhanced Quantum Key Distri-

bution (EQKD). Alice follows the BB84 protocol and

prepares photons in four polarizations (0,90,45,135)

on a rectilinear and diagonal basis. Alice starts

preparing the photon, she prepares these to be one

of the three states: Decoy, signal, and vacuum states

(Wang et al., 2014) as described in Table 3. The sig-

nal state represents the actual qubits that Alice uses

to encode the secret key. The decoy state, where the

mean photon number per pulse is 1, is used to detect

potential eavesdropping. The vacuum state refers to

a situation where Alice sends no photons. Bob mea-

sures the received photons using one of two possible

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

588

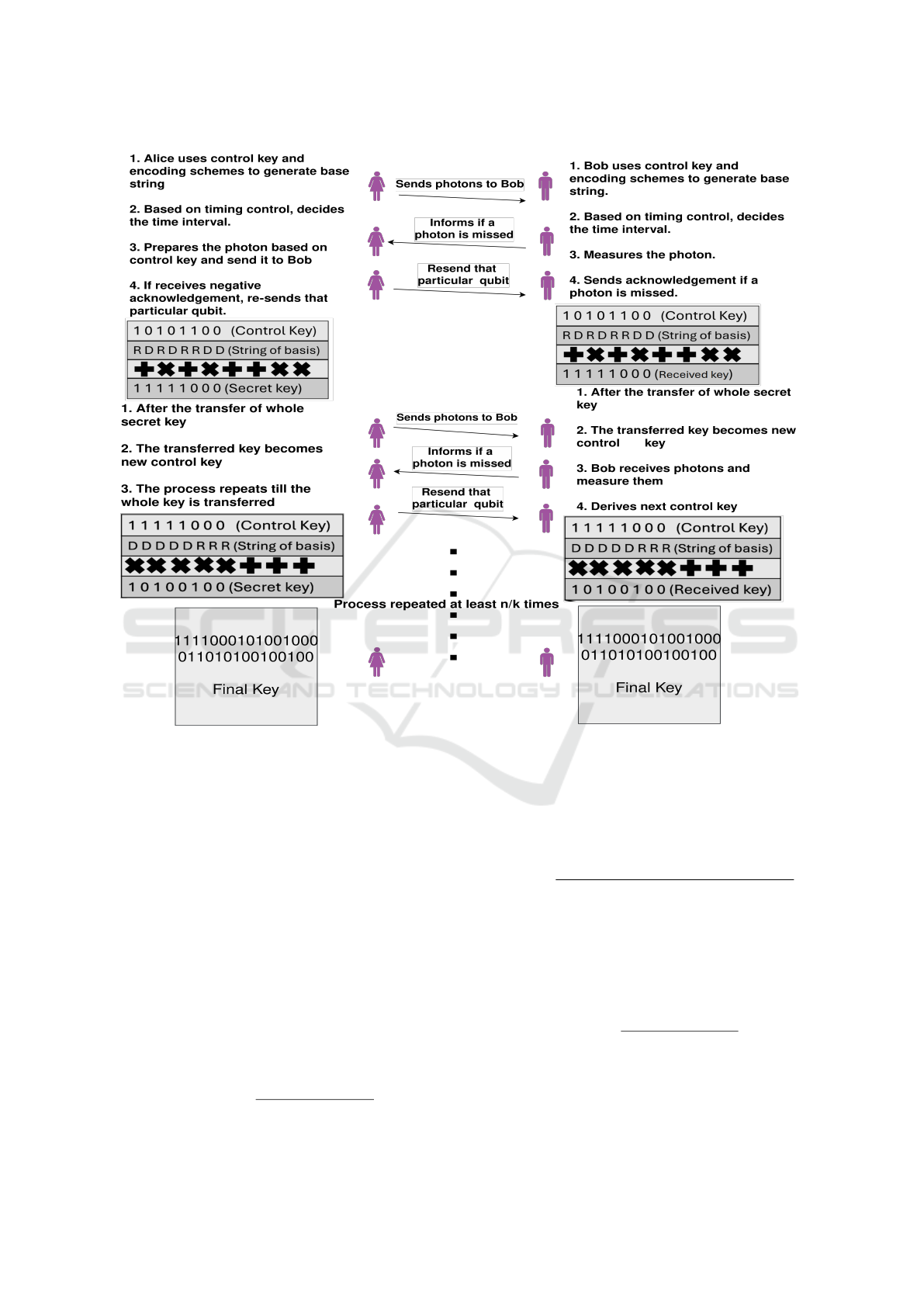
Figure 3: Dynamic key exchange process.

basis (rectilinear or diagonal). Alice and Bob then ex-

change their chosen basis through the classical chan-

nel. After the transmission phase is over, Alice cal-

culates the Yield Y

, Signal Yield Y

signal

, and Decoy

Yield Y

decoy

The expected photon number dependent yield is

given by

= Y

+ [1 − (1 − η)

] (1)

Where Y

is the noise or dark counts, and η is the

detection efﬁciency.

Alice calculates signal photon number dependent

yield Y

Signal

= Y

+ [1 − (1 − η

Signal

)

] (2)

Where η

Signal

is signal state efﬁciency. Alice then

ﬁnds that signal state efﬁciency is given by :

Signal

= −

ln[1 +Y

− Q

Signal

]

(3)

The µ is the mean signal state photon number (de-

scribed in Table 3), and the Q

Signal

is the signal state

gain, representing the probability that Bob success-

fully detects a signal state pulse sent by Alice. The

signal state gain Q

Signal

is calculated as follows:

Signal

Number of signal state detections

Total number of signal state pulse sent

(4)

Similarly, Alice determines the decoy photon

number-dependent yield Y

Decoy

for the decoy state.

Decoy

= Y

+ [1 − (1 − η

Decoy

)

] (5)

Alice then calculates the decoy state efﬁciency

Decoy

= −

ln[1 +Y

− Q

Decoy

]

(6)

Where v is the mean number of photons in the decoy

state (described in Table 3).

After ﬁnding out the signal photon number de-

pendent yield, she then determines the decoy photon

EDQKD: Enhanced-Dynamic Quantum Key Distributions with Improved Security and Key Rate

589

Table 3: Decoy state protocol conﬁguration as explained

(Wang et al., 2014).

State MPN Occurrence percentage

Signal “µ” 0.65 87.5%

Decoy “ν” 0.1 6.25%

Vacuum “ Y

” ∼0.0 6.25%

number dependent

Decoy

Number of decoy state detections

Total number of signal state pulse sent

(7)

If there is no eavesdropper in the system, then the

following condition will be satisﬁed,

η = η

Signal

± σ = η

Decoy

± ∆ (8)

Where σ and ∆ are variations in calculations due

to non-ideal devices.

= Y

Signal

= Y

Decoy

(9)

However, if any attacker is present in the commu-

nication channel, the respective yields will be differ-

ent. The below-mentioned condition will detect PNS

attack and notify us.

= Y

Signal

̸= Y

Decoy

(10)

Meanwhile this equation

̸= Y

Signal

= Y

Decoy

(11)

will tell about a successful Beam splitter attack on the

system. If any discrepancies indicating eavesdrop-

ping are found, discard the current key and stop the

communication. If no eavesdropper is present, the

communication will proceed as usual.

4 SECURITY ANALYSIS

For security analysis of our proposed schemes, We

are assuming that eavesdropper (Eve) has inﬁnite re-

sources and somehow obtains the control key. After

this, several scenarios can be considered:

1. Eve Secures the Initial Segment Basis:

Until entire control key is compromised Eve can-

not determine the encoding scheme.

Suppose she knows the encoding basis and the

time intervals between consecutive qubit trans-

missions. Eve would need to brute-force it to de-

termine the exact exchanged key. The complex-

ity of this brute force process would be 2

, where

k is the length of the control key. Since the key

exchange does not involve a classical channel for

transmitting the key, Eve would need to guess or

brute-force each key, resulting in a total complex-

ity of 2

× 2

× . . . 2

, n/k times, which is equiva-

lent to 2

2. Eve Does not Have Access to the Control Key:

If Eve does not have access to the control key, she

will still need to brute-force all the keys, adding

up to a complexity of 2

× 2

× . . . 2

, n/k times),

again equivalent to 2

3. Eve Obtains a Partial Key of Length k

If Eve somehow gains a partial key of length k,

she knows the basis for the next partial key trans-

mission. In this case, the complexity reduces to

n−k

, as Eve only needs to guess the remaining

portion of the key.

5 DISCUSSION

To overcome key generation inefﬁciency, we pro-

posed a dynamic scheme that uses (i) control key ex-

change and (ii) dynamic basis generation and key ex-

change. Let n represent the total number of qubits that

need to be transmitted. Initially, m qubits are trans-

mitted using the BB84 protocol, where m = n/4, rep-

resenting one-fourth of the actual key size.

Using BB84, approximately m/2 qubits are suc-

cessfully measured by Alice and Bob after basis

matching, which accounts for n/8 of the total key

length n. The mismatched bits are discarded.

For the remaining n − m = 3n/4 qubits, the pro-

posed scheme transmits and generates keys dynam-

ically. In this phase, no basis matching is required,

and all the bits are successfully exchanged without

any loss. Size of control key must be chosen care-

fully as, longer control key allows the entire key to be

exchanged in fewer iterations. But, if the control key

length is very small, it increases the risk of an attacker

obtaining the key through brute force with less effort.

The total key exchange rate for the proposed

scheme is:

Key Exchange Rate =

≈ 87.5%

The improvement in the key exchange rate over

the state-of-the-art BB84 protocol is calculated as fol-

lows:

Improvement =



−



× 100 =

× 100 ≈ 75%

Thus, DQKD achieves a 50% improvement in the

key exchange rate compared to the standard BB84. As

a result, we overcame the inefﬁciency part of BB84.

We address security aspect with, EQKD, the Decoy

signals, detects eavesdropper presence in the channel.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

590

During PNS attack the Eve will unknowingly

block most of the decoy state pulses. However, she

will not block signal states entirely; this causes the

change in yield of decoy states. Thus, leading to

̸= Y

signal

and Y

̸= Y

decoy

In the case of a beam splitter attack, the Eve in-

troduces a universal loss in the channel, affecting

both signal and decoy states, creating this result Y

̸=

signal

= Y

decoy

. If there is no eavesdropping, then

= Y

signal

= Y

decoy

6 CONCLUSION

This literature highlights the limitations of existing

QKD protocols, particularly BB84, in terms of low

key generation rates and vulnerabilities to advanced

attacks. To address these challenges, we proposed

two innovative schemes: Dynamic Quantum Key Dis-

tribution (DQKD) and Enhanced Quantum Key Dis-

tribution (EQKD). The DQKD scheme introduces a

dynamic approach to key exchange, achieving a sig-

niﬁcant improvement in efﬁciency with a key ex-

change rate of 87.5%, representing a 75% enhance-

ment compared to the traditional BB84 protocol. This

improvement is achieved by dynamically generating

and transmitting the remaining key segments without

the need for basis matching in most transmissions.

EQKD extends the DQKD by incorporating

decoy-state BB84, providing resilience against

photon-number-splitting (PNS) and beam-splitter at-

tacks while maintaining a high key generation rate.

The security of the proposed EQKD was rigorously

analyzed in Section 4, with potential attack scenarios

discussed to highlight the robustness of the scheme.

While EQKD demonstrates strong theoretical perfor-

mance, its practical behavior under simulation and

real-time implementation remains an area for future

exploration.

ACKNOWLEDGMENTS

This work was supported by an Indo-Japanese Joint

Lab Grant and Security of Futuristic Technology

sponsored by MEITY, Government of India.

REFERENCES

Anghel, C. (2009). Base selection and transmission

synchronization algorithm in quantum cryptography.

arXiv preprint arXiv:0909.1315.

Anghel, C. (2011). New quantum cryptographic protocol.

The Annals of “Dunarea de Jos “University of Galati.

Fascicle III, Electrotechnics, Electronics, Automatic

Control, Informatics, 34(2):7–13.

Bennett, C. H. and Brassard, G. (2014). Quantum cryptog-

raphy: Public key distribution and coin tossing. The-

oretical computer science, 560:7–11.

Chong, S.-K. and Hwang, T. (2010). Quantum key agree-

ment protocol based on bb84. Optics Communica-

tions, 283(6):1192–1195.

Difﬁe, W. and Hellman, M. E. (2022). New directions in

cryptography. In Democratizing Cryptography: The

Work of Whitﬁeld Difﬁe and Martin Hellman, pages

365–390. ACM.

sek, M., Haderka, O., and Hendrych, M. (1999). Gen-

eralized beam-splitting attack in quantum cryptogra-

phy with dim coherent states. Optics communications,

169(1-6):103–108.

Ekert, A. K. (1991). Quantum cryptography based on bell’s

theorem. Physical review letters, 67(6):661.

Hankerson, D. and Menezes, A. (2021). Elliptic curve cryp-

tography. In Encyclopedia of Cryptography, Security

and Privacy, pages 1–2. Springer.

Hassan, M. and Abouelazm, O. (2024). Improving bb84

efﬁciency with delayed measurement via quantum

memory. arXiv preprint arXiv:2410.21191.

Hwang, W. Y., Koh, I. G., and Han, Y. D. (1998). Quantum

cryptography without public announcement of bases.

Physics Letters A, 244(6):489–494.

Imran, M., Altamimi, A. B., Khan, W., Hussain, S., Al-

saffar, M., et al. (2024). Quantum cryptography for

future networks security: A systematic review. IEEE

Access.

Nwaga, P. C. and Nwagwughiagwu, S. (2024). Explor-

ing the signiﬁcance of quantum cryptography in future

network security protocols. World J Adv Res Reviews,

24(3):817–833.

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A

method for obtaining digital signatures and public-

key cryptosystems. Communications of the ACM,

21(2):120–126.

Tom, J. J., Anebo, N. P., Onyekwelu, B. A., Wilfred, A., and

Eyo, R. (2023). Quantum computers and algorithms:

a threat to classical cryptographic systems. Int. J. Eng.

Adv. Technol, 12(5):25–38.

Ur Rehman, J., Qaisar, S., Jeong, Y., and Shin, H. (2017).

Security of a control key in quantum key distribution.

Modern Physics Letters B, 31(11):1750119.

Wang, S., Chen, W., Yin, Z.-Q., Li, H.-W., He, D.-Y., Li,

Y.-H., Zhou, Z., Song, X.-T., Li, F.-Y., Wang, D.,

et al. (2014). Field and long-term demonstration of

a wide area quantum key distribution network. Optics

express, 22(18):21739–21756.

Wang, X.-B. (2005). Beating the photon-number-splitting

attack in practical quantum cryptography. Physical

review letters, 94(23):230503.

EDQKD: Enhanced-Dynamic Quantum Key Distributions with Improved Security and Key Rate

591