Model Quality and Student Satisfaction in BPMN Education: A

Quasi-Experiment

Matheus Ribeiro Brant Nobre

, J

essyka Vilela

and Lucas Migge de Barros

Centro de Inform

atica, Universidade Federal de Pernambuco (UFPE),

Av. Jornalista An

ıbal Fernandes, s/n – Cidade Universit

aria, Recife-PE, Brazil

Keywords:

Emotions, BPMN Modeling, Teaching BPM, Quasi-Experiment, Collaborative Modeling, Individual

Modeling.

Abstract:

Context: Teaching Business Process Management Notation (BPMN) is challenging due to its complexity.

Understanding how to improve BPMN education is crucial for technical accuracy and conceptual clarity.

Objective: This study examines how individual and collaborative BPMN modeling impact model qual-

ity—correctness and completeness—as well as students’ emotional experiences, including motivation, en-

joyment, and relaxation. It also explores the inﬂuence of psychological proﬁles, based on the Keirsey typol-

ogy, on these outcomes. Method: A quasi-experiment with 19 Information Systems students involved three

BPMN modeling exercises of increasing complexity. Participants alternated between individual and collabo-

rative modeling. Evaluations were based on BPMN quality criteria and emotional responses collected through

Likert-scale questionnaires. Statistical analyses included Wilcoxon tests, Spearman correlations, and ANOVA.

Results: There were no signiﬁcant differences in correctness and completeness between approaches, though

individual modeling slightly outperformed in technical metrics. Collaborative modeling increased enjoyment

and relaxation without reducing technical performance, indicating a trade-off between emotional engagement

and cognitive precision. Psychological proﬁles inﬂuenced outcomes, with Rationals achieving the highest

quality models and Idealists the lowest. Conclusion: The study highlights the need to balance technical rigor

and emotional engagement in BPMN education. Future research should explore long-term effects and collab-

orative tools to enhance BPMN training.

1 INTRODUCTION

Business Process Management (BPM) education

must extend beyond technical expertise, integrating

analytical, modeling, and communication competen-

cies essential for success in process-driven environ-

ments (Sarvepalli and Godin, 2017; Bandara and

et al., 2010)(Nobre and Vilela, 2024).

The Business Process Modeling Notation

(BPMN) is widely used in industry to describe an

organization’s business processes, particularly valued

for bridging communication between business and

IT teams. However, mastering BPMN presents

signiﬁcant challenges for students due to its complex

syntax and extensive range of elements, which

require high cognitive effort to accurately model

business processes.

https://orcid.org/0009-0000-0471-9280

https://orcid.org/0000-0002-5541-5188

https://orcid.org/0009-0000-2323-5345

This diversity in pedagogical strategies under-

scores the importance of evaluating how these ap-

proaches inﬂuence critical metrics, such as BPMN

model quality and student engagement. An under-

explored area in BPM education is how individ-

ual versus collaborative modeling approaches inﬂu-

ence model quality and students’ learning experiences

(Paschoal and et al., 2020). Besides the students’ per-

sonality that inﬂuence the learning process, emotions

play an important role in learning, inﬂuencing stu-

dents’ performance in challenging tasks.

Computing students often experience negative

emotions, such as frustration and anxiety, during

complex activities, but they also report positive emo-

tions, such as satisfaction and pride, when overcom-

ing obstacles (Atiq and Loui, 2022). This emotional

dynamic underscores the need for instructional strate-

gies that not only enhance technical skill but also

address the emotional challenges inherent in BPMN

modeling tasks.

620

Nobre, M. R. B., Vilela, J. and Migge de Barros, L.

Model Quality and Student Satisfaction in BPMN Education: A Quasi-Experiment.

DOI: 10.5220/0013483100003932

In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 1, pages 620-627

ISBN: 978-989-758-746-7; ISSN: 2184-5026

We conducted a quasi-experiment examining the

effects of individual and collaborative BPMN model-

ing on model quality and students’ satisfaction. 19 In-

formation Systems students alternated between mod-

eling individually and in groups, enabling a compar-

ative analysis of correctness, completeness, and self-

reported emotions, including enjoyment, motivation,

and relaxation.

The remaining of the paper is organized as

follows. Section II explores background as well

as related work. Section III outlines the quasi-

experimental design.Section IV presents results. Sec-

tion V contextualizes the ﬁndings within the existing

literature, and Section VI offers pedagogical recom-

mendations and directions for future research.

2 BACKGROUND

This section provides an overview of BPM, discusses

how personality proﬁles and emotions inﬂuence the

learning process, and reviews related work investi-

gating the effectiveness of individual and group ap-

proaches in BPM education.

2.1 Keirsey Proﬁle and Emotions

The Keirsey Proﬁle, developed based on Jung’s the-

ory of personality types and the Myers-Briggs Type

Indicator (MBTI), classiﬁes individuals into four pri-

mary temperaments: Guardian, Artisan, Idealist, and

Rational (Yilmaz and O’Connor, 2015).

These temperaments reﬂect behavioral predispo-

sitions that inﬂuence decisions and interactions in

the work environment. When combined with PBL,

Keirsey’s analysis can reveal patterns of behavior and

learning preferences (Arruda et al., 2019).

2.2 Related Work

Research on individual and collaborative modeling

approaches in BPM education has yielded mixed re-

sults, reﬂecting the complexity of their impact.

An experimental study of (Paschoal and et al.,

2020) compared BPMN modeling in individual and

group contexts, ﬁnding no signiﬁcant differences in

correctness or completeness. However, collabora-

tive activities enhanced engagement and participa-

tion, suggesting that teamwork’s beneﬁts extend be-

yond technical performance. In this context, the So-

cial BPM Lab explored collaborative modeling using

social software tools, emphasizing the development

of communication and teamwork skills (Caporale and

et al., 2013).

Although collaborative activities increased stu-

dent engagement and knowledge exchange, they did

not produce signiﬁcantly better technical quality than

individual modeling. This highlights the potential

for cooperative activities to build interpersonal skills,

even when their impact on technical outcomes is lim-

ited.

Despite these insights, notable gaps persist. We

did not ﬁnd studies that comprehensively examine the

role of emotions in BPMN modeling or how emo-

tional states relate to technical performance.

Moreover, the interplay between individual traits,

such as personality proﬁles and collaborative dynam-

ics, still needs to be explored. Addressing these gaps

is relevant for advancing BPM education and ensur-

ing that technical and interpersonal competencies are

effectively developed.

3 RESEARCH METHOD

In this section, we describe the methodological ap-

proach employed in this study.

3.1 Participants

This paper focuses on an in-person BPM course, de-

livered in Portuguese, with 36 undergraduate students

of the 4th semester from an Information Systems pro-

gram who had little to no prior experience with BPM.

The course spans 60 hours and incorporates a method-

ological approach that includes theoretical lectures,

multiple modeling exercises, exams, and the execu-

tion of an interdisciplinary PBL project (dos Santos

et al., 2023) in teams.

Six groups of six students were formed using the

team formation method (TFM) (dos Santos, 2023),

which integrates various aspects of students’ proﬁles

(Keirsey proﬁles, professional experience, gender and

age, and work preferences). Previous studies have ex-

amined the impact of this method compared to self-

selected teams on team performance (Vilela et al.,

2024).

The ﬁrst author were not involved in teaching or

designing the studied course, and his only role was a

researcher. The second author was the professor of

the course.

3.2 Quasi-Experimental Design

The use of a quasi-experimental design in this study

is justiﬁed by the organizational structure of the in-

terdisciplinary PBL project [omitted due to blind re-

Model Quality and Student Satisfaction in BPMN Education: A Quasi-Experiment

621

view], which naturally groups students into prede-

ﬁned teams.

The primary goal of this study is to investigate the

impact of individual and group modeling approaches

on the quality of BPMN models and students’ emo-

tions during the learning process. To achieve this ob-

jective, we deﬁne three research questions:

RQ1: What emotions do students report when per-

forming individual and group BPMN modeling?

RQ2: What are the differences in the technical qual-

ity of BPMN models (correctness and completeness)

between individual and group modeling?

RQ3: Does personality proﬁle, as deﬁned by Keirsey’s

typology, inﬂuence the technical quality of models or

students’ emotions during modeling activities?

Aims to answer these questions, this quasi-

experiment occurred in three main phases:

1. Training and Familiarization. Students partici-

pated in three classes about BPMN, covering the-

oretical foundations and practical modeling tech-

niques using BPMN tools. A categorization ques-

tionnaire was administered to measure students’

prior experience with process modeling, ensuring

a baseline for future comparisons.

2. Experimental Sessions. This phase occurred in

three stages:

Stage 1. All 36 participants individually modeled

a process in BPMN.

Stage 2. The six groups were randomly assigned

by drawing lots. Groups 2, 3, and 6 performed

the modeling activity in groups, while Groups 1,

4, and 5 completed the exercise individually.

Stage 3. Students modeled another business pro-

cess. Roles were reversed for the subsequent

task, enabling cross-comparisons between indi-

vidual and collaborative conditions.

3. Feedback and Data Collection. After each

session, students completed self-report question-

naires to assess their emotional experiences (mo-

tivation, enjoyment, and relaxation) using a Lik-

ert scale represented by emojis. BPMN models

were evaluated for correctness (accuracy in us-

ing BPMN elements and relationships) and com-

pleteness (including all relevant information for

the modeled scenario) by assistant teachers using

predeﬁned criteria.

3.3 Hypotheses, Variables and

Measurements

The formulation of research hypotheses, outlined in

Table 1, was guided by the study’s central questions

and objectives research.

Table 1: Research Hypotheses.

ID H

(Null Hypothesis) H

(Alternative Hypothesis)

H1 There is no signiﬁcant differ-

ence in correctness of BPMN

models produced individually

and in groups.

There is signiﬁcant difference

in correctness of BPMN mod-

els between individual and

group approaches.

H2 There is no signiﬁcant dif-

ference in completeness of

BPMN models produced indi-

vidually and in groups.

There is signiﬁcant difference

in completeness of BPMN

models between individual

and group approaches.

H3 There is no signiﬁcant dif-

ference in students’ emotions

(motivation, enjoyment, and

relaxation) between individual

and group modeling.

There is signiﬁcant differ-

ence in students’ emotions be-

tween individual and group

approaches.

H4 Keirsey proﬁles do not signif-

icantly inﬂuence correctness

and completeness of BPMN

models.

Keirsey proﬁles signiﬁcantly

inﬂuence correctness and

completeness of BPMN

models.

The variables were categorized to provide a struc-

tured understanding of the interactions between the

treatments applied and the observed outcomes, as out-

lined in Table 2.

Table 2: Variables and Attributes.

Category Description

Independent

Variables (Pa-

rameters)

Tool used (Bizagi Modeler), model structures

(AS-IS and TO-BE), evaluation method.

Independent

Variables (Fac-

tors)

Modeling approach (individual or group),

Keirsey proﬁle (Guardian, Artisan, Idealist,

Rational).

Dependent Vari-

ables

Quality of BPMN models (Correctness and Com-

pleteness), Students’ emotions (Motivation, En-

joyment, and Relaxation).

Correctness (CR) and completeness (CM) were

chosen as critical indicators of model quality, sup-

ported by prior BPMN evaluation studies (Paschoal

and et al., 2020). CR was calculated using a weighted

formula for error severity (light, medium, severe), of-

fering a nuanced assessment of technical accuracy.

This weighted system provides a more detailed

evaluation than binary correctness measures, captur-

ing the practical signiﬁcance of different error types

for the model’s usability. The formula for CR is:

CR =

EC + (1 × EI

Light

) + (2 × EI

Medium

) + (3 × EI

Severe

)

The maximum correctness value (CR = 1) is

achieved when all model elements are correct, with

no errors. Conversely, CR = 0 reﬂects all elements

being incorrect and classiﬁed as severe errors.

Completeness (CM) was calculated similarly, in-

corporating the presence of relevant information and

the severity of omissions. This metric evaluates

the quantity of information included and the impact

CSEDU 2025 - 17th International Conference on Computer Supported Education

622

of missing elements, emphasizing model compre-

hensiveness’s practical signiﬁcance in BPM contexts

(Paschoal and et al., 2020).

By adhering to best practices in empirical re-

search, these domain-speciﬁc metrics ensure reliable

and objective technical assessments (Wohlin et al.,

2012). The formula for CM is:

CM =

IR + (1 × FI

Light

) + (2 × FI

Medium

) + (3 × FI

Severe

)

A completeness value of 1 indicates that all rel-

evant information is included in the model, while 0

reﬂects the absence of all relevant information, with

omissions classiﬁed as severe.

3.4 Data Collection and Analysis

Procedures

Before the experimental activities began, in the in-

terdisciplinary PBL project, participants completed a

questionnaire with information such as group iden-

tiﬁer, gender, age, years of work experience, and

Keirsey proﬁle.

The categorization questionnaire collected base-

line data on participants’ prior experience with mod-

eling.This step was essential to control for confound-

ing variables, ensuring that outcome differences could

be attributed to the experimental treatments rather

than external factors.

The BPMN modeling tasks were designed to

replicate real-world scenarios involving AS-IS and

TO-BE processes. The tasks ensured consistency

across participants by using predeﬁned case studies

and a standardized tool (Bizagi Modeler) while allow-

ing for variations in approach (individual or group).

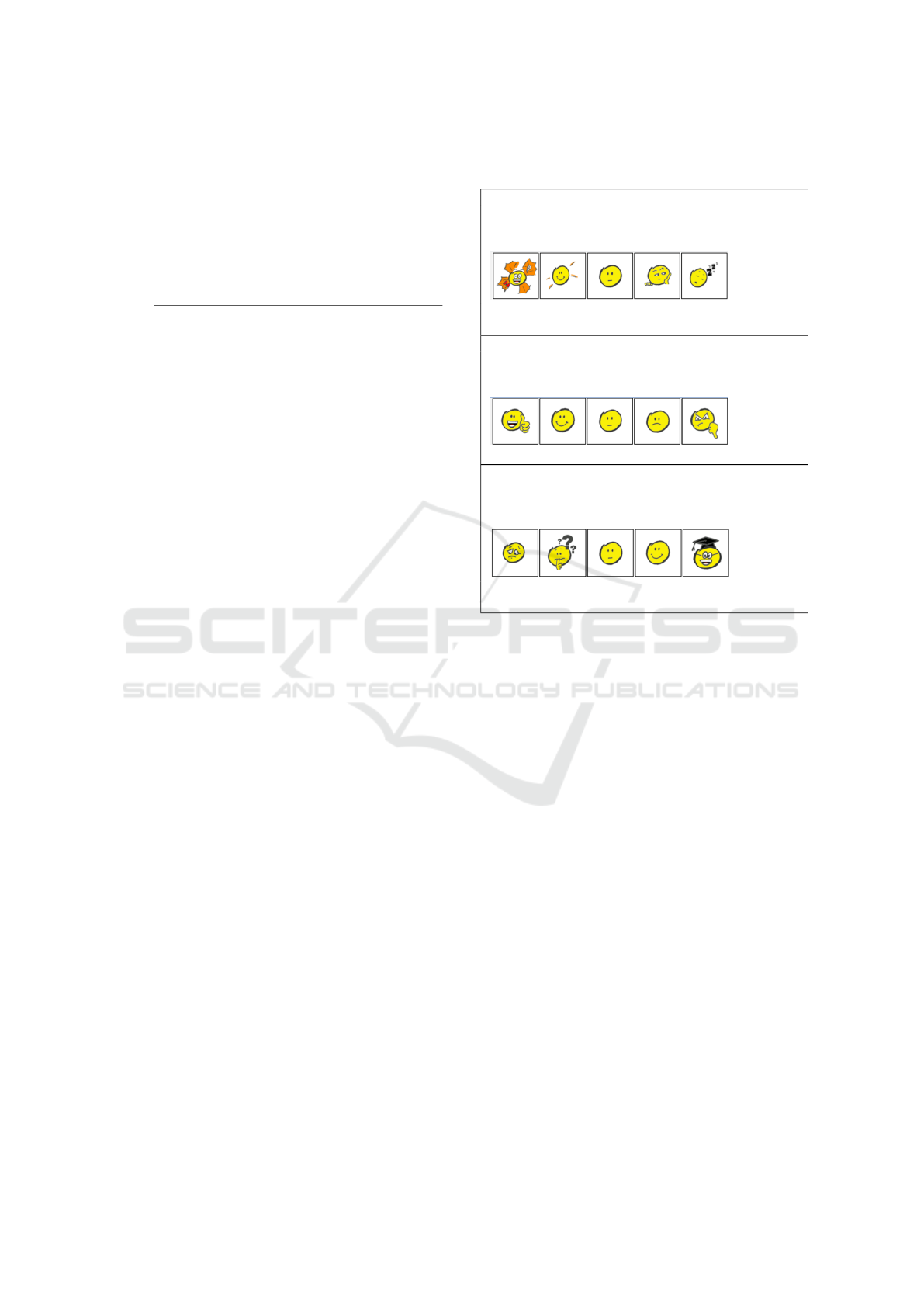
Emotion questionnaires, as illustrated in Table 3,

represented visually with emojis on a Likert scale,

were employed to reduce subjectivity and ensure par-

ticipant engagement.

The data analysis followed a multi-step approach,

leveraging a combination of statistical methods tai-

lored to the research questions and the nature of the

data. Each method was selected based on its suitabil-

ity for addressing speciﬁc aspects of the experiment:

1. Spearman’s Correlation. This non-parametric

test was employed to identify relationships be-

tween variables, such as the impact of prior ex-

perience on technical and emotional outcomes.

2. Wilcoxon Signed-Rank Test. The Wilcoxon

test compared paired samples from individual and

group modeling conditions. This test was selected

for its ability to handle small sample sizes and

non-normal data distributions, common in educa-

tional experiments.

Table 3: Questionnaire used to collect students’ feedback

regarding their emotions.

MOTIVATION

Regarding your MOTIVATION when learning about business process

modeling. How did you feel before process modeling activity? (observe

and select the image that best represents your MOTIVATION)

Totally motivated, Partially motivated, Neutral Partially, unmotivated

Totally unmotivated.

FUN

Regarding FUN when learning about business process model-

ing. How did you feel during the process modeling activity?

(observe and select the image that best represents your FUN)

Totally fun, Partially fun, Neutral, Partially boring, Totally boring.

RELAXATION

Regarding your feeling of RELAXATION during the modeling activity.

How did you feel after the process modeling activity? (observe and

select the image that best represents your RELAXATION)

Totally relaxing Partially relaxing Neutral, Partially stressful, Totally

stressful.

3. Repeated Measures ANOVA. To evaluate vari-

ations across sessions and interactions between

factors (e.g., Keirsey proﬁle, modeling approach),

a Repeated Measures ANOVA was conducted.

The study minimized the risks of type I and type

II errors by triangulating ﬁndings across multiple sta-

tistical methods, ensuring robust and credible con-

clusions (Wohlin et al., 2012). These comprehen-

sive procedures underscore the study’s methodolog-

ical rigor and contribution to advancing empirical re-

search in BPM education.

3.5 Ethics and Transparency

Following best practices for empirical research

(Wohlin et al., 2012; Kitchenham and et al., 2017),

ethical procedures addressed concerns regarding vol-

untary participation, data conﬁdentiality, and the sep-

aration of academic requirements from research com-

ponents.

The Informed Consent Form clariﬁed that partici-

pation in emotion assessments and feedback question-

naires was voluntary and anonymous, ensuring stu-

dents could opt out without academic repercussions.

The BPMN modeling activities, mandatory for

course evaluation, were explicitly separated from op-

tional research elements, preventing coercion and up-

Model Quality and Student Satisfaction in BPMN Education: A Quasi-Experiment

623

holding ethical standards.

Transparency was emphasized, with participants

informed about how their data would contribute to

pedagogical improvements and academic literature.

The consent form included detailed explanations of

how the data would be aggregated, analyzed, and re-

ported, ensuring that no personal identiﬁers would be

linked to the results.

3.6 Threats to Validity

Following the guides proposed by (Wohlin et al.,

2012), we addressed four key validity concerns.

Internal Validity: Participants’ prior BPMN experi-

ence potentially threatened internal validity by in-

ﬂuencing model quality. To mitigate this, a cate-

gorization questionnaire assessed participants’ back-

grounds, and standardized training sessions were con-

ducted to equalize BPMN competencies.

Another factor is the mix of parametric (ANOVA)

and non-parametric (Wilcoxon, Spearman) tests. We

applied ANOVA to compare personality proﬁles be-

cause the data approximated normality, while using

Wilcoxon and Spearman for paired and ordinal data.

External Validity: The limited sample size (19 partici-

pants after data processing) and the academic context

restricted the generalizability of ﬁndings to broader

professional or cross-institutional settings.

Moreover, the controlled academic environment

may only partially capture the complexities of profes-

sional BPMN tasks, such as time constraints and orga-

nizational challenges. Interdisciplinary PBL projects

were employed to simulate real-world scenarios, but

caution is needed when extrapolating ﬁndings to in-

dustrial contexts.

Construct Validity:

Validated criteria from BPMN literature, reviewed

by domain experts, were used to deﬁne correctness

and completeness. The emoji-based Likert scale en-

hanced emotional engagement and clarity, but inte-

grating additional validated emotion scales could pro-

vide more excellent reliability and nuance in future

research.

Ecological Validity: While the academic setting of-

fered controlled conditions for studying BPMN mod-

eling, it differed from professional contexts involv-

ing higher stakes, collaborative dynamics, and larger

datasets. The interdisciplinary PBL framework par-

tially addressed this by simulating real-world chal-

lenges, but further studies in industrial environments

would strengthen ecological validity.

4 RESULTS

The dataset was derived from 33, 30, and 19 students

for Exercises 1, 2, and 3, respectively. After exclud-

ing incomplete data, 19 participants who completed

all three questionnaires were retained to ensure reli-

able analysis.

4.1 RQ1: What Emotions Do Students

Report when Performing Individual

and Group BPMN Modeling?

Participants’ emotional responses were evaluated us-

ing Wilcoxon tests and Spearman correlations. As

shown in Table 4, the Wilcoxon test revealed no statis-

tically signiﬁcant differences between individual and

group modeling for motivation (p = 1.000), enjoy-

ment (p = 1.000), and relaxation (p = 0.824).

These results suggest that the modeling activity

format did not substantially inﬂuence the reported

emotions, leading to the retention of the null hypoth-

esis (H

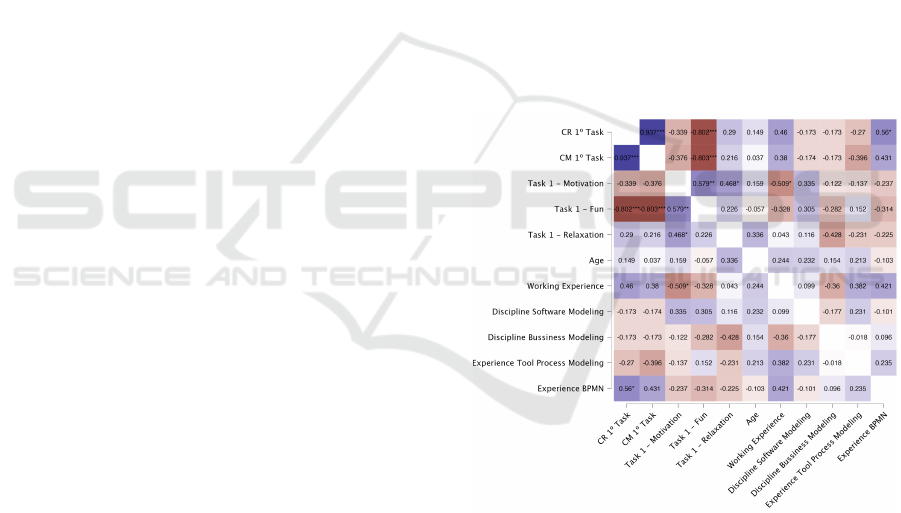
Figure 1: Spearman Correlation - Task 1.

The Spearman correlations analysis for the ﬁrst

BPMN modeling, visualized in Figure 1, highlighted

signiﬁcant relationships between emotional dimen-

sions. Motivation strongly correlated with enjoyment

(ρ = 0.579, p < 0.01) and relaxation (ρ = 0.468, p <

0.05), indicating an intrinsic link between these posi-

tive emotional states.

Additionally, a strong negative correlation be-

tween correctness and enjoyment (ρ = −0.802, p <

0.001) emerged, suggesting an inverse relationship

where higher enjoyment corresponded to lower cor-

rectness scores. This points to a potential tension be-

CSEDU 2025 - 17th International Conference on Computer Supported Education

624

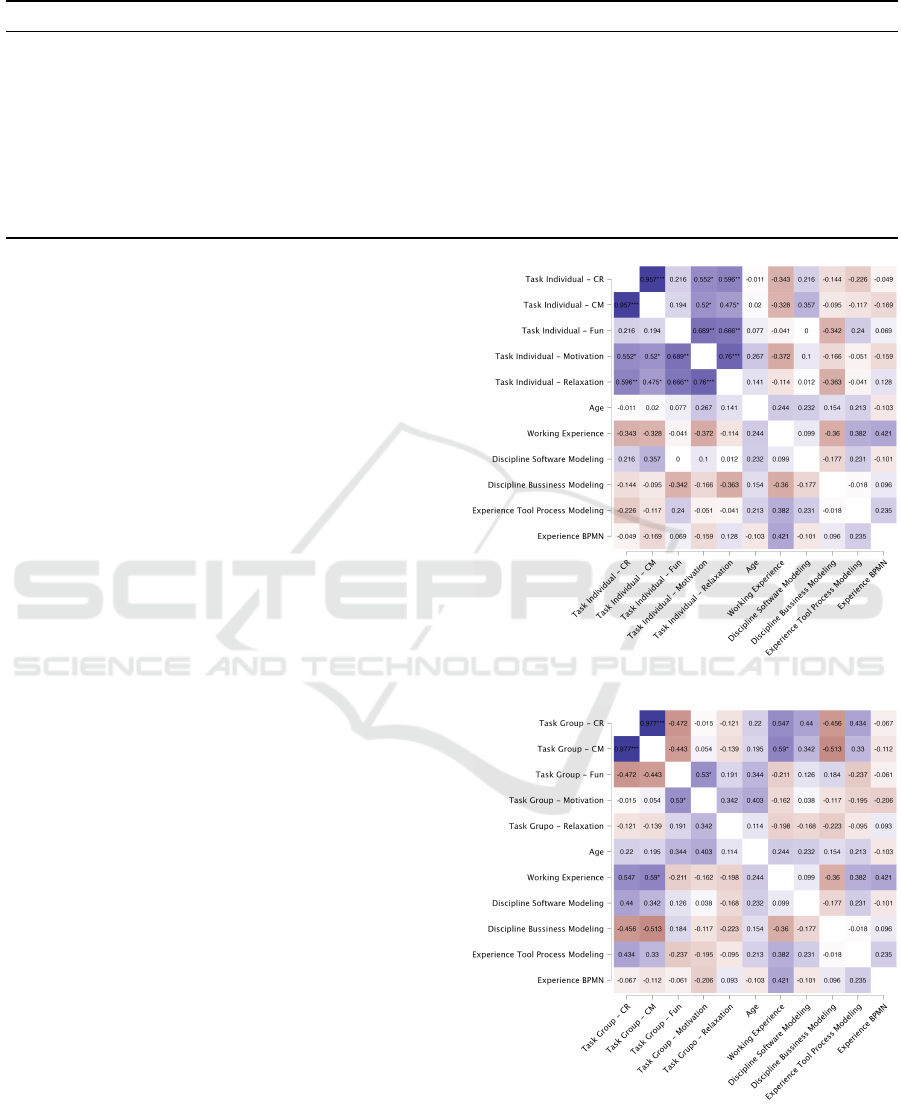
Table 4: Paired Samples T-Test.

Measure 1 Measure 2 Test Statistic z df p Effect Size SE Effect Size

Individual Task - Correctness - Group Task - Correctness Student 0.892 12 0.390 0.248 0.434

Wilcoxon 47.000 0.628 0.556 0.205 0.316

Individual Task - Completeness - Group Task - Completeness Student 1.039 12 0.319 0.288 0.424

Wilcoxon 58.000 0.874 0.414 0.275 0.305

Individual Task - Fun - Group Task - Fun Student −0.195 18 0.848 −0.045 0.241

Wilcoxon 52.000 −0.031 1.000 −0.010 0.294

Individual Task - Motivation - Group Task - Motivation Student 0.000 18 1.000 0.000 0.179

Wilcoxon 22.500 0.000 1.000 0.000 0.358

Individual Task - Relaxation - Group Task - Relaxation Student 0.271 18 0.790 0.062 0.197

Wilcoxon 30.000 0.255 0.824 0.091 0.342

tween emotional engagement and technical precision.

Participants with prior modeling experience re-

ported greater enjoyment, underscoring the role of

familiarity and competence in shaping emotional re-

sponses. These ﬁndings emphasize the need for fu-

ture studies to consider how prior knowledge and task

complexity interact to shape emotional and technical

outcomes in BPM learning environments.

4.2 RQ2: What Are the Differences in

the Technical Quality of BPMN

Models (Correctness and

Completeness) Between Individual

and Group Modeling?

To examine differences in technical quality, we ana-

lyzed correctness (CR) and completeness (CM) using

Wilcoxon tests and Spearman correlations.

As shown in Table 4, the Wilcoxon test found no

signiﬁcant differences between individual and group

modeling in correctness (p = 0.628) or completeness

(p = 0.874).

This supports the null hypotheses (H

and H

indicating that the modeling format did not signiﬁ-

cantly impact technical quality. Notably, both con-

ditions yielded high average scores in CR and CM,

reﬂecting students’ solid grasp of BPMN concepts.

The individual modeling correlations, depicted in

Figure 2, showed a strong positive association be-

tween correctness and completeness (ρ = 0.957, p <

0.001). This relationship underscores the intercon-

nectedness of technical precision and conceptual un-

derstanding in BPMN modeling.

Similarly, Figure 3 highlights how prior work

experience positively inﬂuenced completeness (ρ =

0.590, p < 0.05) in group tasks, suggesting that real-

world exposure plays a crucial role in enhancing

model quality.

These results align with prior studies suggesting

that while collaboration fosters interpersonal skills

and engagement, its impact on technical quality may

Figure 2: Spearman Correlation - Individual Task.

Figure 3: Spearman Correlation - Group Task.

depend on participants’ experience levels and task

complexity.

Model Quality and Student Satisfaction in BPMN Education: A Quasi-Experiment

625

4.3 RQ3: Does Personality Proﬁle, as

Deﬁned by Keirsey’s Typology,

Inﬂuence the Technical Quality of

Models or Students’ Emotions

During Modeling Activities?

To assess the impact of Keirsey proﬁles, ANOVA

analyzed differences across personality types, and

Wilcoxon tests evaluated emotional variations.

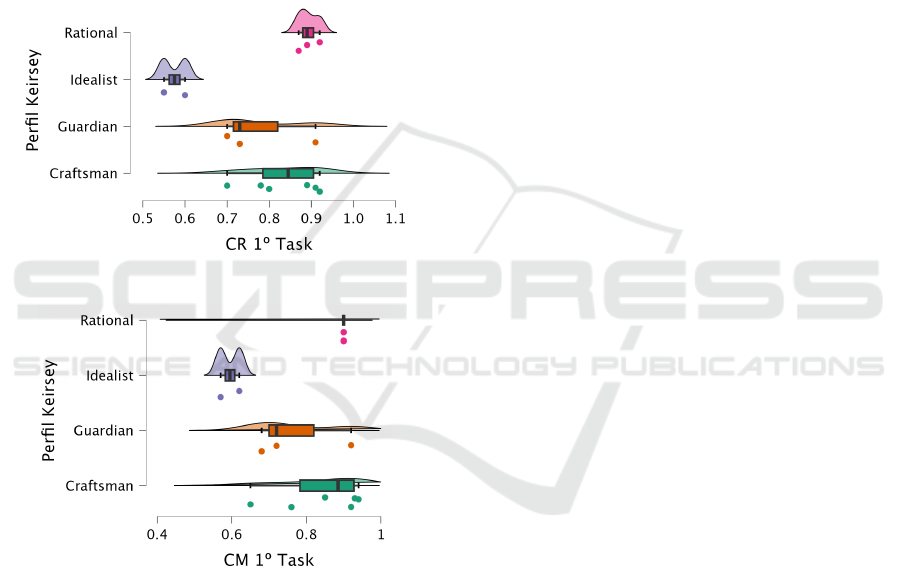
The ANOVA results, illustrated in Figures 4 and

5, demonstrated signiﬁcant differences in correct-

ness (F = 6.761, p < 0.01) and completeness (F =

4.153, p = 0.038) across proﬁles.

Figure 4: ANOVA - Keirsey CR.

Figure 5: ANOVA - Keirsey CM.

Rationals achieved the highest CR (M = 0.893)

and CM (M = 0.900), while Idealists scored the low-

est (CR: M = 0.575, CM: M = 0.595). These ﬁnd-

ings reject the null hypothesis (H

), conﬁrming that

personality traits signiﬁcantly inﬂuence technical out-

comes.

Conversely, Wilcoxon tests revealed no signiﬁcant

differences in emotional responses between proﬁles

(p > 0.05). This indicates that while personality inﬂu-

ences technical performance, emotional experiences

during modeling activities remained consistent across

types.

These insights suggest that personality traits, par-

ticularly those of Rationals, can be strategically lever-

aged to enhance team performance and task out-

comes. Idealists, however, may beneﬁt from targeted

support and technical reinforcement.

Future research could explore how adaptive teach-

ing methods cater to diverse personality proﬁles, op-

timizing technical precision and emotional engage-

ment.

5 DISCUSSION

A notable contribution of our study is the examination

of emotions alongside technical indicators. We de-

tected a negative correlation between enjoyment and

correctness, suggesting that greater enjoyment might

correspond to lower perceived cognitive effort, align-

ing with the idea that high “fun” can sometimes de-

tract from meticulous task execution (Van Merrien-

boer and Ayres, 2005).

Further, incorporating Keirsey personality proﬁles

showed that Rationals performed best in terms of cor-

rectness and completeness, whereas Idealists lagged.

This ﬁnding reinforces the idea that personal traits

and learning preferences can inﬂuence modeling out-

comes, offering actionable insight for educators who

might tailor support or team composition accordingly.

Taken together, our results support earlier argu-

ments that collaboration boosts positive emotions and

interpersonal engagement but does not inherently in-

crease technical quality in BPMN modeling. They

also expand the conversation by linking personality

factors to outcomes.

Despite the limited sample, this research extends

BPM education literature by weaving together techni-

cal metrics, emotional measures, and personality pro-

ﬁles within a single quasi-experimental study. Such

an approach underlines the complexity of BPMN in-

struction, where cognition, affect, and interpersonal

dynamics all converge.

6 CONCLUSIONS AND FUTURE

WORK

This study provides new insights into the intersec-

tion of technical performance, emotional engagement,

and individual characteristics in BPM education. Our

ﬁndings demonstrate no statistically signiﬁcant differ-

ences in the correctness and completeness of BPMN

models between individual and collaborative model-

ing approaches.

CSEDU 2025 - 17th International Conference on Computer Supported Education

626

This suggests that while collaborative activities

may enhance interpersonal dynamics and engage-

ment, they do not inherently improve technical accu-

racy or comprehensiveness. Furthermore, the strong

correlations between emotional states—such as mo-

tivation and enjoyment—and technical performance

highlight the multifaceted nature of the learning ex-

perience.

By integrating personality proﬁles and prior ex-

perience as variables, our study goes beyond tradi-

tional analyses to emphasize the individualized fac-

tors inﬂuencing BPM learning. Identifying personal-

ity traits, such as the Rational proﬁle’s tendency for

higher technical quality, offers valuable insights for

educators seeking to design tailored learning strate-

gies.

Longitudinal studies examining how personal-

ized interventions based on personality proﬁles af-

fect long-term learning outcomes are recommended.

Comparative analyses across different institutions and

cultural contexts could offer a more comprehensive

understanding of BPM education’s global applicabil-

ity.

ACKNOWLEDGEMENTS

The authors extend their heartfelt thanks to all the stu-

dents who participated in this study for their dedica-

tion and valuable contributions. We also thank the

educators and administrative staff whose support fa-

cilitated the experimental sessions. Finally, this work

was only possible with the collaborative efforts of the

interdisciplinary teaching team, whose insights and

guidance enriched this research.

REFERENCES

Arruda, F., Dos Santos, S. C., and Bittencourt, R. A. (2019).

Understanding the relationship between pbl princi-

ples, personality types and learning proﬁles: An initial

analysis. In 2019 IEEE Frontiers in Education Con-

ference (FIE), pages 1–7. IEEE.

Atiq, Z. and Loui, M. C. (2022). A qualitative study of

emotions experienced by ﬁrst-year engineering stu-

dents during programming tasks. ACM Transactions

on Computing Education (TOCE), 22(3):1–26.

Bandara, W. and et al. (2010). Business process manage-

ment education in academia: Status, challenges, and

recommendations. Communications of the Associa-

tion for Information Systems, 27(1):743–776.

Caporale, T. and et al. (2013). Social bpm lab–

characterization of a collaborative approach for busi-

ness process management education. In 2013 IEEE

15th Conference on Business Informatics, pages 367–

373. IEEE.

dos Santos, S. C. (2023). Transforming Computing Edu-

cation with Problem-Based Learning: From Educa-

tional Goals to Competencies. Cambridge Scholars

Publishing.

dos Santos, S. C., Vilela, J., and Vasconcelos, A. (2023).

Promoting professional competencies through inter-

disciplinary pbl: An experience report in computing

higher education. In 2023 IEEE Frontiers in Educa-

tion Conference (FIE), pages 1–9. IEEE.

Kitchenham, B. and et al. (2017). Robust statistical methods

for empirical software engineering. Empirical Soft-

ware Engineering, 22:579–630.

Nobre, M. and Vilela, J. (2024). Content and skills for

teaching bpm in computer science courses: A system-

atic mapping study. In Proceedings of the 16th Inter-

national Conference on Computer Supported Educa-

tion (CSEDU).

Paschoal, L. N. and et al. (2020). What are the differences

between group and individual modeling when learn-

ing bpmn? In Proceedings of the XVI Brazilian Sym-

posium on Information Systems, pages 1–8.

Sarvepalli, A. and Godin, J. (2017). Business process man-

agement in the classroom. Journal of Cases on Infor-

mation Technology (JCIT), 19(2):17–28.

Van Merrienboer, J. J. and Ayres, P. (2005). Research on

cognitive load theory and its design implications for

e-learning. Educational Technology Research and De-

velopment, 53(3):5–13.

Vilela, J., Santos, C. d., and Maia, D. (2024). Impact

of team formation type on students’ performance in

pbl-based software engineering education. In Interna-

tional Conference on Computer Supported Education

(CSEDU).

Wohlin, C., Runeson, P., H

ost, M., Ohlsson, M. C., Reg-

nell, B., and Wessl

en, A. (2012). Experimentation in

software engineering. Springer Science & Business

Media.

Yilmaz, M. and O’Connor, R. V. (2015). Understand-

ing personality differences in software organisations

using keirsey temperament sorter. IET Software,

9(5):129–134.

Model Quality and Student Satisfaction in BPMN Education: A Quasi-Experiment

627