Verifying LLM-Generated Code in the Context of

Software Veriﬁcation with Ada/SPARK

Marcos Cramer

1 a

and Lucian McIntyre

2 b

secunet Security Networks AG, Dresden, Germany

International Center for Computational Logic, Technical University Dresden, Germany

Keywords:

Software Veriﬁcation, LLM, Code Generation, Proof Generation, Ada/SPARK.

Abstract:

Large language models (LLMs) have demonstrated remarkable code generation capabilities, but the correct-

ness of the generated code cannot be inherently trusted. This paper explores the feasibility of using formal

software veriﬁcation, speciﬁcally the SPARK framework for Ada, to ensure the reliability of LLM-generated

code. We present Marmaragan, a tool that leverages an LLM in order to generate SPARK annotations for ex-

isting programs, enabling formal veriﬁcation of the code. The tool is benchmarked on a curated set of SPARK

programs, with annotations selectively removed to test speciﬁc capabilities. The performance of Marmaragan

with GPT-4o on the benchmark is promising, with correct annotations having been generated for 50.7% of the

benchmark cases. The results establish a foundation for future work on combining the power of LLMs with

the reliability of formal software veriﬁcation.

1 INTRODUCTION

Large language models (LLMs) have attracted signiﬁ-

cant attention within both the AI research community

and the general public due to their generative capa-

bilities. Tools such as ChatGPT have demonstrated

the potential of LLMs to automate and accelerate pro-

cesses in diverse ﬁelds, with software development

beneﬁting particularly from their ability to generate

code. However, while LLMs showcase impressive

creativity and adaptability, they also present risks. As

these models operate as black boxes, the code they

generate cannot inherently be trusted to be correct or

error-free, posing challenges for real-world applica-

tions where reliability and safety are essential.

To address the uncertainties associated with LLM-

generated code, formal veriﬁcation techniques offer

a promising solution. Formal software veriﬁcation

employs rigorous mathematical methods to prove the

correctness of code against a speciﬁed set of proper-

ties, which can help ensure that software meets its in-

tended speciﬁcations reliably. Integrating formal ver-

iﬁcation with LLM-generated code has the potential

to mitigate risks, making it possible to harness the

creative beneﬁts of LLMs while maintaining a high

https://orcid.org/0000-0002-9461-1245

https://orcid.org/0009-0008-0408-4340

standard of code quality and safety.

The paper is motivated by the need to bridge the

gap between the creative potential of LLMs and the

necessity for reliable, error-free code. By leveraging

formal veriﬁcation, speciﬁcally through the SPARK

programming language, we aim to explore the feasi-

bility of combining LLMs with formal veriﬁcation to

produce code that is innovative and provably correct.

This study investigates whether LLMs can generate

annotations for SPARK programs, facilitating formal

veriﬁcation of the resulting code.

For this purpose, we have implemented Marmara-

gan, a tool that leverages an LLM in order to generate

SPARK annotations for existing programs, enabling

formal veriﬁcation of the code using the GNATprove

tool. Marmaragan can be viewed as a prototype for

the backend of an AI-powered annotation generator

that could run in the background of a SPARK editor. It

incorporates features such as generating multiple so-

lution attempts, retrying with additional context from

GNATprove, and providing pre-compiled error mes-

sages to improve performance. Marmaragan can cur-

rently be combined with any LLM in the OpenAI API

and has been most throughly tested with GPT-4o. It

has parameters for the number of solutions generated

in parallel, for the number of retries that Marmara-

gan attempts before giving up as well as for toggling

a special chain-of-thought mode.

Cramer, M. and McIntyre, L.

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK.

DOI: 10.5220/0013461900003964

In Proceedings of the 20th International Conference on Software Technologies (ICSOFT 2025), pages 39-50

ISBN: 978-989-758-757-3; ISSN: 2184-2833

In order to evaluate how well Marmaragan per-

forms depending on the value of its parameters, we

created a benchmark based on a curated set of SPARK

programs, from which annotations were selectively

removed following various removal schemata. Ex-

periments on the benchmark demonstrate Marmara-

gan’s competence in generating annotations: Over-

all, it generates correct annotations for 50.7% of the

benchmark programs. Furthermore, the experiments

shed light on what is the optimal balance between par-

allel solution attempts and retries in the light of lim-

ited computational resources.

Through this, we establish a foundation for future

work: In the near to medium-term future, our research

could contribute to making applications of formal ver-

iﬁcation much more efﬁcient. In the long term this

could be a building block towards a hybrid tool that

combines the power of LLMs with the reliability of

software veriﬁcation for generating fully veriﬁed pro-

grams.

In Section 2, we discuss the preliminaries of this

paper in the areas of logic, formal software veriﬁca-

tion (with a focus on SPARK 2014) and large lan-

guage models. The implementation of Marmaragan is

presented in Section 3. In Section 4, we describe the

methodology applied to create a benchmark for eval-

uating Marmaragan. The results of running Marama-

ragan with varying parameters on the benchmark are

presented in Section 5, and in Section 6 we discuss

these results. Section 7 presents related work. In sec-

tion 8, we discuss future work.

2 PRELIMINARIES

This section discusses the foundations the work is set

upon and the work it relates to and is inspired by.

2.1 Formal Software Veriﬁcation

Formal software veriﬁcation is the process of proving

the correctness of a software program with respect to

a speciﬁed formal speciﬁcation or property, using for-

mal mathematical methods. It ensures that the soft-

ware behaves as intended in all possible scenarios. In

contrast with common non-formal testing techniques,

which always cover only a limited number of scenar-

ios and are thus vulnerable to having missed out on a

scenario in which a bug takes effect, formal software

veriﬁcation covers all potential runs of the program.

From here, “formal veriﬁcation” is used as a short-

hand for “formal software veriﬁcation”.

There are different methodological approaches to

formal veriﬁcation. For this paper, we don’t need to

consider model checking and instead focus on deduc-

tive veriﬁcation, which is “the process of turning the

correctness of a program into a mathematical state-

ment and then proving it” (Filli

atre, 2011). In deduc-

tive veriﬁcation, the desired behaviour of the program

needs to be speciﬁed in a formal language. The task is

to prove that the program actually satisﬁes the speci-

ﬁcation for all possible inputs.

At the level of single functions in the program, this

is realized through pre- and postconditions, which are

assertions on values of variables that enter and exit

given functions within our program, specifying prop-

erties and relationships (Hoare, 1969). A precondi-

tion deﬁnes the conditions that must be met, so that a

given function can be executed. Analogously, a post-

condition deﬁnes the conditions that must be met di-

rectly subsequent to function execution. For example,

a function computing F(x, y) = x − y could have the

precondition x > y for ensuring that one stays in the

realm of positive numbers. In this case, a sensible

postcondition would be F(x, y) > 0, as this postcon-

dition logically follows from the precondition and the

deﬁnition of the function F(x, y). This kind of logi-

cal entailment needs to hold for every postcondition

of a function, and this needs to be established through

a formal proof. We say that there is proof obligation

for deriving the postcondition.

2.2 SPARK 2014

SPARK 2014 (Moi, 2013) is a formally deﬁned subset

of the Ada programming language (AdaCore, 1980),

designed to support the development of reliable and

provably correct software (Barnes, 2012). Its un-

ambiguous semantics ensures that programs behave

consistently and predictably. SPARK allows only

speciﬁc constructs from Ada, ensuring compatibility

with formal veriﬁcation methods. Programs written

in SPARK can be annotated with assertions, including

preconditions and postconditions, to support modular

deductive veriﬁcation (Hoare, 1969).

SPARK has found application in multiple areas,

including train control systems and space transporta-

tion (Dross et al., 2014), commercial aviation (Moy

et al., 2013), air trafﬁc management (Chapman and

Schanda, 2014) and GPU design (Chapman et al.,

2024).

Annotations in SPARK take the form of pragma

statements, such as:

pragm a As s ert i on ( c o n di t i on ) ;

These include constructs like Assert,

Loop Invariant (see section 2.2.1 below), and

Loop Variant, which facilitate detailed speciﬁcation

and veriﬁcation. Additionally, SPARK ensures the

ICSOFT 2025 - 20th International Conference on Software Technologies

absence of runtime errors, such as array bounds

violations or division by zero, by verifying adherence

to deﬁned rules.

In SPARK, code is organized into two types of

ﬁles: .ads and .adb. The .ads ﬁles, known as

speciﬁcation ﬁles, deﬁne the interface of modules,

including function and procedure declarations along

with their associated preconditions and postcondi-

tions. In contrast, the .adb ﬁles, or implementa-

tion ﬁles, contain the executable code and additional

annotations such as Assert, Loop Invariant, and

Loop Variant pragmas. This separation supports a

clear distinction between the speciﬁcation and imple-

mentation, facilitating modular reasoning and veriﬁ-

cation of SPARK programs.

The GNATprove toolchain is the primary mecha-

nism for verifying SPARK programs. It operates in

three stages:

• Check: Ensures SPARK compatibility.

• Flow: Analyzes data and information ﬂow.

• Proof: Veriﬁes code against assertions and con-

ditions using third-party theorem provers via

Why3 (Filli

atre and Paskevich, 2013).

GNATprove translates SPARK code into proof

obligations, resolving them using automated provers.

This ensures compliance with user-deﬁned and

language-level constraints, making SPARK programs

highly reliable.

GNATprove provides feedback as errors or medi-

ums. Errors typically indicate issues, such as syntax

or type errors, that prevent the program from being

executed. Mediums, on the other hand, result from

proof obligations that could not be discharged, either

because the statement being proved is false or due to

missing annotations. When a statement is false, these

mediums may include counterexamples generated by

the tool to help identify the source of the issue.

2.2.1 Loop Invariants

A loop invariant is a property that holds during each

loop iteration. It can be viewed as the induction hy-

pothesis in an inductive proof over the number of loop

iterations. Consider the example in Listing 1.

Here, the invariants state that the Result is twice

the Count and that the loop counter does not exceed X.

2.3 Large Language Models and

Transformers

The development of large language models (LLMs)

has been a signiﬁcant leap forward for AI develop-

ment, spurred by the introduction of the transformer

Listing 1: Example of loop invariants for a SPARK function

that doubles a number.

pr o c ed u r e Do u b le_ N u mbe r ( X : in N atu r al ; R es u lt :

out N at u ra l ) is

Co unt : Nat u ra l := 0;

be gin

Re s ul t := 0;

wh ile Co un t < X l oo p

pr a gm a Lo o p _ Inv a r i ant ( R esu lt = Cou nt * 2) ;

pr a gm a Lo o p _ Inv a r i ant ( C ou nt < X ) ;

Re s ul t := Re sul t + 2;

Co unt := Co unt + 1;

end lo op ;

end D o ubl e _ N um b e r ;

architecture by Vaswani et al. in “Attention Is All You

Need” (Vaswani et al., 2017).

LLMs, which are specialized neural models with

billions of parameters, excel at capturing patterns in

text data to perform a variety of language tasks. These

models evolved from earlier statistical language mod-

els that relied on n-gram techniques to predict word

sequences but struggled with long-range dependen-

cies. Innovations like Word2Vec (Mikolov et al.,

2013) and GloVe (Pennington et al., 2014), combined

with the transformer’s attention mechanisms, enabled

the modeling of complex relationships between words

(or rather between tokens), addressing the limitations

of traditional approaches.

The transformer architecture, central to LLMs,

employs a multi-layer encoder-decoder struc-

ture (Vaswani et al., 2017). Its core innovation, the

self-attention mechanism, calculates the importance

of tokens relative to one another, enhancing the

model’s ability to understand context. Multi-head

attention further improves performance by allowing

the model to focus on different aspects of input simul-

taneously. The ﬁnal stages of transformers generate

predictions through a combination of linear layers

and softmax functions, transforming embeddings into

meaningful output. These advancements, coupled

with signiﬁcant increases in model scale and training

data, underpin the capabilities of state-of-the-art (as

of 2024) LLMs like OpenAI’s GPT-4 and GPT-4o

models, which are the basis of this thesis.

2.3.1 Chain-of-thought Prompting

LLM performance has been shown to depend on

the formulation of the prompt that is passed to the

LLM. One prompting technique that is relevant to our

work is chain-of-thought-prompting (Jason Wei et al.,

2023), whose applicability to generating SPARK an-

notations we have studied (see Section 3). This

prompting technique enhances reasoning by guiding

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK

LLMs through a series of intermediate natural lan-

guage steps before generating the ﬁnal output. For

this, the prompt is extended by a note about the in-

tended structure of the response, e.g. “Let’s think step

by step”. This technique has been shown to sig-

niﬁcantly improve model performance on reasoning-

heavy tasks, both for few-shot prompting (Jason Wei

et al., 2023) and for zero-shot prompting (Kojima

et al., 2023).

3 IMPLEMENTATION

This section provides a detailed description of Mar-

maragan, a tool that leverages an LLM in order to

generate SPARK annotations for existing programs,

enabling formal veriﬁcation of the code.

3.1 Marmaragan

Marmaragan [GitHub] is a tool, developed in Python,

designed for the SPARK 2014 language. The tool

implements a hybrid AI approach that combines the

power of LLMs with the trustworthiness of logic-

based reasoning to generate annotations required for

formal veriﬁcation within SPARK 2014 programs.

Use is made of the LangChain (Chase, 2022) Li-

brary to handle the calls to the OpenAI API and make

LLM interaction seamless.

Marmaragan takes as input an existing Spark

project consisting of the speciﬁcation and implemen-

tation ﬁles as well as any dependencies. Using this, it

queries an LLM to generate missing pragma state-

ments and then allows GNATprove to compile and

verify the resulting code. The tool incorporates a

range of strategies to assist in generating correct pro-

grams, including features for retrying with GNAT-

prove errors and mediums as well as post-processing

of LLM output.

In the following, we describe the motivation and

concepts behind Maramaragan. We survey the fea-

tures of the tool and discuss each of the steps that are

taken to transform input into output.

3.2 Proof of Concept

The aim was to develop a proof of concept for au-

tomatic annotation generation in SPARK. This con-

cept stemmed from the hypothesis that generating for-

mally veriﬁed code with an LLM circumvents the typ-

ical problems encountered with LLM-generated code.

3.3 Environment Emulation

Marmaragan is designed to emulate a tool which runs

in the background of a SPARK 2014 editor, such as

GNAT Studio (Brosgol, 2019). With this setup, a user

may send requests to the tool, such that annotations

are generated for their SPARK code.

As Marmaragan is a proof of concept, the idea was

to design a tool which, given existing SPARK code,

is capable of generating annotations. The resulting

added annotations should lead to GNATprove running

free of errors and mediums. Given this premise, the

prompting strategy and setup of Marmaragan is de-

veloped in such a way as to optimally emulate these

conditions.

3.4 Implementation Details

Here we deal with the implementation details of Mar-

maragan. Figure 1 provides an overview

3.4.1 Marmaragan as a Benchmarking Tool

Marmaragan is developed as a proof of concept, im-

plemented as a benchmarking application in order to

evaluate its functionality and performance. It works

by taking a benchmark as input, then iterating over

each of the ﬁles. For each task, it attempts to generate

all required annotations, such that the code runs error-

and medium-free. This procedure may be conﬁgured

in multiple ways.

3.4.2 Prompting in Marmaragan

As described in Figure 1, an important step of the

workﬂow in Marmaragan is prompting the LLM. A

good prompt is key to generating useful LLM re-

sponses, thus we delve into the details of this step.

In Marmaragan prompting works by inserting the

given SPARK 2014 ﬁles into the prompt, format-

ting and subsequently invoking the LLM. The prompt

used for all queries can be found below in listing 2.

Listing 2: The base prompt used to query the LLM

Try t o so l ve the fo l l ow i n g p r obl e m l o g ic a l ly an d

st ep b y st ep . T he fi na l an sw e r s h ou l d t he n be

de l i mi t e d in t he fo l low i ng wa y :

‘‘ ‘ a da

co de here

‘‘ ‘

The f oll o win g are t he spe c i f ica t i o ns an d

de p e n den c i es of a S p a rk 2 0 14 / AD A p roj e ct :

{ de p e nde n c ies }

ICSOFT 2025 - 20th International Conference on Software Technologies

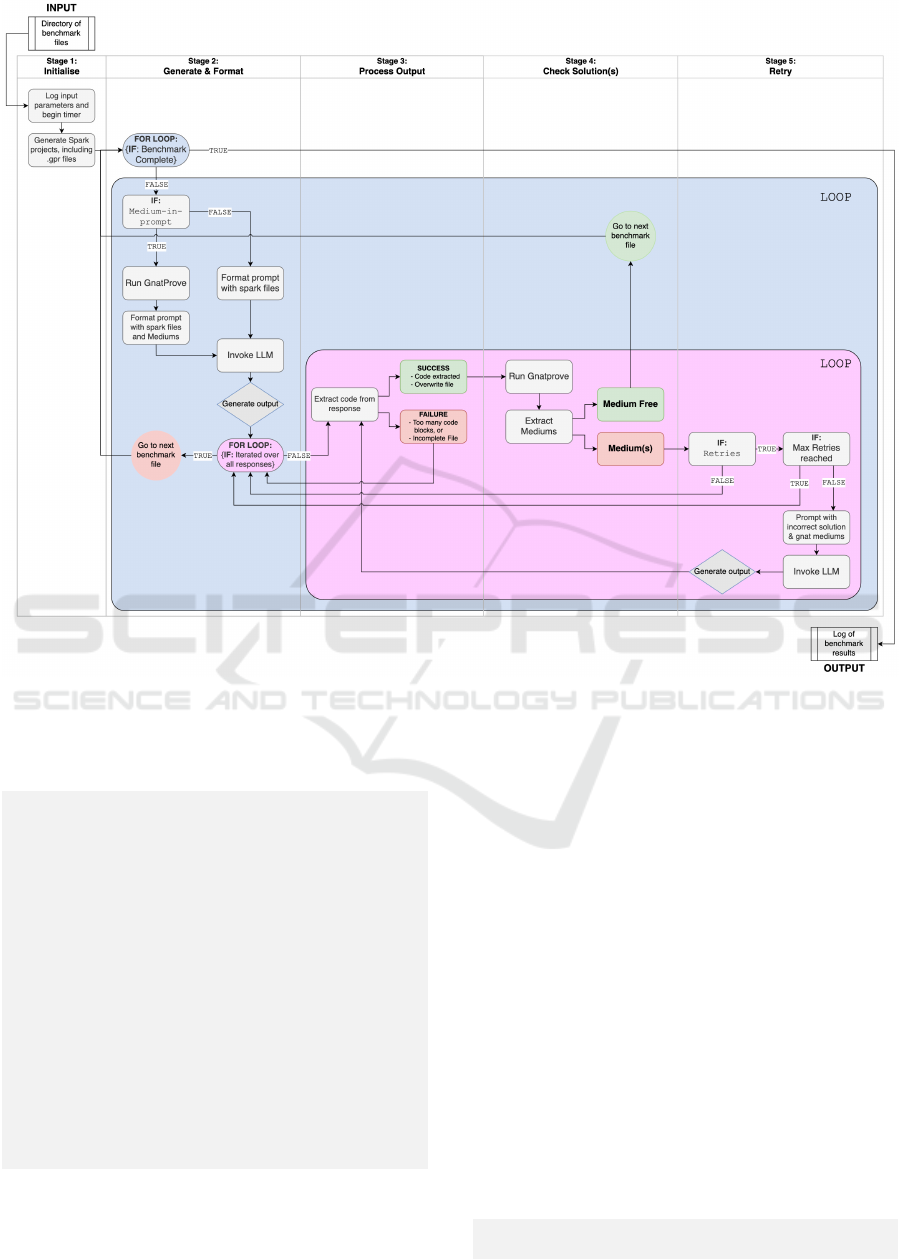
Figure 1: Overview of the control ﬂow in Marmaragan. Stage 1 initializes input parameters and generates the SPARK

directory. Stage 2 begins the iteration over each of the ﬁles in the benchmark, formatting the prompt and invoking the LLM.

Stage 3 is output processing, in Stage 4 GNATprove is run and mediums are extracted. Processes in Stage 5 only run if

enabled: the prompt is reformatted with the previous incorrect solution and GNATprove medium(s) are also included.

Th is i s t he pa c ka g e b od y ( im p l e men t a t ion ) :

{ pa c k age _ b ody }

Add one o r m ul t i pl e pr agm a st a tem e n ts

(e.g. p rag ma L o op _ In v ari a nt , p rag ma A ss e rt ) to th e

pa c ka g e bo dy , so t ha t th e c od e r un s e rro r and

me d iu m f ree .

Ma ke use of t he me diu m s p r o vi d ed in the p r om p t to

gu ide you r so lut i on .

You mu st not mo dif y t he cod e in a ny othe r way ,

ex c ep t to a dd " f or " lo ops a nd " if " sta t e men t s t hat

en c lo s e o nly pr ag m a s t a tem e n ts .

Do no t m odi fy th e f u n cti o n a lit y in a ny way . R e tu r n

the ent ire i mpl e m e nta t i o n f il e w it h t he re qui r ed

ad d i ti o n s .

The prompt is designed to be as general as pos-

sible, in order to adhere to the goal of emulation.

Therefore, no direct speciﬁcation is given as to which

pragma statements to generate.

It also includes the request that the code not be

modiﬁed in any way, other than to add pragma state-

ments and possibly “for” loops and “if” statements

that enclose only pragma statements. Such “for”

loops and “if” statements are sometimes needed in or-

der to support GNATprove’s veriﬁcation of universal

or conditional statements.

Additionally, when prompting LLMs with

LangChain, it is possible to provide a system mes-

sage. The system message conveys to the LLM its

context and which role it should take within the given

context. As the system message for OpenAI GPT

models is capped at 512 characters, the message

chosen sticks to the key points the model should

adhere to. The system message used is displayed

below, in listing [3].

Listing 3: The system message passed to the LLM

You are a S par k 201 4 / A DA pr o g ram m er w it h

st r on g lo gic a l r e a son i ng a b ili t i es .

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK

You wi ll be gi ven a n I m ple m e n tat i o n of a p ro gr am ,

a sp e c i fic a t i on of the p r ogr a m and the m e diu m s

th at GN A T pro v e r a ise d f or it .

You mu st com p let e t he pa c ka g e b od y of t he give n

pr og ra m , i n s ert i ng on e or m u l ti p le p rag ma

st a t eme n t s .

You mu st not mo dif y t he cod e in a ny othe r way ,

ex c ep t to a dd f or lo op s a nd if st a t eme n ts t ha t

en c lo s e o nly pr ag m a s tat em ent s , and d o not

mo d if y t he fu n c t ion a l i ty .

3.4.3 Medium in Prompt

Further, the prompt may be enhanced with additional

context, by enabling the medium-in-prompt feature.

When this feature is enabled, GNATprove compiles

the SPARK project and any mediums from the out-

put are extracted and formatted. In this case, format-

ting involves taking the line number and extracting

the related line of code (and the one below) from the

SPARK ﬁle. The line of code and the medium mes-

sage is then appended to the prompt. Figure 2 gives

an example of this.

3.4.4 Chain-of-Thought Prompt

As discussed in Section 2.3.1, chain-of-thought

prompting (Jason Wei et al., 2023; Kojima et al.,

2023) is a strategy that helps to increase the perfor-

mance of LLMs on complex reasoning tasks. To

gain some insight into the effectiveness of different

prompting techniques, a chain-of-thought prompt was

developed, which deviates from the standard prompt

only in the ﬁrst section:

Listing 4: The beginning of Marmaragan’s chain-of-thought

prompt

Try t o so l ve the fo l l ow i n g p r obl e m by f irs t

ex p l ain i n g in na tu r al l a ng u a ge wh at the und e r ly i n g

pr ob le m , l e adi n g to the m edium , m ig ht be an d ho w

it c ou ld be s olv ed .

...

Based on the results of the papers presented in

2.3.1, this prompt aims to make the LLM explain,

in natural language, how it will go about proving the

code. The hope is that this approach forces the model

to reason more soundly. After explaining how it will

solve the given program, it is then tasked with imple-

menting this solution, all in one step, similar to the

Zero-Shot Chain-of-Thought approach (Kojima et al.,

2023).

3.4.5 N-Solutions

The N-Solutions and Retries parameters are funda-

mental instruments which can be employed to in-

crease the benchmarking success rate. N-Solutions

determines the number of responses an LLM returns,

per individual prompt. At N = 1, the LLM supplies a

single response to a given prompt, at N = 5 it returns

ﬁve responses. Due to how generation is affected by

the temperature parameter, each of the N-Solutions

are in most cases distinct.

3.4.6 Retries

Setting the Retries parameter to a value graeater than

0 makes Marmaragan continue with retries after a

ﬁrst failed attempt at generating pragmas that verify

the code. The Retries mechanism works by provid-

ing the LLM with additional context in the form of

the previous failed attempt and the medium messages

generated by GNATprove in that attempt. This ad-

ditional context helps the model to formulate a new

solution attempt. Increasing the number of Retries

leads to the additional solution attempts, each con-

taining more context than the last.

4 BENCHMARKING

This section discusses the programs selected for

benchmarking. This includes why the programs were

chosen, where they were sourced from and how dif-

fering benchmarks were assembled from these.

4.1 Programs

In total, 16 SPARK 2014 programs were selected,

from three differing sources:

• Five programs originate from the Argu Reposi-

tory, [Link](Cramer, 2023), which is a veriﬁed

tool written by Marcos Cramer for computing ab-

stract argumentation semantics, with a focus on

ﬁnding the grounded extension of an argumenta-

tion framework and proving its uniqueness. It was

ﬁrst published after the cutoff dates for the train-

ing of GPT-4 and GPT-4o, so that unlike for the

other programs in the benchmark, we can be cer-

tain that it was not included in the training data of

these LLMs.

• The spark tutorial [Link], where the

linear search and show map programs were

taken from.

ICSOFT 2025 - 20th International Conference on Software Technologies

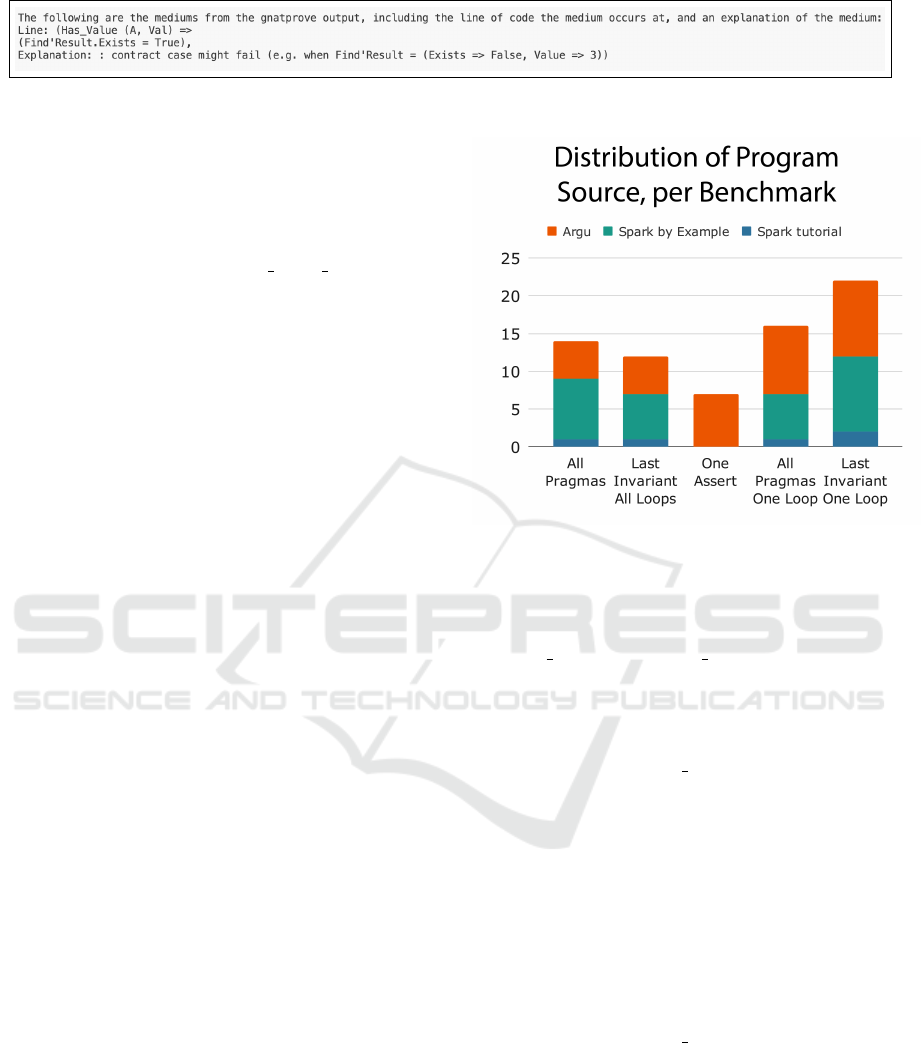
Figure 2: Example of GNATprove precompiled and formatted medium messages, which are added to the prompt

• A repository of SPARK 2014 implementations

of common algorithms, known as spark-by-

example [Link], where the ﬁnal 11 programs

were taken from, including basic implementations

of copy and f ind algorithms, but also more com-

plex programs such as search lower bound.

4.2 Determining a Metric for Results

Evaluation

We chose to work with pre-existing, formally veriﬁed

SPARK 2014 projects, as this made the task of evalu-

ating the results from the benchmarks possible.

Quantifying how close a solution is to being

formally veriﬁed is very challenging. GNATpove

provides no feedback in regards to this, excepting

medium messages. These tell us which statements

lead to a failure in veriﬁcation, but the total number

of medium messages is not indicative of the close-

ness to a completed veriﬁcation. A manual analysis is

also not feasible, given the number of benchmark pro-

grams and the total number of solutions generated.

Thus, it is only possible to evaluate correctness by

checking whether the program is free of errors and

mediums. By taking programs which are already ver-

iﬁed, we ensure that a correct solution exists. Addi-

tionally, utilizing existing programs makes it possible

curate which types of annotations to generate.

4.3 Five Benchmarks

In total, from the 16 programs, ﬁve benchmarks were

developed with differing aims. For each benchmark,

a separate schema for removing pragma statements

from the programs was devised. For some schemas,

it was possible to do this multiple times per program.

pragma statements are removed only from the imple-

mentation ﬁle (.adb) of the SPARK project. After re-

moving pragmas from a program, we run GNATprove

to check whether any mediums are generated. A pro-

gram with removed pragmas is only included in the

benchmark if GNATprove generates mediums for it,

because otherwise it can be considered to be already

fully veriﬁed, requiring no work from Marmaragan.

Figure 3: This chart details the distribution of programs

from each of the three sources across the ﬁve benchmarks.

All Pragmas

• All pragma statements of the form

Loop Invariant, Loop Variant, and Assert

are removed.

• 14 programs total

Last Invariant All Loops

• The last pragma Loop Invariant is removed from

each loop in the ﬁle. If multiple loops occur in the

same ﬁle, then multiple statements are removed.

• 12 programs total

All Pragmas One Loop

• All pr agma statements are removed from a single

loop, only for loops with two or more loop invari-

ant statements.

• 16 programs total

Last Invariant One Loop

• The last pragma Loop Invariant is removed from

a single loop.

• 22 programs total

One Assert

• A single Assert is removed.

• 7 programs total

Figure 3 displays a bar for each of the benchmarks,

detailing the distribution of the source programs.

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK

5 RESULTS

This section presents the ﬁndings from experiments

with Marmaragan. The aim was to evaluate Mar-

maragan’s performance across various benchmarks,

while varying the individual parameters of the tool.

Through a series of experiments, we attempt to mea-

sure the effectiveness of the tool and extract how

the parameter N-Solutions and Retries interact with

each other.

5.1 GPT-4o Release

Early experiments conducted on the benchmark with

vanilla GPT-4 demonstrated promising, albeit not

entirely satisfying, results. However, shortly after

these initial trials, GPT-4o was released. Not only

did small scale experiments indicate that this new

model was more successful overall, importantly, they

also demonstrated that GPT-4o was far more cost-

effective. This made larger experiments feasible. The

main experiments were performed with the model

gpt-4o-2024-05-13.

5.2 Experiment Setup

Adjusting for these new possibilities, a large scale ex-

periment to test the capabilities of Marmaragan was

devised. The aim was to derive the effectiveness of

the N-Solutions and Retries parameters. Various com-

binations of each of the parameters were conceived to

test this. A central goal of these tests was to determine

what balance between n (N-Solutions) and r (Retries)

was ideal in order to get the best results given a ﬁxed

amount of computational resources.

Given the values n and r for the N-Solutions and

Retries parameters, the number of solutions generated

by the program is limited to a maximum of n(r + 1),

because n solutions are generated for the ﬁrst attempt

and n further ones for each of the r retries. The total

number of solutions to be generated per benchmark

program was set to 12, as this made various combina-

tions of n and r possible, while keeping costs within

the limits set. The resulting combinations were the

following:

(n , r ) c o m bin a t i on s :

(12 , 0) , (6 , 1) , (4 , 2) , (3 , 3 ) , (2 , 5)

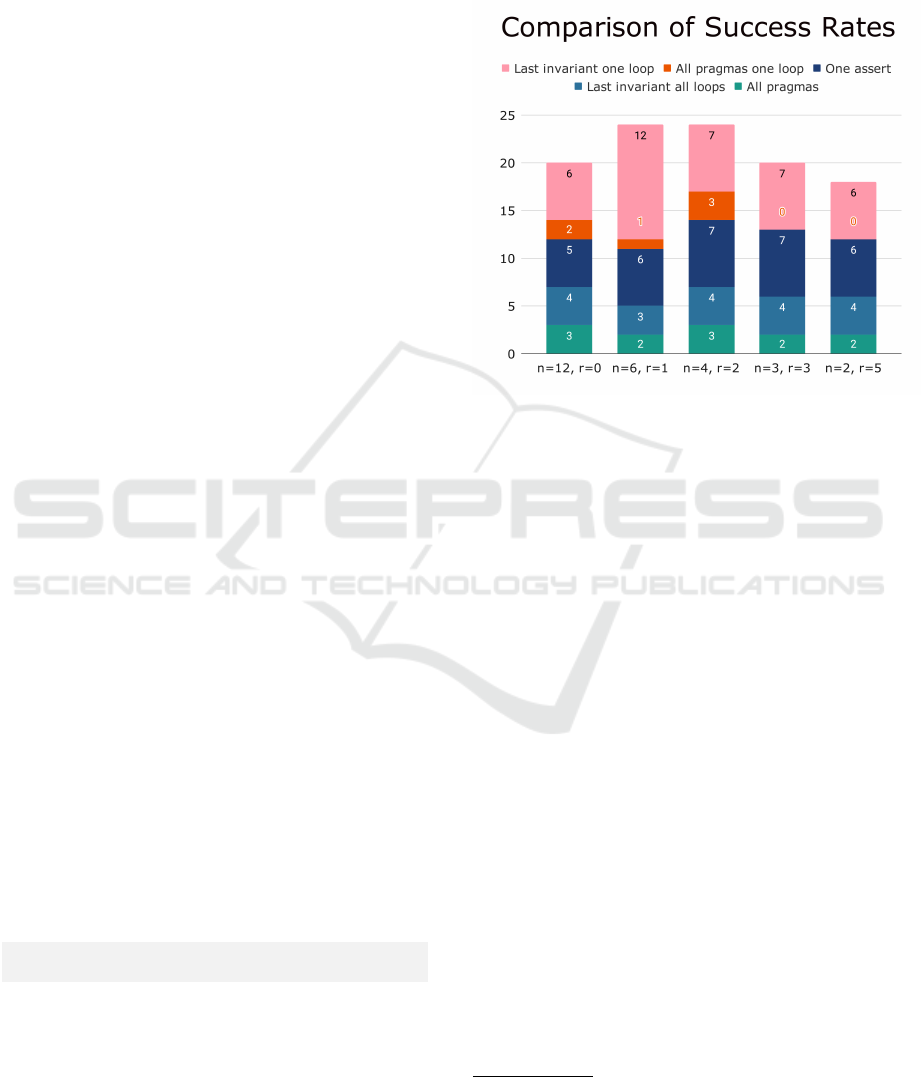
5.3 Experiment Results

Table 1 details the results of each of the ﬁve experi-

ments on each of the ﬁve benchmarks.

In total 36 programs out of 71 were solved across

all ﬁve benchmarks, meaning a solution was found for

50.7% of all benchmark problems.

Figure 4 is a graphical interpretation of Table 1.

Figure 4: Comparison of the number of programs solved per

experiment. The bar is composed of the stacked number of

solutions per benchmark.

A further graphical representation of the data is

Figure 5. The number of successfully solved pro-

grams, compared to the total number of programs in

the benchmark, is depicted through a 100% bar chart,

to contrast performance on each of the benchmarks,

per experiment.

Figures 6 and 7 contrast the effectiveness of suc-

cessive retries and N-Solutions. Important to note

here is that while one parameter is varied, the other

is kept constant. In essence, each of the selected ex-

periments was analyzed and the number of successful

solutions was counted at each step, keeping one of the

two parameters constant.

5.4 Argu Results

The programs that originate from Argu (see Sec-

tion 4.1) are of high signiﬁcance, as the programs

cannot be part of GPT-4o’s training data

. Thus, this

makes it a notable benchmark, as the solutions could

not have been learned, but had to be produced by

the LLM without having seen the full program dur-

ing pre-training.

Along with the programs being completely new

for the LLM, the subject matter of the programs is

If we take the statistics from Open AI’s website to be

up-to-date, at the time of writing, and provided the informa-

tion is reliable.

ICSOFT 2025 - 20th International Conference on Software Technologies

Table 1: The results of ﬁve experiments with unique combinations of N-Solutions and retries, over ﬁve different benchmarks.

The ﬁnal column displays the total number of programs solved across all benchmarks.

All pragmas Last invariant all loops One assert All pragmas one loop Last invariant one loop Sum

n=12, r=0 3 4 5 2 6 20

n=6, r=1 2 3 6 1 12 24

n=4, r=2 3 4 7 3 7 24

n=3, r=3 2 4 7 0 7 20

n=2, r=5 2 4 6 0 6 18

Table 2: Breakdown of the number of programs solved in total, for each benchmark. The bottom row is the number of

programs in the benchmark.

All pragmas Last invariant all loops One assert All pragmas one loop Last invariant one loop Sum

Total solved 5 6 7 4 14 36

Total in benchmark 14 12 7 16 22 71

also niche. Abstract argumentation theory is likely

not among the major ﬁelds of academic research, and

literature surrounding this topic is likewise uncom-

mon. This makes the programs from the Argu repos-

itory potentially the most challenging in the bench-

mark. With these premises in place, the results

achieved by Marmaragan are surprising. Argu pro-

grams comprised just over half of the programs in the

benchmark, totaling 36 out of 71. Out of these 36

programs, 16 were solved.

5.5 Veriﬁcation of Results

Despite additional API costs, a replication of the two

most successful experiments was conducted to at-

tempt to show reproducibility. The two most success-

ful runs were n = 6, r = 1 and n = 4, r = 2, each

reaching 24/71 solutions. These two were rerun, in

order to check reproducibility. The results from this

rerun were more successful than the initial runs, lead-

ing to a total of 25/71 successfully solved programs

for n = 4, r = 2 and 26/71 for n = 6, r = 1.

5.6 Chain of Thought Experiment

The Chain-of-Thought experiment refers to a fur-

ther experiment conducted, which differentiates itself

from the main experiment in its prompting strategy.

See section 3.4.4 for an explanation.

Using the set of parameters with the highest rate

of successfully generated solutions: n = 6, r = 1, the

experiment was conducted. In total, 25/71 programs

were solved, equaling the average of the success rates

from the original experiment and the veriﬁcation run.

6 DISCUSSION

This section analyses the results of the experiments

conducted with Marmaragan.

6.1 General Observations

Experiments on the benchmark demonstrate Mar-

maragan’s competence in generating annotations,

both in the case of Assert statements and in the

case of loop invariants, with a higher level of compe-

tence for Assert statements than for loop invariants.

Overall, it generated correct annotations for 36 out

of 71 (50.7%) of the benchmark cases. These results

highlight the potential for integrating formal veriﬁca-

tion into AI-assisted development, paving the way for

safer and more reliable AI-generated software.

6.2 N-Solutions and Retries Parameters

Increasing the N-Solutions parameter, which deter-

mines the number of initial solution attempts, gener-

ally led to improved success rates in solving bench-

mark problems. The retry mechanism, which allows

Marmaragan to attempt corrections based on error

feedback, also proved to be an effective strategy. In

many cases, experiments that incorporated retries out-

performed those that relied solely on generating new

solutions. This suggests that the model can effectively

use error information to reﬁne its approach.

The experiments reveal a complex interplay be-

tween N-Solutions and retries. The combinations of

n = 6, r = 1 and n = 4, r = 2 yielded the best results,

solving 24 out of 71 programs each. This suggests

that a balance between initial solution attempts and

correction opportunities is more effective than relying

on either approach alone.

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK

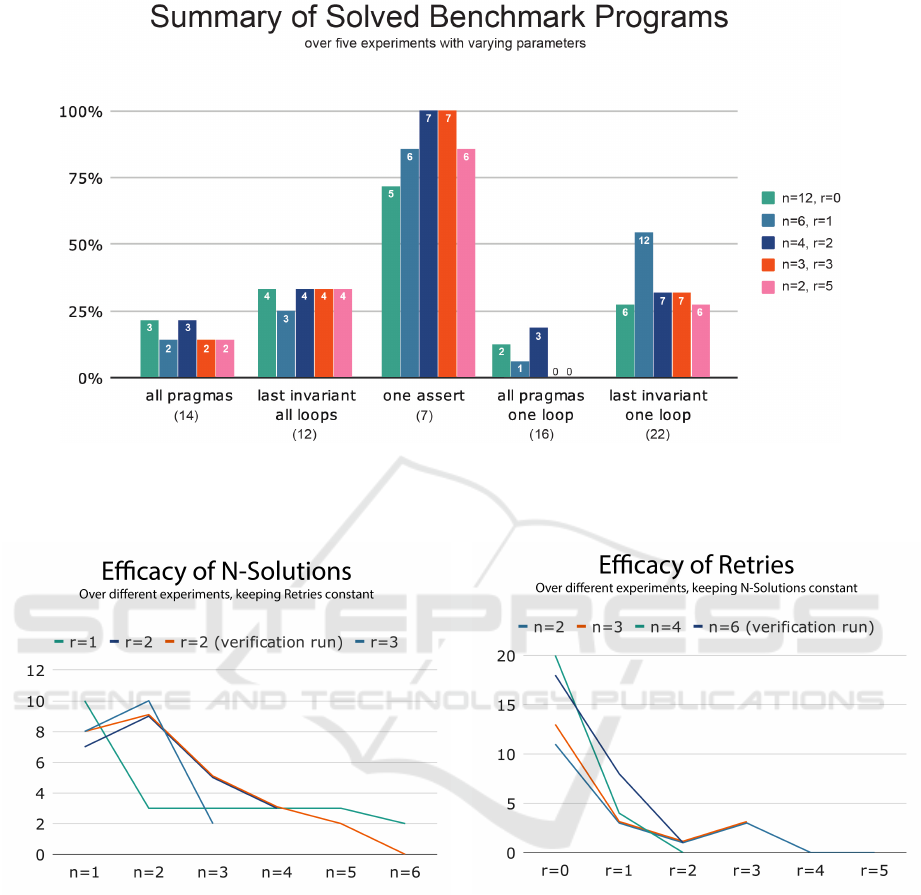
Figure 5: Summary of the total amount of programs solved, per benchmark, across all ﬁve experiments. The chart is a 100%

bar chart, thus the y-axis represents the amount of programs that were solved, as a percentage of the total number of programs

in the benchmark.

Figure 6: An overview of the efﬁcacy of N-Solutions, be-

tween n=1 and n=6. The retries parameter is kept constant.

As can be seen in Figures 6 and 7, higher values

of the N-Solutions end Retries parameters have demi-

nishing returns. This is not surprising, as the model

exhausts its most promising approaches in the ﬁrst

few attempts, with subsequent attempts becoming less

likely to yield new solutions.

7 RELATED WORK

We are not aware of any work that brings LLMs and

formal software veriﬁcation together in the same way

Figure 7: An overview of the efﬁcacy of successive retries,

between r=0 and r=5 (N-Solution parameter constant).

as we have proposed in this paper. But there is related

work on leveraging LLMs for theorem proving and

autoformalization in mathematics, from which valu-

able insights can be drawn for applying these tech-

niques to the veriﬁcation of software. This section

reviews key works that inform our approach. These

studies provide context for the capabilities and limita-

tions of LLMs in formal reasoning, which Marmara-

gan seeks to extend to software veriﬁcation.

Thor (Jiang et al., 2023a) combines language

models (LMs) with automated theorem proving sys-

tems using hammers to improve formal proof gen-

eration. Hammers are tools that bridge the gap be-

ICSOFT 2025 - 20th International Conference on Software Technologies

tween Interactive Theorem Provers (ITPs), which as-

sist users in formulating proofs, and Automated The-

orem Provers (ATPs), which independently verify

conjectures. They achieve this by translating proof

steps into ATP-compatible formats, selecting relevant

premises, and integrating the ATP’s solutions back

into the ITP, enabling automated reasoning for indi-

vidual proof steps (Blanchette et al., 2016). Sledge-

hammer (Paulson, 2012) is a hammer for the Is-

abelle (Paulson, 1994) ITP. Thor functions as follows:

given a theorem and assumptions, it proves the con-

jecture by ﬁrst allowing the LM to devise the proof

steps, then appending < hammer > annotations to

individual sections, allowing Sledgehammer to com-

plete the rest of the proof. Tested on the PISA and

MiniF2F benchmarks, Thor demonstrated higher suc-

cess rates than individual components like Sledge-

hammer, solving 57% of PISA benchmark problems.

Despite its innovative approach, subsequent methods

like Baldur have surpassed Thor’s results, utilizing

newer LLM technologies.

Baldur (First et al., 2023) generates entire for-

mal proofs from theorem statements using LLMs and

features a proof-repair mechanism that utilizes error

messages to reﬁne failed proofs. Unlike step-by-step

proof generation, Baldur constructs full proofs and as-

sesses their validity. It achieves a 47.9% success rate

on the PISA benchmark and demonstrates the effec-

tiveness of proof repair and additional context for im-

proving performance. Combining Baldur with Thor

enhances results, solving 65.7% of PISA problems,

showcasing complementary strengths.

The Draft-Sketch-Prove (DSP) approach (Jiang

et al., 2023b) addresses autoformalization by trans-

forming informal mathematical proofs into veriﬁed

formal proofs through three steps: drafting informal

proofs, generating formal sketches, and completing

gaps using automated provers. Using human-written

and LLM-generated informal proofs, DSP achieves

state-of-the-art performance on the MiniF2F bench-

mark, solving 42.6% and 40.6% of validation prob-

lems, respectively. Ablation studies highlight the im-

portance of comments, multi-step reasoning, and in-

tegrating ATP tools like Sledgehammer.

Magnushammer (Mikuła et al., 2024) uses a

transformer-based architecture to address premise se-

lection, bypassing the need for extensive engineering.

By training on premise selection datasets, it combines

SELECT and RERANK algorithms to embed proof

states and premises into a shared latent space, en-

abling relevance scoring. Magnushammer achieves

state-of-the-art results on PISA, solving 59.5% of

problems, and boosts Thor’s performance to a 71%

success rate when replacing Sledgehammer as the

premise selection tool.

8 FUTURE WORK

Marmaragan demonstrates the feasibility of an AI-

powered annotation generator for SPARK 2014, but

there remain several opportunities for further research

and development.

One potential direction is enabling the generation

of pre- and postconditions by the LLM itself. Devel-

opers could deﬁne contracts for high-level functions,

while the AI reﬁnes contracts for the invoked lower-

level functions to preserve program correctness.

Testing Marmaragan on a benchmark of 16 pro-

grams yielded initial results, but validating its robust-

ness and generalizability requires a larger dataset. Fu-

ture benchmarks should include diverse SPARK pro-

grams spanning various domains and complexities.

Long-term goals include evolving Marmaragan

into an industrial-grade tool, akin to how Copilot in-

tegrates into IDEs, by providing real-time annotation

suggestions during SPARK code development.

Finally, an exciting avenue for long-term research

based on the ideas in this paper would be to explore

the possibility of employing LLMs to generate entire

formally veriﬁed programs based on a conversation

between a human project manager and an LLM about

the intended behavior of the program.

9 CONCLUSION

This paper introduced Marmaragan, a proof-of-

concept tool for generating SPARK 2014 annota-

tions using LLMs. It integrates GNATprove to check

whether the annotations complete the veriﬁcation of

the code. Marmaragan is thus a hybrid AI system that

combines the power of LLMs with the trustworthiness

of logic-based reasoning tools. Key techniques in the

implementation of Marmaragan include utilizing pre-

compiled GNATprove mediums, generating multiple

solutions, retrying with additional context, and op-

tional chain-of-thought prompting.

Benchmarking on 16 curated SPARK programs

demonstrated Marmaragan’s capabilities, particularly

in generating Assert statements. The tool was able

to solve 36 out of 71 benchmark cases.

This work highlights the potential for integrat-

ing formal veriﬁcation into AI-assisted development,

paving the way for safer and more reliable AI-

generated software.

Verifying LLM-Generated Code in the Context of Software Veriﬁcation with Ada/SPARK

ACKNOWLEDGEMENTS

We would like to acknowledge the work done by Em-

manuel Debanne. Based on ideas of the ﬁrst co-

author of this paper, Emmanuel developed Sparkilo, a

closed-source tool similar to Marmaragan for generat-

ing annotations for SPARK 2014 programs, including

features such as retries and chain of thought prompt-

ing. Sparkilo provided a great foundation for the ideas

presented in this paper and laid out the groundwork

for many of the features implemented in Marmaragan.

Two functions authored by Emmanuel were included

in Marmaragan.

Additionally, we would like to acknowledge the

support of Tobias Philipp from secunet Security Net-

works AG, who supported the two co-authors of this

paper in the development of Marmaragan through his

expertise in SPARK 2014.

REFERENCES

AdaCore (1980). Ada programming language. https://ada-

lang.io/.

Barnes, J. (2012). High Integrity Software: The SPARK

Approach to Safety and Security. Addison-Wesley.

Blanchette, J. C., Kaliszyk, C., Paulson, L. C., and Urban,

J. (2016). Hammering towards QED. Journal of For-

malized Reasoning, 9(1):101–148.

Brosgol, B. M. (2019). How to succeed in the software busi-

ness while giving away the source code: The AdaCore

experience. IEEE Software, 36(6):17–22.

Chapman, R., Dross, C., Matthews, S., and Moy, Y. (2024).

Co-developing programs and their proof of correct-

ness. Commun. ACM, 67(3):84–94.

Chapman, R. and Schanda, F. (2014). Are we there yet?

20 years of industrial theorem proving with SPARK.

In Klein, G. and Gamboa, R., editors, Interactive The-

orem Proving, pages 17–26, Cham. Springer Interna-

tional Publishing.

Chase, H. (2022). LangChain Python Library.

https://github.com/langchain-ai/langchain.

Cramer, M. (2023). argu.

https://github.com/marcoscramer/argu.

Dross, C., Efstathopoulos, P., Lesens, D., Mentr, D., and

Moy, Y. (2014). Rail, space, security: Three case stud-

ies for SPARK 2014.

Filli

atre, J.-C. and Paskevich, A. (2013). Why3 — where

programs meet provers. In Felleisen, M. and Gard-

ner, P., editors, Programming Languages and Systems,

pages 125–128, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Filli

atre, J.-C. (2011). Deductive software veriﬁcation. In-

ternational Journal on Software Tools for Technology

Transfer, 13:397–403.

First, E., Rabe, M. N., Ringer, T., and Brun, Y. (2023).

Baldur: Whole-proof generation and repair with large

language models.

Hoare, C. A. R. (1969). An Axiomatic Basis for Computer

Programming. Communications of the ACM.

Jason Wei, X. W., Schuurmans, D., Bosma, M., Ichter, B.,

Xia, F., Chi, E., Le, Q., and Zhou, D. (2023). Chain-

of-thought prompting elicits reasoning in large lan-

guage models.

Jiang, A. Q., Li, W., Tworkowski, S., Czechowski, K.,

Odrzyg

z, T., Miło

s, P., Wu, Y., and Jamnik, M.

(2023a). Thor: Wielding hammers to integrate lan-

guage models and automated theorem provers. Jour-

nal of Formal Methods.

Jiang, A. Q., Welleck, S., Zhou, J. P., Li, W., Liu, J., Jam-

nik, M., Lacroix, T., Wu, Y., and Lample, G. (2023b).

Draft, sketch, and prove: Guiding formal theorem

provers with informal proofs.

Kojima, T., Gu, S. S., Reid, M., Matsuo, Y., and Iwasawa,

Y. (2023). Large language models are zero-shot rea-

soners.

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).

Efﬁcient estimation of word representations in vector

space.

Mikuła, M., Tworkowski, S., Antoniak, S., Piotrowski,

B., Jiang, A. Q., Zhou, J. P., Szegedy, C., Łukasz

Kuci

nski, Miło

s, P., and Wu, Y. (2024). Magnusham-

mer: A transformer-based approach to premise selec-

tion.

Moi, Y. (2013). SPARK 2014 rationale. Ada User Journal,

34(4):243–254.

Moy, Y., Ledinot, E., Delseny, H., Wiels, V., and Monate,

B. (2013). Testing or formal veriﬁcation: DO-178C

alternatives and industrial experience. IEEE Software,

30(3):50–57.

Paulson, L. (2012). Three years of experience with sledge-

hammer, a practical link between automatic and inter-

active theorem provers. In Schmidt, R. A., Schulz, S.,

and Konev, B., editors, PAAR-2010: Proceedings of

the 2nd Workshop on Practical Aspects of Automated

Reasoning, volume 9 of EPiC Series in Computing,

pages 1–10. EasyChair.

Paulson, L. C. (1994). Isabelle: A generic theorem prover.

Pennington, J., Socher, R., and Manning, C. D. (2014).

Glove: Global vectors for word representation. Con-

ference on Empirical Methods in Natural Language

Processing (EMNLP), pages 1532–1543.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L., and Polosukhin, I.

(2017). Attention is all you need. Advances in Neu-

ral Information Processing Systems (NeurIPS), pages

5998–6008.

ICSOFT 2025 - 20th International Conference on Software Technologies