An Extensible MARL Framework for Multi-UAV Collaborative
Path Planning
Mingxuan Li
a
, Boquan Zhang
b
, Zhi Zhu
c
and Tao Wang
College of Systems Engineering, National University of Defense Technology,
Kaifu District, Changsha City, Hunan Province, China
Keywords: UAVs Path Planning, MARL, POMDP, Modeling and Simulation.
Abstract: Automatic path planning of unmanned aerial vehicles (UAVs) can reduce human operational errors and min-
imize the risk of flight accidents. Generally, path planning requires UAVs to arrive at the target points safely
and timely. The commonly utilized dynamic programming algorithms and heuristic bionic algorithms are
characterized by their intricate designs and suboptimal performance, making it challenging to achieve the
goal. Some methods based on Reinforcement Learning (RL) are only suitable for specialized scenarios and
have poor scalability. This paper proposed an Extensible Multi Agent Reinforcement Learning (MARL)
Framework. It includes System Framework and Learning Framework. System Framework sets up the scenario
of path planning problem, which can be extended to different scenarios, including dynamic/static targets,
sparse/dense obstacle, etc. Learning framework reconstruct the models and scenarios of System Framework
as Partially Observable Markov Decision Process (POMDP) problem and adapt MARL algorithms to solve
it. Learning framework can be compatible with a variety of MARL algorithms. To test our proposed frame-
work, preliminary experiments were conducted on three MARL algorithms: IQL, VDN, and QMIX, in the
constructed scenario. The experimental results have verified the effectiveness of our proposed framework.
1 INTRODUCTION
Collaborative path planning for multiple unmanned
aerial vehicles (UAVs) represents a quintessential au-
tomatic control challenge.In comparison to traditional
manual control, automatic control for multiple UAVs
exhibits significant advantages in terms of efficiency
and safety.
At present, some algorithms have achieved signif-
icant results in path planning for single /distributed
UAVs. However, in complex environments charac-
terized by the presence of multiple targets and a sig-
nificant number of obstacles, a single UAV often
struggles to efficiently accomplish the task. Such sce-
narios typically necessitate the collaboration of mul-
tiple UAVs to effectively perform path planning in
these challenging conditions. Coordinating multiple
UAVs has brought many new challenges (Raap, M.
et al. 2019). For example, algorithms tailored for the
single UAV-single target path planning problem
a
https://orcid.org/0009-0000-3137-0133
b
https://orcid.org/0009-0003-8742-3777
c
https://orcid.org/0000-0003-3758-8568
solely require consideration for minimizing the dis-
tance between the UAV and the target point. But for
multiple UAVs, the relationship between the UAV
and the target points may change as the environment
dynamically changes.In addition, when dealing with
multiple target points, competition among UAVs
should be taken into account to prevent redundant vis-
its to the same target point. Furthermore, the fuel en-
durance limit must be considered, ensuring that the
UAV reaches the target point within a specified
timeframe.
In recent years, various methods and algorithms
have emerged in the field of multi-UAV path plan-
ning research. Mainly including dynamic program-
ming algorithms, heuristic algorithms, reinforcement
learning methods, etc. Ni et al. (Ni, J., Tang, G. et al.
2020) designed an innovative latent game model and
optimized binary logarithmic linear learning algo-
rithm, which can address the challenges of collabora-
Li, M., Zhang, B., Zhu, Z. and Wang, T.
An Extensible MARL Framework for Multi-UAV Collaborative Path Planning.
DOI: 10.5220/0013461100003970
In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 217-225
ISBN: 978-989-758-759-7; ISSN: 2184-2841
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
217

tive control and comprehensive coverage of search ar-
eas in multi-UAV collaborative search tasks. Zheng J
et al. (Zheng, J., Ding, M. et al.2023) developed an
overall UAV search objective function in a finite time
domain, which not only considers the need for re-
peated searches, but also considers the maintenance
of connectivity and collision avoidance between
UAVs. This study decomposes the overall search ob-
jective function and establishes a Distributed Con-
strained Optimization Problem (DCOP) model,
which enables all UAVs to optimize the overall
search objective by interacting with their neighbors.
A method based on Enhanced Genetic Algorithm
(EGA) is proposed to explore the global optimal so-
lution of DCOP. Zhang M et al. (Zhang M, Han Y,
Chen S. et al., 2023) proposed a RIME algorithm
based on multi elite policy enhancement for 3D UAV
path planning. This algorithm achieves exploration
and development behavior in optimization methods
by simulating the formation process of ice. Update the
population during the optimal solution selection stage
through an improved greedy selection mechanism.
Traditional dynamic programming algorithms are
limited to controlling small-scale UAV swarms and
require tailored designs for different scenarios, lead-
ing to limited flexibility. Heuristic biomimetic algo-
rithms can address these issues to some extent. How-
ever, most heuristic algorithms only utilize infor-
mation from a single step or a few steps to determine
UAV behavior and are unable to account for the im-
pact of long-term benefits on current decisions.
Currently, reinforcement learning (RL) algo-
rithms stand as one of the most efficient methods for
implementing collaborative path planning for multi-
ple UAVs. Through interaction with the environment,
RL learns the optimal policy and adapts to real-time
environmental changes.It utilizes historical experi-
ence via Q-networks to integrate long-term benefits
into UAV behavior decision-making. However, RL
still encounters unresolved challenges in UAV path
planning for dynamic targets, including: 1. some stud-
ies still use centralized DQN(Mnih, V. et al,2015) or
IQL(Kostrikov, I. et al,2021) algorithms to solve
multi-UAV collaborative path planning problems
(Fei, W. et al, 2024) (Fang, W. et al, 2024). These al-
gorithms cannot fully integrate the observed infor-
mation of all agents, which results in agents are una-
ble to make optimal decisions.2. Many studies focus
on improving algorithms for specific scenarios, and
algorithms are inflexibility.
This paper presents an Extensible Multi Agent
Reinforcement Learning (MARL) Framework.The
Extensible MARL Framework consists of two parts,
the System Framework and the Learning framework.
The contributions are as follows:
1. System Framework defines the multi-objec-
tive optimization function and the constraints of the
problem, and constructs a scenario for multi-UAV
path planning, and develops models for UAVs, obsta-
cles, and targets.
2. Learning Framework reconstructs the multi-
UAV trajectory planning process into a Partially Ob-
servable Markov Decision Process (POMDP), and
combines the MARL algorithm with the recon-
structed problem. To ensure the smooth operation of
the algorithm, the reward function of the MARL al-
gorithm is constructed using environmental infor-
mation such as the number of discovered targets and
the distance between the UAV and the targets.
3. We conducted preliminary experiments using
three MARL algorithms, IQL,VDN(Sunehag, P. et
al,2017),and QMIX(Rashid, T. et al.,2020), to verify
the effectiveness of the proposed method.
2 SYSTEM FRAMEWORK
To describe solve the problem of UAVs collaborative
path planning. Firstly, we define the problem as a
nonlinear multi-objective optimization problem and
establish its constraints. Subsequently, based on the
problem setting, we depict the scenario and identify
the models within it, including drones, obstacles, tar-
gets, among others. Lastly, we formulate these mod-
els, determining their behavioral and interaction rules.
2.1 Problem Formulation
The ability of multi-UAV collaborative path planning
can be represented by the number of discovered tar-
gets. The objective function is established as follows:
𝐹

=𝑚𝑎𝑥
1|𝑑𝑖𝑠(𝐿(𝑡𝑎𝑟
,
)−𝐿(𝑢
,
))≤𝑑

0|𝑑𝑖𝑠(𝐿(𝑡𝑎𝑟
,
)−𝐿(𝑢
,
))>𝑑



(1)
For 𝑡𝑎𝑟
,
represents the information of i-th target
at time t,𝑢
,
represents the information of j-th UAV
at time t. L (.) is used to obtain location, and dis(.) is
used to calculate distance. The total number of targets
is m. When at a certain moment t’, the overall envi-
ronment reaches the condition F
t’
=m,the overall goal
reaches the ideal optimum.
Meanwhile, the behaviours of UAVs in the scene
must meet the following constraints:
|
|𝐿(∀𝑈

)−𝐿(𝑧)
)
||<𝑑𝑧
(2)
𝐿
(
∀𝑈

)
∈
[
(
0,𝑀

)
,
(
0,𝑀

)
]
(3)
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
218

𝑡∈[0,𝑇] 𝑎𝑛𝑑 𝑡∈𝑁
(4)
𝑐ℎ𝑎𝑛𝑔𝑒(𝑒
 
)
𝑇 |𝑑𝑖𝑠(𝐿(𝑢
,
)−𝐿(𝑢
,
))≤𝑑

𝐹|𝑑𝑖𝑠(𝐿(𝑢
,
)−𝐿(𝑢
,
))>𝑑

(5)
For constraint (2), z representing obstacles, the
positions of all UAVs cannot coincide with the posi-
tions of obstacles. Constraint (3) means that the posi-
tion of the UAV cannot exceed the specified area map
boundary. Constraint (4) means that the advancement
of timestamps must be a discrete integer, without con-
sidering the situation where a model is located be-
tween multiple grids at a certain time node. Constraint
(5) means that the UAV can only exchange 𝑒

in-
formation with other UAVs within its communication
range.𝑒

records the information about all targets is
heading by which UAV. 𝑒

is an important attribute
used to help UAVs avoid accessing duplicate targets.
This is defined in Section 2.3.
2.2 Scenario Design
Figure 1 shows the overall scenario designed accord-
ing to the System Framework.Set the size of the spec-
ified area to (Mx, My), which can be divided into
multiple grids of size (mx, my). UAVs, targets, and
partially changing obstacles are all active within the
grid. The field of view (FOV) of a UAV can obtain
the information including the location of obstacles
and targets, within the grids in its detection range.
When the timestamp advancement, UAVs, and some
mobilizable targets can move to nearby grids. There
are also some immovable targets in the scenario. The
condition for mission victory is that n UAVs reach all
m target points (n≥m).
Ly
Lx
communication
Target
Target
Target
Obstacle / No-fly zone
Obstacle / No-fly zone
Figure 1: Schematic diagram of multi-UAV collaborative
path planning scenario.
2.3 Behavioral Modeling
UAV model:The UAV model is defined as follows:
𝑢=
{
𝑥,𝑦,𝑑

,𝑑

,𝑒

}
(6)
x and y represent the coordinate positions of the
UAV. 𝑑

and 𝑐𝑜𝑚𝑚

represent the detec-
tion range and communication range of the UAV, re-
spectively. With the UAV's own position as the center,
it can perceive the presence of targets and obstacles
within the 𝑑

, and can communicate with other UAVs
within the 𝑑

. 𝑒

is a list recording the target points
of each UAV. The UAV cannot obtain the complete
𝑒

in real time and can only obtain it through com-
municating with other UAVs.
The definition of 𝑒

is shown in Equation 6,
where 𝑡𝑎𝑟𝑔𝑒𝑡


represents that UAV
i
is heading to-
wards target
j
, n represents the number of UAVs, and
j represents the identification number of the targets.
𝑒

={𝑡𝑎𝑟𝑔𝑒𝑡


| 𝑖=0,1,2,…𝑛 ,
𝑗
∈𝑚}
(7)
In order to make the overall system scalable, n can
also be set to a slightly larger integer than the total
number of UAVs. For example, there are three UAVs
in the scene, and at a certain moment ct, the infor-
mation recorded in the 𝑒

of UAV
i
may be {0, -1,1}.
The three elements represent that UAV
0
is heading
towards target
0
and currently unable to obtain target
information tracked by UAV
1
, while UAV
2
is head-
ing towards target
1
. As shown in algorithm 1. Based
on the information stored in 𝑒

, UAVs can dynam-
ically allocate tasks more reasonably, avoiding multi-
ple UAVs from repeatedly reaching the same target.
Input: e
list
of UAV
i
Result: Updated e
list
of UAV
i
U_list←Ø
add UAV
i
to U_list
for j=0 to count (UAVs) do:
if ( UAV
j
is within the comm_range of UAV
i
):
add UAV
j
to U_list
END for
new_e_list← Ø
#Calculate the closest target to UAV
i
and record it
new_e_list[i]←record (UAV
i
)
for j=0 to count (UAVs) do:
cache← Ø
if(new_e_list[j] has no record),then:
for k=0 to count(U_list) do:
if (e
list,k
has a record about UAV
j
),then:
cache←cache+record(UAV
j
)
END for
#Find the latest record in cache,update list
new_e_list ← update (new_e_list,cache,j)
END for
Algorithm 1: UAVs communication.
An Extensible MARL Framework for Multi-UAV Collaborative Path Planning
219

The definition of UAVs movement rules is as fol-
lows: each UAV has 8 selectable search directions at
each time step. The position of UAV
i
at time step t is
denoted as 𝐿(𝑢
,
), which is updated by the selected
action a=𝛥(𝑥,𝑦), represented as:

𝜕𝐿(𝑢
,
)/𝜕𝑥=𝜕𝐿(𝑢
,
,𝑥)/𝜕𝑥+𝛥𝑥
𝜕𝐿(𝑢
,
)/𝜕𝑦=𝜕𝐿(𝑢
,
,𝑦)/𝜕𝑦+𝛥𝑦
(8)
𝛥
(
𝑥,𝑦
)
=
⎩
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎧
(
1,0
)
,𝑖𝑓 𝑎=0
(
𝑒𝑎𝑠𝑡
)
(
0,1
)
,𝑖𝑓 𝑎=1
(
𝑛𝑜𝑟𝑡ℎ
)
(
−1,0
)
,𝑖𝑓 𝑎=2
(
𝑤𝑒𝑠𝑡
)
(
0,−1
)
,𝑖𝑓 𝑎=3
(
𝑠𝑜𝑢𝑡ℎ
)
(
1,1
)
,𝑖𝑓 𝑎=4
(
𝑒𝑎𝑠𝑡 𝑛𝑜𝑟𝑡ℎ
)
(
−1,1
)
,𝑖𝑓 𝑎=5
(
𝑤𝑒𝑠𝑡 𝑛𝑜𝑟𝑡ℎ
)
(
1,−1
)
,𝑖𝑓 𝑎=6
(
𝑒𝑎𝑠𝑡 𝑠𝑜𝑢𝑡ℎ
)
(
−1,−1
)
,𝑖𝑓𝑎=7
(
𝑤𝑒𝑠𝑡 𝑠𝑜𝑢𝑡ℎ
)
(9)
Due to the presence of obstacles and area bound-
aries, at certain times, the movement actions of the
UAV may become unavailable, as shown in Figure 2.
For units near obstacles or at the edge of the map, the
corresponding action selection will become unavaila-
ble.
Figure 2 Schematic diagram of UAV action selection.
Target model: some targets can be moved to ad-
jacent grids according to the same movement rules as
UAVs. Some targets are immovable.
Obstacle model: There are multiple obstacles at
random positions within the designated area.To guar-
antee the solvability of the overall problem, we define
an obstacle model in its initial state, subject to the fol-
lowing constraints:
∄𝑧
|
𝐿
(
𝑧
)
=𝐿(∀𝑢

)
𝑜𝑟 𝐿
(
𝑧
)
=𝐿(∀𝑡𝑎𝑟

)
(10)
∄𝑧 |𝑠𝑝
(
∀𝑢,𝑧
)
=0 𝑜𝑟𝑠𝑝
(
∀𝑡𝑎𝑟,𝑧
)
=0
(11)
Constraint (10) indicates that the generation of ob-
stacles cannot coincide with the positions of the target
and the UAV. For constraint (11), sp(.) is the number
of positions that can be reached by the computing unit.
In the case of complete obstacle free and map bound-
ary free influence, sp(.)=8.This constraint indicates
that obstacles cannot completely surround the UAV
and target, making it impossible for the UAV to move
or for the target location to be reached.
3 LEARNING FRAMEWORK
For multi-UAV path planning, UAVs are required to
continuously detect and update information during
flight. However, due to hardware limitations and
other factors, they often cannot accurately observe the
overrall environment. Consequently, UAV path plan-
ning is aptly considered as a POMDP, and MARL is
one of the most efficient algorithms to solve POMDP
problems.
In this section, we introduce a Learning Frame-
work that reconstructs the scenarios and models es-
tablished in Section 2 into POMDP components. Sub-
sequently, we design a simulation flow to generate the
episodes required for training the MARL algorithm.
Lastly, we detail how the MARL algorithm interacts
with the episode data to optimize network parameters
and produce drone actions that are responsive to epi-
sode generation.
3.1 Scenario Reconstructing
To solve the problem built by System Framework.
We reconstruct the scenario and models proposed by
the System Framework as POMDP system.
Agent: A UAV is defined as an agent in the envi-
ronment. The agent obtains information about the sur-
rounding environment from its own sensors, selects
an action and provides feedback to the system.
A: the action of the UAV at time t is expressed as:
𝐴

=𝑎
,
,𝑎
,
,…,𝑎
,
 (12)
Where 𝑎
,
represents the encoding of the move-
ment rules defined in Section 2.2.
O: Each agent can observe its own information
and some environment information, expressed as:
𝑂

=𝑜
,
,𝑜
,
,…,𝑜
,
 (13)
𝑜
,
=𝑜𝑓
,
,𝑒𝑓
,
 (14)
𝑜𝑓
,
={𝐿𝑢
,
,𝑑

(


)
,𝐿

𝑚𝑖𝑛

,

,
𝐷

𝑚𝑖𝑛

,
,𝑢
,

,𝑒

}
(15)
𝑒𝑓
,
=ℎ𝑢
,
,𝐸

 (16)
O

represents the sum of observation information
obtained by all agents at time t in the current environ-
ment.o
,
represents the observation information of
the agent i at time t, which consists of two parts.For
of
,
,Lu
,
 represents the coordinates of agent i in the
map at time t, d

(
u

)
represents the sensing range of
UAV i. Lmtar
,
 represents the coordinate position
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
220

of the target closest to the agent i at time t.
Dmtar
,
,u
,
 represents the distance between the
target and the UAV. For 𝑒𝑓
,
, ℎ𝑢
,
,𝐸

 means that
at time t,the targets in each cell within the detection
range 𝑑

.
S: The overall state of the system is the sum of
global observation information and timestamp infor-
mation, expressed as:
𝑆

={𝑂

,𝑡/𝑇}
(17)
T is the maximum that the timestamp can advance
to, and 𝑡/𝑇 indicates the time advance of the current
environment.
R: The value calculated by the system according
to the current environment information is used to
guide Q network fitting. According to the problem
definition, we build the reward function as follows:
𝑅

=𝑐𝑜𝑢𝑛𝑡
(
𝑡𝑎𝑟


)
−
𝑑
,,
𝐿

+𝑏𝑤
(18)
𝑐𝑜𝑢𝑛𝑡
(
𝑡𝑎𝑟′

)
represents the number of targets
found at time t. 𝑑
,,
represents the sum of the dis-
tance between each UAV u and its nearest target e at
time t.Directly put 𝑑
,,
into the reward value is
likely to dilute other incentives factor, So we use 𝐿

to narrow its processing. 𝑏𝑤 is an indication function
that, at the end of an episode, bw=1 if battle_won sta-
tus has been reached, bw=0 otherwise.
3.2 Simulation Algorithm
In this paper, the purpose of repeating environmental
simulations is to obtain a large number of "episodes".
The simulation events of the environment follow the
principle of discrete event simulation. Episode is the
complete process of an intelligent agent starting to ex-
plore the environment and reaching a termination state
(or reaching a predetermined step limit). In the MARL
framework, the intelligent agent network can learn
from a large amount of "episode" data, continuously
optimize network parameters, thereby improving deci-
sion-making efficiency and ultimately achieving intel-
ligent acquisition of excellent strategies.
The specific process of environment simulation
is :(1) input the episode and time step t to be updated.
Obtain the actions of the UAVs. The actions come
from the output of the Q network. (2) Execute the ac-
tions to update the status of the UAVs. (3) Targets
movement.(4) UVAs communicate with each other to
update their observations. (5) To calculate the overall
reward. According to RL definition, it is necessary to
calculate the difference between the reward value of
this time step and the reward value of the previous
time step as the one-step reward for an episode. (6)
Record environmental information. (7) Check if the
environment has reached the 'battle won' state. If it
has, stop the environment and end the episode early.
(8) Check if the timestamp of the environment has
reached the maximum number of advances, to reach
the end of the episode. (9) Output updated episode.
Algorithm 2 describes the above process, where the
code marked with * is the behaviours that requires in-
teraction with MARL.
Input: episode,t
Result: updated episode
history_reward←0, reward←0
done←False
episode ←Ø
*Obtain_actions from Q network
UVAs←UAVs_move(UAVs,actions)
targets←Targets_move(targets, obstacles)
UVAs←UVAs_communicate(UAVs)
*reward ←Get_reward(UAVs,targets) #eq17
*reward ←reward - history_reward
*history_reward← reward
terminated←False
if episode gets victory conditions,then:
battle_won←True
done←True
if t reaches the maximum simulation time T,then:
terminated←True
done←True
episode←update(episode)
Algorithm 2: Simulation: update episode.
3.3 MARL Learning Procedure
MARL algorithms need to adaptively learn how to
control the UAV to complete the mission according
to real-time episode information.
The network that controls the action of the agent
in MARL is called Q network, and the Q network
training process is as follows:(1) initialize Q net-
work parameter θ and target network parameter
θ
-
,total training time steps T (2) Create two timers,
train_t to record the training progress and e_t to
record the progress of the episode. Initialize an ep-
isode. Initialize buffer D (3) The movements of the
UAVs are obtained from the Q network, the status
of the episode is updated, and the data is stored in
D. (4) When the data in D is sufficient for network
training, parameters θ of the main network and θ-
of the target network are trained.(5) When the ca-
pacity of D is full, it is cleaned. The cleanup
method is usually to delete some of the data that
enters the buffer first. (6) get training-finished θ.
An Extensible MARL Framework for Multi-UAV Collaborative Path Planning
221

Inputs: Initialize parameters θand θ
-
, T
Results: training completed θand θ
-
Initialize replay buffer D, episode
train_t←0
e_t←0
Reset the episode
while t ≤ T do:
actions←𝜀_greedy(UAVs,Q(θ))
# Algorithm2
episode←update_episode(episode,t)
train_t←train_t +1
e_t←e_t+1
episode←add_steps(episode)
if(episode has been finished),then:
Reset the episode
e_t=0
D←update_ episode(episode)
if(The episode stored in D is enough
to train the Q network), then:
Sample a random batch of episode in D
*Update the parameters of networkθ
c←0
if(θ has been trained step c),then:
*Update the parameters of networkθ
-
if(capacity(D) +capacity(e) >=M), then:
D←clean_buffer(D)
END while
Algorithm 3: MARL learns environment information and
outputs UAVs actions.
In algorithm 3,the parameter update of the target
network θ
-
behind that of the main network θ. This
can avoid the frequent change of the target value, re-
duce the instability in the training process, and make
the main network converge to the optimal strategy
more smoothly. QMIX uses the Mixing Network to
mix the individual Q values of multiple agents into a
global Q value. The global Q value represents the ex-
pected return of all agents acting together. VAN ob-
tains this global Q value through a linear function,
and IQL does not consider global Q values.
4 SIMULATION RESULT AND
ANALYSIS
In this section, MARL algorithms: IQL, VDN and
QMIX, are tested in the scenarios with different ob-
stacle rate settings to test the effectiveness of the Ex-
tensible MARL Framework. Then the experimental
results are described and analysed.
4.1 Experiment Settings
This section introduces the operating environment of
the experiment, the setting of MARL algorithm hy-
perparameters and the setting of simulation environ-
ment. The experimental hardwares are ： NVIDIA
GeForce RTX 3080Ti and AMD EPYC 9754. The
softwares are Ubuntu22.04,torch 2.3.0&CUDA
12.1,and PYMARL (Samvelyan, M. et al. 2019). Set-
tings of the MARL hyper-parameters are: batch
size:64 ,buffer_size:5000,and lr:0.001. We conducted
experiments on maps with grid sizes of 20 × 20. Ob-
stacle rate refers to the percentage of cells set as ob-
stacles, which is set to 20 or 40. The scenario involves
6 agents and 6 targets.For a single agent,dr=1 and
dc=1. The maximum of simulation time is 200.
4.2 Analysis of Algorithm Performance
In this section, we analyse the performance of three
MARL algorithms: IQL, VDN, and QMIX. Figures 3
and 4 show the variation of reward values over simu-
lation time for three algorithms in a simulation envi-
ronment with a map size of 20 × 20. T is the total run-
ning time of the simulation environment, measured in
millions. Statistics are performed at fixed intervals of
10k time steps, and the average value of 10k time
steps is taken as the experimental result.It can be seen
that IQL and VDN fit faster than QMIX. When the
obstacle rate is 20, the reward value of IQL and VDN
is slightly higher compared to QMIX. When the ob-
stacle rate is 40, the performance of the VDN algo-
rithm is slightly higher. This is because QMIX re-
quires additional use of global information to train a
hypernetwork. In our simulation environment, using
a combination of local observations as global infor-
mation may not provide sufficient data for the hyper-
network. Additionally, it is possible that the structure
of QMIX's hypernetwork is not suitable for our task.
Table 1 shows the comparison of the average re-
ward values of the three algorithms in the last 50 time
steps. It can be seen from the time-reward curve that
the three algorithms are close to fitting when ap-
proaching the end of training. By comparing the av-
erage reward of the three algorithms in the last 50
Time steps, the specific performance gap of the algo-
rithms can be more intuitively identified. It can be
seen that VDN performs slightly better than the other
two algorithms. This is because VDN uses linear
functions to combine the Q values of agents, which
avoids the lack of interaction between agents like IQL,
and the difficulty of combining Q values caused using
complex hypernetworks like QMIX.
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
222

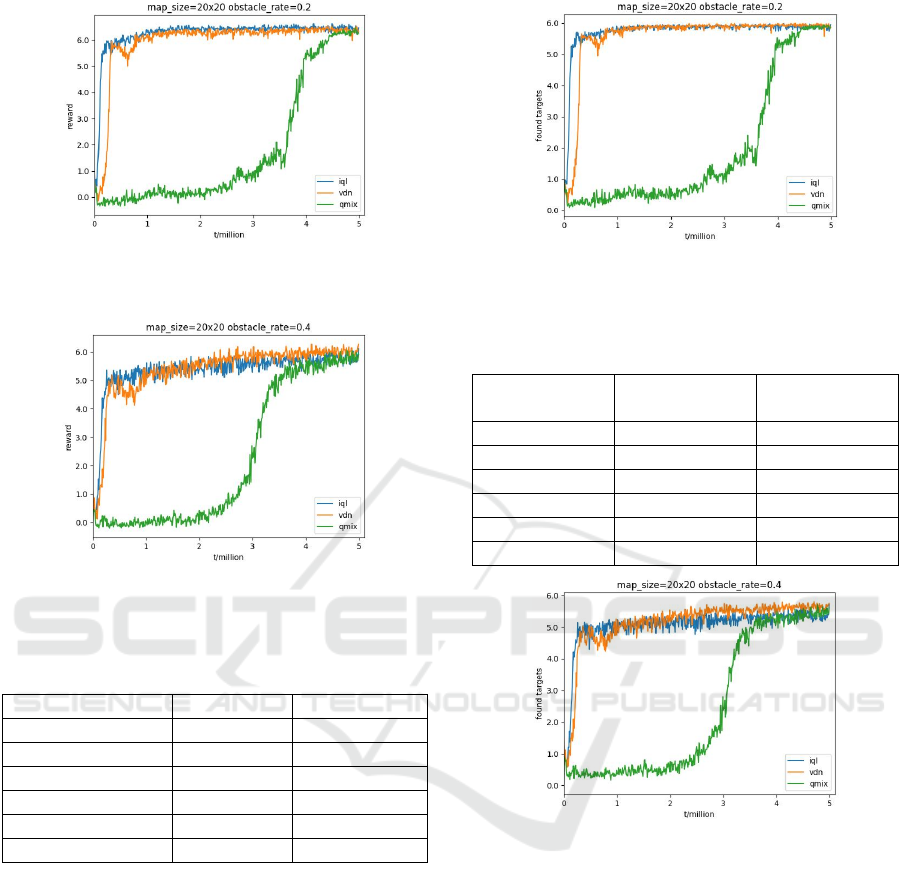
Figure 3 Time-reward curve of three algorithms at an ob-
stacle rate of 20.
Figure 4 Time-reward curve of three algorithms at an ob-
stacle rate of 20.
Table 1 Comparison of the average reward values of the
three algorithms in the last 50 time steps.
O
b
stacle rate (%) Metho
d
Rewar
d
20 IQL 6.45
20 VDN 6.35
20 QMIX 6.27
40 IQL 5.81
40 VDN 6.01
40 QMIX 5.75
4.3 Analysis of Mission Completion
Level
Figure 5 and Figure 6 show the time-target discovery
number curves of the three algorithms, and Table 2
shows how many targets were discovered by each of
the three algorithms in the last 50 time steps. The re-
sults of this experiment are similar to result of the re-
ward comparison experiment, but the performance
gap between the algorithms is not as significant as the
previous experiment. In the case where the total num-
ber of target points is 6, the number of targets found
using the three algorithms exceeds 5, indicating that
Extensible MARL Framework can effectively com-
plete the path planning task.
Figure 5 Time-Number of targets found curve of three al-
gorithms at an obstacle rate of 20.
Table 2: Comparison of the average number of targets
found of the three algorithms in the last 50 time steps.
Obstacle
rate(%)
Method Number of
tar
g
ets foun
d
20 IQL 5.89
20 VDN 5.91
20 QMIX 5.86
40 IQL 5.38
40 VDN 5.64
40 QMIX 5.43
Figure 6 Time-Number of targets found curve of three al-
gorithms at an obstacle rate of 40.
5 CONCLUSION
In order to solve the problem of multi-UAV coopera-
tive path planning, we propose the Extensible MARL
Framework. Extensible MARL Framework can be
applied to scenarios built with a variety of environ-
mental factors and is compatible with a variety of
MARL algorithms. The Extensible MARL Frame-
work consists of two parts, the system framework and
the learning framework. The system framework de-
fines the scenario, including the problems to be
solved, the models, and the behavioural interactions
between the models. The learning framework aims to
reconstruct the problems and models of the system
An Extensible MARL Framework for Multi-UAV Collaborative Path Planning
223

framework into POMDP, then solve the problems of
the system framework through MARL algorithm.
In the experiment part, to verify the validity of Ex-
tensible MARL Framework, the paper tests three
MARL algorithms: IQL, VDN and QMIX, and it
evaluates these algorithms in two scenarios featuring
different obstacle rates: 20% for sparse and 40% for
dense. The experiment results show that IQL and
VDN adapt to the environment faster than QMIX, and
the reward value of IQL and VDN is slightly higher
than QMIX when the proportion of obstacles is 20%.
When the proportion of obstacles increases to 40%,
the performance of the VDN algorithm is slightly
higher than the other two algorithms.
In future research, we will further optimize the al-
gorithm for the poor performance of QMIX's hybrid
network. At the same time, we will design more dy-
namic complex scenarios to test the robustness of var-
ious algorithms. At the same time, we consider de-
signing more realistic experimental scenarios to en-
sure that the MARL algorithm can be truly integrated
with practical applications.
REFERENCES
Aggarwal, S., & Kumar, N. (2020). Path planning tech-
niques for unmanned aerial vehicles: A review, solu-
tions, and challenges. Computer communications, 149,
270-299.
Cao, X., Li, M., Tao, Y., & Lu, P. (2024). HMA-SAR:
Multi-Agent Search and Rescue for Unknown Located
Dynamic Targets in Completely Unknown Environ-
ments. IEEE Robotics and Automation Letters.
Cetinsaya, B., Reiners, D., & Cruz-Neira, C. (2024). From
PID to swarms: A decade of advancements in drone
control and path planning-A systematic review (2013–
2023). Swarm and Evolutionary Computation, 89,
101626.
Fang, W., Liao, Z., & Bai, Y. (2024). Improved ACO algo-
rithm fused with improved Q-Learning algorithm for
Bessel curve global path planning of search and rescue
robots. Robotics and Autonomous Systems, 182,
104822.
Fei, W. A. N. G., Xiaoping, Z. H. U., Zhou, Z. H. O. U., &
Yang, T. A. N. G. (2024). Deep-reinforcement-learn-
ing-based UAV autonomous navigation and collision
avoidance in unknown environments. Chinese Journal
of Aeronautics, 37(3), 237-257.
Hildmann, H., & Kovacs, E. (2019). Using unmanned aerial
vehicles (UAVs) as mobile sensing platforms (MSPs)
for disaster response, civil security and public
safety. Drones, 3(3), 59.
Hou, Y., Zhao, J., Zhang, R., Cheng, X., & Yang, L. (2023).
UAV swarm cooperative target search: A multi-agent
reinforcement learning approach. IEEE Transactions on
Intelligent Vehicles.
Kostrikov, I., Nair, A., & Levine, S. (2021). Offline rein-
forcement learning with implicit q-learning. arXiv pre-
print arXiv:2110.06169.
Lyu, M., Zhao, Y., Huang, C., & Huang, H. (2023). Un-
manned aerial vehicles for search and rescue: A survey.
Remote Sensing, 15(13), 3266.
Martinez-Alpiste, I., Golcarenarenji, G., Wang, Q., & Al-
caraz-Calero, J. M. (2021). Search and rescue operation
using UAVs: A case study. Expert Systems with Appli-
cations, 178, 114937.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., ... & Hassabis, D. (2015).
Human-level control through deep reinforcement learn-
ing. nature, 518(7540), 529-533.
Moon, J., Papaioannou, S., Laoudias, C., Kolios, P., & Kim,
S. (2021). Deep reinforcement learning multi-UAV tra-
jectory control for target tracking. IEEE Internet of
Things Journal, 8(20), 15441-15455.
Ni, J., Tang, G., Mo, Z., Cao, W., & Yang, S. X. (2020). An
improved potential game theory based method for
multi-UAV cooperative search. IEEE Access, 8,
47787-47796.
Raap, M., Preuß, M., & Meyer-Nieberg, S. (2019). Moving
target search optimization–a literature review. Comput-
ers & Operations Research, 105, 132-140.
Rashid, T., Samvelyan, M., De Witt, C. S., Farquhar, G.,
Foerster, J., & Whiteson, S. (2020). Monotonic value
function factorisation for deep multi-agent reinforce-
ment learning. Journal of Machine Learning Re-
search, 21(178), 1-51.
Samvelyan, M., Rashid, T., De Witt, C. S., Farquhar, G.,
Nardelli, N., Rudner, T. G., ... & Whiteson, S. (2019).
The starcraft multi-agent challenge. arXiv preprint
arXiv:1902.04043.
Shixin, Z., Feng, P., Anni, J., Hao, Z., & Qiuqi, G. (2024).
The unmanned vehicle on-ramp merging model based
on AM-MAPPO algorithm. Scientific Reports, 14(1),
19416.
Sunehag, P., Lever, G., Gruslys, A., Czarnecki, W. M.,
Zambaldi, V., Jaderberg, M., ... & Graepel, T. (2017).
Value-decomposition networks for cooperative multi-
agent learning. arXiv preprint arXiv:1706.05296.
Tampuu, A., Matiisen, T., Kodelja, D., Kuzovkin, I., Kor-
jus, K., Aru, J., ... & Vicente, R. (2017). Multiagent co-
operation and competition with deep reinforcement
learning. PloS one, 12(4), e0172395.
Vaswani, A. (2017). Attention is all you need. Advances in
Neural Information Processing Systems.
Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M.,
& Freitas, N. (2016, June). Dueling network architec-
tures for deep reinforcement learning. In International
conference on machine learning (pp. 1995-2003).
PMLR.
Zhang, J., Li, M., Xu, Y., He, H., Li, Q., & Wang, T. (2024).
StrucGCN: Structural enhanced graph convolutional
networks for graph embedding. Information Fusion,
102893.
Zhang, M., Han, Y., Chen, S., Liu, M., He, Z., & Pan, N.
(2023). A multi-strategy improved differential evolu-
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
224

tion algorithm for UAV 3D trajectory planning in com-
plex mountainous environments. Engineering Applica-
tions of Artificial Intelligence, 125, 106672.
Zheng, J., Ding, M., Sun, L., & Liu, H. (2023). Distributed
stochastic algorithm based on enhanced genetic algo-
rithm for path planning of multi-UAV cooperative area
search. IEEE Transactions on Intelligent Transporta-
tion Systems, 24(8), 8290-8303.
Zhou, W., Liu, Z., Li, J., Xu, X., & Shen, L. (2021). Multi-
target tracking for unmanned aerial vehicle swarms us-
ing deep reinforcement learning. Neurocompu-
ting, 466, 285-297.
An Extensible MARL Framework for Multi-UAV Collaborative Path Planning
225