Correlation Power Analysis on Ascon with Multi-Bit Selection Function

Viet Sang Nguyen

, Vincent Grosso

and Pierre-Louis Cayrel

Universit

e Jean Monnet Saint-Etienne, CNRS, Institut d Optique Graduate School, Laboratoire Hubert Curien UMR 5516,

F-42023 Saint-Etienne, France

Keywords:

Correlation Power Analysis, Selection Function, Ascon.

Abstract:

Ascon has recently been selected by NIST as the new standard for lightweight cryptography. This highlights

the need to evaluate its resilience against implementation attacks such as Correlation Power Analysis (CPA).

Traditional CPA on Ascon uses a 1-bit selection function, modeling power consumption based on a single bit

of an machine word. However, actual power leakage depends on the entire word. Therefore, the hypothesized

power consumption aligns better with the measured values when more bits of the word are involved in the

selection function. This paper investigates the use of multi-bit selection functions in CPA on Ascon. We

show that the bitsliced-oriented design of Ascon leads the multi-bit selection functions to produce a group of

key candidates with high correlations, rather than a single candidate as typically expected in CPA. Through

theoretical analysis and experimental validation, we examine this behavior in detail. Based on these insights,

we propose an efﬁcient key recovery algorithm tailored for the multi-bit selection functions. Our results

demonstrate that this approach signiﬁcantly reduces the number of CPA runs required for full key recovery.

1 INTRODUCTION

Nowadays, small computing devices like RFID tags,

sensors, and smart cards are becoming increasingly

widespread. Although the Advanced Encryption

Standard (AES, 2001) is a highly reliable and se-

cure cipher, it is often too resource-intensive for de-

ployment in such constrained environments. In this

context, NIST initiated a competition to look for a

new lightweight cryptography standard. In February

2023, NIST announced that Ascon was selected to be

standardized. Before that, Ascon had also been in-

cluded in the ﬁnal portfolio of the CAESAR competi-

tion. The rigorous evaluations conducted during both

selection processes have solidiﬁed conﬁdence in As-

con’s security under the traditional black-box model,

where the adversary can only access the inputs and

outputs.

However, such a model does not always capture

the security for physical implementations. When

deployed in embedded devices, cryptographic algo-

rithms can be vulnerable to power analysis attacks,

a potent category of side-channel attacks that ex-

ploit the power consumption of the devices during

https://orcid.org/0009-0004-2939-8478

https://orcid.org/0000-0002-3874-7527

https://orcid.org/0000-0002-6708-868X

algorithm execution. Since the introduction of Dif-

ferential Power Attack (DPA) (Kocher et al., 1999),

power analysis attacks have emerged as a prominent

research area. DPA distinguishes the correct key

candidate from the incorrect ones by the difference

of means. Correlation Power Analysis (CPA) (Brier

et al., 2004), a variant of DPA, leverages a speciﬁc

power consumption model, such as Hamming weight,

and uses Pearson correlation to identify the correct

key candidate. CPA is a versatile and powerful at-

tack, as it requires only the observation of power con-

sumption leakages during the execution of the crypto-

graphic algorithm. Detailed knowledge of the device

is not needed. Knowing the algorithm that is executed

by the device is usually sufﬁcient. The goal of CPA

is to recover the key through a statistical analysis of

key-dependent power leakages.

So far, CPA attacks for Ascon have received rel-

atively little attention. The ﬁrst successful CPA at-

tack was presented in (Samwel and Daemen, 2017)

targeting a noisy hardware implementation. A no-

table contribution of (Samwel and Daemen, 2017) is

the development of an effective selection function for

computing the intermediate variable targeted by the

attack. Unlike the popular choice of the S-box out-

put in CPA attacks on AES, selecting a suitable func-

tion for Ascon is more complex due to the bitsliced-

oriented design. In fact, directly using the S-box

Nguyen, V. S., Grosso, V. and Cayrel, P.-L.

Correlation Power Analysis on Ascon with Multi-Bit Selection Function.

DOI: 10.5220/0013460000003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 72-83

ISBN: 978-989-758-760-3; ISSN: 2184-7711

output as the selection function in Ascon can result

in a failed CPA attack, as evidenced in (Ramezan-

pour et al., 2020). Samwel and Daemen constructed

their selection function through a careful analysis of

how information leaks during computation. Using the

same selection function, the CPA attacks in (Roussel

et al., 2023; Weissbart and Picek, 2023) also success-

fully recovered the key. These attacks targeted a hy-

brid CMOS/MRAM hardware implementation and an

ARMv7m software implementation, respectively.

In the design of Ascon, the state is represented by

64-bit variables. Depending on the device architec-

ture, a 64-bit variable can be implemented using mul-

tiple smaller machine words, such as 8-bit or 32-bit

words. While effective, the selection function pro-

posed by Samwel and Daemen is limited to operate on

a single bit (referred to as the 1-bit selection function

hereafter). In other words, the power consumption

hypotheses are modeled based solely on the value of

a single bit within a machine word. However, in prac-

tice, the leaked information depends on the value of

the entire machine word (Brier et al., 2004; Tunstall

et al., 2007). As a result, the 1-bit selection func-

tion may not fully exploit all available leakage in the

power consumption traces.

Contributions. In this paper, we explore the fea-

sibility of employing multi-bit selection functions to

CPA attacks on Ascon. We begin by extending the 1-

bit selection function proposed by Samwel and Dae-

men to operate on multiple bits. Our ﬁndings reveal

that, due to the bitsliced-oriented design of the Sbox

implementation, using multi-bit selections function

results in a small group of key candidates with high

correlations, rather than a single candidate as typi-

cally expected in CPA. Through both theoretical anal-

ysis and experimental validation, we provide a com-

prehensive examination of the underlying causes of

this behavior.

Second, based on the insights from our analy-

sis, we propose an efﬁcient algorithm to identify the

correct key candidate when employing multi-bit se-

lection functions. We show that the multi-bit ap-

proach signiﬁcantly reduces the number of CPA runs

required for full key recovery. Speciﬁcally, the num-

ber of CPA runs is reduced to 26 and 19 for 2-bit and

3-bit selection functions, respectively, compared to 48

for 1-bit selection function. Additionally, this also

facilitates the application of second-order success in

CPA, i.e., choosing the top two candidates with the

highest correlations.

For the sake of reproducibility, we publish the

source code of the experiments as well as the traces

at: https://github.com/nvietsang/multibitcpa-ascon.

Outline. This paper is organized as follows. Sec-

tion 2 provides the background knowledge. Section

3 presents the extension from 1-bit to multi-bit selec-

tion function. Section 4 provides an efﬁcient key re-

covery algorithm for CPA using a multi-bit selection.

Section 5 discusses countermeasures and future work,

and concludes our work.

2 PRELIMINARIES

In this section, we begin by brieﬂy outlining the prin-

ciple of the Correlation Power Analysis (CPA) attack.

We then provide the overview of the Ascon cipher.

Next, we recall the 1-bit selection function proposed

by Samwel and Daemen, which is the foundation for

our extension to a multi-bit selection function. Lastly,

we describe the experimental setup and the device

used in our experiments.

2.1 CPA Attack

In a CPA attack, the attacker analyzes the dependence

between the power consumption at speciﬁc points in

time and the data being processed. The attack in-

volves the following ﬁve steps:

• Choose an Intermediate Variable as the Attack

Point. This variable should be a function f (d, k),

referred to as the selection function, which de-

pends on part of the key k and the known non-

constant data d (e.g., plaintext).

• Measure the Power Consumption. Let the de-

vice execute the algorithm ℓ times with different

inputs. For each execution, the attacker records

the data value d involved in the selection function

and a power trace of s samples. This process re-

sults in a vector of data values d = (d

,...,d

ℓ

and a power trace matrix T of size ℓ × s.

• Calculate Hypothetical Intermediate Values.

Let k = (k

,...,k

) represent the p possible key

candidates. Using the selection function f (d,k),

the attacker calculates the hypothetical intermedi-

ate values for each combination of d and k. This

produces a matrix V of size ℓ × p.

• Derive Hypothetical Power Consumption Val-

ues. The attacker uses a leakage model to map

each value in V to a hypothetical power consump-

tion value. In this work, we choose the Hamming

weight model. This step produces a hypothetical

power consumption matrix H of size ℓ × p.

• Compare Hypothetical and Measured Power

Values. The attacker uses the Pearson’s correla-

tion coefﬁcient to compare the hypothetical power

Correlation Power Analysis on Ascon with Multi-Bit Selection Function

consumption values with the measured power

traces. Speciﬁcally, he calculates the correlation

between each column h

of H and each column t

of T. The correlation is expressed as:

i, j

∑

ℓ

u=1



u,i

− h



u, j

−t

)

∑

ℓ

u=1



u,i

− h



∑

ℓ

u=1

u, j

−t

)

Here, h

u,i

and t

u, j

(and their respective means h

and t

) denote the u-th elements of the columns h

and t

. The resulting matrix R, of size p × s, con-

tains the correlation coefﬁcient r

i, j

for each key

candidate and trace sample.

The key can be recovered based on the fact that

the higher value of r

i, j

indicates the better match be-

tween the columns h

and t

. Let ck denote the index

of the correct key k

in the vector k, and ct denote

the index of the power consumption values t

, which

depend on the intermediate values v

. The columns

and t

should have a strong correlation. Conse-

quently, the highest value r

ck,ct

in the matrix R re-

veals the indexes of the correct key ck and the corre-

sponding location ct.

2.2 Ascon

Ascon (Dobraunig et al., 2021) is a suite of Au-

thenticated Encryption with Associated Data (AEAD)

and hashing algorithms based on the duplex sponge

construction (Bertoni et al., 2012b). This paper fo-

cuses on the recommended authenticated cipher vari-

ant, Ascon-128 (referred to simply as Ascon here-

after). Figure 1 illustrates the encryption process.

Its inputs include a key K of 128 bits, a nonce N of

128 bits, an initialization vector IV, associated data

,...,A

, each of 64 bits, and plaintexts P

,...,P

each of 64 bits. It produces as output a tag T of 128

bits and ciphertexts C

,...,C

, each of 64 bits. The

tag T is used during the decryption process to verify

the authenticity of the ciphertexts.

The permutations, denoted by p

and p

, form the

core of the Ascon construction. These permutations

consist of a = 12 rounds and b = 6 rounds, respec-

tively. Each round is composed of three steps op-

erating on a 320-bit state: (1) addition of constants,

(2) substitution layer (S-box), and (3) linear diffu-

sion layer. The three steps are depicted in Figure 2.

The 320-bit state is divided into ﬁve 64-bit variables,

which can be stored in one or more smaller-sized

words (or registers in hardware). This design facili-

tates the transition from the mathematical description

to practical and efﬁcient implementations.

Implementations for 8-bit, 32-bit, 64-bit architectures

can be found at https://github.com/ascon/ascon-c

Let x

,...,x

represent the ﬁve 64-bit variables of

the round input. In the ﬁrst step, a round constant

is added to the rightmost eight bits of x

. Since the

constant addition step is not relevant to our attack, we

simplify the notation by continuing to denote the out-

put of the ﬁrst step as x

,...,x

. The second step in-

volves a non-linear transformation applied to on ﬁve

bits, with one bit taken from each variable of the ﬁrst

step’s output x

,...,x

. Let y

,...,y

represent the

output state of the S-box, and let 1 (in bold) denote

a variable ﬁlled with 64 bit 1s. The algebraic nor-

mal form (ANF) of the S-box, with all operations per-

formed on the full 64-bit variables (in bitsliced form)

can be expressed as:

= x

⊕ x

= x

⊕ x

= x

⊕ x

⊕ 1,

= x

⊕ x

= x

⊕ x

(1)

At the beginning of the initialization phase (Fig-

ure 1), the 64-bit initialization vector IV is stored in

. The two 64-bit halves of the key, (k

) = K,

are stored in x

and x

. The two 64-bit halves of the

nonce, (n

) = N, are stored in x

and x

. The S-

box computation during the ﬁrst round of the initial-

ization phase, where our attack focuses on, can thus

be written as follows (with the constant addition step

omitted for simplicity):

= n

⊕ n

⊕ k

IV ⊕ k

⊕ IV,

= n

⊕ n

⊕ k

⊕ IV,

= n

⊕ n

⊕ k

⊕ 1,

= n

IV ⊕ n

⊕ n

IV ⊕ n

⊕ k

⊕ IV,

= n

⊕ n

⊕ k

IV ⊕ k

(2)

The third step, linear diffusion layer, applies a ro-

tation to each variable at the S-box output twice. The

rotated variables are then XOR-ed with the original

one. Let z

,...,z

denote the output of the linear dif-

fusion layer. The linear functions applied to each vari-

able are deﬁned as:

= y

⊕ (y

≫ 19) ⊕ (y

≫ 28),

= y

⊕ (y

≫ 61) ⊕ (y

≫ 39),

= y

⊕ (y

≫ 1) ⊕ (y

≫ 6),

= y

⊕ (y

≫ 10) ⊕ (y

≫ 17),

= y

⊕ (y

≫ 7) ⊕ (y

≫ 41).

(3)

2.3 Selection Function

This work relies on the selection function in the at-

tack of (Samwel and Daemen, 2017). The output of

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

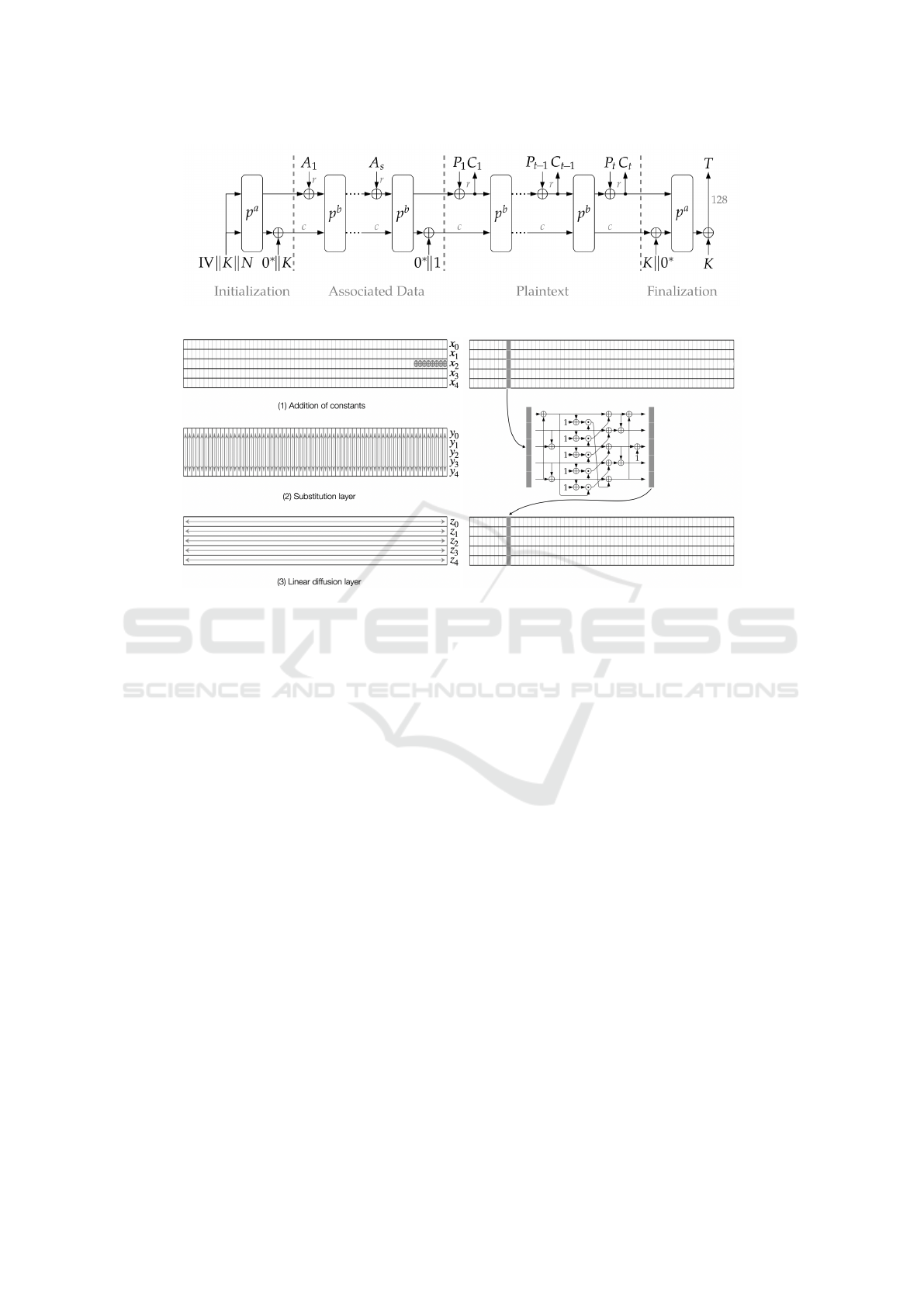
Figure 1: Encryption in Ascon (Dobraunig et al., 2021).

(a) Three steps of a round. (b) An S-box computation.

Figure 2: Each step in a round (Dobraunig et al., 2021).

the linear diffusion layer is chosen as the attack point.

The selection function is derived by analyzing how in-

formation leaks through the S-box computation. As in

(Samwel and Daemen, 2017), we only focus on y

and y

in Equation 2 as their computations contain

non-linear terms between the key and the nonce.

We consider y

as an example. Let the superscript

j denote the index of the j-th bit of a 64-bit variable,

where 0 ≤ j ≤ 63. The j-th bit of y

is computed as:

= n

⊕ 1) ⊕ n

⊕ k

Following Bertoni et al. (Bertoni et al., 2012a), the

term k

⊕k

can be removed because, for the ﬁxed

correct key in the device, this term is independent of

the nonce and contributes a constant amount to the

activity that drives the targeted power consumption of

the register containing y

. This removal results in ˜y

where:

˜y

= n

⊕ 1) ⊕ n

. (4)

We next account the linear diffusion operation.

Recall from Equation 1 that the 64-bit output variable

of this layer is computed as:

= y

⊕ (y

≫ 7) ⊕ (y

≫ 41).

The computation of the j-th bit of z

(0 ≤ j ≤ 63) thus

is:

= y

⊕ y

j+57

⊕ y

j+23

. (5)

The additions j + 57 and j + 23 are implicitly taken

modulo 64. Applying Equation 4 to Equation 5 results

in the selection function ˜z

, which is used to recover

(three bits at a time):

˜z



⊕ 1) ⊕ n



⊕



j+57

⊕ 1) ⊕ n

j+57



⊕



j+23

⊕ 1) ⊕ n

j+23



(6)

Similarly, we can derive the selection functions ˜z

for recovering k

, and ˜z

for recovering k

. The de-

tailed derivation steps are provided in Appendix A.

Here, we present the ﬁnal result of ˜z

˜z



⊕ 1) ⊕ n



⊕



j+3

⊕ 1) ⊕ n

j+3



⊕



j+25

⊕ 1) ⊕ n

j+25



(7)

where k

= k

⊕ k

. Note that k

is not directly re-

covered, instead, k

is recovered when ˜z

is used as

the selection. Then, k

is derived as k

= k

⊕ k

with k

recovered from the CPA using ˜z

as the selec-

tion function. In this following sections, we will use

Correlation Power Analysis on Ascon with Multi-Bit Selection Function

Equation 6 and Equation 7 as the selection functions

to recover the two key halves k

and k

2.4 Experiment Setup

We use a ChipWhisperer Lite board, integrated with

an STM32F303 32-bit ARM target microcontroller,

to record the power consumption traces. The device

operates with a default clock frequency of 7.37 MHz.

The ChipWhisperer board is connected to a MacBook

Air M1 with 16 GB of RAM via a USB cable. To cre-

ate a scenario as realistic as possible, we record the

power traces during the executions of the 32-bit opti-

mized ARMv6 implementation by the Ascon team,

which is well-suited to our microcontroller.

3 MULTI-BIT SELECTION

FUNCTION

Using Equation 6 and Equation 7 as the selection

functions, as in some successful CPA attacks (Samwel

and Daemen, 2017; Weissbart and Picek, 2023; Rous-

sel et al., 2023), means to exploit the leakages of sin-

gle bits z

and z

(in 64-bit variables z

and z

). These

leakages are modeled as the Hamming weight of ˜z

and ˜z

, denoted by HW(˜z

) = ˜z

and HW(˜z

) = ˜z

since the Hamming weight of a bit is the bit value it-

self. In software implementations, the 64-bit variables

and z

are usually implemented by eight 8-bit or

two 32-bit words, depending on device architecture.

The activity of these words (load/store) is known to

leak information about their contained data through

power consumption. The ideal attack scenario is to

consider the entire word length to make hypotheses.

In this scenario, the hypothetical power consumption

tends to highly correlate to the power traces. For ex-

ample, using all 8 bits of an S-box output as the in-

termediate variable in a CPA attack on an 8-bit AES

implementation is more efﬁcient than using only the

most signiﬁcant bit (Brier et al., 2004). However, this

makes the attack computationally infeasible for large

word size such as 32 bits, since the CPA needs to be

performed a large number of times.

The CPA attacks on Ascon in the literature

(Samwel and Daemen, 2017; Weissbart and Picek,

2023; Roussel et al., 2023) only use one bits z

and

of z

and z

for the hypothetical power consump-

tion. These attacks were still successful because, as

pointed out by Brier et al. (Brier et al., 2004), a par-

https://github.com/ascon/ascon-c/tree/v1.2/

crypto aead/ascon128v12/armv6

tial correlation still exists if only a part of the word is

used. Speciﬁcally, the partial correlation coefﬁcient

calculated from d independent bits among m bits

(d ≤ m) and the correlation coefﬁcient ρ

calculated

from all m bits has a the following relation:

= ρ

The attacks in (Samwel and Daemen, 2017; Weissbart

and Picek, 2023; Roussel et al., 2023) correspond to

d = 1. The above equation also indicates that increas-

ing the value of d results in the partial correlation ρ

becoming closer to ρ

. In this section, we extend z

and z

in Equation 6 and Equation 7 to multi-bit se-

lection functions (d > 1) for CPA attacks on software

implementations (in common architectures where m

can be 8, 16, 32 or 64 bits). In Subsection 3.1, we

provide the details of the extension and its advantages.

Then, we present the experiment for this extension in

Subsection 3.2 and discuss the results in Subsection

3.3.

3.1 Extension Method

We consider the selection function ˜z

in Equation 6

here. The same approach is applied for ˜z

. We present

the practical results for both of them. Let z

j.. j+d

de-

note d bits of the 64-bit variable z

, from index j to

j + d − 1 (d ≥ 1). We extend the 1-bit function ˜z

(Equation 6) to the d-bit function ˜z

j.. j+d

as follows:

˜z

j.. j+d



j.. j+d

⊕ 1) ⊕ n

j.. j+d



⊕



j+57.. j+57+d

⊕ 1) ⊕ n

j+57.. j+57+d



⊕



j+23.. j+23+d

⊕ 1) ⊕ n

j+23.. j+23+d



(8)

For better understanding, Figure 3 depicts the

bit locations involving in the computation of ˜z

j.. j+d

Using this d-bit selection function, we can re-

cover 3d bits of the key, k

j.. j+d

, k

j+57.. j+57+d

, and

j+23.. j+23+d

, after each CPA run. This means that

the higher value of d, the more recovered key bits.

These 3d key bits are indexed by the following set

determined by the value of j:

{ j, ..., j + d − 1} ∪ { j + 57, . . . , j + 56 + d}

∪ { j + 23, . . . , j + 22 + d},

where 0 ≤ j ≤ 63 (with additions implicitly mod-

ulo 64). To recover the full 64-bit k

, we need to

run the CPA multiple times with different values of

j such that the recovered key bit indexes cover the

range from 0 to 63. This implies that the effort re-

quired for the attack can be minimized by determining

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

Table 1: Number of CPA runs for the full key recovery.

Number of bits

Selection function d 1 2 3

Key recovery 3d 3 6 9

Involved nonce bits 6d 6 12 18

Number of CPA runs 48 26 19

the minimum number of CPA runs. In other words,

we try to minimize the overlaps among the recovered

key bit indexes. For example, when d = 2, perform-

ing CPA with j = 0 and j = 34 leads to the recov-

ered of the key bits at indexes (0,1,57,58,23,24) and

(34,35,27,28,57,58). We see that the bits indexed by

57 and 58 are recovered twice, which is redundant.

To address this, we formalize a set cover problem

and employ a SAT solver to solve it.

A similar ap-

proach is applied to ﬁnd the minimum number of CPA

runs for the full 64-bit k

recovery. The total number

of CPA runs for recovering the full 128-bit key is the

sum of those of k

and k

. Appendix B includes the

sets of indexes j from our ﬁnding.

Table 1 compares the results for different values

of d. While our extension is generic and works with

any d, this paper focuses on speciﬁc cases where

d ∈ {1,2,3}. This is due to the need of traversing all

possible nonce values to evaluate the distribution

of hypothetical power consumption for our analyses

in the next sections. This becomes computationally

infeasible on classical computers when d ≥ 4. We

will detail this issue in the subsequent section.

From Table 1, we can infer the following ad-

vantages of CPA using multi-bit selection functions

(d > 1):

• The number of CPA runs needed is signiﬁcantly

reduced. Speciﬁcally, for d = 1, 48 CPA runs are

required, while this number decreases to 26 for

d = 2 and 19 for d = 3.

• As a result of the reduction in the number of CPA

runs, using multi-bit selection functions enables

second-order success. This involves selecting the

top two candidates with the highest correlation af-

ter each CPA run, rather than just the single top

candidate. A brute-force search is then performed

across these candidates to determine the correct

key. The brute-force space is 2

for d = 2 and 2

for d = 3, both of which are computationally fea-

sible. In contrast, the brute-force space for d = 1,

, likely remains inefﬁcient on a classical com-

puter.

The source code is included in https://github.com/

nvietsang/multibitcpa-ascon

3.2 Experimental Results

We now conduct an experiment to validate our exten-

sion. We perform the CPA using selection functions

corresponding to d = 1, d = 2 and d = 3 and mea-

sure the success rate for each case. Measuring suc-

cess rate for the full key recovery is time-consuming,

as it requires repeating the analysis numerous times

(typically a hundred or more) for various numbers of

traces. Instead, we estimate this success rate by fo-

cusing on the recovery of 3d bits of k

and 3d bits

of k

. Speciﬁcally, we repeat the 3d-bit key recov-

eries 100 times for k

and k

with different indexes

j. These two success rates for these partial recoveries

are each raised to the power of the number of CPA

runs needed, and then multiplied together to estimate

the success rate for the full key recovery.

We present in Figure 4 the success rates corre-

sponding to selection functions with different values

of d. In this experiment, the CPA uses the ﬁrst-order

success, i.e., the key candidate with the highest cor-

relation is chosen as the best candidate. For d = 1,

the success rate begins to converge toward 100% at

around 5600 traces. However, for d = 2 and d = 3,

we observe an unexpected outcome: the success rates

remain at 0% regardless the number of traces. This

anomaly prompts a deeper investigation into the un-

derlying cause of this behavior.

3.3 Factors Inﬂuencing Performance

We now investigate the cause behind the poor perfor-

mance of multi-bit selection functions, as observed in

Figure 4. While we detail here the analysis for d = 2,

the same analysis approach is applicable for d > 2.

We ﬁrst consider a CPA run and look at the corre-

lations between the hypothetical power consumption

for each key candidate and the recorded power traces.

The multi-bit selection function with d = 2 is sup-

posed to recover 3d = 6 key bits after each CPA run.

There are thus 2

= 64 possible key candidates.

Figure 5 shows the convergence of the correla-

tions for all key candidates as the number of traces

increases. It is evident that a small group of key can-

didates, containing the correct one, is distinguishable

from the rest. This behavior is unlike the traditional

case, where only the correct candidate exhibits a dis-

tinctly high correlation. Even when experimented

with a larger number of traces, this outcome remains

unchanged.

Table 2 shows the ranks of the key candidates cor-

responding to Figure 5, sorted by their correlations.

We can align that the distinct group includes 15 key

candidates. Notably, the correlation of the correct

Correlation Power Analysis on Ascon with Multi-Bit Selection Function

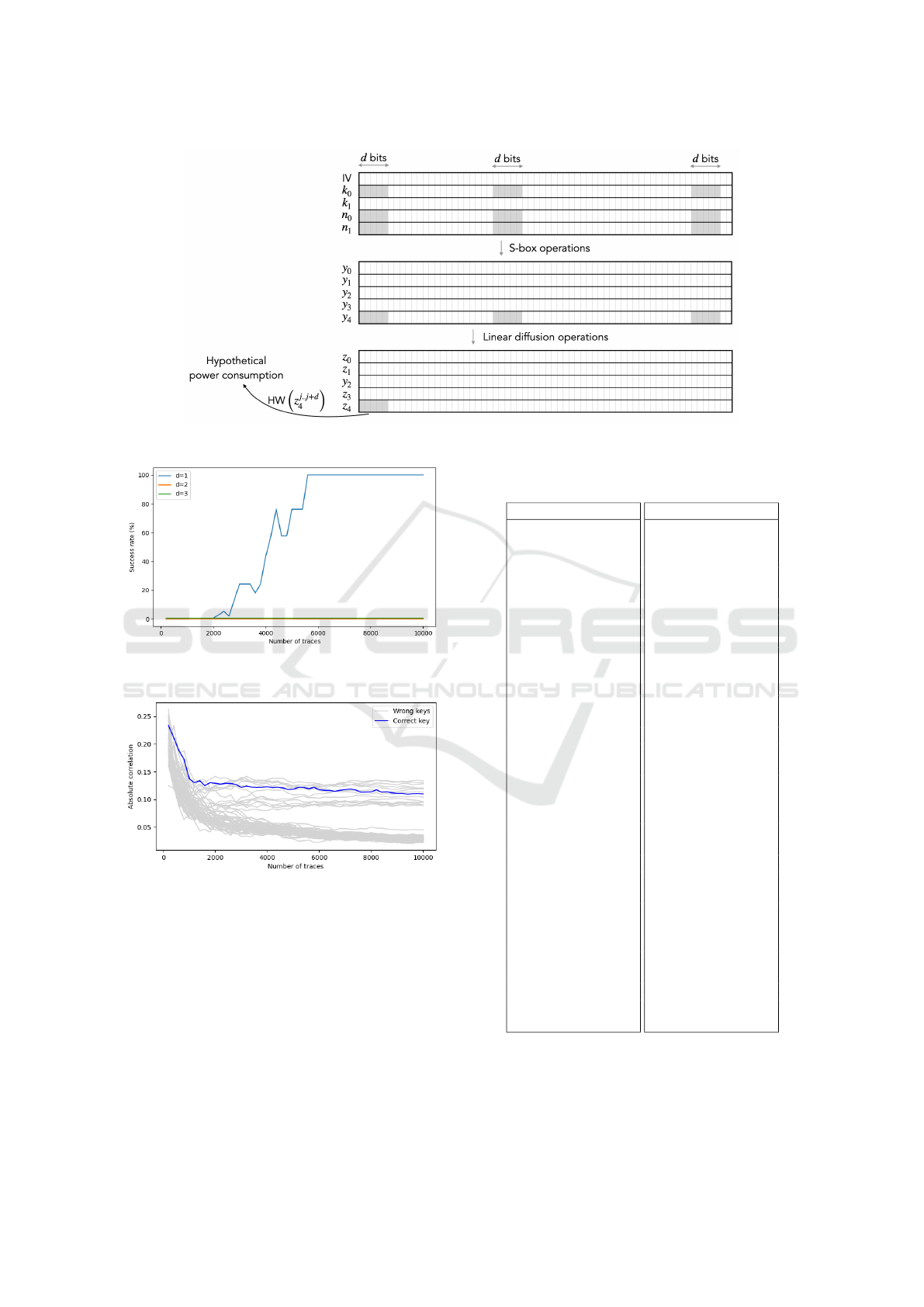
Figure 3: Illustration of d-bit selection function (Equation 8) for j = 0.

Figure 4: Success rates of the full key recovery for different

values of d.

Figure 5: Correlations for all key candidates over increasing

number of traces.

candidate is not the highest and is close to those of

the other candidates in the group. Consequently, the

CPA picks the incorrect candidate at the top-ranked

choice, leading to the success rate of 0% as shown in

Figure 4. However, this issue does not occur with the

CPA using the 1-bit selection function (d = 1), as its

success rate still converges to 100%. This suggests

that the root cause may lie in the differences between

the selection functions.

Table 2 further indicates that, in addition to the

correct key, several incorrect candidates are also

Table 2: Key candidates ranked by correlations at 10000

traces. The correct candidate is highlighted in blue.

Rank Key Corr.

1 10 0.133

2 32 0.130

3 2 0.128

4 42 0.121

5 40 0.119

6 8 0.119

7 34 0.113

8 0 0.110

9 1 0.104

10 5 0.096

11 4 0.095

12 17 0.095

13 16 0.090

14 21 0.089

15 20 0.089

16 31 0.045

17 60 0.036

18 61 0.035

19 15 0.035

20 23 0.034

21 11 0.033

22 19 0.033

23 22 0.033

24 39 0.033

25 7 0.033

26 43 0.032

27 18 0.032

28 56 0.031

29 14 0.030

30 30 0.030

31 36 0.030

32 52 0.030

Rank Key Corr.

33 6 0.030

34 26 0.030

35 27 0.030

36 35 0.029

37 53 0.029

38 55 0.029

39 44 0.028

40 3 0.028

41 57 0.028

42 50 0.028

43 45 0.028

44 37 0.027

45 41 0.027

46 12 0.026

47 46 0.026

48 49 0.026

49 33 0.026

50 54 0.026

51 47 0.026

52 58 0.026

53 48 0.026

54 62 0.026

55 13 0.025

56 28 0.025

57 24 0.025

58 25 0.023

59 59 0.023

60 51 0.023

61 38 0.023

62 63 0.022

63 9 0.022

64 29 0.022

highly correlated to the power traces. To investigate

this, we analyze the distributions generated by each

key candidate across all possible values of the asso-

ciated nonce bits. For every possible key pair, we

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

Figure 6: Correlations between distributions of all possible

key pairs when d = 1. Blue and white cells correspond to

correlation coefﬁcient of 1 and 0, respectively.

calculate the correlation of their distributions to de-

termine whether they are partially correlated. Figure

6 presents the results of this calculation for d = 1,

and Figure 7 presents the results for d = 2. It is clear

that, for d = 2, the distributions of some key pairs are

partially correlated (represented by light blue cells in

Figure 7). In contrast, this behavior does not occur for

d = 1. Furthermore, we observe that the small group

of key candidates with high correlations in the CPA

corresponds to the group of key candidates whose dis-

tributions are partially correlated to that of the cor-

rect key. For example, the top 15 candidates in Ta-

ble 2 align with the (light) blue cells in the ﬁrst row

of Figure 7, indicating the correlations between cor-

rect key’s distribution (0 in this case) and those of the

other key candidates. This conﬁrms the inﬂuence of

the partial correlations between the key candidates.

These partial correlations are absent for d = 1, im-

plying that the root cause lies in the extension of the

selection function to d > 1. Indeed, the extension can

be seen as concatenating multiple identical 1-bit se-

lection functions, which introduces the partial corre-

lations between the distributions of key candidates ob-

served when d > 1. In fact, this concatenation is un-

avoidable if we want to use multi-bit selection func-

tions due to the bitsliced-oriented design of Ascon.

Speciﬁcally, the S-box operates in the vertical dimen-

sion, taking 1 bit per 64-bit variable as input and pro-

ducing 1 bit per 64-bit variable as output (see Figure

2b). Meanwhile, the words (whose activities consume

power) store bits in the horizontal dimension, repre-

senting the bits within a 64-bit variable (see Figure

2a). In other words, the bits in a variable have the in-

volvement of multiple independent S-box operations.

Given the poor performance of the multi-bit selec-

tion functions compared to the 1-bit selection func-

tion, as shown in Figure 4, the question arises: is it

still possible to use them for key recovery? We will

give a positive answer for this question in the next

section.

4 EFFICIENT KEY RECOVERY

ALGORITHM

As established in the previous section, CPA with

multi-bit selection functions fails in key recovery due

to partial correlations among the distributions pro-

duced by many key candidates. In this section, we

show how these partial correlations can be utilized to

develop an efﬁcient key recovery algorithm. The pro-

posed algorithm is described in detail in Subsection

4.1 and experimentally validated in Subsection 4.2.

4.1 Proposed Algorithm

We use the case d = 2 for explanation of the algo-

rithm’s idea hereafter, however, the proposed algo-

rithm is generic and works with any d > 1. We present

the results for both d = 2 and d = 3 below. From

Figure 7, we observe that the distribution of each key

candidate is (partially) correlated to itself and those of

14 other candidates (15 non-white cells in each row).

These 15 candidates form a group which is unique for

each key candidate. For example, the groups corre-

sponding to the candidates 0 and 1, denoted by G[0]

and G[1], are:

G[0] = [0, 1,2,4,5,8,10,16,17,20,21,32,34,40,42],

G[1] = [0, 1,3, 4, 5, 9, 11, 16, 17, 20, 21, 33, 35, 41,43].

We note that the total 2

groups, G[0], . . . , G[2

−

1], can be precomputed from the correlation matrix of

distributions (as in Figure 7).

Let R be a ranking array containing all 2

key

candidates, sorted by descending correlations after the

classical CPA steps in Section 2. R[0] holds the candi-

date with the highest correlation (rank 1). An example

of R is the column of key candidates in Table 2. Let t

be the number of elements in each group G[k], where

0 ≤ k ≤ 2

− 1. In our experiment, t = 15 for d = 2

and t = 169 for d = 3, and these values are the same

for all groups.

The core idea of the algorithm is to determine the

group G[k] that the top t candidates R[0], . . . , R[t − 1]

most likely belong to. The candidate k is then re-

turned as the best choice for the correct key. We refer

to t as a threshold in the algorithm. To measure the de-

gree of the matching between the top t candidates and

a group G[k], a score S[k] is used, for 0 ≤ k ≤ 2

−1.

Each score S[k] ranges from 0 to t, where t denotes a

perfect match. Algorithm 1 presents the details of the

key recovery steps. In this algorithm, we use a param-

eter o for the success order. It returns o key candidates

with the top o highest scores in S.

Correlation Power Analysis on Ascon with Multi-Bit Selection Function

Figure 7: Correlations between distributions of all possible key pairs when d = 2. Blue, light blue and white cells correspond

to correlation coefﬁcient of 1, 0.5 and 0, respectively.

Data: set of traces T , number of bits d,

groups G, threshold t, success order o

Result: top o key candidates

R ← classical CPA on T ;

S ← [0, 0, . . . ,0];

for i from 0 to t − 1 do

for k from 0 to 2

− 1 do

if R[i] ∈ G[k] then

S[k] ← S[k] + 1;

end

L ← indexes of elements in S sorted by

descending scores;

L[0],. . . , L[o − 1];

Algorithm 1: Key recovery for CPA using multi-bit selec-

tion functions (d > 1).

Let us take an example where d = 2. Suppose

R contains 64 key candidates ranked as in Table 2.

By applying the scoring strategy described in Algo-

rithm 1, we obtain the scores shown in Table 3. Here,

S[0] = 15 is the highest score, implying that k = 0 is

the most likely correct key candidate. This is because

the elements R[0], . . . , R[14] perfectly match the group

G[0]. This outcome aligns with our expectation, as

k = 0 is indeed the correct key.

Although our method is generic for any d > 1, a

bottleneck lies in the reliance on precomputed groups

G[k], where 0 ≤ k ≤ 2

− 1. This computation re-

quires determining the distribution of the selection

function output for all key candidates. Speciﬁcally, it

necessitates evaluating the selection function for each

of 2

associated nonce values and 2

key candi-

dates, resulting a time complexity of 2

. A high d

value makes this computation challenging for a clas-

sical computer. For instance, the time complexity

reaches 2

when d = 4, which may exceed the ca-

pabilities of a classical computer. Therefore, we limit

our experiments in the next section to d = 2 and d = 3,

which are computationally feasible on our personal

laptop.

4.2 Experimental Results

We now conduct an experiment to validate the pro-

posed key recovery algorithm. The experimental

setup is identical to that described in the previous sec-

tion. In particular, we reuse the same set of traces and

apply the proposed algorithm for multi-bit selection

functions (d = 2 and d = 3). For comparison, we also

perform an analysis using the classical CPA with the

1-bit selection function (d = 1).

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

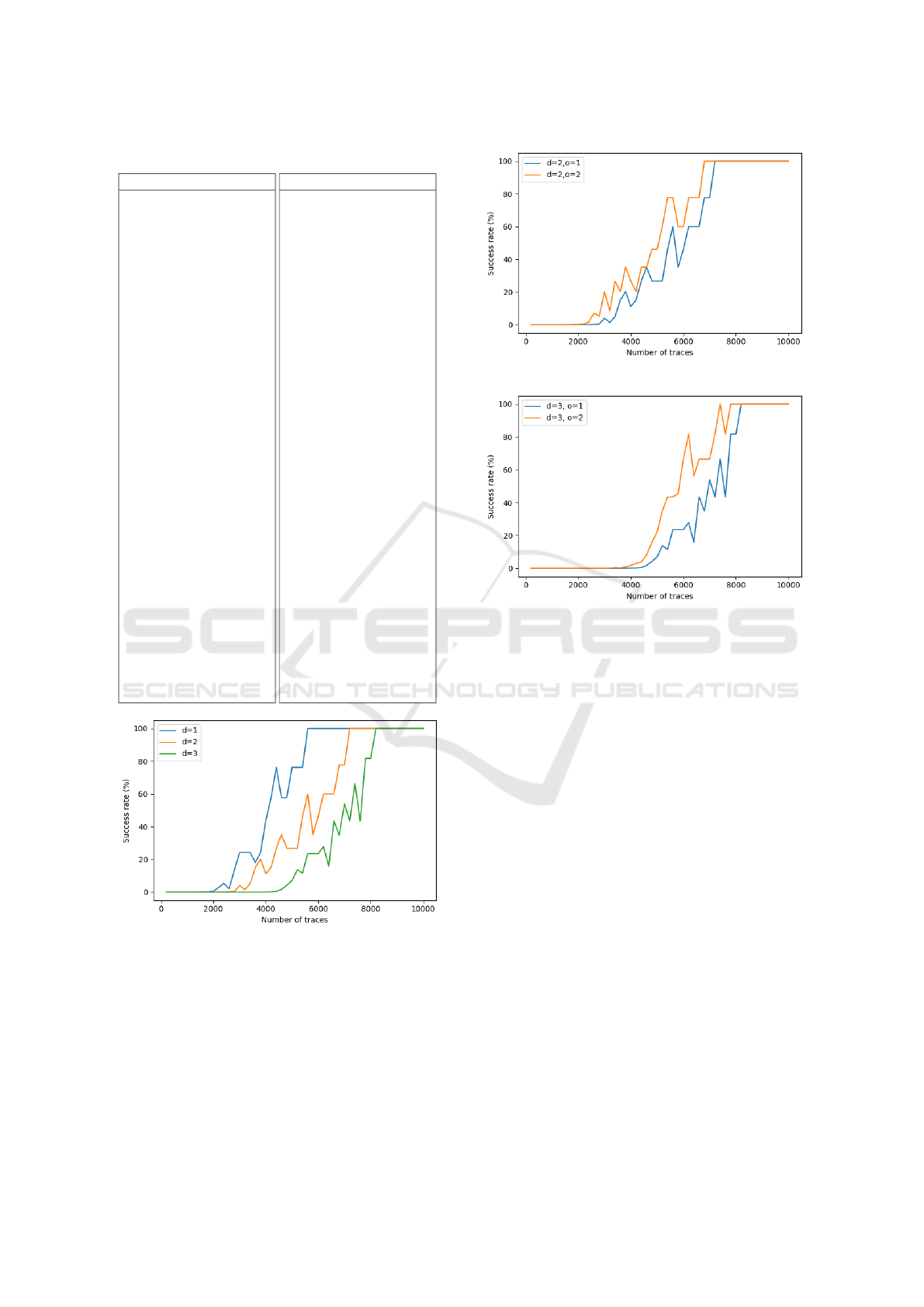
Table 3: Scores of 64 key candidates for d = 2.

Candidate k Score S[k]

0 15

1 8

2 8

3 2

4 8

5 8

6 2

7 2

8 8

9 2

10 8

11 2

12 2

13 2

14 2

15 2

16 8

17 8

18 2

19 2

20 8

21 8

22 2

23 2

24 2

25 2

26 2

27 2

28 2

29 2

30 2

31 2

Candidate k Score S[k]

32 8

33 2

34 8

35 2

36 2

37 2

38 2

39 2

40 2

41 8

42 2

43 8

44 2

45 2

46 2

47 2

48 2

49 2

50 2

51 2

52 2

53 2

54 2

55 2

56 2

57 2

58 2

59 2

60 2

61 2

62 2

63 2

Figure 8: Full key recovery success rates after applying ef-

ﬁcient algorithm for d = 2 and d = 3. The success order is

o = 1 for all cases.

Figure 8 shows the success rates of the full key

recovery using the d-bit selection functions with dif-

ferent values of d. For multi-bit selection functions

(d = 2 and d = 3), their success rates gradually con-

verge to 100% as the number of traces increases, in

contrast to the 0% success rates observed in Figure

4. Speciﬁcally, the successes rates reach 100% for

(a) d = 2.

(b) d = 3.

Figure 9: Full key recovery success rates with ﬁrst- and

second-order successes for d = 2 and d = 3.

d = 2 with 7200 traces and for d = 3 with 8200 traces.

This demonstrates the effectiveness of our proposed

key recovery algorithm.

Nevertheless, compared to the 1-bit selection

function, the multi-bit selection functions require

more traces to achieve 100% success rates. Addition-

ally, it can be observed that the convergence speed

decreases with increasing d. This is likely because

more traces are needed to make the correlations as-

sociated to a group of key candidates stand out from

the rest. A higher d corresponds to a bigger group.

Meanwhile, the 1-bit selection function only requires

the correlation of a single key candidates to stand out.

As discussed in Subsection 3.1, there are two main

advantages of using multi-bit selection functions, in-

cluding the signiﬁcant reduction in the number of

CPA runs and the application of second-order success.

We now consider the latter. It can be seen that Algo-

rithm 1 is generic for o-order success. We conduct

an experiment for the case where o = 2 (i.e., second-

order) with d = 2 and d = 3. Figure 9 compares the

success rates for o = 2 and o = 1. As expected, the

success rates for o = 2 are higher than those for o = 1

in both cases.

Correlation Power Analysis on Ascon with Multi-Bit Selection Function

5 CONCLUSION & DISCUSSION

In this paper, we extended the 1-bit selection function

to a multi-bit selection function. Initially, this exten-

sion caused the CPA to fail in identifying the correct

key candidate due to Ascon’s bitsliced-oriented de-

sign. To address this, we conducted a comprehensive

analysis from both theoretical and experimental per-

spectives to uncover the reasons behind this failure.

Leveraging the insights from this analysis, we pro-

posed an efﬁcient key recovery algorithm tailored for

the multi-bit selection function. We further provided

experimental results demonstrating the effectiveness

of this algorithm. Additionally, we showed that the

multi-bit selection function offers advantages, includ-

ing a reduction in the number of CPA runs required

for full key recovery and the ability to apply second-

order success in CPA.

Countermeasures. CPA attacks exploit the depen-

dency between a device’s power consumption and in-

termediate values of the executed cryptographic al-

gorithms. A well-known mitigation strategy is to

eliminate or at least reduce this dependency. One

approach involves randomizing power consumption

by performing intermediate computations at differ-

ent time moments. This can be achieved by ran-

domly inserting dummy operations during execution

to disrupt the power trace alignment, or by shufﬂing

the operations (Kocher et al., 1999). Another widely

studied approach is masking intermediate values with

randomness (Chari et al., 1999; Goubin and Patarin,

1999), ensuring that power consumption is indepen-

dent of these intermediate values. This technique is

typically implemented at the algorithm level.

Future Work. A potential direction for future work

is the development of a more efﬁcient key recovery

algorithm for the multi-bit selection function. As dis-

cussed earlier, while our proposed algorithm is effec-

tive for key recovery, it becomes computationally in-

feasible for d > 3. Additionally, the resulting success

rates remain lower than those achieved with the 1-bit

selection function, while we expect that incorporat-

ing more bits into the hypotheses for power consump-

tion could improve success rates. A promising direc-

tion to address these challenges is exploring machine

learning-based and proﬁling-based techniques.

ACKNOWLEDGEMENTS

This work was supported by the French Agence Na-

tionale de la Recherche through the grant ANR-22-

CE39-0008 (project PROPHY).

REFERENCES

AES (2001). Advanced Encryption Standard (AES). Na-

tional Institute of Standards and Technology, NIST

FIPS PUB 197, U.S. Department of Commerce.

Bertoni, G., Daemen, J., Debande, N., Le, T.-H., Peeters,

M., and Van Assche, G. (2012a). Power analysis of

hardware implementations protected with secret shar-

ing. In 2012 45th Annual IEEE/ACM International

Symposium on Microarchitecture Workshops, pages

9–16.

Bertoni, G., Daemen, J., Peeters, M., and Van Assche, G.

(2012b). Duplexing the sponge: Single-pass authen-

ticated encryption and other applications. In Miri, A.

and Vaudenay, S., editors, SAC 2011, volume 7118 of

LNCS, pages 320–337. Springer, Berlin, Heidelberg.

Brier, E., Clavier, C., and Olivier, F. (2004). Correlation

power analysis with a leakage model. In Joye, M. and

Quisquater, J.-J., editors, CHES 2004, volume 3156 of

LNCS, pages 16–29. Springer, Berlin, Heidelberg.

Chari, S., Jutla, C. S., Rao, J. R., and Rohatgi, P. (1999). To-

wards sound approaches to counteract power-analysis

attacks. In Wiener, M. J., editor, CRYPTO’99, vol-

ume 1666 of LNCS, pages 398–412. Springer, Berlin,

Heidelberg.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schl

affer,

M. (2021). Ascon v1.2: Lightweight authenticated

encryption and hashing. Journal of Cryptology,

34(3):33.

Goubin, L. and Patarin, J. (1999). DES and differential

power analysis (the “duplication” method). In Koc¸,

C¸ etin Kaya. and Paar, C., editors, CHES’99, volume

1717 of LNCS, pages 158–172. Springer, Berlin, Hei-

delberg.

Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differential

power analysis. In Wiener, M. J., editor, CRYPTO’99,

volume 1666 of LNCS, pages 388–397. Springer,

Berlin, Heidelberg.

Ramezanpour, K., Abdulgadir, A., Diehl, W., Kaps, J.-

P., , and Ampadu, P. (2020). Active and passive

side-channel key recovery attacks on Ascon. NIST

Lightweight Cryptography Workshop.

Roussel, N., Potin, O., Dutertre, J., and Rigaud, J. (2023).

Security evaluation of a hybrid CMOS/MRAM as-

con hardware implementation. In Design, Automa-

tion & Test in Europe Conference & Exhibition, DATE

2023, Antwerp, Belgium, April 17-19, 2023, pages 1–

6. IEEE.

Samwel, N. and Daemen, J. (2017). DPA on hardware im-

plementations of Ascon and Keyak. In Proceedings

of the Computing Frontiers Conference, CF’17, page

415–424, New York, NY, USA. Association for Com-

puting Machinery.

Tunstall, M., Hanley, N., McEvoy, R., Whelan, C., Murphy,

C., and Marnane, W. (2007). Correlation power analy-

sis of large word sizes. http://www.geocities.ws/mike.

tunstall/papers/THMWMM.pdf.

Weissbart, L. and Picek, S. (2023). Lightweight but not

easy: Side-channel analysis of the ascon authenti-

cated cipher on a 32-bit microcontroller. Cryptology

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

ePrint Archive, Paper 2023/1598. https://eprint.iacr.

org/2023/1598.

APPENDIX A: SELECTION

FUNCTIONS

The j-th bit of y

and y

are computed as:

= k

⊕ 1) ⊕ n

⊕ k

⊕ IV

= n

⊕ k

⊕ 1) ⊕ n

⊕ k

⊕ IV

In y

, we remove k

⊕ k

⊕ IV

as they

contribute a constant amount to the power consump-

tion. For the same reason, k

⊕ k

⊕ IV

is re-

moved from y

˜y

= k

⊕ 1) ⊕ n

˜y

= n

⊕ 1) ⊕ n

where k

= k

⊕ k

Recall the linear operations applied on the y

and

= y

⊕ (y

≫ 19) ⊕ (y

≫ 28),

= y

⊕ (y

≫ 61) ⊕ (y

≫ 39).

The j-th bit of z

and z

are thus computed as:

= y

⊕ y

j+36

⊕ y

j+45

= y

⊕ y

j+3

⊕ y

j+25

We then apply the linear operations for ˜y

and ˜y

˜z



⊕ 1) ⊕ n



⊕



j+36

⊕ 1) ⊕ n

j+36



⊕



j+45

⊕ 1) ⊕ n

j+45



(9)

˜z



⊕ 1) ⊕ n



⊕



j+3

⊕ 1) ⊕ n

j+3



⊕



j+25

⊕ 1) ⊕ n

j+25



(10)

APPENDIX B: KEY INDEXES FOR

CPA RUNS

The script of the SAT problem is included in https://

github.com/nvietsang/multibitcpa-ascon. We present

here the minimum number of CPA runs for different

values of d.

For d = 1:

• 24 indexes j for k

recovery: 1, 6, 7, 9, 11, 12, 17,

22, 23, 25, 27, 28, 33, 34, 38, 39, 43, 44, 48, 49,

54, 55, 59, 60.

• 24 indexes j for k

recovery: 3, 5, 6, 7, 13, 15, 17,

22, 24, 26, 32, 33, 34, 39, 41, 43, 45, 50, 51, 52,

53, 58, 60, 62.

For d = 2:

• 12 indexes j for k

recovery: 3, 9, 14, 19, 24, 30,

35, 41, 46, 51, 56, 62.

• 14 indexes j for k

recovery: 2, 10, 11, 20, 22, 28,

30, 37, 39, 43, 46, 48, 55, 57.

For d = 3:

• 10 indexes j for k

recovery: 20, 23, 33, 36, 39,

42, 45, 48, 51, 60.

• 9 indexes j for k

recovery: 1, 7, 13, 20, 29, 32,

39, 48, 58.

Correlation Power Analysis on Ascon with Multi-Bit Selection Function