A Comparative Experimental Evaluation of iPI and iPI-Fuzzy

Controllers for a Thermal Process with a Long Dead Time

Sebastian Vega

1 a

, Johny Iza

1 b

, William Cruz

1 c

, Juan J. Gude

2 d

and Oscar Camacho

1 e

Colegio de Ciencias e Ingenier

ıas ¨El Polit

ecnico”, Universidad San Francisco de Quito USF, Quito, Ecuador

Department of Computing, Electronics and Communication Technologies, Faculty of Engineering,

University of Deusto, 48007, Spain

Keywords:

Temperature Control, Model-Free Control, Intelligent PID, Fuzzy Control, TCLab, Nonlinear Systems.

Abstract:

This paper introduces a control approach integrating intelligent proportional-integral (iPI) control with fuzzy

logic, speciﬁcally designed for temperature management using the Temperature Control Laboratory (TCLab)

platform. The proposed controller leverages a model-free methodology that transcends traditional PID con-

straints by incorporating real-time parameter estimation and adaptive algorithms. The system is adaptable to

handle dynamic temperature variations and external disturbances by combining intelligent control techniques

with fuzzy logic. Experimental validation in the TCLAB reveals signiﬁcant improvements in temperature

tracking precision and system robustness across diverse operational conditions.

1 INTRODUCTION

Thermal processes are fundamental to the success

of chemical engineering and drive innovation across

ﬁelds such as reaction engineering, biomedicine, en-

ergy production, materials science, and green chem-

istry (Plawsky, 2020). Although chemical engineer-

ing was historically centered on the petrochemical

and heavy chemical industries, its scope has expanded

to include biomedicine, environmental sustainabil-

ity, advanced materials, and the mitigation of cli-

mate change (Jain and Goodson, 2011). Achieve-

ments such as the development of antibiotics, vac-

cines, and immunological advancements are heavily

based on precise thermal regulation to ensure reaction

efﬁciency and product stability, signiﬁcantly improv-

ing global health and longevity. Similarly, the fabri-

cation of semiconductor materials (May and Spanos,

2006), a key to the microelectronics revolution, re-

quires meticulous temperature control to achieve the

precision required for modern computing and the dig-

ital era. In these diverse applications, temperature

control is a critical challenge to ensure the stability,

https://orcid.org/0009-0001-3840-8189

https://orcid.org/0009-0002-0051-8216

https://orcid.org/0009-0007-0434-66220.

https://orcid.org/0000-0003-4210-2454

https://orcid.org/0000-0001-8827-5938

safety and performance of chemical processes in labo-

ratory experiments, advanced manufacturing, and in-

dustrial systems (V

asquez et al., 2023; Obando et al.,

2023).

Effective control systems are essential for thermal

processes in chemical engineering, addressing two

primary objectives: regulation and tracking. Regu-

lation involves maintaining process temperatures at

speciﬁc set points to ensure stable and consistent op-

eration, which is critical to meeting industrial re-

quirements such as cost efﬁciency, production targets,

safety standards, and product quality. Precise temper-

ature control is indispensable for chemical reactions

and material synthesis, where deviations can com-

promise efﬁciency or safety. However, tracking en-

tails guiding the process temperature from one oper-

ating state to another, often to accommodate changes

in economic conditions, product requirements, op-

erational constraints, environmental regulations, or

safety protocols. Reliable tracking ensures smooth

transitions while minimizing disruptions and main-

taining compliance with quality and operational ob-

jectives. Together, these functions enable thermal

process control systems to meet dynamic industrial

demands effectively and safely (Smith and Corripio,

2005; Liptak et al., 2018).

Thermal process control strategies vary accord-

ing to the complexity and needs of the system, con-

sidering process dynamics, delays, and goals. Com-

Vega, S., Iza, J., Cruz, W., Gude, J. J. and Camacho, O.

A Comparative Experimental Evaluation of iPI and iPI-Fuzzy Controllers for a Ther mal Process with a Long Dead Time.

DOI: 10.5220/0013459700003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 209-216

ISBN: 978-989-758-759-7; ISSN: 2184-2841

209

mon approaches include PID Control, which balances

fast response, eliminates steady-state error, and antic-

ipates future errors, though it requires tuning for best

performance; Cascade Control, which uses two loops

to enhance accuracy and disturbance rejection, often

in heat exchangers and reactors; Feedforward Con-

trol, which predicts disturbances and adjusts proac-

tively, typically used in systems with measurable dis-

turbances; Model Predictive Control (MPC), which

utilizes process models to predict and optimize future

behavior, ideal for complex systems with constraints;

Smith Predictor, designed for systems with signiﬁ-

cant time delays to improve stability and response;

Adaptive Control, which adjusts parameters based

on real-time changes, maintaining performance un-

der varying conditions; Fuzzy Logic Control, which

handles nonlinearities and uncertainties by mimicking

human decision-making (Smith and Corripio, 2005;

Kocaarslan et al., 2006; Liptak et al., 2018; Schwen-

zer et al., 2021; Mejia et al., 2022).

Previous approaches depend on precise models

and parameters. Analytical models offer insights but

are complicated by nonlinearities, increasing compu-

tational demands (Sardella et al., 2019). Building

comprehensive models is challenging due to the com-

plexity of the system and the accuracy of the param-

eters (Gude et al., 2024), making phenomenological

models difﬁcult to implement in industrial settings

(Gude, 2023). Empirical models such as First-Order

Plus Dead Time (FOPDT) are effective alternatives

for control design, accurately representing the core

dynamics of many industrial processes (Gude et al.,

2024; Obando et al., 2023; Liptak et al., 2018).

Model-free control (MFC) emerges as an aus-

picious approach in this context, offering remark-

able adaptability by eliminating the need for com-

plex mathematical modeling (Fliess and Join, 2013).

Instead, it relies on dynamic, data-driven parameter

estimation, and continuous system adaptation. This

methodology proves especially valuable in systems

characterized by inherent nonlinearities and unpre-

dictable variations, such as temperature control en-

vironments. MFC is characterized by its remarkable

adaptability, making it an ideal choice for complex

or poorly understood systems, as adequately as those

subjected to frequent disturbances and constant varia-

tions (Fliess and Join, 2013; Precup et al., 2017). An

innovative control strategy derived from MFC prin-

ciples is the intelligent PID approach (iPID), as dis-

cussed in (Fliess and Join, 2013; Precup et al., 2017).

This method marks important progress in control the-

ory by overcoming the traditional PID drawbacks

through adaptive parameter alterations and nonlinear

gain methods.

The Arduino-based Temperature Control Lab

(TCLab) was developed to study process dynamics

and control. This lab provides an online experience

with basic programming modules in Matlab, Python,

or Java for students. Participants gain access to sen-

sor data and devices for feedback control. Prelimi-

nary evidence indicates that TCLab enhances learn-

ing; however, further research is required to evaluate

its effect on students’ understanding of system dy-

namics and process control (de Moura Oliveira et al.,

2022). Additional uses of control systems on the

TCLab device are examined in (Mejia et al., 2022;

Patel, 2023).

In this study, iPI controllers were employed for

thermal processes that exhibit long delays, explor-

ing two alternatives: traditional iPI as introduced by

Fliess (Fliess and Join, 2013) and a fuzzy iPI control

applied to TCLab. The concept involves incorporat-

ing fuzzy logic into the iPI to determine whether such

integration could enhance the system’s robustness and

responsiveness in temperature control (Zhang and

Liu, 2006). A comparative analysis of both con-

trollers was conducted for set-point changes and dis-

turbance rejection.

The paper is divided as follows: In Section 2,

some fundamentals are described, Section 3 shows the

methodology of design, Section 4 presents the results

in the TCLab, and ﬁnally the conclusions are drawn

in Section 5.

2 TIME DELAY BASICS

This section outlines the theoretical foundation and

motivation behind the proposed control methodology,

emphasizing its relevance in tackling the challenges

inherent to temperature control with long delays.

2.1 Challenges

Time delays in industrial processes can arise from

various sources, and understanding these delays is

critical for optimizing and controlling systems effec-

tively (Smith and Corripio, 2005; Espin et al., 2022).

Such delays can signiﬁcantly affect the performance

of closed-loop control systems, especially when dead

time is considerable. Increased dead time results in

several issues, including reduced crossover frequen-

cies and critical gains, which make the controller

more sensitive to noise. Additionally, corrective ac-

tions by the controller are delayed, leading to slower

transient responses and an increased risk of system

instability (Mejia et al., 2022; Sardella et al., 2019).

The primary difﬁculty with time delays is that they

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

210

prevent the timely detection of disturbances and de-

lay the corresponding corrective actions, leading to

mismatched responses and potential loss of stability.

From a classical control perspective, time delays in-

troduce negative phase shifts, reducing the critical fre-

quency and phase margin. This, in turn, limits the

permissible control gain and response speed. A com-

mon mitigation strategy is to decrease the gain and

increase the integration constant; however, while this

can reduce the effects of delays, it often compromises

system performance by producing sluggish responses

and poor disturbance rejection. Such performance

degradation is typically unacceptable in industrial set-

tings. These limitations highlight the need for ad-

vanced control strategies speciﬁcally designed to ad-

dress the challenges posed by systems with signiﬁ-

cant time delays. Fuzzy controllers are particularly

suited for systems with dominant time delays due

to their heuristic rule-based adaptability to nonlin-

ear dynamics and parametric variations. Recent stud-

ies (Tanaka et al., 2023; Wang et al., 2022) demon-

strate their effectiveness in industrial thermal pro-

cesses, where real-time estimation and adaptive tun-

ing mitigate delay-induced instability.

3 INTELLIGENT PID

CONTROLLER APPROACHES

This section employs the Fliess recommended

method to develop an iPI fuzzy controller. The layout

of this section is as follows. In section 3.1, we de-

tail the controller design following Fliess’s approach.

Section 3.2 delves into fuzzy methodology and sec-

tion 3.3 focuses on the preliminary tuning via the par-

ticle swarm optimization (PSO) algorithm.

3.1 iPI Controller Proposal by Fliess

One promising approach to designing model-free

controllers is the intelligent PID (iPI) methodology.

Replaces the conventional process model with an ul-

tralocal model and incorporates an estimator to up-

date it dynamically. Inspired by traditional PID con-

trollers, this method leads to several variations, in-

cluding iP, iPI, iPI, and iPI controllers. The ultralocal

model for an SISO system is represented as:

˙y(t) = F(t)+αu(t). (1)

where F(t) captures the unmodeled dynamics and dis-

turbances, α ∈ R is a positive design parameter cho-

sen to align the magnitudes of ˙y(t) and αm(t), and

m(t) is the control input.

The control objective is deﬁned through the track-

ing error:

e(t) = R(t) − y(t). (2)

Here, R(t) denotes the desired reference temper-

ature, while y(t) corresponds to the measured sys-

tem output temperature. This error metric provides

the foundation for designing the control law, ensur-

ing that the system output converges to the reference

value with minimal deviation, even in the presence of

disturbances or model uncertainties.

For the iPI controller, the control law takes the

form:

(t) =



−

F(t)+

R(t) + K

e(t) + K

e(τ)dτ



(3)

where K

and K

are the proportional and integral

gains, respectively, and are tuned to ensure accurate

tracking of R(t). Substituting the model equation into

the control law results in the closed-loop error dynam-

ics:

˙e(t) + K

e(t) + K

e(τ)dτ = 0. (4)

which indicates that disturbances and unmodeled

components encapsulated in F(t) are effectively can-

celed.

The gains for a PI-Fuzzy is necessary to ﬁrst cre-

ate the control law that the derivative part entails. In

this case, we proposed to add the derivative part keep-

ing a ﬁrst ultra local model.

(t) =

[−

F(t) +

R(t) + K

e(t) + K

˙e]. (5)

To estimate ˙y(t), various methods can be em-

ployed, such as numerical differentiation or ﬁltering.

A ﬁrst-order low-pass ﬁlter is commonly used, de-

ﬁned as

(s) =

s + 1

, (6)

where K

and T

are the gain of the ﬁlter and the

time constant, chosen to balance the noise reduction

and delay. Using this ﬁlter, the disturbance estimation

is given by:

F(t) = ˙y(t) − αu(t). (7)

where ˙y(t) represents the estimated derivative of the

output of the system.

A Comparative Experimental Evaluation of iPI and iPI-Fuzzy Controllers for a Thermal Process with a Long Dead Time

211

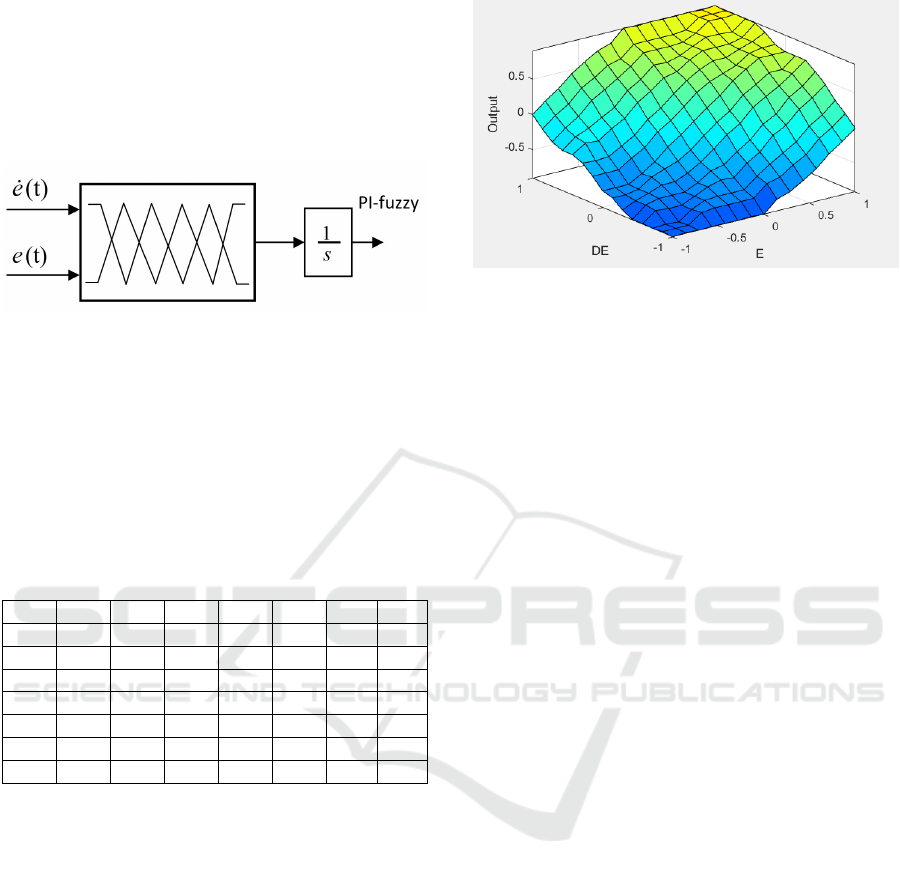
3.2 iPI Fuzzy Controller Proposal

A fuzzy PI controller is designed based on the struc-

ture of the previously described fuzzy PD controller.

To implement the fuzzy PI conﬁguration, the output

of the fuzzy PD controller is integrated, as illustrated

in Fig. 1.

Figure 1: Control PI-fuzzy Scheme.

Table 1 displays the PD-fuzzy rules utilized in the

TcLab. In this context, the terms NB and PB repre-

sent ”negative big” and ”positive big,” respectively.

These labels belong to a set of rules that establish con-

nections between the input and output variables using

fuzzy values. Speciﬁcally, NB refers to a highly nega-

tive value, while PB corresponds to a strongly positive

value within the framework of the fuzzy logic system.

Table 1: Fuzzy Table.

˙e/e NB NM NS ZE PS PM PB

NB NB NB NB NB NM NS ZE

NM NB NB NM NM NS ZE PS

NS NB NM NM NS ZE PS PM

ZE NB NM NS ZE PS PM PB

PS NM NS ZE PS PM PB PB

PM NS ZE PS PM PB PB PB

PB ZE PS PM PB PB PB PB

The three-dimensional surface depicted in 2 illus-

trates how these rules are employed to generate a con-

tinuous output from the fuzzy system. The surface’s

shape and colors reveal how the output values change

based on different input combinations, offering a vi-

sual representation of the way the fuzzy rules convert

inputs into a corresponding output.

3.3 Initial Tuning Parameters Based on

Particle Swarm Optimization (PSO)

Particle Swarm Optimization (PSO) is a renowned

metaheuristic algorithm inﬂuenced by the behavior of

a ﬂock of birds searching for food. Each bird com-

municates its ﬁndings with the group, helping to lo-

cate the most advantageous prey collectively (Wang

et al., 2018). This process involves every bird seeking

its own best solution within a multidimensional space,

and the most effective solution identiﬁed by the entire

Figure 2: Fuzzy Surface.

swarm becomes the optimal result in the PSO.

A minimization objective function dependent on

the error is proposed, known as the Integral Squared

Error (ISE), This function allows the reference to

reach fast, as described in (Campos et al., 2018), re-

sulting in the cost function presented in (8).

= ISE (8)

The optimization focused on adjusting the initial

PID controller parameters and α, while the derivative

values H

LP1

and H

LP2

were kept constant at 1.

4 RESULTS AND DISCUSSIONS

This section presents the performance assessment of

the proposed controllers by examining a scenario that

involves an experimental setup using the TCLab de-

vice. The results include setpoint and disturbance

changes.

4.1 Thermal Process - TCLab

The TCLab device, shown in Fig. 3 is an Arduino

Kit that consists of two heaters and two temperature

sensors that emulate a real-life process in which dif-

ferent control techniques can be implemented. The

heaters are controlled through Pulse Width Modula-

tion (PWM) as detailed in (Mejia et al., 2022)

According to previous works (Mejia et al., 2022),

for example, the FOPDT model of the TCLab device

exhibits a dead time t

signiﬁcantly shorter, almost

one-tenth, compared to the time constant τ. Conse-

quently, to evaluate controller schemes for long de-

lay systems, a software-induced time delay of 175 [s]

was incorporated into the TCLab to make a dominant

time delay system, as depicted in Fig. 4. This conﬁg-

uration was utilized throughout the remainder of the

article.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

212

Figure 3: TCLab diagram.

Disturbance

Temperature

Output

Controller

Temperature

measurement

Temperature

Measurement with

Delay

Sensor

TCLab

Heater

Delay

Figure 4: Temperature process block diagram.

4.2 iPI Controller Approaches

As observed in Fig.5, the general control architec-

ture is designed to address the application of the con-

trollers to the Temperature Control Lab (TCLAB)

with dominant time delay.

The schematic directly includes this delay, empha-

sizing its importance in developing the control strat-

egy and its impact on system performance. Addi-

tionally, the schematic includes essential components

to improve the controller’s efﬁciency. Low-pass ﬁl-

ters (H

LP1

(s) and H

LP2

(s)) mitigate noise and high-

frequency disturbances, while the gain term

ensures

a stable control response.

The two controllers are implemented to ad-

dress the complexities of TCLAB’s behavior with

the dominant time delay. In this case, the two

alternatives are considered, with the second one

combining the intelligent PID (iPI) control frame-

work with the adaptability of fuzzy logic. This

hybrid control strategy processes the error (e(t))

and its derivative ( ˙e(t)) as input, mapping them into

seven fuzzy subsets. A Takagi-Sugeno inference

mechanism, coupled with a centroid defuzziﬁca-

tion method, generates a succinct control signal

that effectively handles the nonlinearities and un-

certainties inherent in the system. The integral

action, introduced by integrating the output of the

iPI-Fuzzy controller, ensures steady-state error elimi-

nation while preserving the ﬂexibility and robustness

of the fuzzy logic framework.

4.3 Reference Tracking and

Disturbance

Fig.6, which illustrates the output of the transmitter

(TO), captures the thermal response of the TCLAB

system under the control actions of the iPI and iPI-

Fuzzy strategies. Both controllers effectively track

the initial reference, showing their capability to reg-

ulate the system’s output within acceptable bounds.

However, the iPI-Fuzzy controller demonstrates su-

perior accuracy in reference tracking, maintaining be-

havior closer to the desired setpoint with minimal

steady-state error.

During dynamic transitions, including disturbance

around 3500 s, the iPI-Fuzzy outperforms the iPI by

exhibiting reduced overshoot and a smoother recov-

ery to the target value. This superior adaptability

underscores the advantages of the fuzzy logic-based

approach in handling the TCLAB’s dominant delay,

as well as its inherent nonlinearities and uncertain-

ties. Furthermore, the iPI-Fuzzy controller design

ensures enhanced stability, achieving robust perfor-

mance even under challenging conditions, optimizing

the thermal response, and minimizing deviations from

the reference signal.

Fig. 7, depicting the Controller Output (CO) over

time, highlights the system’s response to reference

tracking under both the iPI and the iPI-Fuzzy con-

trol strategies. Both controllers exhibit a rapid rise

to achieve the desired set point, demonstrating their

ability to handle initial dynamic changes effectively.

However, the iPI-Fuzzy demonstrates superior perfor-

mance, as evidenced by its smoother trajectory and

reduced overshoot during the transient phase. Around

3500 seconds, when a disturbance is introduced, the

iPI-Fuzzy controller outperforms the iPI by recover-

ing more quickly and maintaining a steadier output

with signiﬁcantly lower oscillations. This behavior

underscores the enhanced adaptability and robustness

of iPI-Fuzzy in managing dynamic system variations.

Furthermore, the inclusion of low-pass ﬁlters in the

controller design effectively mitigates high-frequency

noise, ensuring the stability and reliability of the con-

trol signals throughout the process. These attributes

make the iPI-Fuzzy a more efﬁcient and precise op-

tion for disturbance rejection and reference tracking.

In reference tracking tests, the iPI-Fuzzy con-

troller exhibited superior performance compared to

the conventional iPI controller. This was reﬂected in

a more accurate response, with fewer overshoots and

A Comparative Experimental Evaluation of iPI and iPI-Fuzzy Controllers for a Thermal Process with a Long Dead Time

213

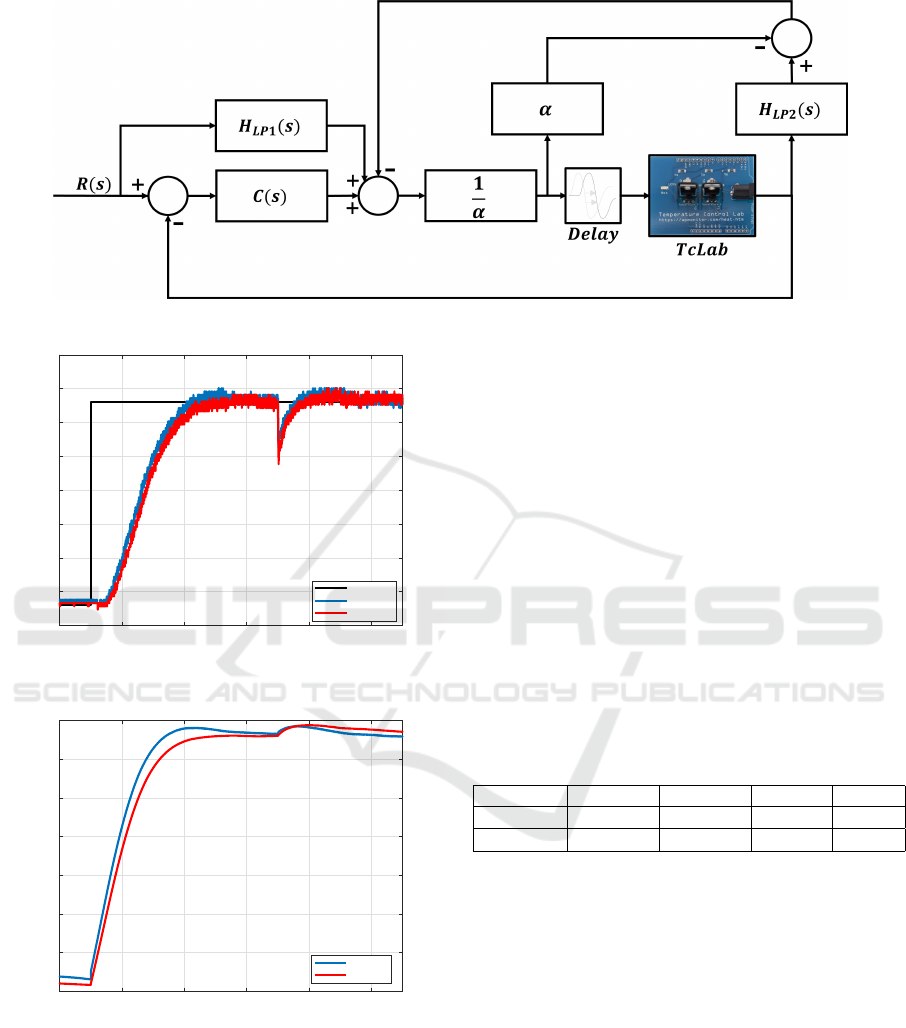
Figure 5: Schematic of Model-Free with Dominant Delay in the TCLab

0 1000 2000 3000 4000 5000

Time [s]

TO [p.u]

Reference

iPI

iPI-Fuzzy

Figure 6: Transmitter Output for iPI vs. iPI-Fuzzy.

0 1000 2000 3000 4000 5000

Time [s]

CO [p.u]

iPI

iPI-Fuzzy

Figure 7: Controller Output for iPI vs. iPI-Fuzzy.

shorter settling times. These improvements can be at-

tributed to the fuzzy logic’s ability to handle nonlin-

earity and adapt to system variations in real-time.

The behavior of the iPI-Fuzzy allowed the system

to efﬁciently reach the target temperature values while

optimizing energy consumption, highlighting its abil-

ity to adapt to the variable dynamics of the TCLab. In

contrast, the iPI controller showed less accurate track-

ing and longer settling times due to its more static de-

sign. In disturbance rejection tests, the iPI-Fuzzy con-

troller proved to be more robust than the conventional

iPI controller. When external disturbances were in-

troduced into the system, such as changes in ambient

temperature, the iPI-Fuzzy quickly compensated for

these disturbances, restoring the temperature to the

target value in less time.

In contrast, the iPI controller experienced a slower

recovery period to reestablish system stability, show-

ing signiﬁcant ﬂuctuations away from the target tem-

perature. This highlights the beneﬁts of integrating

fuzzy logic as it enables adaptive modiﬁcations when

unexpected shifts occur in the system’s operating con-

ditions.

Table 2: Performance evaluation for reference tracking and

disturbance test.

ISE ISCO MP [%] t

[s]

iPI 6.0 × 10

4.8 × 10

3.8 3000.0

iPI-Fuzzy 5.4 × 10

5.0 × 10

0.0 3500.0

Here is the paraphrased text in English:

Table 2 provides a detailed comparative analy-

sis of the iPI and iPI-Fuzzy controllers, focusing on

their performance in two key aspects: reference track-

ing and disturbance rejection. These functionalities

are crucial for ensuring system stability and accuracy,

particularly in thermal processes where delays, distur-

bances, and nonlinear behaviors are common.

The iPI-Fuzzy controller outperforms the conven-

tional iPI controller in reference tracking, as evi-

denced by its signiﬁcantly lower Integral Squared Er-

ror (ISE). This metric quantiﬁes the accumulated er-

ror over time, especially during transient states. A

lower ISE indicates that the controller has effectively

minimized the deviation between the system’s actual

output and the desired reference signal, ensuring a

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

214

closer adherence to the intended trajectory. This im-

proved tracking capability is essential in industrial

applications such as semiconductor manufacturing or

chemical processing, where even small variations in

temperature or other variables can lead to inefﬁcien-

cies, safety risks, or product quality issues.

However, this increased accuracy comes at the ex-

pense of higher control effort, as indicated by the

Integral Squared Control Output (ISCO). This mea-

sure reﬂects the total energy or effort required by

the controller to maintain the desired output. While

the iPI-Fuzzy controller excels at minimizing track-

ing error, it demands greater control effort, which

could result in higher energy consumption or accel-

erated wear on system components. In contrast, the

iPI controller, though less effective in reducing track-

ing error, demonstrates better performance in terms of

ISCO. By balancing error reduction with energy efﬁ-

ciency, the iPI controller is a more suitable option for

applications where minimizing energy consumption

and operational costs is a priority.

Regarding overshoot (Maximum Peak, MP), the

iPI-Fuzzy controller presents a clear advantage. Over-

shoot refers to how much the system output exceeds

the desired reference value before stabilizing at the

steady-state level. In applications where overshoot

is undesirable—such as in precise thermal control,

where excessive heating could cause damage or com-

promise product quality—minimizing this effect is

critical. The iPI-Fuzzy controller achieves this by en-

suring a smooth and controlled approach to the set-

point, making it particularly valuable in industries

where maintaining precise parameter control is essen-

tial for safety and performance.

Conversely, the traditional iPI controller exhibits

a slight but noticeable overshoot, which could pose

challenges in sensitive applications. While this over-

shoot may not signiﬁcantly impact performance in

many cases, it could introduce unwanted ﬂuctuations

in systems that demand high precision or operate un-

der strict safety regulations.

Regarding settling time (t

), the iPI controller pro-

vides a faster response. Settling time represents the

period required for the system to reach and remain

within a speciﬁed range around the setpoint after a

disturbance or reference change. A shorter settling

time indicates that the system stabilizes more quickly,

which is advantageous in applications requiring rapid

adaptation to changing conditions or strict time con-

straints.

However, this faster stabilization comes at the cost

of reduced smoothness in system response. The iPI-

Fuzzy controller, while exhibiting a slightly longer

settling time, prioritizes smoother transitions. This

approach is beneﬁcial in processes where stability

and gradual response are more important than speed.

In industries with long-duration thermal processes or

applications where abrupt changes must be avoided

to preserve material integrity or process stability, the

smoother response of the iPI-Fuzzy controller is often

the preferred choice.

5 CONCLUSIONS

This study has conducted a comprehensive compari-

son between the iPI and iPI-Fuzzy controllers in the

context of the TCLab system. The results demonstrate

that the iPI-Fuzzy controller offers a more robust and

adaptable solution for controlling nonlinear systems

with time delays. This controller excels in maintain-

ing accurate reference tracking and disturbance rejec-

tion, particularly in dynamic environments where tra-

ditional controllers like iPI face limitations. The iPI-

Fuzzy controller’s ability to eliminate overshoot and

adapt more effectively to disturbances underscores its

suitability for real-time thermal process control.

While the iPI controller shows advantages in

terms of quicker settling time and energy efﬁciency,

the iPI-Fuzzy controller provides smoother system

transitions and better stability, making it a superior

choice in applications where robustness and precision

are prioritized over speed. This study validates the po-

tential of fuzzy logic to enhance the performance of

thermal process control, particularly in the presence

of nonlinearities and delays.

For future work, further enhancements to the con-

trol framework are suggested. Integrating machine

learning techniques for real-time parameter tuning

could improve the adaptability of the controller, al-

lowing for automatic adjustments based on changing

system dynamics. Moreover, extending the methodol-

ogy to larger and more complex thermal systems, as

well as to multi-input, multi-output (MIMO) applica-

tions, presents an exciting avenue for future research

and development. This could broaden the applicabil-

ity of the proposed controllers to more industrial-scale

systems and further optimize their performance.

ACKNOWLEDGEMENTS

The authors thank Universidad San Francisco de

Quito for funding this research through the Poli-

Grants Program under Grant 33603.

A Comparative Experimental Evaluation of iPI and iPI-Fuzzy Controllers for a Thermal Process with a Long Dead Time

215

REFERENCES

Campos, J., Jaramillo, S., Morales, L., Camacho, O.,

avez, D., and Pozo, D. (2018). Pso tuning for fuzzy

pd+ i controller applied to a mobile robot trajectory

control. In 2018 International Conference on Infor-

mation Systems and Computer Science (INCISCOS),

pages 62–68. IEEE.

de Moura Oliveira, P., Soares, F., and Cardoso, A. (2022).

Pocket-sized portable labs: Control engineering prac-

tice made easy in covid-19 pandemic times. Ifac-

papersonline, 55(17):150–155.

Espin, J., Castrillon, F., Leiva, H., and Camacho, O. (2022).

A modiﬁed smith predictor based–sliding mode con-

trol approach for integrating processes with dead

time. Alexandria Engineering Journal, 61(12):10119–

10137.

Fliess, M. and Join, C. (2013). Model-free control. In-

ternational journal of control, vol. 86, no. 12, pp.

2228–2252.

Gude, J. J. (2023). Contributions to fractional-order mod-

elling and control of dynamic systems: A theoretical

and practical approach. PhD thesis, Universidad de

Deusto.

Gude, J. J., Garc

ıa Bringas, P., Herrera, M., Rinc

on, L.,

Di Teodoro, A., and Camacho, O. (2024). Fractional-

order model identiﬁcation based on the process reac-

tion curve: A uniﬁed framework for chemical pro-

cesses. Results in Engineering, 21:101757.

Jain, A. and Goodson, K. E. (2011). Thermal microdevices

for biological and biomedical applications. Journal of

Thermal Biology, 36(4):209–218.

Kocaarslan, I., C¸ am, E., and Tiryaki, H. (2006). A fuzzy

logic controller application for thermal power plants.

Energy conversion and management, 47(4):442–458.

Liptak, B. G., Piovoso, M. J., Shinskey, F. G., Eren, H.,

Totherow, G. K., Jamison, J. E., Morgan, D., Hertanu,

H. I., Marszal, E. M., Berge, J., et al. (2018). Instru-

ment engineers’ handbook, volume two: Process con-

trol and optimization. CRC press.

May, G. S. and Spanos, C. J. (2006). Fundamentals of semi-

conductor manufacturing and process control. John

Wiley & Sons.

Mejia, C., Salazar, E., and Camacho, O. (2022). A compar-

ative experimental evaluation of various smith predic-

tor approaches for a thermal process with large dead

time. Alexandria Engineering Journal, 61(12):9377–

9394.

Obando, C., Rojas, R., Ulloa, F., and Camacho, O.

(2023). Dual-mode based sliding mode control ap-

proach for nonlinear chemical processes. ACS omega,

8(10):9511–9525.

Patel, K. M. (2023). A practical reinforcement learning im-

plementation approach for continuous process control.

Computers & Chemical Engineering, 174:108232.

Plawsky, J. L. (2020). Transport phenomena fundamentals.

CRC press.

Precup, R.-E., Radac, M.-B., Roman, R.-C., and Petriu,

E. M. (2017). Model-free sliding mode control of non-

linear systems: Algorithms and experiments. Informa-

tion Sciences, 381:176–192.

Sardella, M. F., Serrano, M. E., Camacho, O., and Scaglia,

G. J. (2019). Design and application of a linear al-

gebra based controller from a reduced-order model

for regulation and tracking of chemical processes un-

der uncertainties. Industrial & Engineering Chemistry

Research, 58(33):15222–15231.

Schwenzer, M., Ay, M., Bergs, T., and Abel, D. (2021).

Review on model predictive control: An engineering

perspective. The International Journal of Advanced

Manufacturing Technology, 117(5):1327–1349.

Smith, C. A. and Corripio, A. B. (2005). Principles and

practices of automatic process control. John wiley &

sons.

Tanaka, K., Wang, L., and Camacho, O. (2023). Fuzzy

control for time-delay systems. IEEE Transactions on

Fuzzy Systems, 31(4):1122–1135.

asquez, M., Yanascual, J., Herrera, M., Prado, A., and

Camacho, O. (2023). A hybrid sliding mode control

based on a nonlinear pid surface for nonlinear chem-

ical processes. Engineering Science and Technology,

an International Journal, 40:101361.

Wang, D., Tan, D., and Liu, L. (2018). Particle swarm op-

timization algorithm: an overview. Soft computing,

22(2):387–408.

Wang, L., Gude, J. J., and Patel, K. M. (2022). Fractional

pid for industrial thermal processes. Journal of Pro-

cess Control, 110:45–58.

Zhang, H. and Liu, D. (2006). Fuzzy modeling and fuzzy

control. Springer Science & Business Media.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

216