A New Numerical Method for Fast Prediction of Wheel Tread Wear

for Stacker Cranes

Minggong Yu

, Enming Zhang

and Johannes Fottner

Chair of Materials Handling, Material Flow, Logistics, Technical University of Munich,

Boltzmannstrasse 15, 85748 Garching near Munich, Germany

Keywords: Wheel-Rail Contact, Wear Prediction, Stacker Crane, Wheel Profile Update, Co-Simulation.

Abstract: With the development of the logistics industry, the demand for efficient, high-capacity material handling

equipment, such as stacker cranes, has grown significantly. As a critical load-bearing component of stacker

cranes, the wheel-rail contact system is subtracted to higher operational speeds and load capacities, which

lead to increased contact stresses and wheel tread wear. The degraded wheel profile caused by wear can

deteriorate wheel-rail interactions, exacerbate vibrations, and subsequently reduce the lifespan of stacker

cranes. This paper proposes a numerical model based on co-simulation to predict wheel tread wear of stacker

cranes. The model combines a multibody dynamics model of the stacker crane, a wheel-rail contact model,

and a worn profile update model. Additionally, a wear superposition method, i.e., a simplified and practical

method, is developed to calculate the accumulated wear, enabling the prediction of the wheel wear under

different work cycles with limited simulation iterations. The results show the accumulated wheel tread wear

depth across various work cycles of stacker cranes, providing quantitative predictions while significantly

reducing simulation time.

1 INTRODUCTION

Stacker cranes are essential components of modern

intralogistics systems, which enable automated

storage and retrieval operations for a wide range of

goods in automated pallet and small-parts

warehouses. As rail-mounted, single-track material

handling equipment, their performance heavily relies

on the reliability of the wheel-rail system. Over the

past decade, the rapid growth of e-commerce and

globalisation has more than doubled the turnover of

the logistics industry (Achouch et al., 2022). To meet

this demand, warehousing operations have

significantly enhanced material handling efficiency.

However, this progress has pushed automated

warehouse systems, particularly stacker cranes, to

operate at their dynamic limits. The resulting increase

in dynamic loads places substantial contact stresses

on the wheel-rail system, accelerating wear and

increasing the risk of damage (Laile & Fottner, 2021).

Wear is a primary damage type affecting the

wheel-rail system, characterised by material loss due

https://orcid.org/0009-0005-8866-0373

https://orcid.org/0009-0008-1177-8404

https://orcid.org/0000-0001-6392-0371

to adhesive and abrasive phenomena (Tunna et al.,

2007). This material loss degrades the wheel and rail

profiles, changing the position and size of the contact

area. These changes influence the distribution of

normal and tangential forces within the contact area,

negatively impacting the system’s dynamic response.

Additionally, wear can lead to wheel out-of-

roundness, causing shock loads and vibrations during

operation. These effects may further damage other

system components (Iwnicki et al., 2023).

Preventive maintenance is commonly conducted

to mitigate the effects of wear, including grinding to

restore the profiles of wheel and rail. Alternatively,

some stacker crane operators choose to replace worn

wheels entirely. Both approaches are scheduled based

on fixed working hours or cycles (Große et al., 2018).

Typically, preventive maintenance strategies rely on

empirical data or manufacturer recommendations.

However, this does not guarantee the prevention of

premature wear failures or ensure that maintenance is

performed only when necessary.

Yu, M., Zhang, E. and Fottner, J.

A New Numerical Method for Fast Prediction of Wheel Tread Wear for Stacker Cranes.

DOI: 10.5220/0013458800003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 193-200

ISBN: 978-989-758-759-7; ISSN: 2184-2841

193

This paper proposes a numerical solution for

predicting the wheel wear behaviour of stacker cranes

using a co-simulation approach that integrates a

Simpack multibody model with a MATLAB-based

wear prediction model. The method accounts for

wheel profile changes due to wear, incorporating

updated wheel profiles into subsequent simulation

iterations. Additionally, a wear scaling strategy based

on a normal distribution is developed, which enables

the simulation of numerous real-world work cycles

within fewer simulation runs. This approach

significantly reduces simulation time while ensuring

reliability.

2 RELATED RESEARCH

Wear is a gradual and slow process that occurs over

significant wheel-rail relative displacements and

under substantial load conditions. To accelerate

simulation processes, it is commonly assumed that

the wheel and rail profiles remain unchanged within

a single simulation iteration. A multiplier is then

applied to amplify material wear and update the

profiles. This approach has been widely used in wear

studies in the field of railways. Zhang et al. (Zhang et

al., 2013) developed a simulation tool using

Simpack’s built-in wear model, where they applied a

distance factor as a multiplier to scale wear results to

a total distance of 10,000 km. However, Bosso et al.

(Bosso & Zampieri, 2019) noted that using a high

multiplier could lead to unrealistic wear

concentrations in the initially calculated wear areas,

resulting in overestimation. To address this, they

proposed an interpolation smoothing method based

on surface curvature to improve accuracy even with a

high multiplier. Braghin et al. (Braghin et al., 2006)

assumed that wear depth was uniformly distributed

along the circumferential direction. They applied a

moving average approach to smooth wear depth and

updated the worn profile using cubic spline

interpolation. Their study recommended updates for

wear depth increments of 0.1 mm. Yang et al. (Yang

et al., 2023) investigated wheel tread wear using a

vehicle-track dynamics model based on a non-

Hertzian contact algorithm. Their results showed that

wear progressively expands in depth and width with

increasing iterations, with wear propagation

occurring faster in earlier iterations than in later ones.

The reviewed literature highlights various

numerical methods for calculating wear in wheel-rail

systems. However, most of these methods face the

following challenges:

• Accurately determining wear depth

distribution and updating the wheel-rail

profile;

• Developing a practical approach to amplify

wear accumulation

Furthermore, existing research primarily focuses

on railway applications, with limited attention given

to wheel-rail systems in logistics equipment such as

stacker cranes. Compared to rail vehicles, stacker

cranes exhibit bidirectional, intermittent movement

patterns and operate under distinct load conditions.

Additionally, stacker cranes use rimless wheels,

which differ in dimensions from those used in railway

applications (Yu & Fottner, 2024). These distinctive

characteristics highlight the need for a comprehensive

study of the wear behaviour of stacker crane wheel-

rail systems. Given the lack of detailed experimental

data on the wheel-rail wear behavior of stacker cranes,

numerical methods provide a suitable approach for

investigation.

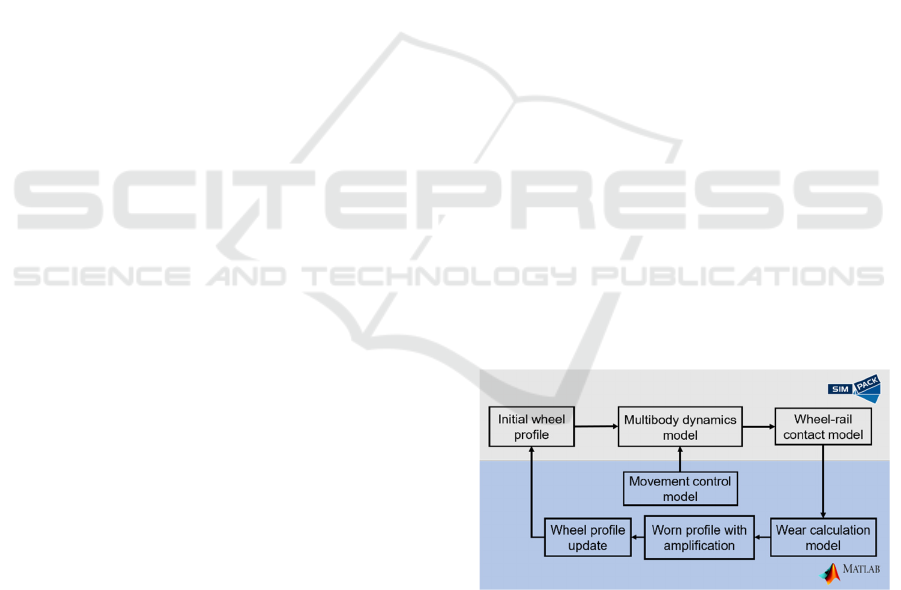
3 NUMERICAL MODEL

The wheel wear prediction model for stacker cranes

proposed in this paper consists of the following sub-

models: a multibody dynamics model, a movement

control model, a wheel-rail contact model, a wear

calculation model and a worn profile update model.

The overall framework is illustrated in Figure 1,

where arrows indicate the flow of output results

between submodel. Detailed descriptions of each

submodel are provided in the following sections.

Figure 1: Overall framework of proposed wear prediction

model based on co-simulation.

3.1 Multibody Dynamics Model of

Stacker Crane

The multibody dynamics model of a single-mast

stacker crane was developed using the multibody

simulation software Simpack (Yu & Fottner, 2024).

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

194

Figure 2 illustrates the model structure along with a

typical application scenario of stacker cranes.

Figure 2: Schematic representation of stacker crane and its

working scenario.

The model comprises a mast, a traverse, a lift

carriage, two running wheels, and a rail. The wheel-

rail system is modelled using Simpack’s built-in Rail

module. The initial wheel profile is rimless, while the

rail uses the standard UIC60 profile, commonly used

in railway applications. Key parameters for modelling

the stacker crane system, such as mast height, average

load capacity, operating velocity, and wheel diameter

and width, are detailed in the study (Yu & Fottner,

2024).

3.2 Movement Control Model

Since Simpack cannot model the complex

movements of a stacker crane, this paper integrates an

external movement control program developed by

Rücker et al. (Rücker et al., 2020) in

MATLAB/Simulink. The program determines the

rack positions required for movement within a single

work cycle based on the selected stacker crane

operation mode. It then computes the corresponding

acceleration, velocity, and displacement signals for

each time step. These signals are then transmitted to

the joint points of the multibody model via co-

simulation, thereby enabling precise control of the

stacker crane’s movements. Figure 2 shows three

typical operation modes of stacker cranes: single

cycle, double cycle, and quadruple cycle. In practice,

stacker cranes operate using a combination of these

modes to improve efficiency (Siciliano et al.).

However, for simplification, this study excludes such

combinations from the simulation.

3.3 Wheel-Rail Contact Model

The wheel-rail contact model is a critical component

of the wear prediction framework, as it defines the

contact area and normal force distribution within the

contact patch, significantly influencing wear results.

This paper uses Simpack’s Rail module for wheel-rail

contact calculations (Vollebregt et al., 2011). The

outputs from the contact model are transferred to the

discrete outer surface of the wheel in MATLAB,

where they are used for subsequent wear calculation

and profile updates.

3.3.1 Wheel-Rail Contact Calculation in

Simpack

Since the wheel and rail have quasi-identical material

properties, the wheel-rail contact can be treated as an

uncoupled normal and tangential contact problem that

is solved sequentially (Sichani, 2013). The normal

contact problem is addressed using Hertzian theory,

while the tangential contact problem is solved using

the FASTSIM algorithm based on Kalker’s simplified

theory. Results from the wheel-rail contact

calculations in Simpack—such as the lateral contact

point position and normal contact force—are used to

determine the position and size of the elliptical

contact area and the normal contact pressure within

that area.

3.3.2 Discretization of the Outer Surface of

Wheel

To further investigate wheel-rail contact and wear

behaviour, the outer surface of the wheel tread should

be discretized. This discretization divides the global

contact problem into discrete cells on the wheel

surface, enabling the local computation of worn

material within each cell of the contact area.

The wheels on stacker cranes are generally

rimless and can be approximated as cylindrical. When

the wheel is unfolded along its axis, the outer surface

can be represented as rectangular, where the length of

the rectangle corresponds to the wheel’s

circumference and the width represents the wheel

tread width. This rectangular surface is discretized

into a grid of 1×1 mm square cell, as shown in Figure

3. For illustrative purposes, the figure does not

represent the actual 1×1 mm cell size to scale.

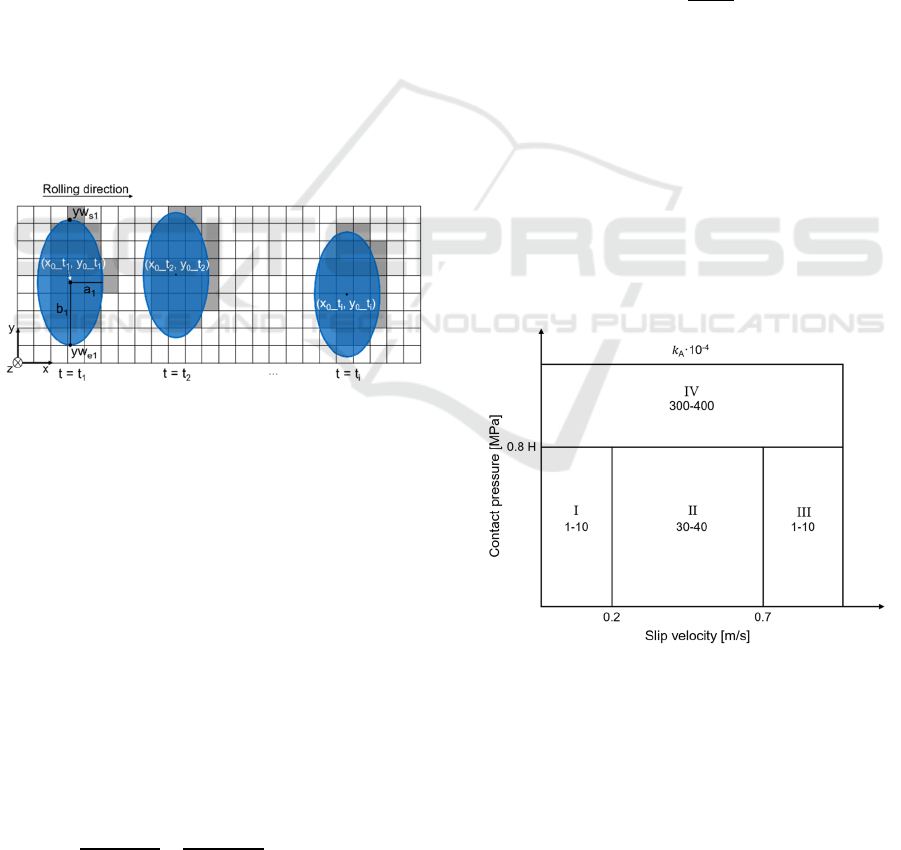
Figure 3: Discretization of wheel outer surface.

A New Numerical Method for Fast Prediction of Wheel Tread Wear for Stacker Cranes

195

The three-dimensional coordinate information of

each grid node, as shown in Figure 3, is stored in a

MATLAB cell array. The 𝑥 and 𝑦 coordinates define

the node’s position on the wheel’s outer surface,

while the 𝑧 coordinate represents the wear depth at

that node. Each cell is referenced by its lower-left

node, which serves as the reference point for

subsequent contact area searches. As illustrated in

Figure 3, the representative node for the cell

highlighted in red is indicated by the black node at its

lower-left corner.

3.3.3 Search for Contact Area on Discrete

Wheel Surface

In this step, the wheel-rail contact area determined by

Simpack is mapped onto the corresponding discrete

wheel surface in MATLAB. Figure 4 shows the

wheel-rail contact area at each time step during the

stacker crane’s movement. The blue elliptical region

represents the contact area calculated by Simpack,

while the grey cells depict the corresponding discrete

representation of the contact area on the wheel’s outer

surface.

Figure 4: Search for contact area at each time step 𝑡



As shown in Figure 4, the position and size of the

elliptical contact area are determined by the wheel’s

lateral contact positions 𝑦

,

and 𝑦

,

at the contact

point, as well as the semi-axis lengths 𝑎 and 𝑏 of the

elliptical contact area.

To discretize the elliptical contact area (blue region

in Figure 4) onto the grid, it is necessary to identify

which grid cells (grey region in Figure 4) lie within the

contact area. This paper uses the positional relationship

between a point and an ellipse, as defined in Equation

(1), where (𝑥



,𝑦



) represents the centre of the

elliptical contact area, (𝑥,𝑦) the lower-left node of a

cell. Specifically, the formula determines whether the

lower-left node of a cell lies inside or on the boundary

of the ellipse. If it does, the corresponding cell is

considered part of the contact area.

(

𝑥−𝑥



)



𝑎



(

𝑦−𝑦



)



𝑏



 1

)

3.4 Wear Calculation Model

This paper applies the Archard wear model to

calculate the volumetric worn material on the wheel.

The wear depth is then determined using the wear

distribution model developed in this study.

3.4.1 Archard Wear Model

In the Archard wear model, the volume of worn

material is directly proportional to the normal contact

force and the sliding distance, while inversely

proportional to the hardness of the softer material in

the wheel-rail pair. This relationship is expressed by

Equation (2),

𝑉



=𝑘⋅

𝐹



⋅𝑠

𝐻

)

where 𝑉



is the worn volume, 𝑘 the wear

coefficient, 𝐹



the normal contact force, 𝐻 the

hardness of the softer material in the wheel-rail

material pair in MPa, and s the sliding distance. The

wear coefficient 𝑘 is a dimensionless factor that

depends on normal contact pressure and sliding

velocity, as shown in Figure 5 (Jendel, 2002). The

values of 𝑘 were experimentally determined under

dry and clean wheel-rail contact conditions. For

simplification, this paper uses the mean values of the

wear coefficients for different regions, i.e. 𝑘



𝑘



= 5×10

-4

, 𝑘



= 35×10

-4

, and 𝑘



= 350×10

-4

Figure 5: Archard wear chart (Jendel, 2002).

3.4.2 Wear Depth Distribution

According to Hertzian theory, normal contact

pressure follows a parabolic distribution across the

contact area. The maximum pressure 𝑃



occurs at

the centre of the contact area, as expressed in

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

196

Equation (3) (Mostofi & Gohar, 1980), and gradually

decreases toward the edges of the contact area.

𝑃



⋅

𝐹



𝐴

(3)

According on the Archard wear model, wear

volume is proportional to the normal contact force. As

a result, wear depth across the contact area is also

expected to follow a parabolic distribution (Heinrich

& Klüppel, 2008). Building on this assumption, we

developed a parabolic wear depth distribution model

based on the Euclidean distance between discrete

nodes and the centre of the contact area. The

Euclidean distance is calculated using Equation (4):

𝑑=



(

𝑥−𝑥



)



(

𝑦−𝑦



)



(4)

where 𝑥 and 𝑦 are the coordinates of any node

within the discretized contact area, 𝑥



and 𝑦



the

coordinates of the contact area centre, 𝑑 the

Euclidean distance between these two points. When

𝑑= 0, meaning the node is located at the centre of the

contact area, the wear depth reaches its maximum

value. Conversely, when 𝑑 reaches its maximum

value 𝑑



, indicating the node is at the edge of the

contact area, the wear depth becomes zero.

If the contact area is divided into cells of size

𝛥𝑥 × 𝛥𝑦, the wear depth 𝛥𝑧 can be expressed by

Equation (5), where 𝛥𝑠 represents the sliding

distance between two time-steps, and 𝑃(𝛥𝑥,𝛥𝑦) the

contact pressure within a cell.

∆z = 𝑘 ⋅

𝑃(𝛥𝑥,𝛥𝑦)⋅∆𝑠

𝐻

(5)

By combining Equation (2), (3) and (5), the wear

depth distribution 𝑧 in the contact area is given by

Equation (6):

𝑧=

⋅1−

𝑑









/

⋅

𝑉



𝐴

(6)

3.5 Worn Profile Amplification and

Update

Wear is a slow and gradual process that develops over

long-term wheel-rail contact. The operational

lifespan of a stacker crane’s wheel can reach up to 10

rotations. However, simulating the complete wear

process over its entire lifecycle is impractical due to

the enormous computational resources and time

required. To address this, the wear results must be

magnified to effectively represent long-term wear

behaviour. The calculated wear depth is subtracted

from the initial wheel profile to model the changes in

the wheel profile due to wear. The updated wheel

profile is then used in subsequent simulation

iterations.

Chapter 2 reviews relevant research on

magnification of wear results. A common approach is

to linearly scale the wear results of a single simulation

iteration using a user-defined multiplier factor. For

example, if 10 simulated cycles correspond to 1,000

actual working cycles, a multiplier factor of 100 is

applied. While higher multiplier factors can

significantly reduce simulation time, they may also

lead to unrealistically concentrated wear distribution

within the contact area. Additionally, they can

generate excessively steep or discontinuous updated

wheel profiles, leading to instability in subsequent

numerical iterations.

When the stacker crane moves along a linear rail,

wheel lateral displacements vary due to movement-

induced excitation. These displacements shift the

contact position, subsequently altering the wear

position. According to the wear distribution model,

wear is concentrated at the centre of the wheel-rail

contact area, with intensity decreasing toward the

edges of the contact area. Based on this principle,

subsequent wear is assumed to accumulate in both

lateral and longitudinal directions along the initial

wear profile. Each accumulation includes a lateral

displacement 𝑦



at each node within the contact

area, while the wear depth at the original position is

simultaneously added onto the displacement position.

The lateral displacement 𝑦



follows a normal

distribution, as expressed in Equation (7):

𝑦



~𝑁(𝜇,𝜎)

(7)

where 𝜇 = 0, indicating that subsequent wear

accumulates at the centre of the initial wear area. The

value of 𝜎 determines the spread of the wear

distribution across the wheel surface, where a higher

𝜎 results in a more evenly distributed wear pattern

across the wheel tread. 𝑁 is the wear amplification

factor, representing the number of iterations in the

accumulated wear process described above. After

wear depth amplification, the wheel profile is updated

and used as the initial profile for the subsequent

dynamics simulation iterations.

4 MODEL VERIFICATION AND

RESULTS DISCUSSION

This section performs a verification of the proposed

model by comparing it with Simpack’s built-in wear

calculation model. While Simpack includes a built-in

wear calculation model, it does not account for the

A New Numerical Method for Fast Prediction of Wheel Tread Wear for Stacker Cranes

197

progressive expansion of the worn area over extended

simulation iterations, resulting in an overestimation

of wear accumulation (Bosso & Zampieri, 2019).

However, since experimental validation with real

measurements is planned for future work, the current

results should be regarded as a verification rather than

a comprehensive validation.

To evaluate the developed wear calculation

model, the unaccumulated result is compared with the

Simpack’s calculation result, which serves as the

baseline. The simulation parameters provided by (Yu

& Fottner, 2024) are used for comparison. The

simulated stacker crane has a height of 30 meters and

an average load capacity of 2,000 kg. The wheels,

made of 42CrMo4 steel material with a Poisson’s

ratio of 0.3, have a diameter of 500 mm. The wheel-

rail friction coefficient is 0.2. The simulation was

conducted for 100 work cycles using the double-cycle

operation mode.

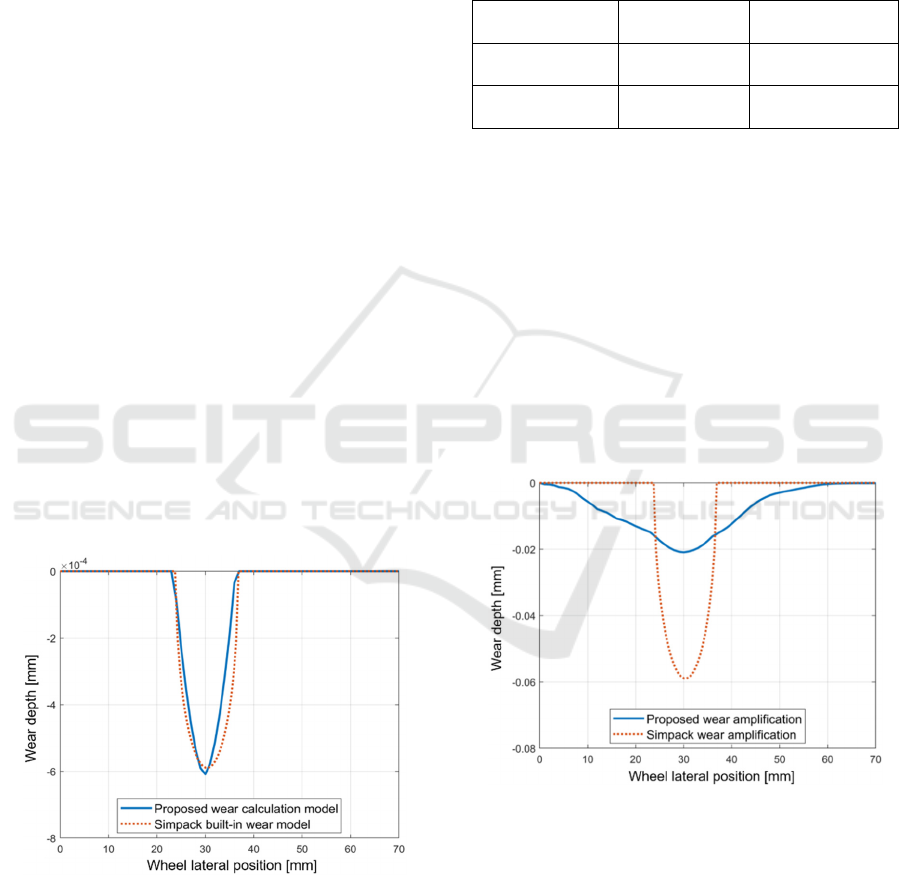
Figure 6 shows wheel wear depth at different

lateral positions for two simulation results. The red

dashed line represents the result obtained using

Simpack’s built-in Archard wear model, while the

blue solid line corresponds to the MATLAB-based

wear calculation model developed in this paper. As

shown in the figure, the maximum wear depth

calculated by the proposed wear model is slightly

higher than that calculated with the Simpack model.

Additionally, the wear distribution predicted by the

proposed method shows a minor shift away from the

centre of the contact area compared to the Simpack

result.

Figure 6: Comparison between the proposed wear model

and Simpack built-in wear model.

Table 1 compares the maximum wear depth and

its corresponding lateral position. The results indicate

that the wear calculation model developed in this

paper is highly consistent with Simpack’s built-in

model results. This consistency emphasises the

reliability of the proposed MATLAB-based wear

calculation model, establishing it as a robust

foundation for subsequent wear amplification and

wheel profile updates.

Table 1: Comparison of two wear calculation models for the

maximum wear depth and the lateral position it occurs.

Proposed wear

model

Simpack’s built-

in wea

model

Maximum wear

-4

6.08 5.89

Wheel lateral

osition

30.00 30.55

To verify the developed wear amplification

method, an amplification factor of 𝑁 = 100 is

selected. Similarly, a distance factor of 100 is applied

in the Simpack wear model to enable a direct

comparison with the wear amplification approach

proposed in this study. The results, shown in Figure

7, compare the two methods. The red dashed line

represents the Simpack result, while the blue solid

line corresponds to the result from the wear

amplification developed in this paper. The results

indicate that the amplified wear depth calculated in

Simpack is significantly higher than that obtained

using the proposed method. Additionally, the wear

area predicted by Simpack is narrower.

Figure 7: Comparison of wear amplification results with a

factor of 100 for one simulation iteration.

The significant differences arise from the

fundamentally different methods of wear

superposition. In Simpack, the distance factor directly

amplifies the results of a single simulation run,

keeping the wear zone consistent with the initial wear

profile. Consequently, subsequent wear is

proportionally amplified along the same profile. In

contrast, the amplification method proposed in this

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

198

paper accounts for the lateral expansion of the wear

profile as wear accumulates over time. This approach

considers the dynamic redistribution of wear,

providing a more refined representation of the wear

process over multiple iterations.

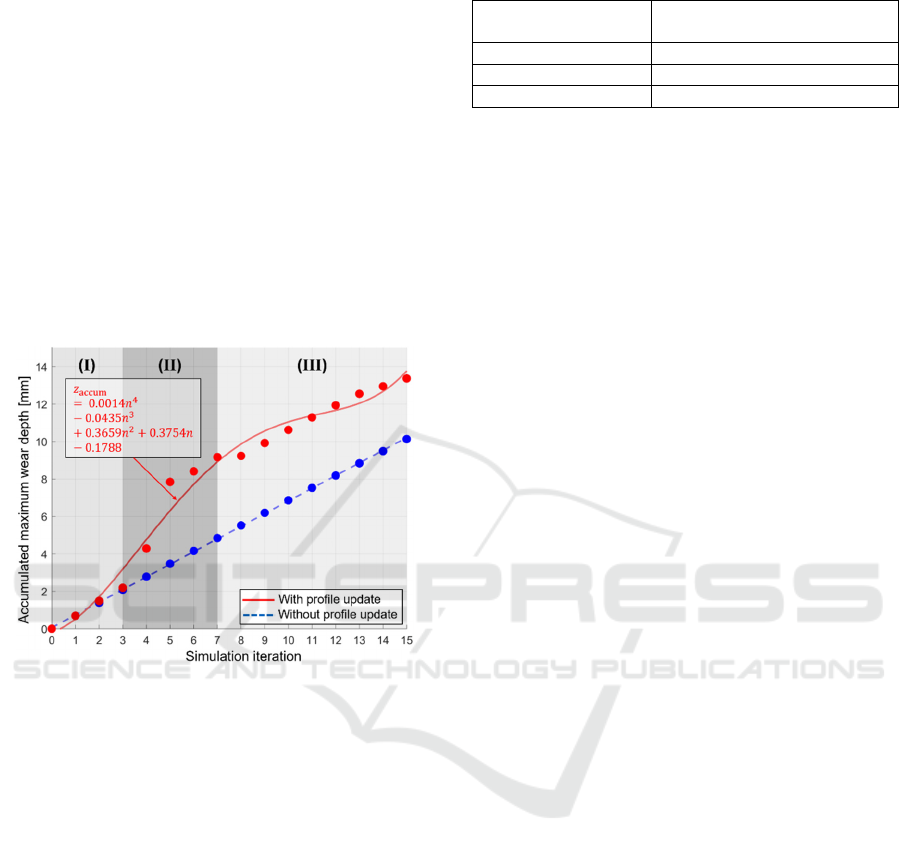
At this stage, the impact of the worn profile

update on simulation results is analysed. To simulate

the long-term work cycles of a stacker crane within a

finite number of simulation runs, a wear amplification

factor of 𝑁 = 100 is applied, with the profile updated

every hundred simulated work cycles. Each profile

update represents one simulation iteration, equivalent

to 10,000 actual work cycles of stacker cranes. In this

simulation, fifteen wear iterations are performed to

analyse the wear behaviour under profile updates,

with the results presented in Figure 8.

Figure 8: Comparison of results with/without worn profile

update regarding multiple simulation iterations.

The blue dashed line shows that wear behaviour

without profile updates follows a quasi-linear trend

throughout the iteration process. In contrast, when

profile updates are considered, the wheel wear

process demonstrates three distinct wear regimes as

work cycles increase, as shown by the red solid curve.

These regimes can be categorized as early stable wear

(I), mid-rapid wear (II), and late stable wear (III).

The red curve in Figure 8 represents a fourth-

degree polynomial fit to the red discrete points. The

fitting result is expressed by the equation next to the

red line in Figure 8, where 𝑧



is the accumulated

maximum wear depth on the wheel tread in mm, 𝑛

the number of simulation iterations, each

corresponding to 10,000 actual work cycles of stacker

cranes.

To quantitatively analyse wheel wear behaviour,

the wear rate is determined at different work cycle

stages. It represents the average maximum wear depth

per 10,000 actual work cycles at each stage. The

summarized results are shown in Table 2.

Table 2: Wheel wear rate under different work cycles.

Number of actual

wor

cycles

Predicted wear rate/ (mm/10

wor

cycles)

–

30,000 0.73

30,000

–

70,000 2.8

> 70,000 0.56

During the initial operation stage (work cycles

less than 30,000), wear has just begun and has

minimal impact on the wheel profile. In the middle

operation stage (work cycles between 30,000 and

70,000), wear may alter the wheel profile, leading to

a mismatch between the wear and rail profiles. This

mismatch reduces the contact area, accelerating

wheel wear. In the later operation stage (work cycles

more than 70,000), the wheel-rail profiles form a

better match, reducing the wheel wear rate.

5 CONCLUSION AND OUTLOOK

This paper presents a numerical investigation into the

wheel wear prediction for stacker cranes. A co-

simulation framework is developed by integrating the

Simpack multibody model with a MATLAB-based

wear calculation model. Additionally, a wear

amplification approach is introduced to simulate the

lifecycle of a stacker crane’s wheel within a feasible

number of simulation iterations. Instead of applying a

simple linear multiplier to the wear results, the

proposed approach accounts for the wear

amplification along the traverse contact position,

providing a more refined estimation of long-term

wear progression. The developed wear calculation

model is compared with Simpack’s built-in wear

model. Results indicate that the proposed approach

produces a similar wear depth distribution to

Simpack’s model, while significant differences are

observed when applying a wear amplification factor

of 100. This discrepancy occurs because the wear

accumulation method proposed in this paper

considers the lateral expansion of the contact area due

to wear.

This paper also investigates the influence of worn

profile changes on wheel wear behaviour across

different operation stages. It is found that the wheel

wore slowly first, then wore rapidly and finally

slowed again. The proposed calculation method

enables a quantitative prediction of stacker crane

wheel wear at various work cycle stages, providing

specific research significance and practical value for

the maintenance planning of stacker cranes.

Future research will focus on experimental

validation of the proposed method to further ensure

A New Numerical Method for Fast Prediction of Wheel Tread Wear for Stacker Cranes

199

its reliability and accuracy. Real-world wheel wear

data from stacker cranes will be used to assess the

consistency between simulated and observed wear

behaviour. These experiments are excepted to provide

valuable insights for validating the proposed wear

amplification method, thereby enhancing its practical

applicability in industrial fields.

ACKNOWLEDGEMENTS

The research has been conducted within the

industrielle Gemeinschaftsforschung [collective

industrial research] (IGF) project “VerStaRad:

Verschleißverhalten von Stahllaufrädern an

Regalbediengeräten” (IGF project number 23053)

basis of a decision of the German Bundestag [Federal

Parliament].

REFERENCES

Achouch, M., Dimitrova, M., Ziane, K., Sattarpanah

Karganroudi, S., Dhouib, R., Ibrahim, H., & Adda, M.

(2022). On Predictive Maintenance in Industry 4.0:

Overview, Models, and Challenges. Applied Sciences,

12(16). https://doi.org/10.3390/app12168081

Bosso, N., & Zampieri, N. (2019). Numerical stability of

co-simulation approaches to evaluate wheel profile

evolution due to wear. International Journal of Rail

Transportation, 8(2), 159–179. https://doi.org/10.1080/

23248378.2019.1672588

Braghin, F., Lewis, R., Dwyer-Joyce, R., & Bruni, S.

(2006). A mathematical model to predict railway wheel

profile evolution due to wear. Wear, 261(11-12), 1253–

1264. https://doi.org/10.1016/j.wear.2006.03.025

Große, K., Sartorius, J., & Fittinghoff, M. (2018).

Predictive Maintenance at Automatic Storage Retrieval

Machines (ASRS) with Vibration Sensors. Logistics

Journal. Advance online publication. https://doi.org/

10.2195/LJ_NOTREV_GROSSE_EN_201812_01

Heinrich, G., & Klüppel, M. (2008). Rubber friction, tread

deformation and tire traction. Wear, 265(7-8), 1052–

1060. https://doi.org/10.1016/j.wear.2008.02.016

Iwnicki, S., Nielsen, J. C. O., & Tao, G. (2023). Out-of-

round railway wheels and polygonisation. Vehicle

System Dynamics, 61(7), 1787–1830. https://doi.org/

10.1080/00423114.2023.2194544

Jendel, T. (2002). Prediction of wheel profile wear—

comparisons with field measurements. Wear, 253(1–2),

89–99.

Laile, M. M., & Fottner, J. (2021). Computing a Realistic

Load Collective for the Rail-wheel Contact of Stacker

Cranes. In 2021 The 8th International Conference on

Industrial Engineering and Applications(Europe) (pp.

46–50). ACM. https://doi.org/10.1145/3463858.346

3862

Mostofi, A., & Gohar, R. (1980). Pressure distribution

between closely contacting surfaces. Journal of

Mechanical Engineering, 22(5), 251–259.

Rücker, A., Rief, J., & Fottner, J. (2020). An investigation

of mean energy demand, performance and reference

cycles for stacker cranes. FME Transactions, 48(2),

307–312. https://doi.org/10.5937/fme2002307R

Sichani, M. (2013). Wheel-Rail Contact Modelling in

Vehicle Dynamics Simulation [Disseration]. KTH

Royal Institute of Technology, Stockholm,Sweden.

Siciliano, G., Durek-Linn, A., & Fottner, J. Optimization of

the Bottleneck Caused by Stacker Cranes in Dynamic

Hybrid Pallet Warehouses and Investigation of the

Influence of the Input/Output Area on Performance. In

12th International Conference on Simulation and

Modeling Methodologies, Technologies and

Applications (SIMULTECH 2022) (pp. 123–130).

https://doi.org/10.5220/0011313600003274

Tunna, J., Sinclair, J., & Perez, J. (2007). A Review of

wheel wear and rolling contact fatigue. Proceedings of

the Institution of Mechanical Engineers Part F Journal

of Rail and Rapid Transit, 221

(2), 271–289.

https://doi.org/10.1243/0954409JRRT72

Vollebregt, E. A., Weidemann, C., & Kienberger, A. (Eds.)

(2011). Use of "CONTACT" in multi-body vehicle

dynamics and profile wear simulation: initial results.

Yang, Y., Ling, L., Wang, J., & Zhai, W. (2023). A

numerical study on tread wear and fatigue damage of

railway wheels subjected to anti-slip control. Friction,

11(8), 1470–1492. https://doi.org/10.1007/s40544-022-

0684-8

Yu, M., & Fottner, J. (Eds.) (2024). Entwicklung und

Validierung einer praxisgerechten Methode zur

Verschleißberechnung im Rad-Schiene-System von

Regalbediengeräten (German). Logistics Journal.

Zhang, J., Xu, B., & Guan, X. (2013). A combined

simulation procedure for wear assessment of the HXN5

locomotive. Wear, 314(1-2), 305–313. https://doi.org/

10.1016/j.wear.2013.11.042

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

200