Building a Decision Landscape Model for Software Development: From

Empirical Insights to Formal Theory

Hannes Salin

School of Information and Engineering, Dalarna University, Borl

ange, Sweden

Keywords:

Decision-Making, Value Stream Mapping, Formal Model, Software Engineering, Software Development.

Abstract:

Value stream mapping is a well known method for identifying waste and bottlenecks in production processes.

It is also used in the software engineering context, to map value streams of different processes in software

development. By regarding decision-making processes as value streams, we can describe and further analyze

decision-making ﬂows in an organization for optimization such as reduced lead times or decision making

efﬁciency. Using empirical data from three different software development organizations in Sweden, we

develop a formal model to describe decision-making ﬂows in a software development organizational context,

in a compact and systematic syntax. Our formal model can thus be used for analyzing decision-making ﬂows

and support management in better understanding how decisions are made within their organizations.

1 INTRODUCTION

As for any organization in software engineering that

produces value of some sort, decision-making is

crucial, e.g. for improved managerial perspectives

with metrics (Salin et al., 2022), architectural de-

sign (Razavian et al., 2019), or product development

(Mendes et al., 2018). In an organization with many

different collaborative teams, units and processes, it

may be complicated to fully understand the overall

decision-making landscape, namely the mapping of

all necessary decision ﬂows that needs to be executed

for efﬁcient or optimal productivity. For this reason,

it would be beneﬁcial to identify and map decision

processes and associated bottlenecks in the organiza-

tion, in order to better understand how these ﬂows can

be optimized. Also, it might be the case that formal

decision-making processes are described in documen-

tation and policies, but works differently in practice.

For that reason, organizations need to map such cur-

rent processes to better understand their own work-

ﬂows.

Value stream mapping (VSM) is a powerful tool

in the lean (and agile) toolbox, which also has been

shown to be suitable for managerial analysis (Eleft-

herios Andreadis and Kumar, 2017). VSM is a sys-

tematic approach used to visualize and analyze the

ﬂow of a process, identifying inefﬁciencies, bottle-

https://orcid.org/0000-0001-6327-3565

necks, and potential improvements. Such mapping

supports decision-making for prioritizing and coordi-

nating continuous improvement initiatives, by map-

ping each step of the workﬂow and thereby distin-

guishing value-added from non-value-added activi-

ties. The typical method to perform a VSM is via

workshops (M

akinen, 2024), although different qual-

itative and/or quantitative methods and other type

of documenting activities works as well. VSM is

predominantly used in manufacturing and operations

contexts, however, also used in software engineering

and DevOps contexts (Botero et al., 2024; M

akinen,

2024; Murphy and Kersten, 2020; Tankhiwale and

Saraf, 2020). The term value is broad and can include

anything that the organization regards (and deﬁne) as

valuable, either in time, monetary units or other type

of metrics. The value of a decision outcome would be

one example.

Given a compact and understandable formal

model for decision-making processes in any context

of software engineering, we aim to provide a sup-

portive tool to perform a VSM directed towards de-

cision value ﬂows, easy to analyze for optimizations.

Moreover, by introducing a formal model as basis

for running a VSM, it could potentially be analyzed

with more depth compared to standard approaches us-

ing multiple step workshops or ﬂow-chart based pro-

cesses with natural language descriptions (Qin and

Liu, 2022; Meudt et al., 2017). Since VSM is not

necessarily only suited for one context or domain, any

Salin, H.

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory.

DOI: 10.5220/0013457300003964

In Proceedings of the 20th International Conference on Software Technologies (ICSOFT 2025), pages 15-26

ISBN: 978-989-758-757-3; ISSN: 2184-2833

improvements that support such approach would be

general in nature.

1.1 Paper Outline

The rest of the paper is outlined as follows: the re-

maining of this section includes related work and

formulated research question. Section 2 describe

the chosen methodology and theoretical foundation,

whereas section 3 presents the results from the empir-

ical data collection. Section 4 describe the developed

model, and section 5 the discussion including threats

to validity and future work. Section 6 concludes our

research.

1.2 Related Work

We underscore that our research is not within the

ﬁeld of traditional decision theory (Kumar, 2025),

nor the cognitive sciences in decision-making (Wall-

sten, 2024). Instead, our work is in particular focused

on the ability to transform observed decision-making

processes in software engineering organizations into

compact and comprehensible formal language. In

contrast, much research is made in general methods

for logic of decision-making, e.g. a general model

for decisions under incomplete knowledge (Markovi

et al., 2024), or different decision-making methods

for artiﬁcial intelligence and systems such as prompt-

ing and reinforcement learning (Yang et al., 2023).

Closest to our approach is the Managerial

Decision-making Description Model (MDDM) that

has been proposed, which can be used for visualiza-

tion of decision-making processes that changes the

business structure states (Kunigami et al., 2019). Fo-

cus for MDDM is on graphical representations via di-

agrams connecting agents’ goals, events, objectives

and other business components. However, the model

does not provide a compact mathematical syntax for

describing the decision-making landscape.

Regarding supportive methods to VSM for

decision-making mapping, discrete events simulation

has been proposed with VSM towards investment de-

cisions (Helleno et al., 2015), and another type of sim-

ulation to enhance lean optimization calculations (Liu

and Yang, 2020). One study implemented a multi-

agent system for dynamic VSM for manufacturing

systems, where the proposed method consisted of a

cyber-physical system with hardware components and

sensors (Huang et al., 2019). However, none of these

approaches has utilized a formal syntax model for de-

scribing decision-making processes.

Finally, a strict formal approach is the Burrows-

Abadi-Needham (BAN) logic for analyzing and rea-

son about authentication in security protocols (Bur-

rows et al., 1990). However, decision-making pro-

cesses are not in scope for BAN logic, although our

proposed model uses a similar formalized syntax with

deﬁned relations in order to systematically describe

complex processes. Thus, to our knowledge, there

are no proposed formal models to describe decision-

making ﬂows using a more syntax-based approach,

with the aim to support VSM.

1.3 Research Question

Given the importance of understanding a software de-

velopment organization’s current decision landscape,

we need a model where decision boundaries, un-

clear mandates and other challenges can be identiﬁed.

Also, to better optimize the organization, a decision

landscape map is required, thus a model for how to

efﬁciently construct such mapping is needed. A for-

mal model is a mathematical or logical representation

of a system or phenomenon, deﬁned by precise rules

and structures to analyze, predict, and/or verify its be-

havior. For that reason, we formulate the following

research question:

• RQ1: How can a formal model of decision-

making in software development organizations be

used for supporting value stream mapping?

By constructing a formal model, our study aims to

provide a compact way to describe decision-making

processes as a supporting tool for VSM, hence ensur-

ing practical applicability for studying software de-

velopment organizational decision-making. Thus, we

seek a way for engineering managers to better under-

stand and optimize their organizations using formal

language to describe current decision-making ﬂows.

2 METHOD

The chosen research methodology follows an induc-

tive approach aimed at theory building from empiri-

cal data (Sjøberg et al., 2008), collected in several in-

stances of the software development context (different

roles from three Swedish software engineering com-

panies). The approach is exploratory in the sense of

identifying current decision-making processes, which

then render a theoretic model construction. Data was

gathered through semi-structured interviews and an

open question survey to capture decision-making pro-

cesses, potential conﬂicts, and dependencies across

different organizational teams, roles and units. Target

companies were chosen via convenience sampling.

An iterative process of qualitative pattern identiﬁca-

tion, using thematic-inspired analysis, was used to

ICSOFT 2025 - 20th International Conference on Software Technologies

summarized a set of key insights. These insights were

then used to develop the proposed formal model of

decision-making.

The aim is to develop a descriptive model since its

primary goal is to provide a compact but structured

language to represent and analyze observed decision-

making processes (Wang et al., 2004). It should cap-

ture relationships and to some degree the dynamics

of decisions without prescribing how these processes

should ideally function or be optimized. Therefore,

unlike normative models, it does not aim to deﬁne op-

timal decision-making practices but instead serves as

a tool for understanding and documenting real-world

workﬂows in conjunction with VSM practices.

2.1 Theoretical Foundation

Based on the guidelines in theory building for soft-

ware engineering (Sjøberg et al., 2008), a theory

should be presented with certain archetypes. We

have chosen to use two of the deﬁned concepts: ac-

tors and activities, where actors are different roles

in an organization and activities refers to different

decision-making relations, e.g. making a success-

ful/unsuccessful decision and so on. Moreover, we

use the notion of constructs, propositions, explana-

tions and scope to construct and present the proposed

model. Constructs are explicit classes or attributes,

e.g. a design, a concept or an organizational entity. A

proposition is a statement aligned with one or many

constructs, e.g. ”decisions in a team are not vio-

lated by a ﬁrst line manager”. Explanations are de-

scriptions of why the propositions are formulated, and

scope details the motivation for the whole theory.

We construct the decision-making model on the

basis of bounded rationality (Simon, 1955) for how

agents behave, and extends this foundation by in-

corporate Hackman’s unit authority theory (Hack-

man, 1986). By combining bounded rationality

as the underlying principle with inspiration from

Hackman’s authority classiﬁcations, our model cap-

tures the nuances of hierarchical and collaborative

decision-making.

2.1.1 Bounded Rationality

The notion of bounded rationality is the assumption

that individuals and teams make decisions within the

limits of their knowledge, resources, and cognitive ca-

pacities (Simon, 1955). We use bounded rationality

as a foundational principle in our model, recognizing

that decision-makers in software development orga-

nizations cannot evaluate all possible options exhaus-

tively due to time constraints, limited information,

and complex inter-dependencies. Instead of seeking

optimal solutions, we assume the decision-maker in-

stead aims for satisfactory outcomes by using heuris-

tics. This assumption aligns with the realities of ag-

ile and dynamic environments in software engineer-

ing, where exhaustive decision-making is impracti-

cal (Erbas and Erbas, 2009; Moe et al., 2012). Al-

though bounded rationality and similar rational de-

cision models are the commonly used assumptions

used in software engineering (Ralph, 2018), other

standpoints exists as well such as empirical natural-

istic theory (Pretorius et al., 2024). However, this

is more studied towards software design decision-

making context, whereas our study focus on the soft-

ware development organizational context.

2.1.2 Hackman’s Theory

Hackman’s unit authority theory (Hackman, 1986)

classiﬁes decision-making authority within teams into

three levels: managerial control (decisions are cen-

tralized with managers), shared control (authority

is distributed between managers and team mem-

bers) and self-control (teams operate autonomously

with full decision-making power). This classiﬁcation

provides a conceptual foundation for understanding

how authority impacts team dynamics and decision-

making processes. The theory has been used pre-

viously in the agile software engineering context to

study team autonomy (Moe et al., 2021).

3 RESULTS

In this section we describe the resulting data collec-

tion procedure, along with the data. We summarize

the ﬁndings in the data into a set of key insights,

which are later used for motivating the model. These

key insights describes identiﬁed themes from the data,

i.e. expressions and descriptions from the participants

that align within certain themes.

3.1 Data Collection

The data collection included three Swedish organi-

zations with software development as part of their

operations: two in banking/ﬁnancial institutions (re-

ferred to as company A and company B, respectively)

and one public sector agency. These companies were

selected by convenience sampling, and all three had

similar product based organizations with agile soft-

ware development.

Semi-structured interviews and one online survey

was created for collecting data about current decision-

making processes. The survey was open-ended with

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory

a free text answer ﬁeld, where participants was asked

to describe what roles that made what type of deci-

sions, and if there were any necessary decisions that

could not be made for a certain role, and how these

were handled in the organization. The survey was

sent to N = 61 employees in total after a convenience

sampling across the three companies. The sampling

stemmed from initial discussions with representatives

from each company, which directed/recommended

subsets of employees to include in the data collection

phase. Four different roles were represented (software

developers, architects, project managers, engineering

managers) with n = 34 respondents in total. The sur-

vey questions are detailed in Tab. 1 and was further

elaborated in the interviews, i.e. the interview proto-

col was not different from the survey questions. The

survey had an introductory text highlighting that all

questions were related to decision-making processes

in the organization and not towards cognitive aspects;

one example was also given to underscore this.

Four interviews were conducted, with two soft-

ware developers (one from the public sector agency

and one from bank/ﬁnance company B), one architect

(bank/ﬁnance company A) and one engineering man-

ager (bank/ﬁnance company B). All interviews were

remote and scheduled for 20 minutes each. All inter-

viewees were also respondents to the survey.

Table 1: Questions stated in the survey, and used for elabo-

ration in the semi-structured interviews.

ID Question

Can you describe how decisions are made

in your role, from the need of a decision to

when it is executed?

Can you describe what decisions you need

but are not within your mandate?

Can you describe what decisions you may

need to take for someone else that does not

have the same mandate?

Can you describe what challenges you face

during decision-making processes in your

organization?

If you cannot take a decision immediately,

can you describe the steps you need to take

in the organization in order to make the de-

cision?

From the respondents of the survey, n

= 17 were

from the public sector agency, n

= 9 from company

A, and the remaining n

= 8 from company B. We

did not collect data on the respondents’ gender, age or

other personal data. The validity of the sample cannot

be used for generalization, but rather indicative.

3.2 Data Summary

From the survey results we collected and grouped dif-

ferent clusters of similar themes. From the clustering

we then formulated different insights, representing

each cluster. The discovered clusters were labeled:

same role - different authority, no decision, lack of in-

formation, need for escalation, decision dependency;

and denoted KI

− KI

respectively. We continued to

ﬁll these clusters with data from the interviews. One

additional cluster, denoted KI

, was discovered from

the interviews: enforced decisions. We summarize

the clusters into key insights that were discovered dur-

ing the data collection phase in Tab. 2. We acknowl-

edge that these insights have their limitations due to a

small-size sample, and further data collection would

be helpful to reﬁne the development of future versions

of the model.

Table 2: Key insights extracted from the data collection

phase.

ID Key insight

One context (team, role) can contain sev-

eral employees with the same appointed

role, but with different decision mandate

on the same decision type.

Employees with same roles and same man-

date might stall in a decision-making pro-

cess. The same can happen even if one role

has higher mandate than the other, and no

decision is made.

In several cases, a decision could be stalled

due to lack of information or knowledge of

the decision-maker. The typical implica-

tion was that an investigation and/or meet-

ings were scheduled to analyze the deci-

sion further.

Similar to KI

and KI

, in several occasions

a stalled decision could not proceed even

though more information was gathered. In

these cases, the typical scenario was esca-

lation to management and/or architects for

ﬁnal decision-making.

In several cases, a decision-maker was hes-

itant to make a decision before another de-

pendent decision was made. This could

happen both within a team or between dif-

ferent organizational units.

Decisions can be enforced, by actors that

lack the sufﬁcient mandate. Decisions can

also be overridden by actors with- and

without sufﬁcient mandates.

ICSOFT 2025 - 20th International Conference on Software Technologies

4 MODEL DEVELOPMENT

This section describes the proposed formal model for

describing decision-making processes in a software

development context. We use standard set theory to

describe constructs, and relations using the notation

a ⊕b where a, b are any constructs and ⊕ any deﬁned

relation operator within the model. A construct is any

set or element of a set deﬁned in model. The basis for

our chosen notation is inspired by the work of (Wang

et al., 2004).

4.1 Decision-Making Context Boundary

Let C represent a speciﬁc context, such as a develop-

ment team, architecture role, IT infrastructure team or

a managerial context. The Decision-Making Context

Boundary (DCB) for context C, denoted as DCB(C),

is the set of all decisions that can be made by the ac-

tors operating within C, subject to the constraints and

scope of C. To avoid vagueness of what a context is,

we formally deﬁne it using actors and mandate sets.

Deﬁnition 1 (Actor Set). Let a

be an actor, i.e. a

role within an organization with speciﬁed task assign-

ments. For the contexts in this model we use actors

such as system developer, architect, agile actor, man-

agerial actor. The set of all a

that belongs to a speciﬁc

decision-making context is denoted A and called actor

set.

Deﬁnition 2 (Mandate Set). Let a tuple (a

, (d

, m

))

be a mandate description, which specify the level of

mandate m

∈ N actor a

has for decision d

. The

positive integer m

thus represents the hierarchical

authority level of actor a

where higher numbers indi-

cate greater decision-making power. For (a

, (d, m

))

and (a

, (d, m

∗

)) where m

> m

∗

then a

has a higher

authority level than a

and can override a

in deci-

sion d. The set of all tuples that belongs to a speciﬁc

decison-making context is denoted M and called the

mandate set.

Deﬁnition 3 (Context). Let C be a context within a

software engineering organization. A context C is de-

ﬁned as a tuple C = (A, M) where A is the actor set

(or roles), and M the mandate set given to the actors.

From the underlying theoretical assumptions of

bounded rationality and Hackman’s theory, we are

able to deﬁne three constraints for an agent when

making a decision: authority, knowledge and resource

constraints. These are necessary to be managed by the

decision-making agent in order to make a decision:

Deﬁnition 4 (Context Decisions). We call d ∈ D a de-

cision, where D is the universal decision space of all

possible decisions in the organization. The element

⊥∈ D represents the absence of a decision, signifying

that no explicit action or choice has been made within

the context. For a given decision d that is valid to ex-

ecute in context C, we denote it as d ⇌ C, unless there

are no constraints on d. The following constraints are

deﬁned:

• Authority Constraint: d can only belong to

DCB(C) if d is within the mandate deﬁned in M

for an actor in A.

• Knowledge Constraint: d can only belong to

DCB(C) if the necessary information for d is ac-

cessible to the actors in A, i.e. information that

enables an informed decision instead of just make

a decision by chance.

• Resource Constraint: d can only belong to

DCB(C) if the resources required for d are avail-

able within the scope of C, i.e. people, organiza-

tions or assets to be included in the decision.

If d is constrained by any of the three constraint types,

we denote that by d ⇀ C, meaning that this decision

attempt will not be valid in C (unsuccessful).

We now deﬁne the DCB(C) as the set of all deci-

sions d for which d ⇌ C, satisfying the context con-

straints:

Deﬁnition 5 (Decision-Making Context Boundary).

DCB(C) = {d ∈ D | d ⇌ C} (1)

where D is the universal set of all possible decisions

in the system or organization, d an individual deci-

sion and C a speciﬁc context, such as a team, organi-

zational unit, or domain.

For instance, let C be an unrealistic (for illus-

trative purposes) context of a developer team that

only has the ability to prioritize a backlog, with

actor set A = {system developer, scrum master}

and a corresponding mandate set M =

{(system developer, (d, 2)), (scrum master, (d, 1))},

where d is a decision to prioritizing the backlog. In

this DCB(C) the scrum master has less mandate in

decisions regarding the backlog. An extension to this

context would be to add tuple (product owner, (d, 3))

indicating that in this particular context the product

owner has the right to ﬁnal decisions of the backlog

over the rest of the team. The ﬁnal DCB(C) would

then be: DCB(C) = {d, ⊥} over the sets A and M.

We note that for an organization ORG, we can de-

scribe the complete decision landscape by:

DCB

ORG

[

i=1

DCB(C

) (2)

where DCB

org

represents the set of all valid decisions

across all contexts {C

, . . . ,C

} in the organiza-

tion.

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory

Note that mandate sets are not exclusive, i.e. for

an actor a

∈ A

that belongs to C

may have de-

cision authority for a decision in multiple contexts.

For example, given a decision d ∈ DCB(C

) but also

d ∈ DCB(C

) the actor a

may have decision man-

dates m

in C

and m

in C

, and m

̸= m

. This cap-

tures a managerial role that can have limited decision

power in one context for d but full mandate in another

context.

4.2 Decision Conﬂicts

In the case where different actors have the same man-

date level m

, say (a

, (d, m

)) ∈ M

and (a

, (d, m

)) ∈

there might be possible conﬂicts in the decision-

making process. For a subset C

= (A

, M

) to a

context C, we deﬁne the decision conﬂict function

f : C

× D → D that either render a decision d ∈ D

or the no decision ⊥∈ D. This function represents the

process where a decision is made (thus to be executed

in a context), including mandate conﬂicts.

Deﬁnition 6 (Decision Conﬂict Function). Let C

, M

) where A

⊆ A and M

⊆ M for a certain con-

text C = (A, M). Let f : C

× D → D be function de-

ﬁned as:

f (C

, d) =











if ∃a

, a

∈ A

s.t (a

, (d, m

)) ∈ M

, (d, m

)) ∈ M

and m

= m

d if ∃a

∈ A

s.t (a

, (d, m

)) ∈ M

and m

> m

for all i ̸= k

(3)

where d

is a particular decision d ∈ D with proba-

bility δ and has the possibility to yield ⊥.

Note that the decision mandate hierarchy holds

trivially when no conﬂicts arise. The probabilistic

outcome d

represents that if there is a conﬂict, it

can be resolved in multiple ways. One such exam-

ple is when an actor outside the current DCB(C) may

interfere and make a decision that is not normally

within the context decision space (e.g., upper man-

agement). In these cases, the likelihood of d

resolv-

ing to ⊥ or a speciﬁc decision, depends on the used

conﬂict resolution strategy or external organizational

policies. Hence, it is up to the analyzing organization

to deﬁne the probability distribution for δ associated

to each possible d. We illustrate this function as fol-

lows: in ORG it is concluded that for a certain context

= (A

, M

) there is a risk of decision conﬂict for

decision d. Given the current policies and empirical

knowledge, it is estimated that f (C

, d) = d

′

is given

by Pr[d =⊥] = 0.5 and Pr[d

′

= d] = 0.5, i.e. the deci-

sion resolves to either no decision or the desired deci-

sion d with a uniform distribution. Therefore δ = 0.5

when resolving d into d

′

, and similarly δ = 0.5 when

resolving d into no decision.

To summarize, to model a particular decision

outcome, we use the decision conﬂict function

f (C

, d) = d

′

such that d

′

= d, d

′

= d

for some d

∈ D

with probability δ, or d

′

=⊥.

4.3 Relation Deﬁnitions

We already deﬁned the ⇌ and ⇀ relations, but we

also need several more to fully describe decision

ﬂows. In this section we deﬁned four additional re-

lations in the model, derived from the key insights.

4.3.1 Enforced Decisions

It might happen that a decision d for which it holds

that d ⇌ C

in DCB(C

) where C

= (A

, M

), but

is enforced and executed by a

that belongs to A

= (A

, M

) with corresponding DCB(C

). Regard-

less if d ⇀ C

or not due to violations to the con-

straints in Def. 4 it might be the case the decision is

executed anyway. This could happen if the decision-

maker has high mandates in many other decisions (but

not necessarily in d) or enforce the decision by also

violating organizational constraints. As an example,

a very high inﬂuencing employee could manipulate or

make decisions without anyone noticing. In order to

capture a violating decision d into another context C

where d does not belong, we denote that by the ⇁

relation:

Deﬁnition 7. Let d be a decision such that d ̸∈

DCB(C) due to violation of any of the constraints in

Def. 4. Then if d is enforced by actor a

in DCB(C),

we denote that relation as d ⇁ (C, a

4.3.2 Decision Dependencies

Decision dependencies represent situations where a

decision d in one context C

is dependent upon an-

other decision d

′

in context C

can be the same

as C

as well). These dependencies often arise in

software engineering organizations when intercon-

nected teams or units must align their decisions to

achieve shared objectives, such as a development

team depending on an architectural decision to pro-

ceed. Moreover, from key insight KI

we conclude

the need for such relation in the model. Capturing

these relationships with the relation d ← d

′

provides

a way to model and analyze the interplay between de-

cisions within and across contexts.

Deﬁnition 8. Let d ∈ C

, d

′

∈ C

be two decisions in

any two contexts C

and C

. If there exists a depen-

dency between d and d

′

, i.e. d cannot be made before

ICSOFT 2025 - 20th International Conference on Software Technologies

′

is decided, we denote that relation as d ← d

′

where

the left-hand side is the dependent decision.

4.3.3 Feedback-Driven Decisions

From the key insights we identiﬁed an reoccurring

theme of decisions that required several feedback

loops before execution (KI

). Especially when the

information and/or knowledge of the decision-maker

was lacking, such feedback loop is needed. There-

fore, due to its common nature, we introduce the rela-

tion of a decision requiring feedback, denoted d ⟳ a

where a

is the actor that is requested for feedback.

If a decision d cannot be decided upon due to lack of

information, it corresponds to this relation.

Deﬁnition 9. Let d be a decision for which d ⇀ a

due to the knowledge constraint, we denote that rela-

tion as d ⟳ C if there is a request of retrieving more

information for decision d from actor a

4.3.4 Decision for Escalation

A typical relation identiﬁed in the study were esca-

lated decisions (KI

), namely that an actor could not

make a decision within its own context, hence esca-

lated the decision to someone with a higher mandate

level (often a manager or architect). In a sense, this

relation occurs trivially in any organization with au-

thority levels, and aligns with Hackman’s theory. This

relation is naturally cross-context and we deﬁne it as

follows:

Deﬁnition 10. Let d be decision for which d ⇀ C. If

the decision is escalated to another actor a

we de-

note that relation as d ↑ a

4.4 Summary of Relations

A relation in the model translates to a state, namely

a state within a context where a particular outcome is

about to be reached. For example, d ⇌ C indicates

that a decision d will be successful if executed within

C (not that d was successfully executed). Similarly,

d ⇀ C indicates that d will not be able to be success-

fully executed in C, and d ↑ a

indicates that d is go-

ing to be escalated to a

as a next step. All deﬁned

relations are summarized in Tab. 3.

4.5 Model Syntax

To describe decision-making processes using the pro-

posed model, we introduce a syntax that captures the

ﬂow of decisions within organizational contexts. This

syntax includes both operators and symbols to rep-

resent sequential, conditional, and iterative ﬂows, as

Table 3: Summary of decision relations in the proposed

model.

Notation Relation/Construct

d ⇌ C Valid decision in context C

d ⇀ C Invalid decision in context C

d ⇁ (C, a

) Enforced decision into context C by

actor a

where d ̸∈ DCB(C)

d ⟳ a

Decision requires feedback from ac-

tor a

d ↑ a

Decision escalated to actor a

d ← d

′

Dependency for d ∈ C to d

′

∈ C

′

⊥ No decision

well as termination states. The syntax is pseudo code

inspired, thus universally understandable. A relation

or a combination of relations and/or symbols and/or

operators is called an expression and is denoted ⟨exp⟩.

The following operators and symbols are deﬁned for

constructing decision ﬂow expressions:

START: Represents the initial condition or state of

the decision-making process, which sets a starting

point of the ﬂow and provides the starting context.

Example: START (d ⇀ C

) THEN d ⟳ a

UNTIL d ⇌ C

THEN: Represents a sequential ﬂow, where one re-

lation follows another.

Example: d ⇀ C

THEN d ⟳ a

IF: Represents a conditional branch based on con-

straints or conditions.

Example: IF d ← d

′

THEN d

′

⇌ C

OTHERWISE: Represents an alternative branch

when the condition in IF is not satisﬁed.

Example: IF d ← d

′

THEN d

′

⇌ C

OTH-

ERWISE d

′

⇀ C

UNTIL: Represents an iterative ﬂow that continues

until a speciﬁc condition is met.

Example: d ⟳ a

UNTIL d ⇌ C.

AND: Represents parallel dependencies, where mul-

tiple relations must hold simultaneously.

Example: d

⇌ C

AND d

⟳ a

OR: Represents alternative paths where at least one

relation must hold.

Example: d

⟳ a

OR d

↑ a

NOT: Represents the negation of a relation or con-

dition. We use the equivalence relation ≡ to ex-

plicitly show a negated relation.

Example: NOT d ⇌ C indicates that d can-

not be valid made in context C. Can also be

expressed as NOT d ⇌ C ≡ d ⇀ C.

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory

CONFLICT: Represents a case of a decision con-

ﬂict that occurs. This implicitly indicates the need

for computing the decision conﬂict function.

Example: d CONFLICT (A, M) indicates

that d has a conﬂicting situation given actors

in A with mandates speciﬁed in M.

RESOLVE: Represents when the decision conﬂict

function f is used for yielding a decision outcome

given a conﬂict.

Example: d RESOLVE (A, M) → d

indi-

cates that d was resolved into d

, where d

is determined by a given probabilistic func-

tion speciﬁc to the organization.

END: The end of a decision ﬂow is indicated using

END, together with either d → □ (successful ex-

ecution) or d ←⊥ (no decision).

Example: d ⇌ C THEN d → □ END.

Example: d ⇀ C THEN d →⊥ END.

Parentheses: Used to group sub-expressions and

deﬁne precedence in decision ﬂows. Follows the

conventional rules for parentheses for logic ex-

pressions.

Example: d ⇌ C

THEN (IF d ← d

′

THEN

′

⇌ C

OTHERWISE d

′

⇀ C

To illustrate the usage of the syntax, consider a

scenario where a decision d

is needed in context C

but is invalid due to information constraints, requires

feedback from actor a

, escalates to actor a

if un-

resolved, and concludes with either successful execu-

tion or no decision:

START (d

⇀ C

)

THEN (d

⟳ a

UNTIL d

⇌ C

)

OTHERWISE (d

↑ a

)

THEN IF d

⇌ C

THEN d

→ □

OTHERWISE d

→⊥

END.

Another example illustrates the process where a

decision d

(e.g. architectural decision in a team) is

not valid due to a dependency to d

(e.g. architect

team approval):

START (d

⇀ C

)

AND (d

← d

)

THEN (d

↑ a

UNTIL d

⇌ C

)

THEN d

→ □

THEN d

⇌ C

THEN d

→ □ END.

These examples show the compactness and build

up to sub expressions within a complete expression

for an analyzed process. As seen in both examples,

the THEN operator works as an implication and rep-

resents a logical next step in the process. This com-

bined with a VSM, where details on why certain ex-

pressions are reached, would thus give a compact yet

comprehensive mapping of a decision ﬂow.

4.6 Axiomatic Rules

To ensure logical consistency in the model, we also

introduce a set of fundamental rules. These are con-

sidered valid in the model given the caveat that they

also assume a simpliﬁed worldview, e.g. strict se-

quential steps in a process and no detailed consider-

ation to temporal aspects of a process. We use the

standard mathematical notation of =⇒ to show that

a certain expression ⟨exp⟩

logically leads to another

expression ⟨exp⟩

, namely: ⟨exp⟩

=⇒ ⟨exp⟩

Deﬁnition 11 (Dependency Resolution Rule). A de-

pendent decision cannot proceed unless its prerequi-

site decision is completed.

d ← d

′

=⇒ (d ⇀ C OR d

′

⇀ C

′

)

This ensures that decision d cannot be valid in context

C unless the dependent decision d

′

is valid in context

′

Deﬁnition 12 (Feedback Resolution Rule). A deci-

sion requiring feedback must resolve its feedback loop

before proceeding.

(d ⟳ a

UNTIL d ⇌ C) =⇒ d ⇀ C OR d ⟳ a

where a

is another feedback actor. This ensures that

a decision in a feedback loop cannot proceed to va-

lidity until the necessary feedback is addressed.

Deﬁnition 13 (Escalation Termination Rule). An es-

calated decision must either reach a valid state or ter-

minate with ⊥.

d ↑ a

=⇒ (d ⇌ C

′

OR ⊥)

This ensures that escalation leads to a resolution, ei-

ther by validating the decision in a higher context C

′

or terminating without resolution.

Deﬁnition 14 (Mutual Exclusion Rule). A decision

cannot be escalated and resolved within the same

context at the same time (simplifying temporal as-

pects), thus we have the implication that.

d ⇌ C =⇒ NOT d ↑ a

for any actor a

∈ A where C = (A, M).

ICSOFT 2025 - 20th International Conference on Software Technologies

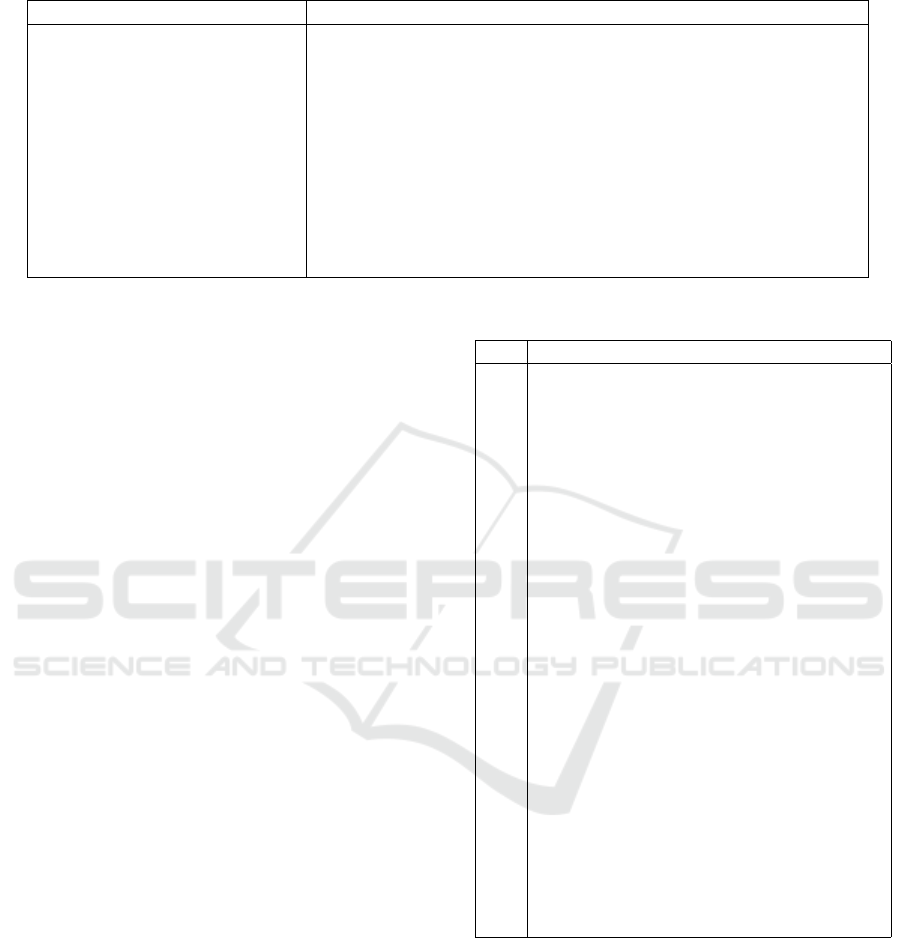
Table 4: Summary of the decision ﬂow syntax, where ⟨exp⟩ is any valid expression constructed from the model.

Syntax Description

START ⟨exp⟩ Speciﬁes the initial condition of the decision process.

⟨exp⟩ THEN ⟨exp⟩ Sequential ﬂow, where one expression follows another.

IF ⟨condition⟩, THEN ⟨exp⟩ Conditional branch based on a speciﬁed condition.

OTHERWISE ⟨exp⟩ Speciﬁes the alternative path if the condition in IF is not met.

⟨exp⟩ UNTIL ⟨condition⟩ Iterative ﬂow that continues until a speciﬁc condition is satisﬁed.

⟨exp⟩ AND ⟨exp⟩ Parallel dependencies, where both expressions must hold.

⟨exp⟩ OR ⟨exp⟩ Alternative paths, where at least one expression must hold.

NOT ⟨exp⟩ Negation of an expression or condition.

⟨exp⟩ THEN □ END Indicates the decision process ends with successful execution.

⟨exp⟩ THEN ⊥ END Indicates the decision process ends with no decision.

Parentheses () Groups sub-expressions and deﬁnes precedence.

Deﬁnition 15 (Loop Consistency Rule). A decision

d that depend on decision d

′

cannot at the same time

have a dependency relation for d

′

; either d is depen-

dent on d

′

or vice versa, otherwise there will be an

inﬁnite loop of dependency.

d ← d

′

=⇒ NOT d

′

← d

We acknowledge that these axiomatic rules are not

complete nor exclusive; in this preliminary work we

provide a ﬁrst attempt to construct the model which

needs to be further tested and evaluated.

4.7 Propositions and Explanations

In this section we summarize the developed model’s

propositions and associated explanations, based on

the nomenclature and theory presentation structure in

(Sjøberg et al., 2008). These are summarized in Tab. 5

and Tab. 6. Explanations are associated to the propo-

sitions of the theory, i.e. the model. The rationale is to

have a sufﬁciently good motivation to the formulated

proposition.

4.8 Scope

The scope of the model is that it is designed to cap-

ture and analyze decision-making processes within

software development organizations, using a compact

and efﬁcient syntax, as a supportive tool in VSM ac-

tivities. The model includes the capture of hierar-

chical, cross-context, and dependency-related chal-

lenges. While the model is grounded in the software

engineering domain, its principles could possibly be

generalized to other knowledge-intensive ﬁelds with

similar organizational dynamics. The model’s pri-

mary scope is thus to complement VSM activities and

thereby provide insights into decision-making con-

straints, conﬂicts, and dependencies, enabling organi-

zations to identify and address inefﬁciencies in their

decision landscapes.

Table 5: Formulated propositions for the developed model.

ID Proposition

Explicitly modeling decision dependencies

and constraints enhances the the structural

and relational understanding of decision-

making processes.

Using pseudo-code syntax enables system-

atic mapping and analysis of decision ﬂows

across multiple organizational contexts, sup-

porting consistent representation of diverse

decision processes.

Using actor sets, mandate sets, and context

boundaries with pseudo-code syntax allows

for a compact and precise representation of

decision processes, reducing ambiguity in

process analysis.

Using authority, knowledge, and resource

constraints, along with mandate sets, enables

the model to identify factors impacting deci-

sion validity.

Integrating the model with VSM approaches

supports the identiﬁcation of process waste

in decision-making workﬂows.

Using explicitly deﬁned relations such as

dependencies, feedback loops, escalations,

enforced decisions, systematically captures

both linear and non-linear decision-making

ﬂows.

5 DISCUSSION

In our model, Hackman’s framework is used as ba-

sis for the design of the mandate set M by highlight-

ing the hierarchical relationships and distribution of

decision-making power within and between contexts.

For example, contexts operating under shared control

often experience decision conﬂicts that require reso-

lution mechanisms, which our decision conﬂict func-

tion f addresses. In our model we can provide a more

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory

Table 6: Explanations for the propositions of the developed

model.

ID Explanation

Explicitly modeling decision dependencies

and constraints provides an overview of th

whole process. This is particularly im-

portant for addressing scenarios like KI

where decisions are delayed due to unre-

solved dependencies, however, all insights

-KI

indicate the need for a structured

way to model a decision path.

Using pseudo-code syntax introduces a

standardized representation of decision

ﬂows, making it easier to analyze, repli-

cate, and communicate decision-making

processes across different contexts. Such

syntax is natural in software engineering,

and allows for potential usage in other for-

mal methods or tools for automatic syntax

validation.

By deﬁning actors and mandates as sets,

with context boundaries, provide a struc-

tured (mathematical) way to model de-

cision landscapes by capturing roles, re-

sponsibilities, and constraints in decision-

making, since these are fundamental con-

cepts in organizational structures.

Authority, knowledge, and resource con-

straints are key factors that inﬂuence de-

cision validity, as motivated by KI

-KI

By integrating these constraints, the model

thus enables the identiﬁcation of barriers in

the decision-making process.

Integrating the model with VSM supports

the identiﬁcation of process waste, such as

delays, hinders and unnecessary steps, by

using the compact notation of the model

with the practical application of VSM ap-

proaches. This explanation draws futher on

lean management principles that empha-

size waste reduction through process anal-

ysis.

Explicitly deﬁned relations, such as depen-

dencies, feedback loops, escalations, and

enforced decisions, allow for the system-

atic representation of both linear and non-

linear decision ﬂows, capturing the com-

plexity of real-world processes. This ex-

planation is justiﬁed by KI

-KI

granular view on the decision mandates compared to

Hackman’s framework, since we deﬁne sets of deci-

sions with corresponding pre-speciﬁed mandate lev-

els m

. This aligns well with proposition P

due to its

simple nomenclature.

The foundation of bounded rationality directly

connects to the proposed relations in the model, such

as feedback loops and escalation, since it highlights

how decision-makers operate with the different con-

straints. For example, this is captured in P

, show-

ing the need to identify factors impacting decision

validity when actors cannot exhaustively evaluate all

options. Similarly, Hackman’s theory has indeed

shaped the model’s constructs, such as decision con-

text boundaries, which relates directly to the hierar-

chical decision-making processes described in P

and

. The escalation relation explicitly reﬂects Hack-

man’s classiﬁcations of authority by demonstrating

how decisions transition from self-control to manage-

rial control when lower-level actors lack the authority

(or has other constraints) to proceed. By integrating

these theories, the model thus provides a structured

way to formalize the interplay between decisions and

decision-makers in a software engineering organiza-

tion. As shown in the developed constructs and re-

lations, it indeed provides a compact language to de-

scribe the decision ﬂows (illustrated with the exam-

ples in Sec. 4.5), hence it would be supportive in VSM

activities. Especially to describe the decision ﬂows

for both comparison and formal analysis within the

same organization. The model is yet to be evaluated

in single, but preferably multi-case studies, to show

how well the support of the model gives a decision

landscape VSM. This is our working hypothesis for

future work, and concludes proposition P

The proposed model could have potential for

automation in decision-support systems, supporting

even more efﬁcient VSM approaches. From this for-

malizing of decision-making processes with clearly

deﬁned constructs, rules, and relations, the model

could potentially be implemented algorithmically to

analyze workﬂows, identify bottlenecks, and suggest

optimizations in real-time. Additionally, its pseudo-

code-inspired syntax and logical structure would

make it suitable for integration with tools for formal

reasoning, enabling automated validation of decision

ﬂows, conﬂict detection, and different type of com-

plex patterns. Moreover, considering different type of

use cases where the model could be useful, the model

syntax and rules most likely allow for both simple and

more complex ones such as cross-organizational (thus

cross-contextual) decision ﬂows between different ac-

tors.

5.1 Example Scenario

We illustrate the syntax with another example. A

project manager (a

) needs to allocate cloud re-

ICSOFT 2025 - 20th International Conference on Software Technologies

sources for a new microservice (d

), but this re-

quires prior technical approval for security compli-

ance from the infrastructure team (a

). The decision-

making process is captured in steps: ﬁrstly, a

at-

tempts to make a decision to allocate resources with-

out approval (d

⇀ C

) and is identiﬁed to depend

on a compliance decision (d

← d

). The decision

is escalated to the infrastructure team (d

↑ a

) which

makes the decision (d

⇌ C

). If the infrastructure

team provides approval, the decision is successfully

made (d

→ □) and the project manager is now able

to proceed (d

⇌ C

). The ﬁnal decision is success-

fully made: d

→ □. However, if the infrastructure

team identiﬁes security concerns, a feedback loop is

initiated where the project manager must address the

issues before resubmitting the request. If the concerns

remain unresolved, the decision process may result in

a failure (d

→⊥). The full description in the model

is:

START (d

⇀ C

)

AND (d

← d

)

THEN (d

↑ a

UNTIL d

⇌ C

)

THEN (d

→ □)

THEN d

⇌ C

THEN d

→ □ END.

OR (d

→⊥) IF unresolved.

From this analysis, it is possible to complement

a VSM in resource allocation decisions to better un-

derstand the overall workﬂow with dependencies and

parties.

5.2 Threats to Validity

This model is subject to certain limitations that may

affect both its validity and applicability. The for-

malization make several assumptions that may not

fully capture real-world scenarios, e.g. static actor-

and mandate sets that does not fully reﬂect the dy-

namic nature of roles and responsibilities which fre-

quently change. Moreover, while the model captures

key decision relations such as escalation and feed-

back, it simpliﬁes complex interactions like resource-

and knowledge dependencies, which may require ad-

ditional constructs. Also, the model builds on logical

rules which assumes deterministic behavior, thus the

current model does not include human factors, such

as biases or conﬂicts that inﬂuence decision-making.

However, this would complicated the model signif-

icantly, and could instead be captured in the VSM

method. Finally, the sampling for the empirical data

collection is limited due to its small size and respon-

dents volume, however, it was collected from three

different companies including both private and public

sector.

5.3 Future Work

We are currently collaborating with one Swedish

company to evaluate the model, aiming for a case

study to further validate and reﬁne the model. For

future work we suggest a multi-case study with sev-

eral different companies, thus potentially different de-

cision processes, to map using VSM and the model.

For more efﬁcient analysis we also suggest that re-

search into automation of VSM analysis based on our

model should be done, including development of tools

and/or complementary support systems. Most impor-

tantly, the model itself should be further analyzed and

developed as in evaluating if additional rules or syntax

is needed. Moreover, extensions to our work could be

utility theoretic approaches where decision outcome

and prediction could be additional parameters to con-

sider.

6 CONCLUSIONS

We have provided a mathematical framework, derived

from empirical data on real-world decision-making

processes in software engineering organizations, to

be used for better analysis and optimization of orga-

nizational decision-making. The model can express

decision-making processes with a pseudo code syn-

tax and expressions based on relations between de-

cisions, actors and contexts. The model allows for

identiﬁcation of mandate hierarchies, decision ﬂows

and decision boundaries.

The proposed model is presented with the descrip-

tion of constructs, propositions with explanations,

and scope, all according to theory presentation by

(Sjøberg et al., 2008). Additionally, we also deﬁned

a model syntax and an axiomatic rule set within the

model. From the propositions P

-P

, we conclude

that an answer to RQ1 is provided, since the model

shows that it can indeed be used for describing deci-

sion ﬂows in accordance to VSM (or any other value

ﬂow technique for that matter). Although not exten-

sively tested in practice, the theoretical framework

is deﬁned. The compact notation is illustrated with

examples. We have contributed with a theoretical

model for describing and analyzing decision-making

ﬂows in software engineering organizations, which

can support managers with organizational work-ﬂow

or decision-making optimizations.

Building a Decision Landscape Model for Software Development: From Empirical Insights to Formal Theory

REFERENCES

Botero, D., Monsalve, E. S., and Pardo, C. (2024). Practices

for conducting value stream traceability in devops: A

systematic literature mapping. Periodicals of Engi-

neering and Natural Sciences (PEN), 12(3):541–564.

Burrows, M., Abadi, M., and Needham, R. (1990). A logic

of authentication. ACM Transactions on Computer

Systems (TOCS), 8(1):18–36.

Eleftherios Andreadis, J. A. G.-R. and Kumar, V. (2017).

Towards a conceptual framework for value stream

mapping (vsm) implementation: an investigation of

managerial factors. International Journal of Produc-

tion Research, 55(23):7073–7095.

Erbas, C. and Erbas, B. C. (2009). Software develop-

ment under bounded rationality and opportunism. In

2009 ICSE Workshop on Software Development Gov-

ernance, pages 15–20.

Hackman, J. (1986). The psychology of self-management

in organizations. Psychology and Work: Productiv-

ity Change and Employment/American Psychological

Association.

Helleno, A., Pimentel, C., Ferro, R., Santos, P., Oliveira,

M., and Simon, A. (2015). Integrating value stream

mapping and discrete events simulation as decision

making tools in operation management. The Interna-

tional Journal of Advanced Manufacturing Technol-

ogy, 80:1059–1066.

Huang, Z., Kim, J., Sadri, A., Dowey, S., and Dargusch,

M. S. (2019). Industry 4.0: Development of a multi-

agent system for dynamic value stream mapping in

smes. Journal of Manufacturing Systems, 52:1–12.

Kumar, R. (2025). A comprehensive review of mcdm meth-

ods, applications, and emerging trends. Decision Mak-

ing Advances, 3(1):185–199.

Kunigami, M., Kikuchi, T., and Terano, T. (2019). A Formal

Model of Managerial Decision Making for Business

Case Description, pages 21–26. Springer Singapore,

Singapore.

Liu, Q. and Yang, H. (2020). An improved value stream

mapping to prioritize lean optimization scenarios us-

ing simulation and multiple-attribute decision-making

method. IEEE Access, 8:204914–204930.

akinen, S. (2024). Enhancing software development pro-

cesses through value stream mapping–a case study.

Master’s thesis.

Markovi

c, u., Vandevelde, S., Vanbesien, L., Vennekens,

J., and Denecker, M. (2024). An epistemic logic

for modeling decisions in the context of incomplete

knowledge. In Proceedings of the 39th ACM/SIGAPP

Symposium on Applied Computing, SAC ’24, page

789–793, New York, NY, USA. Association for Com-

puting Machinery.

Mendes, E., Rodriguez, P., Freitas, V., Baker, S., and Atoui,

M. A. (2018). Towards improving decision making

and estimating the value of decisions in value-based

software engineering: the value framework. Software

Quality Journal, 26:607–656.

Meudt, T., Metternich, J., and Abele, E. (2017). Value

stream mapping 4.0: Holistic examination of value

stream and information logistics in production. CIRP

Annals, 66(1):413–416.

Moe, N. B., Aurum, A., and Dyb

a, T. (2012). Challenges of

shared decision-making: A multiple case study of ag-

ile software development. Information and Software

Technology, 54(8):853–865.

Moe, N. B.,

Smite, D., Paasivaara, M., and Lassenius, C.

(2021). Finding the sweet spot for organizational

control and team autonomy in large-scale agile soft-

ware development. Empirical Software Engineering,

26(5):101.

Murphy, G. C. and Kersten, M. (2020). Towards bridging

the value gap in devops. In Bruel, J.-M., Mazzara,

M., and Meyer, B., editors, Software Engineering As-

pects of Continuous Development and New Paradigms

of Software Production and Deployment, pages 181–

190, Cham. Springer International Publishing.

Pretorius, C., Razavian, M., Eling, K., and Langerak, F.

(2024). When rationality meets intuition: A research

agenda for software design decision-making. Journal

of Software: Evolution and Process, page e2664.

Qin, Y. and Liu, H. (2022). Application of value stream

mapping in e-commerce: a case study on an amazon

retailer. Sustainability, 14(2):713.

Ralph, P. (2018). The two paradigms of software develop-

ment research. Science of Computer Programming,

156:68–89.

Razavian, M., Paech, B., and Tang, A. (2019). Empirical re-

search for software architecture decision making: An

analysis. Journal of Systems and Software, 149:360–

381.

Salin, H., Rybarczyk, Y., Han, M., and Nyberg, R. G.

(2022). Quality metrics for software development

management and decision making: An analysis of at-

titudes and decisions. In International Conference

on Product-Focused Software Process Improvement,

pages 525–530. Springer.

Simon, H. A. (1955). A behavioral model of rational choice.

The quarterly journal of economics, pages 99–118.

Sjøberg, D. I., Dyb

a, T., Anda, B. C., and Hannay, J. E.

(2008). Building theories in software engineering.

Guide to advanced empirical software engineering,

pages 312–336.

Tankhiwale, S. and Saraf, S. (2020). Value stream map-

ping (vsm) led approach for waste and time to market

reduction in software product development process.

Telecom Business Review, 13(1):27.

Wallsten, T. S. (2024). Cognitive processes in choice and

decision behavior. Taylor & Francis.

Wang, Y., Liu, D., and Ruhe, G. (2004). Formal descrip-

tion of the cognitive process of decision making. In

Proceedings of the Third IEEE International Confer-

ence on Cognitive Informatics, 2004., pages 124–130.

IEEE.

Yang, S., Nachum, O., Du, Y., Wei, J., Abbeel, P., and Schu-

urmans, D. (2023). Foundation models for decision

making: Problems, methods, and opportunities. arXiv

preprint arXiv:2303.04129.

ICSOFT 2025 - 20th International Conference on Software Technologies