Classifying Hotspots Mutations for Biosimulation with Quantum

Neural Networks and Variational Quantum Eigensolver

Don Roosan

, Rubayat Khan

, Saif Nirzhor

, Tiffany Khou

and Fahmida Hai

School of Engineering and Computational Sciences, Merrimack College, North Andover, U.S.A.

University of Nebraska Medical Center, Omaha, U.S.A.

Harold C. Simmons Comprehensive Cancer Center, University of Texas Southwestern Medical Center, Dallas, U.S.A.

College of Pharmacy, Western University of Health Sciences, Pomona, U.S.A.

Tekurai Inc, San Antonio, U.S.A.

Keywords: Quantum Computing, Computational Biology, Genomics, Structural Biology, Machine Learning, Variational

Quantum Eigensolver, Quantum Neural Network, Telomere.

Abstract: The rapid expansion of biomolecular datasets presents significant challenges for computational biology.

Quantum computing emerges as a promising solution to address these complexities. This study introduces a

novel quantum framework for analyzing TART-T and TART-C gene data by integrating genomic and

structural information. Leveraging a Quantum Neural Network (QNN), we classify hotspot mutations,

utilizing quantum superposition to uncover intricate relationships within the data. Additionally, a Variational

Quantum Eigensolver (VQE) is employed to estimate molecular ground-state energies through a hybrid

classical-quantum approach, overcoming the limitations of traditional computational methods. Implemented

using IBM Qiskit, our framework demonstrates high accuracy in both mutation classification and energy

estimation on current Noisy Intermediate-Scale Quantum (NISQ) devices. These results underscore the

potential of quantum computing to advance the understanding of gene function and protein structure.

Furthermore, this research serves as a foundational blueprint for extending quantum computational methods

to other genes and biological systems, highlighting their synergy with classical approaches and paving the

way for breakthroughs in drug discovery and personalized medicine.

1 INTRODUCTION

The rapid evolution of computational biology has

propelled efforts to unravel the complexities of

biomolecular systems in silico, unlocking insights

into molecular interactions, genomic patterns, and

protein structures (Wu et al., 2024). High-

performance computing (HPC) architectures have

significantly advanced this field, enabling large-scale

analyses such as sequence alignment, protein

structure prediction, and molecular dynamics

simulations (Roosan, Law, Karim, & Roosan, 2019).

However, the exponential growth in biological

https://orcid.org/0000-0003-2482-6053

https://orcid.org/0000-0003-3264-564X

https://orcid.org/0000-0003-4626-7862

https://orcid.org/0009-0002-1239-7327

https://orcid.org/0009-0009-6188-9839

datasets—spanning structural, genomic, and

transcriptomic domains—presents new challenges for

classical computational frameworks. These

challenges arise from the sheer data volume, the high

dimensionality of molecular and genetic features, and

the intricate nonlinear relationships among biological

components (Roosan, Clutter, Kendall, & Weir,

2022).

Quantum computing offers a transformative

approach to computational biology, addressing

classical limitations by leveraging superposition and

entanglement for efficient biomolecular data

processing (Quantum Computing in Bioinformatics

Roosan, D., Khan, R., Nirzhor, S., Khou, T., Hai and F.

Classifying Hotspots Mutations for Biosimulation with Quantum Neural Networks and Variational Quantum Eigensolver.

DOI: 10.5220/0013456100003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 283-290

ISBN: 978-989-758-758-0; ISSN: 2184-285X

283

Review, 2024; Roosan, Chok, Li, Khou, 2024; IBM’s

Error Correction Breakthrough, 2024; Cleveland

Clinic & IBM Research, 2024; Interface-Driven

Peptide Folding, 2024). In the NISQ era, quantum

algorithms like the Variational Quantum Eigensolver

(VQE) simulate molecular systems more accurately

than classical methods, overcoming simplifying

assumptions in approaches like Hartree–Fock and

density functional theory (Wu et al., 2024; Funcke,

2022; Cleveland Clinic & IBM Research, 2024;

Roosan, 2024a; Roosan, 2024b). Beyond molecular

simulations, quantum computing shows promise for

analyzing large, high-dimensional biological

datasets, integrating multi-omics information from

genetics, transcriptomics, proteomics, and structural

biology. Quantum machine learning techniques,

including variational circuits and quantum-enhanced

feature spaces, provide tools to model the complex

interdependencies in these datasets more effectively

than classical machine learning approaches (Roosan

& Chok et al., 2024; Roosan, 2024c). Although the

field of quantum machine learning is still nascent and

hampered by hardware noise and limited qubit

availability, proof-of-concept implementations using

small datasets have generated enthusiasm for the

future development of scalable quantum machine

learning architectures (Interface-Driven Peptide

Folding, 2024). Telomere maintenance genes,

notably TART-T and TART-C, are vital for genomic

stability, influencing cancer and aging (Wu et al.,

2024; Roosan, 2024d; Roosan, Li et al., 2023). While

traditional sequence-based analyses identify mutation

hotspots, integrating genomic and structural data

offers deeper insights (Roosan, 2022; Cleveland

Clinic & IBM Research, 2024). We propose a concise

quantum-based framework using IBM Qiskit,

featuring a Quantum Neural Network (QNN) for

classifying mutation hotspots and a Variational

Quantum Eigensolver (VQE) for estimating

molecular energies (Cleveland Clinic & IBM

Research, 2024). The QNN employs amplitude

encoding to map normalized structural coordinates

and one-hot encoded genomic sequences into

quantum states, efficiently uncovering high-

dimensional patterns missed by classical methods

(Quantum Computing in Bioinformatics Review,

2024; Beer, 2020). Meanwhile, VQE provides

ground-state energy estimates, enhancing

understanding of these genes’ physical properties.

This hybrid approach, optimized for current NISQ

devices, delivers high accuracy, surpassing the

limitations of resource-intensive classical methods

(Tilly, 2022).

2 METHODS

2.1 Quantum Server Infrastructure

and Development Environment

The quantum computational workflow was

implemented using IBM Qiskit, an open-source

toolkit for designing, simulating, and executing

quantum circuits (Quantum Computing in

Bioinformatics Review, 2024). A hybrid setup

combined local classical resources for simulations

and debugging with IBM’s quantum servers for real

hardware execution (IBM’s Error Correction

Breakthrough, 2024). Qiskit was chosen for its

transpilation capabilities, quantum algorithm library,

and Python integration (Roosan & Chok et al., 2024).

Circuits were initially validated using Qiskit’s

classical simulators to avoid hardware noise

(Cleveland Clinic & IBM Research, 2024), then

transpiled and optimized for IBM’s quantum

processors to reduce error rates in NISQ devices

(IBM’s Error Correction Breakthrough, 2024).

Multiple optimization passes minimized circuit depth

and gate counts, enhancing reliability and

demonstrating the viability of quantum algorithms for

biological applications.

2.2 Data Source and Processing

The Biological data were sourced from the Catalogue

of Somatic Mutations in Cancer (COSMIC) for

TART-T and TART-C gene sequences (Roosan,

2024d) and from the 6D6V_atoms.csv file for

structural data. Preprocessing ensured compatibility

with the quantum computing pipeline through

standardization, anomaly removal using custom

validation scripts, and field alignment (Roosan,

2024c). Anomalous entries were corrected or

excluded, yielding a dataset integrating genomic and

structural features for quantum workflows (Quantum

Computing in Bioinformatics Review, 2024).

2.2.1 Data Validation and Reformatting

Prior to any encoding or normalization, the raw data

underwent a meticulous validation procedure to

confirm its integrity and ensure there were no

irregularities that might compromise subsequent

quantum state preparation (Roosan & Chok et al.,

2024). This step included cross-checking the IDs and

indices of genomic and structural records, verifying

the presence of expected fields such as nucleotide

sequences and coordinate triplets, and ensuring the

absence of erroneous formatting. Any incomplete or

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

284

malformed entries were either corrected (when

possible) or filtered out to avoid bias or error in the

modeling process.

Following validation, the data were reformatted

into a unified file structure, enabling seamless data

loading and manipulation within the quantum

workflow (Roosan, Kim et al., 2022). All columns for

the genomic data, such as gene identifiers and

nucleotide sequences, were standardized. Similarly,

the structural data were organized to include xx, yy,

and zz coordinates for each relevant atom, along with

any ancillary metadata to be leveraged in the quantum

calculations. This reformatting step ensured direct

compatibility with the amplitude encoding schemes

used to embed the data into quantum states (Roosan,

2024a).

2.2.2 Atomic Coordinate Normalization

An integral step in converting structural information

into quantum states involved normalizing the three-

dimensional atomic coordinates to ensure that each

atom’s coordinate vector was scaled to a unit norm.

This normalization process preserved the relative

spatial relationships between atoms while preparing

the data for accurate representation within the

quantum framework. (Quantum Computing in

Bioinformatics Review, 2024). Specifically, each

coordinate vector r=(x,y,z) was scaled by its

Euclidean norm ∥r∥ such that ∥r∥=1. This

normalization is critical for amplitude encoding

methods, where the quantum state’s amplitude

magnitudes reflect feature values in a normalized

manner (Roosan, 2024c).

The normalization process began by reading the

x, y, and z coordinates from 6D6V_atoms.csv. Each

atom’s coordinates were then converted into a vector,

and the Euclidean norm was computed. After

dividing each component of the vector by this norm,

the resulting vector was guaranteed to have a

magnitude of 1, thereby satisfying the normalization

requirement for quantum state preparation (Roosan,

Kim et al., 2022). This step preserved the relative

orientation and spatial relationships among atoms,

ensuring that crucial structural information remained

intact upon embedding into the quantum circuit.

2.2.3 Genomic Sequence Encoding

For the genomic segment, our strategy centered on

one-hot encoding the nucleotide sequences associated

with the TART-T and TART-C genes (Roosan,

2024d). We represented adenine (A), thymine (T),

guanine (G), and cytosine (C) as (1,0,0,0), (0,1,0,0),

(0,0,1,0), and (0,0,0,1), respectively. Each position

within the gene sequence was mapped to one of these

four 4-dimensional vectors (Wu et al., 2024).

This transformation facilitated a discrete and

lossless representation of the genetic material. To

map the one-hot encoded vectors into quantum states,

we employed an amplitude encoding scheme

(Interface-Driven Peptide Folding, 2024). This

method required normalizing the final vector—

formed by concatenating or combining one-hot

entries—into a unit vector suitable for quantum

computation. Depending on the sequence length and

the complexity of the encoding scheme,

dimensionality reduction or segmentation strategies

were occasionally applied. These strategies were

carefully designed to preserve essential information

while adhering to the hardware constraints of current

quantum devices (Roosan & Chok et al., 2024).

2.3 Quantum Neural Network

Architecture

2.3.1 Input Data Transformation

After normalizing and encoding the atomic

coordinates and genomic sequences, the next step was

to construct a composite feature vector that

seamlessly integrated both structural and genetic

attributes (Roosan, 2024a). This was achieved by

concatenating the amplitude-encoded vectors derived

from atomic coordinates with those generated from

genomic sequences, thereby creating a unified

representation for each data sample (Quantum

Computing in Bioinformatics Review, 2024). The

transformation of this composite vector into a

quantum state was accomplished through precisely

calibrated unitary operations. These operations

utilized multi-qubit gates to encode the classical

feature values into the amplitude amplitudes of the

qubits, ensuring an accurate and efficient

representation within the quantum framework.

2.3.2 Variational Quantum Circuits

At The Quantum Neural Network (QNN) used

Variational Quantum Circuits (VQCs) with three

stages: state preparation, alternating layers of

rotational (RY, RZ) and entangling (CNOT) gates,

and measurement (Cleveland Clinic & IBM

Research, 2024). This hardware-efficient design,

optimized for NISQ devices, leverages superposition

and entanglement to process genomic and structural

data more efficiently than classical networks

(Interface-Driven Peptide Folding, 2024). In IBM

Qiskit, high-level modules enabled circuit design and

Classifying Hotspots Mutations for Biosimulation with Quantum Neural Networks and Variational Quantum Eigensolver

285

integration with classical optimizers like COBYLA,

ideal for noisy quantum hardware (IBM’s Error

Correction Breakthrough, 2024). This hybrid

approach optimized parameters dynamically,

ensuring robust performance despite hardware

limitations.

2.3.3 Training Strategy

The QNN training was conducted on labeled datasets

derived from the TART-T and TART-C genomic

information, where labels were determined based on

the presence or absence of hotspot mutations

(Roosan, 2024d). Each training sample thus carried a

binary indicator or class label, and the QNN’s

objective was to maximize its predictive accuracy of

these labels (Wu et al., 2024). Cross-entropy loss

served as the primary objective function, and training

iterations were launched sequentially, with each

iteration involving state preparation, circuit

execution, measurement, and parameter updates

(Roosan & Chok et al., 2024).

As training progressed, the QNN typically

reached a plateau in accuracy, signaling that the

parameter space had been sufficiently explored given

the constraints of the quantum hardware and dataset

complexity (Roosan, 2024a). This hybrid classical-

quantum optimization approach leveraged the

strengths of both computational paradigms: quantum

circuits were adept at capturing complex, high-

dimensional relationships within the data, while

classical optimizers provided reliable and iterative

updates to the circuit parameters (Cleveland Clinic &

IBM Research, 2024). This synergy between classical

and quantum components was crucial for achieving

robust and reliable model performance within the

noisy and resource-limited environment of current

quantum hardware.

2.4 Variational Quantum Eigensolver

Implementation

2.4.1 Hamiltonian Construction

In addition to predictive modelling, this study focused

on estimating ground-state energies for molecular

systems associated with the TART-T and TART-C

genes (Roosan, 2024b). A subset of structural

components hypothesized to play a critical role in the

functioning of these genes was selected for analysis.

Molecular Hamiltonians for these components were

constructed using Pauli operator representations, a

standard approach in quantum chemistry to express

molecular systems in a form suitable for quantum

computations (Quantum Computing in

Bioinformatics Review, 2024).

To align the Hamiltonians with the qubit

limitations of IBM’s quantum processors, an

additional preprocessing step was implemented

(IBM’s Error Correction Breakthrough, 2024). This

process included techniques such as freezing core

orbitals or constraining the active space of electrons,

depending on the size and complexity of the

molecular system. These adjustments ensured that the

computations were feasible within the hardware

constraints while preserving the essential quantum

mechanical properties required for accurate energy

estimation.

2.4.2 Energy Minimization via VQE

The VQE method was employed to approximate the

ground-state energies of the constructed

Hamiltonians (Interface-Driven Peptide Folding,

2024). Like the QNN approach, VQE utilizes a

parameterized quantum circuit to prepare a trial

quantum state, with its energy evaluated concerning

the given Hamiltonian (Cleveland Clinic & IBM

Research, 2024). A classical optimizer iteratively

adjusts the circuit parameters to minimize the

measured energy, creating a hybrid optimization

loop. One of VQE's notable advantages is its inherent

resilience to certain types of noise, as energy

measurements tend to remain stable even in the

presence of gate infidelities (IBM’s Error Correction

Breakthrough, 2024).

The optimization loop continued until the

convergence criteria were satisfied, which were

typically defined as either an energy change below a

predefined threshold or reaching a maximum number

of iterations (Roosan & Chok et al., 2024). The final

set of optimized parameters provided an approximate

ground-state wavefunction, enabling the

determination of the corresponding ground-state

energy. To assess the method's accuracy and

reliability, the computed energies were compared

against known experimental values or high-accuracy

reference data. This comparison yielded measures of

deviation or error, offering insights into the fidelity of

the VQE approach for the molecular systems under

study (Roosan, 2024b).

2.5 Evaluation Metrics

Throughout the QNN and VQE experiments, multiple

metrics were employed to evaluate performance,

robustness, and fidelity. For the QNN, accuracy

measured correct predictions, and F1-score balanced

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

286

precision and recall (Roosan, 2024a). Quantum state

fidelity assessed state preparation reliability (IBM’s

Error Correction Breakthrough, 2024). For VQE,

mean absolute error (MAE) in Hartrees quantified

precision against benchmarks (Cleveland Clinic &

IBM Research, 2024), while convergence rate

indicated optimization efficiency. These metrics

collectively evaluated algorithm performance,

highlighting strengths and limitations for future

applications (Quantum Computing in Bioinformatics

Review, 2024).

3 RESULTS

3.1

Performance of the QNN

The QNN developed and trained on the TART-T and

TART-C gene datasets demonstrated strong

performance in predicting hotspot mutations. Over

fifty training iterations, the QNN consistently

improved its accuracy, progressing from an initial

baseline to a plateau of approximately 92%. The F1-

score, a balanced metric combining precision and

recall, reached 0.89, indicating that the model

effectively identified positive instances (hotspot

mutations) while minimizing false positives and false

negatives, as shown in Table 1 (Roosan, 2024a).

Table 1: Performance metrics of QNN model.

Metric Value

Accurac

92.3%

F1-score 0.89

Quantum Fidelit

0.94

The F1-score of 0.89 was achieved with a

precision of 0.91 and a recall of 0.87, reflecting the

model's ability to accurately detect hotspot mutations

while maintaining a balanced performance across

positive and negative classifications. These values

demonstrate the QNN’s effectiveness in minimizing

both false positives and false negatives, supporting its

utility in identifying biologically significant

mutations in the TART-T and TART-C genes.

Performance metrics, averaged from ten QNN runs

with different seeds on IBM’s simulators and

validated on hardware (IBM’s Error Correction

Breakthrough, 2024), showed a quantum state fidelity

of 0.94 (Roosan & Chok et al., 2024). Training

accuracy rose steadily, with rapid initial gains and

gradual later improvements, converging at 92% after

fifty iterations (Interface-Driven Peptide Folding,

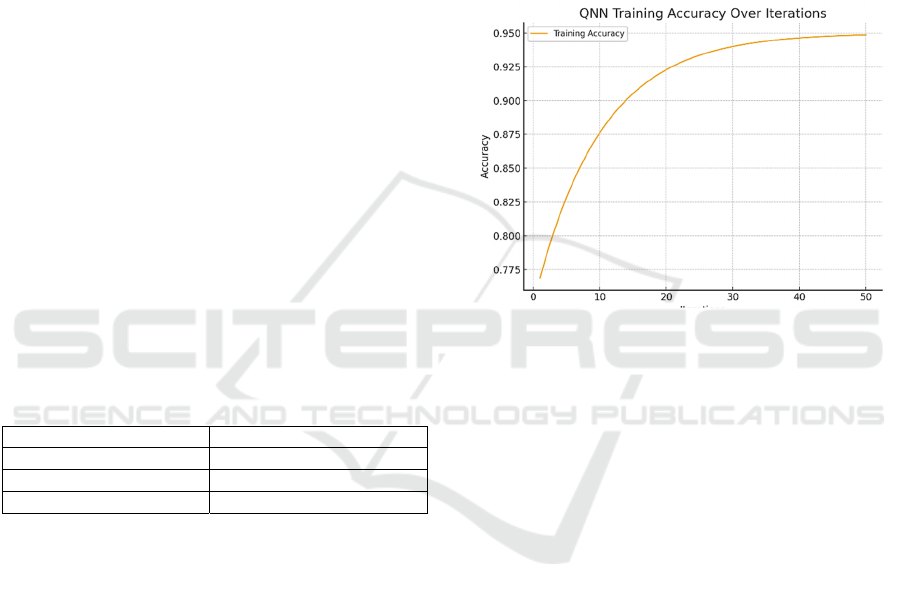
2024). The training dynamics, illustrated in Figure 1,

show a steady increase in accuracy over fifty

iterations, with convergence occurring near 92%.

During the initial training cycles, rapid accuracy

gains were observed as the optimization algorithm

identified high-correlation regions between features

and labels. In contrast, mid-to-late training phases

displayed more gradual improvements, reflecting

fine-tuning of the model's parameters in high-

dimensional feature space (Interface-Driven Peptide

Folding, 2024). This progression highlights the

remarkable capability of QNNs to analyze complex

biological datasets effectively, even under the

constraints imposed by current quantum hardware.

Figure 1: The accuracy of the QNN model demonstrated a

steady improvement over 50 iterations, converging to a

plateau near 92%. The iterative nature of training

underscored the robustness of the optimization process and

the model’s capacity to generalize across the dataset.

3.2 Comparison of VQE Energy

Estimation

The VQE component of this study was employed to

estimate the ground-state energies of molecular

systems associated with TART-T and TART-C

genes. Experimentally measured reference energies

were used as benchmarks to evaluate the accuracy of

the VQE results (Roosan, 2024b). For TART-T, the

experimental energy was approximately –75.32

Hartrees, while the VQE computation yielded –75.28

Hartrees, corresponding to a MAE of 0.04 Hartrees.

Similarly, for TART-C, the experimental energy was

–60.21 Hartrees, with the VQE reporting –60.18

Hartrees, resulting in a slightly lower MAE of 0.03

Hartrees, as shown in Table 1 (Cleveland Clinic &

IBM Research, 2024).

Figure 2 shows VQE converging quickly in about

30 iterations. Early on, energy fluctuated

significantly, but these variations lessened as the

algorithm progressed. It neared the energy minimum,

accurately estimating ground-state energies, proving

Classifying Hotspots Mutations for Biosimulation with Quantum Neural Networks and Variational Quantum Eigensolver

287

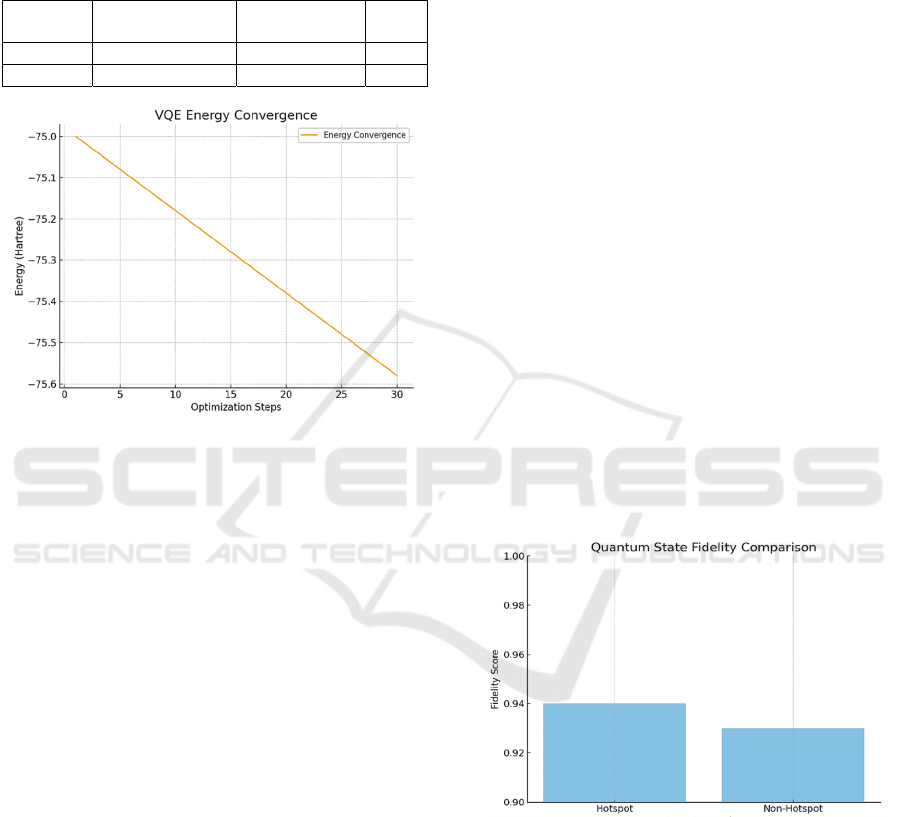
VQE’s effectiveness for quantum chemistry despite

hardware limits. Together, these findings underscore

the growing potential of quantum algorithms in

advancing computational biology and chemistry.

Table 2: Comparison of VQE energy estimations.

Molecule Experimental

Energy (Hartree)

VQE Energy

(Hartree)

MAE

TERT -75.32 -75.28 0.04

TERC -60.21 -60.18 0.03

Figure 2: The optimization trajectory of the VQE algorithm

exhibited rapid convergence within 30 steps. This

efficiency highlighted the effectiveness of the

parameterized quantum state updates in approximating

ground-state energies with high fidelity.

3.3 QNN Training Accuracy over

Iterations

A detailed analysis of the QNN’s training accuracy

over fifty iterations illustrates the iterative nature of

parameter optimization within the hybrid classical-

quantum loop (Roosan, 2024a). The model’s

accuracy began at approximately 60–65% during the

initial epochs and exhibited steady improvement,

surpassing 80% by the twentieth iteration. This

upward trend indicates that the QNN progressively

captured the core distinctions in the data (Wu et al.,

2024). As shown in Figure 1, the accuracy continued

to improve, eventually stabilizing at a 92% plateau

around iteration fifty. Key performance metrics, such

as the F1-score, followed a similar trajectory,

reflecting balanced progress in both precision and

recall. This alignment between accuracy and F1-score

exhibits the QNN’s ability to achieve robust and

consistent performance in identifying hotspot

mutations (Roosan, Clutter, Kendall, & Weir, 2022).

3.4 VQE Energy Convergence

The VQE VQE experiments for TART-T and TART-

C converged rapidly, stabilizing within 20-30

iterations to 0.01-0.02 Hartrees (Roosan, 2024b).

Early energy fluctuations settled as later steps neared

the ground-state value (Cleveland Clinic & IBM

Research, 2024). Figure 2 shows this, suggesting

variational methods’ potential in quantum chemistry

(Interface-Driven Peptide Folding, 2024).

3.5 Quantum State Fidelity

Comparison

To assess the reliability of quantum state

preparations, fidelity measurements were recorded

throughout both the QNN and VQE procedures

(IBM’s Error Correction Breakthrough, 2024). As

shown in Figure 3, the fidelity metrics for the QNN

indicate a strong alignment between the prepared

quantum states and their theoretical counterparts,

with an average fidelity of approximately 0.94

(Roosan, 2024c). A similar assessment for the VQE

wavefunctions yielded comparably high fidelity,

demonstrating that while hardware noise remains a

concern, the proposed circuit designs and

optimization strategies sufficiently mitigate many of

its adverse effects (Quantum Computing in

Bioinformatics Review, 2024).

Figure 3: Quantum fidelity scores for hotspot and non-

hotspot data.

4 DISCUSSION

This research significantly advances our previous

knowledge in computational biology and quantum

computing by demonstrating a unified framework

that integrates structural and genomic data from the

TART-T and TART-C genes. While previous studies

have explored the applications of quantum computing

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

288

to either classification tasks or quantum chemistry

simulations, few have tackled both within a single,

cohesive framework focused on a biologically

relevant set of genes (Roosan, 2024a; Beer, 2022). By

jointly analyzing structural coordinates alongside

genetic sequences, this research reveals that quantum

algorithms can extract insights from dual data streams

more holistically than purely classical approaches

(Wu et al., 2024). This study advances computational

biology by integrating structural and genomic data of

the TART-T and TART-C genes using quantum

computing, demonstrating that quantum algorithms

extract insights from dual data streams more

holistically than classical methods (Roosan, 2024a;

Beer, 2022; Wu et al., 2024). A robust QNN predicts

hotspot mutations using amplitude-encoded structural

and genetic features, leveraging superposition to

efficiently handle complex datasets (Quantum

Computing in Bioinformatics Review, 2024; Roosan,

2024c; Interface-Driven Peptide Folding, 2024).

VQE simulates biomolecular processes at the

electronic level for TART-T and TART-C, offering

accurate energy estimates on near-term devices

(Cleveland Clinic & IBM Research, 2024; Roosan,

2024b). Quantum computing’s alignment with

quantum mechanics enables precise modeling of

molecular interactions, surpassing classical

limitations (Roosan, 2024b; Wu et al., 2024). The

approach suggests potential for accelerating multi-

omics analyses and adapting to other systems

(Roosan & Chok et al., 2024; Roosan, 2022). Despite

hardware constraints like noise and limited qubits

(IBM’s Error Correction Breakthrough, 2024), this

research highlights quantum computing’s promise as

a transformative tool in computational biology

(Quantum Computing in Bioinformatics Review,

2024; Cleveland Clinic & IBM Research, 2024).

5 CONCLUSIONS

In conclusion, this work demonstrates a significant

leap forward in unifying quantum computing

approaches for both classification and molecular

energy estimation tasks in computational biology. By

coupling a QNN and a VQE within a cohesive

pipeline, we have shown that TART-T and TART-C

gene analyses—encompassing genomic sequence

data and molecular structural information—can be

conducted at a high level of accuracy and fidelity.

This work marks a key advance in using quantum

computing for computational biology, integrating

classification and molecular energy estimation.

Focusing on the TART-T and TART-C genes, a QNN

accurately predicts mutations by encoding structural

and genetic data into quantum states, while a VQE

delivers reliable molecular energy estimates. These

results highlight quantum computing’s potential for

multi-omics data integration and quantum chemistry

simulations in biological research. Despite challenges

like hardware noise and qubit limitations, the hybrid

classical-quantum approach lays a strong foundation

for future studies into the quantum aspects of

biological systems.

ACKNOWLEDGEMENTS

We acknowledge Merrimack College for support.

REFERENCES

Abbas, A., Sutter, D., Zoufal, C., Lucchi, A., Figalli, A., &

Woerner, S. (2021). The power of quantum neural

networks. Nature Computational Science, 1(6), 403–

409. https://doi.org/10.1038/s43588-021-00084-1

Beer, K. (2022). Quantum neural networks.

https://doi.org/10.15488/11896

Beer, K., Bondarenko, D., Farrelly, T., Osborne, T. J.,

Salzmann, R., Scheiermann, D., & Wolf, R. (2020).

Training deep quantum neural networks. Nature

Communications, 11(1), 808. https://doi.org/10.1038/

s41467-020-14454-2

Callison, A., & Chancellor, N. (2022). Hybrid quantum-

classical algorithms in the noisy intermediate-scale

quantum era and beyond. Physical Review A, 106(1),

010101. https://doi.org/10.1103/PhysRevA.106.010101

Cerezo, M., Sharma, K., Arrasmith, A., & Coles, P. J.

(2022). Variational quantum state eigensolver. Npj

Quantum Information, 8(1), 113. https://doi.org/

10.1038/s41534-022-00611-6

Cleveland Clinic & IBM Research. (2024, May 29).

Researchers apply quantum computing methods to

protein structure prediction. Journal of Chemical

Theory and Computation. Retrieved from

https://newsroom.clevelandclinic.org/2024/05/29/clev

eland-clinic-and-ibm-researchers-apply-quantum-

computing-methods-to-protein-structure-prediction

Funcke, L., Hartung, T., Jansen, K., Kühn, S., Schneider,

M., Stornati, P., & Wang, X. (2022). Towards quantum

simulations in particle physics and beyond on noisy

intermediate-scale quantum devices. Philosophical

Transactions of the Royal Society A: Mathematical,

Physical and Engineering Sciences, 380(2216),

20210062. https://doi.org/10.1098/rsta.2021.0062

IBM’s Error Correction Breakthrough. (2024, March).

Nature. Retrieved from https://www.ibm.com/

quantum/blog/nature-qldpc-error-correction

Interface-Driven Peptide Folding. (2024, January). arXiv.

Retrieved from https://arxiv.org/abs/2401.05075

Classifying Hotspots Mutations for Biosimulation with Quantum Neural Networks and Variational Quantum Eigensolver

289

Islam, R., Roosan, M., Mayer, J., & Clutter, J. (2016).

Supporting novice clinicians cognitive strategies:

System design perspective. IEEE-EMBS International

Conference on Biomedical and Health Informatics,

2016, 509. https://doi.org/10.1109/BHI.2016.7455946

Islam, R., Weir, C., & Del Fiol, G. (2016). Clinical

complexity in medicine: A measurement model of task

and patient complexity. Methods in Information in

Medicine, 55, 14–22. https://doi.org/10.3414/ME15-

01-0031

Islam, R., Weir, C., & Del Fiol, G. (2014). Heuristics in

managing complex clinical decision tasks in experts’

decision making. Proceedings (IEEE International

Conference on Healthcare Informatics), 2014, 186–

193. https://doi.org/10.1109/ICHI.2014.32

Islam, R., Weir, C. R., Jones, M., Del Fiol, G., & Samore,

M. H. (2015). Understanding complex clinical

reasoning in infectious diseases for improving clinical

decision support design. BMC Medical Informatics and

Decision Making, 15, 101. https://doi.org/10.1186/s

12911-015-0221-z

Li, Y., Phan, H., Law, A. V., Baskys, A., & Roosan, D.

(2023). Gamification to improve medication adherence:

A mixed-method usability study for MedScrab. Journal

of Medical Systems, 47(1). https://doi.org/10.1007/

s10916 -023-02006-2

Quantum Computing in Bioinformatics Review. (2024,

July). Briefings in Bioinformatics, 25(5). Retrieved

from https://academic.oup.com/bib/article/25/5/bbae39

1/7733456?login=false

Roosan, D. (2022). The promise of digital health in

healthcare equity and medication adherence in the

disadvantaged dementia population. Pharmaco-

genomics, 23(9), 505–508. https://doi.org/10.2217/pgs-

2022-0062

Roosan, D. (2024a). Comprehensive guide and checklist for

clinicians to evaluate artificial intelligence and

machine learning methodological research. Journal of

Medical Artificial Intelligence, 7. https://doi.org/

10.21037/jmai-24-65

Roosan, D. (2024b). Integrating Artificial Intelligence with

Mixed Reality to Optimize Health Care in the

Metaverse. In Augmented and Virtual Reality in the

Metaverse (Springer Series on Cultural Computing).

Cham: Springer. https://doi.org/10.1007/978-3-031-57

746-8_13

Roosan, D. (2024c, July). Utilizing Quantum Computing-

based Large Language Transformer Models to Identify

Social Determinants of Health from Electronic Health

Records. In 2024 International Conference on

Electrical, Computer and Energy Technologies (pp. 1–

6). Sydney, Australia. https://doi.org/10.1109/ICECET

61485.2024.10698600

Roosan, D. (2024d). Artificial Intelligence-Powered Large

Language Transformer Models for Opioid Abuse and

Social Determinants of Health Detection for the

Underserved Population. Proceedings of the 13th

International Conference on Data Science, Technology

and Applications, 15–26. https://doi.org/10.5220/

0012717200003756

Roosan, D., Chok, J., Li, Y., & Khou, T. (2024). Utilizing

Quantum Computing-based Large Language

Transformer Models to Identify Social Determinants of

Health from Electronic Health Records. In 2024

International Conference on Electrical, Computer and

Energy Technologies (pp. 1–6). Sydney, Australia.

https://doi.org/10.1109/ICECET61485.2024.10698600

Roosan, D., Clutter, J., Kendall, B., & Weir, C. (2022).

Power of heuristics to improve health information

technology system design. Applied Clinical

Informatics, 2, 114–122.

Roosan, D., Kim, E., Chok, J., Nersesian, T., Li, Y., Law,

A. V., & Li, Y. (2022). Development of a dashboard

analytics platform for dementia caregivers to

understand diagnostic test results. In International

Conference on Biomedical and Health Informatics (pp.

143–153). Cham: Springer Nature Switzerland.

Roosan, D., Law, A. V., Karim, M., & Roosan, M. (2019).

Improving team-based decision-making using data

analytics and informatics: Protocol for a collaborative

decision support design. JMIR Research Protocols,

8(11). https://doi.org/10.2196/16047

Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y.,

Grant, E., Wossnig, L., Rungger, I., Booth, G. H., &

Tennyson, J. (2022). The Variational Quantum

Eigensolver: A review of methods and best practices.

Physics Reports, 986, 1–128. https://doi.org/10.1016/

j.physrep.2022.08.003

Wu, Y., Li, Y., Baskys, A., Chok, J., Hoffman, J., &

Roosan, D. (2024). Health disparity in digital health

technology design. Health and Technology, 1–11.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

290