Citation Steadiness Analysis with GraphSAGE Approach

Renata Avros

, Dvora Toledano Kitai

and Zeev Volkovich

Software Engineering Department, Braude College of Engineering, Snonit st., Karmiel, Israel

Keywords: Citation Manipulation, Network Perturbations, GraphSAGE Algorithm.

Abstract: Citation manipulation occurs when references are deliberately included in academic works for reasons

unrelated to their genuine scholarly merit. Instead of serving their primary purposes—such as supporting

arguments, providing context, or guiding readers—these citations are often utilized to inflate metrics like

citation counts artificially. Manipulated citations tend to deviate from the standard patterns and structures

found in authentic citation networks. Consequently, when such networks are perturbed by removing certain

nodes or connections, these manipulated citations are more likely to exhibit inconsistencies. This paper

introduces a method for detecting citation manipulation by studying how citation patterns change under

random perturbations of the citation graph. The method employs the GraphSAGE algorithm to generate

embeddings of the altered graph in an Euclidean space, thereby reconstructing the removed edges. The

approach assumes that legitimate citations are bolstered by a network of indirect connections, leading to

closely related embeddings for nodes linked by authentic citations that facilitate the accurate prediction of

missing edges. By iteratively perturbing the graph and assessing the accuracy of edge reconstruction, the

method highlights suspected manipulated citations, which consistently exhibit poor reconstruction

performance, signifying supposed anomalous comportment. Numerical experiments validate the effectiveness

of this approach in identifying anomalies within citation networks, highlighting its potential as a reliable tool

for enhancing the integrity of scholarly communication.

1 INTRODUCTION

Citation consistency is a fundamental issue to

research integrity, as it directly impacts the reliability

and trustworthiness of scientific literature.

Inappropriate, particularly manipulated citations

often occur in scientific literature when references are

deliberately included in academic works for reasons

other than genuine scholarly merit. Instead of

supporting arguments, providing background, or

guiding readers, these citations are predominantly

used to escalate metrics like citation counts

artificially. This practice is frequently employed to

enhance the perceived impact and prestige of

researchers, journals, or institutions and has

significant detrimental effects, eroding the core

principles of academic discourse: accuracy,

objectivity, and scientific integrity.

https://orcid.org/0000-0001-9528-0636

https://orcid.org/0009-0002-1923-3640

https://orcid.org/0000-0003-4636-9762

Corresponding author

The paper (Prabha, 1983) emphasizes the scale of this

subject, indicating that more than two-thirds of

references in a typical paper may be superfluous,

underscoring the widespread occurrence of

questionable citation practices. Others (Fong and

Wilhite, 2017) explore unethical practices in

scholarly publishing, focusing on honorary

authorship and coercive citation. The study exposes

the widespread prevalence of these manipulative

practices across various academic disciplines such

that a significant number of respondents reported

instances of including honorary authors in their

research projects and facing pressure to incorporate

unnecessary citations.

Common schemes to increase citation amount

described by (Jacobes, 2016), (Falaga ang Alexiou,

2008), (Wilhite, Fong and Wilhi, 2019), and

(Ioannidis and Thombs, 2019), include:

• Self-Citation Clusters: Excessive self-citation to

heighten personal citation counts.

Avros, R., Kitai, D. T., Volkovich and Z.

Citation Steadiness Analysis with GraphSAGE Approach.

DOI: 10.5220/0013455600003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 769-777

ISBN: 978-989-758-758-0; ISSN: 2184-285X

769

• Mutual Citation Agreements (citation cartels):

Groups of researchers or journals decide to cite

each other's work or publish special issues with

highly cited specific articles.

• Citation Stacking: Journals citing their own

articles to inflate impact factors.

• Inclusion of Irrelevant Citations: Referencing

unrelated works to benefit cited authors or

journals.

• Strategic publication: Publishing articles likely

to receive disproportionate attention (e.g.,

reviews or editorials).

These manners distort evaluations of academic

performance and the significance of scholarly

contributions, erode the trustworthiness of academic

publishing, and mislead stakeholders, including

researchers and funding bodies. Manipulation also

impacts younger researchers by promoting shortcuts

over developing rigorous scholarly habits. They

undermine the integrity of citation systems and

scholarly evaluation systems. To combat this issue,

the academic community needs stricter editorial

policies, promote transparent citation practices, and

employ advanced algorithms to detect anomalous

citation patterns.

Several surveys (Resnik, Gutierrez-Ford, and

Peddada, 2008), (Wilhite and Fong, 2012) and (Wren

and Georgescu, 2022) have been conducted to

explore the prevalence and characteristics of

reference list manipulation, underscoring the critical

need for attention to this issue.

Many studies reveal that manipulated citations

often deviate significantly from the established norms

and ethical standards of scholarly referencing.

Numerous authors have likened these citations to

rumours, emphasizing their tendency to propagate

without genuine relevance or merit. While we do not

delve into a comprehensive review of all studies cited

in these reviews, we briefly recall several.

Citation network analysis usually incorporates

three key aspects: the number of citations, the

structure of the citation network, and the topical

relevance reflected in citation relationships. The

Paper (Liu, Bai, Wang, et al., 2024) employs semantic

main path network analysis to generate a precise and

comprehensive understanding of domain evolution,

revealing more coherent development trajectories.

The article (Wren and Georgescu, 2022) presents

a combination of statistical techniques to identify

peculiar citation manners in academic articles to

uncover instances where authors might intentionally

manipulate reference lists to boost their citation

counts artificially.

Surveys cited in this paper have explored various

dimensions of reference list manipulation, such as the

prevalence of coercive citation practices. For

instance, the paper (Fong and Wilhite, 2017)

examines the frequency of pressure on authors to

include specific citations. A survey (Resnik,

Gutierrez-Ford, and Peddada, 2008) of 283 authors

reveals that a significant proportion (22.7%) had

experienced situations where a reviewer insisted on

including unnecessary references to their own work.

Furthermore, another survey by (Wilhite and Fong,

2012) reported that over 20% of respondents had

faced pressure from journal editors to include specific

citations.

The current study is built on the framework

introduced in (Avros, Keshet, Toledano Kitai.,

Vexler, and Volkovich, 2023), aiming to analyse

connections within a citation graph by examining

their behavior under network perturbations using the

Node2Vec method (Grover and Leskovec, 2016)

employing a graph embedding technique designed to

capture node representations through random walks

within the graph. The underlying hypothesis suggests

authentic relationships within the graph are inherently

more robust to conceivable graph disruptions.

The presented research also operates on the

premise that manipulated or fraudulent citations

create irregularities in the citation network, making

them more prone to detection under specific network

perturbations. These anomalies are introduced

intentionally to boost publications' perceived impact

or credibility artificially. Such manipulation citations

diverge from the natural citation patterns and

structures within the network. As a result, when the

network undergoes perturbations, such as removing

specific nodes or edges, these anomalous citations are

more likely to exhibit detectable inconsistencies,

distinguishing them from legitimate citations.

Following this general standpoint, this paper

explores a method for detecting citation manipulation

by examining how citation patterns respond to the

random removal of elements from the citation graph.

The approach leverages the GraphSAGE algorithm

(Hamilton, Ying, and Leskovec, 2017) to generate

embeddings of the permuted graph in an Euclidean

space, thereby reconstructing the removed edges. The

underlying assumption is that legitimate citations are

supported by a robust network of indirect

connections, resulting in closely related embeddings

for nodes connected by genuine citations.

This proximity aids in accurately predicting the

missing edges. By systematically perturbing the

graph and evaluating the reconstruction accuracy, the

approach identifies manipulated citations, which tend

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

770

to demonstrate poor reconstruction performance,

thereby revealing their anomalous nature. The

provided numerical experiments demonstrate that this

technique effectively identifies anomalies within

citation networks, supplying a valuable tool for

detecting citation manipulation.

The suggested approach in this paper, while

focusing on identifying "aberrant" citation patterns,

has inherent restrictions that can lead to inaccuracies,

especially when applied to multidisciplinary articles

or phenomena like "sleeping beauties”. A "sleeping

beauty" article receives minimal attention primarily

but later experiences a surge in citations due to

significant developments or rediscovery.

Additionally, mentions of ancient works by historical

figures like Newton and Archimedes often are uncited

due to their common knowledge, so citing such an

article can be comprehended as an anomaly.

Multidisciplinary articles integrating datasets and

methodologies from multiple fields pose another

challenge. One potential strategy is to match each

citation to its relevant dataset within its respective

domain, though alternative approaches may be

considered.

The manuscript proceeds as follows: Section 2

introduces the GraphSAGE model embedding.

Subsequently, Section 3 details the proposed model

for detecting citation manipulation. Experimental

evaluation is presented in Section 4, followed by a

summary and concluding remarks in Section 5.

2 GraphSAGE MODEL

EMBEDDING

GraphSAGE (Hamilton, Ying and Leskovec, 2017)

stands as a notable model in the realm of Graph

Convolutional Networks (GCNs), drawing

inspiration from the Weisfeiler-Lehman graph

isomorphism test to deliver advanced capabilities for

inductive representation learning on large and

dynamic graphs. Unlike transductive learning

methods, which rely on the entire graph being present

during training and inference, GraphSAGE is

uniquely suited for evolving graph structures and

scenarios where new nodes are introduced post-

training. One of the approach's core strengths lies in

its ability to harness rich node attributes—such as

user profiles in social networks, chemical properties

in molecular graphs, or bibliometric metadata in

citation networks—while also considering the

graph’s structural context. By aggregating

information from a node's local neighborhood, the

model generates embeddings that effectively capture

topological relationships and feature-based nuances,

enabling it to learn highly expressive node

representations.

A notable feature of GraphSAGE is its flexibility

in choosing aggregation functions, such as mean,

LSTM-based, or pooling, allowing practitioners to

tailor the model to the specific needs of their

applications. This versatility, efficiency, and

scalability have made GraphSAGE a cornerstone for

various graph-related tasks, such as Community

Detection, Node Classification, Link prediction, etc.

To aggregate feature information from a node's local

neighbourhood, including attributes like degrees or

textual features of neighboring nodes, GraphSAGE

employs a powerful and flexible framework, which

generates node embeddings through a forward

propagation process using learned model parameters.

This procedure iteratively gathers information from a

node's neighbors, combines it, and transforms it into

a compact and meaningful representation.

The algorithm describes a method for generating

node embeddings in a graph. It iteratively updates

node representations, starting with the graph and

initial node features. During each iteration, a node's

representation is updated by aggregating information

from its neighbours and merging it with its current

representation.

This merged information is passed through a

neural network layer to generate the updated

representation. Repeating this process for a fixed,

appropriately chosen number of iterations produces

final embeddings that capture local and global graph

structure.

Data:

• A graph 𝐺= (𝑉,𝐸), where 𝑉 is the set of

nodes, input features {𝑥



,∀𝑣 ∈ 𝑉}, and 𝐸 is

the set of edges.

• Feature matrix 𝑋∈ℝ



×

, where 𝑑 is the

dimension of node features.

• Aggregation function AGGREGATE.

• Number of layers 𝐾.

• Weight matrices 𝑊



for 𝑘 = 1,2,…,𝐾.

• Non-linearity 𝜎(⋅) (e.g., ReLU).

• Neighbourhood sampling size 𝑆.

• Embedding dimension 𝐷𝑖𝑚

Result: Node embeddings 𝑍∈ℝ



×

;

1. Initialize node representations:

For each node 𝑣∈𝑉, initialize the node

Citation Steadiness Analysis with GraphSAGE Approach

771

representation: ℎ





=𝑥



, where 𝑥



is the initial

feature vector for the node 𝑣.

2. Message passing and aggregation:

For each layer 𝑘=1 𝑡𝑜 𝐾:

a. For each node 𝑣∈𝑉:

• Sample a fixed-size set of neighbors

𝑁



(

𝑣

)

⊂𝑁

(

𝑣

)

(if sampling is used),

where 𝑁(𝑣) refers to the neighborhood of

a node 𝑉 in a graph 𝐺= (𝑉,𝐸).

• Aggregate the representations of neighbors

𝑁



(

𝑣

)

𝑚





𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸



({ℎ





:𝑢 ∈ 𝑁



(𝑣)})

• Concatenate the aggregated message 𝑚





with the current ℎ





ℎ





=𝜎(𝑊



⋅𝐶𝑂𝑁𝐶𝐴𝑇(ℎ





,𝑚





)).

3. Normalize embeddings:

Normalize ℎ





to maintain numerical stability if

required.

4. Output final embeddings:

After 𝐾 iterations, the final node embeddings

are: 𝑧



= ℎ





∀𝑣 ∈ 𝑉.

Algorithm 1: GraphSAGE- Embedding Generation

Algorithm.

Key Components:

1. Aggregation Function (AGGREGATE):

Examples of aggregation functions include:

• Mean Aggregator.

• Pooling Aggregator.

• LSTM Aggregator: Applying an LSTM over the

sequence of neighbour embeddings.

2. Sampling Neighbourhood:

To scale to large graphs, only a subset of neighbors is

sampled for aggregation.

Dimension outlines refer to the size of the hidden

layers within a neural network. This is a crucial

parameter that the user must specify. A common

practice is keeping the dimension consistent

throughout all layers or gradually reducing it as the

network's depth increases.

3 APPROACH

This section outlines the presented method for

estimating the reliability of citations in academic

systems, which may signal manipulation or

fraudulent activity grounded in the premise that

manipulated citations are intentionally added to

inflate the perceived impact of specific publications.

Such citations are expected to exhibit inconsistencies

and become detectable when a citation network is

subjected to perturbations. So, it is hypothesized that

it is possible to identify these irregularities and

expose suspicious citations by examining the stability

of citations under arbitrary disturbances introduced to

the citation network involving randomly removing

edges in a controlled manner. These modifications

simulate different scenarios to evaluate the network’s

robustness, stability, and structural integrity.

Applying these perturbations aims to expose

vulnerabilities within the network and increase the

likelihood of anomalies or manipulated elements

displaying abnormal behaviour, thereby

distinguishing them from authentic components.

A link prediction is conducted to maintain the

network’s coherence following these perturbations.

This step utilizes node embeddings of the permuted

network to measure the similarity or proximity

between node pairs. Various similarity metrics are

employed, such as cosine similarity, Euclidean

distance, and graph-based measures like mutual

neighbours and the Jaccard coefficient.

The citation graph is treated as undirected in this

study, focusing on the overall connectivity between

papers rather than the direction of citations. This

undirected perspective allows for a comprehensive

analysis of the network’s structure and patterns,

capturing relationships and dependencies among

papers irrespective of whether they are cited.

A pseudocode of the proposed approach is given

as Algorithm 2.

Data:

• A graph 𝐺= (𝑉,𝐸), where V is the set of

nodes, input features {𝑥



,∀𝑣 ∈ 𝑉}, and 𝐸 is

the set of edges.

• Feature matrix 𝑋∈ℝ



×

, where 𝑑 is the

dimension of node features.

• Aggregation function 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸.

• Number of layers 𝐾.

• Embedding dimension 𝐷𝑖𝑚

• Weight matrices 𝑊



for 𝑘 = 1,2,…,𝐾..

• Non-linearity 𝜎(⋅) (e.g., ReLU).

• Neighbourhood sampling size 𝑆.

• 𝑁_𝑖𝑡𝑒𝑟—Number of perturbations.

• 𝐹𝑟—Fraction of edges randomly omitted in each

iteration.

• 𝑆𝑖𝑚—Similarity measure.

• 𝑇𝑟—Similarity threshold.

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

772

Result: a sorted array 𝑅𝑒𝑠𝑢𝑙𝑡0 in ascending order;

1. Load the dataset 𝐺= (𝑉,𝐸),

2. Initialize an array 𝑅𝑒𝑠𝑢𝑙𝑡0 of zeros with a

length equaling the number of edges in 𝐺,

3. For 𝑖𝑡𝑒𝑟 = 1: 𝑁_𝑖𝑡𝑒𝑟 do:

• Create a temporary dataset 𝐺_𝑇 by removing the

𝐹𝑟 fraction of edges in 𝐺 without replacement.

• Create an embedding of 𝐺_𝑇: 𝑊(𝐺_𝑇) =

GraphSAGE (𝐺_𝑇, 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸, 𝑊



, 𝜎, 𝑆,

𝑁_𝑖𝑡𝑒𝑟, 𝐹𝑟, 𝑆𝑖𝑚, 𝑇𝑟).

• Calculate for all pairs of nodes of 𝐺_𝑇 the

similarity values between all nodes,

• Compose a set 𝐸𝐷_𝑅 of the edges reconstructed

using the procedure:

Link_prediction (𝐺_𝑇,𝑊(𝐺_𝑇), 𝑆𝑖𝑚, 𝑇𝑟),

• For edge in 𝐸𝐷_𝑅 do:

𝑅𝑒𝑠𝑢𝑙𝑡(𝑒𝑑𝑔𝑒) = 𝑅𝑒𝑠𝑢𝑙𝑡(𝑒𝑑𝑔𝑒) + 1

4. Summarize by sorting the array 𝑅𝑒𝑠𝑢𝑙𝑡0 in

ascending order.

Algorithm 2: A pseudocode of the proposed approach.

The process starts by downloading the examined

citation graph and initializing a zero-filled array

named 𝑅𝑒𝑠𝑢𝑙𝑡0, whose length matches the number of

edges in 𝐺 . Then, it proceeds through 𝑁_𝑖𝑡𝑒𝑟

sequential iterations. In each iteration, a temporary

graph, 𝐺_𝑇 is generated by randomly removing a

fraction 𝐹𝑟 of edges from 𝐺. This temporary graph is

then embedded into ℝ



using the GraphSAGE

algorithm. A similarity measure ( 𝑆𝑖𝑚 ) and a

threshold (𝑇𝑟) are introduced to enhance the method.

A similarity measure quantifies the similarity

between node pairs and the threshold (𝑇𝑟) determines

whether a pair is considered "connected" if the

similarity score between two nodes is greater than 𝑇𝑟,

they are classified as connected; otherwise, they are

considered disconnected. This criterion is then used

in the link prediction procedure to distinguish

between connected and disconnected nodes within

the graph.

𝐿𝑖𝑛𝑘_𝑝𝑟𝑒𝑑𝑖𝑐𝑡𝑖𝑜𝑛 (𝐺_𝑇, 𝑊(𝐺_𝑇), 𝑆𝑖𝑚, 𝑇𝑟) is a

procedure designed to predict the presence of an edge

between two nodes.

Data:

• 𝐺—Graph of paper citations.

• 𝑛



,𝑛



-two nodes in 𝐺.

• 𝑊(𝐺)—Embedding of Graph 𝑇.

• 𝑆𝑖𝑚—Similarity measure.

• 𝑇𝑟—Similarity threshold.

Result: If it is feasible to predict potential links

amid nodes 𝑛



and 𝑛



: false or true.

1. If the similarity score 𝑆𝑖𝑚 (𝑛



,𝑛



) is bigger

than 𝑇𝑟, the procedure returns 1 (true),

indicating that an edge could suppositionally be

between 𝑛



and 𝑛



2. Otherwise, if the similarity score is less than or

equal to 𝑇𝑟, the procedure returns 0 (false),

indicating that there is likely no edge between

𝑛



and 𝑛



Algorithm 3: A link_prediction procedure.

4 NUMERICAL EXPERIMENTS

To investigate the datasets, we conduct numerical

experiments with 500 (number of perturbations)

iterations per experiment and explore different

parameter settings. These tests explored three key

parameters: 𝐹𝑟 (set at 0.3, 0.4, and 0.5), 𝑇𝑟 = 0.95,

and the cosine similarity. The number of layers 𝐾 is

10. All weights in 𝑊



for 𝑘=1,2,…,𝐾 are equal to

1. Non-linearity activation function 𝜎(⋅) is ReLU.

The neighbourhood sampling size 𝑆 is 2.

The main goal is to assess the distribution of the

reconstruction rate for the edges. An edge is deemed

"non-reconstructed absent" when the similarity

between the two nodes it connects does not surpass

established thresholds. The results are presented

using histograms that illustrate the distribution of

edge recovery success rates obtained during an

iterative procedure. In these visualizations, color

coding highlights critical areas:

• Red: Represents the lower bound of

reconstructed edges for the bottom 10% of the

data.

• Blue: Covers the range of reconstructed edges

between 10% and 50%.

• Yellow: Indicates 50% and 90% of reconstructed

edges.

• Green: Covers the range of reconstructed edges

above 90% of reconstructed edges.

4.1 Cora Dataset

The Cora dataset, a widely recognized benchmark for

machine learning and network analysis research,

consists of 2,708 scientific papers categorized into 7

distinct classes within the machine learning field. It

features 5,429 citation connections, making it well-

suited for evaluating algorithms for tasks like

document classification and link prediction.

GraphSAGE embedding dimensions are influenced

Citation Steadiness Analysis with GraphSAGE Approach

773

by factors such as the number of layers, hidden layer

dimensions, and aggregation methods, which are

explored by testing dimensions (32, 16, 64, 128, 256).

This hyperparameter tuning process identified

𝐷𝑖𝑚 = 256 as our application's most apposite

embedding dimension.

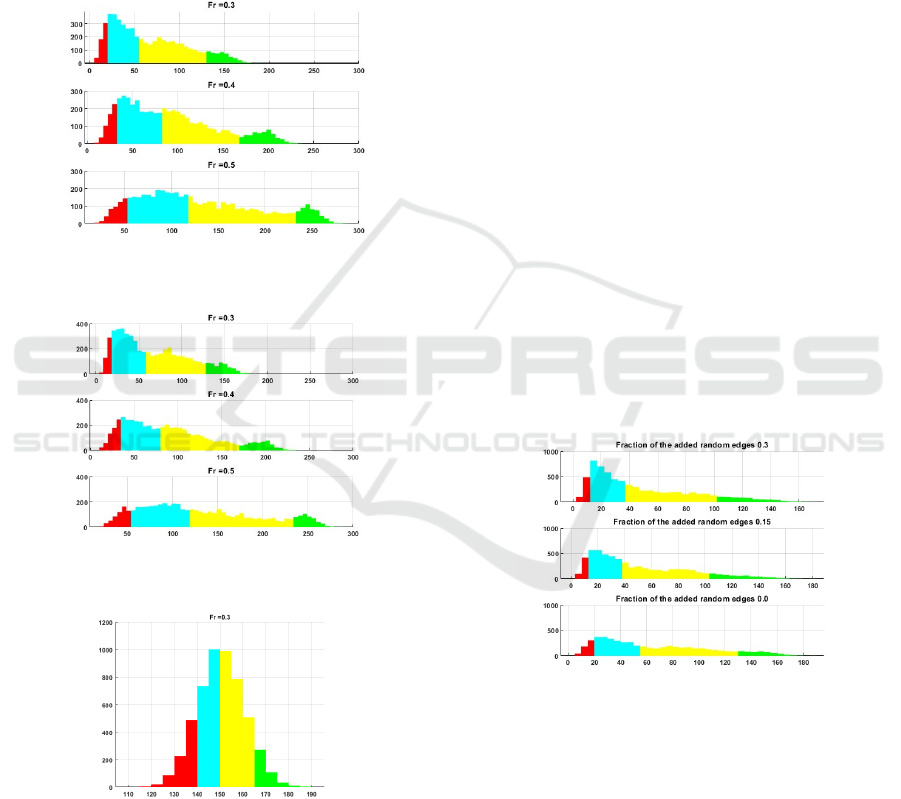
4.1.1 Experiments with Real Data

The following 3 figures demonstrate the results of the

given Aggregation function (𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸).

Figure 1: Histograms of reconstruction rate obtained for the

Cora dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=’Mean’.

Figure 2: Histograms of reconstruction rate obtained for the

Cora dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=’Pool’.

Figure 3: Histograms of reconstruction rate obtained for the

Cora dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=’LSTM’.

First, it must be noted that it is highly uncommon

to observe a normal distribution in subjects connected

to citation distributions, as this goes against the well-

established trend that citation distributions are

typically skewed with a long-tail pattern. This implies

that a small proportion of highly cited papers

accumulate most citations, while the vast majority

receive relatively few. Such skewness is often

explained by phenomena like the "Matthew effect"

(where highly cited papers attract even more

citations), the influential nature of groundbreaking

works, and the impact of prevailing research trends.

So, in citation networks, the Matthew effect posits

that highly cited papers tend to attract further

citations, thereby contributing to a skewed

distribution of citations within the scholarly

landscape. Moreover, it contradicts the results stated

in (Avros, Keshet, Toledano-Kitai, Vexler, and

Volkovich, 2023) and (Avros, Haim., Madar, Ravve,

and Volkovich, 2024).

The observation of a normal citation distribution

might indicate an inappropriate choice of the

aggregation function. It appears that an LSTM-based

aggregation is not appropriate for this relatively small

dataset.

4.1.2 Sanity Checks

The Modified versions of the CORA dataset are

tested to evaluate the model's performance

thoroughly. The variation includes a 15% and 30%

increase in edges, simulating noise or unexpected

connections. These changes allow us to assess the

model's ability to generalize and adapt to

transformations in the graph's underlying structure.

The experiments are provided for 𝐹𝑟=0.3.

Figure 4: Histograms of reconstruction rate obtained for

noise versions of the Cora dataset with

𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=’Mean’.

As was expected, the injected noises significantly

increase the distribution of positive asymmetry, i.e.,

the tail of the distribution extends towards the right

side of the number line. The most visible influence

occurs in 30% noise attitude (the upper panel). To

ensure consistency in analysis, the distributions of all

three dataset versions are presented using the

identical binning structure of 4 colored areas as that

utilized for the original, "clean" dataset without any

added noise.

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

774

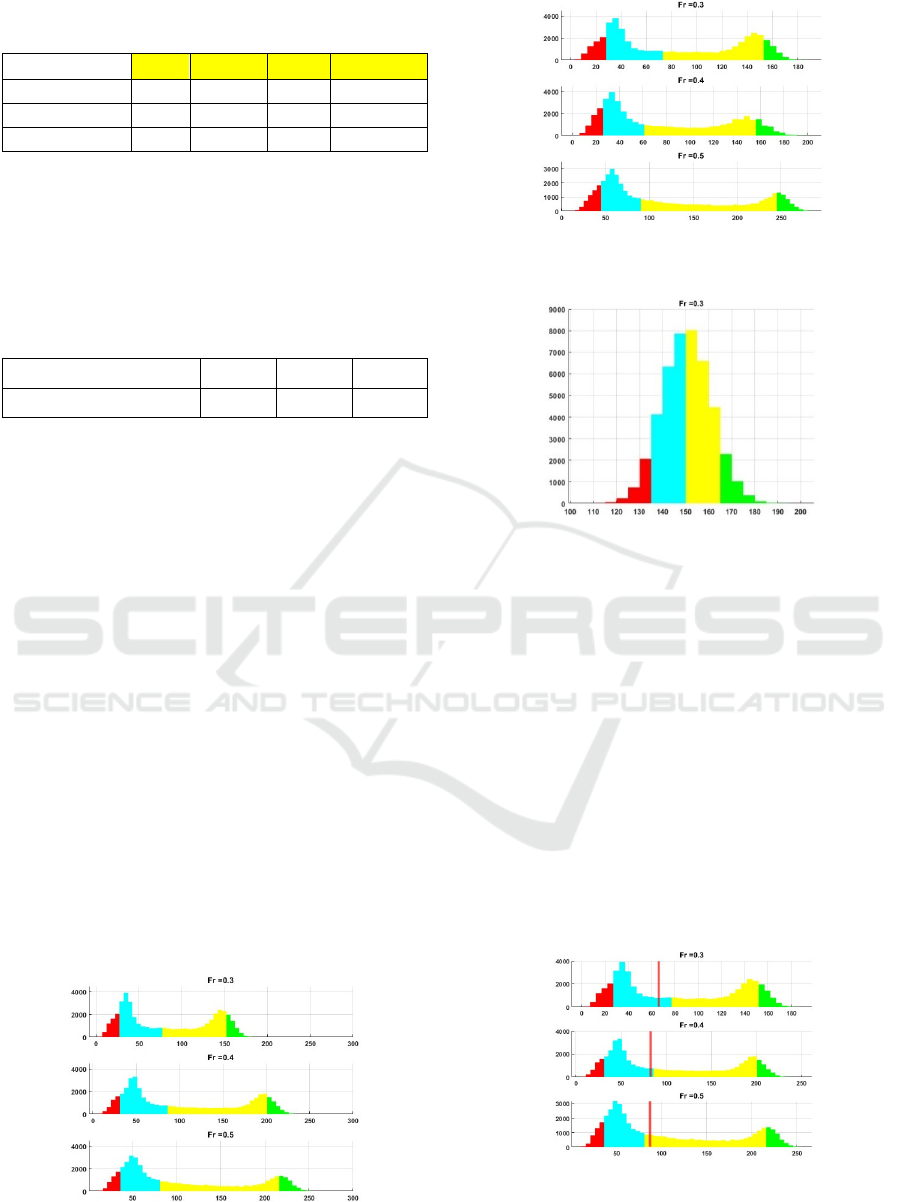
Table 1: The reconstructed edges in 3 dataset versions

within 4 colored areas.

Noise attitude 1 2 3 4

0.3

740

2890 2778 705

0.15

519

2401

2667 683

0.0

131

1553

2575 1119

The presented results provide evidence of the

model's readiness for deployment. A notable

observation is an increase in the frequencies of the

two first categories, accompanied by shifts in the

frequency of the last group. The appropriate skewness

values also support this conclusion.

Table 2: The skewness attitude calculated for 3 datasets.

Noise attitude 0.30 0.15 0.0

Skewness 0.19 0.37 0.58

4.2 PubMed Dataset

PubMed is a freely available database curated by the

U.S. National Library of Medicine (NLM), a part of

the National Institutes of Health (NIH). It serves as a

comprehensive platform for accessing biomedical

and life sciences literature. The database primarily

includes references and abstracts from scientific

journals, spanning various disciplines such as

medicine, biology, healthcare, bioinformatics,

biochemistry, and public health. The core of

PubMed's content is sourced from **MEDLINE**,

NLM’s primary bibliographic database. Additionally,

it integrates literature from **PubMed Central

(PMC)**, a free repository for full-text biomedical

articles. Hosting over **35 million citations and

abstracts**, PubMed offers coverage that extends

back to the 1940s and is regularly updated with the

latest research findings. The dataset exhibits a

network structure with 19,717 nodes representing

papers and 88,648 edges representing citation links

between them. The articles are classified into 3

distinct thematic categories.

Figure 5: Histograms of reconstruction rate obtained for the

PubMed dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=’Mean’.

Figure 6: Histograms of reconstruction rate obtained for the

PubMed dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=Pool’.

Figure 7: Histograms of reconstruction rate obtained for the

PubMed dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=LSTM’.

In all considered circumstances except for the

“LSTM” case, the appearing histograms are bimodal,

suggesting a mixture distribution where the observed

data originates from two separate underlying

components. This pattern typically indicates that the

data is not homogeneous but fairly composed of two

subpopulations governed by its own distribution. The

“Expectation-Maximization (EM) algorithm” can be

employed to uncover these subpopulations. The

resulting clusters, derived from the histogram's

bimodal nature, enable a deeper understanding of the

data's composition, allowing researchers to explore

each subpopulation's distinct properties and

templates. Examples of such partitions are given in

the following figure.

Figure 8: Histograms of reconstruction rate obtained for

the PubMed dataset with 𝐴𝐺𝐺𝑅𝐸𝐺𝐴𝑇𝐸=Mean’ with

clusters boundary.

Citation Steadiness Analysis with GraphSAGE Approach

775

The vertical red lines assign the boundary

between clusters. As can be seen, the partitions are

about the same in all cases, which can indicate the

presence of two subpopulations in the edge

community.

5 SUMMARY AND

CONCLUSIONS

This research introduces a new methodology for

detecting suspicious citations in scientific literature

using the GraphSAGE algorithm and enhanced

citation graph embeddings. The method has shown

effectiveness in uncovering citation anomalies

through extensive testing. However, challenges arise

in handling interdisciplinary research and "sleeping

beauties"—articles initially overlooked but later

recognized due to delayed breakthroughs—making it

difficult for the model to differentiate genuine citation

dynamics from anomalies.

Approximately 80% of citation edges studied in

the study are identified as vulnerable to distortion,

revealing their lack of robustness within the citation

graph. These edges are flagged as potentially

manipulated, highlighting the fragile nature of

citation datasets and the significant impact that

individual edges can have on network stability and

reliability. Despite structural differences between

datasets, shared characteristics are identified,

suggesting universal tendencies within citation

systems. The Cora dataset displayed a homogeneous

structure with a higher proportion of suspicious

citations, while an analysis of the larger and more

heterogeneous PubMed dataset reveals two distinct

citation groups: one associated with suspicious edges

and another with more stable, well-reconstructed

citations.

All datasets considered exhibit a stable core of

reliable connections, reflecting the gradual

accumulation of trustworthy citations over time.

Nonetheless, even in datasets regularly updated with

new publications, a substantial number of edges are

found to be unstable or irrelevant, suggesting that

citation datasets inherently include connections

disposed to manipulation or unreliability.

Reconstruction score distributions demonstrated a

positively skewed, unimodal pattern, where most

citations clustered around lower scores, with a right-

skewed tail influenced by higher scores. This

distribution implies that a significant portion of

citations may lack reliability, raising concerns about

potential manipulation.

To validate the proposed approach, an experiment

is conducted with artificially augmented citation

graphs obtained by adding random noise expressed in

random edges. The results validate the model's

effectiveness in detecting such anomalies, further

reinforcing its value as a reliable tool for identifying

citation manipulation. The proposed method provides

a framework for dynamically monitoring research

trends and integrating new articles into citation

graphs, leveraging a stable core of knowledge to

evaluate individual links. Exploring positions within

the recovery histogram offers insights into citation

reliability and susceptibility to manipulation.

This research proposes new avenues for

understanding citation dynamics, emphasizing the

role of stable reconstructed edge clusters in

maintaining citation network integrity. It also

highlights universal patterns within citation systems,

offering valuable insights for developing robust tools

for citation analysis and anomaly detection.

REFERENCES

Avros, R., Haim, M. B., Madar, A., Ravve, E., &

Volkovich, Z. (2024). Spotting suspicious academic

citations using self-learning graph transformers.

Mathematics, 12(6), 814.

https://doi.org/10.3390/math12060814.

Avros, R., Keshet, S., Kitai, D. T., Vexler, E., & Volkovich,

Z. (2023). Detecting pseudo-manipulated citations in

scientific literature through perturbations of the citation

graph. Mathematics, 11(18), 3820.

https://doi.org/10.3390/math11123820.

Avros, R., Keshet, S., Kitai, D. T., Vexler, E., & Volkovich,

Z. (2023). Detecting manipulated citations through

disturbed node2vec embedding. In Proceedings of the

25th International Symposium on Symbolic and

Numeric Algorithms for Scientific Computing

(SYNASC), Nancy, France, 2023 (pp. 274–278). IEEE.

https://doi.org/10.1109/SYNASC61333.2023.00047

Falagas, M. E., & Alexiou, V. G. (2008). The Top-Ten in

Journal Impact Factor Manipulation. Archives of

Immunology and Therapy Experimental (Warsz),

56(4), 223–226. https://doi.org/10.1007/s00005-008-

0024-5.

Fong, E. A., & Wilhite, A. W. (2017). Authorship and

citation manipulation in academic research. PLOS

ONE, 12(12), e0187394.

https://doi.org/10.1371/journal.pone.0187394.

Grover, A., & Leskovec, J. (2016). Node2vec: Scalable

feature learning for networks. In Proceedings of the

22nd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining (KDD '16),

San Francisco, CA, USA, 13–17 August 2016 (pp. 855–

864). ACM. https://doi.org/10.1145/2939672.2939754.

Hamilton, W., Ying, Z., & Leskovec, J. (2017). Inductive

representation learning on large graphs. Advances in

Neural Information Processing Systems, 30, 1024–

1034.

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

776

Ioannidis, J. P. A., & Thombs, B. D. (2019). A user’s guide

to inflated and manipulated impact factors. European

Journal of Clinical Investigation, 49(7), e13151.

https://doi.org/10.1111/eci.13151.

Jacobs, J. A. (2016, June 30). Manipulated journal

rankings? Inside Higher Ed. Retrieved from

https://www.insidehighered.com/views/2016/07/01/ex

amination-whether-academic-journal-rankings-are-

being-manipulated essay.

Liu, J., Bai, X., Wang, M., et al. (2024). Anomalous

citations detection in academic networks. Artificial

Intelligence Review, 57, 103.

https://doi.org/10.1007/s10462-023-10375-w.

Prabha, C. G. (1983). Some aspects of citation behaviour:

A pilot study in business administration. Journal of the

American Society for Information Science, 34(4), 202–

206. https://doi.org/10.1002/asi.4630340404.

Resnik, D. B., Gutierrez-Ford, C., & Peddada, S. (2008).

Perceptions of ethical problems with scientific journal

peer review: An exploratory study. Science and

Engineering Ethics, 14(3), 305–310.

https://doi.org/10.1007/s11948-008-9077-2.

Wilhite, A., & Fong, E. (2012). Coercive citation in

academic publishing. Science, 335(6072), 542–543.

https://doi.org/10.1126/science.1210353.

Wilhite, A., Fong, E. A., & Wilhi, S. (2019). The influence

of editorial decisions and the academic network on self-

citations and journal impact factors. Research Policy,

48(6), 1033–1044.

https://doi.org/10.1016/j.respol.2019.03.003.

Wren, J. D., & Georgescu, C. (2022). Detecting anomalous

referencing patterns in PubMed papers suggestive of

author-centric reference list manipulation.

Scientometrics, 127(3), 5753–5771.

https://doi.org/10.1007/s11192-022-04362-w.

Citation Steadiness Analysis with GraphSAGE Approach

777