
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to
Cheng and Church Algorithm
Shokofeh VahidianSadegh
1 a
, Alberto Ibarrondo
2 b
and Lena Wiese
1 c
1
Computer Science Department, Goethe University Frankfurt, Frankfurt am Main, Germany
2
Arcium, France
Keywords:
Biclustering Algorithm, Privacy-Preserving AI, Secure Multi-Party Computation, Function Secret Sharing.
Abstract:
High-throughput technologies (e.g., the microarray) have fostered the rapid growth of gene expression data
collection. These biomedical datasets, increasingly distributed among research institutes and hospitals, fuel
various machine learning applications such as anomaly detection, prediction or clustering. In particular, un-
supervised classification techniques based on biclustering like the Cheng and Church Algorithm (CCA) have
proven to adapt particularly well to gene expression data. However, biomedical data is highly sensitive, hence
its sharing across multiple entities introduces privacy and security concerns, with an ever-present threat of
accidental disclosure or leakage of private patient information. To address such threat, this work introduces
a novel, highly efficient privacy-preserving protocol based on secure multiparty computation (MPC) between
two servers to compute CCA. Our protocol performs operations relying on an additive secret sharing and func-
tion secret sharing, leading us to reformulate the steps of the CCA into MPC-friendly equivalents. Leveraging
lightweight cryptographic primitives, our new technique named FunBic-CCA is first to exploit the efficiency
of function secret sharing to achieve fast evaluation of the CCA biclustering algorithm.
1 INTRODUCTION
The abundance of biomedical data, thanks to the rapid
advancement and readily available high-throughput
technologies, provides great opportunities for the
knowledge discovery. Machine Learning (ML) has
been widely used to categorise and classify large
amounts of data. Among ML methods, the tradi-
tional one-way clustering methods perform analysis
directly on specific characteristics. More adaptable
approaches to gene expression data are biclustering
algorithms that have become prevalent with a wide
variety of applications, ranging from bioinformatics
to recommender systems, and many more. Biclus-
tering based on Cheng and Church Algorithm (CCA)
groups a set of genes and conditions with a high sim-
ilarity score. This was the first study to apply biclus-
tering algorithms over gene expression data (Cheng
and Church, 2000).
Despite this potential of large biomedical data
analysis, a recent influx of malicious attacks on these
a
https://orcid.org/0000-0002-6464-6842
b
https://orcid.org/0000-0003-4079-4127
c
https://orcid.org/0000-0003-3515-9209
sensitive resources has been increasingly reported.
Since that, there exists an inherent, simultaneous con-
tradiction between utility and privacy. Accordingly,
there must be improved data protection and preven-
tive information leakage measures against unautho-
rised users.
Considering this problem, we propose FunBic-
CCA (Function secret sharing for Biclusterings Ap-
plied to Cheng and Church Algorithm), a privacy-
preserving framework for gene expression data anal-
ysis by biclustering algorithms with well-established
schemes, additive secret sharing (SS (Demmler et al.,
2015)) and Function Secret Sharing (FSS (Boyle
et al., 2015)).
After discussing preliminaries from privacy-
preserving biclustering analysis methods (Section 2),
we detail FunBic-CCA framework (Section 3), which
provides core contributions below:
• An end-to-end privacy-preserving framework
based on additive secret sharing and function se-
cret sharing schemes;
• Support for privacy-preserving evaluation of both
linear and non-linear operations with 100% cor-
rectness in less than 500 seconds;
VahidianSadegh, S., Ibarrondo, A., Wiese and L.
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm.
DOI: 10.5220/0013455400003979
In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 37-48
ISBN: 978-989-758-760-3; ISSN: 2184-7711
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
37

• An extensive discussion on the security aspects of
FunBic-CCA as well as analyses on its accuracy
and efficiency;
• An open-source implementation
1
of our frame-
work, available under the permissive MIT license.
We evaluate the efficacy of FunBic-CCA through
experiments and evaluation measures using our
framework (Section 4). Finally, we present an
overview of related works and elaborate on differ-
ences of existing solutions (Section 5) then conclude
(Section 6).
2 BACKGROUND
We provide an overview of the applied techniques and
methods in FunBic-CCA. We first define our notation
and proceed with a description of Cheng and Church
Algorithm (Cheng and Church, 2000). Afterwards,
an overview of the cryptography methods used in our
framework is discussed.
Notation. We use regular letters for scalars (e.g., s)
and boldface letters for matrices in capitals (A) and
vectors of integers and polynomials (e.g., a). a
i j
de-
notes the element of the matrix A in the i-th row and
j-th column of a polynomial/ vector a with N coef-
ficients/ elements. We write a · b = c to denote the
element-wise two vector multiplication, while show-
ing matrix multiplication like A × B = C.
In a 2PC paradigm, P
0
, P
1
denote two comput-
ing parties or in general, we consider P
d
, where
d ∈ {0, 1}. a
i j
d
is an element of expression ma-
trix A for a party d. We use P
a
: q ⇒ P
b
to show
that party a sends value q to party b. We employ
⟨x⟩ to indicate that value x is arithmetically secret
shared into random shares (x
0
, x
1
), that are held by
two computing parties and verify x = x
0
+ x
1
mod
2
n
. All values are encoded on n-bits, which lives
in Z
2
n
. Z
∗
n
+
represents the range 0 ≤ x ≤ 2
n−1
− 1.
We note U
⌈l
r
·l
c
⌉
2
n
as the uniform distribution in the set
2
n
with the size of maximum number of elements
in a matrix with l
r
rows and l
c
columns. We use
1
r2del
, 1
c2del
, 1
r2sdel
, 1
c2sdel
, 1
r2add
, 1
c2add
to elaborate
on the comparison functions (e.g., 1
x≥0
⇔ x ≥ 0).
Cheng and Church Algorithm (CCA). Cheng
and Church (Cheng and Church, 2000) developed a
greedy algorithm and used a measure to evaluate the
consistency of matrix’s elements and to assess the
quality of a bicluster. Mean square residue score
1
https://github.com/ShokofehVS/FunBic-CCA
(MSR) measures the coherence of genes and condi-
tions of a bicluster by taking means of genes and con-
ditions. CCA focuses mainly on particularly large,
maximal biclusters with score below a predefined
threshold (δ). In other words, given that a matrix A
and a threshold δ ≥ 0, CCA finds δ-biclusters. After
finding values of the mean for rows (µ
r
), columns (µ
c
)
and all of elements (µ
i j
), the residue of the entry a
i j
for a bicluster B
k
= (r
k
, c
k
) is
r
i j
= a
i j
− µ
r
− µ
c
+ µ
i j
. (1)
which is needed to determine MSR (or H
i j
):
H
i j
=
∑
i∈r
k
∑
j∈c
k
r
2
i j
|r
k
||c
k
|
. (2)
Score for rows, and columns separately can be sum-
marised as follow in which:
H
r
=
1
|c
k
|
∑
j∈c
k
r
2
i j
, H
c
=
1
|r
k
|
∑
i∈r
k
r
2
i j
. (3)
The three different phases in CCA include mul-
tiple node deletion, single node deletion and node
addition. First step is the removal of multiple
rows/columns over the input data matrix, which is
followed by the single row/column deletion step. At
this point, the result may not be maximal and, there-
fore, a node addition step is required to insert some
rows/columns without increasing MSR. CCA takes as
input, the expression matrix (A), maximum accept-
able mean squared residue score threshold (δ), a pa-
rameter for multiple node deletion step (α), and num-
ber of δ-biclusters (k) (Cheng and Church, 2000).
Additive Secret Sharing. Additive secret sharing
(SS) focuses on rings with distributed secret x into
two random shares x
0
and x
1
, given that x = x
0
+ x
1
mod N (where N is the ring size) among two comput-
ing parties P
d
. Since then, two parties are able to per-
form local addition/subtraction of two secret shared
values. However, parties require one round of com-
munication to do multiplication by having Beaver’s
multiplication triples (Beaver, 1992). Lastly, the re-
sult is reconstructed by one chosen party, which adds
the two secret shares together. We work with N = 2
n
,
where n ∈ {8, 16, 32, 64}, by considering native inte-
ger types in modern computers that increase the speed
in working with the n-bit modular arithmetic.
Function Secret Sharing. A 2PC Function Secret
Sharing (FSS) scheme unlike standard secret sharing
of individual elements, shares description of a func-
tion f among parties (Boyle et al., 2015). In this
scheme, f is split into two shares ( f
0
, f
1
), where f
d
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
38
hides f and f
0
(x) + f
1
(x) = f (x) for the input value
x that is public for both parties. Due to the public-
ity of the secret input x, a random mask r is added
ˆx = x + r before using in FSS evaluation to keep its
privacy. The used mask is generally known by dealer
and applied for the key generation to blind the input.
We use Interval Containment (IC) gate for com-
parison (≥ γ, γ = 0) in our work
2
. Our equality check
between two secret shares is relied on the Distributed
Point Function (DPF) (Definition 2.5 of (Boyle et al.,
2019)) as an FSS scheme for the family of all point
functions
3
.
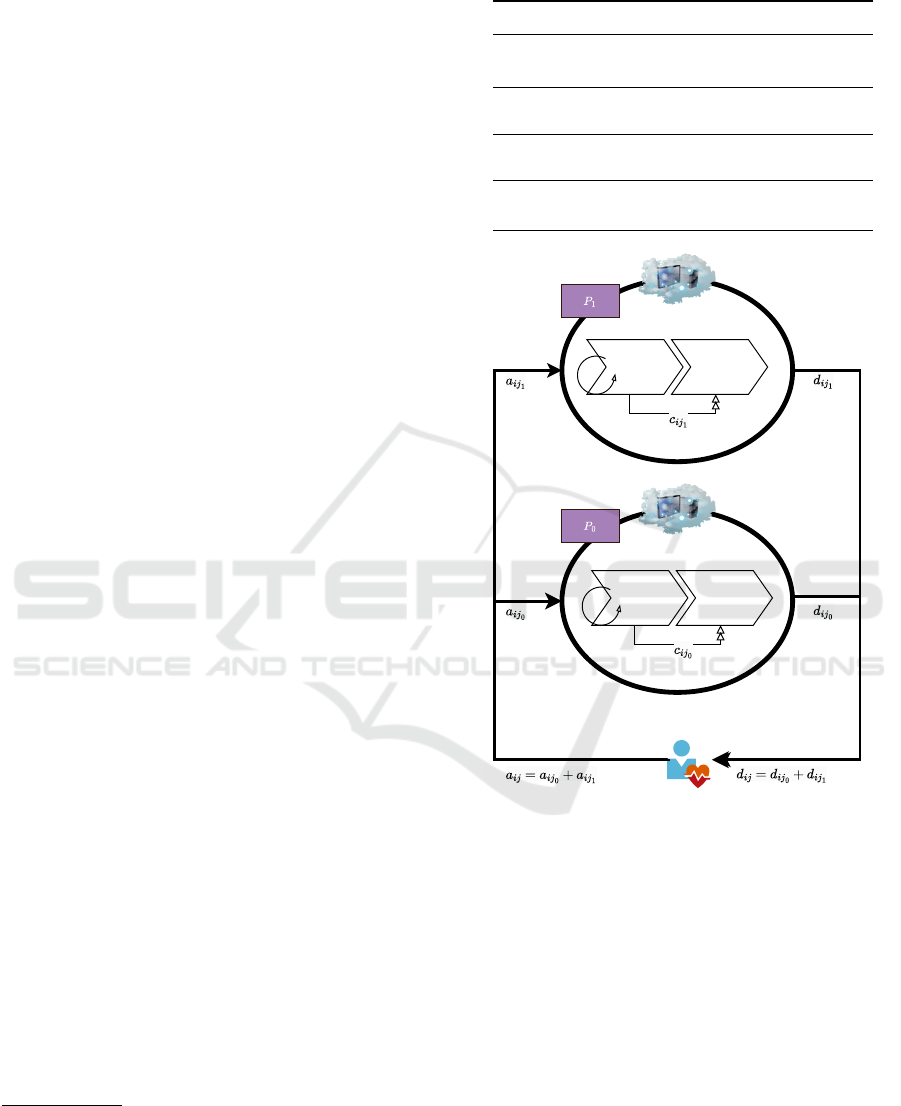
3 FunBic-CCA FRAMEWORK
In this Section, we provide a detailed description of
our FunBic-CCA framework.
Sketch of the Solution. We consider a scenario by
having a data owner and two cloud servers as our
computing parties (P
0
, P
1
):
• Data owner: or patient with his genes sequenced
as matrix A of expression level values a
gp
, con-
sisting of genes g under different conditions p.
• Public cloud servers: by which we intend to exe-
cute biclustering on the secret shared gene expres-
sion data with our algorithmic design.
Different types of computations are needed in the
procedure that can potentially be transferred to the
public cloud services. Table 1 contains these steps
(further explanations on these steps in Section 2) and
Figure 1 represents the general overview of our pro-
posed solution. Prior to the introduction of our main
building blocks, we summarise the main generic func-
tions inside our algorithm (with the steps in Table 1)
that we intend to protect by MPC based operations
(see Section 3.1):
H
i j
, H
r
, H
c
H
r
> αH
i j
, H
c
> αH
i j
H
r
[d(i)] ≥ H
c
[d( j)], H
r
[d(i)] < H
c
[d( j)]
H
r
≤ H
i j
, H
c
≤ H
i j
(4)
2
IC gate in FSS scheme computes f
p,q
(x) = 1
x∈[p,q]
where p = 0, q = 2
n−1
− 1 to finally obtain 1
0≤x≤2
n−1
−1
(Section 4.1 of (Boyle et al., 2021)).
3
This states that for a point function f
α,β
, f (α) = β and
f (x) = 0 for x ̸= α, where α ∈ G
in
, β ∈ G
out
, f : G
in
→ G
out
.
Table 1: Steps within Cheng and Church Algorithm.
Step Description
1 Finding mean squared residue scores
H
r
, H
c
and H
i j
2 Evaluation in multiple node deletion
H
r
> αH
i j
, H
c
> αH
i j
3 Evaluation in single node deletion
H
r
[d(i)] ≥ H
c
[d( j)], H
r
[d(i)] < H
c
[d( j)]
4 Evaluation in node addition
H
r
≤ H
i j
, H
c
≤ H
i j
CCA
Deletion Addition
Deletion Addition
CCA
Figure 1: General overview of FunBic-CCA system.
Two-Party Computation Scenario. Our solution
is based on the two-party computation (2PC) con-
text, having two computing parties (P
0
, P
1
) to per-
form secure computations as well as the data owner.
In this two-server protocol, the data owner interacts
with these two servers that are assumed not to collude
(Boyle et al., 2021).
Our framework is secure against Honest-but-
Curious (“semi-honest”) adversaries. Therefore,
FunBic-CCA provides privacy of all the input data in
the case of corruption of either the two parties by a
semi-honest adversary. This work is designed in MPC
with a preprocessing model, having a setup/offline
phase to benefit from an optimised online phase.
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm
39

3.1 Cryptographic Primitives
Here, we provide details of our building blocks that
form the core of our framework and for which we
decide to apply secret sharing schemes. In all op-
erations, d refers to the number of parties, precisely
d ∈ {0, 1}. Note that, each individual element (a
i j
)
of the input matrix (A) is secret shared among parties
with the following condition: a
i j
= a
i j
0
+ a
i j
1
.
Construction of Secure Linear Operations. We
require to obtain the below-mentioned operations,
such as addition/subtraction, and multiplication:
• Addition/ subtraction: These operations can be
computed locally. Accordingly, both parties are
able to perform the following operations on their
own secret shared input matrix.
– Finding the mean values, residue, scores of the
whole matrix, and nodes are based on addition/
subtraction.
l
r
·l
c
∑
a
i j
d
,
l
r
∑
a
i j
d
,
l
c
∑
a
i j
d
l
r
·l
c
∑
(a
i j
d
− µ
r
d
− µ
c
d
+ µ
i j
d
)
l
r
·l
c
∑
r
2
i j
d
,
l
r
∑
r
2
i j
d
,
l
c
∑
r
2
i j
d
(5)
• Multiplication: Both parties perform SS-based
multiplications in one round of communication
and consumption of the beaver multiplication
triples.
– Squaring the residue (r
i j
0
× r
i j
1
) as part of
the score formula requires parties to perform
element-wise multiplication for the matrices
jointly using beaver triples. We follow the steps
mentioned in (Knott et al., 2021). To square
the residue r
2
i j
= r
2
i j
0
+ r
2
i j
1
+ 2 × r
i j
0
× r
i j
1
, the
parties use a beaver pair ˆa,
ˆ
b, such that
ˆ
b = ˆa
2
.
Then, parties compute ˆe
d
= r
i j
d
− ˆa
d
, decrypt ˆe
d
to obtain result with r
2
i j
=
ˆ
b
d
+ e
2
+ 2 × e × ˆa
d
.
Construction of Secure Non-Linear Operations.
Our algorithm relies on non-linear operations, includ-
ing comparison, argmax and division:
• Comparison: Main comparative functions are de-
noted in Table 2. The threshold in comparison i.e.,
zero (is referred to γ), must be kept private and
hidden by parties by using a random mask. In the
online phase,the parties are required to compute
1
r2del(H
r
d
,α·H
i j
d
)>0
, 1
c2del(H
c
d
,α·H
i j
d
)>0
1
r2sdel(H
r
d
[d(i)],H
c
d
[d( j)])≥0
, 1
c2sdel(H
c
d
[d( j)],H
r
d
[d(i)])>0
1
r2add(H
i j
d
,H
r
d
)≥0
, 1
c2add(H
i j
d
,H
c
d
)≥0
1
stop(H
i j
d
,δ)≥0
1
req(I
d
,I
′
d
)==0
, 1
ceq(J
d
,J
′
d
)==0
(6)
on the secret shares a
i j
d
.
Parties evaluate IC gate to determine whether
the result is greater or equal to the threshold
for 1
r2del
, 1
c2del
, 1
r2sdel
, 1
c2sdel
, 1
r2add
, 1
c2add
. The
DPF gate handles our equality checks, 1
req
, 1
ceq
.
For stopping condition 1
stop
, we reconstruct the
intermediate results o
stop
0
, o
stop
1
after FSS IC gate
to check whether our score H
i j
d
, is below or equal
to the threshold δ.
To this end, our condition to remove columns,
1
con
, is done in the cleartext, since the size of the
input is public and known by both parties. Note
that, each of the comparison function requires one
round of communication and to send two ring el-
ements in the online phase.
• Argmax: Single node deletion step works with re-
moving a single row or column, whichever hav-
ing the largest d(i) or d( j). This is achieved by
finding the argmax of rows and columns with the
largest score:
d(i) = argmax(H
r
), d( j) = argmax(H
c
) (7)
Our argmax function is similar to the algorithm
6 of (Ryffel et al., 2020), using pairwise compar-
isons. It gets as input; secret shared scores of rows
or columns (H
r
, H
c
) and outputs the index of the
row or column with the largest score value.
Algorithm 3 requires a constant number of
rounds. For instance, argmax of rows with length
l
r
requires l
r
(l
r
− 1) parallel comparisons with IC
gate and l
r
equality checks with DPF gate. There-
fore, we need two rounds of communication and
sending O(l
2
r
) values in an online phase.
• Division: Finding mean which is a base function
for calculation of the scores relies on a division.
∑
l
r
·l
c
a
i j
d
|I||J|
,
∑
l
r
a
i j
d
|J|
,
∑
l
c
a
i j
d
|I|
∑
l
r
·l
c
r
2
i j
d
|I||J|
,
∑
l
r
r
2
i j
d
|J|
,
∑
l
c
r
2
i j
d
|I|
(8)
In secured machine learning applications (Ryffel
et al., 2020), it is a standard assumption to keep
the data and model parameters private; however,
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
40

Table 2: FunBic-CCA comparative functions.
Formula Symbol
H
r
> αH
i j
, H
c
> αH
i j
1
r2del
, 1
c2del
H
r
[d(i)] ≥ H
c
[d( j)] 1
r2sdel
, 1
c2sdel
H
r
≤ H
i j
, H
c
≤ H
i j
1
r2add
, 1
c2add
H
i j
≤ δ 1
stop
I == I
′
∧ J == J
′
1
req
, 1
ceq
|J| <= 100 1
con
the shape (number of rows and columns) of the
input and the architecture of the model are public.
In addition, multiplying or dividing by a public
value (Escudero, 2022) such as |I|, |J| can be exe-
cuted locally.
Prior to any changes on nodes (removing, adding),
the dimension of matrix is clear; thus the mean
values are being done as mentioned above. Ad-
ditionally, parties do local operations, including
addition/ subtraction simultaneously by one, once
any node is added/ removed.
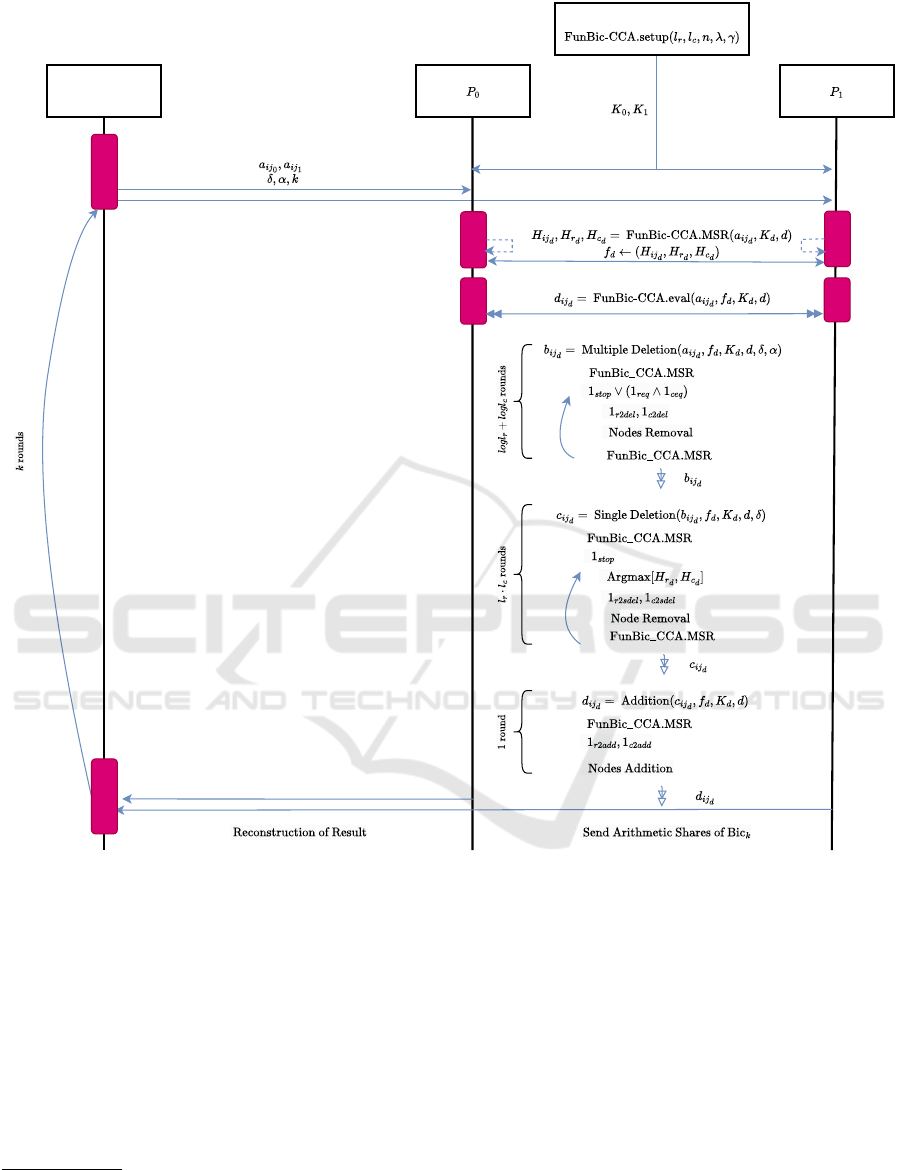
3.2 System Protocol
We describe our protocols needed to deliver the full
solution based on the crytographic primitives in Sec-
tion 3.1. Figure 2 shows these protocol steps.
We follow the below settings in the offline and on-
line phases, having the two parties (P
0
, P
1
):
• Offline phase: Correlated randomness is required
to perform the secured multiplication according to
the discussion in Section 3.1. The generation of
the FSS keys for the comparison functions also
occurs in “FunBic-CCA.setup”. These prepro-
cessing materials are distributed among the par-
ties to be used in the online phase.
We assume a trusted dealer, an individual entity,
to only participate in the offline phase and pro-
vide the computing parties with the preprocessing
materials. We can also realise a trusted dealer by
having our two computing parties in a pure 2PC
scenario jointly generate required preprocessing
materials (Boyle et al., 2021).
• Online phase:
1. Identification of the scores: Calculation of
the mean squared residue for the whole
input matrix and its rows and columns
(i.e., H
i j
d
, H
r
d
, H
c
d
) takes place in “FunBic-
CCA.MSR”.
The parties perform linear operations, addition/
subtraction, along with a non-linear division lo-
cally. Further, the parties square the residue
Algorithm 1: FunBic-CCA.setup (l
r
, l
c
, n, λ, γ) →
K
0
, K
1
.
Input: l
r
· l
c
: length of matrix A.
n: number of bits for secret sharing
ring Z
2
n
.
λ: security parameter.
γ: threshold for comparison
(∈ Z
2
n
, γ = 0).
Output: K
0
, K
1
: keys in preprocessing phase.
Preprocessing Steps:
Beaver triples for multiplication:
① ⟨ ˆa⟩ ≡ ( ˆa
0
, ˆa
1
) ∼ U
l
r
·l
c
2
n
②
ˆ
b
0
← ˆa
2
0
∼ U
l
r
·l
c
2
n
③
ˆ
b
1
← ( ˆa
0
+ ˆa
1
)
2
−
ˆ
b
0
④ ⟨
ˆ
b⟩ ≡ (
ˆ
b
0
,
ˆ
b
1
)
Random masks for FSS gates:
① ⟨r⟩ ≡ (r
0
, r
1
) ← (r
0
+ r
1
) ∼ U
2
2
n
② ⟨r
γ
⟩ ≡ (r
γ
0
, r
γ
1
) ← (r
0
, r
1
− γ)
Distribution of preprocessing materials:
① K
d
≡ ( ˆa
d
,
ˆ
b
d
, r
γ
d
, K
IC
d
, K
EQ
d
), d ∈ {0, 1}
② K
0
⇒ P
0
, K
1
⇒ P
1
(r
i j
d
) by having the correlated randomness from
the setup phase in one round of communication.
Algorithm 2:
FunBic-CCA.MSR (a
i j
d
, K
d
, d) → H
i j
d
, H
r
d
, H
c
d
.
Input: a
i j
d
: input matrix
(∈ {a
i j
0
, a
i j
1
}, Z
l
r
·l
c
2
n
).
K
d
: preprocessing keys containing
ˆa
d
,
ˆ
b
d
.
d: computing parties (∈ {0, 1}).
Output: H
i j
d
, H
r
d
, H
c
d
: similarity scores
(∈ l
r
· l
c
).
Score Steps:
Local linear functions (addition and subtraction):
①
∑
l
r
·l
c
a
i j
d
,
∑
l
r
a
i j
d
,
∑
l
c
a
i j
d
②
∑
l
r
·l
c
(a
i j
d
− µ
r
d
− µ
c
d
+ µ
i j
d
)
③
∑
l
r
·l
c
r
2
i j
d
,
∑
l
r
r
2
i j
d
,
∑
l
c
r
2
i j
d
Local non-linear function (division):
①
∑
l
r
·l
c
a
i j
d
|I||J|
,
∑
l
r
a
i j
d
|J|
,
∑
l
c
a
i j
d
|I|
②
∑
l
r
·l
c
r
2
i j
d
|I||J|
,
∑
l
r
r
2
i j
d
|J|
,
∑
l
c
r
2
i j
d
|I|
Reconstruction of ˆe for multiplication:
① ˆe
d
← (r
i j
d
− ˆa
d
);⟨ˆe⟩ ≡ ( ˆe
0
, ˆe
1
) ∼ U
l
r
·l
c
2
n
② ˆe
d
⇒ P
1−d
; ˆe ← ˆe
0
+ ˆe
1
Squared residue:
① r
2
i j
d
=
ˆ
b
d
+ e + 2 × e × ˆa
d
2. Deletion/ addition of the nodes: Parties do the
comparisons, composing of 1
r2del
, 1
c2del
inside
the multiple node deletion, 1
r2sdel
, 1
c2sdel
of the
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm
41
Data Owner
(1)
(3)
(3.1)
(2)
-
-
-
-
-
-
-
-
-
(3.2)
-
-
(3.3)
-
-
-
(4)
(5)
Trusted Dealer
(1)
Figure 2: System diagram of the end-to-end secured computation of CCA using FunBic-CCA’s algorithm.
single node deletion, 1
r2add
, 1
c2add
in the node
addition, and the stopping function 1
stop
as ex-
plained in Table 2, by performing the “FunBic-
CCA.eval” with the IC gate
4
.
Further, the parties benefit from the DPF gate
5
to obtain 1
req
, 1
ceq
and to also decide which
nodes have to be removed/ added in the deletion
and addition steps. Deletion of a single node
depends on the result of the argmax, which in-
vokes both FSS gates for the comparison and
4
We keep FSS.Gen
IC
, FSS.Eval
IC
calls to the original
protocols 1, and 2 in (Ibarrondo et al., 2023).
5
Construction of FSS.Gen
EQ
, FSS.Eval
EQ
for equality
check maintains a call to DPF gate (Boyle et al., 2019).
equality check. To this end, parties can locally
increase/ decrease with one simultaneously to
track the actual size of the secret shared ma-
trix (i.e., some rows/ columns are masked with
zeros in the deletion steps). The resulting ma-
trices are sent back to the next step.
3. Final result: Parties return their final output
to the data owner for its reconstruction in the
”FunBic-CCA.result”.
3.3 Security Analysis
Overview. As explained earlier in Section 3, our
framework is secure against Honest-but-Curious
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
42

Algorithm 3: Argmax (H
r
d
→ argmax
w∈[1,l
r
]
H
r
d
).
Input: H
r
d
: secret shared score for rows.
Output: argmax
w∈[1,l
r
]
H
r
d
.
for w ← 1 to l
r
do
1 for v ← 1 to l
r
do
2 if w ̸= v then
3 ˆz
γ
d
← H
r
d
[w] − H
r
d
[v] + r
γ
d
4 Comparison of H
r
d
[w] ≥ H
r
d
[v]:
5 ① ˆz
γ
d
⇒ P
1−d
ˆz
γ
← ˆz
γ
0
+ ˆz
γ
1
6 ② geq
d
← FSS.Eval
IC
(d, K
IC
d
, ˆz
γ
)
7 ③ s
d
←
∑
l
r
geq
d
8 Equality check on s
d
== l
r
− 1:
9 ① ˆz
γ
d
← s
d
− (l
r
− 1) + r
γ
d
10 ② ˆz
γ
d
⇒ P
1−d
ˆz
γ
← ˆz
γ
0
+ ˆz
γ
1
11 ③ eq
w
← FSS.Eval
EQ
(d, K
EQ
d
, ˆz
γ
)
12 if eq
w
== 1 then
13 return w
Algorithm 4: FunBic-CCA.eval (a
i j
d
, f
d
, K
d
, d) → d
i j
d
.
Input: a
i j
d
: input matrix
(∈ {a
i j
0
, a
i j
1
}, Z
l
r
·l
c
2
n
).
f
d
: similarity scores (∈ {H
i j
d
, H
r
d
, H
c
d
}).
K
d
: preprocessing keys from setup phase.
d: computing parties (∈ {0, 1}).
Output: d
i j
d
: arithmetic shares of output
matrix after deletion/ addition steps.
Evaluation Steps:
Preparation of input to FSS gate (ˆz
γ
d
):
① 1
r2del
: αH
i j
d
− H
r
d
+ r
γ
d
② 1
r2sdel
: H
r
d
[d(i)] − H
c
d
[d( j)] + r
γ
d
③ 1
r2add
: H
i j
d
− H
r
d
+ r
γ
d
④ 1
stop
: H
i j
d
− δ + r
γ
d
⑤ 1
req
: I
′
d
− I
d
+ r
γ
d
Reconstruction of masked input:
① ˆz
γ
d
⇒ P
1−d
; ˆz
γ
← ˆz
γ
0
+ ˆz
γ
1
Comparison (IC) and equality check (DPF):
① o
geq
d
← FSS.Eval
IC
(d, K
IC
d
, ˆz
γ
)
② o
eq
d
← FSS.Eval
EQ
(d, K
EQ
d
, ˆz
γ
)
(“semi-honest”) adversary (T ) that corrupts up to one
of computing parties (P
0
, P
1
). We consider standard
security model in line with the related works (Ibar-
rondo et al., 2023; Boyle et al., 2021), having a static
corruption model. Therefore, the adversary must
choose a participant to corrupt prior to computations.
We simulate the corruption of a party P
d
by resort-
ing to the standard real world - ideal world paradigm
(Canetti, 2001). The ideal world requires an addi-
tional trusted party that obtains all the inputs from
the involved parties, which will then receive correct
results by the correct computation of the ideal func-
tionality. On the other hand, we execute the afore-
Algorithm 5: FunBic-CCA.result d
i j
d
→ Bic
k
(I, J).
Input: d
i j
d
: output arithmetic shares.
Output:Bic
k
(I, J) : k δ-biclusters.
Result Steps:
① d
i j
= d
i j
0
+ d
i j
1
② return Bic
k
(I, J) = d
i j
mentioned protocols of the FunBic-CCA algorithm
in the real world with T . Accordingly, we begin
with representing our ideal functionality of FunBic-
CCA in FUNCTIONALITY 5 to prove that our secu-
rity works in the I
FunBic-CCA.setup
-hybrid model. Thus,
the model is based on the faithful execution of the
FunBic-CCA.setup by our defined trusted party to
provide designated parties with each piece of setup
material.
Security Proof. We assert that there is a Probabilis-
tic Polynomial Time (PPT) key generation algorithm.
Simulator (S) realises the mentioned ideal function-
ality I
bic-identif
for each individual participant (given
∀A ∈ R
l
r
·l
c
, ∀γ ∈ Z
∗
n
+
) in which S ’s behaviour is com-
putationally or statistically indistinguishable from a
real world execution of our protocols 2,4, and 5, hav-
ing a semi-honest adversary T .
Proof. We prove the security of our framework
by considering S and possible scenarios during exe-
cution of the protocols:
• FunBic-CCA.setup: This offline phase can be
seen as a black-box access in an ideal world that
provides parties with preprocessing materials. We
realise this setup phase as an ideal functionality
I
FunBic-CCA.setup
.
Its simulation is grounded on the security of the
underlying primitive used to instantiate it, generic
2PC for the FSS keys (Appendix A.2 of (Boyle
et al., 2021)), and OT (Oblivious Transfer), HE
(Homomorphic Encryption) for the SS prepro-
cessing materials in (Demmler et al., 2015).
• FunBic-CCA.MSR: For the messages that a par-
ticular party is holding without sharing with the
other one, nothing is needed to be considered by
S , because T does not have access to any mes-
sages. In the other cases in which P
1−d
is the
owner, S still executes the protocols honestly.
Our local functions, including addition/ subtrac-
tion and division do not need to be simulated as of
being done in a non-interactive way. The security
proof of our secured multiplication is the same as
for the Beaver-triple-based secure multiplication
protocol.
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm
43

• FunBic-CCA.eval: In the online phase, S honestly
follows the protocol steps for finding the score us-
ing the data from the MSR phase. This is followed
by the reconstruction of ⟨ ˆz
γ
⟩ as ˆz
γ
= ˆz
γ
0
+ ˆz
γ
1
which is our input to FSS gates.
We argue computationally indistinguishability of
the ideal world - real world executions for FSS
gates based on (Boyle et al., 2021) (Definition 2).
In this simulation, the information in FSS keys
K
0
, K
1
as well as mask r
γ
is preserved.
• FunBic-CCA.result: S simulates the output result
with receiving ⟨o⟩ from T and o
1−d
, associated
with P
1−d
, then can compute o
d
= 1 − o
1−d
. S
provides T with o
d
on behalf of P
1−d
. After all, S
has the output of P
d
from T .
FUNCTIONALITY 5 (I
bic-identif
(A) → D):
Upon receiving a share of input matrix A,
known parameters δ, α, k,
preprocessing materials
ˆa
d
,
ˆ
b
d
, ˆe
d
, K
IC
, K
DPF
, r
γ
from
P
d
, d ∈ {0, 1}, I
bic-identif
reconstructs
ˆe
d
= r
i j
d
− ˆa
d
, computes H
i j
, H
r
, H
c
and
1
r2del
, 1
c2del
, 1
r2sdel
, 1
c2sdel
, 1
r2add
, 1
c2add
,
finally returns the shares of output matrix D.
Correctness Proof. The execution of FunBic-CCA
protocols satisfies:
if FunBic-CCA.setup(l
r
, l
c
, n, λ, γ) → K
0
, K
1
,
and FunBic-CCA.MSR(a
i j
d
, K
d
, d) → f
0
, f
1
then Pr[FunBic-CCA.eval(a
i j
0
, f
0
, K
0
, 0)
+ FunBic-CCA.eval(a
i j
1
, f
1
, K
1
, 1)
= {1
r2del(H
r
d
,α·H
i j
d
)>0
, 1
c2del(H
c
d
,α·H
i j
d
)>0
,
1
r2sdel(H
r
d
[d(i)],H
c
d
[d( j)])≥0
, 1
c2sdel(H
c
d
[d( j)],H
r
d
[d(i)])>0
1
r2add(H
r
d
,H
i j
d
)≥0
, 1
c2add(H
c
d
,H
i j
d
)≥0
} → d
i j
0
, d
i j
1
] = 1
(9)
for threshold γ (∈ Z
∗
n
+
), input matrix A(∈ l
r
· l
c
), and
suitable choice of FSS as well as computing functions
including deletion and addition.
Proof. Our proof on the correctness of IC
gate is grounded on Theorem 3 of (Boyle et al.,
2021). The two protocols FSS.Gen
IC
(λ, n, r),
FSS.Eval
IC
(d, k
IC
d
, ˆz
γ
) establish the IC gate correctly,
maintaining the condition of f (z
γ
, γ) = z
γ
≥ γ. Lastly,
we argue what we mentioned earlier based on the Def-
inition 2 of (Boyle et al., 2021) that
Pr[FSS.Eval
IC
(0, k
IC
0
, ˆz
γ
)+
FSS.Eval
IC
(1, k
IC
1
, ˆz
γ
) = (z
γ
≥ γ)] = 1 (10)
We analyse the correctness of the equality test ac-
cording to Theorem 4.3 of (Boyle et al., 2019). The
correctness can be seen since point function f
α,β
(x)
evaluates to β = 1 once (x
1
− x
2
) = α = (r
in
1
− r
in
2
) or
having (x
1
− r
in
1
) = (x
2
− r
in
2
).
Afterwards, we prove the correctness of SS-based
multiplication (i.e., r
2
i j
) by resorting to the definition
of scheme about random shares (a
i j
d
= a
i j
0
+ a
i j
1
),
beaver multiplication triples ( ˆa
d
,
ˆ
b
d
, e : Dec( ˆe
d
)) and
having secret shares (r
i j
d
= r
i j
0
+ r
i j
1
, ˆe
d
= r
i j
d
− ˆa
d
)
after applying the local functions, including addition/
subtraction and secured division:
e
2
+ (
ˆ
b
0
+
ˆ
b
1
) + 2 × e × ( ˆa
0
+ ˆa
1
)
= e
2
+
ˆ
b + 2 × e × ˆa = e
2
+ ˆa
2
+ 2 × e × ˆa = (e + ˆa)
2
= [(r
i j
1
− ˆa
1
) + (r
i j
0
− ˆa
0
) + ˆa]
2
= [(r
i j
1
− ˆa
1
) + (r
i j
0
− ˆa
0
) + ( ˆa
0
+ ˆa
1
)]
2
= [(r
i j
1
+ r
i j
0
) − ( ˆa
1
+ ˆa
0
) + ( ˆa
0
+ ˆa
1
)]
2
= (r
i j
1
+ r
i j
0
)
2
= r
2
i j
(11)
4 EXPERIMENT
In this Section, we represent our implementation of
the FunBic-CCA framework, evaluation of resulting
biclusters and finally summarise by discussing time
performance and accuracy obtained.
Implementation and Environment. Our privacy-
preserving implementation drives from Funshade
(Ibarrondo et al., 2023) to construct the protocol steps
(1, 2, 4, and 5) efficiently. Additionally, we use sycret
(Ryffel et al., 2020) to implement only the equal-
ity checks. We also rely on biclustlib (Padilha and
Campello, 2017) for the implementation of the origi-
nal CCA, yeast cell cycle dataset and accuracy mea-
sures.
In the original algorithm (Cheng and Church,
2000), rows that form mirror images are added in bi-
cluster throughout the node addition phase. However,
they are not of interest when defining a bicluster in
a general framework (Galvani et al., 2021). Accord-
ingly, we change our focus in this work only on rows
in the addition phase to be applicable to a broader set
of data and increase the performance.
FunBic-CCA is implemented and executed on an
Intel Core i7-1185 CPU, 3.00 GHz with 8 physical
cores available and 31 GB system memory over at
least 10 runs.
Datasets. We have utilised yeast cell cycle (Tava-
zoie et al., 1999) and human expression data (Al-
izadeh et al., 2000) that were used for testing the
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
44

Table 3: Number of rounds and the communication size for
one time execution of the FunBic-CCA protocol steps in the
online phase. n is the bit size of the matrix elements, l
r
· l
c
is the matrix size.
Step No. rounds Communication size (bits)
MSR 1 2n(l
r
· l
c
)
Eval 26 4n[1 + 6(l
r
+ l
c
)]
Result 1 2n(l
r
· l
c
)
Total 28 4n[1 + (l
r
· l
c
) + 6(l
r
+ l
c
)]
implementation of the original algorithm (Cheng and
Church, 2000).
Parameter Selection. In MPC, integers are natu-
rally encoded into native data types, such as uint32 t
or uint64 t, due to the implementation of protocols
over finite rings or fields. We work with n = 64-
bit modular arithmetic with λ = 128, considering the
scale of input matrices and maximum bit width during
secure computations. We leverage the normalisation
of the input matrices and integer division, while such
bounds prevent from inherently impeding any secure
computation protocol.
We assess maximum communication size and
round of communication for each protocol step in the
online phase, and list them in Table 3, given that our
biclustering algorithm runs through logl
r
+ logl
c
iter-
ations in the multiple node deletion, l
r
· l
c
rounds in
the single node deletion with only one iterate of the
node addition for each k bicluster (Cheng and Church,
2000). We consider here, one time execution of the
online protocol steps, including FunBic-CCA.MSR
with local functions (addition, subtraction, division)
and one secured squaring (consists of one round of
communications). Regarding FunBic-CCA.eval, our
node deletion and addition steps rely on the recon-
struction of the masked inputs to FSS gates with one
round of communication.
Accuracy Measures. The quality of a bicluster
needs to be assessed by evaluation functions, aligned
with biclustering algorithms. These external evalua-
tion criteria measure how close FunBic-CCA is to the
ground truth. In this paper, we apply similarity mea-
sures such as Liu and Wang (Liu and Wang, 2007) and
further extend it to the Prelic relevancy score (Preli
´
c
et al., 2006).
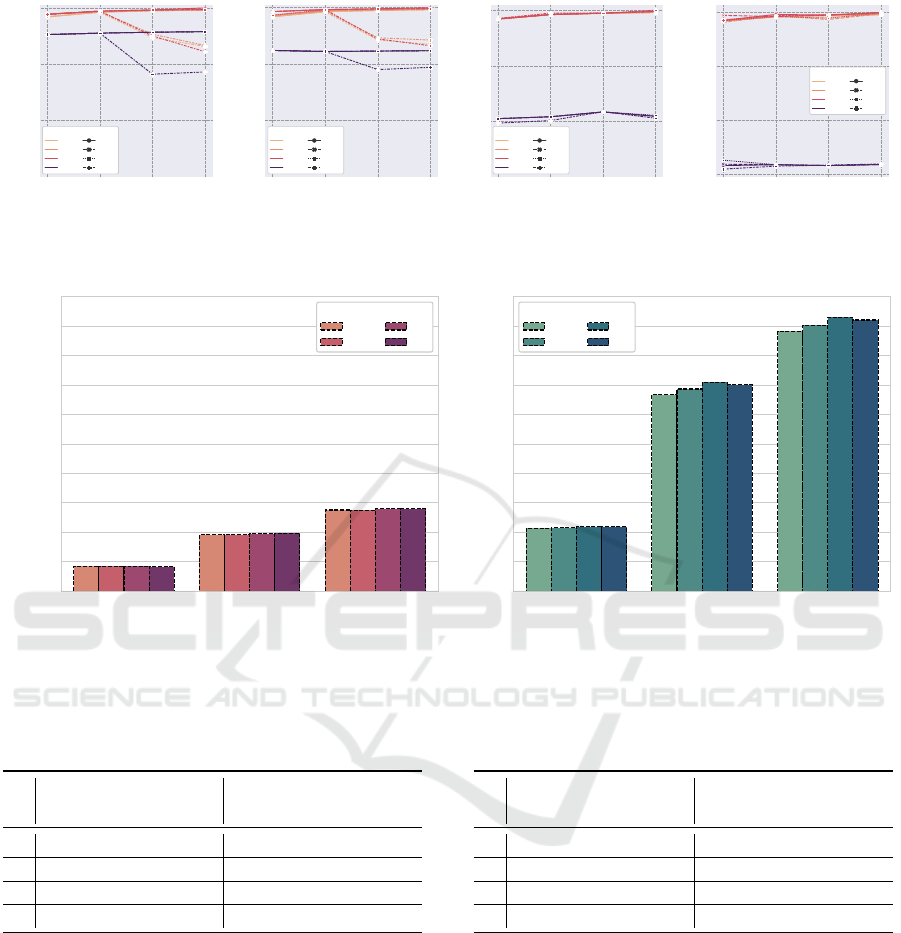
4.1 Results
Impact on Accuracy. Here, we study the accuracy
of our solution based on the above-mentioned key
measures, which range over the interval [0, 1], with
higher values indicating better solutions. Missing el-
ements for both datasets are randomly replaced with
values greater than or equal to 0. We choose α = 1.2
and minimum number of the columns to be 100, ac-
cording to the original study for both datasets (Cheng
and Church, 2000). δ for experiments with yeast
cell cycle and human gene expression data is selected
based on the experiment by Tavazoie et al. (Tavazoie
et al., 1999), whose reported clusters had scores in the
range of between 261 and 996, with a median of 630.
Among the contributing parameters, n has a direct
impact on the accuracy (see Figure 3). Lower numer-
ical precision leads to a drop in accuracy; while its
improvement also occurs as long as natural overflow
is avoided and computation is not exceed [0, 2
n
− 1]
(unsigned integers). Best accurate biclusters are de-
rived from δ being close to the lower end of the range
(δ = 300) (Tavazoie et al., 1999) to detect more re-
fined patterns. Because the size and the variance in
the human data are doable and quadrupling compared
to yeast, the high quality biclusters are achieved with
δ = 1200. In accordance to the findings of (Liu and
Wang, 2007; Preli
´
c et al., 2006), when the number of
the biclusters (k) is small, the match scores decrease;
because CCA itself is not powerful enough when
dealing with small set of biclusters. To conclude,
we record the 100% correctness, when inputting both
datasets, for 100 biclusters, and n = 32-bit.
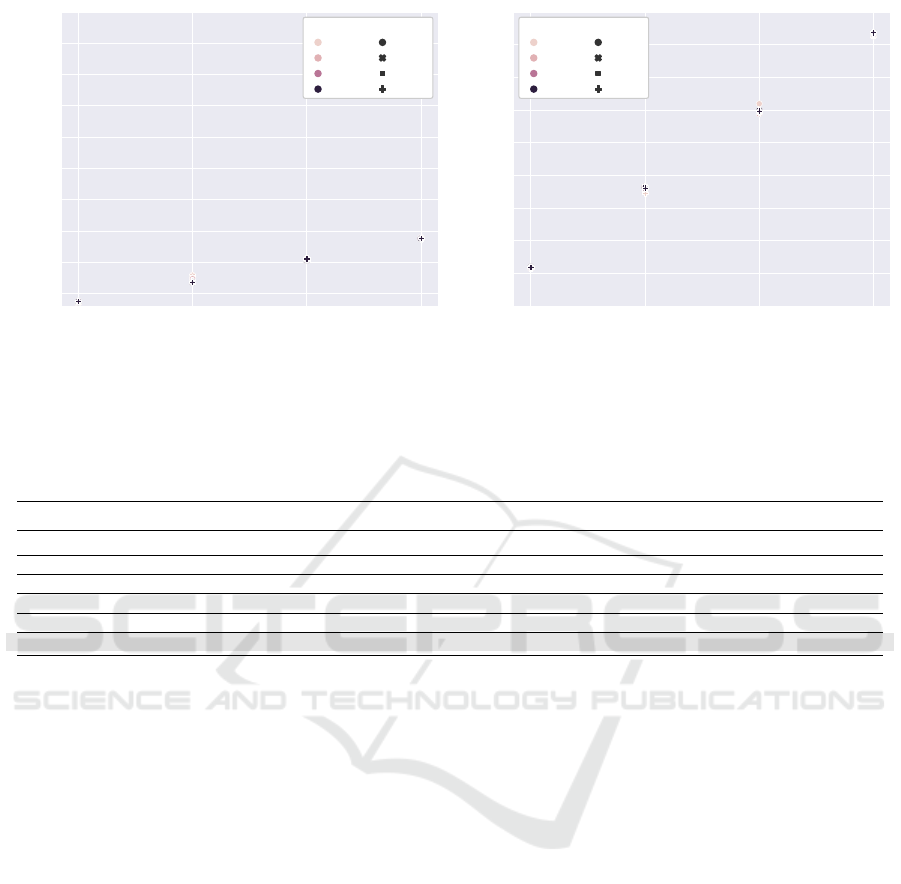
Performance Analysis. In this Section, we analyse
the performance of FunBic-CCA. According to Fig-
ure 4, we notice that by enlarging the bit width of the
input matrix, both latency and bandwidth in the on-
line phase are increased. We set the original values of
δ for the yeast (δ = 300) and human data (δ = 1200).
Parties evaluate “FunBic-CCA.MSR” jointly
∼
=
42
seconds (s), and
∼
=
110 (s) on yeast and human data.
We record on average 96.8225 (s) having yeast cell
cycle, while 345.64 (s) on human data for another step
in the online phase, “FunBic-CCA.eval”. We extend
the analyses to test how other parameters, including
k and δ can affect the overall performance in the on-
line phase. In this regard, k linearly increases the la-
tency, while lowering δ links to the higher number of
computations inside the algorithm, thus increases the
latency (see Figure 5).
In addition, we time the total latency by
each actor, including the data owner plus trusted
dealer (DT), and the parties, in Table 4 and 5.
Timings for parties consist of the three protocol
steps “FunBic-CCA.MSR”, “FunBic-CCA.eval” and
“FunBic-CCA.result” to identify the scores, perform
deletion/ addition on the nodes, then send back the
secret shared of the outputs. We determine the to-
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm
45
25 50 75 100
Number of biclusters (k)
25 %
50 %
75 %
100 %
Prelic relevancy
n
8
16
32
64
δ
300
630
996
1200
(a) .
25 50 75 100
Number of biclusters (k)
25 %
50 %
75 %
100 %
Liu and Wang
n
8
16
32
64
δ
300
630
996
1200
(b) .
25 50 75 100
Number of biclusters (k)
25 %
50 %
75 %
100 %
Prelic relevancy
n
8
16
32
64
δ
300
630
996
1200
(c) .
25 50 75 100
Number of biclusters (k)
25 %
50 %
75 %
100 %
Liu and Wang
n
8
16
32
64
δ
300
630
996
1200
(d) .
Figure 3: Accuracy of the final biclusters with relevance, and Liu and Wang match scores with varying n, k and δ over yeast
cell cycle (a, b) and human expression data (c, d).
MSR Eval Total
Protocol steps over yeast cell cycle
50 s
100 s
150 s
200 s
250 s
300 s
350 s
400 s
450 s
500 s
Online latency
Number of bits (n)
8
16
32
64
MSR Eval Total
Protocol steps over human expression data
50 s
100 s
150 s
200 s
250 s
300 s
350 s
400 s
450 s
500 s
Online latency
Number of bits (n)
8
16
32
64
Figure 4: Computation and communication overhead of FunBic-CCA for each protocol step in the online phase over yeast
cell cycle (δ = 300) and human expression data (δ = 1200).
Table 4: Computation and communication overhead of
FunBic-CCA (online phase) for each actor over yeast cell
cycle with δ = 300.
n
Time (s) Bandwidth (KB)
DT P
d
DT ↔ P
d
P
1−d
↔ P
d
8 14.2383 123.6316 1221.86 400.9778
16 14.2110 123.4150 1370.52 400.9453
32 14.2907 125.4250 1371.9 400.9676
64 14.1132 126.1317 1376.26 403.0315
tal latency of the DT, which is referred to “FunBic-
CCA.setup” and reconstruction of the biclusters. Al-
most 89.93% and 91.81% of the total execution time
allocate to the parties performing the protocol steps
in the online phase, remaining the rest for the DT on
64-bits yeast cell cycle and human expression data re-
spectively.
Besides, the communication size between the DT
and parties is calculated to less than 1380 kilobytes
(kb) for both datasets. According to Figure 2, the
communicated elements are the secret shares of the
input matrix (a
i j
0
, a
i j
1
), known parameters for our al-
gorithm (δ, α, k) and the preprocessing materials (i.e.,
Table 5: Computation and communication overhead of
FunBic-CCA (online phase) for each actor over human data
with δ = 1200.
n
Time (s) Bandwidth (KB)
DT P
d
DT ↔ P
d
P
1−d
↔ P
d
8 36.9292 404.5446 1224.74 2247.0354
16 37.1300 414.5372 1373.26 2247.9475
32 37.7045 427.2254 1373.17 2247.7641
64 37.6850 422.8491 1380.47 2251.3945
K
0
, K
1
or the correlated randomness and FSS keys).
On the other hand, the parties send back the secret
shares of the output matrix to the data owner for its
reconstruction. We also record the communication
size between the two computing parties, exchanging
the masked secret shares in performing multiplication
(refer to Section 3.1) and the comparative functions
(see Table 2). On average, 2248.5353 (kb) is com-
municated between two computing parties for human
data, which is approximately × 5 higher than the size
of communication in yeast data due to the difference
in their range and size.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
46
25 50 75 100
Number of biclusters (k)
50 s
100 s
150 s
200 s
250 s
300 s
350 s
400 s
450 s
500 s
Total online latency
n
8
16
32
64
δ
300
630
996
1200
25 50 75 100
Number of biclusters (k)
50 s
100 s
150 s
200 s
250 s
300 s
350 s
400 s
450 s
500 s
Total online latency
n
8
16
32
64
δ
300
630
996
1200
Figure 5: Total online latency with varying n, k and δ over yeast cell cycle (left) and human expression data (right).
Table 6: Overview of FSS-based secure frameworks. G# indicates semi-honest security model, and : malicious security
model. Primitives include Secret Sharing (SS), Function Secret Sharing (FSS), Replicated SS (RSS), optimized SS (o-SS),
Distributed Comparison Function (DCF), Interval Containment (IC). Online computation blocks are considered for both linear
and non-linear functions: Matrix Multiplication (MatMult), Convolution (Conv), Comparison (Comp), Feature Selection
(FeatSelect), Path Evaluation (PathEval).
Work Online Computation Blocks Type Parties Security Remarks
Funshade (Ibarrondo et al., 2023) Scalar product, Comp. (≥ θ) o-SS, FSS (IC gate) 2PC G# Optimised online phase
AriaNN (Ryffel et al., 2020) MatMult., Conv., Argmax, MaxPool SS, FSS (DCF gate) 2PC G# Reduced FSS key size
FssNN (Yang et al., 2023) MatMult., ReLU, DReLU, MaxPool SS, FSS (DCF gate) 2PC G# Reduced FSS key size
PDTE (Cheng et al., 2024) FeatSelect, Comp., PathEval RSS, FSS (IC, DPF gates) 3PC G# Constant rounds of comm.
Waldo (Dauterman et al., 2022) Additive and arbitrary aggregate RSS, FSS (DCF, DPF gates) 3PC Multi-predicate filtering
FunBic-CCA (OURS) MatMult., Comp. (≥ θ), Argmax SS, FSS (IC, DPF gates) 2PC G# 1st end-to-end secure CCA
5 RELATED WORK
Personal data misuse and theft, especially when deal-
ing with patients’ genomic data, are ever-present
concerns due to carrying highly private information.
Accordingly, privacy-compliant patient data analyses
are among typical applications of privacy-preserving
computation techniques. In line with works on FSS
to name but a few (Boyle et al., 2021; Ryffel et al.,
2020; Ibarrondo et al., 2023), these solutions incur
promising results leading to our framework. Table 6
represents recent FSS-based secure frameworks.
Regarding unsupervised machine learning algo-
rithm based on biclustering, there exist methods in the
literature that use searches reliant on traditional one-
way clustering and combine additional techniques to
analyse the second dimension (Fraiman and Li, 2020).
For instance, clustering based on the singular value
decomposition, whose privacy is protected mainly by
data distortion (Lakshmi and Rani, 2013). Moreover,
co-clustering algorithms with matrix factorisation are
widely used in text clustering and gene expression
analysis demonstrated their superiority to traditional,
one-side clustering (Lin et al., 2019). Their privacy
has been discussed in several recent works, partic-
ularly when using differential privacy (Guo et al.,
2023). Unfortunately, the papers neither targeted
the expression data by biclustering methods such as
Cheng and Church (Cheng and Church, 2000) as one
of the most cited and used algorithms nor building
upon recent advances in FSS. Our proposed solution
can be adaptable to a range of MSR-based algorithms.
6 CONCLUSIONS
In this paper, we introduced our framework upon an
additive secret sharing scheme and function secret
sharing for a full correctness for comparison with
a fixed threshold in an online phase between two
computing parties. Thanks to the proposed solution,
FunBic-CCA is the first protocol that applies func-
tion secret sharing over Cheng and Church Algorithm
and discloses similarity score, all while relying on
lightweight cryptographic primitives. We implement
our solution on top of the open-source libraries and
showcase its 100% correctness with 32-bit precision
FunBic-CCA: Function Secret Sharing for Biclusterings Applied to Cheng and Church Algorithm
47

and latency within
∼
=
500s against 4026 rows and 96
columns. Future research is envisioned for extending
FunBic-CCA to guarantee security with abort against
malicious adversaries, using MACs
6
.
REFERENCES
Alizadeh, A. A., Eisen, M. B., Davis, R. E., Ma, C., Lossos,
I. S., Rosenwald, A., Boldrick, J. C., Sabet, H., Tran,
T., Yu, X., et al. (2000). Distinct types of diffuse large
b-cell lymphoma identified by gene expression profil-
ing. Nature, 403(6769):503–511.
Beaver, D. (1992). Efficient multiparty protocols us-
ing circuit randomization. In Advances in Cryptol-
ogy—CRYPTO’91: Proceedings 11, pages 420–432.
Springer.
Boyle, E., Chandran, N., Gilboa, N., Gupta, D., Ishai, Y.,
Kumar, N., and Rathee, M. (2021). Function se-
cret sharing for mixed-mode and fixed-point secure
computation. In Annual International Conference on
the Theory and Applications of Cryptographic Tech-
niques, pages 871–900. Springer.
Boyle, E., Gilboa, N., and Ishai, Y. (2015). Function secret
sharing. In Annual international conference on the
theory and applications of cryptographic techniques,
pages 337–367. Springer.
Boyle, E., Gilboa, N., and Ishai, Y. (2019). Secure compu-
tation with preprocessing via function secret sharing.
In Theory of Cryptography: 17th International Con-
ference, TCC 2019, Nuremberg, Germany, December
1–5, 2019, Proceedings, Part I 17, pages 341–371.
Springer.
Canetti, R. (2001). Universally composable security: A new
paradigm for cryptographic protocols. In Proceedings
42nd IEEE Symposium on Foundations of Computer
Science, pages 136–145. IEEE.
Cheng, N., Gupta, N., Mitrokotsa, A., Morita, H., and
Tozawa, K. (2024). Constant-round private decision
tree evaluation for secret shared data. Proceedings on
Privacy Enhancing Technologies.
Cheng, Y. and Church, G. M. (2000). Biclustering of ex-
pression data. In Ismb, volume 8, pages 93–103.
Dauterman, E., Rathee, M., Popa, R. A., and Stoica, I.
(2022). Waldo: A private time-series database from
function secret sharing. In 2022 IEEE Symposium on
Security and Privacy (SP), pages 2450–2468. IEEE.
Demmler, D., Schneider, T., and Zohner, M. (2015). Aby-
a framework for efficient mixed-protocol secure two-
party computation. In NDSS.
Escudero, D. (2022). An introduction to secret-sharing-
based secure multiparty computation. Cryptology
ePrint Archive.
Fraiman, N. and Li, Z. (2020). Biclustering with alternating
k-means. arXiv preprint arXiv:2009.04550.
6
Primitive that is used to guarantee data integrity and
authenticate the parties’ shares.
Galvani, M., Torti, A., Menafoglio, A., and Vantini, S.
(2021). Funcc: A new bi-clustering algorithm for
functional data with misalignment. Computational
Statistics & Data Analysis, 160:107219.
Guo, X., Li, X., Chang, X., and Ma, S. (2023).
Privacy-preserving community detection for locally
distributed multiple networks. arXiv preprint
arXiv:2306.15709.
Ibarrondo, A., Chabanne, H., and
¨
Onen, M. (2023). Fun-
shade: Function secret sharing for two-party secure
thresholded distance evaluation. Proceedings on Pri-
vacy Enhancing Technologies.
Knott, B., Venkataraman, S., Hannun, A., Sengupta, S.,
Ibrahim, M., and van der Maaten, L. (2021). Crypten:
Secure multi-party computation meets machine learn-
ing. Advances in Neural Information Processing Sys-
tems, 34:4961–4973.
Lakshmi, M. N. and Rani, K. S. (2013). Svd based data
transformation methods for privacy preserving clus-
tering. International Journal of Computer Applica-
tions, 78(3).
Lin, R., Wang, S., and Guo, W. (2019). An overview of
co-clustering via matrix factorization. IEEE Access,
7:33481–33493.
Liu, X. and Wang, L. (2007). Computing the maximum
similarity bi-clusters of gene expression data. Bioin-
formatics, 23(1):50–56.
Padilha, V. A. and Campello, R. J. (2017). A sys-
tematic comparative evaluation of biclustering tech-
niques. BMC bioinformatics, 18:1–25.
Preli
´
c, A., Bleuler, S., Zimmermann, P., Wille, A.,
B
¨
uhlmann, P., Gruissem, W., Hennig, L., Thiele, L.,
and Zitzler, E. (2006). A systematic comparison and
evaluation of biclustering methods for gene expres-
sion data. Bioinformatics, 22(9):1122–1129.
Ryffel, T., Tholoniat, P., Pointcheval, D., and Bach, F.
(2020). Ariann: Low-interaction privacy-preserving
deep learning via function secret sharing. arXiv
preprint arXiv:2006.04593.
Tavazoie, S., Hughes, J. D., Campbell, M. J., Cho, R. J.,
and Church, G. M. (1999). Systematic determina-
tion of genetic network architecture. Nature genetics,
22(3):281–285.
Yang, P., Jiang, Z. L., Gao, S., Wang, H., Zhou, J.,
Jin, Y., Yiu, S.-M., and Fang, J. (2023). Fssnn:
communication-efficient secure neural network train-
ing via function secret sharing. Cryptology ePrint
Archive.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
48
