A Nested Structure of Anomalies in Academic Publication Citations

Renata Avros

, Gal Farfel

and Zeev Volkovich

Department of Software Engineering, Braude College, P.O. Box: 78, Karmiel, 21982, Israel

Keywords: Citation Anomalies, Graph Wavelet Transform, Beta Wavelet Graph Neural Network.

Abstract: The article presents a novel approach to detecting nested anomalies in citation networks. These anomalies, as

irregularities within citation patterns, significantly threaten the reliability of academic research. Traditional

methods for anomaly detection often study the entire citation graph, missing abnormalities within specific

subfields or research clusters. Unlike these methods, our approach delves deeper by examining articles within

the citation network at different nested scales. Such an approach allows anomalies that might be missed to be

uncovered by focusing on a single level, revealing hidden patterns across various granularities, detecting a

broader spectrum of nested irregularities, and offering a more nuanced understanding of how citation patterns

deviate from the expected. The presented approach supports identifying potential issues, such as citation

manipulation, and uncovering emerging trends within the network. The delivered numerical experiments also

demonstrate the method's ability to estimate the consistency of the dataset structure.

1 INTRODUCTION

The research on anomalies in citation networks, a

complex and pressing issue, is of utmost importance

for the integrity and reliability of scholarly

communication. Understanding these incongruities

involves identifying multiple irregularities or

unexpected outliers within the larger citation patterns.

Investigating citation patterns at multiple levels can

uncover critical insights, including identifying

improper citations, potentially fraudulent activities,

and emerging knowledge-sharing trends. Our

approach aims to recognize potential issues, such as

citation manipulation, and uncover emerging trends

within the citation realm. The need for a more

nuanced understanding of how citation patterns

deviate from the expected is crucial for ensuring the

integrity and reliability of scholarly communication

and enhancing the accuracy of citation-based metrics

and analyses.

The anomaly papers may manifest at multiple

levels of the citation network hierarchy, indicating

deviations or inconsistencies in citation patterns

snuggled within broader citation relationships.

https://orcid.org/0000-0001-9528-0636

https://orcid.org/0009-0005-1672-5924

https://orcid.org/0000-0003-4636-9762

* Corresponding author

Certain articles may exhibit abnormal citation

behavior, such as a disproportionate number of

citations from articles located in other clusters of

papers. These irregularities may indicate citation

manipulation, biased referencing, or emerging

research trends within specific subfields. For

instance, a paper may contain citations to obscure or

irrelevant sources, self-citations intended to

artificially inflate the author's citation count, or

citations to predatory journals or discredited research.

While a paper may conform to expected citation

norms, specific citations within the paper may stand

out as inconsistent. Unethical citation practices are

not just a minor inconvenience but a serious threat to

the core principles of academic discourse – precision,

impartiality, and scientific credibility. Researchers

commonly acknowledge the uneven value of citations

and attempt to differentiate them by type and

importance (e.g., weighting), but this approach

remains limited. Prabha's work (Prabha, 1983)

underscores the gravity of the issue, revealing that

over two-thirds of references in a paper might be

needless. This statistic highlights the prevalence of

dubious citations that undermine the integrity of the

academic record.

Avros, R., Farfel, G., Volkovich and Z.

A Nested Structure of Anomalies in Academic Publication Citations.

DOI: 10.5220/0013455300003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 761-768

ISBN: 978-989-758-758-0; ISSN: 2184-285X

761

Scholarly citation practices are not immune to

author bias, which takes various forms. Excessive

self-citation, for example, occurs when authors cite

their work excessively, potentially to bolster their

publication count or perceived impact. Coercive

citation involves reviewers or editors pressuring

authors to cite specific references, sometimes

including their own or those from journals.

Citation networks can exhibit phenomena like

citation rings, where groups of researchers

reciprocally inflate each other's citation counts, and

ghost citations, fabricated references to strengthen

arguments or create the illusion of broader support.

Data-related issues, such as inaccurate reference

formatting or ambiguity in author names, further

complicate citation tracking. External influences, like

the bias towards citing studies from prestigious

journals or those funded by entities, also skew citation

practices. Moreover, erratic citation patterns may

emerge as scholars establish foundational works and

methodologies in emerging research fields.

As widely acknowledged, citation analysis is

focused on identifying various anomalies. This

attention stems from the concern raised in the

introduction that these anomalies may originate from

inaccurate references in a specific context. The

effectiveness of anomaly detection hinges on

selecting the most appropriate algorithm for the

specific data type and desired data-centric outcome.

Most studies in the mentioned field (see, e.g., (Liu

2022), (Liu, 2024)) concentrate on anomaly citation

recognition, examining a citation graph in its entirety

and losing the graph granularity. An anomaly paper

in a citation network is one whose citation patterns

deviate significantly from the norm for its field and

topic. These deviations can indicate various issues,

potentially impacting the integrity of the academic

record. Such an anomaly is associated with the paper's

position within the citation network. Unexpected co-

citation patterns can signal anomalies, such as a

highly cited paper only co-cited with irrelevant

works.

The community structure is also important to

consider, considering whether the paper belongs to a

cluster of highly interconnected papers that exhibit

unusual citation behavior. So, anomalies can exhibit

a spectrum of deviations from the norm, indicating

that their departure from typical patterns can vary in

severity across different instances, creating a nested

anomaly structure.

Unlike traditional methods, this paper presents a

multi-level analysis for more comprehensive

detection, examining articles at various granularities

to uncover overlooked irregularities. The findings

of this research can be applied to various fields,

including citation analysis, software engineering, and

scholarly communication, to detect irregularities,

uncover emerging trends, and enhance the accuracy

of citation-based metrics and analyses, thereby

improving the quality and trustworthiness of

academic research evaluation.

Aiming to recognize anomaly papers on nested

citation levels, we base our research on the method

proposed in (Tang, 2022). It is an innovative

approach to harnessing spectral information within

Graph Neural Networks (GNNs) to detect anomalies.

It proposes a new network architecture called a Beta

Wavelet Graph Neural Network (BWGNN).

The proposed method involves a detailed

examination of articles' location in a network, starting

from their broad structural attributes and narrowing

down to finer connection elements to identify

anomalies in the citation nested patterns.

Aiming to prepare the initiating anomaly sets in

data clusters, a citation graph is embedded using the

Node2Vec method (Grover, 2016) and clustered in a

linear space. Subsequently, the outer shell of the

clusters—those points most distant from the cluster

centers—is identified as the initial set of anomalies.

We employ the BWGNN network trained on a dataset

with elements assigned as anomalies or normal

elements to better understand the identified

anomalies. After categorizing the data points, the

network identifies anomalies and their connections

within the network. These anomalies are then

removed, resulting in a cleaner dataset. The process

is then repeated using this reduced graph to refine the

detection and analysis of anomalies at further deeper

levels.

2 MATHEMATICAL

FRAMEWORKS

Subsections 2.1 and 2.2 establish the background for

BWGNN to be employed throughout this study.

2.1 Signal on Graphs

An attributed graph, G = {V, E}, is characterized in

this study by a collection of nodes V and unweighted

edges E connecting the nodes. The degree matrix D is

a diagonal matrix where D

denotes the degree, or

number of connections, of vertex i. The adjacency

matrix A is a square matrix where A

signifies the

presence (with a 1) or absence (with a 0) of an edge

between vertices i and j. Let L=D-A be the regular

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

762

Laplacian (not that the normalized one also can be

used) matrix with eigenvalues arranged in ascending

order, 0 = 𝜆



≤⋯≤𝜆



, and a corresponding

orthonormal basis of eigenvectors 𝑈 =

(𝑢



,𝑢



,…,𝑢



Except for the two endpoints 𝜆



and 𝜆



the

remaining eigenvalues can be partitioned into low

frequencies

{

𝜆



,𝜆



,⋯,𝜆



}

and high frequencies

{𝜆



,𝜆



,…,𝜆



} using an arbitrary threshold 𝜆



The paper (Tang, 2022) brings attention to the “right-

shift” phenomenon concept. Anomalies disturb a

graph's spectral energy distribution, causing it to shift

towards higher frequencies. So, regular graphs

display a specific energy pattern, but anomalies

disrupt this pattern by focusing more energy on high-

frequency elements.

This concept can be clarified by considering the

known case of the Fourier transform on graphs. Just

like a regular Fourier transform breaks down a

complex signal into its basic frequencies, the graph

Fourier transform acts as a similar tool for network

data. It decomposes the data into fundamental

components unique to the network's structure.

Here, the spectral energy distribution of a signal

𝑥= (𝑥



,𝑥



,⋯,𝑥



)



∈𝑅



on a graph is given by the

signal's frequency components obtained by the named

transform

𝑥= (𝑥



,𝑥



,⋯,𝑥



)



=𝑈



𝑥 .

Let us introduce

𝑝(𝜆



𝑥





∑

𝑥







as the spectral energy distribution at 𝜆



(1≤𝑘≤

𝑁). The famous coefficient of variation can be

interpreted as the level of anomalies present in the

distribution. An increasing proportion of anomalies

corresponds to a more significant coefficient of

variation in the energy distribution. If the distance

between anomalies and the mean vector expands, the

indicator also rises, designating a greater degree of

anomalies. To quantify the changes in the spectral

energy distribution relative to the degree of

anomalies, a metric called the Energy Ratio is

introduced as follows:

𝜂



(𝑥,𝐿)=

∑













∑











,(1≤𝑘≤𝑁−1).

Generally, as the coefficient of variation increases,

the expected value of the inverse of the low-

frequency energy ratio also increases. This means that

a greater number of outliers or anomalies in the

dataset results in a higher average of the inverse low-

frequency energy ratio. Therefore, a greater degree of

anomaly results in the spectral energy distribution

showing reduced concentration on the low-frequency

eigenvalues. A spectral energy ratio can be used to

detect anomalies in a graph. However, this method is

sufficiently complex and slow for large graphs. A

simpler and faster method has been proposed,

focusing on the spectral domain.

To accomplish this, a piecewise linear function is

introduced within the interval from zero to 𝜆



Between two successive eigenvalues

[

𝜆



,𝜆



]

this

function equals to 𝜂



(𝑥,𝐿) . The residual area

between this simplified curve and a line representing

constant energy (g(t) = 1) is termed the high-

frequency area (S

high

). It can be calculated through

elementary manipulations without the necessity for

eigendecomposition:

𝑆



(𝑥)=













This equation demonstrates the close relationship

between a signal's energy distribution in the spectral

domain and the smoothness in the spatial domain.

Consequently, when the signal x demonstrates similar

values between connected nodes, resulting in a

smaller 𝑥



𝐿𝑥 suggests a lower degree of irregularity.

2.2 Beta Wavelet Graph Network

As indicated in (Tang, 2022), many existing Graph

Neural Networks (GNNs) face challenges from using

low-pass filters and prioritizing information from

lower frequencies, potentially leading to oversight of

high-frequency anomalies of interest. While adaptive

filters allow them to adjust their focus, they may still

need more specificity in targeting the frequency band

where anomalies reside (band-pass) or accurately

pinpointing the location of these anomalies within the

graph (spectral-localized). This issue arises because,

even in anomalies, a substantial portion of the graph's

energy remains concentrated on lower frequencies.

Consequently, these adaptive GNNs may exhibit

behavior akin to low-pass filters, potentially missing

critical high-frequency anomalies.

To better handle anomalies, a new graph neural

network architecture is proposed based on

Hammond's graph wavelet theory (Hammond, 2011),

which is well-known for its band-pass nature. This

theory represents a significant advancement in signal

processing and analysis, as it extends the capabilities

of wavelets to graphs. Researchers can analyze

signals within intricate graph structures, unlike

traditional wavelets limited to Euclidean spaces. It

provides them with a robust toolkit for conducting

A Nested Structure of Anomalies in Academic Publication Citations

763

localized analysis on graphs, like how wavelets

facilitate the examination of signals in time or

frequency domains.

Generally, this graph wavelet transform is created

on a “mother” wavelet ψ and utilizes a set of wavelets

as bases, denoted as 𝑊 = (𝑊





,𝑊





,⋯) . In

formal terms, the application of 𝑊





to a graph signal

∈

can be expressed as:

𝑊





(𝑥) = 𝑈𝑔



(𝛬)𝑈



𝑥.

To avoid computing the eigen decomposition of the

graph Laplacian, the kernel function 𝑔



is chosen

commonly as a polynomial function represented as

𝑈𝑔



(

𝐿

)

𝑈



= 𝑔



(𝐿)

The presented research selects a slightly modified

beta distribution density as the graph kernel function:

𝛽

,

(

𝑤

)





(,)

𝑤



(1 − 𝑤)



, 𝑖𝑓 𝑤 ∈[0,1]

0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

where 𝑝,𝑞∈𝑅



and B is the standard Beta function,

also called the Euler integral of the first kind. Aiming

to cover all eigenvalues 𝜆∈

[

0,2

]

of the normalized

graph Laplacian 𝐿 a modified kernel

(,)() (,)

pq w pq

ββ







𝛽

∗

,

is a polynomial for 𝑝,𝑞 𝜖ℕ



. Thus,

()

()( )

(p,q) (p,q)

L/2 I L/2

WU U

(p 1,q 1)

−

Let us choose a constant 𝑝+𝑞=𝐶 to generate a

set of C+1 the Beta wavelet transforms 𝑊 with the

same order:

𝑊=(𝑊

,

,𝑊

,

,…,𝑊

,

Here is a low-pass filter 𝑊

,

, However, all the other

functions provide band-pass filters of different scales.

Based on the introduced beta graph wavelet, BWGNN

is proposed for anomaly detection.

𝑍



=(𝑊

,

𝑀𝐿𝑃

(

𝑋

)

,𝐻=𝐴𝐺𝐺

(

𝑍



,𝑍



,…,𝑍



)

MLP(

⋅

) represents a multi-layer perceptron, while

AGG(

⋅

) is a basic aggregation function like

summation or concatenation. Following aggregation,

the resultant representation H is forwarded to another

MLP employing the Sigmoid function to determine

the abnormal probability.

2.3 Node2Vec Graph Embedding

Analogous to word embedding, graph embedding

methodologies are designed to distill the fundamental

attributes of nodes and edges within a graph into

continuous vectors of diminished dimensions. In a

manner akin to word embeddings, which elucidate the

semantic nuances and interrelationships among

words in textual contexts, graph embeddings

elucidate the structural layout and interconnections

intrinsic to a graph.

The famous Node2Vec approach (Grover, 2016)

constitutes a particular algorithm employed for graph

embedding, which addresses converting a graph into

numerical representations for each node. Termed

embeddings, these numerical representations

encapsulate the relationships among nodes within the

graph. Analogous to word embedding, where words

with analogous meanings possess similar

embeddings, Node2Vec attempts to generate

embeddings wherein closely interconnected nodes

within the graph exhibit analogous numerical

representations.

Node2Vec uses random walks on graphs, with a

bias, during this exploration process. This bias allows

it to balance two important aspects of a node's

neighborhood: Homophily and Structural

Equivalence. Two settings, namely “return” and

“inout”, regulate the algorithm's exploration behavior

by covering the network. These settings influence the

direction of the random walk, dictating its next steps.

• Local Exploration: “Return(p)” - This setting

governs the likelihood of the walk revisiting

recently traversed nodes. A higher “return” value

results in the walk staying near its starting point,

emphasizing the exploration of the local

neighborhood and capturing the network's

structural characteristics.

• Global Exploration: “Inout(q)” - This setting

determines whether the walk explores outward to

new regions or inward towards previously visited

nodes. A higher “inout” value encourages

outward exploration, facilitating the discovery of

diverse network regions.

Node2Vec balances exploring novel graph areas

and exploiting information from neighboring nodes

by adjusting settings, particularly using probabilities

1/p and 1/q.

After generating random walks, Node2Vec

considers each walk ostensibly a sentence in natural

language and encodes the nodes using Word2Vec

word embeddings. Node2Vec operates with the Skip-

gram approach, where the embedding captures the

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

764

structural similarities between nodes, effectively

translating their proximity or connectivity within the

network. The Skip-gram model is trained on a large

text corpus. For each word (target), the approach

considers a window of surrounding words (context)

and aims to predict these context words based solely

on the internal representation of the target word.

3 NESTED ANOMALIES’

STRUCTURE APPROACH

The proposed procedure seems to unfold as follows:

Algorithm 1.

Pseudocode of the procedure:

Input parameters:

• GraphG -A citations graph.

• Node2Vec procedure:

 p and q – “return” and “inout” parameter values.

 Nwalk- The number of random walks.

 Lwalk-a length of a random walk.

 d- a dimension of the Word2Vec embedding.

• H-a number of levels in the hierarchy.

• Cl- a clustering algorithm with K

- a number of

the clusters in GraphG.

• Fr - a core fraction in clusters.

• C-a constant to generate a set of C+1 the Beta

wavelet transforms

Procedure:

a. Load the dataset GraphG.

b. Initialize the set of anomaly nodes 𝑉



=∅.

c. For iter = 1: H do:

1. Create a temporal dataset G

iter

by omitting all

anomaly nodes from 𝑉



together with the

connections between 𝑉



and 𝐺𝑟𝑎𝑝ℎ𝐺\𝑉



2. Create an embedding of G

iter

W(G

iter

) = Node2Vec(G

iter

, Nwalk ,p, q, d).

3. Cluster W(G

iter

) using Cl into K

clusters.

a. Calculate distances from each point to

its cluster centroid.

b. In each cluster, select a fraction Fr of

the points closest to the centroid as the

cluster core while designating the

remaining points as anomalies.

c. Update 𝑉



as a union of all cluster

anomalies.

d. Update 𝑉



as a union of all cluster cores.

e. Train BWGNN(C) on 𝑉



, 𝑉



f. Assign each node in G

iter

recognized as

an anomaly to set 𝑉



d. Summarize the results.

4 NUMERICAL STUDY

4.1 CORA Dataset

The CORA dataset is famous for machine learning

and natural language processing researchers,

especially those interested in citation networks. It is a

collection of computer science research papers. Each

paper is represented as a bag of words by terms

appearing in the paper. The dataset also includes

information on how these papers cite each other,

forming a network of citations. So, CORA has the

following features:

• 2,708 Scientific Papers (the nodes of the

network)

• 5,429 Citation Links

• A binary bag of words Vector for Each

Paper based on a dictionary of 1,433 unique

terms.

• 7 Paper Categories: The papers are neatly

classified into 7 different areas as presented

in Table 1.

Table 1: Research Areas Presented in the CORA Dataset.

Field Amount

1. Neural Networks 818

2. Probabilistic Methods 426

3. Genetic Algorithms 418

4. Theory 351

5. Case-Based 298

6. Reinforcement Learning 217

7. Rule Learning 180

Figure 1 partially visualizes the CORA dataset

resting upon 2000 nodes. Different categories are

colored another way. The experiments are conducted

using a specified set of parameters.

• p = q = 1.

• Nwalk = 200.

• Lwalk = 50.

• d = 64.

• H =10.

• Cl- the PAM algorithm (see, e.g.,

(Kaufman, 1990)) with the K-means++

initialization and K

=7.

• Fr = 0.7, 0.8, 0.9.

• C= 64

It is important to note that while the number of

clusters used in the algorithm matches the number of

categories, the resulting partition does not correspond

A Nested Structure of Anomalies in Academic Publication Citations

765

to the original categorization. The Cramér's V

correlation coefficient between two partitions is

0.048, indicating an absence of significant

correlation. This discrepancy likely arises due to

differences in how papers are assigned. The applied

embedding method inherently relies on the citation

base partition. The obtained results are presented in

Tables 2-4.

Table 2: Distribution of anomaly papers during the sequential iterations and inherent categories for cora for FR=0.7.

Iteration\

cluster

1 2 3 4 5 6 7 Sum

1 26 2 17 11 11 0 10 77

2 1 16 16 0 15 10 9 67

3 5 4 7 0 9 25 9 59

4 21 17 12 7 25 4 1 87

5 16 8 1 5 1 11 6 48

6 1 7 14 17 2 38 13 92

7 3 7 0 7 6 13 4 40

8 3 15 0 1 7 14 8 48

9 6 13 0 8 2 15 8 52

10 21 9 7 7 6 33 0 83

Sum 103 98 74 63 84 163 68

Table 3: Distribution of anomaly papers during the sequential iterations and inherent categories for cora for FR=0.8.

Iteration\

cluster

1 2 3 4 5 6 7 Sum

1 14 7 10 22 24 17 0 94

2 6 7 6 0 8 6 8 41

3 3 3 15 2 12 1 0 36

4 18 9 4 1 9 0 11 52

5 2 7 8 8 11 0 3 39

6 8 10 0 11 11 1 7 48

7 11 17 6 0 0 11 23 68

8 3 10 12 3 2 1 2 33

9 13 8 11 1 6 0 1 40

10 2 8 15 1 7 6 6 45

Sum 80 86 87 49 90 43 61

Table 4: Distribution of anomaly papers during the sequential iterations and inherent categories for cora for FR=0.9.

Iteration\

cluster

1 2 3 4 5 6 7 Sum

1 14 13 0 4 10 11 1 53

2 4 9 9 1 3 3 5 34

3 4 7 3 9 6 4 0 33

4 4 3 5 5 3 13 1 34

5 2 3 2 2 2 18 0 29

6 1 0 1 0 0 13 0 15

7 3 0 5 0 4 11 0 23

8 2 8 6 1 10 8 3 38

9 9 2 3 8 2 0 6 30

10 0 2 3 0 0 0 0 5

Sum 43 47 37 30 40 81 16

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

766

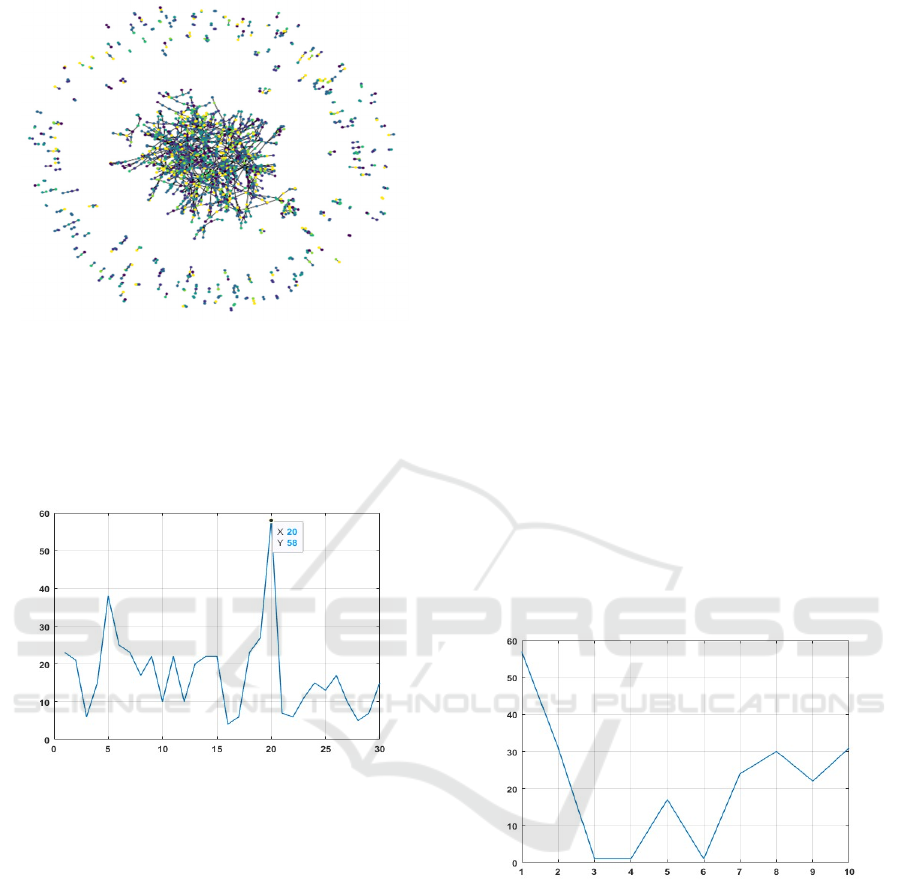
Figure 1: Partial visualization of the CORA dataset.

It appears interesting to consider the behavior of the

number of nested anomalies during iterations. The

following Figure 2 demonstrates an example of such

a performance for Fr=0.9 through 30 sequential

iterations.

Figure 2: The averaged number of anomalies calculated for

CORA data with Fr=0.9 through 30 sequential iterations.

This observation underscores the robustness and

stability of the CORA dataset's structure. As the

number of iterations increases, the characteristic

behavior consistently demonstrates a natural

tendency to decrease, indicating a reliable and well-

defined framework within the dataset.

4.2 PubMed-Diabetes Dataset

The “PubMed-Diabetes Dataset” is a meticulously

curated compilation of scientific articles delving into

diabetes research sourced from the extensive

biomedical literature on PubMed. Managed by the

National Center for Biotechnology Information

(NCBI) and the U.S. National Library of Medicine,

PubMed is a central hub for accessing scientific

advancements across the life sciences. This database

encompasses many publications, including research

papers, reviews, and scholarly articles spanning

various biomedical disciplines. Leveraging this

extensive repository, the PubMed-Diabetes dataset

focuses on articles investigating different aspects of

diabetes, offering valuable insights into this complex

condition.

To delve into the thematic connections among

articles in diabetes research, we adopted a subset

analysis approach. Specifically, we randomly

extracted 3000 nodes from the PubMed-Diabetes

dataset, constituting roughly 10% of the entire

dataset. This sample size is deemed statistically

significant for conducting network analysis.

Remarkably, within this subset, we identified 1995

edges, representing approximately 90% of the total,

indicating links between the respective articles.

Exploring this subset of the PubMed-Diabetes

dataset allows us to analyze thematic relationships

and uncover potential knowledge gaps, like the

CORA dataset analysis. The analysis provided for

this sampled dataset with the exchange of K

value

to 3, which is the inherent number of the categories in

the dataset, supplies the following result for Fr=0.9.

(see, Table 5).

Figure 3 presents the average number of

anomalies calculated for PubMed data with Fr=0.9

through 10 sequential iterations.

Figure 3: The average number of anomalies calculated for

PubMed data with Fr=0.9 through 10 sequential iterations.

This curve exhibits more unstable behavior than

the graph shown in Figure 2.

This instability could be attributed to the random

sampling method used to construct this dataset. The

inherent randomness in the sampling process likely

introduced more significant variability, leading to the

observed fluctuations in the curve. This suggests that

the inborn data structure significantly affects the

resulting stability.

A Nested Structure of Anomalies in Academic Publication Citations

767

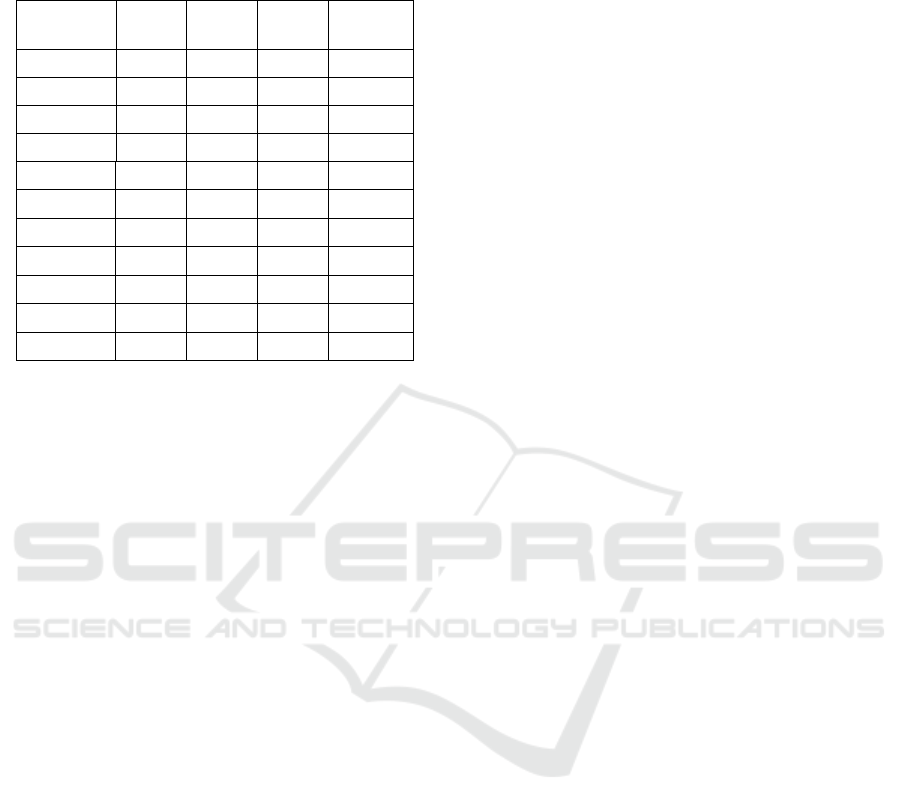
Table 5: Distribution of anomaly papers during the

sequential iterations and inherent categories for PubMed for

Fr=0.9.

Iteration\c

luster

1 2 3 Sum

1 54 1 2 57

2 29 1 1 31

3 1 0 0 1

4 0 0 1 1

5 17 0 0 17

6 0 0 1 1

7 24 0 0 24

8 0 30 0 30

9 0 21 1 22

10 20 1 10 31

Sum 145 54 16

5 CONCLUSIONS

This paper introduces a novel multi-level analysis

approach for detecting anomalies within citation

networks. Unlike traditional methods that focus on a

single level, this approach examines articles at

various granularities, inspired by the work of (Tang,

2022), which leverages Beta Wavelet Graph Neural

Networks (BWGNNs) to utilize spectral information

for pinpointing anomalies. The proposed process

begins with Node2Vec embedding and sequential

clustering to identify initial anomalies. The

Node2Vec approach is applied to embed the current

graph into Euclidian space, making it possible to use

clustering to reveal the initial anomalies set fed into

BWGNN for further refinement. The detected outliers

and their connections are removed, resulting in a

cleaner dataset. This process is repeated, each

iteration revealing at each step a level in a nested

structure of anomalies within the citation network.

This stable structure is essential for conducting

accurate and meaningful analyses, ensuring reliable

results, and genuinely reflecting the inherent

relationships among the data items.

REFERENCES

Grover, A., Leskovec, J. (2016). Node2vec: Scalable

feature learning for networks. In Proceedings of the

22nd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining.

Hammond, D. K., Vandergheynst, P., Gribonval, P. (2011).

Wavelets on graphs via spectral graph theory. Applied

and Computational Harmonic Analysis, vol. 30(2), pp.

129-150.

Kaufman, L., Rousseeuw, P.J. (1990). Finding Groups in

Data: An Introduction to Cluster Analysis, John Wiley

& Sons, Inc.

Liu, J., Bai, X., Wang, M., Tuarob, S., Xia, F. (2024).

Anomalous citations detection in academic networks.

Artif Intell Rev, vol. 57, 103. DOI:

https://doi.org/10.1007/ s10462-023-10655-5.

Liu, J.; Xia, F.; Feng, X., Ren, J., Liu., H. (2022). Deep

Graph Learning for Anomalous Citation Detection.

IEEE Transactions on Neural Networks and Learning

Systems, vol. 33(6), pp. 2543-2557, DOI:

10.1109/TNNLS.2022.3145092.

Prabha, C. G. (1983). Some aspects of citation behavior: A

pilot study in business administration. Journal of the

American Society for Information Science, vol. 34(3),

pp. 202–206.

Tang, J., Li, J., Gao, Z., Li, J. (2022). Rethinking Graph

Neural Networks for Anomaly Detection. International

Conference on Machine Learning,

https://api.semanticscholar.org/ CorpusID:249209972.

DMBDA 2025 - Special Session on Dynamic Modeling in Big Data Applications

768