Modeling and Simulating of Combat: An Empirical Application

Konstantina Founta

Department of Economics, University of Thessaly, Volos, Greece

Keywords: Combat Modeling, Combat Simulation, Decision-Making, Decision Support, Optimization,

Strategic Behavior.

Abstract: This paper proposes a combat model to predict the expected optimal strategic behavior of two participants

engaged in battle, focusing on their interactions throughout the conflict. The model enables the construction

of detailed scenarios, predictions, and analyses of battle outcomes, including potential shifts in the balance of

power. To demonstrate the applicability and effectiveness of the model, three case studies are studied: a naval

battle (Case 1), an island seizure battle (Case 2), and a ground battle (Case 3). This work aims to enhance

strategic planning and provide actionable insights for decision-makers and strategic analysis, guiding their

future decisions.

1 INTRODUCTION

Combat modeling and simulation have become

integral tools for military planning, training, and

decision-making. They leverage advanced

methodologies to simulate complex scenarios, predict

outcomes, and optimize strategies. A wide range of

historical battles can be analyzed with these

methodologies. Analysts use simulations to

investigate system operation, identify critical factors,

and try to isolate time periods in development where

the process could have changed direction (Washburn

& Kress, 2009).

The applications of combat simulation models

emphasize enhanced efficiency, quality, reduce

complexity and cost in model development, while

enabling agile construction of simulation

applications. These models include simulating

human, social, cultural, and behavioral interactions

within complex environments, supporting military

training, operational planning, and decision-making

processes. The models also address core processes

such as movement, communication, and engagement,

providing deeper insights into complex combat

scenarios (Tolk, 2012). The true value of modeling

and simulation lies in their ability to simplify

complex decision-making processes, illustrating how

key operational parameters impact implementation

and final results.

Many researchers use or extend Lanchester’s

equations to represent combat dynamics and

interactions between opposing forces (Taylor (1974),

Protopopescu et al. (1989), Keane (2011), Kress et al.

(2018), Zhang, (2023), Cangiotti et al. (2023)). These

works have significantly shaped the theoretical and

practical understanding of warfare modeling, and

their influence remains evident in modern combat

simulations. In contrast, some researchers advocate

the discrete form of Lanchester’s combat models. Fox

(2010) underscores the difference between

continuous and discrete models in representing

combat interactions. Discrete models offer a more

granular analysis of combat scenarios compared to

the fluid, continuous nature of traditional models.

Furthermore, discrete models reflect situations where

one player’s decisions directly influence the actions

of others, treating decision-making as a game with

multiple equilibria. This approach allows for the

identification of marginal effects arising from both

individual and collective decisions.

Moreover, several studies explore key aspects of

combat through diverse analytical approaches. Peng,

Zhai, and Levitin (2016) examine a strategic game

between an attacker and a defender, incorporating the

use of false targets to deceive the adversary.

Similarly, Zhai et al. (2017) address infrastructure

protection in a two-player zero-sum game context,

offering valuable insights into defensive strategies.

Other research focuses on critical factors

influencing combat outcomes. Jiang et al. (2020)

introduce the Whale Army Optimization Algorithm

(WAOA), an advanced iteration of the Whale

166

Founta and K.

Modeling and Simulating of Combat: An Empirical Application.

DOI: 10.5220/0013430600003970

In Proceedings of the 15th Inter national Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 166-174

ISBN: 978-989-758-759-7; ISSN: 2184-2841

Optimization Algorithm (WOA) developed by

Mirjalili and Lewis (2016). This method leverages

strategic adjustments to solve optimization problems

effectively and proposes an armed force program

based on collective and coordinated battlefield

strategies.

The studies discussed above primarily concentrate

on the factors that influence combat outcomes, while

the evaluation of those outcomes remains a

challenging research problem for analysts. Lee et al.

(2021) emphasize that the battlefield itself should be

considered a critical factor in modeling, as it can

significantly alter the outcome of a battle. They

propose combat winner predictor models that

leverage both battlefield and troop data, alongside a

framework designed to optimize military resources

under constraints.

In addition, the NATO Net-enabled Capability

Command and Control Maturity Model (N2C2M2),

as described by Alberts, Huber, and Moffat (2010),

has been pivotal in shaping discussions on command-

and-control maturity in combat scenarios. The latest

research by Koehler, et al. (2024) explores the

application of complex adaptive systems to combat

simulations of the generation-after-next. Their study

underscores the growing need for dynamic and

adaptive strategies in military decision-making,

further advancing the field of combat modeling and

simulation.

Despite the advancements around combat

modeling and simulation, challenges persist in

formulating optimal strategies and refining the

approaches used to develop them.

In comparison to existing studies, our work aims

to provide a structured mathematical framework that

integrates strategic decision-making within a

dynamical system. Unlike traditional Lanchester-

based models that often assume deterministic

interactions, our approach introduces a game-

theoretic perspective to represent strategic

adaptability. We provide a novel contribution that

blends classical combat modeling with modern

decision-theoretic approaches.

Our contribution focuses on analyzing the

players’ effective strategic behavior during combat,

exploring how these behaviors inform decision-

making processes. Additionally, we aim to predict

both combat outcomes and potential reversals,

providing deeper insights into the dynamics of

strategic interactions on the battlefield.

Combat models are indispensable for simulating

battles and determining the optimal strategic behavior

between two opposing forces. This paper introduces

a methodology to address a pivotal question: What

strategic behavior should a player (state entity) adopt

when external forces threaten its survival as an

autonomous entity?

The proposed model identifies the most critical

factors influencing battle outcomes and predicts the

optimal strategic behavior for each player engaged in

armed conflict. Additionally, the model facilitates the

prediction of battle outcomes by framing the conflict

as a war game. This is achieved through a comparison

of the dynamical system's solution with the Nash

equilibrium of the “Hawk–Dove” game (Smith, and

Price, 1973).

To demonstrate the model's practical application,

we test three case studies, each representing a

different type of battlefield. Case Study 1 examines

a naval battle, Case Study 2 explores an island

seizure battle, and Case Study 3 investigates a

ground battle. These case studies illustrate the

versatility and effectiveness of the model in diverse

combat scenarios.

2 MODEL PRESENTATION

Over the years, numerous simulations have been

developed using a wide variety of modeling

methodologies. This section presents an extended

version of the model developed by Founta and

Zachilas (2021; 2023), which is validated with

historical battle data, enhancing its credibility for

military decision-making. This model captures the

strategic behavior of two opposing forces through a

dynamical system. It reflects the inherent non-

linearity present in real-world combat scenarios. The

model is applicable to any state entities engaged in

interstate conflicts.

In contrast to traditional Lanchester-based

models, we introduce a game-theoretic perspective to

represent strategic adaptability in combat. The

proposed model not only evaluates combat outcomes

but also predicts strategic reversals, identifying

critical turning points where a weaker player could

potentially gain an advantage. Our approach allows

for a more realistic and flexible analysis of battlefield

interactions, capturing the evolution of strategic

behavior over time.

The core of the model lies in its ability to relate

key combat parameters through a system of

equations. These equations express the dynamic

interactions and evolving relationships between the

two opponents over time, providing a comprehensive

framework for analyzing combat scenarios and

strategic decision-making.

Modeling and Simulating of Combat: An Empirical Application

167

The expected optimal strategic behavior of each

player is expressed as:

⎩

⎪

⎨

⎪

⎧

𝑥



=4∙𝑥



∙



1−𝑥





∙𝑃



+𝑇𝑁



+𝑇𝐴



+𝑇𝐿



+𝑇𝐼







−𝐺∙ 𝐷



+𝐸



∙2∙𝑦



∙



1−𝑦





𝑦



=4∙𝑦



∙



1−𝑦





∙𝑃



+𝑇𝑁



+𝑇𝐴



+𝑇𝐿



+𝑇𝐼







−



1−𝐺



∙𝐷



+𝐸



∙2∙𝑥



∙



1−𝑥





(1)

where:

𝑥



: The strategic behavior of the player x at the time

𝑦



: The strategic behavior of the player y at the time

𝑥



: The expected strategic behavior of the player x

at the time t+1.

𝑦



: The expected strategic behavior of the player y

at the time t+1.

We set 𝑥



,𝑦



,𝑥



,𝑦





[0,1]. The value of the

variables is defined as entirely aggressive strategic

behavior for each player, if the value of 𝑥



(or 𝑦



respectively) equals to 1. While we define the entirely

defensive strategic behavior, when the value of 𝑥



(or 𝑦



, respectively) equals to 0.

Table 1: Definitions of the parameters in Eq. (1).

Parameter Definition

𝑃

Military forces (quantity)

Technological capability (quality) in:

Army: 𝑇𝐿

Navy: TN

Air Force: TA

Intelli

ence: TI

𝐺

The difficulty of Geographical terrain of

the armament conflict / Battlefiel

Estimated damage that one player brings

to another during the battle

Expected military expenditures (from

available financial resources

)

for a battle

In Eq. (1), each parameter has an indicator that shows

the player (x or y) we are referring to. We assume that

the parameters (in Table 1) are defined in the closed

interval [0,1].

Explanation of Values of the Parameters

 P: If the value is close to 1, the players have

powerful manpower.

 If the value is close to 0, the players have

weak manpower.

 T: If the value is close to 1, the players have

high technological capabilities,

 If the value is close to 0, the players have

low technological capabilities.

 G: If the value is close to 1, the geophysical

terrain of the area is difficult,

 If the value is close to 0, the geophysical

terrain of the area is favorable.

(The part G (and 1 – G) provides a

battlefield advantage or disadvantage

affecting the players’ estimated strategic

behavior during a battle.)

 D: If the value is close to 1, the player causes

huge damage to its opponent. If the value is

close to 0, the player causes less damage to

its opponent.

 E: If the value is close to 1, the players have

huge military expenditures for the

impending battle. If the value is close to 0,

the players have less military expenditure

for the impending battle.

The terms 4∙𝑥



∙



1−𝑥





and 2∙𝑦



∙



1−𝑦





expresses that the next move of a player depends not

only on how its opponent acts but also the player itself

at the time t. The constant in front of each logistic

equation is defined in [0, 4], and we chose a suitable

value to achieve a smooth behavior of the model.

3 METHODOLOGY

In this section, we outline the step-by-step

methodology used to simulate and analyze combat

scenarios. First, we create a battle scenario by setting

initial conditions. These conditions are then used to

parametrize the data and solve the system of

equations (Eq. (1)). Among the various fixed points,

we consider only those within the interval [0,1]. Each

fixed point represents a strategic combination of the

two players.

Based on the ‘‘Hawk-Dove” game (Smith and

Price, 1973), we conceive that each player one can

behave aggressively (Hawk) or defensively (Dove).

Thus, we assume that if the value of the fixed point is

close to 1, the player has aggressive behavior (Hawk),

while if the value is close to 0, then the player has

defensive behavior (Dove).

Next, we perform stability analysis by evaluating

the Jacobian matrix at each fixed point. A fixed point

is stable if all eigenvalues' absolute values are below

1, otherwise it's unstable (Scheinerman, 2012).

To gain deeper insights, we analyze players'

decision-making processes, particularly focusing on

how battle outcomes can be overturned and

identifying strategic mistakes made during the

conflict. Methodologically, we explore alternative

scenarios by varying a single parameter in each

simulation. These variations represent different

potential battle narratives, with each scenario yielding

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

168

distinct results due to the sensitivity of initial

conditions.

Sensitivity is a hallmark of chaotic systems, where

small changes in initial values can lead to significant

differences in system dynamics (Guckenheimer,

1979). This characteristic highlights the inherent

complexity and unpredictability of combat scenarios,

emphasizing the critical need for accurate modeling

and thorough scenario analysis.

4 NUMERICAL RESULTS – 2D

MODEL

We investigate three case studies, describing different

locations (geographical terrain of battlefield) First,

we examine a naval battle (Case 1), where we set that

the players x and y have any advantage from the

geophysical terrain. Secondly, the two opponents

fight to capture an island (Case 2), where we set that

player x has the advantage in this geographical

location. The last scenario (Case 3) concerns a ground

battle, where we set that player y has the advantage in

this geophysical terrain.

Figure 1: Fiction map with the three case studies (Case 1–

Naval battle, Case 2– Island seizure battle and Case 3–

Ground battle).

Mathematically, battlefield is expressed by

parameter G, and we present below the three case

studies:

 G = 0.5 (Case 1 – Naval Battle),

 G = 0.3 (Case 2 – Island Seizure Battle), and

 G = 0.7 (Case 3 – Ground Battle).

We examine the cases separately.

4.1 Case 1: Naval Battle

In case 1, we explore the strategic behavior of the two

opponents, when the battle is taking place in the

middle of the sea (G = 0.5). We assume no

geographical advantage for each player. Regarding

initial values, we determine the military forces of

each player as 𝑃



=0.4, 𝑃



=0.6, respectively.

Concerning the technological military capabilities of

each one, as follows:

player x: 𝑇𝐿



=0, 𝑇𝑁



=0.06, 𝑇𝐴



=0.07 and

𝑇𝐼



=0.06

player y: 𝑇𝐿



=0, 𝑇𝑁



=0.04, 𝑇𝐴



=0.04 and

𝑇𝐼



=0.04

In addition, the estimated damage caused by x to

y is equal to 𝐷



=0.06, and the estimated damage y

brings to x equals 𝐷



=0.03. Furthermore, the

expected military expenses for the impending battle

for each player are set 𝐸



=0.03, 𝐸



=0.08.

Regarding these initial values, we solve Eq. (1),

and the real equilibrium points, which belong to

closed interval [0, 1], are:

 𝑓𝑝



∶



𝑥

∗

=0.0126,𝑦

∗

=0.6322



Saddle

point

 𝑓𝑝



∶𝒙

∗

=𝟎.𝟓𝟏𝟖𝟔,𝒚

∗

=𝟎.𝟔𝟏𝟐𝟐 Stable

(node)

 𝑓𝑝



∶𝑥

∗

=0.5304,𝑦

∗

=0.0201 Saddle

point

 𝑓𝑝



∶



𝑥

∗

=0,𝑦

∗



trivial

We analyze the stability of the solutions, and we

present the method for 𝑓𝑝



. The Jacobian matrix is

used for stability analysis. Also, a fixed point is called

stable, as the discriminant (Δ) > 0, if and only if the

determinant of Jacobian matrix (det (J

)) > 0 and the

trace (tr (J

)) < 0 (Robinson, 2012).

We calculate the Jacobian matrix:

𝐽

=

2.131 − 𝑥 − 2.13𝑥 0.06𝑦 − 0.061 −𝑦

0.14𝑥 −0.141 − 𝑥 2.721 − 𝑦 − 2.72𝑦



(2)

and substitute the 𝑓𝑝



in Jacobian matrix, as follows:

𝐽







2.0806 0.01586

−0.1364 −0.7209



(3)

We calculate the determinant of matrix 𝐽





, the trace

and the discriminant:

det𝐽





=−1.4977 0 ,

𝑡𝑟𝐽





=1.359 0 ,

𝛥=7.8398 0.

According to the sign of the value, the 𝑓𝑝



saddle point (Robinson, 2012). We analyzed the

stability of the other fixed points following the same

analysis process.

Furthermore, interpreting the equilibrium points,

the 𝑓𝑝



is rejected because it is trivial and has no

interest. 𝑓𝑝



, 𝑓𝑝



and 𝑓𝑝



could determine the

strategic behavior of the two opponents, but the 𝑓𝑝



Modeling and Simulating of Combat: An Empirical Application

169

expresses it more realistic than the other two fixed

points. Thus, we focus on 𝑓𝑝



and its interpretation.

In 𝑓𝑝



∶𝑥

∗

=0.5186,𝑦

∗

=0.6122, the values

of 𝑥

∗

is slightly lower than 𝑦

∗

. On the one hand, it

means that the players have similar behavior during

the battle, because there is no significant divergence

between the values. On the other hand, since the value

of 𝑦

∗

is higher than the value of 𝑥

∗

, we suppose that

y wins the battle, and the victory depends on some key

– moves that y would have done. In addition, we

consider this as a war game and based on the idea of

the game “Hawk – Dove”, we could say that player y

has aggressive behavior (Hawk), because the value of

𝑦

∗

is close to 1, and thus wins the battle.

4.2 Case 2: Island Seizure Battle

In this case, we examine the scenario of fighting to

capture an island (G = 0.3). Also, we set the 𝑇𝐿



0.05 because player x has a supporting army on the

island for protection. The remaining parameters are

constant. Thus, we solve the Eq. (1) again, and there

are four real solutions:

 𝑓𝑝



∶𝑥

∗∗

=0.0063,𝑦

∗∗

=0.6324

Saddle point

 𝑓𝑝



∶𝒙

∗∗

=𝟎.𝟓𝟔𝟓𝟏,𝒚

∗∗

=𝟎.𝟔𝟎𝟑𝟗

Stable (node)

 𝑓𝑝



∶𝑥

∗∗

=0.5708,𝑦

∗∗

=0.0291

Saddle point

 𝑓𝑝



∶𝑥

∗∗

=0,𝑦

∗∗

=0 trivial

We perform stability analysis with the process

shown on the previous section (Section 4.1). The

most realistic solution is 𝑓𝑝



∶𝑥

∗∗

=0.5651,𝑦

∗∗

0.6039. Interpreting the 𝑓𝑝



, we observe that the

players have similar behavior with Case 1 (Section

4.1). Specifically, there is a slight difference between

the values of 𝑥

∗∗

and 𝑦

∗∗

, and the value of 𝑦

∗∗

higher than the value of 𝑥

∗∗

. It means that y wins this

battle through key – moves, as they adopt a mild

strategic behavior.

4.3 Case 3: Ground Battle

In the last case, we explore a ground battle scenario

(G = 0.7). Modeling this case, we change, also, the

value of parameter 𝑇𝐿



=0.07 and retain the other

values of parameters constant.

Summarizing the profile of the two players:

Player x has higher Navy, Air Force, and Intelligence

capabilities, while y has a great Army and a

geographical advantage.

With these specific initial values, we solve again

the Eq. (1) and the real solutions, that belong to [0,1],

are:

 𝑓𝑝



∶



𝑥

∗∗∗

=0.0143,𝑦

∗∗∗

=0.6667



Saddle point

 𝑓𝑝



∶𝑥

∗∗∗

=𝟎.𝟓𝟓𝟕𝟏,𝒚

∗∗∗

=𝟎.𝟔𝟓𝟔𝟖

Stable (node)

 𝑓𝑝



∶𝑥

∗∗∗

=0.571,𝑦

∗∗∗

=0.0104

Saddle point

 𝑓𝑝



∶𝑥

∗∗∗

=0,𝑦

∗∗∗

=0 trivial

Studying these equilibrium points, we observe

that 𝑓𝑝



is more realistic than the other. Interpreting

𝑓𝑝



, we see that the value of 𝑦

∗∗∗

is slightly higher

than the value of 𝑥

∗∗∗

. It means both have a mild

strategic behavior during the battle and player y wins

this battle, because its value is greater than 𝑥

∗∗∗

The following figures show the expected strategic

behavior of each player throughout time (we set that

the time is expressed by days) as well as, the

endurance of each one during the battle. Furthermore,

bifurcation diagrams are presented, indicating how

they behave strategically, as the difficulty of the

battlefield changes (G).

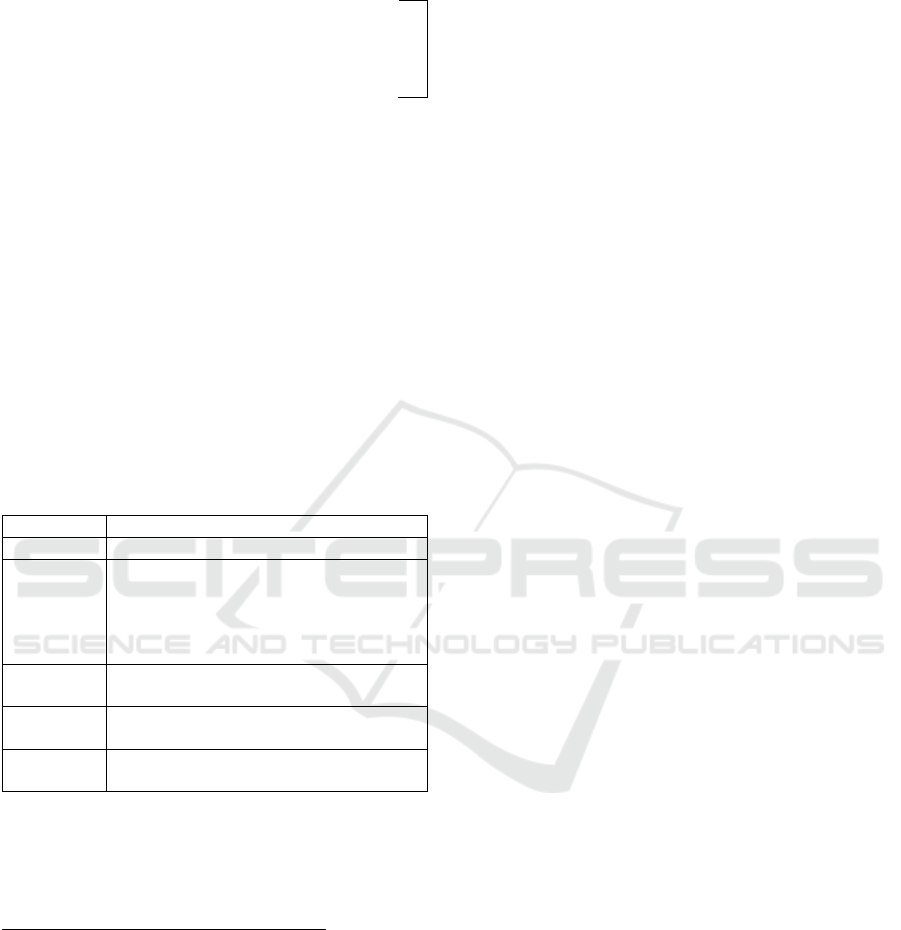
Figure 2: Timeseries diagrams for Cases 1, 2 and 3.

In Fig. 2, the strategic behaviors of x (blue line)

and y (red line) are presented during the battle in each

case. The lines express the expected strategic

behavior of the player, and their oscillation shows the

duration of the battle (in days). Moreover, the

distance of each oscillation represents the endurance

in time. In a nutshell, we observe that in each case the

red line is above the blue, which means that player y

has more aggressive behavior and wins on each

battlefield. In cases 1 and 2, the win comes in a few

days, but in case 3 lasts a month approximately.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

170

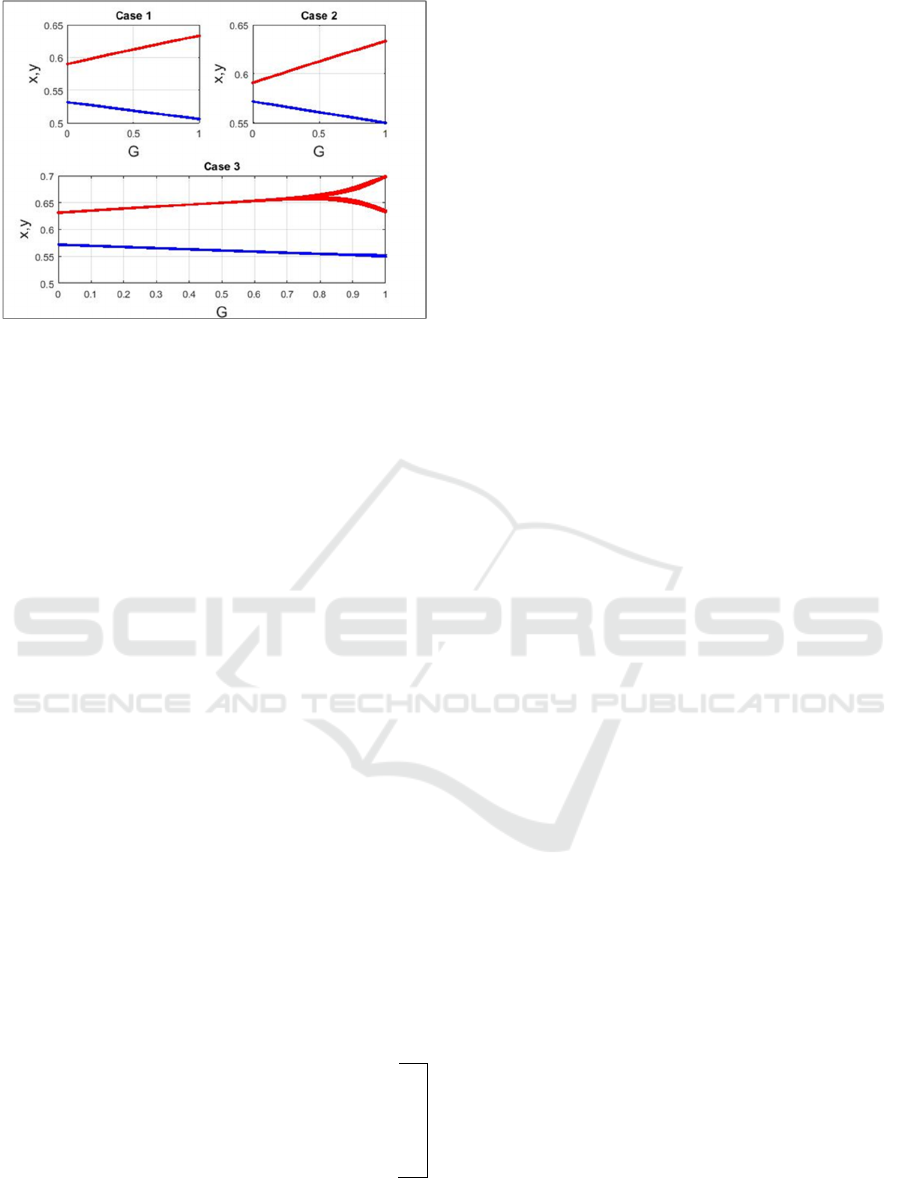
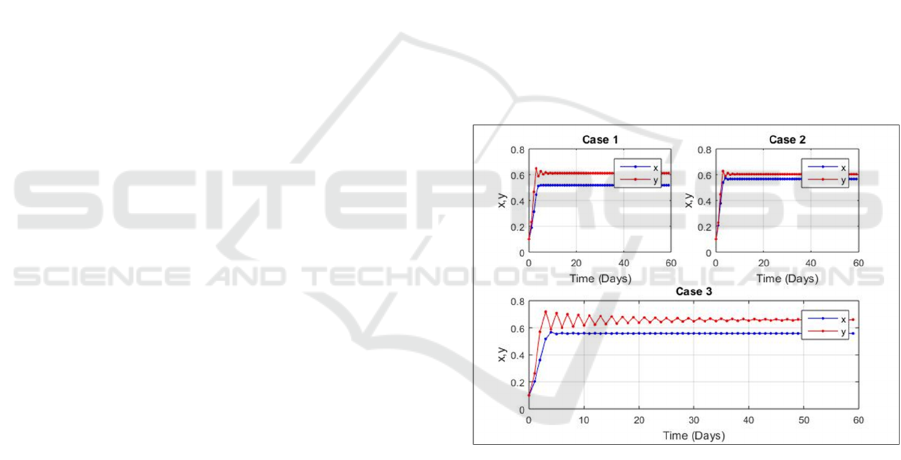
Figure 3: Bifurcation diagrams for Cases 1, 2 and 3. x – blue

line, y – red line.

Fig. 3 illustrates the Bifurcation diagrams for

Cases 1, 2, and 3. In each case, parameter G

represents the difficulty of the battlefield and includes

the weather phenomena (or features) that may affect

each battle. We observe that in each case, the red line

is above the blue (in all plots), which means that y has

aggressive behavior.

5 NUMERICAL RESULTS – 3D

MODEL

Regarding the analysis presented above and

summarizing the results, we observe that player x is

unable to withstand the enemy’s attacks, and player

y emerges victoriously on each battlefield. Thus, the

question is: How could participant x overturn the

outcome of the battle?

Founta and Zachilas (2021) argued that certain

crucial factors (parameters) of the model could

overturn the outcome of the battle. While their

argument is valid, it has limitations. Simply altering a

parameter may not be sufficient to reverse the

outcome. Instead, it is essential to introduce new

actions to achieve a decisive overturn. To address

this, we propose the inclusion of an ally to support

player x in the battle. Thus, we extend Eq. (1) into a

system of three equations, as presented below:

⎩

⎪

⎨

⎪

⎧

𝑥



=4∙𝑥



∙



1−𝑥





∙𝑃



+𝑇𝑁



+𝑇𝐴



+𝑇𝐿



+𝑇𝐼







+𝑎𝑙𝑐∙4∙𝑧



∙



1−𝑧





−𝐺∙𝐷



+𝐸



∙2∙𝑦



∙1−𝑦





𝑦



=4∙𝑦



∙



1−𝑦





∙𝑃



+𝑇𝑁



+𝑇𝐴



+𝑇𝐿



+𝑇𝐼







−1 − 𝐺 ∙[1 − 𝑎𝑙𝑐 + 𝐷



+𝐷



+𝐸



] ∙ 2𝑥



∙1−𝑥





𝑧



=𝑃



+𝑇



∙𝑧



∙1−𝑧



−𝐷



+𝐸



∙𝑦



∙1−𝑦





(4)

where:

𝑧



: The expected strategic behavior of the

player (ally) z at the time t+1.

𝑧



: The strategic behavior of the player (ally) z at the

time t.

𝑃



: represents the military forces (quantity) of

ally z.

𝑇



: indicates the sum of the ally’s technological

military capabilities (quality).

𝑎𝑙𝑐: describes the influence that the ally (z) exerts,

either positively or negatively, on each player. We

describe ally’s intervention through diplomacy,

providing technology, or offering human resources.

𝐷



: represents the estimated damage that z causes to

𝐸



: describes the expected military expenditures of

ally z to support the player x for the impending battle.

The third equation in Eq. (2) represents the expected

strategic behavior of player z and includes the factors

(parameters) that influence the ally’s behavior.

Regarding the initial values, we retain the

previous values constant and set: 𝑃



=0.5,𝑇



0.7,𝐷



=0.03 and 𝐸



=0.015.

This implies that the ally has moderate military

forces and significant technological capabilities

(since the value is close to 1). Additionally, we

assume that player y inflicts minimal damage on z,

and player z allocates 1.5% of their military

expenditures to support.

The parameter 𝑎𝑙𝑐 is analyzed under three

scenarios for each Case:

 𝑎𝑙𝑐=0.3, representing the ally’s

intervention through diplomacy.

 𝑎𝑙𝑐=0.5, indicating that the ally provides

technological support.

 𝑎𝑙𝑐=0.7, which shows that the ally offers

human resources to player x.

Through the analysis, we observed that the ally’s

military forces should satisfy 𝑃



0.5. Based on our

findings, if the value of 𝑃



is lower than 0.5, the

model fails to produce rational solutions that align

with reality. Thus, the minimum military force

required from the ally is 0.5, which serves as a

necessary and sufficient condition for the model and

its analysis.

Further, we revisit the examined cases (different

battlefields) and repeat the analysis process to

observe the differences when the ally intervenes.

Once more we solve the system of equations (Eq.

2) and examine the stability of each equilibrium point.

Additionally, we predict the outcome of the battle and

their expected optimal strategic behavior. For each

case, we present three scenarios, illustrating different

forms of the ally’s intervention during the battle.

The following table summarizes these scenarios.

Modeling and Simulating of Combat: An Empirical Application

171

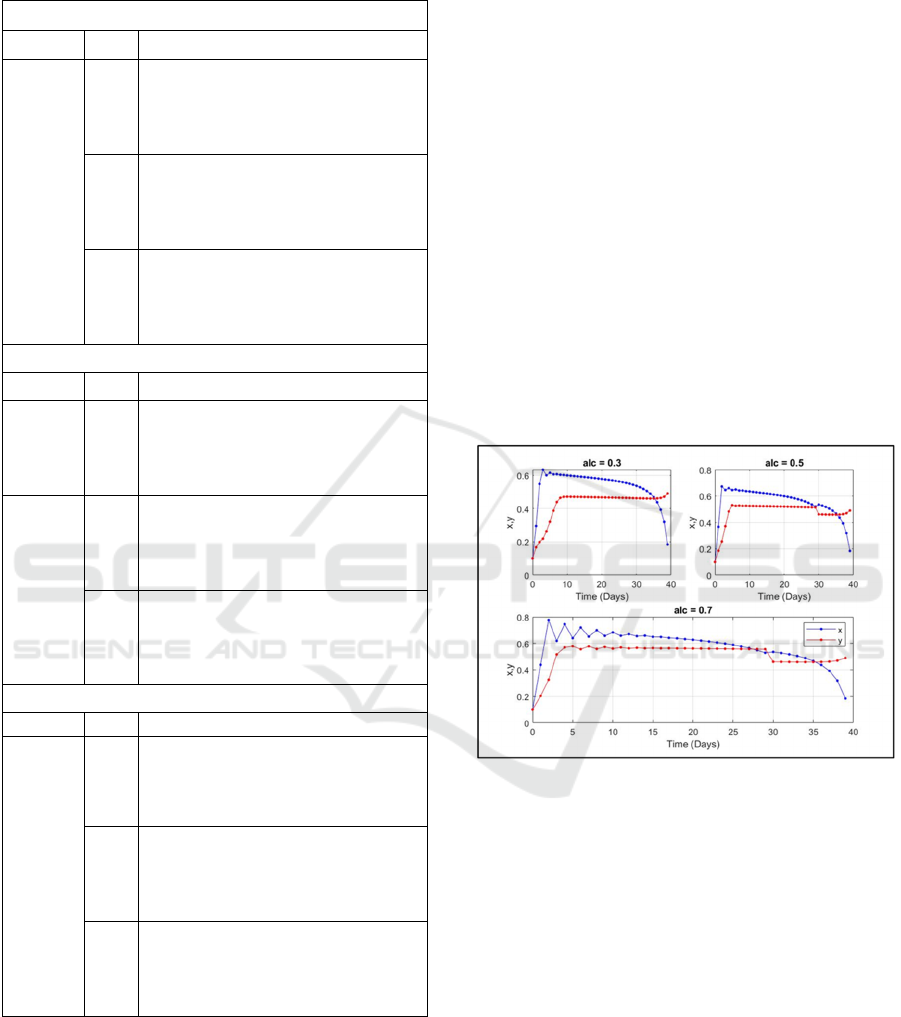
Table 2: Case 1, 2 and 3 - Initial values and equilibrium

points of each scenario.

Case 1

Ally 𝒂𝒍𝒄 Equilibrium Points

𝑃



=0.5

0.3

𝑓𝑝



∶𝒙

∗

=𝟎.𝟔𝟐𝟓𝟕,𝒚

∗

=𝟎.𝟏𝟓𝟔𝟗,𝒛

∗

𝟎.𝟏𝟐𝟕𝟗

𝑓𝑝



∶



𝑥

∗

=0.5648,𝑦

∗

=0.1689,𝑧

∗

0.0423



𝑓𝑝



∶𝑥

∗

=0,𝑦

∗

=0,𝑧

∗

=0

0.5

𝑓𝑝



∶



𝒙

∗

=𝟎.𝟔𝟗𝟒𝟏,𝒚

∗

=𝟎.𝟎𝟗𝟕𝟒,𝒛

∗

𝟎.𝟏𝟒𝟑𝟕



𝑓𝑝



∶



𝒙

∗

=𝟎.𝟓𝟕𝟎𝟖,𝒚

∗

=𝟎.𝟏𝟏𝟔𝟓,𝒛

∗

𝟎.𝟎𝟐𝟕𝟖



𝑓𝑝



∶𝑥

∗

=0,𝑦

∗

=0,𝑧

∗

=0

0.7

𝑓𝑝



∶𝒙

∗

=𝟎.𝟕𝟓𝟓𝟕,𝒚

∗

=𝟎.𝟎𝟓𝟓,𝒛

∗

𝟎.𝟏𝟓𝟒

𝑓𝑝



∶𝑥

∗

=0.5681,𝑦

∗

=0.0759,𝑧

∗

0.0176

𝑓𝑝



∶𝑥

∗

=0,𝑦

∗

=0,𝑧

∗

=0

Case 2

Ally 𝒂𝒍𝒄

Equilibrium Points

𝑃



=0.55

0.3

𝑓𝑝



∶𝑥

∗∗

=0.6659,𝑦

∗∗

0.2872,𝑧

∗∗

=0.1513

𝑓𝑝



∶



𝒙

∗∗

=𝟎.𝟕𝟎𝟓,𝒚

∗∗

𝟎.𝟒𝟎𝟐𝟐,𝒛

∗∗

=𝟎.𝟐𝟓𝟓𝟒



𝑓𝑝



∶𝑥

∗∗

=0,𝑦

∗∗

=0,𝑧

∗∗

=0

𝑃



=0.5

0.5

𝑓𝑝



∶



𝒙

∗∗

=𝟎.𝟕𝟎𝟔𝟕,𝒚

∗∗

𝟎.𝟏𝟒𝟔𝟓,𝒛

∗∗

=𝟎.𝟏𝟑𝟎𝟖



𝑓𝑝



∶



𝑥

∗∗

=0.6263,𝑦

∗∗

0.1762,𝑧

∗∗

=0.0446



𝑓𝑝



∶𝑥

∗∗

=0,𝑦

∗∗

=0,𝑧

∗∗

=0

0.7

𝑓𝑝



∶𝒙

∗∗

=𝟎.𝟕𝟔𝟕𝟗,𝒚

∗∗

𝟎.𝟎𝟕𝟕𝟒,𝒛

∗∗

=𝟎.𝟏𝟒𝟖𝟔

𝑓𝑝



∶𝒙

∗∗

=𝟎.𝟔𝟏𝟕𝟗,𝒚

∗∗

𝟎.𝟏𝟎𝟖𝟔,𝒛

∗∗

=𝟎.𝟎𝟐𝟓𝟕

𝑓

𝑝



∶



𝑥

∗∗

=0,𝑦

∗∗

=0,𝑧

∗∗



Case 3

Ally

𝒂𝒍𝒄

Equilibrium Points

𝑃



=0.5

0.3

𝑓𝑝



∶𝒙

∗∗∗

=𝟎.𝟔𝟔𝟕𝟔,𝒚

∗∗∗

𝟎.𝟎𝟎𝟔𝟒,𝒛

∗∗∗

=𝟎.𝟏𝟓𝟏𝟗

𝑓𝑝



∶𝑥

∗∗∗

=0,𝒚

∗∗∗

=0,𝒛

∗∗∗

=0

0.5

𝑓𝑝



∶



𝒙

∗∗∗

=𝟎.𝟕𝟐𝟓𝟖,𝒚

∗∗∗

𝟎.𝟎𝟒𝟐𝟔,𝒛

∗∗∗

=𝟎.𝟏𝟓𝟔𝟗



𝑓𝑝



∶



𝒙

∗∗∗

=0.5861,𝒚

∗∗∗

0.053,𝒛

∗∗∗

=0.012



𝑓

𝑝



∶



𝒙

∗∗∗

=0,𝒚

∗∗∗

=0,𝑧

∗



0.7

𝑓𝑝



∶𝒙

∗∗∗

=𝟎.𝟕𝟕𝟖𝟓,𝒚

∗∗∗

𝟎.𝟎𝟐𝟓,𝒛

∗

=𝟎.𝟏𝟔𝟎𝟗

𝑓𝑝



∶𝒙

∗∗∗

=0.5861,𝒚

∗∗∗

0.036,𝒛

∗∗∗

=0.0082

𝑓

𝑝



∶



𝒙

∗∗∗

=0,𝒚

∗∗∗

=0,𝒛

∗∗∗



Analysing the stability of fixed points, we find

that all are saddle points (with 𝑓𝑝



omitted as trivial),

reflecting the system's complexity. The bolded

solutions represent the most realistic strategic

behaviour. In Case 1 (𝑎𝑙𝑐=0.5), the ally supports x

through either independent technology use (indirect)

or supervised assistance (direct). As ally intervention

increases, x adopts a more aggressive stance while y

becomes defensive, highlighting the ally’s crucial

role in shifting the outcome. In Case 2 – Island seizure

battle (G = 0.3), player x wins the battle, as the 𝑎𝑙𝑐

varies. Furthermore, when 𝑎𝑙𝑐=0.7 there are two

expected optimal strategic behaviors. This suggests

that the ally can contribute either directly or

indirectly. Specifically, the ally could provide troops

to support the battle (direct approach) or assist player

x in decision making (indirect approach). In the last

case, we analyze a ground battle (G = 0.7), where

player y holds a geographical advantage. The

minimum required ally’s military force (𝑃



=0.5) is

also determined as 𝑎𝑙𝑐 varies. Moreover, we observe

a significant difference between the values of 𝑥

∗∗∗

and

𝑦

∗∗∗

in each scenario. This suggests that this battle

could be a total destruction for player y, regardless of

the support provided by the ally.

The following time-series diagrams illustrate the

duration of the battle in cases 1, 2, and 3, as well as

the endurance of players x and y during the battle.

Figure 4: Case 1 – Time-series diagrams for sub-scenarios:

alc=0.3, alc= 0.5, alc=0.7. x – blue line, y – red line.

Fig. 4 illustrates the strategic behaviour of x (blue

line) and y (red line) during the naval battle (G = 0.5)

over time (days). In all cases, x adopts an aggressive

(Hawk) strategy, while y remains defensive (Dove),

with the red line following a linear pattern. At 𝑎𝑙𝑐=

0.3, a gap exists due to ally’s support, converging

around 𝑡 35 days, marking a critical turning point.

Similar trends appear for (𝑎𝑙𝑐=0.5 and 𝑎𝑙𝑐=0.7)

confirming x’s endurance advantage.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

172

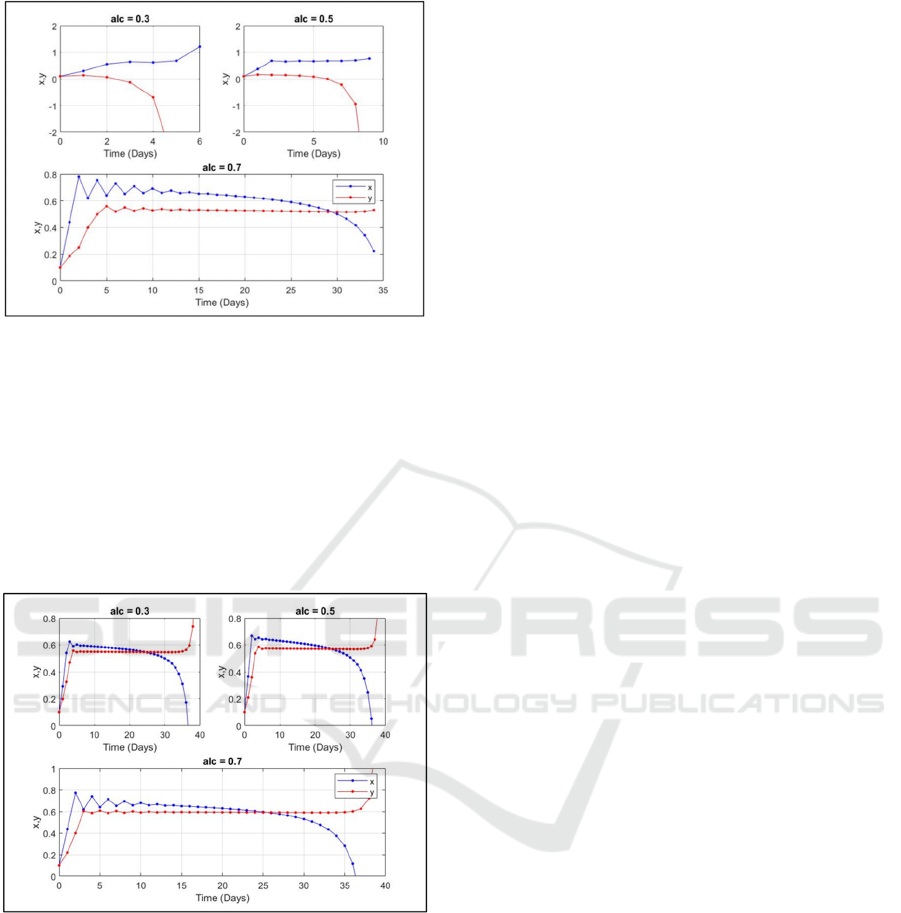
Figure 5: Case 2– Timeseries diagrams for sub-scenarios:

alc=0.3, alc= 0.5, alc=0.7. x – blue line, y – red line.

Fig. 5 shows the strategic behavior of x and y

during the island seizure battle (G = 0.3). In all cases,

x follows an aggressive (Hawk) strategy, while y

remains defensive (Dove). At 𝑎𝑙𝑐=0.3, the battle

lasts 6 days, increasing to 10 days at 𝑎𝑙𝑐=0.5. In the

final scenario (𝑎𝑙𝑐=0.7), initial oscillations lead to

a turning point at 𝑡 28 days, with the battle lasting

34 days. Across all cases, x maintains superiority.

Figure 6: Case 3– Timeseries diagrams for sub-scenarios:

alc=0.3, alc= 0.5, alc=0.7. x – blue line, y – red line.

Regarding Fig. 6, the maximum duration of

ground battle is approximately 𝑡 40 days, with a

critical point at 𝑡 25 days. In all plots, the blue line

is consistently above the red, indicating that player x

adopts aggressive behavior (Hawk) while player y

takes on more defensive strategic behavior (Dove).

In summary, Fig. 6, demonstrates that in all

scenarios, player x maintains a dominant position

until the critical point ( 𝑡 25 days), where the

outcome overturns.

6 CONCLUSIONS

We propose a decision-making combat model to

study the expected optimal strategic behavior of two

players during a battle. Additionally, we analyze the

kind of players’ strategic behavior and provide

predictions concerning the outcome of the battle.

Through the analysis of two-dimensional (2D)

model, we identify the most critical factors

influencing the players' strategic behavior during the

battle. We examined three case studies: a naval battle

(Case 1), an island seizure battle (Case 2), and a

ground battle (Case 3).

Adopting the “Hawk–Dove” game, we

endeavored to interpret the players' strategic behavior

and predict the outcome of the combat. The solutions

derived from the model (in each case study) describe

the Nash equilibria of this game.

According to our findings, player y wins in all

battlefields (case studies). Even if the parameters of

the model are crucial and influence the outcome of

the battle, we observe limitations in their impact. To

tackle this issue, we introduced a new player (player-

z) who acts as ally to player x. We extend the model

(Eq. (1)) into a system of three equations (Eq. (2)) and

re-analyzed the same case studies.

We incorporated three forms of intervention by

the ally: diplomacy, provision of technology, and

human resources. At this stage, we identified the

minimum military forces required from the ally in

each case. Furthermore, we detailed both the direct

and indirect methods of intervention employed by the

ally across all scenarios. Furthermore, we detailed

both the direct and indirect methods of intervention

employed by the ally across all scenarios x.

Consequently, player x won in all battlefields (case

studies) overturning the initial outcomes.

While our model predicts optimal strategic

behaviour and battle outcomes, it is based on certain

assumptions that may limit its applicability in highly

dynamic, multi-player combat environments. One

key limitation is the assumption of deterministic

strategic interactions between players, which does not

account for unpredictable elements such as battlefield

intelligence, morale shifts, or external

reinforcements.

As further research, we could explore the

implications of reducing the parameter space even

further, potentially consolidating the variables into

just two or three dimensions. Another promising

avenue is the application of machine learning

techniques to classify different combat scenarios and

predict strategic outcomes more effectively based on

reduced parameter sets. These approaches could

Modeling and Simulating of Combat: An Empirical Application

173

enhance decision-support systems and improve the

adaptability of combat models to modern, complex

warfare scenarios.

REFERENCES

Anderson, A.D., Bryan, P., Cannon, C., Day, B., Jeffrey, J.

(1972). An Experiment in Combat Simulation: The

Battle of Cambrai, 1917. The Journal of

Interdisciplinary History. The MIT Press, 2(3), 229–47.

https://doi.org/10.2307/202286.

Alberts, D. S., Huber, R. K., & Moffat, J. (2010). The

NATO net enabled capability command and control

maturity model. Technical report, Office of the

Assistant Secretary of Defense, Command and Control

Research Program, Washington, DC.

Tolk, A. (2012). Engineering Principles of Combat

Modeling and Distributed Simulation, Willey, 1–22.

DOI:10.1002/9781118180310

Taylor, J. G. (1974). Lanchester‐type models of warfare and

optimal control. Naval Research Logistics

Quarterly, 21(1), 79-106. https://doi.org/10.1002/

nav.3800210107

Cangiotti, N., Capolli, M., & Sensi, M. (2023). A

generalization of unaimed fire Lanchester’s model in

multi-battle warfare. Operational Research, 23(2), 38.

https://doi.org/10.1007/s12351-023-00776-8

Keane., T. (2011). Combat modelling with partial

differential equations. Applied Mathematical

Modelling, DOI: 10.1016/J.APM.2010.11.057

Kress, M., Caulkins, J.P., Feichtinger, G., Grass, D., Seidl,

A. (2018). Lanchester model for three-way combat,

European Journal of Operational Research,

https://doi.org/10.1016/j.ejor.2017.07.026 .

Founta K., Zachilas L. (2023). Mathematical modeling of

strategic behavior: the Battle of Midway, 1942. The

Journal of Defense Modeling and Simulation. 0(0).

doi:10.1177/15485129231160182

Fox, W. P. (2010). Discrete Combat Models. International

Journal of Operations Research and Information

Systems, 1(1), 16–34. doi:10.4018/joris.2010101302

Guckenheimer, J., (1979). Sensitive dependence to initial

conditions for one dimensional maps.Communications

in Mathematical Physics, 70(2), 133-160.

Jiang, R., Yang, M., Wang, S., Chao, T. (2020). An

improved whale optimization algorithm with armed

force program and strategic adjustment, Applied

Mathematical Modelling. https://doi.org/10.1016/

j.apm.2020.01.002.

Koehler, M. T., Bricio-Neto, J. L., Page, E. H., & Tolk, A.

(2024). Applying complex adaptive systems research

results to combat simulations of the generation-after-

next. The Journal of Defense Modeling and Simulation.

https://doi.org/10.1177/15485129241233608

Lee, D., Kim, M.J., Ahn, C.W. (2021) Predicting combat

outcomes and optimizing armies in StarCraft II by deep

learning, Expert Systems with Applications.

https://doi.org/10.1016/j.eswa.2021.115592.

Mirjalili, S., Lewis, A. (2016). The whale optimization

algorithm, Advances in Engineering Software.

https://doi.org/10.1016/j.advengsoft.2016.01.008.

Founta, K. and Zachilas, L. (2021). Dynamical Systems

Theory Compared to Game Theory: The Case of the

Salamis’s Battle. Applied Mathematics, 12, 882-899.

https://doi.org/10.4236/am.2021.1210058

Peng, R., Zhai, Q., Levitin, G. (2016). Defending a single

object against an attacker trying to detect a subset of

false targets. Reliability Engineering & System Safety,

https://doi.org/10.1016/j.ejor.2016.06.059

Protopopescu., V, Santoro., R.T., Dockery, J. (1989).

Combat modeling with partial differential equations.

European Journal of Operational Research, DOI:

10.1016/0377-2217(89)90102-1

Smith, M.J., Price, G.R. (1973). The Logic of Animal

Conflict. Nature, 246, 15-18. https://doi.org/10.

1038/246015a0

Scheinerman, E. R. (2012). Invitation to dynamical systems.

Dover Publications. ISBN: 978-0486485942.

Robinson, R. C. (2012). An introduction to dynamical

systems: Continuous and Discrete. American

Mathematical Society, 2

Edition, Vol.19, ISBN: 978-

0-8218-9135-3.

Zhai, Q., Ye, Z.-S., Peng, R., Wang, W. (2017). Defense

and attack of performance-sharing common bus

systems. European Journal of Operational Research,

DOI: 10.1016/j.ejor.2016.06.059

Zhang, L. (2023). Combat modelling using Lanchester

equations. International Journal of Mathematical

Education in Science and Technology, 55(2), 224–234.

https://doi.org/10.1080/0020739X.2023.2242863.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

174