Coverage Path Planning Using a Group of UAVs

Bouras Abdelwahhab

1 a

, Bouzid Yasser

2 b

, Cheriﬁ Youcef

and Guiatni Mohamed

2 c

Ecole Sup

erieure Ali Chabati, Reghaia, Algiers, Algeria

Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

ﬁ

Keywords:

Coverage Path Planning, Unmanned Aerial Vehicles, Traveling Salesman Problem, Genetic Algorithms.

Abstract:

This article introduces a novel methodology of path planning within a group of Unmanned Aerial Vehicles

(UAVs) for aerial detection. The primary aim of this method is to ensure comprehensive coverage of a desig-

nated Region of Interest (RoI) while taking measurements from the entire region. The proposed methodology

operates through a structured yet adaptive three-phase process. First, the RoI is transformed into a discrete

representation using a meshing algorithm, ensuring a well-deﬁned and homogeneous spatial structure for sub-

sequent planning. This discretized space is then well partitioned into subregions via the K-means clustering

algorithm, optimizing workload distribution among UAVs while preserving spatial coherence. Finally, the

path of each UAV is formulated as a Traveling Salesman Problem (TSP) and solved using an enhanced Ge-

netic Algorithm (GA). Speciﬁcally, this GA is tailored to accelerate convergence and yield optimized paths.

The principal advantages of the proposed method, as demonstrated through simulation experiments, are its

optimization capabilities, ﬂexibility and reduction in computational time.

1 INTRODUCTION

Over the past two decades, the rapid advancement

in sensor technology and embedded systems for Un-

manned Aerial Vehicles (UAVs) has markedly ex-

panded their applicability across a range of domains,

both civilian and military. These applications include

surveillance, photogrammetry, the Internet of Things

(IoT), search and rescue operations, and agricultural

tasks, etc (see Fig. 1a and Fig. 1b). Additionally, the

deployment of UAV ﬂeets mitigates the limitations in-

herent in single UAV operations, enhancing overall

efﬁciency. This has numerous advantages, particu-

larly in scenarios that pose signiﬁcant risks to human

operators (refer to Fig. 1c), such as reducing exe-

cution time and minimizing human resource involve-

ment. Nonetheless, each application presents its tech-

nical challenges, with control, optimization and path

planning being critical areas requiring advancement.

This paper focuses on coverage path planning

(CPP) (Choset, 2001) using a UAV group (Cabreira

et al., 2019) (Bouras et al., 2022) (Kumar and Kumar,

2023) (Chen et al., 2024). Each UAV must systemat-

ically measure a predeﬁned set of points to gather in-

https://orcid.org/0000-0003-3518-6821

https://orcid.org/0000-0002-8400-9912

https://orcid.org/0000-0002-5899-6862

formation essential for achieving comprehensive cov-

erage while circumventing obstacles. This necessi-

tates the employment of spatial division techniques,

the generation of Points of Interest (PoI), and the op-

timization of planned routes. Moreover, optimizing

these procedures in terms of energy and time (Yu and

Lee, 2024) is crucial.

Typically, research addressing the Multi-Coverage

Path Planning (mCPP) problem within a Region of In-

terest (RoI) follows a four-step process (Bouras et al.,

2019): 1) discretizing the spatial domain; 2) distribut-

ing the workload among UAVs based on their ﬂight

autonomy; 3) employing a planning algorithm to de-

ﬁne the paths; and 4) smoothing the resultant routes.

In reference (Kapoutsis et al., 2017), the authors

tackle the coverage problem by discretizing the space

into small square cells and establishing rules to en-

sure equitable distribution of the RoI, thereby avoid-

ing redundancy and ensuring comprehensive cover-

age. The paths, determined by the Spanning Tree

Coverage (STC) algorithm, navigate around obsta-

cles such as trees. While effective, the STC algo-

rithm’s speed decreases with more UAVs, increasing

memory demands and causing suboptimal paths due

to frequent turns. This issue was addressed in (Gao

et al., 2018) through optimization via Ant Colony Op-

timization (ACO), which improved path efﬁciency.

Abdelwahhab, B., Yasser, B., Youcef, C. and Mohamed, G.

Coverage Path Planning Using a Group of UAVs.

DOI: 10.5220/0013421200003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 159-165

ISBN: 978-989-758-759-7; ISSN: 2184-2841

159

(a) (b) (c)

Figure 1: Examples of UAV ﬂeet applications: (a) Agricul-

tural uses, (b) Internet of Things (IoT), (c) Fire forest uses.

In the work by H. Azp

urua et al. (Azp

urua et al.,

2018), the RoI is partitioned into hexagonal cells, of-

fering greater connectivity to adjacent cells and min-

imizing inter-cell distances, thus reducing the Total

Path Length (TPL). The planning is modeled as a

Traveling Salesman Problem (TSP), the results illus-

trate the impact of UAV involved and coverage line

distance on mission execution time. However, the op-

timization remains requires improvements due to the

non-exact discretization of the RoI.

Another study (Balampanis et al., 2017) employs

triangulation to mesh the RoI, aligning the triangles

with the sensor’s footprint. UAVs are assigned sub-

regions based on their ﬂight autonomy using two

proposed algorithms: Wave Front Propagation and

Reverse Watershed Scheme (AWP & RWS). This

approach also incorporates a Dead Lock Handling

(DLH) algorithm to prevent no-ﬂy zones. However,

the analysis does not address the number of turns or

the energy consumption associated with these paths.

This work introduces a novel three-phase method-

ology that enhances the efﬁciency of multi-UAV path

planning while addressing the limitations of exist-

ing scenario-speciﬁc approaches. Unlike traditional

methods with restricted applicability, our approach

offers greater ﬂexibility in discretization, sensor se-

lection, and path optimization. A key contribution

is the precise discretization of the RoI, overcoming

the approximations common in prior techniques. This

structured representation enables optimized task al-

location via K-means clustering. Additionally, an

enhanced Genetic Algorithm (GA) with problem-

speciﬁc mutation operators accelerates convergence

and improves solution quality. These advancements

collectively lead to faster convergence, greater scala-

bility, superior path optimization, and increased com-

putational efﬁciency compared to standard GA-based

methods.

The structure of this article is organized as fol-

lows: Section II and Section III delineate the method-

ology and provide a detailed description of the algo-

rithms employed. Section IV is devoted to presenting

the results obtained from the simulations. Finally,

Section V concludes the paper with a discussion of

the results and outlines potential avenues for

future research.

2 METHODOLOGY

2.1 Preliminary

Coverage of the RoI using UAVs involves the gener-

ation of PoIs distributed over the surface of this RoI.

The quantity and spatial distribution of these points

are primarily inﬂuenced by the desired extent of cov-

erage (either full or partial) and the range of the on-

board sensors. Each UAV is allocated a ﬁnite set of

PoIs based on its ﬂight capabilities. The objective is

to take measurements at each PoI by tracing an op-

timal path that connects these points. The mission

begins at an initial point, denoted as ”Start”, and con-

cludes at a ”Goal” point, with the caveat that each

UAV ultimately returns to the starting point, effec-

tively considering them as confused, in other words,

each UAV ends the coverage mission by returning to

the starting point.

To achieve this, we model the problem represent-

ing our RoI as a closed region delineated by polyg-

onal segments, which may be either convex or non-

convex. Obstacles are present only in the area outside

the RoI but within the operational workspace. The

conﬁguration of the RoI’s shape and the number of

UAVs are user-deﬁned parameters, and each UAV’s

ﬂight autonomy must be sufﬁcient to accomplish the

assigned mission.

The UAVs employed are considered rotary-wing

aircraft, speciﬁcally quadcopters. Their inherent ma-

neuverability, hovering capability, and ease of control

make them well-suited for such missions, particularly

when equipped with various types of embedded sen-

sors (as illustrated in Fig. 2).

2.2 Mathematical Formulation

Let P ⊆ R

represent the workspace designated for

coverage, with dimensions [l × w], where l and w de-

note the length and width of P , respectively.

Deﬁne A ⊆ R

as the RoI characterized by a list

of n segments S =

{

,...,s

}

, and A ⊆ P , O ⊆ R

and O ⊆ P /A is the non-ﬂy zone or O =

∑

i=0

, such

that o

represents the i

from z small obstacles located

between A and P .

Let c

∈ A denote the set of PoIs, where c

) for i ∈

{

0,...,r

}

and r is the number of the

PoIs. Speciﬁcally, c

= (x

) represents the initial

position of the UAVs’ parking platform, with coordi-

nates x

. Let u ⊆ N

∗

denote the number of UAVs,

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

160

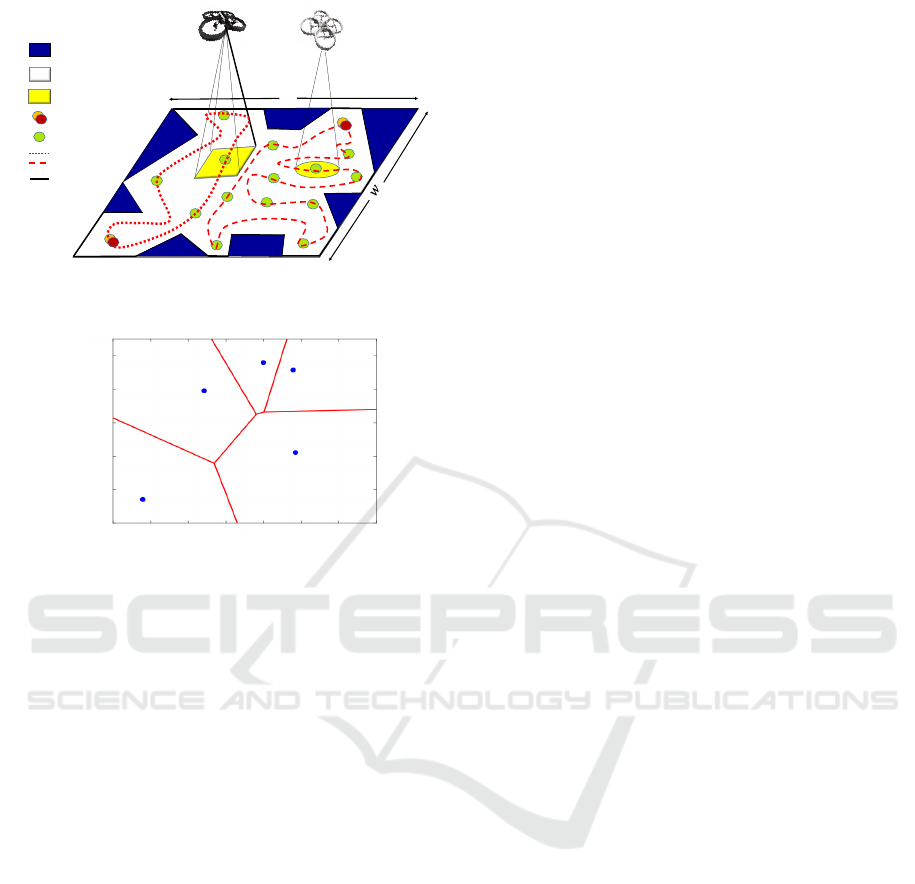
2D workspace

Obstacles

Vertices

𝑙

PoIs

Sensor footprint

RoI

Paths

Start & Goal points

Figure 2: Coverage using a group of UAVs.

0.8

0.6

Y [m]

0.4

0.2

0.4

1.2

1.4

X [m]

0.6

0.8

Figure 3: Voronoi diagram.

and let R

s f

signify the radius of the sensor footprint,

which may take the form of either a square [l

s f

× l

s f

]

or a rectangle [l

s f

× w

s f

], where l

s f

and w

s f

represent

the length and width of the sensor footprint, respec-

tively.

In the initial phase, following the selection of P ,

A and r, we proceed to generate the PoIs within the

RoI A. This generation process utilizes the Voronoi

diagram, deﬁned as follows:

V =



y ∈ Ω | d(y, x

) ≤ d(y, x

), f or j ̸= i



(1)

This function partitions the space into sub-regions

(referred to as cells when dealing with a large number

of r), such that all points p

: p

∈ Ω within each cell

are closer to x

than to x

for j ̸= i. Additionally, the

grid that delineates the r cells consists of the bisectors

of the line segments [x

] (Fig. 3).

The computation of the Voronoi diagram for an ar-

bitrary set X =

{

| i = 0,...,r

}

, followed by the in-

tegration of each resulting cell and the determination

of its centers, constitutes a version of Voronoi Tessel-

lation known as the Lloyd algorithm (Du et al., 1999).

These centers represent our PoIs, with their quantity

being chosen according to the coverage requirements

and the type of sensors employed. A comprehensive

description of this algorithm is provided in the subse-

quent section (Algorithm 1).

The second step involves distributing these PoIs

among UAVs. It is crucial to achieve a homogeneous

distribution that considers the UAVs’ autonomies and

ensures an appropriate grouping of these points to

prevent collisions and balance the loads. This step

is facilitated by the K-means algorithm.

In the third step, we aim to determine the opti-

mal sequence of PoIs C =

,...,c

for

each UAV, which minimizes the TPL. Here, r

rep-

resents the number of points assigned to the i

UAV

. Given the ﬂexibility in selecting the number and

distribution of PoIs, it is assumed that the TPLs are

within the operational range of the UAVs. Therefore,

the objective is to minimize the following function:

T PL

min

−1

∑

i=1

d(N

, N

i+1

) + d



, N



(2)

where d(N

, N

i+1

) is the distance between points N

and N

i+1

. The optimization of these paths is ensured

by adapting it as a TSP and solving it using a GA,

whose details are provided in Algorithm 2.

3 ALGORITHMS DESCRIPTION

The primary focus of this section is to develop the

previously outlined steps in the form of algorithms.

To generate PoIs, the RoI is partitioned into r cells

using an adapted Meshing algorithm (Algorithm 1).

Unlike traditional meshing techniques, this approach

iteratively reﬁnes the spatial subdivision to enhance

uniformity and adaptability. After initializing the in-

put data, the algorithm constructs an initial Voronoi

tessellation and determines the set x

| i = 0,...,r. At

each iteration, the centroids c

of the Voronoi cells are

computed and reallocated as new distribution points

for x

, triggering a re-computation of the tessellation.

This process continues until a predeﬁned convergence

criterion is met or the maximum number of iterations

is reached. As a result, the algorithm progressively

produces more uniform cells, ultimately approximat-

ing a structured grid while preserving adaptability to

the underlying spatial constraints.

The second stage consists of assigning the ﬁnal

cell centers c

| j = 0,...,r to the UAVs by cluster-

ing them into m

subgroups (Clusters), each contain-

ing r

points, while minimizing the intra-cluster dis-

tances. This ensures an efﬁcient workload distribution

among UAVs. To achieve this, we employ K-means

clustering algorithm, which optimally partitions the

PoIs by minimizing the distance between each cluster

Coverage Path Planning Using a Group of UAVs

161

Let Ω be the working ﬁeld, σ a density function on Ω, and r the number of generators. The initial set of

generators is denoted as x

| i = 0,...,r. The Meshing algorithm is deﬁned as follows:

Input: l,w,S,r,X ,numIter,x

Function: [v

, order of v

, x

, y

] = MeshingAlgorithm (x

,S,numIter, r) % v

and its order

represent the Voronoi cell borders and their arrangement, while x

, y

denote cell centroids.

Initialization: Generate an initial set of r points x

| i = 0,...,r.

while the iteration count numIter is not reached do

Voronoi Tessellation: Compute the Voronoi diagram of Ω using the generator set x

| i = 0,...,r.

Centroid Computation: Determine the centroids c

| j = 0,...,r of the Voronoi cells.

Update: Set x

| i = 0,...,r ← c

| j = 0,...,r % Replace the set x

with the computed centroids c

end

Output: [v

, order of v

]

Algorithm 1: Meshing Algorithm.

center and its assigned points, as expressed by:

argmin

∑

i=1

∑

∈M



− µ



(3)

where µ

represents the centroid of cluster M

The clustering process follows an iterative two-

step reﬁnement:

1. Cluster assignment: Each point c

is assigned to

the closest cluster center µ

based on a Voronoi

partitioning:

(t)

= {c

:∥ c

− µ

(t)

∥≤ ∥ c

− µ

(t)

∗

∥∀i

∗

= 1, . . . , m

}

(4)

2. Centroid update: The cluster centers are recom-

puted as the mean of the assigned points:

(t+1)

= (M

(t)

)

−1

∑

∈M

(5)

This iterative process ensures convergence by pro-

gressively reducing the cost function. Given the ﬁnite

number of possible partitions, the algorithm is guar-

anteed to reach a stable solution, making it well-suited

for UAV task allocation in large-scale environments.

The ﬁnal stage involves determining the optimal

sequence of points within each set M

to minimize

the total travel distance (Equation (2)) and establish

the optimal paths R

,...,c

. Given the com-

binatorial nature of this NP-hard problem, it is for-

mulated as a TSP and efﬁciently solved using an en-

hanced GA. For instance, even a modest set of 10

points leads to 181 440 and 362 880 possible arrange-

ments in symmetric and asymmetric TSPs, respec-

tively, highlighting the necessity of an adapted opti-

mization approach.

In this context, GA optimization involves evolving

a population of chromosomes C h

,...,H

where each chromosome represents a candidate route

. The ﬁtness function evaluates each solution based

on the total traveled path length (TPL):

f (C) =

−1

∑

i=1

d(H

, H

i+1

) + d



, H



(6)

where r

denotes the number of waypoints as-

signed to a single UAV.

To efﬁciently explore the (n − 1)! possible per-

mutations, we introduce swap operations (ﬂip, slide,

and swap) (Pham et al., 2017), which signiﬁcantly ac-

celerate convergence, reduce computational complex-

ity, and ensure feasible solutions even for large popu-

lations. Without these adaptive operators, the algo-

rithm struggles to handle populations exceeding 16

elements, resulting in computation times exceeding

( > 2000 sec) seconds.

Algorithm 2 summarizes the third step of our so-

lution. Generating an initial population is necessary,

where each chromosome is assigned a value f

calcu-

lated by the ﬁtness function. We then perform a selec-

tion within this population. Subsequently, new indi-

viduals in the population are created using crossover

and mutation. Finally, we repeat the process.

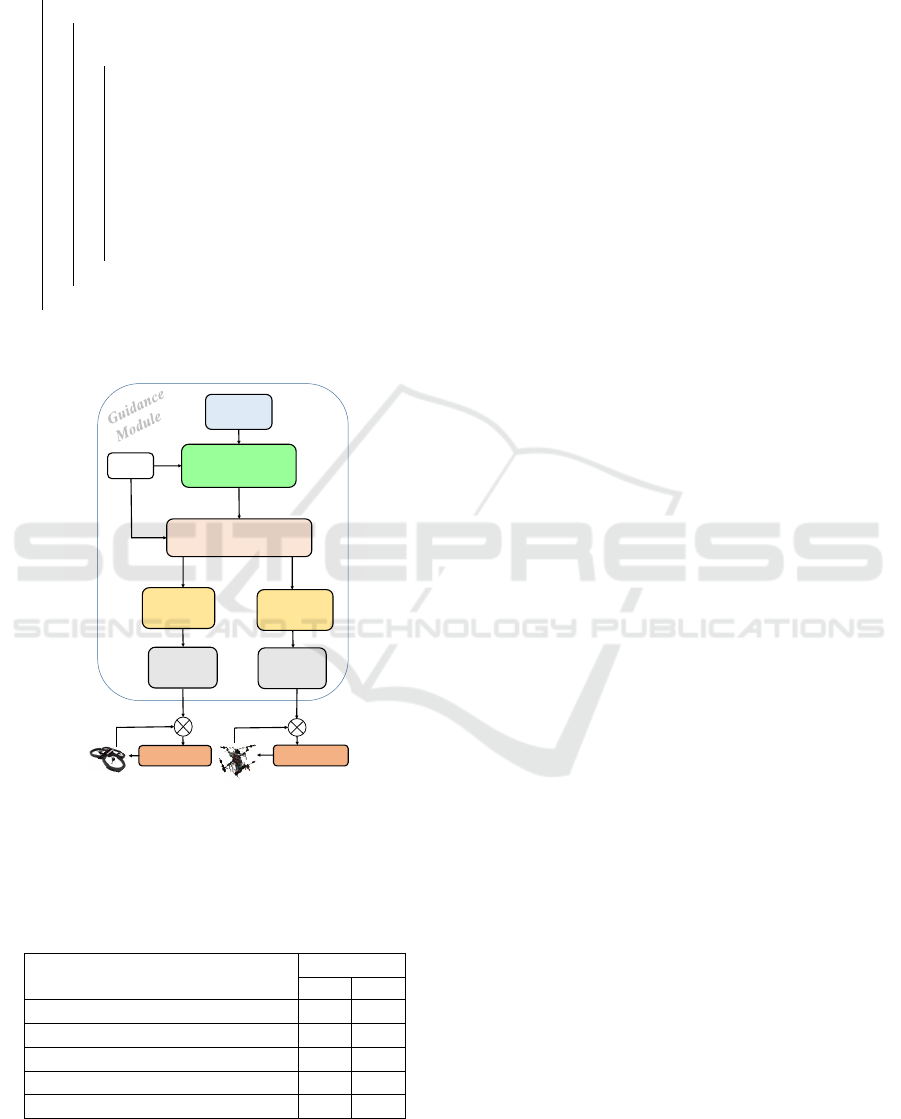
The entire proposed technique and its algorithm

sequence are summarized in Fig. 4. A detailed dis-

cussion of each step, based on the simulation results,

is provided in the next section.

4 SIMULATION RESULTS AND

DISCUSSION

In this section, we tested the effectiveness of the

algorithms presented in the previous section using

two scenarios. We selected a study region, which is

polygon-shaped and located within a square space of

dimensions [3 × 2] Km. In this region, we generated

the PoIs, distributed evenly across the surface to be

studied. The base station is positioned at p

) =

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

162

Data: population size (r

), Number of generations (n

), Number of cities = size (N

), Global min = Inf,

i ← 1 (i is the current iterations), Pop(t) ← (r

) chromosomes Pop

(t).

while not terminating condition do

while i ≤ r

← f (Pop

(t)) % f is the ﬁtness function

while i ≤ r

NewPop

(t + 1) ←rand choose Pop

(t) from Pop(t)

CrossPop(t + 1) ←recombine (NewPop(t +1)) with P

% P

is the crossover probability

MutPop(t + 1) ←mutate (CrossPop(t +1)) with P

% P

is the mutation probability

Switch

case 1 mutate by ﬂipping,

case 2 mutate by swapping,

case 3 mutate by sliding.

Pop(t + 1) ←MutPop(t + 1)

i ← i + 1

end

Algorithm 2: Solving TSP-GA.

Map

definition

Map

decomposition

Solving

TSP-GA

Optimal

route

User

UAV N

Controller

Optimal

route

UAV 01

Controller

Quadrotor 01

Quadrotor N

. . .

K-means

Solving

TSP-GA

Figure 4: Summary of the technique proposed in this work.

(1 Km,1 Km). The parameters of the simulation tests

are illustrated in Table 1.

Table 1: Simulation data.

Scenario

Parametres 1 2

Number of UAVs (u) 01 04

Number of iterations (numIter) 80 180

Number of cities (N

) 20 80

Population size (r

) 20 80

Number of generations (n

) 100 150

In the ﬁrst scenario, we generated 20 measure-

ment PoIs. The Meshing algorithm required 80 it-

erations to establish the distribution of PoIs. Figure

5 (a) illustrates the outcome of this step, where lines

extend from the base station to each cell center, repre-

senting the path during the execution of the Meshing

algorithm. The ﬁnal coordinates of the cell’s centers

obtained from this process are used in the subsequent

step. However, their deployment paths are not consid-

ered in this study.

A single UAV is utilized to provide coverage,

equipped with a circular sensor of radius R

= 200 m.

The path optimized by the TSP-GA (blue line) and

the resulting footprint coverage (red circles) are pre-

sented in Figure 5 (b). The optimization of the TPL

with TSP-GA across generations is shown in Figure 5

(c).

From this ﬁrst test, it appears that:

• The number of iterations is directly related to

the number of PoIs generated. The number of

PoIs depends on the type of application, the on-

board sensor used, and the desired coverage qual-

ity (with or without overlaps).

• The TSP-GA is a crucial step for optimizing the

TPL. Theoretically, there are 19! possible ways to

connect the 20 PoIs and return to the initial point.

Using TSP-GA, this is efﬁciently calculated, re-

sulting in an overall distance of 7.7236 Km.

In the second scenario, 80 measurement points

were generated for four UAVs over the same region.

This setup provides a concrete demonstration of the

advantages of using a group of UAVs in terms of cov-

erage quality. Additionally, it allows us to test the ef-

fectiveness of the proposed algorithms in more com-

plex situations compared to a single UAV.

Such a distribution of the PoIs, as shown in Figure

Coverage Path Planning Using a Group of UAVs

163

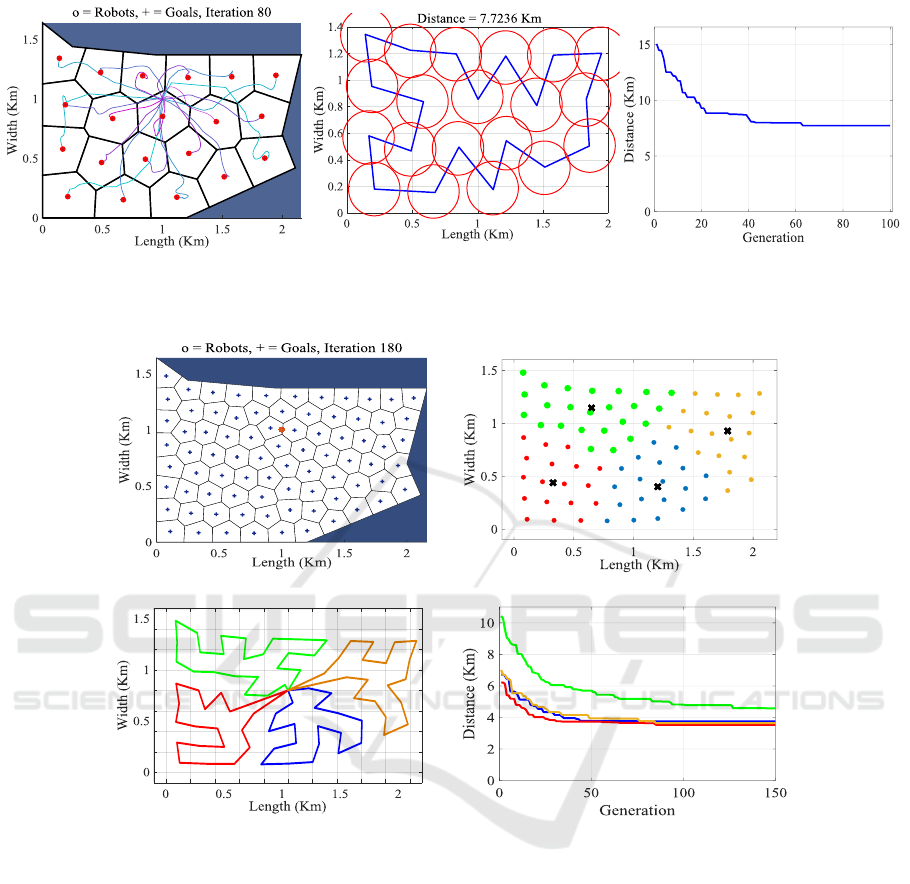
(a)

(b)

(c)

Figure 5: Area division and CPP (Scenario 1): (a) Area discretization, (b) Planned path and coverage results with circular

sensor footprint, (c) TPL according to generation.

(a) (b)

Figure 6: Area division and CPP (Scenario 2): (a) Area discretization with Meshing algorithm, (b) K-means clusters, (c)

Planned paths solving TSP-GA, (d) TPLs according to generation.

6 (a), required 180 iterations. The result of grouping

the PoIs for each UAV using the K-means algorithm

is illustrated in Figure 6 (b), where the black crosses

represent the centroids of each cluster. Figure 6 (c)

presents the ﬁnal planned paths for the UAVs, gener-

ated from the optimization step using TSP-GA. The

TLPs according to generation during optimization are

shown in Figure 6 (d). The results of this scenario

lead us to summarize the following conclusions:

• C1: The Meshing algorithm requires more iter-

ations as the number of PoIs increases, which is

manageable with the number of PoIs.

• C2: A homogeneous distribution of clustered PoIs

by the K-means algorithm has a beneﬁcial effect

on TPLs (Table 2). This clustering also results in

isolated paths relative to each other, which helps

to avoid collisions between UAVs ﬂying at the

same altitude.

• C3: The set of planned paths are optimal in

terms of TPL (and/or energy consumption), feasi-

ble, and ensure passage through all PoIs, thereby

achieving overall coverage of the RoI.

Moreover, from C1 and C2, the choice of the num-

ber of PoIs and the number of UAVs provides another

degree of freedom to accommodate the ﬂight capabil-

ities of UAVs. Additionally, there is the possibility

of implementing sensors of various shapes (circular,

square, rectangular, etc.), which offers a generic solu-

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

164

Table 2: PoIs and TPLs.

Path Number of PoIs TPL (Km)

Green path (R

) 24 4.5744

Red path (R

) 18 3.5241

Blue path (R

) 19 3.7513

Brown path (R

) 19 3.6438

tion for a wide range of applications.

5 CONCLUSION

Our work addresses UAV group path planning for

aerial detection applications (coverage). The primary

objectives are the automation of setup for crossing

points and planning optimized paths for UAVs. The

global approach is structured into three steps: the gen-

eration of PoIs, the clustering of these PoIs, and the

optimal connection of all these points to ensure com-

prehensive coverage of the studied map. Addresses

the limitations of scenario-speciﬁc approaches by

proposing a more ﬂexible methodology that integrates

diverse discretization techniques, sensor types, and

path optimization strategies.

The precise spatial discretization using the Mesh-

ing algorithm ensures comprehensive coverage of the

global RoI, while the K-means clustering method en-

ables balanced task allocation, contributing to colli-

sion avoidance and optimized path planning. The ﬁ-

nal optimization phase formulates the problem as a

TSP, solved using an enhanced GA with modiﬁca-

tions that signiﬁcantly accelerate convergence. These

improvements lead to more efﬁcient path planning,

reduced energy consumption, and overall enhanced

UAV performance, as demonstrated by the simulation

results.

While the proposed method improves UAV path

planning, several limitations remain. Scalability is-

sues may arise with larger UAV ﬂeets due to the com-

putational cost of GA optimization. The approach

also assumes a static environment, lacking adapt-

ability to dynamic obstacles, and does not explicitly

account for UAV constraints, communication limits,

or collision avoidance. To overcome these limita-

tions, future work will focus on adaptive clustering for

improved task allocation and coordination, real-time

obstacle avoidance using Rapidly-exploring Random

Tree (RRT) and RRT*, and trajectory generation to

reﬁne UAV motion planning before real-world de-

ployment.

REFERENCES

Azp

urua, H., Freitas, G. M., Macharet, D. G., and Campos,

M. F. (2018). Multi-robot coverage path planning us-

ing hexagonal segmentation for geophysical surveys.

Robotica, 36(8):1144–1166.

Balampanis, F., Maza, I., and Ollero, A. (2017). Coastal

areas division and coverage with multiple uavs for re-

mote sensing. Sensors, 17(4):808.

Bouras, A., Bouzid, Y., and Guiatni, M. (2019). Multi-uavs

coverage path planning. In International Conference

on Electrical Engineering and Control Applications,

pages 23–36. Springer.

Bouras, A., Bouzid, Y., and Guiatni, M. (2022). Multi-uav

coverage path planning for gas distribution map appli-

cations. Unmanned Systems, 10(03):289–306.

Cabreira, T. M., Brisolara, L. B., and Paulo R, F. J. (2019).

Survey on coverage path planning with unmanned

aerial vehicles. Drones, 3(1):4.

Chen, Y., Mou, Z., Lin, B., Zhang, T., and Gao, F. (2024).

Complete coverage path planning for data collection

with multiple uavs. In 2024 IEEE Wireless Commu-

nications and Networking Conference (WCNC), pages

01–06. IEEE.

Choset, H. (2001). Coverage for robotics–a survey of recent

results. Annals of mathematics and artiﬁcial intelli-

gence, 31:113–126.

Du, Q., Faber, V., and Gunzburger, M. (1999). Centroidal

voronoi tessellations: Applications and algorithms.

SIAM review, 41(4):637–676.

Gao, C., Kou, Y., Li, Z., Xu, A., Li, Y., and Chang, Y.

(2018). Optimal multirobot coverage path planning:

Ideal-shaped spanning tree. Mathematical Problems

in Engineering, 2018(1):3436429.

Kapoutsis, A. C., Chatzichristoﬁs, S. A., and Kosmatopou-

los, E. B. (2017). Darp: Divide areas algorithm for

optimal multi-robot coverage path planning. Journal

of Intelligent & Robotic Systems, 86:663–680.

Kumar, K. and Kumar, N. (2023). Region coverage-aware

path planning for unmanned aerial vehicles: A sys-

tematic review. Physical Communication, 59:102073.

Pham, T. H., Bestaoui, Y., and Mammar, S. (2017). Aerial

robot coverage path planning approach with concave

obstacles in precision agriculture. In 2017 Work-

shop on Research, Education and Development of

Unmanned Aerial Systems (RED-UAS), pages 43–48.

IEEE.

Yu, Y. and Lee, S. (2024). Multi-uav coverage path as-

signment algorithm considering ﬂight time and energy

consumption. IEEE Access, 12:26150–26162.

Coverage Path Planning Using a Group of UAVs

165