Multilevel Hypergraphs: A Conceptual Approach for Complex

System Database Modelling

José Ribas

and Orlando Belo

Higher School of Technology and Management, Polytechnic Institute of Viana do Castelo, Portugal

ALGORITMI R&D Centre / LASI, University of Minho, Portugal

Keywords: Complex System Modelling, Database Models, Graphs, Graph Models, Hypergraphs, Multi-Level

Hypergraphs, and Graph Databases.

Abstract: Graphs are very specialized structures for modelling and representing data objects and their relationships in

real-world applications. The number and diversity of graph-based applications existing today are clear

testimonies of the importance and relevance of the application of graphs in solving real-world problems.

However, more conventional graph structures have difficulty keeping up with the evolving complexity of

problems, particularly when they involve n-ary relationships between data objects. This can be overcome

using hypergraphs, which allow for representing complex relationships between finite sets of data objects.

However, their implementation still has some difficulties, such as the establishment of efficient algebras and

computing mechanisms to deal with relational content between entities of a dataset. In this paper, we present

an extension to conventional hypergraph-based models for modelling real world problems, proposing a new

functional abstraction based on a graph structure with several levels of abstraction. Relationships between

data objects are established at each level in a traditional way, while relationships between levels are defined

by “levelled” virtual data objects, allowing for the establishment of inheritance relationships between other

data objects of sequential levels, through a logical governance structure defining the relational flow between

the various levels of the established model. We named this structure as multilevel hypergraph.

1 INTRODUCTION

Graph theory (Daniel, 2013) (Angles & Gutierres,

2008) (Bondy & Murty, 2008) has been used since

very early in our training process. From the first

moment we saw a map of roads, graphs emerged in a

very natural way as the most appropriate solution to

represent the various data elements and their

relationships presented in a map. Later, in more

advanced study cycles, graphs appeared to us as

simple but very powerful "tools" for modelling real-

world systems. As we study graph theory,

approaching its history, foundations, terminology,

models and algebras, we recognize the importance of

the work of Euler (Biggs et al., 1986), which was the

first to use a graph model to solve a real practical

problem (the "Seven Bridges of Königsberg") or of

Sylvester (1878) that coined the word graph, as well

as the enormous potential and application of graphs.

https://orcid.org/0000-0001-9139-2801

https://orcid.org/0000-0003-2157-8891

In the areas of Medicine, Biology, Economics or

Computer Science, among many others, graphs have

been applied in a very systematic way, to represent

and solve very complex problems (Kanhio, 2023).

However, as problems become more complex, we

find that the most elementary representations of

graphs are not always the most adequate to address

some problems, especially those that require the

establishment of more complex relationships between

data objects than simple binary relationships, between

pairs of data objects. In some applications, the use of

simple relationships can lead to the loss of pertinent

information or even lead to the inability of the model

to represent real data objects. Cases like these require

other modelling approaches for overcoming such

limitations and providing means to represent complex

relationships (n-ary) between data objects. One of the

ways we can use to solve these types of problems is

using hypergraphs.

Ribas, J. and Belo, O.

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling.

DOI: 10.5220/0013356900003929

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 87-98

ISBN: 978-989-758-749-8; ISSN: 2184-4992

Berge (Berge, 1967) (Berge, 1973) introduced the

concept of hypergraph as a form of generalization of

graph-based approaches. In practice, a hypergraph

(Hellmuth et al., 2012) (Voloshin, 2009) (Bretto,

2013) is made up of a set of vertices and a set of

hyperedges that each refer to a diverse set of vertices.

In addition, vertices of a hypergraph can be related to

several hyperedges. Hypergraphs are a natural model

for the representation of networks or systems that

require the representation and manipulation of objects

with complex relationships or need to host higher-

order interaction processes. In fields such as physics,

biology, or engineering, traditional graph models may

not have the capacity to represent adequately the

complexity of the data objects involved. In these

cases, hypergraphs have already proven that they can

help.

From social network analysis to software system

modelling, hypergraphs have had numerous

applications. We can find them in several application

domains (Molnár, 2014), such as image segmentation

processes (Ducournau et al., 2012), representing

structures of non-classical molecules (Konstantinova

& Skorobogatov, 2001), provisioning of new data

models for social networks (Amato et al., 2017),

recommending music in social networks (Tan et al.,

2011), or representing systems (Sarkadi-Nagy &

Molnár, 2019). Despite their proven usefulness,

hypergraphs reveal some practical limitations,

particularly in visualizing and interpreting the

complex objects they represent and host, as well as in

understanding the relationships established, and

mapping them in a real field of application. In

addition, given their complexity, they are much more

demanding in terms of computational resources and

may be less efficient than traditional graphs.

In this paper, we present and discuss a new

conceptual model for hosting hypergraphs: multilevel

hypergraphs (MLHG). A MLHG uses multilevel

graphs to represent complex real-world problems,

presenting several benefits and applications in

different areas of knowledge, namely in the field of

data science and data engineering. The model of a

MLHG is a new functional abstraction for modelling

real world problems, since it allows to make more

complex and detailed representations of relationships

between entities and to sustain analysis processes

along the various levels of abstraction defined in the

structures of the implemented model. A MLHG adds

a new set of features to conventional hypergraphs,

namely: the ability to create and edit a modular data

hierarchy during the construction of the model itself,

or the process of its instantiation; the capability to

perform isolated analyses on a specific set of data,

bounded between two levels of abstraction, within a

virtual vertex; or the simplicity of manipulating the

data structure of a specific set of data contained in any

virtual vertex, without harming the other data or the

overall structure of the model, are just some of them.

These characteristics enable innovative approaches to

solve new problems, especially those related to

models with multiple functional complexities or to

models with irregular hierarchical groupings, whose

hierarchies are not initially defined in the model, and

whose mutations evolve over time, being applicable

in latent scenarios. We organized the remaining part

of this paper as follows. Section 2 exposes the domain

of graphs and hypergraphs, giving emphasis to their

fundamentals and applications, Section 3 presents and

discusses multilevel hypergraphs, an abstract

extension for conventional hypergraphs we propose

for modelling complex systems, and Section 4

demonstrates the application of multilevel

hypergraphs to a specific application case. Finally,

Section 5 presents some conclusions and future work.

2 GRAPHS AND HYPERGRAPHS

The application of graphs (Daniel, 2013) (Angles &

Gutierres, 2008) to real-world problems are quite

common whenever the problem requires, directly or

indirectly, the representation and storage of data that

requires the definition of paired relationships between

one or more data elements. Numerous real-world

domains provide a very broad field of application for

the use and exploration of graph-based structures.

However, it is the emergence of new areas of work

and new services that, today, requires the use of

structures such as graphs, essentially due to the

volume and complexity of the data elements involved

and their relationships.

Many systems involving navigation or

transportation problems that people use in their

decision services use graphs, such as the one that

Dijkstra used many years ago (Dijkstra, 1959).

Graphs help to decide which is the shortest path

between two points (Johnson, 1977), to find the

shortest path between any pair of points in a directed

heavy graph, or to help allocate rental cars to people

who need to get around (Kuhn, 1955). These are

typical optimization problems in which graphs can be

naturally applied. But there are a lot more of fields

where graphs can be applied with very success. For

example, in Chemistry non-oriented graphs are used

to represent molecules (Wigh et al., 2022), in Biology

to represent bio entities such as proteins, genes, or

molecules (Georgios et al., 2018), or in Medicine to

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

support the interpretation of proteomic data (Brin &

Page, 1998). In Process Management and Control

applications, some of the data representation models

are used to represent the execution of tasks or

processes, considering their sequence, scaling, or

execution time.

Graph models have enormous application

potential. We can prove this through the numerous

applications in various scientific fields, supporting a

wide variety of solutions to problems in networks of

chemical reactions, access to web pages,

establishment of usage profiles, or in the analysis of

population dynamics. But probably the most relevant

application was in Google's PageRank System (Brin

& Page, 1998). Finally, we want to mention the use

of graphs in the implementation of database systems

(Angles & Gutierres, 2008), in which we can find

very high-level graph structures to host and relate

data elements, in large volume and diversity. Take,

for example, the cases of the database management

systems Neo4J (Neo4J, 2024), JanusGraph

(JanusGraph, 2024), Memgraph (Memgraph, 2024)

or NebulaGraph (NebulaGraph, 2024), which have

been gaining popularity over the last few years, or

other hybrid systems, which integrate graphs with

other types of data structures to cover a wide

spectrum of applications.

Generally, a graph G is abstractly defined as a

structure G (V, E), where V represents the vertices

and E the edges that support connections among

vertices, allowing the establishment of relationships

between different entities or data objects, defining

semantic relationships, interrelating characteristics,

and promoting inference of new information. Over

the years, graph structures and their conceptualization

processes have evolved, encompassing new

representation schemes and embracing increasingly

sophisticated and complex levels of abstraction. But

in many real-world problems, relationships between

objects require more complex connections than

simple relationships between pairs of vertices. The

eventual representation of these complex

relationships through simple relationships could be

done, but it would lead to some kind of loss of

information, deteriorating the real representation of

the model in its field of application (Schölkopf et al.,

2007).

Hypergraphs (Hellmuth et al., 2012) (Ouvrard,

2020) can be a good solution for receiving complex

relationships, since they allow for the representation

of relationships between more than two vertices.

Hypergraph theory is not new, having been studied by

many researchers over the years. The concept of the

hypergraph was introduced by Claude Berge in 1967

(Berge, 1967). Since then, hypergraphs have been

used in a variety of applications, including problem

optimization, network analysis, machine learning, or

data science, among other areas (Molnár, 2014).

However, one of the biggest applications of

hypergraphs, probably the most impactful, has been

in graph partitioning, which is a technique widely

used in several areas, such as Computer Science,

Mathematics, Engineering or Physics. In these areas,

hypergraphs are used for solving combinatorial

optimization problems, data clustering, social

network analysis, or data routing, among many other

problems. Contrarily to traditional graphs,

hypergraphs are composed of vertices and

hyperedges. Hyperedges are sets of two or more

vertices identified as a single entity. The definition of

hyperedges provides essential means to receive and

deal with complex relationships among communities

of vertices, not only among simple vertices. In

scientific collaboration networks (Ouvrard et al.,

2017), for example, the use of hyperedges allows for

modelling the co-authorship of articles. In this case,

each vertex represents an author, and each hyperedge

represents an article on which those authors

collaborated. Using a hypergraph, we can effectively

model the (complex) relationships between authors

and papers, rather than simply relating pairs of

authors as would happen in a traditional graph.

Hypergraphs can represent higher-order relationships

between vertices, while traditional graphs are limited

to representing relationships of order 2 (edges). This

is the big distinction between conventional graphs

and hypergraphs. Furthermore, hypergraphs have

specific properties that differentiate them even more

from traditional graphs. For example, the cardinality

of a hyperedge is the number of vertices it contains,

while the cover of a hypergraph is the smallest set of

vertices that intersects all hyperedges. These

properties have important implications for the

analysis and understanding of hypergraphs. They

promote the investigation of richer structures and

provide greater flexibility in the relationships that

must be represented.

Formally, a hypergraph (HG) can be defined as a

structure (V, E, I), in which V is a non-empty set of

vertices, E a set of hyperedges, and I the incidence

function that associates each hyperedge of E with a

non-empty subset of V. The incidence function I is

defined as I: And → P(V), where P(V) is the set of

all subsets of V. Figure 1a illustrates a small example

of a hypergraph. The representation of hypergraphs

can be performed using algebraic, incidence,

adjacency matrices and their respective lists, as well

as through set-based approaches (Ouvrard, 2020).

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling

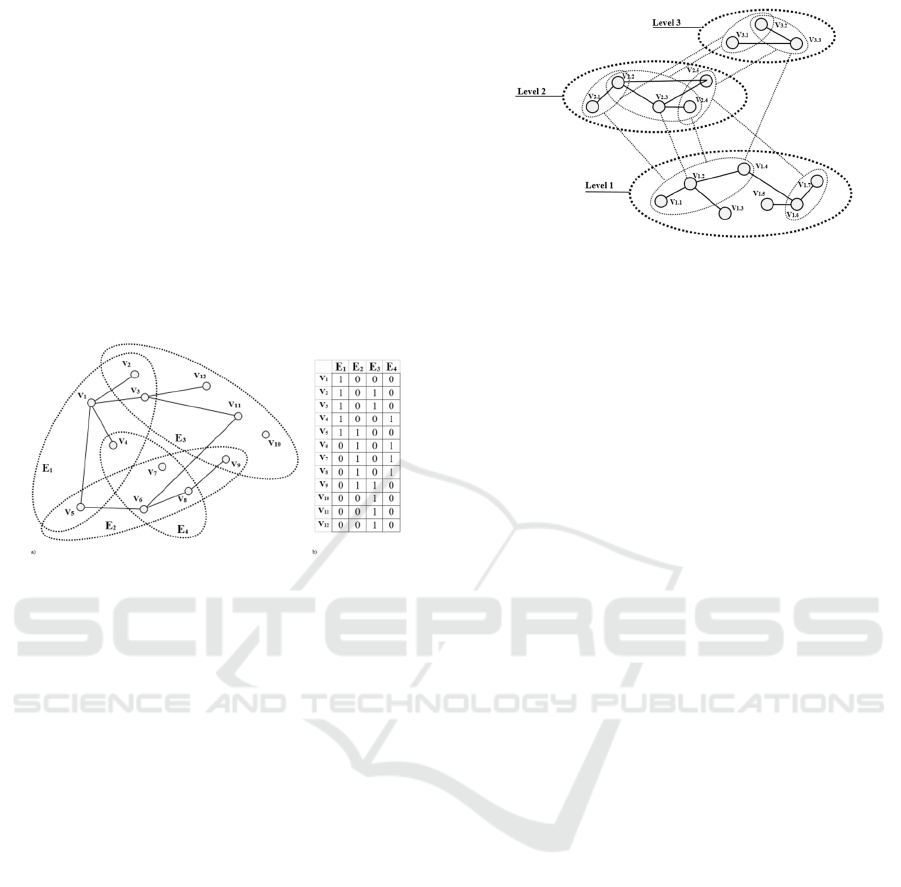
Each of these representations must be carefully

chosen, considering the field of application and the

desired modelling, as each of them has specific

advantages and applications. In Figure 1a we can see

an example of a hypergraph and in Figure 1b the

corresponding matrix representation. However,

despite their advantages, hypergraphs pose some

difficulties, not only in terms of their complexity of

their computational representation and processing,

but also in their subsequent visualization,

manipulation, and analysis of their various data

elements. To work with a hypergraph, it is necessary

to use several techniques, such as, for example,

decomposition trees (Habib et al., 2022).

Figure 1: A hypergraph and its adjacency matrix.

In addition, modelling a hypergraph can also be quite

challenging, sometimes requiring the use of machine-

learning techniques (Gao et al., 2022), as well as

interpreting the information we obtain from a

hypergraph, given the complexity of the data and the

relationships that are included in it. To interpret data

like these, Frieze and Karoński (2015) proposed some

specific random graph-based techniques, namely for

applying in processes of pattern and relationship

analysis in scientific literature.

Over time, depending on the needs of the

problems and their domains of knowledge, several

types of hypergraphs have been created, which are

basically extensions to the original model of a

hypergraph. Today, in the literature, we can find a

large diversity of references about hypergraphs,

ranging from random hypergraphs (Frieze &

Karoński, 2015) (Ghoshal et al., 2009), incident

hypergraphs (Grilliette et al., 2022), to hierarchical

hypergraphs (Ancona & De Floriani, 1989), among

many others. Although the importance of all these

types of hypergraphs in their own fields of

application, in this work we have relied in a particular

type of hypergraphs, hierarchical (Figure 2), in which

vertices and hyperedges are organised at different

levels.

Figure 2: An example of a hierarchical hypergraph.

This type of hypergraph is used effectively in very

interesting areas of application. Of note is their

application in rule-based modelling of biochemical

systems (Lemonset al., 2011), representing structural

properties of robotic systems (Scioni et al., 2016), or

describing the structure of an application and its

computing architecture (Yang & Shen, 2015).

Inspired by all these works, we designed a new

definition for a multilevel hypergraph structure, as a

new class of hypergraphs, which has greater

flexibility in modelling complex systems, involving

multiple levels of hierarchy. With this type of

hypergraph, it will be possible to create connections

that are more complex, with greater granularity, when

compared to traditional hierarchical hypergraphs,

which we think are an interesting alternative for

representing and manipulating complex systems, at

different areas of knowledge. In the next section, we

will approach this new class of hypergraphs: MLHG.

3 MULTILEVEL HYPERGRAPHS

The nature of a problem determines what kind of data

model we need to use. Different problems impose

different data models. Obviously. Each type of

problem requires a specific data model, supported by

a particular type of graph. There are problems having

complex natures that require sophisticated graph

structures for modelling and receiving data, capable

of representing entities whose characterization (and

relationships) is done through the establishment of

several levels of abstraction, with some kind of

defined hierarchy. To accommodate this kind of

modelling problems, we propose MLHG as an

alternative functional abstraction.

A MLHG (Figure 3) is a generalization of a

hypergraph, which allows for describing complex

relationships between multiple data objects

distributed by distinct abstraction levels. The

mathematical-computational representation of

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

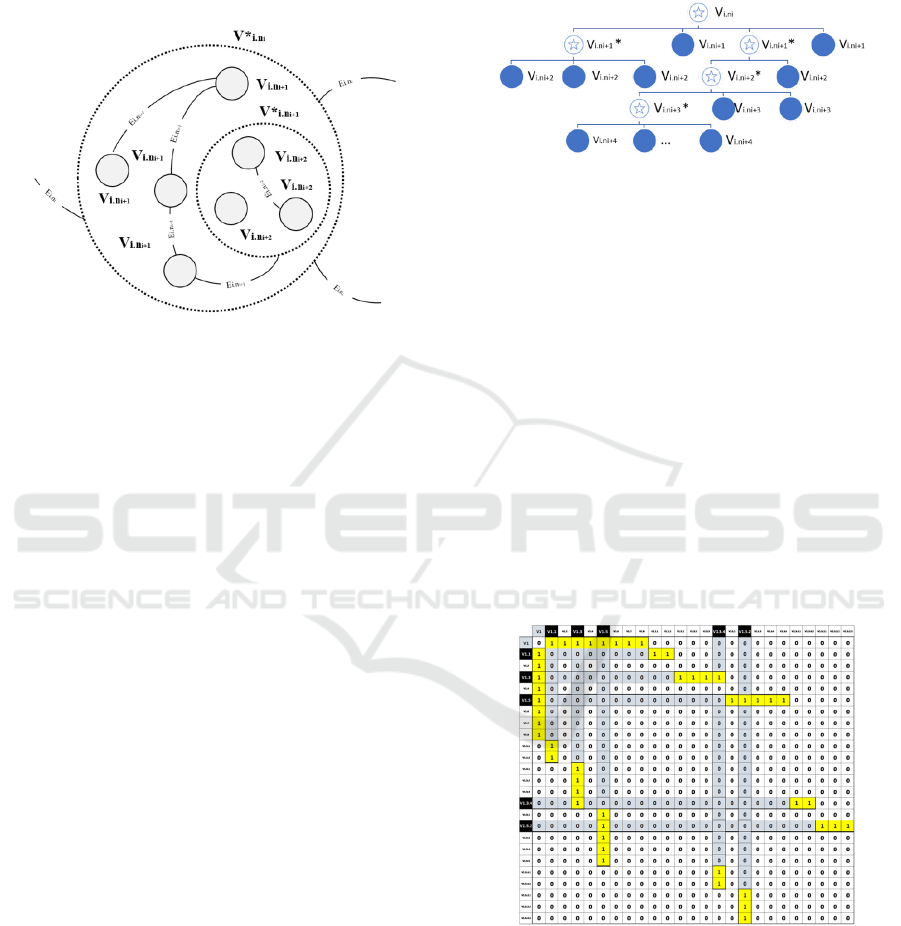
problems using a MLHG provides the basis for

modelling relationships between objects belonging to

different levels, which often cannot be described in an

adequate manner by other hypergraph approaches,

even by hierarchical hypergraphs.

Figure 3: Illustration of a MLHG conceptual structure.

The MLHG model proposal we propose uses a

structure (V

i,n

, A

i,n

, V

i,n

, E

i,n

) (Figure 3), in which V

i,n

represents the set of regular vertices, A

i,n

the set of

level trees, V

i,n

the set of virtual vertices, and E

i,n

the

set of edges of the hypergraph. The vertices V

i,n

which are organized at different levels of abstraction,

represent the entities at a given level of abstraction n,

while the logical structure trees of levels (Ai,n)

manage the relational flow between the vertices of the

various levels. The virtual vertices (V

i,n

) are

candidates for hypergraphs at the n-level, and the

edges (E

i,n

) materialize the relationships between the

vertices V

i,n

and V

i,n

The mathematical-computational representation

of an MLHG is obtained using an adjacency matrix

structure supported by a dictionary of labels, in which

each vertex is represented on a specific line and a

column. The graphical representation of a MLHG

allows for visualizing different entities and

relationships present at a certain level of abstraction,

making it easier to understand and analyse any system

model. The level trees (A

i,n

) (Figure 4) play an

essential role in defining the flow of relationships

between different levels of abstraction of the MLHG.

Each tree starts with a specific root, which represents

the various regular vertices (V

i,n

) and the virtual

vertices (V

i,n

), at the n

level. As the tree may grow

to higher levels, virtual vertices (V

i,n

) turn into

branches, feeding other branches and providing

leaves (vertices) at the next higher level, n+1.

Level trees provide a clear hierarchical structure

of the various relationships between different levels

of abstraction of a MLHG. This provides a way for

establishing a coherent and efficient organization in

the representation of graphs of diverse multi levels of

abstraction, facilitating the understanding of the

relationships between all the entities involved in each

level of abstraction.

Figure 4: An example of a level tree of a MLHG.

Additionally, using virtual vertices (V

i,n

) allows

MLHG to represent models in which an entity has not

yet been fully defined or is not relevant to an ongoing

analysis process. Furthermore, we have created a

structure for labelling vertices representing entities at

a given level of abstraction n. This structure uses a

unique index for each vertex V, in the form

<i(n1).i(n2).i(n3).i(n4)…i(nn)>. The size of the index

allows for setting the cardinal of the level, as well as

the cardinal of the vertex at each level it crosses. For

example, a label having the format <1.3.4.2> refers to

a vertex, V

1.3.4.2

, at the maximum level, n=4,

representing, respectively, the second vertex of that

level, the fourth vertex of level 3, the third vertex of

level 2, and the first vertex of level 1. Labelling these

elements is important for identifying uniquely each

vertex in a MLHG.

Figure 5: An adjacency matrix of a MLHG.

Figure 5 shows the mapping of an MLHG in an

adjacency matrix. Through the adjacency matrix of

the level tree, it is possible to identify directly the

virtual vertices (V

i,n

) and the edges (E

i,n

) associated

with each level of abstraction of the MLHG. Thus, a

more organized and efficient representation of a

MLHG is achieved, facilitating the analysis of the

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling

relationships established between the entities

involved, using the labels of their vertices. The

adjacency matrix of a MLHG is a square matrix of

dimensions (V x V), which can be represented simply

by [V

]. This type of structure was chosen because it

is possible to know its dimensions in advance. It is a

structure commonly recommended for the

representation of dense graphs, which allows for

creating algebraic operators, and it is especially

oriented for representing digraphs.

The algorithm used for constructing the adjacency

matrix of an MLHG (Figure 6), as well as its vertex

labelling dictionary, was developed to ensure its

integrity. This is important, because there is an

inheritance relationship between the relationships of

each abstraction level (n) and its successor level

(n+1). This means that for a given relationship E

i,ni+1

existing at the level ni+1 between two vertices of this

level (V

i,ni+1

) and another virtual vertex (V

i,ni+1

candidate to be managed by each of the elements

integrated in the higher level, ni+2, it is necessary to

ensure the replication by inheritance of the

relationships, E

i,ni+1

(of edges) and of the vertex V

ni+1

, for all vertices E

i,ni+2

constituents of V

i,ni+1

which in this process will no longer be part of the ni+2

level.

Figure 6: Building an adjacency matrix for a MLHG.

In the process of inheritance between levels (Figure

7), due to a certain relationship E

i,ni+1

of the ni+1

level, relating the vertex V

i,ni+1

with the virtual vertex

i,ni+1

at the level ni+2, it can be observed that three

new relationships arise, one for each vertex of V

i,ni+1

despite the loss of another relationship. The

inheritance relations defined with the relationships

established between each abstraction level (n) and its

successor level (n+1) are defined through the

algorithm, which allows for constructing the

adjacency matrix for the MLHG, for any level n. The

adjacency matrix, AdjM(MLHG), at the first level, is

initialized according to the standard convention for

labelled graphs. The algorithm iterates through each

virtual vertex V

i.ni+1

with edges E

i,n+1

, at each level

n+k, and establishes a new adjacency matrix

AdjM(V

i.ni+2

i,n+2

), having dimension V

x V

, where

is the number of vertices in V

i.ni+2

. For expanding

the dimension of the current Madj array, and

accommodate a new Madj array (V

i.ni+2

i,n+2

), the

algorithm performs three steps, namely it:

1) expands dimensionally the matrix in the (i-th+1)

row and column referring to the position of the

vertex V

i.ni+1

, by adding |V

|-1;

2) replicates the constant values with respect to the

virtual vertex V

i.ni+1

in the new coordinates

resulting from step 1, per column and per row;

3) develops the new Madj matrix from the correct

coordinates of the current Madj matrix, from the

initial coordinates of the vertex V

i.ni+1

Figure 7: Illustrating inheritance between levels.

For virtual vertices with no edges (E

i,n+1

), the

algorithm performs a similar process, but performing

a dimensional expansion from the origin of the

adjacency matrix, assigning zeros to all new

coordinates. The result is an adjacency matrix

AdjM(MLHG) representing an MLHG with levels

and no virtual vertices. The algorithm uses constant

values and straightforward development processes, to

minimize the number of calculations required to

construct the final adjacency matrix. MLHG are

designed to represent systems having multiple

hierarchies, or complex interactions between

different levels, being particularly adequate for

modelling systems. For example, in transportation

systems, Bezrukova (2019) demonstrated the

practical application of MLHG, and Yu Gu (2022)

their applications in the field of distributed data

processing, proposing a partitioning algorithm for

graph division for facilitating the distributed

processing of hypergraphs. All the experiments

revealed very interesting results. In the next section

we will look at how we can apply the model proposed

in this paper in a real-world application domain

4 AN APPLICATION CASE

Today, the application of hypergraphs has some

prominence in several application areas. By

modelling complex interactions between structural

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

elements, hypergraphs allow the visualization of

global relationships defined in a system model,

making simple to understand how these interactions

influence the project. In this section, we will show

how to explore a MLHG for representing (and see)

relationships in a Rowing Club, which will allow us

to understand how the different elements of the club

are related and interact with each other. Using a

MLHG for representing them, it will be possible to

identify patterns and structures that would not be as

evident just by looking at the raw data. We can get a

more detailed view seeing the relationships between

different elements of the club, such as athletes,

coaches, competitions, and boats.

4.1 The Case: General Overview

Rowing, as a sport, has a deeply intertwined history

with the regattas that emerged along the River

Thames in England around 1700. Initially used for

transportation, even in war contexts, rowing has

evolved to become an emblematic sporting activity.

Historic competitions, such as the Oxford-Cambridge

regatta, established in 1829 and still held in London

today, were essential in consolidating rowing as a

prominent sport. Rowers compete in narrow

watercraft, sitting on movable benches with their

backs to the bow. In this speed competition, athletes

are challenged to propel the boat as fast as possible,

using oars and controlling the rudder by means of

cables attached to the feet.

There is a wide variety of categories, from

individual boats to teams of eight rowers. The number

of oars used depends on the type of boat and the

modality. On certain types of boats, especially larger

ones, a helmsman is present to guide the team and

dictate the pace of the paddling. Rowing clubs are

institutions dedicated to the training and competition

of rowers of all athletic levels. The management of

rowing clubs presents a series of complex difficulties

requiring well-defined strategies for ensuring the

success of the institution in competitions, namely to:

organize and coordinate training and competitions

ensuring that athletes are prepared for the

competitions, manage available resources – e.g.

boats, equipment or technical personnel – efficiently

to improve the performance of the club, or make

strategic decisions in various areas, to hire technical

staff, set training goals or plan competitions, for

example.

4.2 A MLHG Model

The MLHG allows for representing the diverse range

of relationships and interactions between the different

elements involved in the club. Its flexible structure is

essential to capture the complexity of the

management environment, which involves a variety

of intricate and dynamic relationships between its

elements, namely athletes, coaches, boats and

competitions, etc. The possibility of achieving a

multi-level representation of the relationships within

the club is an aspect that enhances the relationships

that can be visualized and analysed at different levels

of granularity. From the individual level of athletes

and coaches to the functional level of the competition

boats, as well as the management of the club. On the

other hand, club managers can conduct an integrated

analysis of the interactions between the different

members of the club, which includes identifying

patterns, trends, and correlations that may not be

easily perceived in a traditional management

approach. Faced with a chaotic scenario of the

dynamic management of the club, which is subject to

constant changes, such as the entry of new athletes,

the hiring of new coaches or the scheduling of new

competitions, we consider that the MLHG is

adequate, as it welcomes any changes that may occur

over time, which allows new elements to be easily

incorporated into a graph-based database and

relationships to be adjusted accordingly is necessary.

Let’s focus now specifically on our case study and

how modelling it is using a MLHG. The club has nine

different boats for the competitions (Table 1).

Table 1: Types of boats.

Each boat is identified by a unique label, B

. The club

has its own facilities, in which the athletes perform

specific daily training in water tanks and ergometers.

Within the group of athletes, only 12 are selected to

occupy the positions (A

), previously established for

each boat. Figure 8 shows the structure of the HGMN

and Figure 9 its corresponding adjacency matrix. The

matrix was defined as a general structure of the club

management, with hyperedges/vertices for athletes

(A), coaches (T), boats (B), helmsmen (TM),

competitions (C) and directors (D).

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling

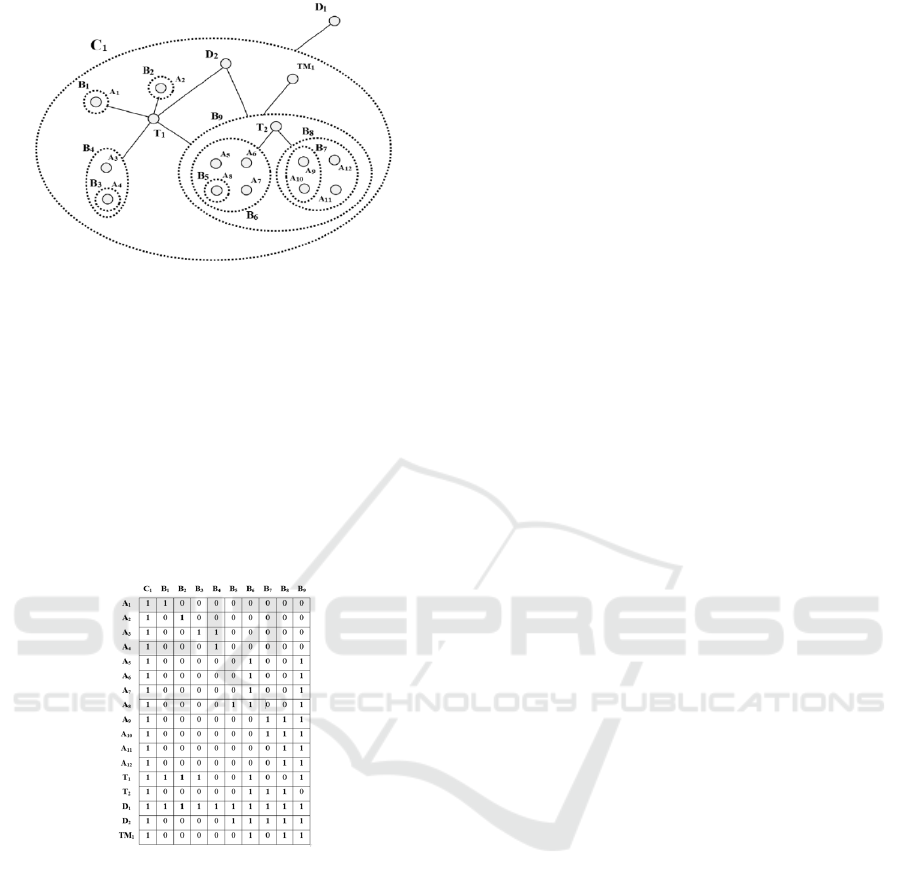
Figure 8: Illustration of the club management MLHG.

Edges indicate the various relationships established

between the entities of the club, such as the

assignment of athletes to coaches or their

participation in competitions, for example. Since we

are dealing with an MLHG, hyperedges could be

associate some relationships by inheritance, which in

turn can connect different entities, such as athletes,

coaches, competitions, and types of boats. Each entity

(hyperedge) may have several attributes and be

associated with specific relationships established

between entities.

Figure 9: The adjacency matrix of the MLHG.

Let's now take a closer look at the various entities we

defined for the club and the MLHG adjacency matrix

representing the various relationships established

between them. In the adjacency matrix, each column

corresponds to a relationship (hyperedge) between

the entities of the club, namely:

- Competition (C

), represents athletes, coaches

and types of boats that participate in the

competitions; they provide information that

allows for determining which athletes and

coaches are involved in each competition, and

what types of boats can be used.

- Type of boat (B

..B

), defines each of the types

of competition boats. Each type of boat has a

specific relationship with the athletes and

coaches. For example, we can identify which

athletes are assigned to each type of boat, and

which coaches are responsible for their training.

- Athlete (A

1..

A12

), represents the athletes of the

club; they are related to the types of boats which

they compete on and the coaches who supervise

them. The adjacency matrix defined does not

allow us to determine which athletes are in each

boat and which are their coaches.

- Coach (T

, T

), which characterizes the club's

coaches, are associated with the athletes he

supervises and the types of boats they are

involved in. This information allows us to know

how the distribution of coaches is done among

the different types of boats and athletes.

- Helmsman (TM

), who represents the helmsmen

of the boats; each helmsman is associated with

the various types of boats he drives and implicitly

with the athletes who are involved in each boat.

This information can be used to know its

influence on the results between different types

of boats and athletes.

- Director (D

, D

), who characterizes the

members of the club involved in the organization

and logistics of competitions and training. Their

relationships can be inferred indirectly based on

the relationships between athletes, coaches, and

competitions.

Using the MLHG presented earlier in Figure 8,

let's analyse some practical application cases.

Athletes are directly related to the types of boats

available. Each athlete is associated with one or more

types of boats, which indicates they compete in these

boats. For example, the athlete A

is related to the

boats B

, B

and B

, which means that he participates

in competitions with these three types of boats.

Coaches are directly related to the types of boats

available. Each trainer is related to one or more types

of boats, indicating supervision and training actions

on these vessels. For example, the trainer T

is related

to all types of boats available. The director D

is not

directly related to the types of boats, but rather to the

competitions. On the other hand, director D

is related

to boat B

– this boat, with eight seats, is the one that

will bring the most prestige to the club, if it is

successful in the competition. The helmsman is

related to the types of boats available, which require

his steering. For example, the helmsman TM

associated with boats B

, B

and B

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

4.3 A Graph-Based Database

To establish a schema for a graph-based database

from the structure of an MLHG, it is important that

its creation is carried out according to the schema

presented in Figure 10, and the trees of the levels

logical structure reflect the hierarchical organization

of the all the aspects considered in the management

of the club. The MLHG framework provides a

flexible basis for representing information by

defining hierarchical dimensions. It allows for

creating a database model with different levels of

detail and complex relationships, having the ability to

represent the large number of relationships between

the club's entities.

Figure 10: The club’s graph-based database schema.

The schema for the database should be defined to

capture all relevant elements of the management of

the club, including the entities, relationships and

attributes necessary to represent the data involving

athletes, coaches, competitions, resources and other

aspects involving the club management. The scheme

depicted in Figure 10 represents the club and the

relationships between management elements.

However, it could, if necessary, include other vertices

to represent other aspects, such as the coordination of

training and competitions, or the performance of

athletes, among others. As mentioned earlier, logical

level structure trees are essential for breaking down

club management into several hierarchical layers.

Each level of the tree includes a specific set of

elements and their relationships, which allows us to

get a detailed and structured view of the management

of the club (Figure 11).

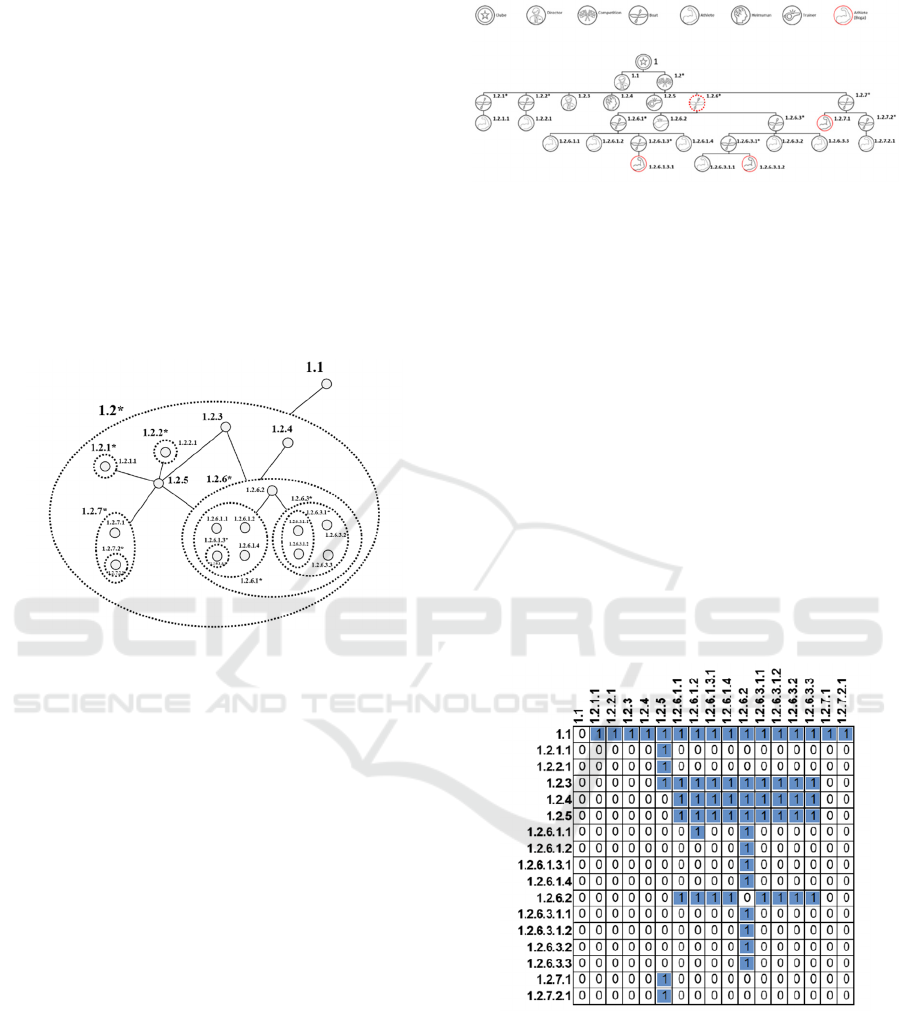
The logical framework defined for the MLHG in

the context of the modelling of the management of the

rowing club shows how the 6 levels of abstraction are

linked, from the individual level of athletes and

coaches to the level of competitions.

Figure 11: Logical structure of the club’s levels.

To create an instance of a given competition (Figure

13), after the conclusion of the aggregation process

presented in section 3, an aggregate subgraph

representative of the instance is incorporated into the

database, through its dictionaries and its adjacency

matrix, Figure 12, which at the limit, may be

coincident with the overall adjacency matrix of the

scheme. This matrix provides a visual mapping

representation of the relationships established

between the club's entities for the competition

instance. In the array, each cell indicates whether

there is a relationship between two entities. This

visual representation of relationships is essential to

understanding the connections established within the

club's organizational structure. For example, if a cell

contains a value that indicates a relationship between

an athlete and the competition, it suggests the athlete's

participation in that competition.

Figure 12: The adjacency matrix of an instance.

By associating this matrix with the formal definition

of relationships (Table 2), it is possible to establish

the labelled subgraph, as shown in Figure 14, to

support a representative instance of a particular

competition. After having typified the relationships

involved, using the MLHG adjacency matrix to

support the instantiation process of the competitions,

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling

we can obtain the support subgraph presented in

Figure 13.

Table 2. Definition of the relationships.

Entity Relationship Description

Director RELATED_TO The person in charge to coordinate the

members of the club.

Helmsman ACCOUNTABLE The responsible for a specific set of boats

during competitions or training.

Trainer TRAINS The one that trains a specific set of athletes.

Athlete TRAINE An athlete trained by one or more coaches

specialized in a given sport.

This subgraph offers a detailed view of the various

relational flows between the various entities of the

club, for a given competition, even without revealing

the identity of the athletes, coaches or directors,

where, for example, it is verified that the athlete

(1.2.6.1.3.1) relates exclusively to the two coaches

(1.2.5) and (1.2.6.2), who in turn report directly to

(1.1) and (1.2.3), your situation as an athlete. In the

final populating stage of the database, a careful

selection was made of the individuals to be included

in the database, such as athletes.

Figure 13: Support aggregate subgraph.

The athletes were chosen based on their performance

history, which includes their technical level,

endurance and physical strength. In addition to

physical capabilities, the potential of athletes was also

evaluated based on their mental capabilities, so that

we can achieve higher competitive results. The

willingness of the athletes to train and compete, along

with their commitment to the club, were also

considered as determining factors in the selection of

the athletes. This process resulted in the formation of

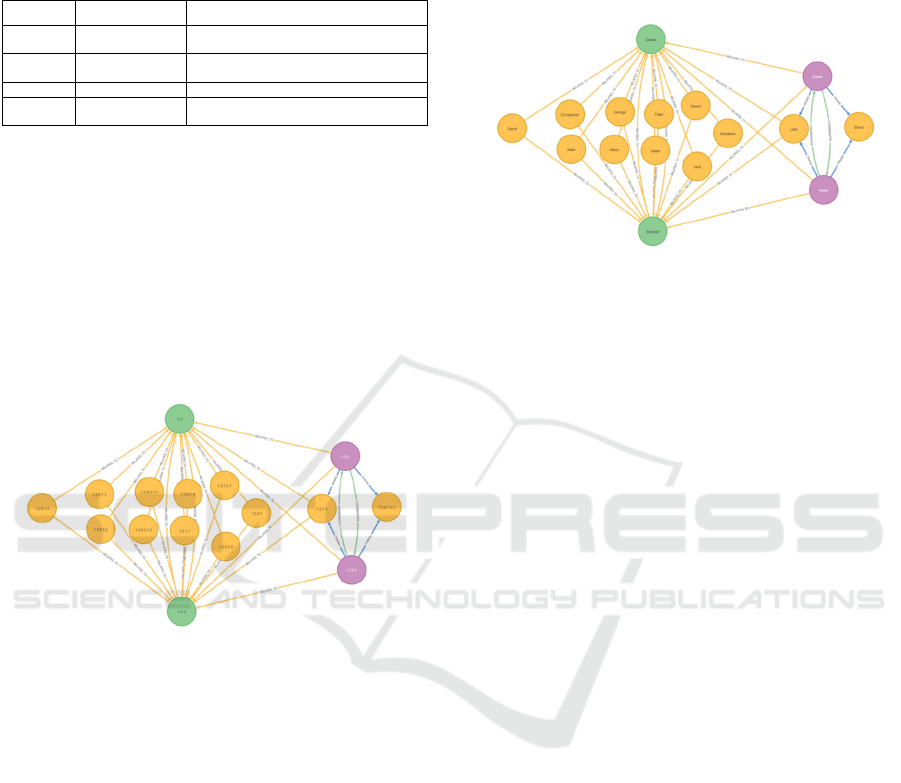
a very refined subgraph (Figure 14), which allows the

identification of all the participants in each

competition, where, for example, it turns out that

Ethan relates exclusively to the two coaches David

and Henry, who in turn report directly to the directors

James and Michael, his situation as an athlete.

To conclude, we want to emphasize once again

the importance of creating a graph-based database for

the club, using a HGMN model for representing the

complex relationships that can be established

between one or more entities of the club. The

database created is a robust structure to store and

organize information related to athletes, coaches,

competitions, types of boats and other essential

aspects in the management of the club.

Figure 14: Participant Aggregate subgraph.

By using a HGMN as the fundamental model of

the database, we can capture and model the

interactions and interdependencies between the

different entities of the club, which facilitates the

implementation of analysis and decision-making

processes, and provides a high-level conceptual

model of the database.

5 CONCLUSIONS AND FUTURE

WORK

The growing demand for advanced approaches for

analysing complex systems has driven to the

exploration of mathematical structures with the

ability for capturing interconnections and

interdependencies present in the various system’s

data elements. Graphs, in general, and hypergraphs,

in particular, stood out in this domain as adequate and

very versatile instruments, capable of dealing with the

complexity of the intricate way data elements are

related to (and aggregate). Graphs offer an elegant

mathematical representation for creating very

intuitive, easy-to-understand visual abstract models.

It is not surprising, therefore, that it is adopted and

applied in modelling systems requiring reliable

representations of real systems and effective

mechanisms for manipulating their data elements,

using specific languages for selecting and combining

data elements, different types of data, and other types

of data.

In this paper, we presented a new strain of

hypergraphs, as a new functional abstraction for

modelling real world problems. This kind of graphs,

MLHG, allows for receiving complex and detailed

representations of relationships between entities as

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

well as the ability for sustaining analysis processes

along the multilevel architecture of a hypergraph.

MLHG allow for solving complex problems,

involving models with multiple functional

complexities or with irregular hierarchical groupings,

not defined initially and involving mutations evolve

over time. Their basic characteristics sustain the

definition of modular data elements hierarchies

during the construction of a system model,

performing isolated analyses on a specific set of data,

bounded between two levels of abstraction, within a

virtual vertex, and allowing handling autonomously

data element structures contained in virtual vertices,

without affecting other data elements of a specific

model.

MLHGs stand out for their ability to deal with

systems that exhibit unpredictable behaviours, in

which the so-called global properties arise from local

interactions between individual components. On the

other hand, they have great potential in large-scale

systems, helping to identify problems and improve

the performance of complex systems. It is important

that, in a near future, we develop more efficient

algorithms, and increase the understanding of

complex systems, to improve MLHG-based

solutions.

ACKNOWLEDGEMENTS

This work has been supported by FCT – Fundação

para a Ciência e Tecnologia within the R&D Units

Project Scope: UIDB/00319/2020.

REFERENCES

Daniel, G. (2013). Graph Theory. In: Runehov, A.L.C.,

Oviedo, L. (eds) Encyclopedia of Sciences and

Religions. Springer, Dordrecht.

Angles, R., Gutierrez, C. (2008). Survey of graph database

models. ACM Comput. Surv. 40, 1, Article 1, February.

Bondy, J. A., Murty (2008). U. S. R., Graph Theory,

Springer.

Biggs, N., Lloyd, E., Wilson, R. (1986). Graph Theory,

1736-1936, Oxford University Press.

Sylvester, J. (1878). Chemistry and Algebra. Nature. 17

(432): 284. Bibcode, 1878.

Kanhio, M. (2023). Scope of Graph Theory in Real Life.

http://dx.doi.org/10.2139/ssrn.4651239

Berge, C. (1967) Graphes et hypergraphes. Dunod, Paris.

Berge, C. (1973). Graphs and hypergraphs, volume 7.

North-Holland publishing com-pany Amsterdam.

Hellmuth, M., Ostermeier, L. & Stadler, P.F. (2012). A

Survey on Hypergraph Products. Math.Comput.Sci. 6,

1–32.

Voloshin, V. (2009). Introduction to graph and hypergraph

theory. Nova Science Publ. ISBN 978-1-60692-372-6.

Bretto, A. (2013). Applications of Hypergraph Theory: A

Brief Overview. In: Hyper-graph Theory. Mathematical

Engineering. Springer, Heidelberg.

Molnár, B. (2014.) Applications of Hypergraphs in

Informatics: A Survey And Oppor-tunities For

Research. Annales Universitatis Scientiarum

Budapestinensis De Rolando Eotvos Nominatae Sectio

Computatorica (Issn: 0138-9491). 42. 261-282.

Ducournau, A., Bretto, A., Rital, S., Laget, B. (2012), A

reductive approach to hypergraph clustering: An

application to image segmentation, Pattern

Recognition, Volume 45, Is-sue 7.

Konstantinova, E. V., & Skorobogatov, V. A. (2001).

Application of hypergraph theory in chemistry.

Discrete Mathematics, 235(1-3), 365-383.

Amato, F., Moscato, V., Picariello, A., Sperlí, G. (2017).

Influence Maximization in So-cial Media Networks

Using Hypergraphs. In: Au, M., Castiglione, A., Choo,

KK., Palm-ieri, F., Li, KC. (eds) Green, Pervasive, and

Cloud Computing. GPC 2017. Lecture Notes in

Computer Science, vol 10232. Springer, Cham.

Tan, S., Bu, J., Chen, C., Xu, B., Wang, C., He, X. (2011).

Using rich social media in-formation for music

recommendation via hypergraph model. ACM Trans.

Multimedia Comput. Commun. Appl. 7S, 1, Article 22

(October 2011), 22 pages.

Sarkadi-Nagy, B., Molnár, B. (2019). System Modeling by

Representing Information Systems as Hypergraphs. In:

Abramowicz, W., Corchuelo, R. (eds) Business Infor-

mation Systems. BIS 2019. Lecture Notes in Business

Information Processing, vol 354. Springer, Cham.

https://doi.org/10.1007/978-3-030-20482-2_8

Dijkstra, E. W. (1959). "A note on two problems in

connexion with graphs". Numer-ische Mathematik. 1:

269–271.

Johnson, D. B. (1977), "Efficient algorithms for shortest

paths in sparse networks", Journal of the ACM, 24 (1):

1–13..

Kuhn, H. W. (1955). "The Hungarian method for the

assignment problem". Naval Re-search Logistics

Quarterly. 2 (1–2): 83–97.

Wigh, D., Goodman, J., Lapkin, A. (2022). A review of

molecular representation in the age of machine

learning. WIREs Comput Mol Sci.

Georgios A Pavlopoulos, Panagiota I Kontou, Athanasia

Pavlopoulou, Costas Bouyiou-kos, Evripides Markou,

Pantelis G Bagos (2018), Bipartite graphs in systems

biology and med-icine: a survey of methods and

applications, GigaScience, Volume 7, Issue 4, April.

Santos, A., Colaço, A.R., Nielsen, A.B. et al. (2022). A

knowledge graph to interpret clinical proteomics data.

Nat Biotechnol 40, 692–702.

Brin, S., and Page, L. (1998). The anatomy of a large-scale

hypertextual web searchen-gine. Computer networks

and ISDN systems 30, 1, 107–117.

Multilevel Hypergraphs: A Conceptual Approach for Complex System Database Modelling

Neo4J (2024). Neo4J, GenAI apps, grounded in your data.

Homepage, https://neo4j.com/, last accessed

2024/12/11.

JanusGraph (2024). JanusGraph, Distributed, open source,

massively scalable graph database. Homepage,

https://janusgraph.org/, last accessed 2024/12/11.

Memgraph (2024). Memgraph, Scales to billions of nodes

and edges, and delivers real-time performance.

Homepage, https://memgraph.com/, last accessed

2024/12/11.

NebulaGraph (2024). NebulaGraph, Open Source,

Distributed, Scalable, Lightning Fast. Homepage,

https://www.nebula-graph.io/, last accessed

2024/12/11.

Schölkopf, B., Platt, J., Hofmann, T. (2007). Learning with

Hypergraphs: Clustering, Classification, and

Embedding," in Advances in Neural Information

Processing Systems 19: Proceedings of the 2006

Conference , MIT Press, pp.1601-1608.

Ouvrard, B. (2020). Hypergraphs: an introduction and

review. arXiv:2002.05014, 2020.

Molnár, B. (2014). Applications of Hypergraphs in

Informatics: A Survey and Oppor-tunities for Research.

Annales Universitatis Scientiarum Budapestinensis de

Rolando Eotvos Nominatae Sectio Computatorica

(ISSN: 0138-9491). 42. 261-282.

Ouvrard, B., Le Goff, J., Marchand-Maillet, S., (2017).

Networks of Collaborations: Hypergraph Modeling and

Visualisation.

Habib, M., de Montgolfier, F., Mouatadid, L., Zou, M.

(2022). A general algorithmic scheme for combinatorial

decompositions with application to modular

decompositions of hypergraphs. Theoretical Computer

Science, 923, 56-73.

Gao, X., Zhu, Y., Yang, Y., Zhang, F., Zhou, F., Tian, X.,

... & Chen, Y. (2022). A sei-zure detection method

based on hypergraph features and machine learning.

Biomedical Signal Processing and Control, 77, 103769.

Frieze, A., Karoński, M. (2015). Introduction to Random

Graphs. Cambridge University Press.

Ghoshal, G., Zlatić, V., Caldarelli, G., Newman, M.E.J.

(2009). Random hypergraphs and their applications.

Phys. Rev. E 2009, 79, 066118,

https://doi.org/10.1103/physreve.79.066118

Grilliette, W., Reynes, J., Rusnak, L. (2022). Incidence

hypergraphs: Injectivity, uni-formity, and matrix-tree

theorems, Linear Algebra and its Applications, Volume

634, Pages 77-105.

https://doi.org/10.1016/j.laa.2021.10.023.

Ancona, M., De Floriani, L. (1989). A hypergraph-based

hierarchial data structure and its applications, Advances

in Engineering Software, Volume 11, Issue 1, Pages 2-

11. https://doi.org/10.1016/0141-1195(89)90030-2

Lemons, N.W., Hu, B., Hlavacek, W.S. (2011).

Hierarchical graphs for rule-based modeling of

biochemical systems. BMC Bioinformatics 12, 45.

https://doi.org/10.1186/1471-2105-12-45

Scioni, E., Huebel, N., Blumenthal, S., Shakhimardanov,

A., Klotzbuecher, M., Garcia, H., & Bruyninckx, H.

(2016). Hierarchical Hypergraph for Knowledge-

centric Robot Systems: a Composable Structural Meta

Model and its Domain Specific Language NPC4. In

JOSER: Journal of Software Engineering for Robotics

(Vol. 7, Issue 11, pp. 55–74).

Yang, F., Shen, L. (2015). Reconfigurable architecture

model based on layered hyper-graph. In 2015 Chinese

Automation Congress (CAC), Wuhan, pp. 1868-1873.

https://doi.org/10.1109/CAC.2015.7382808

Bezrukova, T., Tereshkina, T., Nesterov, S., Kuksova, I.,

Pecherskaya, O. (2019). Management of transport and

logistic infrastructure of the territory: methodological

tools and their improvement, IOP Conference Series:

Materials Science and Engineer-ing, Volume 817, 28-

29 November 2019, St. Petersburg, Russia

Gu, Y., Yu, K., Song, Z., Qi, J., Wang, Z., Yu, G., Zhang,

R. (2022). Distributed Hy-pergraph Processing Using

Intersection Graphs, in IEEE Transactions on

Knowledge and Data Engineering, vol. 34, no. 7, pp.

3182-3195, 1 July.

https://doi.org/10.1109/TKDE.2020.3022014.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems