Incentive Design in Hedonic Games with Permission Structures

Yuta Akahoshi, Yao Zhang, Kei Kimura, Taiki Todo and Makoto Yokoo

Graduate School of ISEE, Kyushu University, Fukuoka, Japan

Keywords:

Hedonic Games, Diffusion Mechanism Design, Social Networks, Approximation Ratios.

Abstract:

This paper investigates which coalition structure generation algorithms guarantee the incentive of agents to

invite as many colleagues as possible in symmetric additively-separable hedonic games. We ﬁrst clarify that,

the incentive of invitation is not compatible with each of Nash stability and Pareto efﬁciency. Furthermore,

we show that the worst-case ratio of social surplus achieved by any algorithm satisfying the incentive of

invitation, compared to the best possible social surplus, is unboundedly small. We then introduce two problem

restrictions to achieve somewhat positive results. More speciﬁcally, we showed that, when the utility graph of

a hedonic game only contains three values, {−p,0, p}, for some positive number p, there exists a polynomial-

time algorithm to achieve both the incentive of invitation and 1/n-approximation with respect to the social

surplus.

1 INTRODUCTION

A coalition formation game is one of the central prob-

lem in the ﬁeld of multi-agent systems. Given set of

multiple agents participating into the game, each of

which has its own characteristics, it is desired to de-

velop a coalition structure generation algorithm that

partitions the whole set of agents into a certain num-

ber of subgroups (coalitions) that appropriately per-

forms according to the given characteristics. Applica-

tions of such coalition formation problems includes,

but not limited to, human resource allocations to jobs

in the labor market and supply-chain management.

In the literature of coalition formation games, a

hedonic game is well-studied, where each agent has a

preference only over the set of coalitions in which he

or she belongs to. An outcome, returned by a coali-

tion structure generation algorithm, is usually evalu-

ated based on various criteria related to some kind of

stability, including Nash stability, individual stability,

and individual rationality. Clarifying the complexity

of showing the existence of stable outcomes has been

one of the research trends in the domain of computa-

tional social choice in last few decades.

In practical situations, however, the set of partic-

ipating agents is not given a priori. Instead, agents

usually invite their colleagues to participate in the

decision making. If we assume that each agent

prefers having more members in his/her coalition,

such an invitation process will be naturally incen-

tivized. On the other hand, if agents dislike some

others, agents may pretend inviting colleagues to the

decision making. The main purpose of this paper is to

design incentive-compatible coalition structure gen-

eration algorithms, which incentivizes agents to in-

vite as many colleagues as possible to the decision

making. Such a research direction has recently been

called as permission structures in the ﬁeld of coali-

tional games and operations research, and as diffusion

mechanism design in the ﬁeld of multi-agent systems

and artiﬁcial intelligence.

As a ﬁrst application of the perspective of diffu-

sion mechanism design to the literature of hedonic

games, we focus on a special class of hedonic games,

so called as symmetric additively-separable hedonic

games (SASHG) (Burani and Zwicker, 2003). In an

SASHG, there is an undirected weighted graph, in

which the set of vertices corresponds to the set of

agents. Given a coalition, each agent’s utility is given

as the sum of the weights of the edges connecting the

agent to other members in the coalition. Each agent

then prefers coalitions that give her higher utilities.

At the same time, the set of agents has a permis-

sion structure, given as a directed unweighted graph,

in which the set of vertices again corresponds to the

set of agents. Intuitively, the existence of a directed

edge from agent i to agent j in a permission structure

means that agent i has a right to invite agent j to the

SASHG. We then call agent i as a parent of agent j,

and agent j as a child of agent i. Technically speak-

184

Akahoshi, Y., Zhang, Y., Kimura, K., Todo, T. and Yokoo, M.

Incentive Design in Hedonic Games with Permission Structures.

DOI: 10.5220/0013320400003890

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 1, pages 184-195

ISBN: 978-989-758-737-5; ISSN: 2184-433X

ing, we consider two variants of incentives of invi-

tations, namely the conjunctive variant and the dis-

junctive variant. In the conjunctive variant, an agent

participates if all her parent invite her. On the other

hand, in the disjunctive variant, an agent participates

if at least one of her parents invites her.

To sum up, the problem we tackle in this paper

is the symmetric additively-separable hedonic games

with permission structures, SASHG-PS in short. An

SASHG-PS instance has two graphs, one of which

is deﬁnes an SASHG, and the other deﬁnes its per-

mission structures. Given an SASHG-PS instance,

a coalition structure generation algorithm returns a

coalition structure, hopefully guaranteeing incentives

for agents to invite as many colleagues as possible,

along with some stability properties. The main focus

in this paper is then to clarify the existence of such

coalition structure generation algorithms for SASHG-

PS.

In this paper, we ﬁrst give a formal deﬁnition of

the new class of games, SASHG-PS. We then show

three impossibility results and one possibility result,

according to various combinations of stability, fair-

ness, and efﬁciency properties. We also investigate

approximating the social surplus, deﬁned as the sum

of the utilities of participating agents, by incentive-

compatible algorithms. On this direction, we ﬁrst pro-

vide a general impossibility result, and then introduce

two problem restrictions under which some positive

results have been clariﬁed.

2 RELATED WORKS

Hedonic games are a special class of coalition for-

mation games, in which each agent only cares about

which members does she have in the same coalition

with her and ignores the structures of other coali-

tions (Dreze and Greenberg, 1980; Bogomolnaia and

Jackson, 2002). Gairing and Savani (2019) focused

on symmetric additively-separable hedonic games

and provided several complexity results on ﬁnding

various stable outcomes. Flammini et al. (2021) con-

sidered additively-separable hedonic games from the

viewpoint of strategy-proof mechanism design. The

main difference with this paper is that, while this

paper focuses on information diffusion strategies by

agents, they considered the cases where agents can

misreport their valuation functions. A survey on he-

donic games by Aziz and Savani (2016) summarizes

solution concepts and known results on several vari-

ants of hedonic games, from the viewpoints of algo-

rithms and computational complexity.

The research of diffusion mechanism design, also

known as mechanism design over social networks,

was initiated by Li et al. (2017), which considered

single-item auctions and proposed a strategy-proof

mechanism. After that, several works investigated

strategy-proof resource allocation mechanisms with

monetary compensations, e.g., multi-unit auctions

and redistributions (Zhao et al., 2018; Kawasaki et al.,

2020; Li et al., 2020; Zhang et al., 2020; Jeong and

Lee, 2024). On the other hand, there is limited re-

search on decision making without money from the

perspective of diffusion mechanism design. Recently,

Kawasaki et al. (2021) and You et al. (2022) consid-

ered diffusion mechanism design for house allocation

problems, which do not allow monetary compensa-

tions. Cho et al. (2022) studied two-sided matching

over social networks, and Ando et al. (2024) studied

facility location games. However, as far as the authors

know, this paper is a very ﬁrst attempt to study hedo-

nic games from the perspective of diffusion mecha-

nism design.

While the paradigm of diffusion mechanism de-

sign has recently been introduced in the ﬁeld of com-

puter science, a quite similar approach has also been

considered in the ﬁeld of operations research, which

is known as cooperative games with permission struc-

tures. The two variants of cooperative games with

permission structures, namely the conjunctive vari-

ant (Gilles et al., 1992) and the disjunctive vari-

ant (van den Brink, 1997), has been originally intro-

duced for the domain of general coalitional games.

The main difference between the diffusion mecha-

nism design and the cooperative games with permis-

sion structures is that, while the former considers the

decision making process from the viewpoint of mech-

anism design, the latter is deﬁned consistently with

the traditional cooperative games. The main purposes

of these two directions are therefore a bit different;

diffusion mechanism design focuses on designing al-

gorithms/mechanisms that incentivises agents to in-

vite other agents, and the cooperative games with

permission structures focuses on analysing the exis-

tence of appropriate solution concepts and their char-

acterization/axiomatizations. For more detail on per-

mission structures, please refer to a recent survey on

games with permission structures by van den Brink

(2017).

3 MODEL

As explained in Section 1, the problem we consider

in this paper is deﬁned as a combination of two well-

studied models, namely the symmetric additively-

separable hedonic games and the coalition games with

Incentive Design in Hedonic Games with Permission Structures

185

permission structures. Now we deﬁne the model of

symmetric additively-separable hedonic games with

permission structures (SASHG-PS).

Let N be the set of all the potential agents, and let

n := |N| be the number of potential agents. A subset

C ⊆ N is called as a coalition. Given agent i ∈ N, let

be the set of coalitions that contains i, i.e.,

:= {C ⊆ N | C ∋ i}

Also, given N, a partition π = {C

,. ..} of N is

called as a coalition structure, such that

∀k, ℓ(̸= k),C

∩C

ℓ

and

[

k=1,2,...

= N.

Let Π

be the set of all the possible coalition struc-

tures that partitions the set N of agents. Furthermore,

given coalition structure π ∈ Π

and agent i ∈ N, let

π(i) be the coalition in π in which agent i belongs, i.e.,

π(i) := C ∈ π s.t. C ∋ i.

There is a utility graph G(N,E,w), which is an

undirected edge-weighted graph, where w

∈ R de-

notes the weight of edge e ∈ E. For notation sim-

plicity, we assume w

̸= 0, i.e., the edges with a zero

weight is removed from the set E of edges. When an

edge e ∈ E has agent (vertex) i ∈ N in one of its end-

points, we denote e ∋ i. Furthermore, when both of

the endpoints of edge e belongs a coalition C, we de-

note e ∈ C. Given utility graph G(N,E, w) and agent

i ∈ N, a symmetric additively-separable preference ≿

of agent i, over the set N

of coalitions, is deﬁned as

follows:

∀C,D ∈ N

,C ≿

D ⇔

∑

e∋i|e∈C

≥

∑

e∋i|e∈D

Also, given utility graph G(N,E,w), agent i ∈ N, and

a coalition structure π ∈ Π

, agent i’s utility is deﬁned

(π) :=

∑

e∋i|e∈π(i)

SASHG-PS also has another graph, the permis-

sion graph H(N,A), represented as an unweighted di-

rected acyclic graph. The set of vertices corresponds

to the set of agents N. Also, the set A ⊆ N × N

of directed edges is assumed not to contain multi-

edges and self-loops. The existence of directed edge

(i, j) ∈ A means that agent i can send an invitation

to agent j. Given permission graph H(N, A), the set

O ⊆ N of vertices that have no incoming edges is re-

ferred to as the original agents, who is assumed to

participate in the game even without any invitation.

Given permission graph H(N, A) and agent i ∈ N, let

∈ N

≥0

be the distance of agent i, deﬁned as the

minimum distance from an original agent, i.e.,

:= min

o∈O

Also, given permission graph H(N,A) and agent i ∈

N, let S(i) be the set of agents (vertices) that agent i

can send an invitation, i.e.,

S(i) := { j ∈ N | (i, j) ∈ A}

An important note here is that, although both the

utility graph and the permission graph are compo-

nents of an SASHG-PS instance, these are not di-

rectly observed by a coalition structure generation al-

gorithm. Instead, agents ﬁrst decide who to invite to

the game, and then the algorithm is able to observe

who invite which agents and ﬁnally who participate

in the game.

To sum up, an instance I(G,H) of SASHG-PS has

two graphs, the utility graph G(N,E, w) and the per-

mission graph H(N,A), where the set N of potential

agents is in common in these two graphs. Now let us

explain how an SASHG-PS proceeds.

1. The Nature determines both the utility graph and

the permission graph, while the both are not di-

rectly observable by anyone.

2. A coalition structure generation algorithm is pub-

licly announced.

3. Observing the description, i.e., the rule of a game,

each agent decide which colleagues to invite to the

game.

4. According to the invitation strategies of the

agents, the set of participating agents is ﬁxed.

Then, the algorithm returns the outcome.

3.1 Optimization Criteria

Before introducing several properties related to sta-

bility, fairness, and efﬁciency, we ﬁrst deﬁne an eval-

uation criteria for quantitatively measuring the worst-

case performance of coalition structure generation al-

gorithms. A social surplus, deﬁned as the sum of the

utilities of all the participating agents, is a well-known

evaluation criteria in the ﬁeld of micro-economics.

Deﬁnition 1 (Social Surplus). Given SASHG-PS in-

stance, a social surplus SW(π) of a coalition structure

π ∈ Π

is deﬁned as

SW(π) :=

∑

i∈N

(π

We then deﬁne the approximation ratio for the so-

cial surplus, which enables evaluating the worst-case

performance of (potentially incentive-compatible) al-

gorithms, compared to the global optimal solution

that is not necessarily incentive-compatible.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

186

Table 1: Comparisons of four incentive-compatibility properties. Properties on top-left direction is more demanding. No

inclusion relation exists between D-DSIC and C-EPIC.

Equilibrium Concept

Dominant Strategy Ex-Post

Permission Type

Conjunctive C-DSIC C-EPIC

Disjunctive D-DSIC D-EPIC

Deﬁnition 2 (Approximation Ratio). Given SASHG-

PS instance I, an optimal coalition structure π

∗

(I) ∈

is a coalition structure that has the maximum so-

cial surplus, i.e.,

∗

(I) := arg max

π∈Π

SW(π).

An approximation ratio α

of a coalition structure

generation algorithm M is the minimum ratio of the

social surplus of a coalition structure obtained by the

algorithm, against the optimal social surplus. For-

mally,

:= min

SW(M (I))

SW(π

∗

(I))

The optimal approximation ratio is one, and any

algorithm has an approximation ratio weakly less than

one. Designing coalition structure generation algo-

rithms having a larger approximation ratio is desir-

able. If there is an algorithm achieving the approxi-

mation ratio of one, we call it optimal.

3.2 Properties

In this subsection we deﬁne several properties that

coalition structure generation algorithms should sat-

isfy. We ﬁrst deﬁne incentive compatibilities. Ac-

cording to the characteristics of SASHG-PS, speciﬁ-

cally the permissions’ types and the equilibrium con-

cepts, we deﬁne four variants of incentive compatibil-

ity properties, summarized in Table 1.

Deﬁnition 3 (Incentive Compatibility). Given

SASHG-PS instance I(G,H), a coalition structure

generation algorithm M is said to satisfy

• dominant-strategy incentive compatibility for

conjunctive permissions (C-DSIC) if, for each

agent i ∈ N, inviting as many colleagues in S(i)

as possible is a dominant strategy, under the as-

sumption that an agent participates in the game if

and only if all her parents invite her.

• dominant-strategy incentive compatibility for dis-

junctive permissions (D-DSIC) if, for each agent

i ∈ N, inviting as many colleagues in S(i) as pos-

sible is a dominant strategy, under the assumption

that an agent participates in the game if and only

if at least one of her parents invites her.

• ex-post incentive compatibility for conjunctive

permissions (C-EPIC) if, for each agent i ∈ N,

inviting as many colleagues in S(i) as possible

is a best strategy when all the other participating

agents invite as many colleagues as possible, un-

der the assumption that an agent participates in

the game if and only if all her parents invite her.

• ex-post incentive compatibility for disjunctive

permissions (D-EPIC) if, for each agent i ∈ N,

inviting as many colleagues in S(i) as possible

is a best strategy when all the other participating

agents invite as many colleagues as possible, un-

der the assumption that an agent participates in

the game if and only if at least one of her parents

invites her.

By deﬁnition, C-DSIC implies both D-DSIC and

C-EPIC, and both D-DSIC and C-EPIC imply D-

EPIC. Between D-DSIC and C-EPIC, there is no in-

clusion relation in general.

We next deﬁne stability, fairness, and efﬁciency

properties that are quite popular in the literature of

hedonic games. Both individual rationality and Nash

stability have been known as a stability property,

where the latter implies the former.

Deﬁnition 4 (Individual Rationality). Given SASHG-

PS instance I(G,H), a coalition structure π ∈ Π

said to be individually rational if

∀i ∈ N, u

(π(i)) ≥ 0

holds. A coalition structure generation algorithm M

is said to satisfy individual rationality (IR) if M (I) is

individually rational for any SASHG-PS instance I.

Deﬁnition 5 (Nash Stability). Given SASHG-PS in-

stance I(G,H), a coalition structure π ∈ Π

is said to

be Nash stable if

∀i ∈ N, u

(π(i)) ≥ u

(C ∪ {i})

holds for any C ∈ π ∪ {

0}. A coalition structure gen-

eration algorithm M is said to satisfy Nash stability

(NS) if M (I) is Nash stable for any SASHG-PS in-

stance I.

Incentive Design in Hedonic Games with Permission Structures

187

Pareto efﬁciency is one of the most popular efﬁ-

ciency property in the ﬁeld of economics. Intuitively,

it requires that there is no other outcome that is better

for all the participating agents.

Deﬁnition 6 (Pareto Efﬁciency). Given SASHG-PS

instance I(G,H), a coalition structure π ∈ Π

is said

to be Pareto efﬁcient if there is no other coalition

structure π

′

∈ Π

such that both

∀i ∈ N, u

(π

′

(i)) ≥ u

(π(i))

and

∃ j ∈ N,u

(π

′

( j)) > u

(π( j))

hold. A coalition structure generation algorithm M is

said to satisfy Pareto efﬁciency (PE) if M (I) is Pareto

efﬁcient for any SASHG-PS instance I.

Envy-freeness is a fairness property, which re-

quires that for each agent, changing her position with

any other agent is not beneﬁcial.

Deﬁnition 7 (Envy-Freeness). Given SASHG-PS in-

stance I(G,H), a coalition structure π ∈ Π

is said to

be envy-free if

∀i, j ∈ N s.t. π(i) ̸= π( j),

(π(i)) ≥ u

((π(i) \ { j}) ∪ {i})

holds. A coalition structure generation algorithm M

is said to satisfy envy-freeness (EF) if M (I) is envy-

free any SASHG-PS instance I.

In the literature of hedonics games, there are sev-

eral other properties, including individual stability,

contractually individual stability, the core, and the

strict core. For more detail on these solution concepts,

please refer to a survey chapter by Aziz and Savani

(2016).

4 (IM)POSSIBILITIES

We are now ready to present our technical contribu-

tion. We ﬁrst show that, although all the properties

introduced in the previous section seems to be de-

sirable, various combinations among them result in

the non-existence of algorithms. On the other hand,

Theorem 4 shows that just keeping every participat-

ing agent as a singleton satisﬁes IR, EF, and C-DSIC.

Theorem 1. There exists no coalition structure gen-

eration algorithm that simultaneously satisﬁes D-

EPIC and NS.

Proof. Consider an SASHG-PS instance described in

Fig. 1, and focus on the strategic invitation by agent

a. When agent a invite agent c, all the three agents

G(N,E, w) H(N,A)

-3

Figure 1: An SASHG-PS instance for which D-EPIC and

NS are incompatible, used in the proof of Theorem 1.

G(N,E, w) H(N,A)

2 1

-10

Figure 2: An SASHG-PS instance for which PE and either

D-DSIC or C-EPIC are incompatible, used in the proof of

Theorem 2.

participate. Then, the unique Nash stable coalition

structure is

π = {{a},{b,c}},

under which agent a’s utility is 0.

When agent a does not invite agent c, there are

only two participating agents a and b. Then, the

unique Nash stable coalition structure is

π = {{a,b}},

under which agent a’s utility is 1. Thus, agent a is

better off by not inviting agent c. Since the permis-

sion graph H(N,A) has only one directed edge, the

weakest variant of IC condition, namely D-EPIC, is

violated.

Theorem 2. There exists no coalition structure gen-

eration algorithm that simultaneously satisﬁes PE

and either D-DSIC or C-EPIC.

Proof. Consider an SASHG-PS instance described in

Fig. 2, in which there are ﬁve Pareto efﬁcient coalition

structures:

1. {{a, b},{c,d}}

2. {{a, c},{b,d}}

3. {{a, b,d},{c}}

4. {{a, c,d},{b}}

5. {{a, b,c,d}}

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

188

G(N,E, w) H(N,A)

-10

Figure 3: An SASHG-PS instance for which PE, IR, and

D-EPIC are incompatible, used in the proof of Theorem 3.

When a Pareto efﬁcient algorithm returns coalition

structure 1., 2., 3., or 5. above, agent b’s utility is

strictly less than 5. Therefore, agent b has an incen-

tive not to invite agent c; the unique Pareto efﬁcient

coalition structure is {{a,b, d}} if agent c does not

participate, in which agent b’s utility is 5.

When a Pareto efﬁcient algorithm returns coali-

tion 4. above, agent d’s utility is 5. Therefore, agent

d has an incentive not to invite agent b; the unique

Pareto efﬁcient coalition structure is {{a, c,d}} if

agent b does not participate, in which agent d’s utility

is 6.

The existence of these two beneﬁcial manipula-

tions violates both D-DSIC and C-EPIC (and thus C-

DSIC), which completes the proof. Note that D-EPIC

is not violated in this instance, since agent c is not ex-

cluded by any sole manipulation by either agent b or

Theorem 3. There exists no coalition structure gen-

eration algorithm that simultaneously satisﬁes PE,

IR, and D-EPIC.

Proof. Consider an SASHG-PS instance described in

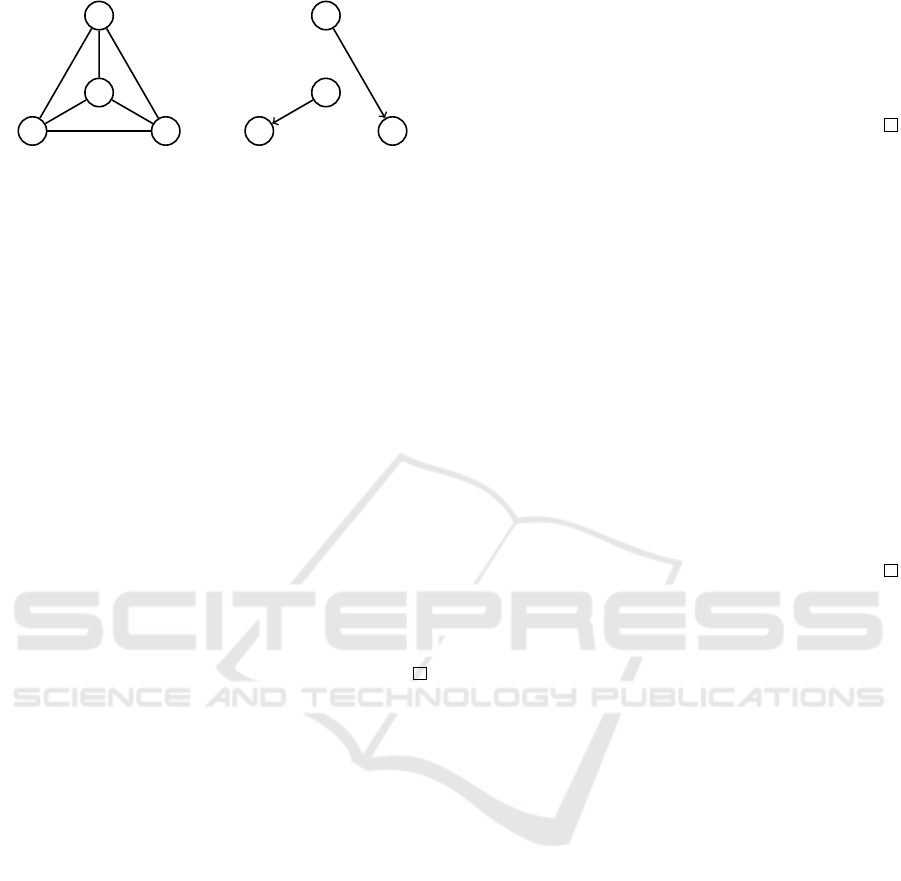
Fig. 3, in which there are four coalition structures that

is both Pareto efﬁcient and individually rational:

1. {{a, b},{c,d}}

2. {{a, c},{b,d}}

3. {{a, b,d},{c}}

4. {{a, c,d},{b}}

When a Pareto efﬁcient algorithm returns coalition

structure 1., 2., or 4. above, agent a’s utility is strictly

less than 4. Therefore, agent a has an incentive not

to invite agent c; the unique Pareto efﬁcient coalition

structure is {{a,b,d}} if agent c does not participate,

in which agent a’s utility is 4.

When a Pareto efﬁcient algorithm returns coali-

tion structure 3. above, agent d’s utility is 5. There-

fore, agent d has an incentive not to invite agent

b; the unique Pareto efﬁcient coalition structure is

{{a,c, d}} if agent b does not participate, in which

agent d’s utility is 6.

The existence of these two beneﬁcial manipula-

tions, which are independent with each other, implies

that D-EPIC is violated. Thus, IR, PE and D-EPIC

are incompatible.

Theorem 4. There exists a coalition structure gener-

ation algorithm that simultaneously satisﬁes IR, EF,

and C-DSIC.

Proof. Consider a coalition structure generation al-

gorithm M that returns, for any SASHG-PS instance,

a coalition structure in which every agent constructs a

singleton coalition.

In such an algorithm, every agent has utility zero

for any instance, regardless of the invitation strate-

gies of all the agents. Thus, M satisﬁes C-DSIC,

the strongest incentive compatibility, and individual

rationality

Furthermore, when a coalition structure π ∈ Π

such that every agent constructs a singleton coalition,

it holds that

∀i, j ∈ N, (π( j)\ { j})∪ {i} = π(i).

Thus, the condition of envy-freeness is satisﬁed.

5 DESIGNING APPROXIMATION

ALGORITHMS

The impossibility results presented in the previous

section, regarding the incentive compatibility proper-

ties in SASHG-PS, are quite negative. Now we fo-

cus only on the incentive compatibility and analyze

the worst-case performance of incentive compatible

algorithms with respect to the social surplus.

The theorem below has a quite negative implica-

tion. The property D-EPIC is the weakest among the

four deﬁnitions. This theorem states that, even with

the weakest incentive requirement on strategic invita-

tion, there is a chance that the achievable social sur-

plus becomes nearly zero.

Theorem 5. The approximation ratio of any coalition

structure generation algorithm satisfying D-EPIC is

zero.

Proof. Consider an SASHG-PS instance described in

Fig. 4, where the weight m of edge between agents

b and c is sufﬁciently large. The optimal coalition

structure for this instance is the grand coalition, i.e.,

all the three agents belong to the same coalition, in

which the social surplus is m + 1.

Incentive Design in Hedonic Games with Permission Structures

189

G(N,E, w) H(N,A)

-1

Figure 4: An SASHG-PS instance for which D-EPIC and

NS are incompatible, used in the proof of Theorem 5.

Since m is arbitrarily large, any coalition structure

generation algorithm that has bounded approximation

ratio must put both agents b and c in a single coalition.

Under such a coalition structure, agent a’s utility is at

most 1.

Also, when agent a does not invite agent b, the op-

timal coalition structure for two agents a and c is the

grand coalition that contains both agents a and c in a

single coalition, in which the social surplus is 2. Thus,

any coalition structure generation algorithm that has

bounded approximation ratio must put both of these

two agents a and c in a single coalition, when agent b

does not participate.

Therefore, agent a has an incentive not to invite

agent b; agent a’s utility is 2 when she does not invite

agent b, while it is at most 1 when she invite agent

b. Since agent a can solely decide the participation

of agent b, such an algorithm violates D-EPIC, the

weakest incentive compatibility.

6 ALGORITHMS FOR

RESTRICTED GRAPHS

In the previous section we have presented a negative

results on the approximability of social surplus by in-

centive compatible coalition structure generation al-

gorithms. A natural question is then how can we over-

come the negative results by introducing some prob-

lem restriction to SASHG-PS.

A quite trivial case is such that the permission

graph H(N, A) has no edge, i.e., A =

0, where any

incentive compatibility constraint becomes void and

we can simply apply known algorithms in the litera-

ture. However, when the permission structure is not

observable a priori, which seems to be very likely in

practical situations, assuming such a restriction is not

quite reasonable.

We therefore focus on the restriction to the utility

graph in this paper. At ﬁrst, we provide a sufﬁcient

condition to guarantee an optimality of the social sur-

plus. Namely, when the edges with non-zero weights

G(N,E, w)

-1

-5

Figure 5: An example of forest utility graph.

of a utility graph construct a forest, there exists an

optimal coalition structure generation algorithm that

also satisﬁes C-DSIC.

Theorem 6. There exists an optimal C-DSIC coali-

tion structure generation algorithm when the utility

graph is given as a forest.

Proof. Consider a coalition structure generation al-

gorithm M that (i) ﬁrst remove all the negative edges

from the utility graph G and then (ii) choose each of

the connected component in the modiﬁed utility graph

as a coalition. Note that, when the original utility

graph G is assumed to be a forest, it is still a forest af-

ter the removal of all the negative edges. Obviously, it

returns the optimal coalition structure for such a forest

graph.

Now let us show that this algorithm M satisﬁes C-

DSIC. In this algorithm, agent i belongs to the same

coalition with any agent j if and only if there is an

edge with a strictly positive weight. Here, for any

whole set N of agents, any agent i ∈ N, and any subset

′

⊆ N such that N

′

∋ i, let π ∈ Π

and π

′

∈ Π

′

the coalition structure provided by M for each of two

participating sets, N and N

′

, of agents, respectively.

Then, we have

(π(i)) ≥ u

(π

′

(i)),

which implies C-DSIC.

Example 1. Now we demonstrate how the algorithm

M proposed in the proof of Theorem 6 works for the

SASHG-PS instance described in Figure 5.

The algorithm ﬁrst removes all the edges with neg-

ative weights in the utility graph G(N, E,w). In the

ﬁgure, there are two such edges, between agents a

and b, and between agent c and s. Then, the algo-

rithm returns each of the connected components as a

coalition. The outcome is therefore,

{{a},{b, q,r}, {c,t},{s},}

which is clearly optimal as it contains all the edges

with positive weights and does not contain any edge

with a negative weight.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

190

G(N,E, w) H(N,A)

Figure 6: An SASHG-PS instance showing the upper bound

of approximation ratio for the case of n = 3, used in the

proof of Theorem 7. The dashed edge has a positive weight

+p, while the dotted edge has a negative weight −p.

7 ALGORITHMS FOR

RESTRICTED WEIGHTS

Restricting the domain of weights of the utility graph

is also a natural approach to overcome impossibil-

ity results in the literature. Even for our problem of

SASHG-PS, there is a quite trivial case where such

a restriction works. For example, when the weights

of the utility graph is assumed to be non-negative, in

which returning the grand coalition is the optimal.

Here we provide a quite different condition to

guarantee the tight approximability results for the so-

cial surplus, by either D-DSIC or C-EPIC coalition

structure generation algorithms. Namely, while we al-

low the existence of negative weights, all the non-zero

weights have the same absolute value. We ﬁrst show,

in Theorem 7, that any coalition structure generation

algorithm satisfying either D-DSIC or C-EPIC has an

approximation ratio of at most

for n = 3, and at

most

n−1

for n ≥ 4, which works as an upper bound.

We then show, in Theorem 8, the existence of D-DSIC

algorithm which has an approximation ratio of

for

odd n and

n−1

for even n. That is, the approximation

ratio obtained in this section is asymptotically tight.

We further show that the proposed algorithm runs in

polynomial-time.

Theorem 7. Assume that the weights of the utility

graph are restricted to {−p,0, p} for some constant

p ∈ R

. Then, the approximation ratio of any coali-

tion structure generation algorithm satisfying either

D-DSIC or C-EPIC is at most 1/n for n = 3, and

n−1

for n ≥ 4.

Proof. We ﬁrst show the upper bound

for the case

of n = 3, and then show the upper bound

n−1

for the

case of n ≥ 4.

To show the bound for n = 3, we begin with an

SASHG-PS instance with n = 4, described in Fig-

ure 6. Note that the dashed edges in the ﬁgure have a

G(N,E, w) H(N,A)

Figure 7: An SASHG-PS instance obtained by removing

both agents c and d from Figure 6.

G(N,E, w) H(N,A)

Figure 8: An SASHG-PS instance obtained by removing

agents d from Figure 6.

positive weight +p, and the dotted edges have a neg-

ative weight −p.

Consider that agent b is now willing to strategi-

cally invite her colleagues, agents c and d. When all

those four agents participate, agent b’s utility would

be p in coalition {a,b}, and 0 in any other coalition. If

an algorithm returns a coalition structure where agent

b does not belong to coalition {a, b}, agent b has an

incentive not to invite both agents c and d, resulting in

the graphs shown in Figure 7; agent b’s utility would

then be 1, to guarantee that the approximation ratio

is bounded. The existence of such an incentive vio-

lates both C-EPIC (where agent b can solely prevent

the participation of both c and d) and D-DSIC (where

agent b can still prevent the participation of agents

c and d if agent a also chooses not to invite them).

Therefore, in the case of Figure 6, an algorithm with

a bounded approximation ratio must return a coalition

structure containing a coalition {a, b} as its member.

Note that in this coalition, agent a’s utility is also 1.

Now let us consider that agent a is also willing to

strategically invite agent b (see Figure 8). When agent

b does not participate, agent a’s utility cannot exceed

1; otherwise agent a has an incentive to prevent agent

b’2 participation, violating D-EPIC. Therefore, the

set of possible coalition structures in Figure 8 is one

of the followings:

{{a,c}, {d}}, {{a,d},{c}},

{{a},{c, d}}, {{a},{c}, {d}}.

The maximum social surplus is then 1, while the op-

timal social surplus is 3. Thus the target ratio 1/3 is

proved.

Incentive Design in Hedonic Games with Permission Structures

191

G(N,E, w) H(N,A)

·· ·

Figure 9: An SASHG-PS instance showing the upper bound

of approximation ratio for the case of n ≥ 4, used in the

proof of Theorem 7.

G(N,E, w) H(N,A)

·· ·

Figure 10: An SASHG-PS instance obtained by removing

agent b from Figure 9.

Now we turn to show that the upper bound is

n−1

for the case of n ≥ 4. Consider the case described

in Figure 9, where there are n − 1 agents, agent a is

connected to all the other agents, b, c, d, ···, x, with

an edge with a positive weight +p in the utility graph

G, while agent b is connected to those agents c, d, ···,

x, with an edge with a negative weight −p (except for

agent a). Also, in the permission graph H, both of

agents a and b are able to invite those agents to which

they are connected to in G, respectively.

Since agent b has only one edge with a positive

weight, connected with agent a, agent b’s utility is 1

if and only if coalition {a, b} is in the coalition struc-

ture, and zero otherwise. From a similar argument

with the case of n = 3, coalition {a,b} must be formed

for the case of Figure 9; otherwise both C-EPIC and

D-DSIC are violated. Note that in this case agent a’s

utility is 1.

We then consider that agent a is also willing to

strategically invite agent b (see Figure 10, where there

are n agents). Again, from a similar argument with

the case of n = 3, agent a’s utility cannot exceed 1;

otherwise D-EPIC is violated. Therefore, the possible

coalition structures in Figure 10 are such that agent

a forms a coalition with at most one another agent.

The social surplus is then at most 1, while the optimal

social surplus is n − 1. Thus the target ratio

n−1

proved.

Theorem 8. Assume that the weights of the utility

graph are restricted to {−p,0, p} for some constant

p ∈ R

. Then, there is a polynomial-time coalition

structure generation algorithm that satisﬁes D-DSIC

and has an approximation ratio of 1/n when n is odd,

and

n−1

when n is even.

Proof. The theorem is separately shown in the two

propositions below, Propositions 1 and 2.

We now propose a polynomial-time algorithm that

satisﬁes D-DSIC and has an asymptotically optimal

approximation ratio. Brieﬂy speaking, the proposed

algorithm tries to ﬁnd a maximum matching by fo-

cusing on the edges with a positive weights. Obvi-

ously, such a maximum matching can be found in

polynomial time. However, a na

ıve implementation

of maximum matching algorithm fails to satisfy even

D-EPIC, which will be explained later in this section.

Deﬁnition 8 (Proposed Algorithm). Given SASHG-

PS instance I, runs the following procedure:

1. Initialization: Remove all the edges with a nega-

tive weight in the utility graph. Also, label all the

edges with a positive weight in the utility graph

with pre-update. Let n be the number of partici-

pating agents, and let h = 1.

2. Construct a linear order ▷ of all the participating

agents so that, for any two agents i, j, if either

• δ

< δ

, or

• δ

= δ

and |S(i)| > |S( j)|

holds, then we order i ▷ j, i.e., agent i is more

prioritized than agent j. When both δ

= δ

and

|S(i)| = |S( j)| holds, we break the tie based on

a consistent way under which agents’ invitation

strategies does not affect.

3. For the most prioritized remaining agent i in the

order ▷:

• Update the weight of all edges e ∋ i that have

labeled as pre-update (if any) with the weight

n−h

, and then label them with post-update.

• Let h ← h+1, remove i from the top of the order

▷, and go to 3. if h ≤ n; otherwise go to 4.

4. Obtain a maximum weight matching for the util-

ity graph with updated weights, where the tie-

breaking among the edges with the same (up-

dated) weight is determined based on the linear

order ▷.

Intuitively, the algorithm works like a “serial dic-

tatorship mechanism” in the literature of strategy-

proof mechanism design, which is a powerful tool to

guarantee incentive compatibility in various decision

making situations. First, the most prioritized agent,

say i, in ▷ chooses the whole set of outcomes in

which agent i is matched with another agent. Among

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

192

them, the second prioritized agent, say j, chooses a

subset in which agent j is also matched.

It is clear that the proposed algorithm runs in a

polynomial-time. Step 1. completes in O(E). Step

2. is just sorting the agents based on the information

available from the algorithm, which runs in O(N).

Updates in Step 3. occur E times, since every edge

is updated exactly once. Finally, in Step 4., we obtain

the maximum weight matching in a polynomial-time,

e.g., in O(N

E) by Edmonds’ algorithm (Edmonds,

1965). Since these steps are processed in a series, the

total runtime is O(N

E).

We now demonstrate how the proposed algorithm

works, by applying it to the case of Figure 9.

Example 2. Consider the situation described in Fig-

ure 9, and assume that there are three agents in the

list d, . .., x. That is, there are totally six agents. In

Step 1., the algorithm removes all the negative edges,

and label all the positive edges with pre-update. Then,

in Step 2., the participating agents will be linearly or-

dered. When all the agents participates, the order is,

say,

a ▷ b ▷ c ▷ d ▷ ··· ▷ x.

After that, in Step 3., the weights are updated. Now

that all the remaining positive edges has agent a at

one of their endpoints, all the weights are updated as

By applying a maximum weight matching for

this modiﬁed utility graph, with the tie-breaking rule

based on ▷, the edge between a and b is chosen, and

the algorithm terminates. From agent a’s perspec-

tive, removing agent b does not help, since agent a

is already satisﬁed by being connected with an agent.

Note that the utility is calculated based on the origi-

nal weights of the utility graph.

From agent b’s perspective, any removal of her

colleagues does not help, since agent b is also con-

nected. Note that, if an arbitrary tie-breaking rule

would be used for achieving a maximum weight

matching in Step 4., it may possible that agent c is

matched with agent a. In such a case, agent b has

an incentive not to invite agent b (and possibly all the

others, so that they cannot participate if agent a also

does not invite them ), violating D-DSIC.

We ﬁrst brieﬂy explain why the proposed algo-

rithm satisﬁes D-DSIC. Due to space limitations, we

present a proof sketch. Also, Example 2 above will

also help the readers to understand the intuition why

we need to carefully choose the tie-breaking methods.

Proposition 1. When the weights are restricted to

{−p,0, p} for some constant p ∈ R

, algorithm 8 sat-

isﬁes D-DSIC.

Proof Sketch. By deﬁnition, the linear order ▷ satis-

ﬁes the property such that, for any agent i, removing

any of her colleagues from the games never changes

the order of the agents who are originally more priori-

tized than agent i. Furthermore, as we have mentioned

in Example 2, using the tie-breaking rule based on ▷

is essential to guarantee D-DSIC. Therefore, there ex-

ists no case in which agent i can get matched and re-

ceives utility +p by removing some of her colleagues,

while agent i would not be matched with anyone by

inviting all her colleagues.

We then present that the proposed algorithm

asymptotically matches the upper bound presented in

Theorem 7. While an approximation ratio O(

) is

quite negative from the viewpoint of algorithm de-

sign, this is unavoidable as we require incentive com-

patibility property.

Proposition 2. When the weights are restricted to

{−p,0, p} for some constant p ∈ R

, algorithm 8 has

an approximation ratio of

when n is odd, and

n−1

when n is even.

Proof. Arbitrarily choose an SASHG-PS instance

with n agents, and let m be the number of unmatched

agents, i.e., the number of singleton coalitions, in the

coalition structure π returned by the proposed algo-

rithm. Since the proposed algorithm only constructs

two-agent matchings as coalitions except for the sin-

gletons, there are

n−m

matchings, and thus the social

surplus is

n−m

When m is either 0 or 1, it is obvious that adding

an arbitrary edge to the same instance does not in-

crease the number of two-agent matchings. By re-

peating this argument with adding a positive edge, we

ﬁnally obtain the complete graph with n vertices as a

utility graph, under which the optimal social surplus

n(n−1)

p. Thus, the minimum ratio is

n−1

for m = 0

and

for m = 1, which coincides with the theorem

statement.

Now we consider the case of m ≥ 2. First, ob-

serve that there is no edge between any pair of agents

who are left as singletons; otherwise the algorithm

matches these agents, violating the property of maxi-

mum weight matching in the algorithm. Also, observe

that the number of edges among the matched n − m

agents are at most

(n−m)(n−m−1)

, which corresponds

to the case where these n − m agents form a clique in

the utility graph.

Now we count the total number of edges between

those two sets of agents, namely the set M

of m sin-

gleton agents and the set M

of matched n−m agents.

For each pair i, j ∈ M

of agents who forms a two-

agent coalition {i, j} ∈ π, the number of edges con-

Incentive Design in Hedonic Games with Permission Structures

193

necting {i, j} and M

is at most m, all of which are

connected to the exactly same vertices, say i; oth-

erwise we can ﬁnd an augmenting path, which also

violates the property of maximum weight matching.

Since there are

n−m

matched pairs, the number of

such edges is at most

m(n−m)

Therefore, the number of edges in the utility graph

is at most

(n − m)(n − m − 1)

m(n − m)

(n − m)(n − 1)

Thus, the ratio of the number of matchings to this

value is at least

n−1

, which coincides with the the-

orem statement.

One might feel that, since the algorithm can di-

rectly observe the utility graph among the participat-

ing agents, constructing a grand coalition whenever

all the edges have a positive weight achieves a better

social surplus. However, such an algorithm must also

return as large coalition as possible even with negative

weights; otherwise some agents have incentive to re-

move their colleagues with which edges with a nega-

tive weight exist, violating e.g., D-EPIC. We strongly

believe that there is no much improvement from the

above proposed algorithm, even in the average-case

performance.

8 CONCLUSIONS

In this paper we clariﬁed under which problem re-

strictions an appropriate coalition structure genera-

tion algorithm exist. Restricting the structure of util-

ity graph worked well; we ﬁnd an optimal algorithm

that also satisﬁes C-DSIC, the most demanding incen-

tive property. On the other hand, while restricting the

weights provided a slightly positive ﬁndings, it might

be possible that under some other weight restriction

we may ﬁnd an optimal algorithm.

As future works, there still exist various possible

extensions of general hedonic games with permission

structures, including joint manipulations by a group

of agents (also known as group-strategyproofness),

non-obvious manipulability, and randomized decision

making. Also, some combinations of desirable prop-

erties introduced in this paper have not yet com-

pletely clariﬁed, along with those incentive compat-

ibility properties. Furthermore, it would be promising

to clarify the key structure in the utility graphs that is

essential to make the design of incentive compatible

algorithms difﬁcult.

REFERENCES

Ando, R., Kimura, K., Todo, T., and Yokoo, M. (2024).

Parameterized voter relevance in facility location games

with tree-shaped invitation graphs.

Ando, R., Kimura, K., Todo, T., and Yokoo, M. (2025).

Parameterized voter relevance in facility location games

with tree-shaped invitation graphs. To appear in Proceed-

ings of the 19th International Conference and Workshops

on Algorithms and Computation (WALCOM ’25).

Aziz, H. and Savani, R. (2016). Hedonic Games, pages

356–376. In Handbook of Computational Social Choice,

chapter 15. Cambridge University Press.

Bogomolnaia, A. and Jackson, M. (2002). The stability of

hedonic coalition structures. Games and Economic Be-

havior, 38(2):201–230.

Burani, N. and Zwicker, W. S. (2003). Coalition formation

games with separable preferences. Mathematical Social

Sciences, 45(1):27–52.

Cho, S.-H., Todo, T., and Yokoo, M. (2022). Two-sided

matching over social networks. In Proceedings of the

31st International Joint Conference on Artiﬁcial Intelli-

gence (IJCAI-ECAI ’22), pages 186–193.

Dreze, J. and Greenberg, J. (1980). Hedonic coalitions: Op-

timality and stability. Econometrica, 48(4):987–1003.

Edmonds, J. (1965). Maximum matching and a polyhedron

with 0,1-vertices. Journal of Research of the National

Bureau of Standards Section B Mathematics and Mathe-

matical Physics, page 125.

Flammini, M., Kodric, B., Monaco, G., and Zhang, Q.

(2021). Strategyproof mechanisms for additively sepa-

rable and fractional hedonic games. Journal of Artiﬁcial

Intelligence Research, 70:1253–1279.

Gairing, M. and Savani, R. (2019). Computing stable out-

comes in symmetric additively separable hedonic games.

Mathematics of Operations Research, 44(3):1101–1121.

Gilles, R. P., Owen, G., and van den Brink, R. (1992).

Games with permission structures: The conjunctive

approach. International Journal of Game Theory,

20(3):277–93.

Jeong, S. E. and Lee, J. (2024). The groupwise-pivotal

referral auction: Core-selecting referral strategy-proof

mechanism. Games and Economic Behavior, 143:191–

203.

Kawasaki, T., Barrot, N., Takanashi, S., Todo, T., and

Yokoo, M. (2020). Strategy-proof and non-wasteful

multi-unit auction via social network. In Proceedings

of the 34th AAAI Conference on Artiﬁcial Intelligence

(AAAI ’20), pages 2062–2069.

Kawasaki, T., Wada, R., Todo, T., and Yokoo, M. (2021).

Mechanism design for housing markets over social net-

works. In Proceedings of the 20th International Con-

ference on Autonomous Agents and Multiagent Systems

(AAMAS ’21), pages 692–700.

Li, B., Hao, D., and Zhao, D. (2020). Incentive-compatible

diffusion auctions. In Proceedings of the 29th Interna-

tional Joint Conference on Artiﬁcial Intelligence (IJCAI

’20), pages 231–237. Main track.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

194

Li, B., Hao, D., Zhao, D., and Zhou, T. (2017). Mechanism

design in social networks. In Proceedings of the 31st

AAAI Conference on Artiﬁcial Intelligence (AAAI ’17),

pages 586–592.

van den Brink, R. (1997). An Axiomatization of the Dis-

junctive Permission Value for Games with a Permis-

sion Structure. International Journal of Game Theory,

26(1):27–43.

van den Brink, R. (2017). Games with a permission struc-

ture - A survey on generalizations and applications. TOP:

An Ofﬁcial Journal of the Spanish Society of Statistics

and Operations Research, 25(1):1–33.

You, B., Dierks, L., Todo, T., Li, M., and Yokoo, M.

(2022). Strategy-proof house allocation with existing

tenants over social networks. In Proceedings of the 21st

International Conference on Autonomous Agents and

Multiagent Systems (AAMAS ’22), pages 1446–1454.

Zhang, W., Zhao, D., and Chen, H. (2020). Redistribution

mechanism on networks. In Proceedings of the 19th In-

ternational Conference on Autonomous Agents and Mul-

tiagent Systems (AAMAS ’20), pages 1620–1628.

Zhao, D., Li, B., Xu, J., Hao, D., and Jennings, N. R.

(2018). Selling multiple items via social networks. In

Proceedings of the 17th International Conference on Au-

tonomous Agents and MultiAgent Systems (AAMAS ’18),

pages 68–76.

Incentive Design in Hedonic Games with Permission Structures

195