Multiple Sequence Alignment Using Ant Colony Optimization with

Chaotic Jump

Matheus Lino de Freitas

, Matheus Carreira Andrade

, Anderson Rici Amorim

Vitoria Zanon Gomes

, Bruno Rodrigues da Silveira

, Gabriel Augusto Prevato

Luiza Guimar

aes Cavarc¸an

, Carlos Roberto Val

encio

and Geraldo Francisco Doneg

a Zafalon

Department of Computer Science and Statistics, Universidade Estadual Paulista (UNESP),

Rua Crist

ao Colombo, 2265, Jardim Nazareth, S

ao Jos

e do Rio Preto - SP, 15054-000, Brazil

Keywords:

Multiple Sequence Alignment, Ant Colony Optimization, Hybrid Approaches, Chaotic Jump.

Abstract:

Multiple sequence alignment is one of the most relevant techniques in the bioinformatics. The next generation

sequencing technologies produces a large volume of data that is later analised by biologists, biomedicals and

geneticists. Due to this huge volume, computational effort are necessary to aid in the data analisys, as an

example, for sequence alignment. This works aims to introduce a novel method that combines the KAlign and

Clustal Omega tools in order to produce a seed alignment that will later be reﬁned by Ant Colony Optimization

and Chaotic Jump. The results showed that for every test the ACO produced better alignments than the MSA-

GA tool and at least for 50% of tests the proposed method was able to improve the initial alignments produced

by the KAlign and Clustal Omega tools.

1 INTRODUCTION

After the discovery of the chemical structure of the

deoxyribonucleic acid (DNA) molecule in 1953, the

genetic code and the ﬂow of biological information

from the molecules, a new area, bioinformatics, oc-

curred. This area involves several lines of knowledge

and has the fundamental role of providing computa-

tional solutions to various real biological problems

(Prosdocimi et al., 2002). After more than 30 years

this area has gained more and more expressiveness,

thanks to the evolution of hardwares and the growth

in the number of information available, but there are

still many problems to be faced (Zafalon, 2009). Con-

sequently, sequence alignments have become relevant

and necessary for the analysis of this large amount of

https://orcid.org/0009-0004-7969-5729

https://orcid.org/0000-0002-1670-266X

https://orcid.org/0000-0001-7862-7530

https://orcid.org/0000-0003-4176-566X

https://orcid.org/0009-0003-5941-9869

https://orcid.org/0009-0001-7091-9763

https://orcid.org/0009-0007-9589-3217

https://orcid.org/0000-0002-9325-3159

https://orcid.org/0000-0003-2384-011X

information (Sievers and Higgins, 2014). With this,

the present work proposes a contribution to a concept

widely used in bioinformatics, which is the multiple

alignment of sequences.

Because sequence alignment is from the prob-

lem class called Non-Deterministic Polynomial-Time

Hard or NP-Hard, the exact and even approximate

approaches are not used for large volumes of se-

quences (Zafalon et al., 2021). They use heuristics

and stochastic models, because these approaches can

ﬁnd solutions with good biological quality within a

feasible time. Even heuristics may not converge to

a result considered acceptable because they can stag-

nate at local maximum or minimum points. There-

fore, in addition to a good model that helps prevent

these situations, chaotic approaches, for example, are

also applied for this purpose in the literature.

In addition, hybrid solutions are another option

used to improve the expected result. The work of

Lee et al. (2008) proposes a hybrid approach using

Genetic Algorithm for construction of alignment and

optimization by ant colony for reﬁnement. Another

line of hybrid solution is the combination of tools,

as can be seen in the Rubio-Largo et al. (2016) work

that uses the KAlign tool to perform a realignment

of sequence fragments. The present work takes these

Lino de Freitas, M., Andrade, M. C., Amorim, A. R., Gomes, V. Z., Rodrigues da Silveira, B., Prevato, G. A., Cavarçan, L. G., Valêncio, C. R. and Zafalon, G. F. D.

Multiple Sequence Alignment Using Ant Colony Optimization with Chaotic Jump.

DOI: 10.5220/0013293800003929

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 2, pages 237-244

ISBN: 978-989-758-749-8; ISSN: 2184-4992

237

practical questions into consideration and proposes

a solution for multiple alignment of sequences us-

ing a hybrid solution with two tools: KAling (Lass-

mann, 2019) and Clustal Omega (Sievers and Hig-

gins, 2014) together with an optimization reﬁnement

by ant colony combined with chaotic jump in order

to reduce the probability of reaching local maximums

and achieve higher quality results.

The aim of this work is to present a method for

multiple alignment of sequences, using the meta-

heuristic Ant Colony Optimization and seeking to ob-

tain results that are biologically relevant. Thus, hybrid

strategies were employed, such as the combination

of tools for generating a base alignment, reﬁnement

of the alignment through the meta-heuristic cited and

application of the concept of chaotic jump combined

with partial realignment of sequences, if the algorithm

enters a local maximum point.

This work is organized as follows: In Section 2,

we present the related works, In Section 3 we detail

our methodology to develop the approach. In Section

4, we show the results of our method, focusing on

time execution improvement. Finally, in Section 5,

we make our conclusions about the work.

2 RELATED WORK

2.1 Multiple Sequence Alignment Based

on Chaotic PSO

The work of Lei et al. (2009) presents a multi-

sequence alignment approach, combining chaotic

jump with Particle Swarm Optimization. The authors

propose this solution to deal with the problem of pre-

mature convergence, which often means that the al-

gorithm has reached a local maximum or minimum

point (Gomes et al., 2022). Basically, the proposed

method perceives premature convergence by observ-

ing two points, ﬁrst if the average distance of particles

is less than a threshold and second if the variance of

the particle satisfaction function is less than another

parameter of threshold.

When identifying the situation of premature con-

vergence, the algorithm uses a logistic map function

to generate values in the chaotic interval between 0

and 1. These values are then mapped to entire posi-

tions corresponding to gaps that will be inserted into

the target sequence. In situations where there is al-

ready a gap in the given position, a random posi-

tion is chosen, the previous gap is maintained, and

the new gap is inserted into that position. The algo-

rithm presented better solutions for a set of Ribonu-

clease sequences extracted from the BAliBase dataset,

which are sequences with an identity above 35%. For

other sequences, with smaller identities, such as Cy-

tochrome c, the results are not much better, but still,

the difference between the minimum and maximum

scores is small, which denotes robustness in the solu-

tion.

2.2 Chaotic Step Length Artiﬁcial Bee

Colony Algorithms for Protein

Structure Prediction

An important area of bioinformatics, in addition to

pattern recognition and multiple alignment of se-

quences, is the area of prediction of the protein struc-

ture. Originally, nuclear magnetic resonance and X-

ray crystallography techniques were used to deter-

mine the structure of the protein. However, these ap-

proaches require a costly laboratory equipment and

also consume a lot of time.

The work of Saxena et al. (2020) is in the predic-

tion of the protein structure ﬁeld through a computa-

tional physical model. In general, the physical models

of protein prediction are constructed in two phases:

initially, a model with unknown energy is created and

optimization functions are applied on this model to

minimize protein-free energy.

To build and optimize free energy models, meta-

heuristics are often used, one of these meta-heuristics

is the Artiﬁcial Bee Colony. In the work of Saxena

et al. (2020), the hypothesis of applying chaotic func-

tions in a step of the algorithm Artiﬁcial Bee Colony

(ABC) is validated for best results. Originally, the

ABC algorithm updates bee velocity using the equa-

tion 1, where Φ is a randomly generated number in the

interval [−1, 1]. Saxena’s proposition is to replace the

random value with a method called Chaotic Length

Separator. The modiﬁed function is represented ac-

cording to the equation 2.

i j

= x

i j

+ φ(x

best j

− x

i j

) (1)

i j

= x

i j

+CLS

best j

− x

i j

) (2)

To calculate Chaotic Length Separator, ten chaotic

map functions were chosen. The method were now

named Enhance Chaotic Artiﬁcial Bee colony and

for each function an indice was assigned. Some of

them are: Chebyshev chaotic (ECABC1), Sinusoidal

chaotic (ECABC9) and Tent chaotic (ECABC10).

After computing the functions, the result is normal-

ized using the equation 3, in the interval [0.2,1

e−10

]

where, t denotes the current iteration and T the maxi-

mum number of iterations.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

238

Table 1: Results of chaotic PSO optimization.

Identity Sequence Average Maximum Minimum

< 25% SH3 0.5971 0.9461 0.4559

twitchin 0.4721 0.5248 0.4215

20% - 40% SH2 0.6235 0.6807 0.5723

Cytochrome c 0.5346 0.5731 0.4822

> 35% Ribonuclease 0.8256 0.8761 0.7778

immunophilin c 0.5146 0.5739 0.4611

(t) = N

max

−



max

− N

min



∗t (3)

The results pointed out by the study indicate bet-

ter efﬁcacy in the conversion of the ABC algorithm

with the use of chaotic maps. In addition, this ap-

proach, with ten distinct functions, allowed exploring

and highlighting the differences and behavior of the

algorithm with its use of each of them.

3 THE PROPOSED METHOD

The present work deals with the reﬁnement of mul-

tiple alignment of sequences through a hybridization

of techniques, aiming to obtain more biologically rel-

evant results. To achieve this objective, several ap-

proaches have been implemented and the main one,

which is at the heart of the proposed method, is the

ant colony optimization algorithm. It is through this

method that other approaches, such as the realign-

ment of sequence fragments and the application of the

chaotic method, are applied.

This section is subdivided into 5 parts: Method

Overview, Ant Colony Optimization, Multiple Se-

quence Alignment, Subsequence Realignment, and ﬁ-

nally, Chaotic Jump. In the overview, a pseudocode of

the method is presented to facilitate understanding. In

the Ant Colony Optimization section, the ant colony

optimization algorithm, its modeling for the sequence

alignment problem and the parameters used will be

detailed.

3.1 Method Overview

The proposed method is to apply Ant colony opti-

mization to reﬁne the multiple alignment of sequences

constructed by the KAlign and Omega Clustal tools.

To achieve this goal, this method captures the initial

alignment produced and performs reﬁnement using

ACO optimization, recomputate the pair-by-par align-

ment, and realigns with the Center Star technique.

When the alignment resulting from reﬁnement is

better than the previous one, this alignment is stored

as a possible ﬁnal solution, otherwise a counter is in-

cremented. If the counter obtains a predetermined

threshold, the algorithm enters a realignment phase.

At this stage, a position of the sequences is chosen us-

ing chaotic draw, where the chaotic jump is applied at

an initially random value. Only the ﬁrst random val-

ues drawn are used, because in the next occurrences,

the value is backfed in the chaotic formula itself to

recalibrate the initial position of the realignment.

The realignment step selects the starting position

and size that will be recalibrated and performs a mul-

tiple alignment of only that piece of the sequences and

then inserts them back into the original positions. Af-

ter this realignment, a new iteration will be performed

with the sequences modiﬁed to re-measure the quality

of the alignment performed. This cycle repeats until

the limit of iterations is reached. The Algorithm 1 il-

lustrate these steps that were described in the previous

paragraphs.

Algorithm 1. Overview of the proposed method.

for ant = 1, 2, . . . , N do

for iteration = 1, 2, . . . , N do

Generate initial multiple alignment

(ClustalW and KAlign)

Computing pair-by-par alignments

Run Center Star for Multiple Alignment of

Sequences

Calculate the score of multiple sequence

alignment

if Multiple alignment better than the previ-

ous one then

Store better alignment

else

Compute execution without improving

if Reached limit of executions without

improving then

Realign fragments of all sequences

end if

end for

Multiple Sequence Alignment Using Ant Colony Optimization with Chaotic Jump

239

3.2 Ant Colony Optimization

The approach of the proposed method, speciﬁcally

with regard to ant colony optimization is based on the

work of Amorim (2017). In his work, multiple align-

ment of sequences is improved by mutations in pre-

aligned sequences using a simpliﬁed grid to displace

ants and update the pheromone track by this grid. As

ants select the paths by grid, they also deposit the

pheromones on the chosen track, so that the trail that

generates the best biological result will be preferred

and trails with lower results will be discarded.

During the trail offset, when the ant takes a path

in the grid of the top line or infer line, a gap is in-

serted into the unchosen line, if the ant follows the

middle line, no gap is inserted and the two sequences

are not modiﬁed. Because of mutations, the result-

ing sequences are previously resized to a size of (2 *

max) positions, where max corresponds to the largest

size sequence and empty spaces are ﬁlled with gaps.

This procedure is done only to normalize the size of

the sequences and allow the realignments to ﬁt in the

sequences in their initial positions.

At the beginning of the process, ants use the

ClustalW and KAlign tools to produce an initial ba-

sic alignment. These tools were chosen because their

response time is in the millisecond to seconds and

the quality of the alignment produced is reasonable.

After the construction step of the initial alignment,

the pair-by-par alignment of each sequence is per-

formed, using the meta-heuristic Ant Colony Opti-

mization (ACO) to converge on biologically more rel-

evant alignments.

The equation 4 denotes the probability of transi-

tioning to the grids of the pair-by-par alignment. The

dimension i = (0, 1, 2) corresponds to the path that the

ant will choose, 0 for the top row, 1 for the middle

line, and 2 for the bottom row. Dimension j = 1..N

corresponds to the residue or amino acid of the se-

quence, and the dimension k = 1..T corresponds to

the number of the initial sequence of the pair-by-pair

alignment, where T is the total number of sequences.

The value of eta is set at 1, since because the simpli-

ﬁed grid has only 3 options, this value does not inter-

fere with convergence. The value of al pha and beta

are method parameters and their values will be set by

the user. All parameter values and their choice criteria

will be presented in section 4.

i jk

(t)

i jk

∑

i jk

(t)

i jk

(4)

After each pair is aligned, a score is computed

for the alignment. This score is used to update the

intensity of the pheromone track, which serves as

a guide for ants to decide between one path or an-

other. The equation representing the evaporation of

path pheromones can be observed in 5. In this equa-

tion, p is a parameter in the [0, 1] range and represents

the evaporation rate. The value of ∆τ

i jk

is deﬁned by

the equation 6, in which Q and MaxScore are param-

eters for the algorithm, and Score

is the calculated

score for the newly aligned sequence pair and is de-

ﬁned by the 7 equation.

i jk

(t + 1) = (1 − p) ∗ τ

i jk

(t) + ∆τ

i jk

(5)

∆(τ

i jk

) =











Q ·

Score

+ MaxScore

, if the ant z

transit through the grid (i, j, k)

0, if the ant z

do not transit through the grid (i, j, k)

(6)

Score(a, b) =

len

∑

i=1

α(A

′

[i], B

′

[i]) (7)

This pair-by-par alignment process is repeated for

all sequences, and upon completion, a 2-dimensional

array is generated. This array has 2 dimensions to al-

low storing all alignments against all sequences. In

addition, another resulting vector stores the cumula-

tive score of all alignments for each sequence. Both

artifacts are used in the next step, which is multiple

alignment of sequences.

3.3 Multiple Sequence Alignment

Among several multiple alignment methods, this

work uses the Center Star Zou et al. (2015) method.

This method consists of selecting the sequence

that scored the highest, starting multiple alignment

through it, and progressively inserting the other se-

quences, taking into account the pair-by-par align-

ment matrix.

In Figure 1, we observe the process of construct-

ing multiple alignment by this technique, this process

is divided into three steps, with a left enumeration in-

dicating each step. In step 1, the sequences are to be

aligned. In step 2, a representation of the par-to-par

alignment score can be observed, the objective is to

ﬁnd the sequence that obtains the highest score in this

matrix, for this each sequence is positioned in the ma-

trix with a score that corresponds to the result of the

pair-by-par alignment performed for each of the other

sequences present. And ﬁnally, in step 3, the s1 se-

quence was selected as center star and the alignment

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

240

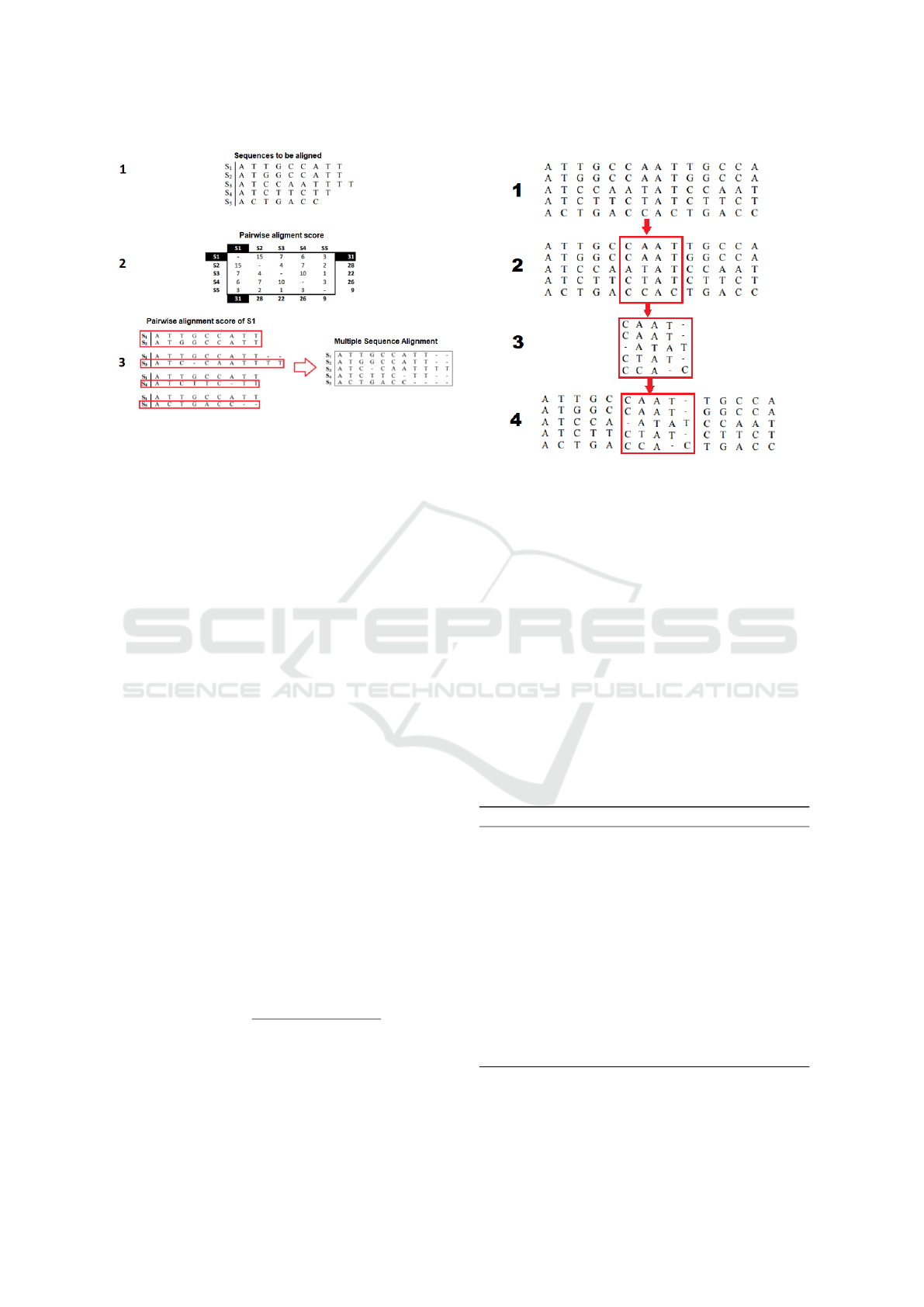
Figure 1: Multiple sequence alignment by Center Star algo-

rithm - Source: Adapted of Amorim (2017).

is constructed from the pair-by-par alignments with

that sequence.

To calculate the score of multiple sequence align-

ment, this work used the weighted sum-of-pairs

(WSP) Rubio-Largo et al. (2015) function. This is

the objective function that is maximized in the heuris-

tics developed in the present work. In the equation 8,

which deﬁnes the WSP function, AL is the size of the

aligned sequences and k is the total sequences. There-

fore, l corresponds to each residual or position of the

sequence and s

′

corresponds to the sequence resulting

from the multiple alignment. The SP(l) function is

deﬁned by the equation 9.

WSP(S

′

) =

∑

l=1

SP(l) −

∑

i=1

AGP(s

′

) (8)

SP(l) =

k−1

∑

i=1

∑

j=1

i j

× δ(s

′

i,l

, s

′

j,l

) (9)

In 9, delta corresponds to some replacement ar-

ray (BLOSUM, PAM). The function of this matrix

in the equation is to weigh the weight of replacing

one amino acid with another. In the present work,

we used the BLOSUM62 Eddy (2004) matrix. The

i, j

(a, b) function is deﬁned by the equation refdis-

tance, in which LD(s

, s

) corresponds to the distance

of Levenshtein and s

and s

correspond to the un-

aligned sequences.

i, j

(a, b) = 1 −

LD(s

, s

)

max(len(s

), len(s

))

(10)

Finally, in the equation 11, you have the penalty

function for gaps, where g

is the weight for each

opening of a new gap and g

is the weight applied to

the total of gaps consecutive after each new opening.

Figure 2: Example of the realignment phase.

AGP(s

′

) = (g

× N

gaps

) + (g

× N

spaces

) (11)

3.4 Subsequence Realignment

When the algorithm performs a certain number of iter-

ations and the quality of multiple sequence alignment

does not improve, a realignment step is performed on

subsequences of all sequences involved in multiple

alignment. The value of the number of iterations is

the limiting factor for selecting the position in the se-

quence, in which the subsequences will be extracted,

in which the logistic map function is applied. The re-

sult of this function is translated to a position in the se-

quence and alignment is performed using the KAlign

tool. This realignment phase can be observed through

the algorithm 2:

Algorithm 2. Realignment algorithm overview.

Calculate realignment limits

Extract fragments the same size from all sequences

Generate new ﬁle with only fragments of the origi-

nal sequences

Run KAlign

Get sequences aligned by KAlign

Inject aligned sequences into the originally ex-

tracted ranges

Multiple Sequence Alignment Using Ant Colony Optimization with Chaotic Jump

241

3.5 Chaotic Jump

Chaotic Jump is used in the method proposed in the

sequence position selection step to perform realign-

ment. First, the logistic map function was deﬁned ac-

cording to the equation 12. For the present study, the

value of α = 4 was used, because with this value the

result of the function, for any value of x, will always

occur in the range [0, 1]. Because this function ex-

pects a value to calculate the next, the initial value is

randomly generated in the same range.

= x

n+1

= αx

(1 − x

) (12)

In the 3 algorithm, how the value of delta

transformed into a sequence position and how the

block size that will be realigned is determined. In

the ﬁrst two lines, the minimum and maximum lim-

its of the block size that will be realigned are calcu-

lated respectively. In the third line, the fact size of the

block is calculated randomly in the range of the previ-

ously deﬁned limits. Therefore, the limit size is set for

the draw of the position, to prevent the drawn num-

ber from exceeding the length of the sequences. After

that, the start and end positions are calculated, and the

extraction process takes place as demonstrated in the

previous section. The values of P

textmin

and P

textmax

are algorithm parameters and initialized by default at

5 and 25 of the total sequence size, respectively.

Algorithm 3. Algorithm used to determine realignment po-

sitions and sizes.

Block

min

= P

min

∗ T

seq

Block

max

= P

max

∗ T

seq

Block

size

= Rand(Block

min

, Block

max

)

limit

= T

seq

− Block

size

initial

= δ

∗ T

limit

f inal

= P

initial

+ Block

size

4 RESULTS AND DISCUSSION

All tests of this work were run under a computer

with Windows Operating System(R) 10 Enterprise, 16

GB RAM, an Intel(R) Core(TM) i7-8665U CPU @

1.90GHz 2.11GHz with 4 cores and 8 threads and a

240GB SSD.

4.1 Parameters Used in the Present

Work

The parameters used for ACO, WSP and Realignment

methods are shown in table 2.

In order to compare the efﬁciency of the proposed

method, the same set of sequences was, in paral-

lel, aligned using the MSA-GA, KAlign and Clustal

Omega tool. The parameters used by the MSA-GA

tool are in Table 3:

All tests performed were performed on the BAl-

iBase 3 benchmark. 10 random regions of all BAl-

iBase families were selected, and the tests were re-

peated at least 3 times in each tool to obtain the mean

and standard deviation of the metrics. To measure the

quality of alignment, the QScore tool was used, which

is a customized version of the BAliScore tool to ac-

cept the .fasta ﬁle format.

The comparison of the alignments made by the

tools are shown in tables 4, 5, 6, 7 and 8. In the ta-

bles’ columns are presented: the region of BaliBase

(column Region), the method used (column Method),

the average score of Q (column Avg. Q), the maxi-

mum score of TC (column Max TC) and the standard

deviation of Q score (column SD Q).

5 CONCLUSIONS

In this work, a method for multiple alignment of

sequences using Ant Colony Optimization was pro-

posed and implemented in conjunction with a chaotic

state approach. To validate the results, the propo-

nent made comparations of the new method with

three other methods also implemented in tools, called

MSA-GA, KAlign and Clustal Omega.

Through the analysis of the results and the

comparative table we can observe that the proposed

method showed better results, regarding the quality of

the alignment produced, in more than ﬁfty percent of

the executions, for all regions used in the benchmark.

In tables 4, 5, 6, 7 and 8, it can be observed that

the value of the ACO method is at least as good as

the best alignment between the Omega clustal and

KAlgin tools. This behavior is expected, since to

perform the realignments, these tools are used to gen-

erate an initial alignment. And because the proposed

method is a reﬁnement of multiple alignment, the

quality will be at least as good as the alignment pro-

duced by the initial alignment. When observing the

values of the standard deviations, it is also perceived

that the method offers a robust solution, because in

more than half of the cases, the result value always

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

242

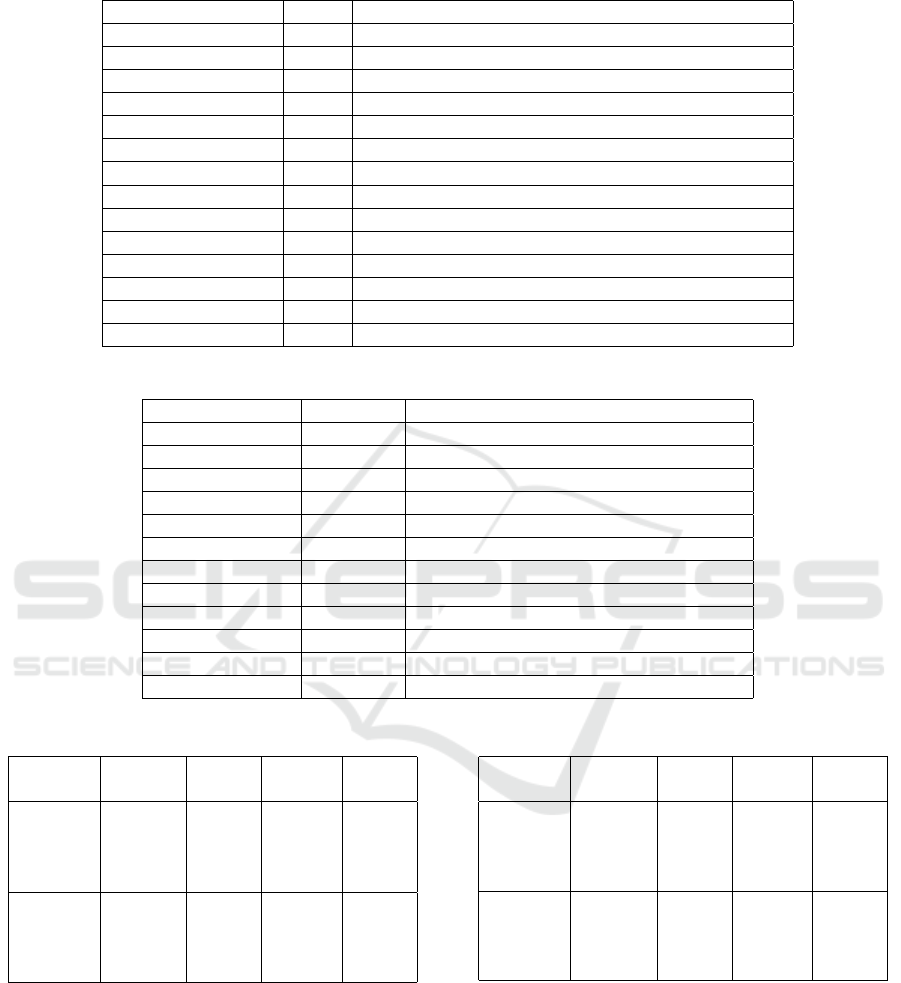
Table 2: Parameters for the ACO, WSP and Realignment methods.

Name Value Description

NumberOfAnts 20 Amount of ants used

NotImprovedLimit 10 Minimum number of iterations

NumberOfIterations 300 Maximum number of iterations per ant

α 1.0 Value of alpha to ACO

β 5.0 Value of beta to ACO

0.3 Value of Q0 to ACO

RO 0.2 Value of RO to ACO

Q 0.001 Value of Q to ACO

10 Initial pheromone value to ACO

MaxScore 200.0 Value of MaxScore to ACO

0.85 Value of Gap Extension penalty for the WSP function

6 Value of Gap Open penalty for the WSP function

MinFragmentPerc 0.05 Minimum percent of the sequence block size

MaxFragmentPerc 0.25 Maximum percent of the sequence block size

Table 3: Parameters used in the MSA-GA tool.

Name Value Description

PopulationSize 1000 Population size

Generations 10000 Number of Generations

BlockMutation 0.01 Mutation rate

GapExtMutation 0.05 Gap Extension Mutation

GapRedMutation 0.05 Gap Reduction Mutation

HorCrossover 0.8 Horizontal Cross-over rate

VerCrossover 0.8 Vertical Cross-over rate

HorVerRation 0.5 Horizontal/Vertical Ratio

TournamentSize 2 Tournament Size

OffSet 0 Offset value

MaxSeqSize 1.2 Maximum size of the sequence alignment

Matrix Blosum62 Substitution matrix

Table 4: Results for the regions BB11001 and BB11010.

Region Method Avg.

Max

SD Q

BB11001 ACO 0.969 0.943 0.05

BB11001 ClustalO 0.907 0.83 0

BB11001 KAlign 0.874 0.727 0

BB11001 MSAGA 0.728 0.5 0.02

BB11010 ACO 0.299 0.175 0.02

BB11010 ClustalO 0.287 0.14 0

BB11010 KAlign 0.283 0.148 0

BB11010 MSAGA 0.141 0.00388 0.13

generates the same value and therefore the devi-

ation is zero.

As a future works, we intend to investigate the

improvement to this method in order to reduce the

execution time. Since the Ant Colony Optimization

allows to share minimum state between ants, a par-

allel approach would be viable and recommended to

achieve this goal.

Table 5: Results for the regions BB12012 and BB12022.

Region Method Avg.

Max

SD Q

BB12012 ACO 0.564 0.42 0.05

BB12012 ClustalO 0.558 0.41 0

BB12012 KAlign 0.538 0.387 0

BB12012 MSAGA 0.138 0.0173 0.09

BB12022 ACO 0.783 0.558 0

BB12022 ClustalO 0.772 0.532 0

BB12022 KAlign 0.719 0.468 0

BB12022 MSAGA 0.628 0.374 0.03

ACKNOWLEDGEMENTS

The authors would like to thank S

ao Paulo Research

Foundation (FAPESP) for the ﬁnancial support, un-

der grants, 20/08615-8, 23/13399-0, 23/13576-0,

23/13610-3, and Coordenac

ao de Aperfeic¸oamento

de Pessoal de N

ıvel Superior - Brasil (CAPES) for

the partial ﬁnancial support.

Multiple Sequence Alignment Using Ant Colony Optimization with Chaotic Jump

243

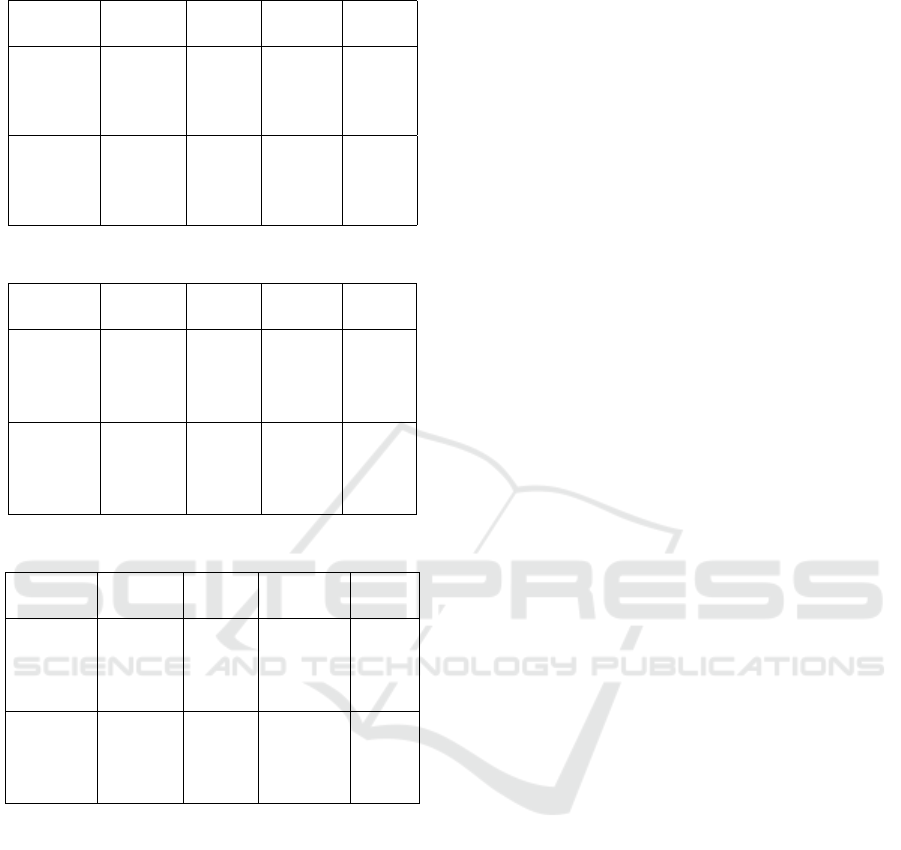
Table 6: Results for the regions BB20010 and BB20030.

Region Method Avg.

Max

SD Q

BB20010 ACO 0.852 0.535 0

BB20010 ClustalO 0.852 0.535 0

BB20010 KAlign 0.826 0.44 0

BB20010 MSAGA 0.298 0.00152 0.08

BB20030 ACO 0.895 0.0955 0

BB20030 ClustalO 0.883 0.0892 0

BB20030 KAlign 0.781 0.052 0

BB20030 MSAGA 0.441 0.024 0.11

Table 7: Results for the regions BB30016 and BB30024.

Region Method Avg.

Max

SD Q

BB30016 ACO 0.414 0.0641 0

BB30016 ClustalO 0.414 0.0641 0

BB30016 KAlign 0.311 0.0148 0

BB30016 MSAGA 0.0907 0.0148 0

BB30024 ACO 0.726 0.448 0

BB30024 ClustalO 0.726 0.448 0

BB30024 KAlign 0.706 0.392 0

BB30024 MSAGA 0.0171 0 0.12

Table 8: Results for the regions BB40011 and BB50014.

Region Method Avg.

Max TC SD Q

BB40011 ACO 0.363 0 0

BB40011 ClustalO 0.358 0.000569 0

BB40011 KAlign 0.363 0 0

BB40011 MSAGA 0.00291 0 0.09

BB50014 ACO 0.811 0.398 0.02

BB50014 ClustalO 0.803 0.395 0

BB50014 KAlign 0.756 0.27 0

BB50014 MSAGA 0.231 0.0184 0.01

REFERENCES

Amorim, A. R. (2017). Alinhamento m

ultiplo de

sequ

encias utilizando algoritmo gen

etico multifunc¸

e col

onia de formigas. Master’s thesis, Universidade

Estadual Paulista (UNESP).

Eddy, S. R. (2004). Where did the blosum62 alignment

score matrix come from? Nature biotechnology,

22(8):1035–1036.

Gomes, V. Z., Andrade, M. C., Amorim, A. R., and Zafalon,

G. F. D. (2022). A hybrid genetic algorithm using pro-

gressive alignment and consistency based approach

for multiple sequence alignments. In Proceedings of

the 24th International Conference on Enterprise In-

formation Systems - Volume 2: ICEIS, pages 167–174.

INSTICC, SciTePress.

Lassmann, T. (2019). Kalign 3: multiple sequence align-

ment of large datasets. Bioinformatics, 36(6):1928–

1929.

Lee, Z.-J., Su, S.-F., Chuang, C.-C., and Liu, K.-H. (2008).

Genetic algorithm with ant colony optimization (ga-

aco) for multiple sequence alignment. Applied Soft

Computing, 8(1):55–78.

Lei, X.-j., Sun, J.-j., and Ma, Q.-z. (2009). Multiple se-

quence alignment based on chaotic pso. In Interna-

tional Symposium on Intelligence Computation and

Applications, pages 351–360. Springer.

Prosdocimi, F., Coutinho, G., Ninnecw, E., Silva, A. F.,

dos Reis, A. N., Martins, A. C., dos Santos, A. C. F.,

unior, A. N., and Camargo Filho, F. (2002). Bioin-

form

atica: manual do usu

ario. Biotecnologia Ci

encia

& Desenvolvimento, 29:12–25.

Rubio-Largo,

A., Vega-Rodr

ıguez, M. A., and Gonz

alez-

Alvarez, D. L. (2015). A hybrid multiobjective

memetic metaheuristic for multiple sequence align-

ment. IEEE Transactions on Evolutionary Computa-

tion, 20(4):499–514.

Rubio-Largo,

A., Vega-Rodr

ıguez, M. A., and Gonz

alez-

Alvarez, D. L. (2016). Hybrid multiobjective artiﬁcial

bee colony for multiple sequence alignment. Applied

Soft Computing, 41:157–168.

Saxena, A., Shekhawat, S., Sharma, A., Sharma, H., and

Kumar, R. (2020). Chaotic step length artiﬁcial bee

colony algorithms for protein structure prediction.

Journal of Interdisciplinary Mathematics, 23(2):617–

629.

Sievers, F. and Higgins, D. G. (2014). Clustal omega, ac-

curate alignment of very large numbers of sequences.

In Multiple sequence alignment methods, pages 105–

116. Springer.

Zafalon, G. F. D. (2009). Algoritmos de alinhamento

ultiplo e t

ecnicas de otimizac¸ao para esses algorit-

mos utilizando Ant Colony. PhD thesis, Universidade

Estadual Paulista (UNESP), R. Crist

ao Colombo,

2265 - S

ao Jos

e do Rio Preto - SP, Brasil.

Zafalon, G. F. D. Z., Gomes, V. Z., Amorim, A., and

Val

encio, C. R. (2021). A hybrid approach using pro-

gressive and genetic algorithms for improvements in

multiple sequence alignments. In Proceedings of the

23rd International Conference on Enterprise Informa-

tion Systems - Volume 2: ICEIS, pages 384–391. IN-

STICC, SciTePress.

Zou, Q., Hu, Q., Guo, M., and Wang, G. (2015). Halign:

Fast multiple similar dna/rna sequence alignment

based on the centre star strategy. Bioinformatics,

31(15):2475–2481.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

244