Optimizing 2D+1 Packing in Constrained Environments Using Deep
Reinforcement Learning
Victor Ulisses Pugliese
1 a
, Os
´
eias Faria de Arruda Ferreira
2 b
and Fabio A. Faria
1,3 c
1
Universidade Federal de S
˜
ao Paulo, S
˜
ao Jos
´
e dos Campos, S
˜
ao Paulo, Brazil
2
EMBRAER S.A., S
˜
ao Jos
´
e dos Campos, S
˜
ao Paulo, Brazil
3
Instituto Superior Tecnico, Universidade de Lisboa, Av. Rovisco Pais 1, Lisboa, Portugal
Keywords:
Deep Reinforcement Learning, Packing, PPO, A2C.
Abstract:
This paper proposes a novel approach based on deep reinforcement learning (DRL) for the 2D+1 packing prob-
lem with spatial constraints. This problem is an extension of the traditional 2D packing problem, incorporating
an additional constraint on the height dimension. Therefore, a simulator using the OpenAI Gym framework
has been developed to efficiently simulate the packing of rectangular pieces onto two boards with height con-
straints. Furthermore, the simulator supports multidiscrete actions, enabling the selection of a position on
either board and the type of piece to place. Finally, two DRL-based methods (Proximal Policy Optimization –
PPO and the Advantage Actor-Critic – A2C) have been employed to learn a packing strategy and demonstrate
its performance compared to a well-known heuristic baseline (MaxRect-BL). In the experiments carried out,
the PPO-based approach proved to be a good solution for solving complex packaging problems and highlighted
its potential to optimize resource utilization in various industrial applications, such as the manufacturing of
aerospace composites.
1 INTRODUCTION
Manufacturing has undergone significant changes in
recent decades, primarily driven by market trends that
encourage companies to transition from traditional
mass production lines to more dynamic and flexible
manufacturing systems, essential for competitiveness
in the global market. This shift, known as smart man-
ufacturing, is currently reinventing itself through ad-
vances in Digital Transformation, Internet of Things
(IoT), and Artificial Intelligence (AI) (Alem
˜
ao et al.,
2021), (Xia et al., 2021), and (Ramezankhani et al.,
2021).
Consequently, various approaches to manufactur-
ing scheduling have been studied and implemented to
optimize production and resource allocation. Despite
these efforts, most scheduling uses manual methods
or basic software, resulting in limited improvements
in system performance. Historically, the production
lines produced many of the same products, always
following the same process. However, this is not the
a
https://orcid.org/0000-0001-8033-6679
b
https://orcid.org/0009-0007-4066-8709
c
https://orcid.org/0000-0003-2956-6326
case for Smart Manufacturing (Alem
˜
ao et al., 2021).
Aerospace manufacturing, particularly using com-
posite materials, presents a complex scheduling chal-
lenge characterized by high demand variability, ex-
tended lead times, and the integration of diverse sup-
pliers and work practices. Although composites of-
fer advantages such as superior strength, corrosion
resistance, and efficient forming, their higher cost
than traditional metallic materials requires careful op-
timization (Xie et al., 2020) and (Azami et al., 2018).
The manufacturing process typically involves two pri-
mary stages: layup and curing (Azami, 2016). Au-
toclave packing, a critical aspect of the curing pro-
cess, involves meticulous placement of composite
parts within the autoclave to achieve desired prod-
uct properties (Haskilic et al., 2023) and (Elkington
et al., 2015). This intricate task, involving manual po-
sitioning, presents a unique optimization problem that
surpasses the classical packing problem due to addi-
tional constraints and resource management require-
ments (Collart, 2015).
Certain constraints can be relaxed to simplify the
optimization process. For instance, since composite
materials cannot be stacked within an autoclave, the
placement strategy can focus on the width and length
Pugliese, V. U., Ferreira, O. F. A. and Faria, F. A.
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning.
DOI: 10.5220/0013292100003929
In Proceedings of the 27th Inter national Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 501-511
ISBN: 978-989-758-749-8; ISSN: 2184-4992
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
501

of the parts. Additionally, the height of each part must
be verified to ensure it does not exceed the capacity of
the tooling cart.
The introduction of Reinforcement Learning (RL)
methods to solve packing problems has shown
promising results in the literature. For instance,
(Kundu et al., 2019) employed RL to take an image
as input and predict the pixel position of the next
box, while (Li et al., 2022) explored RL in 2D and
3D environments. Furthermore, combining heuristics
with RL, as in (Fang et al., 2023a), has proven to
be effective, and RL has also been applied to sev-
eral other types of problem, as discussed in (Wang
et al., 2022). One of the advantages of RL is that
it does not require an explicit model of the environ-
ment; the agent learns to make decisions by observ-
ing the rewards of its actions from a state, as described
in (Sutton and Barto, 2018), and continuously adapts
to its environment through exploration and exploita-
tion. This makes RL particularly suitable for sequen-
tial decision-making in games, robotics, control sys-
tems, and scheduling problems (Cheng et al., 2021).
Our approach distinguishes itself by relying solely
on RL methods, using actor-critic to explore and ex-
ploit. This contrasts with other packing studies that
frequently incorporate heuristics to guide or direct the
RL algorithm, thereby limiting its scope and creativ-
ity. To our knowledge, no scientific study has ever
addressed this topic in the literature. Therefore, this
paper aims to apply Reinforcement Learning meth-
ods to address a 2D+1 packing problem with spatial
constraints. This problem is an extension of the tra-
ditional 2D packing problem, incorporating an addi-
tional constraint on the height dimension. We also
compare the PPO and A2C as the unique methods that
support multi-discrete action spaces. This research,
inspired by the challenges of aerospace composite
manufacturing, has potential applications in many in-
dustry sectors, including the packing of components
in vehicles, organizing parts in boxes or pallets for
transport and storage, arranging products in-store dis-
plays, and similar optimization tasks across different
sectors.
2 BACKGROUND
This section briefly describes the types of packing
problem and the deep reinforcement learning (DRL)
methods used in this paper.
2.1 Packing
The packing problem is a classic challenge in combi-
natorial optimization that has been extensively stud-
ied for decades by researchers in operations research
and computer science, as noted in (Li et al., 2022).
The primary objective is to allocate objects within
containers, minimizing wasted space efficiently. The
problem can work with regular (Kundu et al., 2019)
and (Zhao et al., 2022b) or irregular shapes
(Crescitelli and Oshima, 2023), often explored in
streaming/online or batching/offline approaches.
Several works based on heuristic approaches have
been proposed for solving packing problems as de-
scribed in (Oliveira et al., 2016), such as the Max-
imum Rectangles - Bottom-Left (Max Rects-BL),
Best-Fit Decreasing Height (BFDH), and Next-Fit
Decreasing Height (NFDH). Max Rects-BL approach
places the largest rectangle in the nearest available
bottom-left corner of a 2D space (Fang et al., 2023a).
BFDH sorts items by descending height and then at-
tempts to place each item, left-justified, on the ex-
isting level with the minimum remaining horizon-
tal space (Seizinger, 2018). In the NFDH approach,
it first arranges the pieces in descending order of
heigthen places each piece on the current level, start-
ing from the left side, as long as there is enough space;
otherwise, it starts a new level (Oliveira et al., 2016).
2.2 Deep Reinforcement Learning
Deep Reinforcement Learning (DRL) addresses the
challenge of autonomously learning optimal decisions
over time. Although it employs well-established su-
pervised learning methods, such as deep neural net-
works for function approximation, stochastic gradi-
ent descent (SGD), and backpropagation, RL applies
these techniques differently, without a supervisor, us-
ing a reward signal and delayed feedback. In this
context, an RL agent receives dynamic states from an
environment and takes actions to maximize rewards
through trial-and-error interactions (Kaelbling et al.,
1996).
The agent and the environment interact in a se-
quence at each discrete time step, t = 0, 1, 2, 3, · · · . At
each time step t, the agent receives a representation
of the environment’s state s
t
∈ S, where S is the set of
possible states, and selects an action a
t
∈ A(s
t
), where
A(s
t
) is the set of actions available in the state s
t
. At
time step t + 1, as a consequence of its actions, the
agent receives a numerical reward r
t+1
∈ R and tran-
sitions to a new state s
t+1
(Sutton and Barto, 2018).
During each iteration, the agent implements a
mapping from states to the probabilities of each possi-
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
502

ble action. This mapping, known as the agent’s policy,
is denoted as π
t
, where π
t
(s, a) represents the proba-
bility that a
t
= a given s
t
= s. Reinforcement learn-
ing methods specify how the agent updates its policy
based on experience, intending to maximize the cu-
mulative reward over the long term, according (Sut-
ton and Barto, 2018).
2.2.1 Proximal Policy Optimization (PPO)
PPO employs the actor-critic method and trains on-
policy, meaning it samples actions based on the most
recent policy iteration (Schulman et al., 2017). In
this framework, two neural networks typically serve
as the “actor” and “critic.” The “actor” learns the pol-
icy, while the “critic” estimates the value function or
the advantage, which is used to train the “actor”.
The training process involves calculating future
rewards and advantage estimates to refine the policy
and adjust the value function. Both the policy and
value function are optimized using stochastic gradi-
ent descent algorithms, as described in (Keras, 2022).
The degree of randomness in action selection de-
pends on the initial conditions and the training pro-
cedure. Typically, as training progresses, the pol-
icy becomes less random due to updates that encour-
age the exploration of previously discovered rewards
(S
´
aenz Imbacu
´
an, 2020).
2.2.2 Advantage Actor-Critic (A2C)
A2C, often perceived as a distinct algorithm, is re-
vealed in “A2C is a special case of PPO” as a specific
configuration of Proximal Policy Optimization (PPO)
operating within the actor-critic approach. A2C
shares similarities with PPO in employing separate
neural networks for policy selection (actor) and value
estimation (critic). Its core objective aligns with PPO
when the latter’s update epochs are set to 1, effec-
tively removing the clipping mechanism and stream-
lining the learning process (Huang et al., 2022).
A2C is a synchronous adaptation of the Asyn-
chronous Actor-Critic (A3C) policy gradient ap-
proach. It operates deterministically, waiting for ev-
ery actor to complete its experience segment before
initiating updates, averaging across all actors. This
strategy improves GPU utilization by accommodating
larger batch sizes (Mnih et al., 2016).
3 RELATED WORKS
The field of 2D regular packing problems has seen
significant progress in recent years, with various
methods proposed to optimize space utilization and
minimize waste, using Reinforcement Learning. This
review connects several key research papers, high-
lighting the diverse strategies to tackle these chal-
lenges.
In online 2D bin packing, where items are placed
sequentially without prior knowledge of future in-
puts, (Kundu et al., 2019) propose a variation of DQN
for the 2D online bin packing problem, to maximize
packing density. This method takes an image of the
current bin state as input and determines the precise
location for the next object placement. The reward
function encourages placing objects in a way that
maximizes space for future placements. The method
is extendable to 3D online bin-packing problems.
For grouped 2D bin packing, common in indus-
tries like furniture manufacturing and glass cutting,
where orders are divided into groups and optimized
within each group, (Ao et al., 2023) presents a hierar-
chical reinforcement learning approach. The method
was successfully developed in a Chinese factory, re-
ducing the raw material costs. (Li et al., 2022) pro-
poses SAC with a recurrent attention encoder to cap-
ture inter-box dependencies and a conditional query
decoder for reasoning about subsequent actions in 2D
and 3D packing problems. This approach demon-
strates superior space utilization compared to base-
lines, especially in offline and online strip packing
scenarios.
To address uncertainties in real-world packing
problems, (Zhang et al., 2022) presents a hybrid
heuristic algorithm that combines enhanced scoring
rules with a DQN, which dynamically selects heuris-
tics through a data-driven process, to solve the truck
routing and online 2D strip packing problem.
We can mention other works which combine RL
with scoring rules. (Zhao et al., 2022b), for in-
stance, employed Q-learning for sequencing and the
bottom-left centroid rule for positioning. Fang et
al. (Fang et al., 2023a) leveraged REINFORCE
with the MaxRect-BL algorithm to exploit under-
lying packing patterns. It (Zhu et al., 2020) Re-
inforcement Learning-based Simple Random Algo-
rithm (RSRA) algorithm, integrating skyline-based
scoring rules with a DQN, has demonstrated effec-
tiveness.
This section shows a range of RL methods ap-
plied to 2D regular packing problems. As research
in this area advances, there is also an increasing focus
on expanding 3D solutions (Wu and Yao, 2021; Zhao
et al., 2022a; Puche and Lee, 2022; Zuo et al., 2022)
and tackling irregular shapes (Crescitelli and Oshima,
2023; Fang et al., 2023b; Fang et al., 2022; Fang et al.,
2021; Yang et al., 2023).
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning
503

4 DRL APPROACH FOR 2D+1
PACKING PROBLEM
This section describes our DRL solution for a 2D+1
packing environment, inspired by real-world scenar-
ios related to aerospace composite manufacturing.
The environment simulates the task of efficiently
packing rectangular pieces onto two distinct boards
with limited height. It was built using the OpenAI
Gymnasium framework and represents the packing
scenario with the following key components:
1. Observation Space. It consists of two matrices,
each one representing a board of length X width
dimensions. Additionally, four integer values are
included, corresponding to the quantities of four
different types of piece.
2. Action Space. It comprises a multi-discrete
space, encompassing the (x, y) coordinates for the
top-left corner of a piece placement, an index se-
lecting the target board, and another index spec-
ifying the piece to be chosen from the available
set.
3. Algorithm. It is structured to reward the agent for
positive actions that effectively fill the available
spaces in the environment. Conversely, penalties
are applied for invalid actions, such as selecting a
piece with zero remaining quantity, attempting to
place a piece on an already occupied coordinate,
or putting a piece that exceeds the tooling cart’s
height. The process proceeds in Algorithm 1.
The agent and our simulator interact during
each episode in a discrete-time sequence, t =
0, 1, 2, 3, · · · . At each time step t, the agent is pro-
vided with a representation of the boards and the
quantities of pieces to be placed, s
t
∈ S, where
S represents the set of available positions on the
board and the piece’s type. The action taken by
the agent, denoted as a
t
∈ A(s
t
), consists of se-
lecting the coordinates (x, y), the index board, and
the index piece in-state s
t
for placement. At time
step t + 1, as a result of this action, the agent re-
ceives a numerical reward r
t+1
∈ R and transitions
to a new state s
t+1
, as shown in Figure 1.
The R
height
is determined by the following condi-
tions:
• If
piece height
board height
× 100 ≤ 50, then R
height
= 0
• Else if
piece height
board height
× 100 ≤ 80, then R
height
= 1
• Else if
piece height
board height
× 100 ≤ 100, then R
height
= 2
(Optimal)
• Else if
piece height
board height
× 100 > 100, then R
height
=
−2
Algorithm 1: Packing2D Environment - Step Function.
Data: Action a = [x, y, b, p], where:
• (x, y): Placement coordinates on the board
• b: Board index (0 or 1)
• p: Piece type index (0 to 3)
Result: Observation s
′
, Reward r, Done flag
B
0
, B
1
, B
H
0
, B
H
1
← Current states of boards and height
maps
Q
0
, Q
1
, Q
2
, Q
3
← Remaining quantities of piece
types 0, 1, 2, 3
empty ← count zeros(B
0
) + count zeros(B
1
)
if Q
0
, Q
1
, Q
2
, Q
3
> 0 and empty > 0 then
piece ← Shape matrix of piece type p
x ← clip(x, 0, board weight − w)
y ← clip(y, 0, board lenght − l)
occupied ← 0
for i = 0 to l − 1 do
for j = 0 to w − 1 do
if piece[i][ j] == 1 then
if x + i < board lenght and y + j <
board weight then
B
b
(x+i, y+ j) ← B
b
(x+i, y+ j)+
1
B
H
b
(x + i, y + j) ← B
H
b
(x + i, y +
j) + piece height(p)
if B
b
(x + i, y + j) > 1 then
occupied ← 1
end
end
end
end
end
r
height
← check height(b, piece height(p))
if occupied == 0 and r
height
≥ 0 then
dim = (w, l) ← Dimensions of piece type p
r ← dim × r
height
else
r ← −8
Revert B
b
and B
H
b
to previous state
end
done ← False
Q
p
← Q
p
− 1
else
done ← True
r ←
calculate
reward(B
0
)+calculate reward(B
1
)
2
end
return (B
0
, B
1
, Q
0
, Q
1
, Q
2
, Q
3
), r, done
4. Training and Testing. We only employed PPO
and A2C methods in the Stable Baselines library,
because they support multi-discrete action spaces.
PPO, a state-of-the-art model-free reinforcement
learning algorithm (Sun et al., 2019), is partic-
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
504

Figure 1: Our simulator pipeline based on reinforcement
learning methods.
ularly effective in this context. Standard imple-
mentations of Deep Q-Network (DQN) and Soft
Actor-Critic (SAC) are not directly applicable to
multi-discrete action spaces.
Our agents were trained in a 2D+1 packing en-
vironment for 10 million episodes. Evaluations
were conducted every 50 episodes under deter-
ministic conditions, and each experiment was re-
peated 10 times. For both PPO and A2C, we used
a linear learning rate of 0.0005 and a discount fac-
tor (gamma) of 0.95 as hyperparameters.
5 EXPERIMENTS
This section presents the experimental protocol and
results achieved by DRL methods.
5.1 Experimental Methodology
In this work, we conducted six different experiments:
three of them using even board dimensions (8×8) and
three using odd board dimensions (7 × 7). Each set of
experiments followed these conditions: (1) the pieces
and boards were constrained to a uniform height, (2)
the board 1 was taller than the board 2, and (3) the
board 2 was taller than the board 1. Table 1 summa-
rizes the setup adopted in the experiments.
Table 1: Setup of the experiments.
Exp. ID Even/Odd Weight Length Height 0 Height 1
1 Even 8 8 100 100
2 Even 8 8 120 80
3 Even 8 8 80 120
4 Odd 7 7 100 100
5 Odd 7 7 120 80
6 Odd 7 7 80 120
We also employed four types of pieces: 2 × 2 and
2 × 1, with heights of either 115 or 75 centimeters.
These pieces are placed within two boards that define
the environment’s boundaries. Figure 2 shows their
shapes.
Figure 2: The types of piece available to be placed into the
boards.
Table 2 shows the amount of pieces was used for
each experiment.
Table 2: The sets of pieces used for each experiment.
Exp. ID Qty Piece 1 Qty Piece 2 Qty Piece 3 Qty Piece 4
1 8 8 16 16
2 8 8 16 16
3 8 8 16 16
4 6 6 9 9
5 6 6 9 9
6 6 6 9 9
In a real-world aerospace manufacturing setting,
the number of parts in an autoclave can vary signifi-
cantly based on available volume and batch size. We
can expect around 30 to 50 parts per curing cycle.
However, the number may be lower, such as when
dealing with aircraft fairings. It is important to note
that the packing phase does not involve irregular parts
due to the safety margins necessary to achieve the de-
sired product properties. Furthermore, since it oper-
ates on batches of parts, we should abstract these con-
straints, focusing on the packing process.
In the experiments carried out, the PPO, A2C and
MaxRect-BL methods have been compared. We se-
lected the MaxRect-BL approach, aligning with the
bottom-left placement strategies employed in prior
work by (Zhao et al., 2022b) and (Fang et al., 2023a)
within the context of RL. To address the limitations of
MaxRect-BL in handling height constraints, we im-
plemented a modified version inspired by the BFDH.
This modified approach prioritizes the height orienta-
tion of the pieces before considering their size during
the packing process, effectively improving the pack-
ing efficiency. Furthermore, the simulations were per-
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning
505

formed on a Core i7 processor with 16 GB of RAM.
Each PPO training session lasted approximately 7
hours.
5.2 Even Experiments
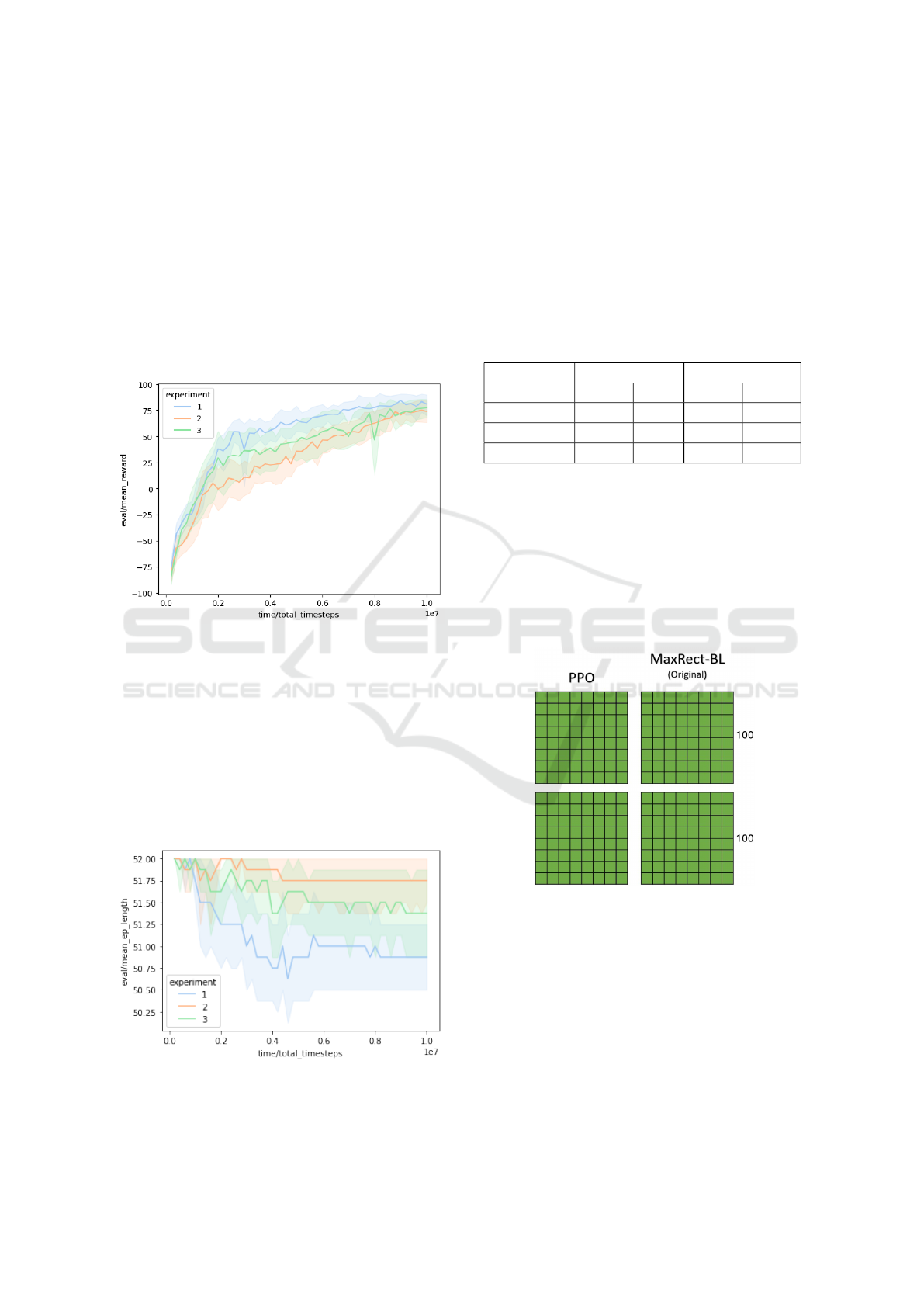
Figure 3 illustrates the evaluation curves for 10 inde-
pendent PPO runs across the three experimental con-
ditions. These experiments demonstrated optimal per-
formance by achieving the maximum reward through
100% correct board fillings. Negative reward values
signify incorrect board configurations.
Figure 3: Evaluation curves of the three even experiments
using PPO.
Figure 4 presents the curves depicting the mean
episode length across 10 independent PPO runs un-
der the three experimental conditions. These re-
sults highlight the progression of the mean episode
length throughout iterations, providing insights into
the agent’s performance dynamics and its efficiency
in solving the problem. The optimal episode length
occurs approximately when the maximum number of
pieces is successfully packed onto a board.
Figure 4: Mean episode length over even experiments using
PPO.
In the experiments carried out, the A2C method
proved to be less practical than the PPO due to its sig-
nificantly longer convergence time and greater insta-
bility during training. Furthermore, A2C often fails
to achieve optimal performance compared to PPO
method. We selected 4 results from each experimental
setup to compare these RL methods. Table 3 contains
the mean percentage of correct board fills (Mean) and
its standard deviation (Std).
Table 3: Comparative analysis between PPO and A2C
methods for correctly board filling.
Experiment
PPO A2C
Mean Std Mean std
1 96.0% 3.0% 88.0% 6.0%
2 96.0% 5.0% 34.0% 23.0%
3 94.0% 5.0% 74.0% 5.0%
5.2.1 Experiment 1
All of pieces and boards were constrained to a uni-
form height for this experiment. Both the PPO and
MaxRect-Bl algorithms achieved complete coverage
(100%) of the boards, as demonstrated in Figure 5.
The green regions highlight the optimal placements
determined by the algorithms during the packing pro-
cess.
Figure 5: Experiment 1 - All of pieces and boards were
constrained to a uniform height for this experiment.
5.2.2 Experiment 2
Both PPO and MaxRect-BL achieved 100% cover-
age. However, MaxRect-BL’s optimal performance
was contingent on a specific piece sorting strategy:
first by descending height, then by descending dimen-
sions. The BFDH heuristic could also achieve optimal
performance. Figure 6 shows the convergence behav-
ior of the experiment.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
506

Figure 6: Experiment 2 - board 1 taller than board 2.
Without sorting by height, the MaxRect-BL fails
to converge as effectively, as indicated in Figure 7.
This occurs because MaxRect-BL initially places 8
Pieces 1 (with R
height
= 2) and 8 Pieces 2 (with
R
height
= 1), which fill all the available space on
board 0. It then attempts to add 16 Pieces 3 (whose
height exceeds the board’s height, causing them to be
skipped) and finally places 16 Pieces 4 (with R
height
=
2) on board 1. The yellow areas highlight suboptimal
placement choices resulting from R
height
< 2, while
the white areas represent unused space on the board.
Figure 7: Experiment 2 without order pieces for MaxRect-
BL.
5.2.3 Experiment 3
In this experiment, both PPO and MaxRect-BL
achieved 100% coverage. While MaxRect-BL re-
quired a specific piece sorting strategy (ascending
height, descending dimensions) for optimal perfor-
mance, the BFDH heuristic could also achieve opti-
mal results in this scenario. Figure 8 illustrates the
convergence behavior of the experiment.
Without sorting by height, the MaxRect-BL fails
to converge as effectively, as indicated in Figure 9.
Figure 8: Experiment 3 - board 2 taller than board 1.
This occurs because MaxRect-BL first attempts to
place 8 Pieces 1 (whose height exceeds the board’s
limit, causing them to be skipped), but successfully
adds 8 Pieces 2 (with R
height
= 2). It then tries to
add 16 Pieces 3 (again skipped due to their excessive
height) and finally places 16 Pieces 4 (which meet the
optimal condition of R
height
= 2) on board 0.
Figure 9: Experiment 3 without order pieces for MaxRect-
BL.
5.3 Odd Boards
Figure 10 illustrates the evaluation curves for 10 inde-
pendent PPO runs across the three experimental con-
ditions. These experiments demonstrated optimal per-
formance by achieving the maximum reward through
100% correct board fillings. Negative reward values
signify incorrect board configurations.
Figure 11 presents the curves depicting the mean
episode length across 10 independent PPO runs un-
der the three experimental conditions. These re-
sults highlight the progression of the mean episode
length throughout iterations, providing insights into
the agent’s performance dynamics and its efficiency
in solving the problem. The optimal episode length
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning
507

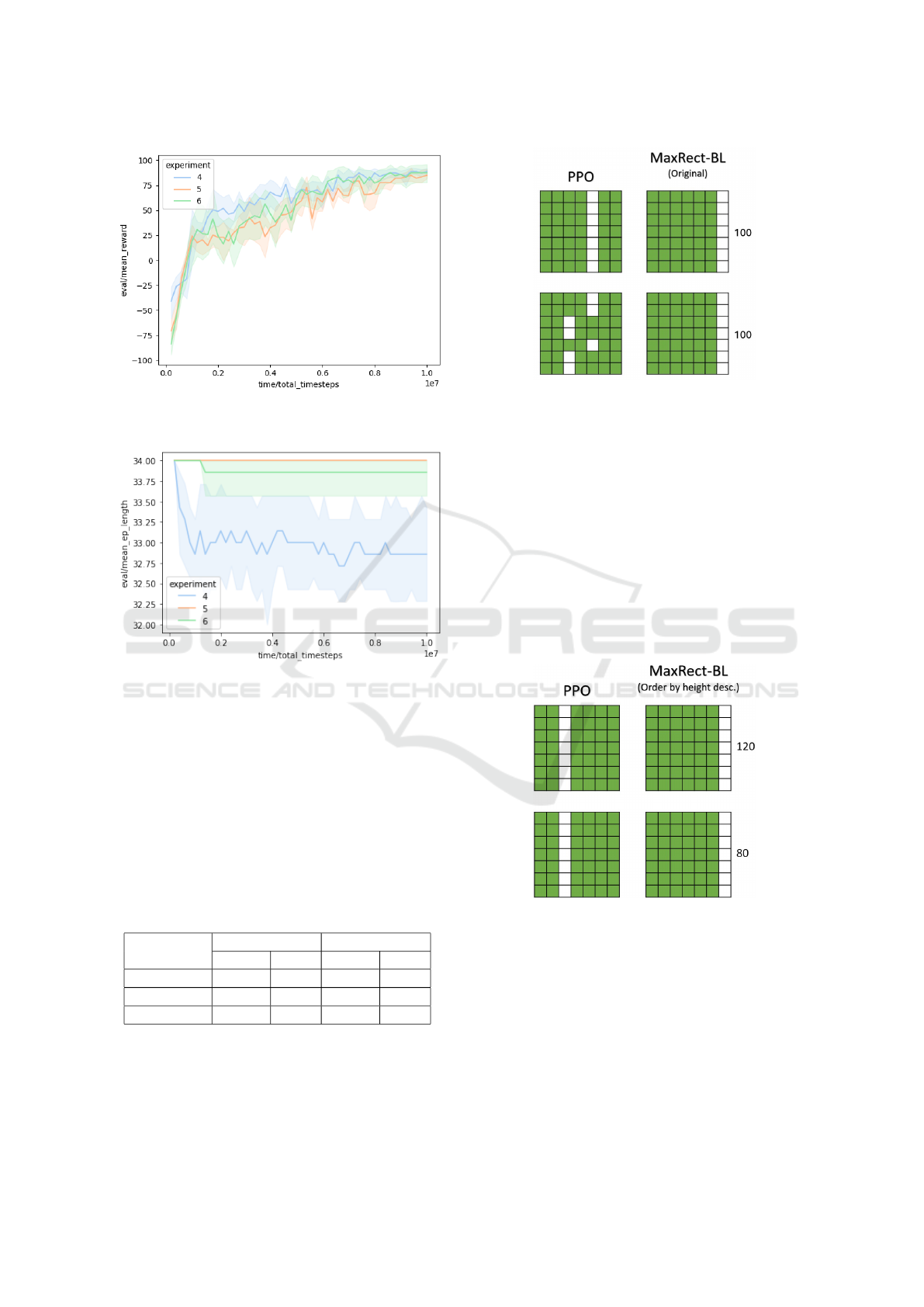
Figure 10: Evaluation curves of the three odd experiments
using PPO.
Figure 11: Mean episode length over odd experiments using
PPO.
occurs approximately when the maximum number of
pieces is successfully packed onto a board.
In these experiments, it was again possible to ob-
serve that A2C method achieved an inferior perfor-
mance when compared to PPO method. We selected
4 results from each experimental condition to com-
pare these RL methods. Table 4 contains the mean
percentage of correct board fills (Mean) and its stan-
dard deviation (Std).
Table 4: Comparative analysis between PPO and A2C
methods for correct board fills.
experiment
PPO A2C
Mean Std Mean Std
4 97.0% 3.0% 82.0% 8.0%
5 97.0% 3.0% 88.0% 4.0%
6 97.0% 4.0% 81.0% 8.0%
5.3.1 Experiment 4
All of pieces and boards were constrained to a uni-
form height for this experiment.
Figure 12: Experiment 4 - All of pieces and boards were
constrained to a uniform height for this experiment.
Both the PPO and MaxRect-Bl algorithms
achieved complete coverage (100%) of the boards, as
demonstrated in Figure 12. The green regions high-
light the optimal placements determined by the algo-
rithms during the packing process.
5.3.2 Experiment 5
PPO and MaxRect-Bl (ordered by height descending)
successfully placed all pieces. MaxRect-BL exhibits
the same limitations as in Experiment 2 without this
ordering. Figure 13 shows the convergence behavior
of the experiment.
Figure 13: Experiment 5 - board 1 taller than board 2.
5.3.3 Experiment 6
PPO and MaxRect-Bl (ordered by height ascending)
successfully placed all pieces. MaxRect-BL exhibits
the same limitations as in Experiment 3 without this
ordering. Figure 14 shows the convergence behavior
of the experiment.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
508

Figure 14: Experiment 6 - board 2 taller than board 1.
6 CONCLUSIONS
This paper proposed a 2D+1 simulator, and devel-
oped a spatially constrained packing problem within
the OpenAI Gymnasium framework, for the pack-
ing problem in the offline approach. This simulator
employs an observation space comprising two boards
and four different types of pieces and their associated
quantities. It supports multi-discrete action space, al-
lowing the selection of a position on a specific board
and the choice of a piece to place. Furthermore, this
paper introduced a new spatial-variant reward func-
tion that maximizes coverage by considering both di-
mension and height of the pieces.
This research conducted a literature review fo-
cused on deep reinforcement learning solutions for
the 2D regular packing problem. Since 2018, pub-
lications involving DRL for this type of problem have
attracted the attention of researchers; however, there
are still research gaps, such as the use of on-policy
actor-critic methods for the target task.
In the performed experiments, it was possible to
observe that PPO and MaxRect-BL (with height or-
dering) have correctly allocated all of the pieces.
However, MaxRect-BL without height ordering ex-
hibited poorer performance, as illustrated in Figures
7 and 9. As the problem complexity increases (e.g.,
multiple boards), the effectiveness of simple heuris-
tics like height-based ordering diminishes. While the
BFDH heuristic is viable for packing items, PPO’s
ability to learn and adapt dynamically through explo-
ration and exploitation provides a more flexible and
potentially superior solution. The A2C did not show
better results than PPO in the experiments.
As future work, to enhance the simulator’s fidelity
as a digital representation of an aerospace industry au-
toclave for composite material curing, we plan to im-
plement key improvements, including material alloca-
tion constraints to ensure accurate material placement
based on specific curing types, thus reflecting real-
world production processes. Additionally, we will
integrate thermocouple and pressure sensor simula-
tions to capture precise temperature and pressure con-
ditions within the autoclave, providing valuable data
for process optimization and quality control. Further-
more, a mechanism will be added to simulate material
delivery deadlines, ensuring the simulator reflects the
time-sensitive nature of production operations. These
enhancements will result in a more comprehensive
and realistic model of the autoclave curing process,
enabling engineers to conduct more effective simula-
tions and optimize production workflows.
ACKNOWLEDGEMENTS
The authors would like to thank the National Coun-
cil for Scientific and Technological Development
(CNPq) for granting a scholarship to Victor Pugliese
through the Academic Master’s and Doctorate Pro-
gram in Innovation (MAI/DAI) in collaboration with
the EMBRAER S.A. company.
REFERENCES
Alem
˜
ao, D., Rocha, A. D., and Barata, J. (2021). Smart
manufacturing scheduling approaches—systematic
review and future directions. Applied Sciences,
11(5):2186.
Ao, W., Zhang, G., Li, Y., and Jin, D. (2023). Learning to
solve grouped 2d bin packing problems in the manu-
facturing industry. In Proceedings of the 29th ACM
SIGKDD Conference on Knowledge Discovery and
Data Mining, pages 3713–3723.
Azami, A. (2016). Scheduling Hybrid Flow Lines of
Aerospace Composite Manufacturing Systems. PhD
thesis, Concordia University.
Azami, A., Demirli, K., and Bhuiyan, N. (2018). Schedul-
ing in aerospace composite manufacturing systems: a
two-stage hybrid flow shop problem. The Interna-
tional Journal of Advanced Manufacturing Technol-
ogy, 95:3259–3274.
Cheng, C.-A., Kolobov, A., and Swaminathan, A. (2021).
Heuristic-guided reinforcement learning. Advances
in Neural Information Processing Systems, 34:13550–
13563.
Collart, A. (2015). An application of mathematical op-
timization to autoclave packing and scheduling in a
composites manufacturing facility.
Crescitelli, V. and Oshima, T. (2023). A deep reinforce-
ment learning method for 2d irregular packing with
dense reward. In 2023 Fifth International Confer-
ence on Transdisciplinary AI (TransAI), pages 270–
271. IEEE.
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning
509

Elkington, M., Bloom, D., Ward, C., Chatzimichali, A.,
and Potter, K. (2015). Hand layup: understanding the
manual process. Advanced manufacturing: polymer
& composites science, 1(3):138–151.
Fang, J., Rao, Y., Ding, W., and Meng, R. (2022). Research
on two-dimensional intelligent nesting based on sarsa-
learning. In 2022 5th International Conference on Ad-
vanced Electronic Materials, Computers and Software
Engineering (AEMCSE), pages 826–829. IEEE.
Fang, J., Rao, Y., Guo, X., and Zhao, X. (2021). A rein-
forcement learning algorithm for two-dimensional ir-
regular packing problems. In Proceedings of the 2021
4th International Conference on Algorithms, Comput-
ing and Artificial Intelligence, pages 1–6.
Fang, J., Rao, Y., and Shi, M. (2023a). A deep reinforce-
ment learning algorithm for the rectangular strip pack-
ing problem. Plos one, 18(3):e0282598.
Fang, J., Rao, Y., Zhao, X., and Du, B. (2023b). A hy-
brid reinforcement learning algorithm for 2d irregular
packing problems. Mathematics, 11(2):327.
Haskilic, V., Ulucan, A., Atici, K. B., and Sarac, S. B.
(2023). A real-world case of autoclave loading and
scheduling problems in aerospace composite material
production. Omega, page 102918.
Huang, S., Kanervisto, A., Raffin, A., Wang, W., Onta
˜
n
´
on,
S., and Dossa, R. F. J. (2022). A2c is a special case of
ppo. arXiv preprint arXiv:2205.09123.
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).
Reinforcement learning: A survey. Journal of artifi-
cial intelligence research, 4:237–285.
Keras, F. (2022). PPO proximal policy optimization.
Kundu, O., Dutta, S., and Kumar, S. (2019). Deep-pack:
A vision-based 2d online bin packing algorithm with
deep reinforcement learning. In 2019 28th IEEE Inter-
national Conference on Robot and Human Interactive
Communication (RO-MAN), pages 1–7. IEEE.
Li, D., Gu, Z., Wang, Y., Ren, C., and Lau, F. C. (2022).
One model packs thousands of items with recurrent
conditional query learning. Knowledge-Based Sys-
tems, 235:107683.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In International conference on machine learning,
pages 1928–1937. PMLR.
Oliveira, J. F., Neuenfeldt, A., Silva, E., and Carrav-
illa, M. A. (2016). A survey on heuristics for the
two-dimensional rectangular strip packing problem.
Pesquisa Operacional, 36(2):197–226.
Puche, A. V. and Lee, S. (2022). Online 3d bin packing
reinforcement learning solution with buffer. In 2022
ieee/rsj international conference on intelligent robots
and systems (iros), pages 8902–8909. IEEE.
Ramezankhani, M., Crawford, B., Narayan, A., Voggenre-
iter, H., Seethaler, R., and Milani, A. S. (2021). Mak-
ing costly manufacturing smart with transfer learning
under limited data: A case study on composites auto-
clave processing. Journal of Manufacturing Systems,
59:345–354.
S
´
aenz Imbacu
´
an, R. (2020). Evaluating the impact of cur-
riculum learning on the training process for an intelli-
gent agent in a video game.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
510

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and
Klimov, O. (2017). Proximal policy optimization al-
gorithms. arXiv preprint arXiv:1707.06347.
Seizinger, M. (2018). The two dimensional bin packing
problem with side constraints. In Operations Research
Proceedings 2017: Selected Papers of the Annual In-
ternational Conference of the German Operations Re-
search Society (GOR), Freie Universi
¨
at Berlin, Ger-
many, September 6-8, 2017, pages 45–50. Springer.
Sun, Y., Yuan, X., Liu, W., and Sun, C. (2019). Model-
based reinforcement learning via proximal policy op-
timization. In 2019 Chinese Automation Congress
(CAC), pages 4736–4740. IEEE.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Wang, X., Thomas, J. D., Piechocki, R. J., Kapoor, S.,
Santos-Rodr
´
ıguez, R., and Parekh, A. (2022). Self-
play learning strategies for resource assignment in
open-ran networks. Computer Networks, 206:108682.
Wu, Y. and Yao, L. (2021). Research on the problem of 3d
bin packing under incomplete information based on
deep reinforcement learning. In 2021 International
conference on e-commerce and e-management (ICE-
CEM), pages 38–42. IEEE.
Xia, K., Sacco, C., Kirkpatrick, M., Saidy, C., Nguyen,
L., Kircaliali, A., and Harik, R. (2021). A digital
twin to train deep reinforcement learning agent for
smart manufacturing plants: Environment, interfaces
and intelligence. Journal of Manufacturing Systems,
58:210–230.
Xie, N., Zheng, S., and Wu, Q. (2020). Two-dimensional
packing algorithm for autoclave molding scheduling
of aeronautical composite materials production. Com-
puters & Industrial Engineering, 146:106599.
Yang, Z., Pan, Z., Li, M., Wu, K., and Gao, X. (2023).
Learning based 2d irregular shape packing. ACM
Transactions on Graphics (TOG), 42(6):1–16.
Zhang, Y., Bai, R., Qu, R., Tu, C., and Jin, J. (2022). A deep
reinforcement learning based hyper-heuristic for com-
binatorial optimisation with uncertainties. European
Journal of Operational Research, 300(2):418–427.
Zhao, H., Zhu, C., Xu, X., Huang, H., and Xu, K. (2022a).
Learning practically feasible policies for online 3d
bin packing. Science China Information Sciences,
65(1):112105.
Zhao, X., Rao, Y., and Fang, J. (2022b). A reinforcement
learning algorithm for the 2d-rectangular strip packing
problem. In Journal of Physics: Conference Series,
volume 2181, page 012002. IOP Publishing.
Zhu, K., Ji, N., and Li, X. D. (2020). Hybrid heuristic
algorithm based on improved rules & reinforcement
learning for 2d strip packing problem. IEEE Access,
8:226784–226796.
Zuo, Q., Liu, X., Xu, L., Xiao, L., Xu, C., Liu, J., and Chan,
W. K. V. (2022). The three-dimensional bin pack-
ing problem for deformable items. In 2022 IEEE In-
ternational Conference on Industrial Engineering and
Engineering Management (IEEM), pages 0911–0918.
IEEE.
Optimizing 2D+1 Packing in Constrained Environments Using Deep Reinforcement Learning
511