Toward Designing a Reduced Phone Set Using Text Decoding Accuracy

Estimates in Speech BCI

Shuji Komeiji

1 a

, Koichi Shinoda

2 b

and Toshihisa Tanaka

1 c

Department of Electronic and Information Engineering, Tokyo University of Agriculture and Technology, Naka-cho,

Koganei-shi, Tokyo, Japan

Department of Computer Science, Tokyo Institute of Technology, Japan

Keywords:

Speech BCI, GPWCR, PWCR, Automatic Speech Recognition, Phone Set.

Abstract:

Reducing the phone set in speech recognition or speech brain-computer interface (BCI) tasks improves phone

discrimination accuracy. This reduction may also degrade text decoding accuracy due to increased homonyms.

To address this, we propose a novel estimator called the Generalized Pronunciation/Word Confusion Rate

(GPWCR), which estimates text decoding accuracy by considering both phone discrimination performance

and the number of homonyms. By minimizing the GPWCR, we designed the optimal reduced phone set.

Experimental results from Japanese large vocabulary speech recognition demonstrate that the optimal phone

set, reduced from 39 to 38 phones, lowered the word error rate from 14.1% to 13.8%.

1 INTRODUCTION

Speech brain–computer interface (BCI) is a tech-

nique to decode text or speech from brain activity

associated with language processing (Martin et al.,

2016; Moses et al., 2018; Akbari et al., 2019; Sun

et al., 2020; Makin et al., 2020; Angrick et al.,

2021; Proix et al., 2022; Komeiji et al., 2022; Wil-

lett et al., 2023; Komeiji et al., 2024; Card et al.,

2024). These interfaces are expected to serve as re-

habilitation tools for damage or degeneration of mo-

tor pathways necessary for speech, such as in stroke,

aphasia, or amyotrophic lateral sclerosis (Luo et al.,

2023), and as next-generation communication de-

vices. To develop speech BCIs, such as those for de-

coding text from neural signals, previous studies have

adopted methodologies from automatic speech recog-

nition (ASR) (Herff et al., 2015; Moses et al., 2018;

Willett et al., 2023). Since the 2010s, ASR has shifted

to directly mapping speech features (mel-frequency

cepstral coefﬁcients) to text, a method known as the

end-to-end (E2E) neural network model, which has

become the de facto standard for ASR. This differs

from traditional ASR, which typically involves two

distinct models: an acoustic model (AM) and a lan-

https://orcid.org/0009-0004-9514-0424

https://orcid.org/0000-0003-1095-3203

https://orcid.org/0000-0002-5056-9508

guage model (LM), where text is decoded by estimat-

ing phones. Speech BCI research has also adopted

this trend, with E2E models being successfully ap-

plied in recent studies (Makin et al., 2020; Komeiji

et al., 2024).

Despite the popularity of E2E models, traditional

ASR systems, which consist of an AM and an LM, re-

main crucial in speech BCI research, where decoding

text by estimating phones (a two-step decoding pro-

cess) is still widely used. This approach allows for

analyzing the relationship between neural signals and

phones, an area that is not yet fully understood, un-

like the well-established relationship between acous-

tic signals and phones in ASR. For example, Wil-

lett et al. (Willett et al., 2023) demonstrated phone

estimation from neural signals using recurrent neu-

ral networks (RNNs) as an AM and sentence con-

struction using n-gram models as an LM. Their ﬁnd-

ings revealed that the neural representations learned

by RNNs resemble the geometric structure of articu-

latory representations of phones.

This insight highlights the continued importance

of applying traditional ASR methods (two-step de-

coding) to speech BCI. By leveraging these tech-

niques, researchers can gain valuable insights into

the neural basis of speech production and poten-

tially improve the accuracy and robustness of speech

BCIs. Our study aims to further explore this ap-

proach, building upon the foundations laid by previ-

980

Komeiji, S., Shinoda, K. and Tanaka, T.

Toward Designing a Reduced Phone Set Using Text Decoding Accuracy Estimates in Speech BCI.

DOI: 10.5220/0013265800003911

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 18th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2025) - Volume 1, pages 980-987

ISBN: 978-989-758-731-3; ISSN: 2184-4305

ous research in both ASR and speech BCI ﬁelds.

To construct text decoding through phone estima-

tion, deﬁning an appropriate phone set is a critical

step. This step is fundamental in developing an ef-

fective two-step decoding process for speech BCI.

Previous research on phone set deﬁnitions for ASR

tasks has shown that redesigning the phone set can

lead to increased recognition accuracy (Vazhenina

and Markov, 2011; Oh et al., 2021), despite typi-

cal sets being based on linguistically deﬁned phonetic

dictionaries. For example, in multilingual ASR tasks,

multilingual phone sets are designed by synthesizing

phones from multiple languages (Hara and Nishizaki,

2017; Sivasankaran et al., 2018). In ASR tasks for

non-native speakers, reduced phone sets improved

recognition accuracy (Wang et al., 2014), while in

rare language ASR tasks, grouping low-frequency

phones enhanced performance (Davel et al., 2015;

Diwan and Jyothi, 2020). For speech BCI, Herff

et al. (Herff et al., 2015) used a reduced phone set

of 20, down from the original 39, by grouping sim-

ilar phones. Komeiji et al. (Komeiji and Tanaka,

2019) introduced a novel approach by considering

homonyms increased by phone set reduction, using a

metric called pronunciation/word sequence confusion

rate (PWCR), calculated with the occurrence proba-

bility of n-grams in an LM.

However, PWCR does not account for phone sim-

ilarity, which may result in the unintended grouping

of acoustically or neurally similar phones, as Wil-

lett et al. (Willett et al., 2023) revealed phone simi-

larities in neural signals. To address this limitation,

we propose a generalization of PWCR that considers

both phone “similarity” and LMs. This generalized

PWCR (GPWCR) provides a more appropriate esti-

mate when evaluating the trade-off between improved

accuracy by reducing phone confusion and reduced

accuracy due to an increased number of homonyms

via phone set reduction. This trade-off suggests the

existence of a minimal GPWCR, where the opti-

mal reduced phone set can be designed, whereas the

conventional PWCR increases monotonically as the

phone set size decreases. To conceptually evaluate

the reduced phone set designed by minimizing GP-

WCR, we conducted experiments on an ASR task.

The phone set by minimizing GPWCR reduced from

39 to 38 phones, lowering the word error rate (WER)

from 14.1% to 13.8%.

2 PHONE SET REDUCTION

2.1 Conventional Research on Phone

Set Reduction

Given a phone set, some acoustically “similar”

phones can be considered a single phone. Using

this, we can obtain a reduced phone set, which has a

smaller number of phones than the original phone set.

The “similarity” is key to generating a reduced phone

set, as similar phones are easily confused and can de-

grade ASR accuracy. The similarity between these

phones can be determined using the Bhattacharyya

distance (Mak and Barnard, 1996).

Conventionally, some studies introduced reduced

phone sets to improve recognition accuracy. For ex-

ample, the accuracy of the Russian ASR was im-

proved by reducing the phone set (Vazhenina and

Markov, 2011). Phone recognition was used to create

a phone confusion matrix, and the phone sets were re-

duced by merging phone pairs with the highest phone

confusion rate. Moreover, there are several publica-

tions on multilingual ASR tasks. For example, Hara et

al. (Hara and Nishizaki, 2017) merged common inter-

national phonetic alphabet (IPA) phones across mul-

tiple languages to design an AM, and Sivasankaran

et al. (Sivasankaran et al., 2018) merged confusing

phone pairs in phone recognition using a bilingual

phone set. In an English ASR task for native Japanese

speakers, phone set reduction was performed us-

ing decision tree clustering for context-independent

phones (Wang et al., 2014).

On the other hand, phone set reduction in a sin-

gle language has the disadvantage of increasing the

number of homonyms, which degrades the accuracy

of text decoding. For example, when the English

phonemes /d/ and /f/ are merged, the words “dish”

and “ﬁsh” become homonyms. This makes it difﬁ-

cult to differentiate them, especially in word recogni-

tion. Although Davel et al. (Davel et al., 2015) con-

sidered homonyms when reducing a phone set in rare

language ASR tasks, they did not measure the degree

to which homonyms affected ASR accuracy quanti-

tatively. To evaluate this, we proposed a PWCR cal-

culated using the occurrence probability of n-grams

in an LM in (Komeiji and Tanaka, 2019). Moreover,

we also proposed a new algorithm to design a reduced

phone set that prevents increases in the PWCR.

2.2 Pronunciation/Word Confusion

Rate (PWCR)

PWCR can determine the degradation of recognition

accuracy due to homonyms using the n-gram occur-

Toward Designing a Reduced Phone Set Using Text Decoding Accuracy Estimates in Speech BCI

981

rence probability of an LM and a pronunciation dic-

tionary. It is expressed by the following equation:

PWCR = 1 −

∑

W = w|

A = a)

× P(A = a|W = w)

× P(W = w), (1)

where w is the n-gram in the LM. In addition, a de-

notes a phone sequence. P(

W = w|

A = a) is the prob-

ability of obtaining n-gram w given the phone se-

quence a, P(A = a|W = w) is the probability of ob-

taining the phone sequence a given n-gram w, and

P(W = w) is the occurrence probability of the n-gram.

Equation (1) corresponds to estimates of the accuracy

of ASR when there are no errors in phone estimation.

2.3 PWCR-Based Reduction Algorithm

This section describes a PWCR-based phone set re-

duction algorithm. The goal is to ﬁnd a reduced phone

set that minimizes PWCR among any combination

of phone sets of size k obtained from a basic phone

set of size n. The number of combinations, which

follows the second-class Stirling number, grows ex-

tremely large as the size n of the basic phone set in-

creases. Computing PWCR for all these combina-

tions becomes impractical due to their astronomical

number. To address this computational challenge, a

greedy algorithm is applied to ﬁnd a reduced phone

set that gives an approximate minimum PWCR within

a realistic computational time. Speciﬁcally, the algo-

rithm iteratively ﬁnds phone sets of size k that mini-

mize PWCR using sets of size k + 1 until the desired

size is reached.

PWCR is calculated from an LM and formulates

only the accuracy degradation due to the increase in

homonyms; it does not consider confusion among

similar phones, which can lead to the grouping of con-

fusing phones. Therefore, while this algorithm can

reduce the phone set size, it is not guaranteed to ﬁnd

a set of phones that improves overall recognition ac-

curacy.

3 GENERALIZED

PRONUNCIATION WORD

CONFUSION RATE (GPWCR)

3.1 GPWCR

To address the limitation of PWCR in not considering

confusion among similar phones, we generalize the

PWCR to consider both the phone decoding and the

LM. This generalization is based on the error rate in

text decoding, given by:

R = 1 −

∑

W = w, W = w), (2)

where W is a sequence of reference words and

W is

a sequence of recognized words. The probability of

W , W) is the joint probability of W and

W , and the

total probability of W = w and

W = w is the correct

answer rate for text decoder. The correct answer rate

is subtracted from 1 because eq. (2) represents an er-

ror rate.

We reconsider the error rate in eq. (2) in general-

izing the PWCR. First, we restrict the sequences of

words W and

W represent n-grams in the LM. Since

eq. (2) is in an abstract form (i.e., W can represent all

possible word sequences), calculating the error rate R

is difﬁcult. Second, a phone sequence A derived from

the correct word sequence W and a sequence of rec-

ognized phones

A are introduced as latent variables.

Then, eq. (2) is rewritten using W ,

W , A, and

A to

deﬁne the GPWCR as follows:

GPWCR = 1 −

∑

ˆa

∑

W = w,

A = ˆa, A = a, W = w).

(3)

Considering that the data ﬂow of information in actual

text decoding is W → A, A →

A →

W , the joint

probability in eq. (3) can be expressed as the product

of four probabilities:

GPWCR = 1 −

∑

ˆa

∑

W = w|

A = a)

× P(

A = ˆa|A = a)

× P(A = a|W = w)

× P(W = w), (4)

where P(

W |

A) is the probability of getting a word

sequence from the phone sequence. Note that GP-

WCR increases as the number of homonyms in-

creases. Also, P(

A|A) is the probability of getting a

recognized phone sequence from the correct phone

sequence, and GPWCR increases as the number of

phone errors increases. In eq. (4), the case where no

phonetic errors are assumed: P(

A = a|A = a) = 1 cor-

responds to PWCR in eq. (1).

3.2 Derivation of Probability P(

A|A)

Unlike PWCR, the derivation of GPWCR requires

an additional calculation of the probability P(

A|A).

There are degrees of freedom to choose P(

A|A). In

this paper, we deﬁne P(

A|A) as the total cost of

dynamic programming (DP) matching between the

phone sequences a and ˆa. Each DP matching cost

is the negative logarithmic probability − logP( ˆp =

BIOSIGNALS 2025 - 18th International Conference on Bio-inspired Systems and Signal Processing

982

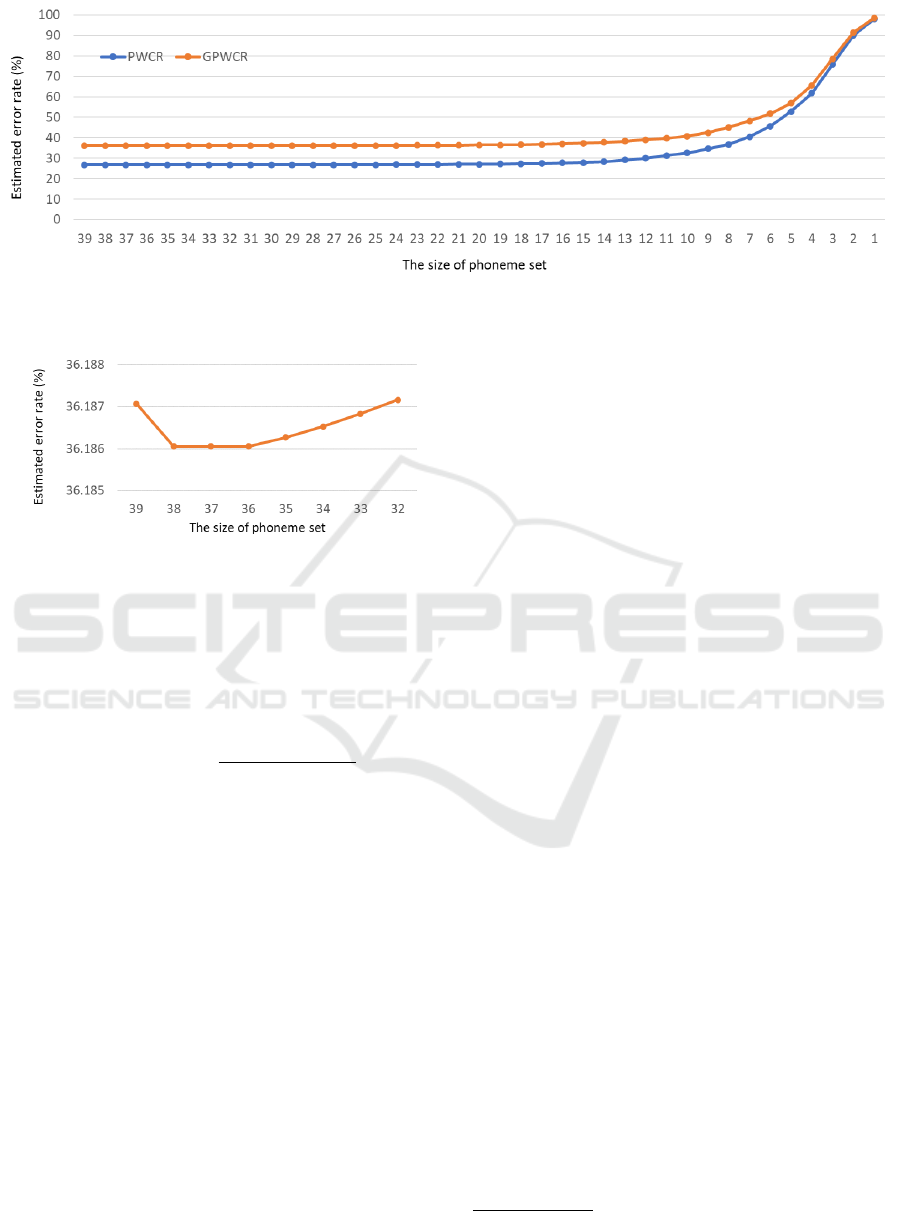
Figure 1: Relationship between the size of the reduced phone set, PWCR, and GPWCR.

Figure 2: Relationship between the size of the reduced

phone set, GPWCR (in detail).

|p = x

) of getting a phone y

from a phone x

where a = {x

, x

, ..., x

} and ˆa = {y

, y

, ..., y

When the total cost of DP matching is expressed by

S( ˆa, a), then P(

A = a|A = a) is given by the follow-

ing:

A = ˆa|A = a) =

exp(−S( ˆa, a))

∑

˜a

exp(−S( ˜a, a))

. (5)

For example, probability P( ˆp|p) can be calculated

from phone recognition results by creating a phone

confusion matrix.

3.3 Relationship Between Reduced

Phone Set and GPWCR

According to eq. (4), reducing the number of phones

tends to reduce the phone estimation errors, thereby

increasing the probability of P(

A = a|A = a). On

the other hand, it tends to increase the number

of homonyms, thereby reducing the probability of

P( ˆw = w|

A = a). While the conventional PWCR in-

creases monotonically as the number of phones de-

creases, making it impossible to identify an optimal

phone set, GPWCR can reach a minimum value by

balancing this trade-off. Therefore, to ﬁnd the opti-

mal phone set, we should minimize the GPWCR.

4 EXPERIMENT

The experimental setup is explained, followed by ap-

plying the algorithm (Section 2.3) based on PWCR

and GPWCR to obtain reduced phone sets. These re-

duced phone sets are evaluated using Japanese large-

vocabulary continuous ASR to assess their impact on

recognition accuracy. This experiment focuses on val-

idating the concept of GPWCR. While our ultimate

goal is to apply this method to speech BCI tasks, we

use ASR for this initial validation due to its well-

established evaluation metrics and the availability of

large-scale datasets.

4.1 Experimental Setup

In the experiment, the corpus of spontaneous

Japanese (CSJ) (Furui et al., 2000) and an open-

source toolkit called Kaldi (Povey et al., 2011) were

used for training and evaluation. To use the CSJ for

training/evaluation in Kaldi, the Kaldi-CSJ recipe was

used (Moriya et al., 2015)

. The Kaldi-CSJ recipe

uses 240 hours of lecture speech recordings as train-

ing data for the AM. The recipe is designed to train

“Gaussian mixture model” - “Hidden Markov model”

(GMM-HMM) and ﬁnally train “time-delay neural

networks” - HMM (TDNN-HMM) (Peddinti et al.,

2015; Povey et al., 2016). In this experiment, we

assumed a small training data task and reduced the

training data to 1/16, which is about 15 hours.

In the recipe, about 450,000 sentences accompa-

nied by 240 hours of training data in the CSJ were

used for the LM training. The Kneser-Ney smoothing

method was also applied. The unigram in the LM was

used to calculate PWCR and GPWCR. The number of

unigrams was 71,940. The basic phone set consists of

https://github.com/kaldi-

asr/kaldi/blob/master/egs/csj/s5/run.sh

Toward Designing a Reduced Phone Set Using Text Decoding Accuracy Estimates in Speech BCI

983

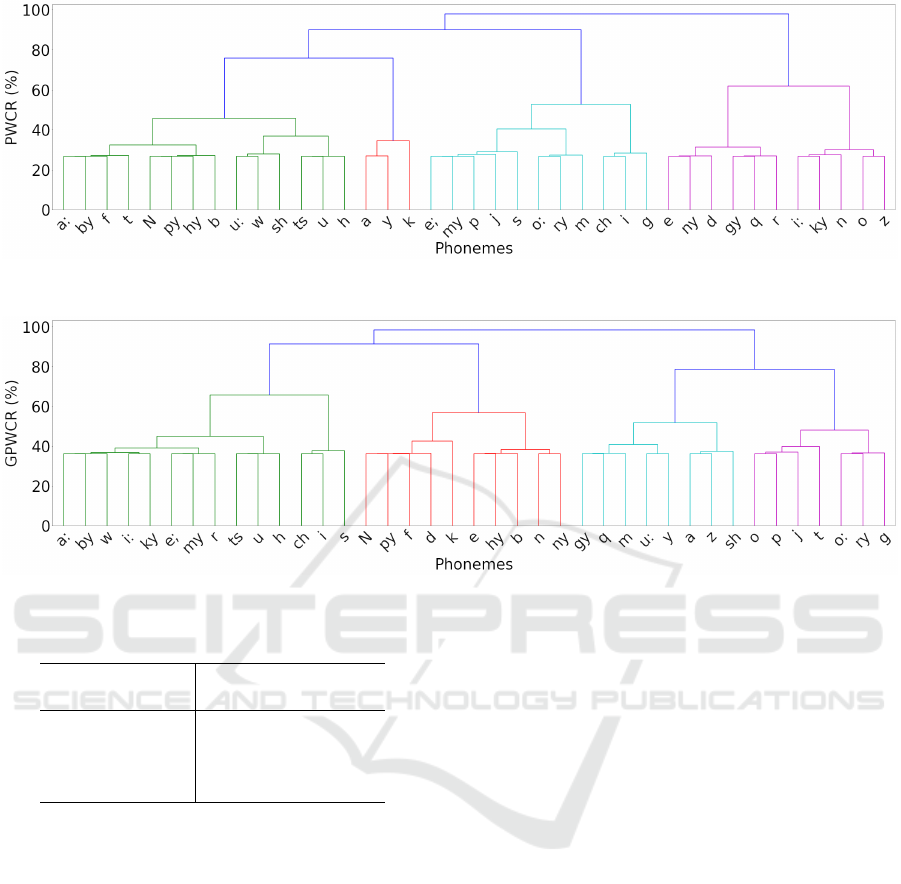
Figure 3: Phone compilation based on PWCR.

Figure 4: Phone compilation based on GPWCR.

Table 1: Basic phoneme set in Kaldi-CSJ recipes.

Vowels (10) a, e, i, o, u

a:, e:, i:, o:, u:

Consonants (29) b, ch, d, f, g, h, j, k,

m, n, N, p, q, r, s, sh,

t, ts, w, y, z, by, gy,

hy, ky, my, ny, py, ry

the 39 phonemes listed in Table 1.

The CSJ standard evaluation sets Eval1, Eval2,

and Eval3 (10 talks each) were used for recognition

evaluation. The recognition process is based on a

weighted ﬁnite state transducer (WFST) (Mohri et al.,

2002).

Probability P(

A|A) in the GPWCR was derived

from a phone confusion matrix, which was created

from the phone recognition results of Eval1 using the

GMM-HMM obtained during the learning process in

the recipe.

4.2 A Comparison of PWCR and

GPWCR

The relationship between the size of the reduced

phone set, PWCR, and GPWCR, is shown in Fig. 1. It

can be seen that the GPWCR has a higher value than

the PWCR. The reason for this is that the GPWCR is a

recognition accuracy estimate that also takes phonetic

errors into account.

Moreover, the PWCR increases monotonically as

the number of phones decreases. On the other hand,

GPWCR has a minimum value (see Fig. 2). Figure 2

is a zoomed-in view of the GPWCR values from 32

to 39 phones. Reduced phone sets with sizes 36 to

38 for the GPWCR are expected to achieve improved

recognition accuracy over the basic phone set with a

size of 39.

The behavior of the reducing process based on the

PWCR and the GPWCR is shown in Figs. 3 and 4, re-

spectively. The horizontal axis represents each phone

and the vertical axis represents the PWCR and GP-

WCR values. In the GPWCR, acoustically similar

phones such as /n/ and /ny/ are grouped when reduc-

ing the size from 39 to 38. On the other hand, it can be

seen from Fig. 4 that acoustically similar phones are

not always grouped in other reducing processes. This

is because merging phones that are acoustically simi-

lar to each other increases the number of homonyms.

4.3 ASR Evaluation

The reduced phone sets obtained in Section 4.2

were applied to actual Japanese large-vocabulary

BIOSIGNALS 2025 - 18th International Conference on Bio-inspired Systems and Signal Processing

984

Table 2: WERs (%) when the reduced phone sets are ap-

plied. The numbers in parentheses show the signiﬁcance

probability (%) of the bootstrap test compared to the accu-

racy of the baseline. Note that these values represent WERs,

not PWCR or GPWCR.

Size Metric Eval1 Eval2 Eval3 AVG

39 Baseline 15.48 12.26 14.71 14.07

38 PWCR 15.08 12.19 14.78 13.91

(98.6) (65.4) (37.4) (93.1)

GPWCR 14.82 12.01 14.84 13.75

(100.0) (93.7) (27.8) (99.8)

37 PWCR 15.07 11.98 14.69 13.80

(98.7) (95.8) (52.5) (99.3)

GPWCR 15.13 12.07 14.83 13.89

(97.6) (88.0) (29.0) (94.7)

36 PWCR 15.33 12.22 14.86 14.03

(79.6) (58.6) (25.3) (62.7)

GPWCR 15.36 12.37 14.75 14.07

(75.1) (26.2) (43.2) (49.3)

35 PWCR 15.26 11.86 14.79 13.85

(89.6) (99.2) (36.2) (97.5)

GPWCR 15.20 12.14 14.89 13.96

(93.3) (75.3) (21.6) (82.9)

18 PWCR 15.99 12.85 15.43 14.66

1(0.4) (0.1) (0.2) (0.0)

GPWCR 15.97 12.52 15.42 14.52

(0.7) (6.7) (0.2) (0.0)

10 PWCR 17.85 14.28 17.64 16.44

(0.0) (0.0) (0.0) (0.0)

GPWCR 17.77 14.43 18.12 16.58

(0.0) (0.0) (0.0) (0.0)

continuous ASR. The process for applying reduced

phone sets is just replacing phone symbols in the

word/pronunciation dictionary used in the Kaldi-CSJ

recipe and training TDNN-HMM from scratch using

the dictionary. The following phone sets were evalu-

ated: the basic phone set of size 39 for baseline, the

reduced phone sets of sizes from 36 to 38 with smaller

GPWCR than the basic phone set, and the extremely

reduced phone sets of sizes 10 and 18 (Komeiji and

Tanaka, 2019).

The results are shown in Table 2 as the WER for

each recognition accuracy. The numbers in parenthe-

ses in the table show the signiﬁcance probability in

the bootstrap test when compared with the baseline

WER. Eval1–Eval3 are the CSJ standard evaluation

set consisting of 10 speeches each, and AVG is the

average of these values. According to Table 2, the

baseline WERs are 15.48%, 12.26%, and 14.71% for

Eval1, Eval2, and Eval3, respectively. These values

are approximately 50% worse than the baseline WER

reported in (Komeiji and Tanaka, 2019), due to the

reduction of training data from 240 hours to 15 hours.

Table 2 shows that both the PWCR and GPWCR

for phone set sizes 36 to 38 generally achieve bet-

ter WERs compared to the baseline. This indicates

that both PWCR and GPWCR effectively reduced the

phone set size. The GPWCR was not always more

accurate than the PWCR. The advantage of using GP-

WCR did not manifest in this task because the differ-

ence between the GPWCR minima and the GPWCR

of the basic phone set was very small. Even when

the number of phones was reduced to extremely small

sizes (i.e., 10 or 18), the GPWCR achieved almost the

same WER as the PWCR.

5 DISCUSSION

In this section, we ﬁrst discuss the effectiveness of

using an LM for reducing the phoneme set size as de-

termined by PWCR or GPWCR, while maintaining

minimal degradation. Second, we highlight the pri-

mary contribution of this paper.

Firstly, regarding the use of PWCR and GPWCR

for phone set reduction, it is surprising that we ob-

served that even with a signiﬁcant reduction in the

phoneme set size–from 39 down to 18 or even 10–

the degradation was kept within 3%. This remark-

able result indicates that the language model (LM)

is strong enough to compensate for the limited vari-

ation in phoneme sequences. In this paper, we em-

ployed an n-gram-based LM, but Transformer-based

LMs, such as the generative pretrained Transformer

(GPT) (Vaswani et al., 2017), (Brown et al., 2020)

known as large LM (LLM), have been highly success-

ful in natural language processing. Using an LLM,

which can handle longer sentence ranges, would

likely better compensate for phoneme sequence con-

fusions and prevent degradation in text decoding ac-

curacy, more so than the n-gram-based LM.

Secondly, the primary contribution of this paper

is that by using GPWCR, we were able to iden-

tify a minimum value in phone set reduction, which

could not be discovered using conventional PWCR.

Since PWCR increases monotonically as the number

of phones decreases, it is challenging to determine the

optimal phone set size. In contrast, GPWCR allows us

to determine the optimal reduction point, making this

a key contribution in this paper.

The small improvement in WER observed in our

experiments is likely due to the characteristics of the

Japanese language (Lu and Morgan, 2020), which

has many homonyms. Reducing the phone set based

on acoustic similarity in Japanese leads to an in-

crease in homonyms, which lowers text decoding ac-

curacy. For example, Komeiji et al. (Komeiji and

Tanaka, 2019) showed that in Japanese ASR, reduc-

ing the phone set based on acoustic similarity (Bhat-

tacharya distance) causes a sharp decline in accuracy

Toward Designing a Reduced Phone Set Using Text Decoding Accuracy Estimates in Speech BCI

985

even in early stages of reduction due to the prolif-

eration of homonyms. Consequently, although GP-

WCR is employed to reduce confusion arising from

both homonyms and phone similarity, in the case

of Japanese, merging similar phones ultimately in-

creases the number of homonyms. As a result, reduc-

ing the phone set using GPWCR yields results that

are similar to those obtained with PWCR, which only

accounts for homonym confusion. This suggests that

in Japanese, the inﬂuence of homonym proliferation

outweighs the beneﬁts of addressing phone similar-

ity when reducing the phone set. In contrast, for lan-

guages with fewer homonyms, such as English, it is

expected that greater phone reductions and larger im-

provements in WER can be achieved. For instance,

Wang et al. (Wang et al., 2014) demonstrated that by

merging similar phones, the number of phones for

non-native English speakers could be reduced from

41 to 27, improving word accuracy from 92.4% to

96.7%.

In the context of speech BCIs, previous stud-

ies by Moses et al. (Moses et al., 2016) and Wil-

lett et al. (Willett et al., 2023) assumed an English

phone set of size 39 for phone decoding. In contrast,

Herff et al. (Herff et al., 2015) reduced this set to

20 phones. Willett et al. (Willett et al., 2023) also

revealed that phone similarity in neural signals mir-

rors that in acoustic signals. This suggests that GP-

WCR, which accounts for confusability between sim-

ilar phones, could be more suitable for speech BCIs

than PWCR. In future work, we will validate the ef-

fectiveness of using a reduced phone set for speech

BCIs with GPWCR.

6 CONCLUSIONS

In this paper, we proposed a method for designing

a reduced phone set by estimating text decoding ac-

curacy using GPWCR. By minimizing GPWCR, we

were able to identify an optimal reduced phone set.

Our experiments on large Japanese vocabulary speech

recognition demonstrated that the phone set designed

with GPWCR, reduced from 39 to 38 phones, im-

proved the WER from 14.1% to 13.8%. In future

work, we aim to apply the proposed GPWCR method

to speech BCI tasks, where deriving phone similarity

from neural signals could enhance phone discrimina-

tion.

ACKNOWLEDGEMENTS

This work was supported in part by JSPS KAKENHI

20H00235 and 23H00548.

REFERENCES

Akbari, H., Khalighinejad, B., Herrero, J. L., Mehta, A. D.,

and Mesgarani, N. (2019). Towards reconstructing in-

telligible speech from the human auditory cortex. Sci-

entiﬁc reports, 9(1):874.

Angrick, M., Ottenhoff, M. C., Diener, L., Ivucic, D., Ivu-

cic, G., Goulis, S., Saal, J., Colon, A. J., Wagner, L.,

Krusienski, D. J., et al. (2021). Real-time synthesis of

imagined speech processes from minimally invasive

recordings of neural activity. Communications biol-

ogy, 4(1):1055.

Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D.,

Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,

Askell, A., et al. (2020). Language models are few-

shot learners. Advances in neural information pro-

cessing systems, 33:1877–1901.

Card, N. S., Wairagkar, M., Iacobacci, C., Hou, X., Singer-

Clark, T., Willett, F. R., Kunz, E. M., Fan, C., Vah-

dati Nia, M., Deo, D. R., et al. (2024). An accurate

and rapidly calibrating speech neuroprosthesis. New

England Journal of Medicine, 391(7):609–618.

Davel, M., Barnard, E., Heerden, C. v., Hartmann, W.,

Karakos, D., Schwartz, R., and Tsakalidis, S. (2015).

Exploring minimal pronunciation modeling for low

resource languages. In Sixteenth Annual Conference

of the International Speech Communication Associa-

tion.

Diwan, A. and Jyothi, P. (2020). Reduce and reconstruct:

ASR for low-resource phonetic languages. arXiv

preprint arXiv:2010.09322.

Furui, S., Maekawa, K., and Isahara, H. (2000). A

Japanese national project on spontaneous speech

corpus and processing technology. In ASR2000-

Automatic Speech Recognition: Challenges for the

New Millenium ISCA Tutorial and Research Workshop

(ITRW), pages 244–248.

Hara, S. and Nishizaki, H. (2017). Acoustic modeling with

a shared phoneme set for multilingual speech recogni-

tion without code-switching. In 2017 Asia-Paciﬁc Sig-

nal and Information Processing Association Annual

Summit and Conference (APSIPA ASC), pages 1617–

1620.

Herff, C., Heger, D., De Pesters, A., Telaar, D., Brunner,

P., Schalk, G., and Schultz, T. (2015). Brain-to-text:

decoding spoken phrases from phone representations

in the brain. Frontiers in Neuroscience, 9:217.

Komeiji, S., Mitsuhashi, T., Iimura, Y., Suzuki, H., Sug-

ano, H., Shinoda, K., and Tanaka, T. (2024). Feasi-

bility of decoding covert speech in ecog with a trans-

former trained on overt speech. Scientiﬁc Reports,

14(1):11491.

BIOSIGNALS 2025 - 18th International Conference on Bio-inspired Systems and Signal Processing

986

Komeiji, S., Shigemi, K., Mitsuhashi, T., Iimura, Y.,

Suzuki, H., Sugano, H., Shinoda, K., and Tanaka, T.

(2022). Transformer-based estimation of spoken sen-

tences using electrocorticography. In ICASSP 2022-

2022 IEEE International Conference on Acoustics,

Speech and Signal Processing (ICASSP), pages 1311–

1315. IEEE.

Komeiji, S. and Tanaka, T. (2019). A language model-based

design of reduced phoneme set for acoustic model.

In 2019 Asia-Paciﬁc Signal and Information Process-

ing Association Annual Summit and Conference (AP-

SIPA), pages 192–197.

Lu, Y. and Morgan, J. L. (2020). Homophone auditory pro-

cessing in cross-linguistic perspective. Proceedings of

the Linguistic Society of America, 5(1):529–542.

Luo, S., Rabbani, Q., and Crone, N. E. (2023). Brain-

computer interface: applications to speech decoding

and synthesis to augment communication. Neurother-

apeutics, 19(1):263–273.

Mak, B. and Barnard, E. (1996). Phone clustering using the

bhattacharyya distance. In Fourth International Con-

ference on Spoken Language Processing, volume 4,

pages 2005–2008.

Makin, J. G., Moses, D. A., and Chang, E. F. (2020). Ma-

chine translation of cortical activity to text with an

encoder–decoder framework. Technical report, Nature

Publishing Group.

Martin, S., Brunner, P., Iturrate, I., Mill

an, J. d. R., Schalk,

G., Knight, R. T., and Pasley, B. N. (2016). Word

pair classiﬁcation during imagined speech using direct

brain recordings. Scientiﬁc Reports, 6:25803.

Mohri, M., Pereira, F., and Riley, M. (2002). Weighted

ﬁnite-state transducers in speech recognition. Com-

puter Speech & Language, 16(1):69–88.

Moriya, T., Tanaka, T., Shinozaki, T., Watanabe, S., and

Duh, K. (2015). Automation of system building for

state-of-the-art large vocabulary speech recognition

using evolution strategy. In Automatic Speech Recog-

nition and Understanding (ASRU), 2015 IEEE Work-

shop on, pages 610–616.

Moses, D. A., Leonard, M. K., and Chang, E. F. (2018).

Real-time classiﬁcation of auditory sentences using

evoked cortical activity in humans. Journal of Neu-

ral Engineering, 15(3):036005.

Moses, D. A., Mesgarani, N., Leonard, M. K., and Chang,

E. F. (2016). Neural speech recognition: continuous

phoneme decoding using spatiotemporal representa-

tions of human cortical activity. Journal of Neural

Engineering, 13(5):056004.

Oh, D., Park, J.-S., Kim, J.-H., and Jang, G.-J. (2021). Hi-

erarchical phoneme classiﬁcation for improved speech

recognition. Applied Sciences, 11(1):428.

Peddinti, V., Povey, D., and Khudanpur, S. (2015). A time

delay neural network architecture for efﬁcient model-

ing of long temporal contexts. In Sixteenth Annual

Conference of the International Speech Communica-

tion Association.

Povey, D., Ghoshal, A., Boulianne, G., Burget, L., Glem-

bek, O., Goel, N., Hannemann, M., Motlicek, P.,

Qian, Y., Schwarz, P., et al. (2011). The kaldi speech

recognition toolkit. In IEEE 2011 Workshop on Auto-

matic Speech Recognition and Understanding, num-

ber EPFL-CONF-192584.

Povey, D., Peddinti, V., Galvez, D., Ghahremani, P.,

Manohar, V., Na, X., Wang, Y., and Khudanpur, S.

(2016). Purely sequence-trained neural networks for

asr based on lattice-free mmi. In Interspeech, pages

2751–2755.

Proix, T., Delgado Saa, J., Christen, A., Martin, S.,

Pasley, B. N., Knight, R. T., Tian, X., Poeppel, D.,

Doyle, W. K., Devinsky, O., et al. (2022). Imagined

speech can be decoded from low-and cross-frequency

intracranial eeg features. Nature communications,

13(1):48.

Sivasankaran, S., Srivastava, B. M. L., Sitaram, S., Bali,

K., and Choudhury, M. (2018). Phone merging for

code-switched speech recognition. In Proceedings of

the Third Workshop on Computational Approaches to

Linguistic Code-Switching, pages 11–19.

Sun, P., Anumanchipalli, G. K., and Chang, E. F. (2020).

Brain2char: a deep architecture for decoding text

from brain recordings. Journal of neural engineering,

17(6):066015.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Vazhenina, D. and Markov, K. (2011). Phoneme set selec-

tion for Russian speech recognition. In 2011 7th Inter-

national Conference on Natural Language Processing

and Knowledge Engineering, pages 475–478. IEEE.

Wang, X., Zhang, J.-S., Nishida, M., and Yamamoto, S.

(2014). Phoneme set design using English speech

database by Japanese for dialogue-based english call

systems. In LREC, pages 3948–3951.

Willett, F. R., Kunz, E. M., Fan, C., Avansino, D. T., Wil-

son, G. H., Choi, E. Y., Kamdar, F., Glasser, M. F.,

Hochberg, L. R., Druckmann, S., et al. (2023). A

high-performance speech neuroprosthesis. Nature,

620(7976):1031–1036.

Toward Designing a Reduced Phone Set Using Text Decoding Accuracy Estimates in Speech BCI

987