Modelling and Clustering Patterns from Smart Meter Data in Water

Distribution Systems

Mariaelena Berlotti

, Sarah Di Grande

, Salvatore Cavalieri

and Roberto Gueli

Department of Electrical Electronic and Computer Engineering, University of Catania, Viale A.Doria n.6, Catania, Italy

EHT, Viale Africa n.31, Catania, Italy

Keywords: Water Distribution System, Decision Support System, Smart Metering, Machine Learning.

Abstract: In recent years, water utilities have increasingly required a deeper understanding of users’ water demand

across their distribution networks to optimize resource management and meet customers' needs. With the

adoption of smart metering solutions, it has become possible to investigate water usage at a finer resolution,

enabling the collection of more detailed consumption data. In the present study, the authors present an

innovative methodology for identifying water usage using data from smart meters. First, a Multiple Seasonal-

Trend Decomposition algorithm is applied to extract seasonality from the raw time-series data. Next, the

Bootstrap sampling technique is used to train an optimized Time Series K-means algorithm on multiple data

configurations. Finally, the clustering results are interpreted graphically and validated, providing valuable

insights into consumption habits and a comprehensive assessment of the methodology's effectiveness and

stability.

1 INTRODUCTION

The increasing global population, along with rapid

urbanization and ongoing climate change, continues

to strain water resources. In many countries

worldwide, it has become increasingly common to

discuss about water crisis, referring to a deficiency in

the water systems. The causes of this crisis vary and

include several factors such as, primarily, the drought

due to climate change; the reduced rainfall and high

temperatures lead to a significant reduction in the

volume of water available in reservoirs (McDonald et

al., 2011). Another major cause is the lack of

maintenance of water infrastructures, which have

become outdated and poorly managed. In regards, the

International Water Association (IWA) estimates that

water losses from water systems worldwide amount

to 346 billion litres per day. The World Bank states

that 8.6 trillion gallons per year of water is lost due to

leakage and breakage in water networks worldwide

(Pearson, 2019). In this context, understanding water

https://orcid.org/0009-0008-8895-2175

https://orcid.org/0009-0007-6564-704X

https://orcid.org/0000-0001-9077-3688

https://orcid.org/0000-0002-8014-0243

usage is becoming crucial for an efficient

management of Water Distribution Systems (WDS).

Recently, the rise and expansion of smart-

metering technologies facilitate the quick and

extensive collection of water usage data at high

spatial and temporal detail (Cominola et al., 2019).

This data provides essential information, crucial for

improving the efficiency and sustainability of WDS

with specific applications including the development

of predictive models for water demand (Di Grande et

al., 2024), the advancement of water reuse and

recycling technologies (Du Plessis et al., 2018), the

classification of users profiles based on individual

water consumption patterns (Mazzoni et al., 2023)

together with the detection of possible anomalies and

irregularities through the investigation of unusual

water consumption behaviours (Berlotti et al., 2023 ).

Profiling consumers and evaluating the water demand

patterns to detect abnormal water consumption

behaviour is strongly requested to achieve a

sustainable management of WDS. Data-driven

approach based on machine learning or artificial

Berlotti, M., Di Grande, S., Cavalieri, S. and Gueli, R.

Modelling and Clustering Patterns from Smart Meter Data in Water Distribution Systems.

DOI: 10.5220/0013200500003929

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 691-698

ISBN: 978-989-758-749-8; ISSN: 2184-4992

691

intelligence algorithms may be of great help to reach

this goal.

In this paper, the authors introduce a novel

clustering approach for identifying different user

profiles from water demand time series. By grouping

users with similar, though not identical, consumption

patterns, the method generates representative profiles

for both residential and non-residential users. This

approach not only allows for user type identification

based on consumption patterns but also makes the

clustering algorithm a robust tool for detecting

abnormal water demands, which may indicate the

presence of issues as leakages, irregularities, or

unauthorized consumption.

The paper is structured as follows: Section 2 is an

overview of the state of the art regarding the paper

subject. In Section 3 the authors give a detailed

description of the proposed approach. Section 4 will

provide a description of the representative patterns

featured by different types of consumers; moreover,

the main results obtained from the final test carried

out during the research, are presented. Finally, in

Section 5 concluding remarks will summarize the

contents of the paper.

2 RELATED WORKS

In this section, the authors provide an overview of the

current state of the art about methods used to identify

user profiles based on water demand data.

Traditionally, research on water consumption has

focused on the residential sector, as residential users

typically represent the largest share of water

consumers (Aksela and Aksela, 2011). Several

studies have been conducted to evaluate residential

water usage at different levels of spatial aggregation,

ranging from large-scale, such as entire cities or

District Metered Areas (DMA), to individual user

levels. Historically, water consumption at the user

level was examined using data collected from water

meters, aggregated on a monthly or yearly basis for

billing purposes. This kind of data provides a broad

view of the aggregate water consumed over a long

period, limiting the ability to analyze detailed

consumption behavior or identify specific trends.

With advancements in technology and the widespread

adoption of smart meters, much more granular data

can now be collected, such as every 15 minutes or

hourly. The availability of such high-resolution data

opens up new possibilities for more accurate profiling

and analysis of water usage, facilitating better

resource management and the identification of

possible anomalies that were previously difficult to

detect.

In their study, (Obringer and White, 2023)

propose a clustering approach to develop a typology

of residential water users. The study focuses on

understanding community-specific attitudes towards

water usage and conservation by applying

unsupervised learning techniques on social survey

data collected in three cities in the Southwestern

United States. The methodology combines social

survey data with unsupervised machine learning,

making it a novel approach to segmenting water users

based on behavioural patterns.

Similarly, (Arsene et al., 2021) explore the

profiling of water consumers in a WDS using K-

Means clustering along with multiple pre-processing

methods. The study analyses a sample of 800

households, and it focuses on improving the

identification of distinct water consumer profiles.

All the aforementioned studies focus specifically

on water consumption in the residential sector.

However, residential users account for only a small

portion of the total water supplied by utilities. A large

share of water is also consumed by industries,

commercial businesses, and other services (Aksela

and Aksela, 2011). On the basis of this consideration,

more recent studies have shifted focus toward

analysing water consumption at the non-residential

level.

In particular, (Cheifetz et al., 2017) proposed a

two-step machine learning approach for exploring

both residential and non-residential user profiles from

water consumption data produced by smart meters.

Their methodology is fully data-driven, applying a

Fourier decomposition algorithm to extract seasonal

patterns from time series data. Two clustering

strategies, K-Means and FReMix generative models,

are then evaluated and compared, providing a

qualitative interpretation of the resulting clusters.

In line with the approach by (Cheifetz et al.,

2017), the authors of this paper propose a multi-step

machine learning method to analyse hourly water

consumption data collected from smart meters of a

WDS in real WDS located in a city of the central Italy.

The first part of the approach focuses on profiling

typical water usage patterns for different consumer

types. To achieve this, several data-cleaning

techniques were applied, including Multiple

Seasonal-Trend time series decomposition using

LOESS (MSTL) (Bandara et al., 2021). Decomposing

the original time series into its main components,

helps isolate recurring consumption patterns,

enabling the clustering algorithm to focus on seasonal

trends instead of noise. An optimized Time Series K-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

692

means algorithm (TSKmeans), rather than the

standard K-Means, was used for profiling the

different users. To ensure stability in the clustering

results, the authors applied Bootstrap Sampling,

testing various clustering solutions with different sets

of hyperparameters during the optimization process.

Differently from (Cheifetz et al., 2017), in the

second part of the approach the authors were able to

validate the clustering results using geo-referenced

users’ information, ensuring that the identified

clusters reflect real-world patterns more reliably.

After validating the clusters, the authors conducted a

final test on a new set of residential users to identify

those whose water usage deviated from typical

patterns.

In conclusion, the integration of clustering with

geographic data represents a significant improvement

over existing methods, making the proposed approach

an effective decision-support tool for water utilities

able not only to profile the water consumption

patterns of user types but also to detect irregularities,

possibly due to billing errors, leakages or even

potential fraud in water consumption.

3 PROPOSED APPROACH

3.1 Data Acquisition

The data used in the analysis refers to the hourly

cumulative water demand in litres per second (l/s)

collected over nine months (September 5th, 2023-

May 31st, 2024) from smart meters monitoring six

District Metered Areas (DMAs) in a central Italian

city. In details, the DMAs consist of varying users

counts: 403 (DMA 1), 295 (DMA 2), 81 (DMA 3), 31

(DMA 4), 84 (DMA 5), 61 (DMA 6).

3.2 Data Preprocessing

Data preprocessing was necessary before proceeding

with clustering users. After downloading and merging

files in different formats, the authors began by

cleaning the data. Specifically, columns with more

than 30% of missing values were removed. Since the

dataset consists of time series, each column

corresponds to the hourly user's cumulative water

consumption. Therefore, removing a column means

deleting that user's data. All remaining missing values

were filled using the K-Nearest Neighbors (KNN)

spatial interpolation (Sahoo and Ghose, 2022). After

cleaning, each DMA counts the following users: 396

(DMA 1), 288 (DMA 2), 81 (DMA 3), 28 (DMA 4),

84 (DMA 5), 61 (DMA 6).

The next step was to transform the cumulative into

effective water consumption data. Smart meters

continuously monitor water use as cumulative litres

per second (l/s) meaning that they store the total

amount of water consumed until that point. However,

these aggregated values were not directly indicative

of how much water was used by the user in each hour.

To derive this information, the difference of

cumulative consumption values between two

consecutive hours was computed.

The final data preprocessing step was data

normalization, essential to establish a uniform

baseline and prevent the clustering bias from feature

scales (Ahsan et al., 2021). In the residential group,

household size can significantly affect total water

consumed, even when the overall consumption

patterns remain similar. To address this issue and

group households by behaviours regardless of size,

Min-Max scaling was applied, standardizing each

variable to 0-1 scale.

3.3 Data Exploration

Before proceeding with the analysis, an initial data

exploration was conducted to gain a basic

understanding of the dataset. Due to the authors'

inability to access information regarding the type of

user contract, a reconstruction of this data was

necessary. Thanks to the availability of geographic

information, it was possible to map the users and

identify the types of activities they were associated

with. An application able to provide the type of the

activity at a given location by providing longitude,

latitude, and address information was developed.

Finally, based on the output generated by the

mapping, a two-class label is assigned to each user,

distinguishing between residential and non-

residential categories.

This initial data exploration revealed that only 60

users in the sample are non-residential. This

imbalance reflects reality, as residential users

typically constitute the majority of water consumers

in a city . To solve this issue, the clustering model was

trained on a balanced dataset consisting of 145 users:

85 residential users were randomly selected from

across the six DMAs of the WDS. The remaining 60

represent the available non-residential user’s data.

3.4 Feature Engineering

Feature engineering is the process of transforming

raw data into more meaningful features to enhance

the performance of machine learning algorithms

(Kumar et al., 2017). The next step in the analysis

Modelling and Clustering Patterns from Smart Meter Data in Water Distribution Systems

693

involves using MSTL to extract seasonal patterns

from the original time series. MSTL iteratively

decomposes the time series into its main components:

seasonality, representing repeating patterns in the

data, trend, capturing the long-term changes, and

residuals, considered as noise or irregular

fluctuations (Bandara et al., 2021). Compared with

other decomposition alternatives, MSTL is highly

efficient and well-suited to handling large datasets

due to its computational scalability. To estimate the

different components, MSTL relies on LOESS (Local

Regression Smoothing), a non-parametric regression

method that fits local polynomial regressions to the

data, smoothing the series at each time point within a

defined window. The outcome of the procedure is a

smooth curve that represents the seasonality in the

data, filtered out from noise to reveal clear patterns

(Cleveland, 1979).

Two key hyperparameters have been set in the

MSTL algorithm: periods, regulating the length of

each seasonal cycle, and windows, referring to the

LOESS smoothing window size. While the window

size was left at its default value, the period was set to

168, to align with weekly water consumption

patterns. This strategic choice enables MSTL to

capture distinct weekly variations, such as residential

users consuming more water on weekends and

commercial users peaking on weekdays. The analysis

of MSTL seasonal components makes it easier to

identify similar user behaviours, allowing a more

effective clustering.

Lastly, seasonal data was aggregated into weekly

patterns by calculating the average hourly

consumption for each day of the week, for each

month. Instead of dealing with 720 observations, the

dataset was reduced to 168 observations (24 hours for

each of the 7 days in a week). By focusing on a

representative week, general daily and weekly

consumption patterns were captured without being

skewed by unusual dates within the month.

3.5 Feature Extraction

Principal Component Analysis (PCA) is an effective

dimensionality reduction technique whose main idea

is to transform the original data into a set of linear

combinations represented in a new space with

reduced dimensions (Pearson, 1901). Several reasons

justify the introduction of PCA in this analysis. First,

by focusing on the components with the most

variance PCA reduces noise and helps filter out less

significant data. Secondly, this technique highlights

dominant water consumption patterns that may not be

immediately visible in the original high-dimensional

space. Additionally, by reducing the number of

features, PCA makes the dataset more manageable

and computationally efficient.

After cleaning and transposition, PCA was

performed on the dataset of seasonal water

consumption patterns consisting of 145 users (rows)

and 1512 features (columns). By retaining 95% of the

variance, PCA results showed that rather than using

the original 1512 features, the dataset could be

reduced to 80 principal components. In essence, 80

components were sufficient to represent most of the

relevant information from the original features,

enabling more efficient data handling while

preserving critical insights into consumption patterns.

3.6 Modelling

This section explains the clustering procedure applied

in the analysis. A key challenge in clustering is

determining the optimal number of clusters while

ensuring stability—meaning the robustness and

consistency of clusters despite data variations or

random initialization. In this paper, the authors use a

Bootstrap sampling technique to test clustering

stability.

3.6.1 Bootstrap Sampling

Bootstrap sampling, or Bootstrapping, is a resampling

technique used in statistics and machine learning,

which consists in drawing multiple samples from the

original data with replacement, meaning that the same

data point can appear more than once in the resampled

dataset (Jain and Moreau, 1987). This technique

enables clustering validation on "fake" datasets that

differ from the original, with some users’ patterns

potentially missing. Starting with an unknown

population, X of n elements, m different bootstrap

samples (S

, S

, …, S

) are created, each containing

the water consumption values over a series of

timesteps for the users, who are equally likely to be

selected. The number of bootstrap samples, m, is a

key hyperparameter that needs to be tuned for optimal

model performance.

3.6.2 Optimization

Hyperparameter optimization, or tuning, involves

selecting the set of hyperparameters that yields an

optimal model by minimizing a predefined loss

function for a given dataset (Claesen and De Moor,

2015). In our analysis, various clustering models were

generated and tested with different sets of

hyperparameters using the Optuna Python library

(Optuna: A Hyperparameter Optimization

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

694

Framework — Optuna 4.0.0 Documentation, n.d.). A

total of 100 trials were conducted to create and

compare 100 different clustering models across

different combinations of the original dataset as

determined by the number of bootstrap samples. The

following hyperparameters directly influencing the

complexity, speed and performance of the model

have been optimized: n_of_bootstraps (number of

samples drawn from the original dataset, range from

10 to 100), n_of_clusters (number of groups, range

from 2 to 20), max_iter (maximum number of

algorithm iterations to find the optimal clusters, range

from 50 to 300), tol (convergence threshold,

measuring centroids changes, range from 1e-6 to 1e-

4), n_init (number of algorithm initializations with

different initial centroids, range from 1 to 10).

3.6.3 Evaluation Metrics

The optimization process determines the best

clustering model, including the number of clusters

using the combined score of three equally weighted

metrics, given by (1).

𝐹𝑖𝑛𝑎𝑙 𝑆𝑐𝑜𝑟𝑒 = Silhouette score



−

𝐵𝐼𝐶



+𝐴𝐼𝐶



(1)

In equation (1), the final score combines the

average silhouette score with the average Bayesian

Information Criterion (BIC) and the average Akaike

Information Criterion (AIC). Each trial yields an

average of the metrics obtained across all

combinations of the original dataset tested.

The silhouette score is a metric to maximize,

while BIC and AIC are metrics to minimize.

Specifically, the silhouette score, ranging from -1 to

+1, measures clusters separation. In details, +1

reflects perfectly distinct clusters, -1 indicates overlap

or misallocation , and 0 suggests ambiguity in data

point assignments (Shahapure and Nicholas, 2020).

BIC and AIC are information criteria used for

model selection. Both metrics balance the model’s

goodness of fit against its complexity by

incorporating a penalty term to discourage complex

models (Gabbay et al., 2011). As a result, these

metrics provide a more nuanced evaluation compared

to the silhouette score.

3.6.4 Clustering

Clustering algorithm used in this study is TSkmeans

(Huang et al., 2016). TSkmeans was specifically

chosen for its ability to account for the sequential

nature and temporal distortions in the data, challenges

that traditional clustering methods struggle to address

(Berlotti et al., 2024). Unlike traditional K-means,

TSkmeans incorporates Dynamic Time Warping

(DTW) metric to account for temporal shifts,

varying speeds, and local distortions in sequences,

providing a more comprehensive measure of

similarity among time-dependent data points

(Tslearn.Clustering.TimeSeriesKMeans — Tslearn

0.6.3 Documentation, n.d.). The integration of DTW

into TSkmeans improves the detection of similar

water usage patterns, leading to more accurate

insights for efficient water resource management.

4 RESULTS

In this section, the authors discuss the obtained

results. The clustering model was trained on a dataset

of 145 users: 85 residentials and 60 non-residential.

Table 1 shows the input dataset used for modelling.

Specifically, after PCA the data was transposed to

place users in columns, ensuring that each user became

a feature in the dataset. This transposition is crucial for

clustering, as it allows the algorithm to make

meaningful comparisons between user’s water

consumption patterns, rather than focusing on time

points or specific measurements. Finally, additional

daytime information (Year, Month, Day of the Week,

and Hour) was added in the dataset.

Table 1: Final input dataset for modelling.

Year Month Day of

wee

Hour User1 … UserN

2023 9 Monday 0 0.47738 … 0.554809

… … … … … … …

2024 5 Sunday 23 0.599534 … 0.459491

The optimization step yielded the following

hyperparameters configuration: {n_of_bootstraps=10,

num_clusters=4, max_iter=158, tol=5.69941e-06,

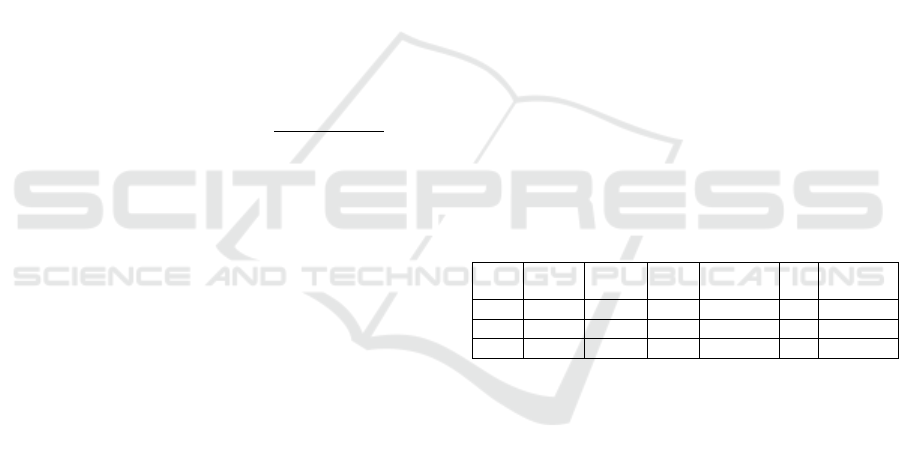
n_init=8}. Figure 1 shows the average weekly pattern

of each cluster for the optimal repartition K=4.

Next, a realistic explanation of the clusters is

given. Clusters 1 and 2 group residential users’

patterns with similar habits. Both show peaks around

1:00–3:00 pm (lunch time), and 7:00–11:00 pm

(dinner time), with higher water consumption on

weekends, especially Sundays. Instead, Cluster 3 and

4 include non-residential users. In Cluster 3, users

typically consume water from 9:00 am to 2:00 pm

(peak at noon) and again from 4:00 pm to 8:00 pm

(peak at 6:00 pm), primarily during weekdays with

minimal activity on weekends. Meanwhile, Cluster 4

groups users whose consumption patterns differ

significantly from those of the other clusters, though

their behaviour still follows a consistent pattern.

Modelling and Clustering Patterns from Smart Meter Data in Water Distribution Systems

695

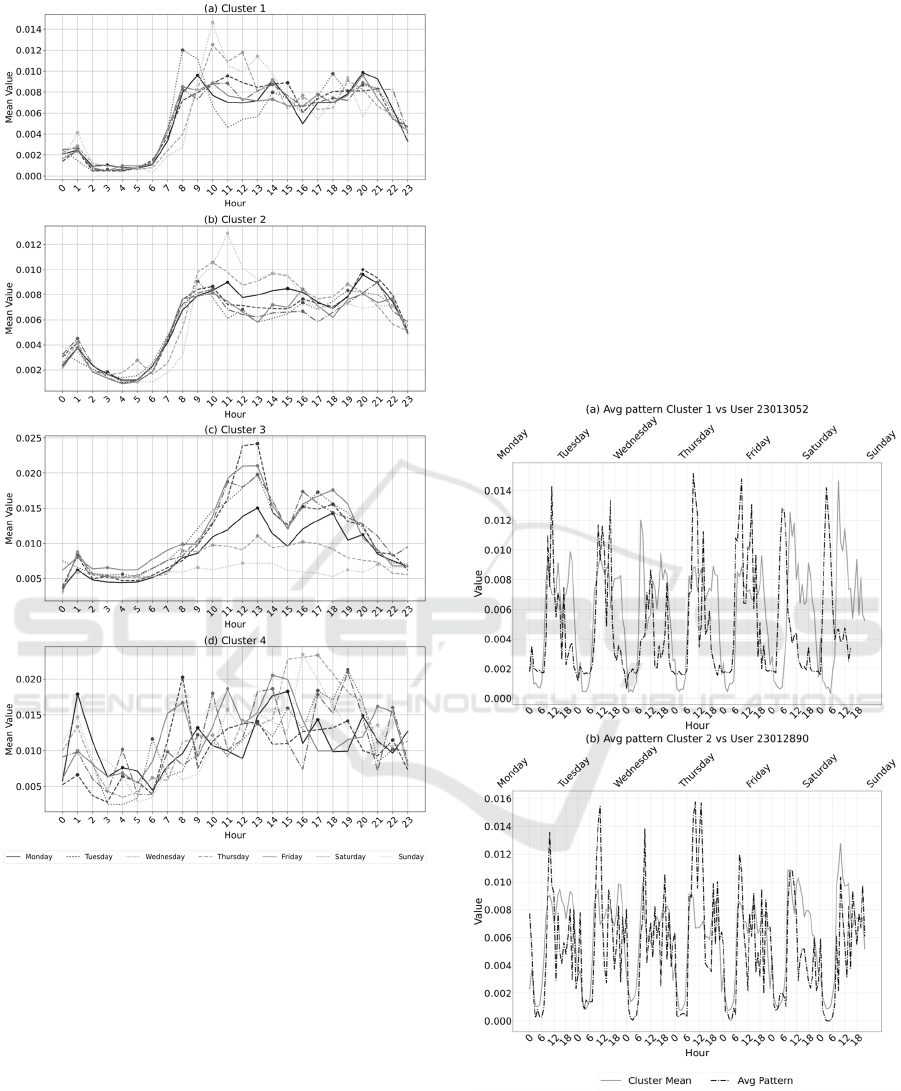
Figure 1: Average weekly pattern for each cluster.

These considerations were confirmed by the

georeferenced information. In particular, Cluster 1

and 2 include 37 and 49 users respectively, all

residential. Cluster 3 consists of 34 non-residential

users, including banks, garages, and service

companies. Finally, Cluster 4 is composed of 25

mixed users, of which only 9 are residential, while the

rest are non-residential, involved in industrial

activities.

As introduced before, in this paper a validation of

the clustering has been done with the aim of verifying

if it was possible to use the four clusters as input for

a decision-support system, capable of identifying the

user’s type from the consumption pattern and of

detecting any irregularities. In concerns, to test the

algorithm a new set of 30 randomly selected users

was considered. Some of the results achieved will be

presented in the following.

The first results shown involve two test users

(23013052 and 23012890) assigned to the residential

Cluster 1 and 2. Using georeferenced information, it

was possible to confirm that the two users were

residentials. To furthermore confirm this result, in

Figure 2 test users’ average hourly patterns (dotted

line) over one week were compared with the typical

residential pattern given by Cluster 1 and 2

(continuous line). Due to space constraints, the

timestamp is illustrated in 6-hour step. As shown in

plots (a) and (b), the two test users’ patterns closely

resemble the average patterns of the two residential

clusters in shape and structure.

Figure 2: Test users grouped as residentials.

The authors provide another example of test user

(23012939) chosen among the set considered. In

Figure 3 (a) and (b), the pattern of the test user is

compared with the average patterns of the residential

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

696

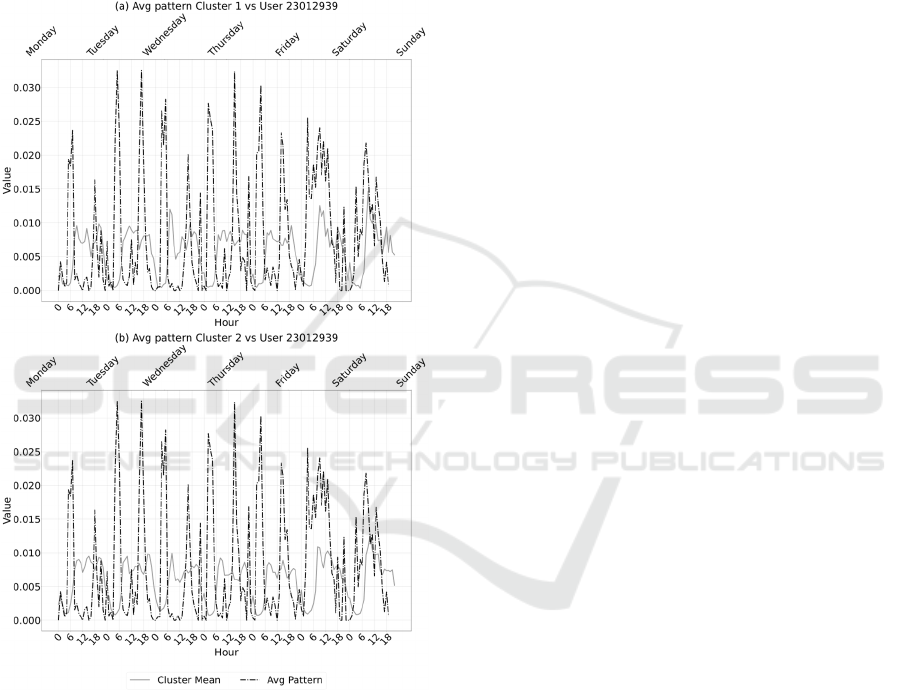
clusters 1 and 2. As shown in the plots, despite being

labelled as residential through georeferenced

information, the user was classified by the algorithm

in Cluster 4. Indeed, the test user exhibits a

completely different pattern compared to the typical

residential patterns of Cluster 1 and Cluster 2.

Specifically, the test user’s water consumption never

drops to zero at night, with unusual peaks which may

indicate an irregularity in consumption as well as the

presence of a leakage.

Figure 3: Strange user vs residential clusters patterns.

5 CONCLUSIONS

In this study, the authors propose a machine learning

approach for identifying users’ profiles from smart

meter water demand data. The data under analysis

refers to hourly time series recording the amount of

water consumed by each user over a period of nine

months. Using the MSTL algorithm, seasonality is

extracted from the original time series. Next, PCA is

performed on the seasonal patterns’ dataset, retaining

95% of the variance. The optimized TSkmeans

algorithm is then used to divide the data into different

clusters. The authors highlight a significant advantage

in using Bootstrap sampling to train the clustering

algorithm on various configurations of the input data.

This technique ensures that the model is less sensitive

to dataset variations, thus enhancing the robustness of

the results. The authors propose not only a graphical

evaluation of the clustering results, providing a

realistic explanation of the patterns' distribution, but

also its validation using the georeferenced

information available for each user. Ultimately,

testing the clustering on a new set of users, the authors

proved the ability of the algorithm to identify not only

the type of user from its pattern but also cases of

irregularities in water consumption.

Future plans involve increasing the size of the

population considered in the analysis, aiming to

include a larger number of both residential and non-

residential users to discover new possible water

consumption habits. Furthermore, the authors also

expect to extend the analysis period to one year,

incorporating users’ water consumption variations

during the summer.

ACKNOWLDEGEMENT

The research here presented has been partially

developed under the Project "DATA-SET: DATA

driven dependencies for Sustainable Energy and

Transport", "PIAno inCEntivi per la RIcerca di

Ateneo" (PIACERI) 2024/2026, Track 1 funded by

the University of Catania.

REFERENCES

Ahsan, M., Mahmud, M., Saha, P., Gupta, K., and Siddique,

Z. (2021). Effect of Data Scaling Methods on Machine

Learning Algorithms and Model Performance.

Technologies, 9(3), 52.

Aksela, K., and Aksela, M. (2011). Demand Estimation

with Automated Meter Reading in a Distribution

Network. Journal of Water Resources Planning and

Management, 137(5), 456–467.

Arsene, D., Predescu, A., Truică, C.-O., Apostol, E.-S.,

Mocanu, M., and Chiru, C. (2021). Profiling consumers

in a water distribution network using K-Means

clustering and multiple pre-processing methods. 2021

13th International Conference on Electronics,

Computers and Artificial Intelligence (ECAI), 1–6.

Bandara, K., Hyndman, R. J., and Bergmeir, C. (2021).

MSTL: A Seasonal-Trend Decomposition Algorithm for

Time Series with Multiple Seasonal Patterns

Modelling and Clustering Patterns from Smart Meter Data in Water Distribution Systems

697

(arXiv:2107.13462). arXiv. http://arxiv.org/abs/2107.1

3462

Berlotti, M., Di Grande, S., and Cavalieri, S. (2024).

Proposal of a Machine Learning Approach for Traffic

Flow Prediction. Sensors, 24(7), Article 7.

Berlotti, M., Di Grande, S., Cavalieri, S., and Gueli, R.

(2023). Detection and Prediction of Leakages in Water

Distribution Networks: Proceedings of the 12th

International Conference on Data Science, Technology

and Applications, 436–443.

Cheifetz, N., Noumir, Z., Samé, A., Sandraz, A.-C., Féliers,

C., and Heim, V. (2017). Modeling and clustering water

demand patterns from real-world smart meter data.

Drinking Water Engineering and Science, 10(2), 75–

82.

Claesen, M., and De Moor, B. (2015). Hyperparameter

Search in Machine Learning (arXiv:1502.02127).

arXiv.

Cleveland, W. S. (1979). Robust Locally Weighted

Regression and Smoothing Scatterplots. Journal of the

American Statistical Association, 74(368), 829–836.

Cominola, A., Nguyen, K., Giuliani, M., Stewart, R. A.,

Maier, H. R., and Castelletti, A. (2019). Data Mining to

Uncover Heterogeneous Water Use Behaviors From

Smart Meter Data. Water Resources Research, 55(11),

9315–9333.

Di Grande, S., Berlotti, M., Cavalieri, S., and Gueli, R.

(2024). A Proactive Approach for the Sustainable

Management of Water Distribution Systems. 115–125.

Du Plessis, J. L., Faasen, B., Jacobs, H. E., Knox, A. J., and

Loubser, C. (2018). Investigating wastewater flow from

a gated community to disaggregate indoor and outdoor

water use. Journal of Water, Sanitation and Hygiene for

Development, 8(2), 238–245.

Gabbay, D., Thagard, P., Woods, J., Bandyopadhyay, P.,

and Forster, M. (2011). Philosophy of Statistics (Vol.

7).

Huang, X., Ye, Y., Xiong, L., Lau, R. Y., Jiang, N., &

Wang, S. (2016). Time series k-means: A new k-means

type smooth subspace clustering for time series data.

Information Sciences, 367, 1-13.

Jain, A. K., and Moreau, J. V. (1987). Bootstrap technique

in cluster analysis. Pattern Recognition, 20(5), 547–

568.

Kumar, A., Boehm, M., and Yang, J. (2017). Data

Management in Machine Learning: Challenges,

Techniques, and Systems. Proceedings of the 2017

ACM International Conference on Management of

Data, 1717–1722.

Mazzoni, F., Alvisi, S., Blokker, M., Buchberger, S. G.,

Castelletti, A., Cominola, A., Gross, M.-P., Jacobs, H.

E., Mayer, P., Steffelbauer, D. B., Stewart, R. A.,

Stillwell, A. S., Tzatchkov, V., Yamanaka, V.-H. A.,

and Franchini, M. (2023). Investigating the

characteristics of residential end uses of water: A

worldwide review. Water Research, 230, 119500.

McDonald, R. I., Green, P., Balk, D., Fekete, B. M.,

Revenga, C., Todd, M., and Montgomery, M. (2011).

Urban growth, climate change, and freshwater

availability. Proceedings of the National Academy of

Sciences, 108(15), 6312–6317.

Obringer, R., and White, D. (2023). Leveraging

Unsupervised Learning to Develop a Typology of

Residential Water Users’ Attitudes Towards

Conservation. Water Resources Management, 37(1),

37–53.

Optuna: A hyperparameter optimization framework—

Optuna 4.0.0 documentation. (n.d.). Retrieved 23

September 2024, from https://optuna.readthedocs.io/

en/stable/index.html

Pearson, D. (2019). Standard Definitions for Water Losses.

IWA Publishing.

Pearson, K. (1901). On lines and planes of closest fit to

systems of points in space. The London, Edinburgh, and

Dublin Philosophical Mangazine and Journal of

Science, 2(11), 559-571, https://doi.org/10.1080/147

86440109462720

Sahoo, A., and Ghose, D. K. (2022). Imputation of missing

precipitation data using KNN, SOM, RF, and FNN. Soft

Computing, 26(12), 5919–5936.

Shahapure, K. R., and Nicholas, C. (2020). Cluster Quality

Analysis Using Silhouette Score. 2020 IEEE 7th

International Conference on Data Science and

Advanced Analytics (DSAA), 747–748.

tslearn.clustering.TimeSeriesKMeans—Tslearn 0.6.3

documentation. (n.d.). Retrieved 25 September 2024,

from https://tslearn.readthedocs.io/en/stable/gen_mod

ules/clustering/tslearn.clustering.TimeSeriesKMeans.h

tml

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

698