Public Transport Network Design for Equality of Accessibility via

Message Passing Neural Networks and Reinforcement Learning

Duo Wang

, Andrea Araldo

and Maximilien Chau

SAMOVAR, Institut Polytechnique de Paris, Palaiseau, France

Keywords:

Transport, Network, Design, Accessibility, Reinforcement Learning, Message Passing Neural Networks.

Abstract:

Graph learning involves embedding relevant information about a graph’s structure into a vector space. How-

ever, graphs often represent objects within a physical or social context, such as a Public Transport (PT) graph,

where nodes represent locations surrounded by opportunities. In these cases, the performance of the graph

depends not only on its structure but also on the physical and social characteristics of the environment. Op-

timizing a graph may require adapting its structure to these contexts. This paper demonstrates that Message

Passing Neural Networks (MPNNs) can effectively embed both graph structure and environmental informa-

tion, enabling the design of PT graphs that meet complex objectives. Speciﬁcally, we focus on accessibility,

an indicator of how many opportunities can be reached in a unit of time. We set the objective to design a

“equitable” PT graph with a lower accessibility inequality. We combine MPNN with Reinforcement Learning

(RL) and show the efﬁcacy of our method against metaheuristics in a use case representing in simpliﬁed terms

the city of Montreal. Our superior results show the capacity of MPNN and RL to capture the intricate relations

between the PT graph and the environment, which metaheuristics do not achieve.

1 INTRODUCTION

Existing Public Transport (PT) is less and less ade-

quate to satisfy mobility needs of the people, in a con-

text of urban sprawl (Sun et al., 2018). The United

Nations estimate that only “1/2 of the urban popula-

tion has convenient access to PT” (UN, 2020). Build-

ing more and more PT lines to keep pace with ur-

ban sprawl, using traditional planning objectives, has

proved to be ineffective.

PT operators generally design PT lines with the

purpose of maximizing overall efﬁciency, measured

in terms of generalized cost (which takes into account

travel times and cost for the operators), or number

of kilometers traveled or number of passengers trans-

ported. This has resulted in unequal development of

PT within urban areas. The level of service offered by

PT is often satisfactory in city centers and poor in the

suburbs. In transportation, there is a consensus that it

is not sustainable that people in the suburbs travel by

car, as private cars are the largest polluters, 60.6% of

all transport (EU, 2019). Therefore, suburban popula-

tion depend on their private cars to perform their daily

https://orcid.org/0009-0007-8567-4707

https://orcid.org/0000-0002-5448-6646

activities (Anable, 2005; Welch et al., 2013). As an

example, the modal share of the car in the city center

of Prague is double that in the city center. The depen-

dence on private cars has negative economic, social

and environmental impacts (Saeidizand et al., 2022,

Section 2.2), which are common to different cities of

the world. For example, 61% of EU road transport

comes from cars, jobseekers with no car have

72% less chances of ﬁnding a job in Flanders, etc.

Therefore, a sufﬁcient condition to achieve sustain-

ability is to improve PT level of service where it is

currently poor. We propose in this paper to set geo-

graphical equality of PT level of service as the main

design objective. We focus in this paper on PT acces-

sibility metric, which measures the ease (in terms of

time and/or monetary cost) of reaching Points of In-

terest (PoIs) via PT. To improve geographical equal-

ity, we prioritize increasing PT accessibility in the un-

derserved areas.

A trivial strategy to do so would be to place more

stops and lines in underserved areas. However, this

may not be the most efﬁcient way to increase ac-

cessibility there. Indeed, the ability to reach PoIs

might be increased even more by improving PT net-

work close to other nodes, possibly far away, that

may enable convenient changes with other important

Wang, D., Araldo, A. and Chau, M.

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning.

DOI: 10.5220/0013166000003890

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 3, pages 619-630

ISBN: 978-989-758-737-5; ISSN: 2184-433X

619

lines. In general the PT network extends the inter-

dependencies between locations and PoIs far beyond

those that are in physical proximity. Therefore, to re-

duce the inequality of the distribution of accessibility

it is always required to take the entire PT graph into

consideration, rather than just around the local areas

where we want improvement. This makes our prob-

lem particularly challenging.

Most cities already have an existing PT network,

and the need to build lines from scratch is very lim-

ited. Re-designing the whole PT network is also not

an option as it would lead to major costs to the oper-

ators. For this reason, in this work, we assume a core

PT network (e.g., metro) that does not change, and we

only tackle the design of some bus lines, which comes

at a limited infrastructure cost. By focusing on bus

network design only, we aim to achieve important re-

duction of accessibility inequality with relatively low

expenses for the operator.

The contribution of this paper is a novel approach

to PT network design, in which the non-trivial inter-

dependencies involved into the accessibility metrics

are captured via a Message Passing Neural Network

(MPNN) (Wang et al., 2023; Gilmer et al., 2017;

Maskey et al., 2022) and a Deep Reinforcement

Learning (RL) agent. While MPNN and RL have

been used to solve canonical optimization problems

on graphs, to the best of our knowledge we are the

ﬁrst to use them for PT network design. To reduce in-

equality, we propose a simple yet effective approach,

consisting in using quantiles of the accessibility met-

rics as objective function.

Numerical results in a scenario inspired by Mon-

treal show that our method effectively reduces acces-

sibility inequality, more effectively than metaheuris-

tics classically used for PT design. This improvement

is due to the capability of the MPNN to capture the

structure of the PT network and its relation with the

PoIs, while metaheuristics do no learn any dependen-

cies and restrict themselves in randomly exploring the

space of designs.

2 RELATED WORK

Transport Network Design Problems (TNDPs), and

in particular Public Transport Network Design Prob-

lems (PTNDPs) can be at a strategic level or an oper-

ational level. At a strategic level, a PT planner aims

to decide the route of the different lines as well as

their frequencies. At an operational level, a PT op-

erator organizes the service in order to match the de-

cisions taken at the strategic level, deciding precise

time tables, as well as crew and vehicle scheduling.

In this paper, we focus on PTNDPs at a strategic

level. Reviews of strategic-level PTNDPs are pro-

vided in (Farahani et al., 2013; Gkiotsalitis, 2022).

The methods generally used to solve PTNDPs can be

divided into two categories: mathematical program-

ming methods (Section 2.1) and search-based heuris-

tics methods (Section 2.2). We use instead graph-

based reinforcement learning (Section 2.3). The latter

has been applied to solve several combinatorial prob-

lems and has also few applications in Transport. How-

ever, it has not been used for PT planning (lines de-

sign), with one exception (Yoo et al., 2023). How-

ever, (Yoo et al., 2023) only designed the bus network

based on some cost function. Their article did not

consider the impact of the structure of pre-existing

metro lines on the design of new bus lines, nor did

it consider optimizing the inequality of accessibility.

Their method is difﬁcult to apply to our problem.

2.1 Mathematical Programming

Methods

TNDPs usually be formulated as non-linear program-

ming models. Solvers are used to solve these mod-

els. To ensure that their models are reasonable, they

usually need to set numerous constraints (Wei et al.,

2021; Quynh and Thuan, 2018). For a realistic sized

problem, it is difﬁcult to ﬁnd a suitable solution with

this method (Chakroborty, 2003). Therefore, instead

of considering a real city, they turned to represent-

ing it with a regular geometrical pattern, such as the

Continuous Approximation method (Calabro et al.,

2023). This method can indeed crudely describe any

city through some characteristics, but in the end they

cannot be applied to any real city. Because real cities

are much more complex than abstract regular geomet-

rical shapes.

Some works try to achieve the purpose of deal-

ing with large-scale real cities by adding more con-

straints, which often limit the solution space. These

works are (Guti

errez-Jarpa et al., 2018), which ﬁrst

proposed to design metro lines in some predeﬁned

corridors, and these corridors with higher passenger

trafﬁc were chosen by a Greedy generation heuristic

step before any optimization, and (Wei et al., 2019),

conducted a real-world case study by predeﬁning cor-

ridors and solving a bi-objective mixed-integer linear

programming model. However, all these works highly

rely on an expert guidance to help reduce the potential

solution space, in other words, the results vary with

different expert guidance. Expert guidance does not

ensure that the optimal solution is not eliminated.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

620

2.2 Heuristics Methods

The most commonly used search-based heuristic

methods are Simulated Annealing, Tabu Search, and

Genetic Algorithm. Their common method is to ini-

tialize a PT design and then gradually optimize the

PT design by changing it through heuristics. (Schit-

tekat et al., 2013) develops a bi-level metaheuristic

to ﬁnd the optimal solution of school bus routing

problem. The upper level repeats greedy randomized

adaptive search followed by a variable neighborhood

descent n

max

times and then ﬁnds the best solution

to bus stops assignment among these n

max

times of

search, while the lower level ﬁnds an exact solution to

a sub-problem of assigning students to stops by solv-

ing a mathematical programming problem. (Owais

and Osman, 2018) uses a Genetic Algorithm to gen-

erate a bus route network from With only the Ori-

gin–Destination matrix and the network structure of

an existing transportation network. In the process of

using GA to evolve route design, the connectivity of

routes is ensured at every stage of the GA. (Kova-

lyov et al., 2020) uses a Particle Swarm Optimiza-

tion method to solve the optimal planning problem

of replacing traditional Public Transport with elec-

tric. (Barcel

o et al., 2018) emphasizes the application

of metaheuristic algorithms in problems of managing

city logistics systems. These methods have a com-

mon limitation, that is, during the iterative process,

some basic characteristics of the graph are retained,

such as connectivity, which is not needed in reality.

Therefore, they often can only ﬁnd local optimal so-

lutions.

Considering all of the above, we need to design a

generic algorithm which requires fewer constraints. It

does not require expert experience, which is the lim-

itation of Mathematical programming method, and it

also can no longer retain some unreasonable charac-

teristics of graph, which is the limitation of Search-

based heuristics method. Therefore, we chose the RL-

based method.

Closer to our work, the work in (Yoo et al., 2023)

solved TNDP by directly using RL, and did not ex-

tract the information of PT graph. The work (Darwish

et al., 2020) used Transformer architecture to pro-

duce the nodes and the graph embeddings, and then

solved TNDP via RL. But to make their method fea-

sible, they assumed that the network is a connected

graph, which is not needed in our paper. The work

(Wei et al., 2020) presented a RL-based method to

solve the city metro network expansion problem. Our

main difference lies in the different methods used to

extract the information on PT graph. They used two

1-dimensional convolutional neural networks to cal-

culate the embeddings for the stations. However, the

graph structure is complex, we believe only applying

1-dimensional convolutional neural network is insuf-

ﬁcient. In this sense, we proposed to use Message

Passing Neural Network (MPNN) to extract the infor-

mation on PT graph.

2.3 Graph-Based Reinforcement

Learning Applications

Some works using Graph-based RL to solve other

problems are as follows: The work (Barrett et al.,

2020) already coupled it successfully to a DQN on

traditional combinatorial problem, such as max-cut

problem. The work (Duan et al., 2020) ﬁrst extracted

the information of graphs, based on the recurrent neu-

ral networks (RNN), and then combined it with RL to

solve the Vehicle Routing Problem. The work (Yoon

et al., 2021) improved the transferability of the so-

lution to trafﬁc signal control problem by combin-

ing Reinforcement learning and MPNN. The work

oksal Ahmed et al., 2022) proposed an algorithm

for the vehicle ﬂeet scheduling problem, by integrat-

ing a reinforcement learning approach with a genetic

algorithm. The reinforcement learning is used to de-

cide parameters of genetic algorithm.

3 MODEL

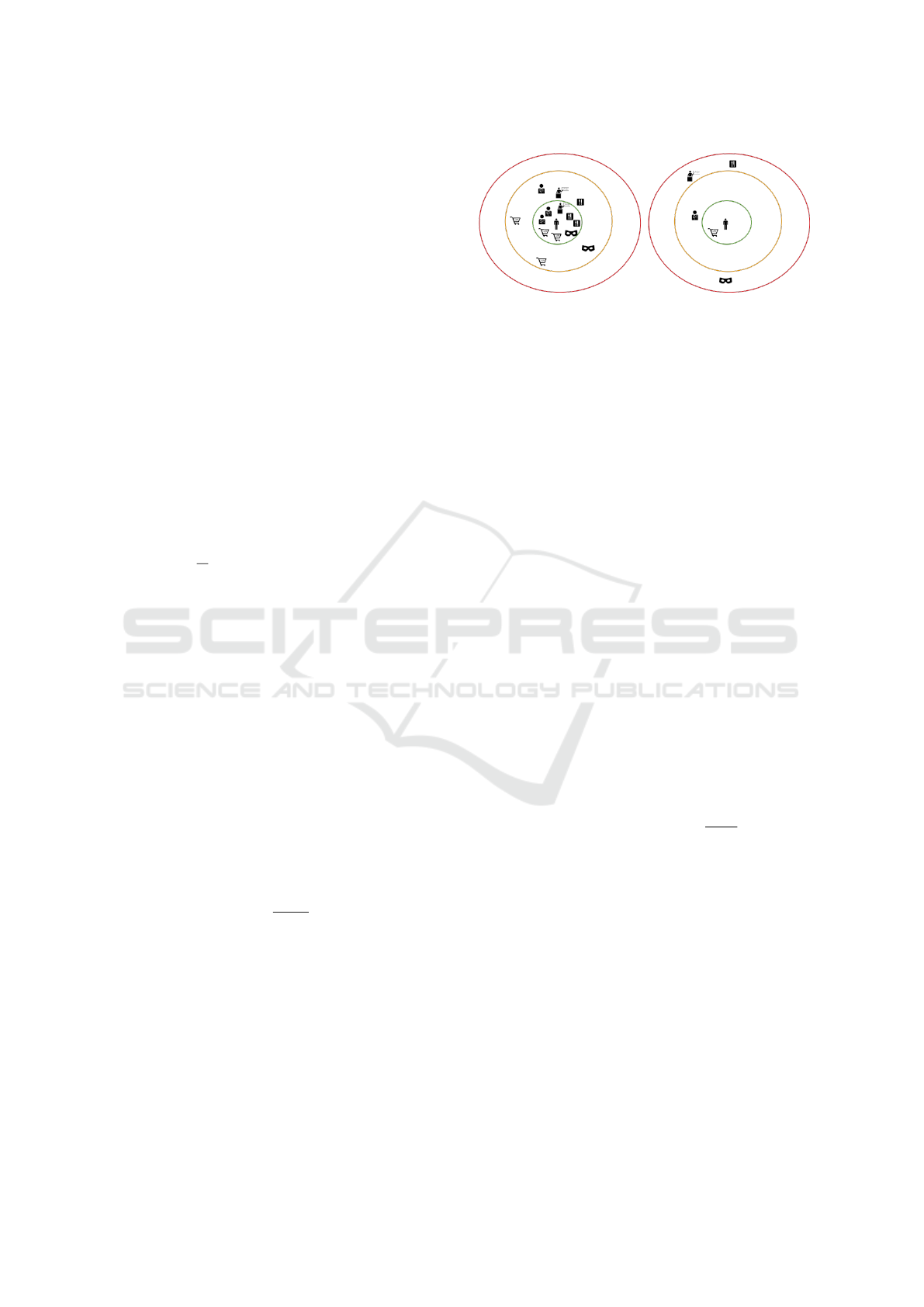
Figure 1: Model of Public Transit: PT graph G has 2 metro

lines (red points represent metro stations) and 2 bus lines

(purple points represent bus stops), in addition, the blue

points are the centroids, and the green points are the points

of interest.

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning

621

3.1 Model of Territory and of Public

Transport

We partition the study area with a regular tessella-

tion (here we adopt square tiles, but any regular shape

can be used), as in Figure 1. The center of each

tile is called centroid (blue points in Figure 1). The

study area also contains Points of Interest (PoIs) often

called ”opportunities” in the literature about accessi-

bility. PoIs can be shops, jobs, schools, restaurants,

etc. PoIs are depicted as green points in Figure 1.

As illustrated in Figure 1, our model of PT is com-

posed of:

1. Metro lines and metro stations (red points).

2. Bus lines and bus stops (purple points).

Changing metro lines is very costly and time con-

suming. On the other hand, redesigning bus lines re-

quires much less infrastructure cost and can be done

in shorter time. In this paper, we only focus on re-

designing bus lines and keep metro lines unchanged.

We model PT as a graph G= (V,E,L), where V is

the set of nodes, composed of centroids and PT stops

V = C

B, E is the set of edges, and L is the set

of lines. Any PT line l (metro line or bus line) is a

sequence of PT stops, linked by edges e ∈ E. Each

edge has a weight, which represents the time used by

a vehicle to go from a PT stop to another. A PT line l

also has a headway t

, which is the time between two

vehicle departures in the same direction. Since we

only optimize bus lines, headway t

of any metro line

remains unchanged. For metro lines, headway t

can

be obtained from real data. Instead, since we build

bus lines, we need to calculate ourselves headway t

for any bus line l. Once we decide the sequence of

bus stops composing l, we can get the total length of

the line d

, to go from the ﬁrst to the last stop. We

assume number N

of buses deployed on line l is ﬁxed

in advance. In this case, the cost is always the same

since the total ﬂeet size (= kN

) is ﬁxed. Denoting

with s

the bus speed, headway t

is:

· N

. (1)

In reality, the headway could also be a bit higher, due

to the time spent by the bus at the terminal before

starting the next run.

As in Figure 1, we include in G the set of cen-

troids C and the set of points of interest P. We also

include edges (in the two directions) between any cen-

troid and all PT stops, between any point of interest

and all PT stops, and between any centroid and any

point of interest. Note that V is deﬁned as the set of

nodes, C is a subset of V.

Figure 2: Accessibility example: the location on the left en-

joys high accessibility as, departing from it, one can reach

many PoIs in little time. On the right, instead, accessibility

is poor: few PoIs are reachable and high travel times are

required. The left and right locations are typical of city cen-

ters and suburbs, respectively.

For a trip from centroid c to point of interest poi, a

traveler can choose between different modes of travel.

For example, a traveler could simply walk to poi at

speed s

or walk from centroid c to a PT stop (metro

station or bus stop), go via PT to another stop, and

from there walk to the destination poi. If the stops

of two lines are close enough, we will also add the

edge between two stops to indicate that passengers

can transfer by walking. We consider an average wait-

ing time t

′

/2 at this station. We assume that travelers

always take the shortest path, i.e., the one that allows

to arrive at destination with the least time.

3.2 Accessibility

Accessibility measures the ease of reaching PoIs

via PT. A simpliﬁed depiction is given in Figure 2.

Accessibility depends on both land use (which de-

termines where PoIs are) and the transport system

(which determines the time to reach each PoI). There

are several ways of mathematically deﬁning accessi-

bility. We deﬁne the accessibility of centroid c as:

acc(c) =

∑

poi∈P

max



0,1 −

c,poi

max



, (2)

where T

c,poi

is the shortest travel time from cen-

troid c to point of interest poi and T

max

is a prede-

ﬁned threshold for travel time (e.g., 30 mins). Intu-

itively, acc(c) measures the number of PoIs that can

be reached by individuals departing from centroid c,

within time T

max

. Such PoIs are weighted by the time

to reach them, so that the closer a PoI, the more it con-

tributes to accessibility. Our deﬁnition is a combina-

tion of two classic deﬁnitions of accessibility, namely

the isochrone and gravity-based (Miller, 2020). The

purely isochrone deﬁnition of accessibility has the is-

sue of counting all PoIs the same, despite the dif-

ference in travel time to reach time. On the other

hand, the purely gravity based deﬁnition of accessibil-

ity, factors in all PoIs, even those that would require

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

622

a prohibitive travel time. By combining the two as-

pects, we solve the aforementioned limitations. Note

that accessibility is agnostic to demand: it does not

describe where people currently go but it measures

where they potentically go (Miller, 2020). When

modifying the PT structure, we modify this “potential

of mobility” and thus we also impact where people

will go. For this reason, mixing current demand with

the deﬁnition of accessibility would be misleading, as

current demand is implicitly invalidated by PT design

actions.

We deﬁne the global accessibility of graph G as

acc(G) =

∑

c∈C

acc(c). (3)

Classic efﬁciency-based optimization of PT would

aim to maximize acc(G). Instead, our aim is to re-

duce the inequality in the geographical distribution of

accessibility, and thus we choose to consider the ac-

cessibility of the centroids that suffer from the worst

accessibility, as we aim to concentrate improvement

in such zones.

One could be tempted to apply max-min optimiza-

tion, trying to maximize the lowest accessibility in the

territory. However, when we tried that, we obtained

poor results. Indeed, we were ending up improving

areas that were remote and often uninhabited. Of-

ten, the improvement was enjoyed by too few loca-

tions. We therefore propose to maximize some bot-

tom quantile of the accessibility distribution. To the

best of our knowledge, this simple yet effective idea

has not been explored so far. We deﬁne the following

accessibility metric, related to the qth quantile:

acc

(G) =

∑

c∈C

acc(c), (4)

where C

deﬁnes the set containing the q% of cen-

troids with the least accessibility. Note that acc(G) =

acc

100

(G).

3.3 Problem Deﬁnition

Let us consider a PT graph G and a set B of n

can-

didate bus stops. Set B is contained in set V of nodes

of G. Set B = V \ C \ B is the set of non candidate

stops, i.e., the ones that will not be used to create the

new lines.

In broad terms, we consider the problem of the PT

operator to design k bus lines {l

,. ..,l

} (where num-

ber k is ﬁxed a-priori), passing by these n

bus stops,

in order to reduce inequality of accessibility. Any stop

in B may be already part of pre-existing lines or not.

The problem at hand may emerge in case a PT op-

erator wishes to build additional bus lines, passing by

stops B. Another case is when a PT operator wishes to

redesign current bus lines, while reusing current bus

stops.

In quantitative terms, we wish to ﬁnd graph G

∗

which is as G but also contains additional lines

,. ..,l

, such that acc

(G) is maximized. Specially,

if we deﬁne:

i, j

(

1, if bus stop j in line l

0, if bus stop j not in line l

(5)

We aim to solve the following optimization

max

σ(l

),σ(l

),...,σ(l

)

acc

(G), (6)

subject to the following constraint:

∑

i=1

i, j

= 1, ∀ j = 1,2...,n

. (7)

∑

j=1

i, j

≥ 2, ∀i = 1,2...,k. (8)

According to the values of x

i, j

, we can deﬁne each

line:

= {b

,. ..,b

},∀i = 1,2...,k. (9)

Calculating accessibility needs to ﬁnd shortest path

in current PT graph, which makes impossible to give

speciﬁc formulation of accessibility. Therefore, this

problem belongs to the integer programming of a

black-box function. Constraint 7 ensures that each

candidate stop is assigned to a line. With this con-

straint, we are forbidding a node to be part of multiple

lines. However, this limitation can be easily removed

by “duplicating” the same real stop into multiple can-

ditate stops in our model. Constraint 8 means that

each line has at least two bus stops. In addition to de-

termining which stops each line contains based on the

value of x

i, j

and Constraint 9, the permutation func-

tion σ(l

) (in Formulation 6) is also needed to deter-

mine the order of the stops in each line l

Note that maximizing the accessibility of the bot-

tom quantiles means, indeed, to improve the accessi-

bility of the poorest locations. Observe that, selecting

only the location with the worst accessibility as the

objective function generally returned, in our prelimi-

nary experiments, not reasonable results, as it concen-

trates all the optimization effort to just few, possibly

very remote, locations, where improving accessibil-

ity is anyways hopeless. Our idea of maximizing the

bottom quantiles avoid this kind of biased results.

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning

623

4 RESOLUTION METHOD

BASED ON GRAPH

REINFORCEMENT LEARNING

We decompose our problem (§3.3) as a bi-level opti-

mization: in the upper level, we partition the candi-

date bus stops in k subsets. In the lower level, each

subset will be transformed in a line, deciding the or-

der of the stops.

4.1 Markov Decision Process

Formulation

Let us denote by G the initial graph, i.e., the one when

no new bus lines have yet been added. We model the

upper level problem as the following Markov Deci-

sion Problem (MDP):

• States. A state is a partition S = (l

,. ..,l

) of can-

didate stops, where l

= {b

,. ..,b

} is the set of

bus stops assigned to line l

Each bus stop is as-

signed to a single line. Given any state S, we build

the line corresponding set l

of stops, i = 1,.. ., k.

To transform set l

in a line we need to decide the

order in which the stops in l

will be visited. Such

an order is calculated via a heuristic (Section 4.4).

Given sate S = (l

,. ..,l

) and having deﬁned the

lines corresponding to l

,i = 1,. .. ,k, we add to

graph G the edges corresponding to those lines

and obtain a new graph G(S).

• Actions. At each step, our optimization agent

shifts a bus stop b

from its current line l

to a

target line l

. The action is deﬁned by a tuple

a = (b

). The state changes from S to S

′

: state S

′

is equal to S, except for line l

which becomes l

\ {b

}, and for l

, which becomes l

= l

The action of changing a bus stop to its own line

is not admitted. Observe that ours is a Determin-

istic MDP (Dekel and Hazan, 2013), i.e., arrival

state S

′

can be deterministically calculated from

departing state S and action a.

• Rewards. The instantaneous reward collected

when applying action a = (b

) on state S, is

r(S,a) = acc



G(S

′

)



− acc

(G(S)), (10)

where parameter q must be chosen in advance.

• Policy: During training, our agent follows an ε-

greedy policy. At test time, actions are chosen

greedily with respect to the Q-values but our agent

keeps exploring with a random action every time

it ﬁnds a local optima.

For simplicity of notation, we use the same symbol l

to denote a line and also the set of stops assigned to it.

The sizes of the state space and the action space

are k · n

, considering a matrix with k lines and n

bus

stops can represent any state and action.

4.2 High-Level View of the

Optimization Approach

Due to the high size of the action and state spaces,

enumerating all the states and actions and learning

a Q-function that takes directly those states and ac-

tions as input is hopeless. Therefore, as common in

graph-related optimization tasks, we resort to a Mes-

sage Passing Neural Network (MPNN) (Wang et al.,

2023; Gilmer et al., 2017; Hameed and Schwung,

2023; Maskey et al., 2022). Via a MPNN, we embed

each node in a low dimension Euclidean space. Such

representation captures the “role” of that node within

the graph, based on the direct or indirect connections

with the other nodes. The process of node embedding

is thus able to capture the structure of a graph, so that

the RL agent can take decisions that take such struc-

ture into account.

A MPNN takes as input PT graph G(S) of current

state S, then it outputs the Q value for each action.

Next, the Greedy Policy performs an action accord-

ing to the Q values. At last, the reward, which is the

change of accessibility metric, helps to update param-

eters of MPNN. The following section will introduce

MPNN in more detail. Every time we shift a bus stop

from a bus line to another line, a reasonable method of

deleting and inserting bus stops in a line is presented

in Section 4.4.

4.3 Message Passing Neural Network

Let us associate to each candidate stop b a feature vec-

tor x

. Let us denote with X the matrix of the feature

vectors of all stops and with M

adj

the adjacency ma-

trix, where element (i, j) is 1 if there is a line in which

bus stop b

comes right before b

, and 0 otherwise.

A MPNN calculates a vector µ

, called embed-

ding, for each candidate bus stop b. Embedding µ

is a function of feature vector x

, of feature matrix X ,

and of adjacency matrix M

adj

In the following, all vectors like Θ

denote param-

eters that learned during training. The embedding of

bus stop b is initialized as

= f (x

,Θ

) ∈ R

. (11)

The vector of edge embeddings, one per each edge, is

initialized as

= g(M

adj

,X,Θ

) ∈ R

. (12)

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

624

Let us denote with N (b) the neighbor bus stops of

bus stop b. Note that since the bus lines change from

a state S to another, N (b) may also changes for bus

stop b.

The information is then shared to each of the

nodes’ neighbors through T rounds of messages. The

message passed to candidate stop b at round t + 1 is:

t+1

= M(µ

,{µ

}

u∈N (b)

,{w

}

u∈N (b)}

,Θ

) ∈ R

′

(13)

where w

is the embedding of edge between bus

stop u and bus stop b after t times iterations.

Embedding u

t+1

of candidate stop b by message:

t+1

= U(µ

t+1

,Θ

) ∈ R

, (14)

M and U are respectively message and update func-

tions at round t. After T rounds of message passing, a

prediction is produced by some Readout function, R.

In our case, the prediction is the set of Q-values corre-

sponding to the actions of the changing bus stops and

their target line:

{Q(S,a)}

a∈A

= R({µ

}

b∈B

,Θ

), (15)

where A is the set of actions, and B is the set of bus

stops. Note that µ

is calculated via Formula 13 and

Formula 14, thus varys for different state S. Mes-

sage function M, Update function U, and Readout

function R, as well as the embedding functions f

and g, are all neural network layers with learnable

weights {Θ

,Θ

,{Θ

}

,{Θ

}

,Θ

}. Every time our

agent takes an action and gets a reward r. The One-

Step Q-learning loss is:

Loss(S,a) = (γ · max

′

Q(S

′

) + r − Q(S

′

,a))

(16)

where γ is a Discount factor. We update learnable

weights via Stochastic Gradient Descent of loss func-

tion 16. (Khalil et al., 2017) also used the same loss

to deal with the combination problem on the graph.

From (Blakely et al., 2021), the total time complexity

of the forward step and the backward step of MPNN is

O(T · (|V| + |E|)) for sparse matrix of PT graph with

embedding vector dimension unchanged. Combined

with action space is k · n

in Section 4.1, the time cost

of each step is linearly related to the sum of the num-

ber of nodes and edges in the graph G.

4.4 Sorting Algorithm

Recall that state S is a partition (l

,. ..,l

) of set B

of candidates nodes. State S just establishes to which

line each candidate node belongs. However, to trans-

form any set l

into a line, a certain ordering of its

stops must be established.

In this section, we will introduce the method of

determining the order of bus stops. This optimal

method should also maximize our accessibility objec-

tive function. However, since it is a Traveler Sales-

man Problem, deﬁning such a function seems utterly

complex or with a very high computational cost. Con-

sidering that order must be determined every time the

RL agent selects a new bus stop subset, we decided to

use the shortest path algorithm as a proxy for the max-

imum accessibility path algorithm. We understand

that this approach is suboptimal as we optimize dis-

tances, but accessibility is a measure completed over

the whole graph. Nevertheless, using this algorithm

optimizes the headway of our bus lines, and thus ren-

ders a good enough accessibility with low computa-

tional costs.

4.5 Reinforcement Learning Equality

Algorithm

Given the number of bus lines k and the PT network

G, we propose a Reinforcement Learning Equality al-

gorithm (Algorithm 1) to plan k bus lines efﬁciently,

in order to optimize the accessibility objective func-

tion acc

(·) (q = 20,50,100.). Our base idea is to

get a better state-action function Q by updating the

MPNN network. Note that only when our objec-

tive function value is better than before, we will up-

date our MPNN network. We still explore different

actions (and thus different graph conﬁgurations) for

each step, also the ones that decrease the score with

respect to the last graph obtained. We just remove

from exploration those graphs that are worse than the

initial one. If acc

(G) has not changed in the past cer-

tain iterations (e.g., 5 iterations), the episode will be

ended. Algorithm 1 terminates when a certain time

threshold (e.g., 1h) is exceeded. In fact, the initial

graph G of our algorithm can be different for each

episode. Therefore, it has the ability to learn among

different PT networks.

5 EVALUATION

5.1 Considered Scenario

To showcase our agent, we consider a simpliﬁed ver-

sion of Montreal. Note that we do not aim to set up

a realistic mobility scenario with all the needed de-

tails for transport planning. This would indeed re-

quire years of effort, by specialized transport consul-

tant companies, and it is out of our scope. Here, our

intention is to show that the proposed approach is ef-

fective from a methodological and algorithmic point

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning

625

Data: Number of lines k, initial graphs G,

quantile q

Result: The best accessibility acc

best

while Running time threshold is exceeded do

Initialization: Randomly partition the

bus stops between the lines to obtain

initial state S;

Sort the lines (§4.4), and update G;

Set acc

best

= acc

(G);

while acc

(G) has not changed in the

past 5 iterations do

Predict Q = MPNN(G,S) (15);

Update the state with action

a = argmax

Q(S,a);

Sort each line l

(§4.4);

Calculate headway t

via (1) for

each l

;

Update graph G with the new bus

lines and headway ;

Compute acc

(G) (see (4)) ;

if acc

best

> acc

(G) then

Set acc

best

= acc

(G);

Compute loss via (16);

Update learnable weights

{Θ

,Θ

,{Θ

}

,{Θ

}

,Θ

} of

MPNN by Gradient Descent;

else

Continue;

end

Algorithm 1: Online Reinforcement Learning Equality al-

gorithm.

Figure 3: Accessibility of Montreal Metro network.

of view. For this reason, any cost-beneﬁt analysis of

our resulting PT network in Montreal, and any de-

tailed environmental assesment is out of scope for this

algorithmic focused paper. Observed that one could

replace accessibility with cost or km traveles or any

other transport related metric. However, we chose to

focus on the most difﬁcult metric among those used in

common PT design problem, as to optimize accessi-

bility quantiles requires the model to be able to deeply

capture the inter-relation between the graph and its

surrounding environment, as well as spatial inequali-

ties. This is the focus and the interest of this paper.

From the General Transit Feed Speciﬁcation

(GTFS) data of Montreal ((STM, 2023)), we take the

station locations, the sequence of stations of all lines.

We assume the PT operators wishes to keep the metro

(subway) network as it is, but wishes to build bus lines

in order to reduce the inequality of the geographi-

cal distribution of accessibility. Therefore, set B of

candidate stops consists of all bus stops, while set B

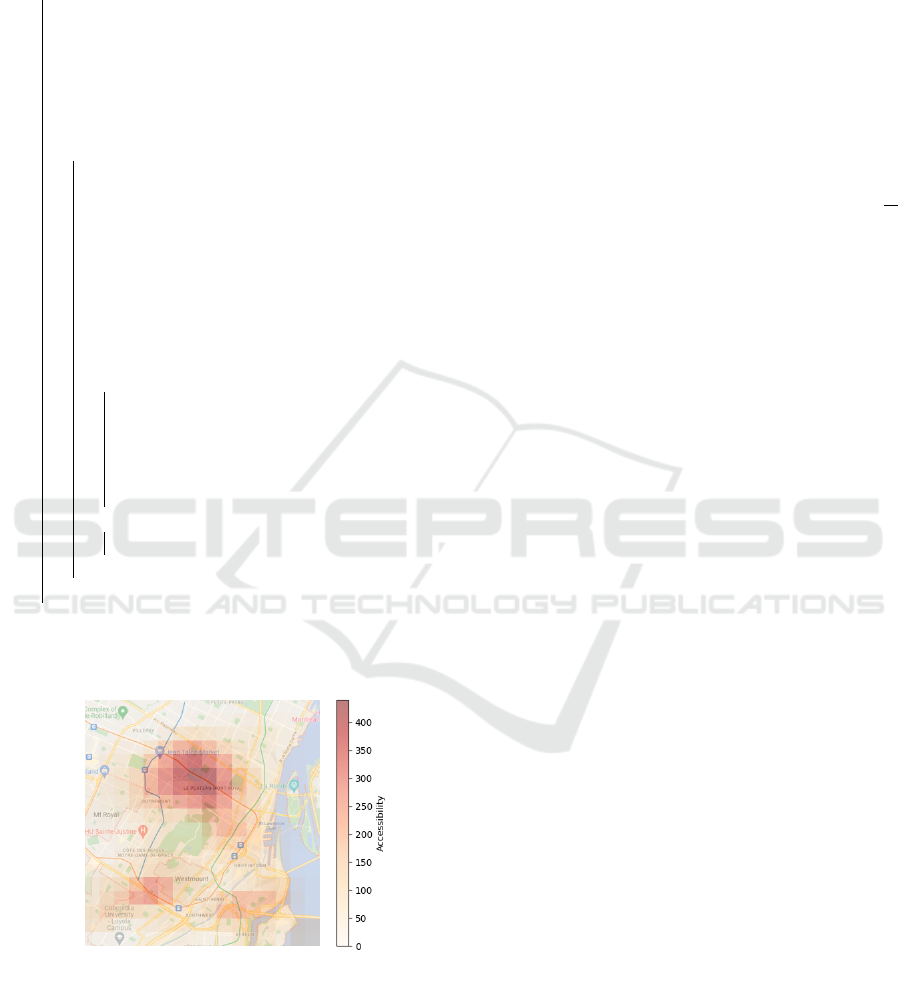
of non-canidate stops are the metro stops. Figure 3

shows the accessibility distribution of accessibility re-

sulting from initial PT graph G of Montreal, which

we assume consists of only the current lines. These

assumptions may correspond to the case in which the

PT operator wishes to completely redesign bus lines

(so that we can remove all bus lines from our initial

graph G). The metro network is composed of 4 lines

of different sizes. It covers mostly the center of Mon-

treal, which delimits our environment boundaries. In

our case, bus stop locations can change over the year.

We wanted to check that our method conveys good re-

sults, no matter the set of stops. This is the reason that

our results are shown for 100 different instances of the

problem, each with a different set of stops. The real

locations of bus stops in Montreal can be easily added

to the training set as an instance. To establish prelim-

inary results, we ﬁrst limit the number of bus stops to

an arbitrary low number of 72. We generate the bus

stops as follows. We tessellate the territory with a reg-

ular grid. Note that this tessellation is not necessarily

the same as the one described in Section 3.1. Within

each cell of such a grid a bus stop is created with a

random location within the cell. By generating bus

stop locations in this way, we ensure uniformity of

the bus stops on a larger scale. Consequently, all ar-

eas of the territory have access to the public transport

network to all regions. We extract points of interest

from Open Street Map (OpenStreetMap contributors,

2017) in combination with the Overpass API and as-

sign to the centroids the point of interest number in

their area. For the points of interest, we select some

of the main amenities in a city (schools, hospitals,

police stations, libraries, cinemas, banks, restaurants,

and bars). Some of these amenities present a distri-

bution which is relatively uniform over the map (e.g.,

schools) while some others have higher densities in

popular streets (e.g., restaurants). Scenario parame-

ters are in Table 1.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

626

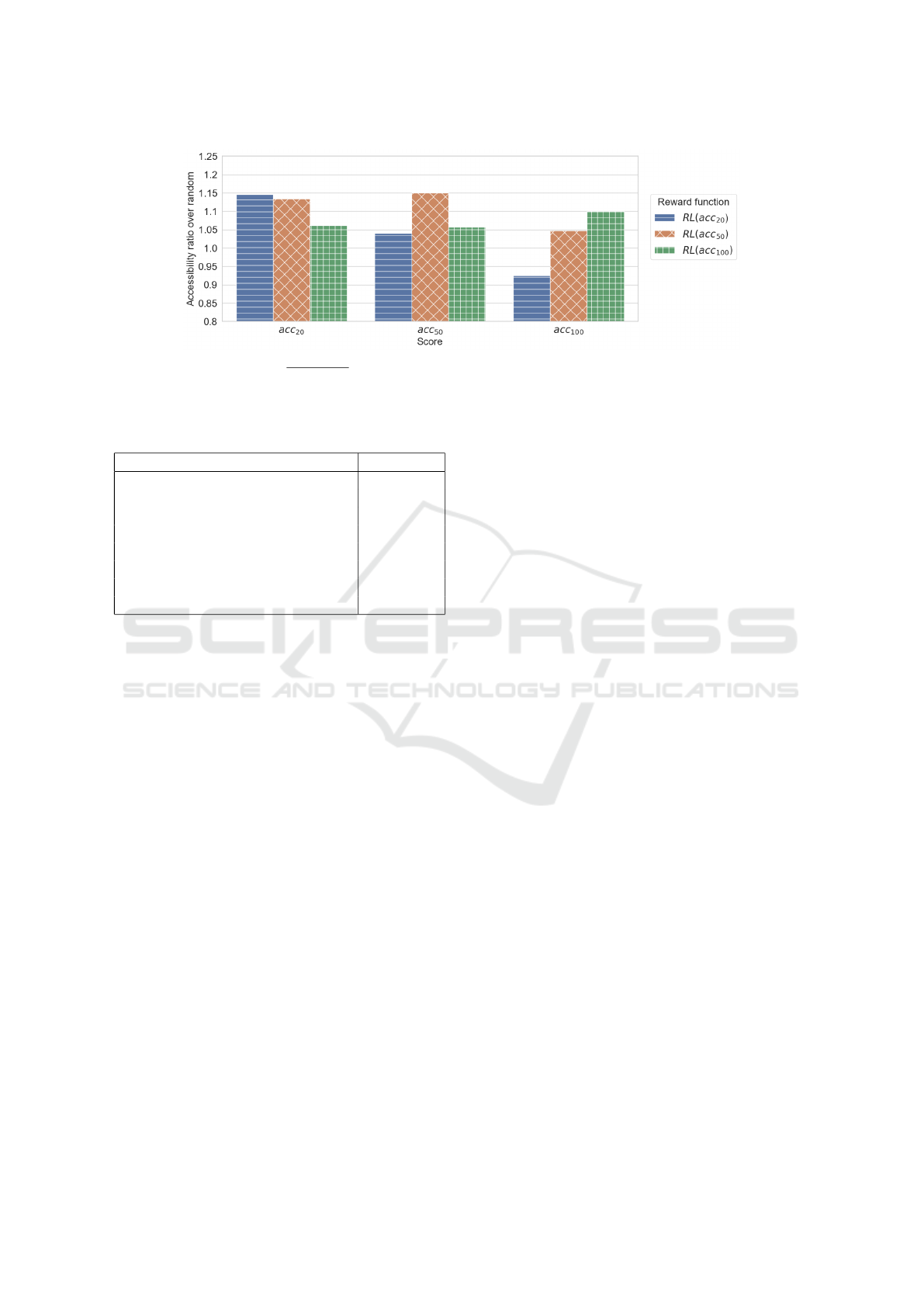
Figure 4: Accessibility ratio (

acc

(RL)

acc

(random)

, a,b = 20,50 or 100) via our Reinforcement Learning Equality algorithm (Algo-

rithm 1) against the random search algorithm. x-axis shows different metrics of the Random search algorithm, and the labels

show the different metrics used by RL methods.

Table 1: Scenario parameters.

Parameter Value

Number of bus stops n

Number of lines k 3

Maximum accessibility time T

max

30 minutes

Walking speed s

(Ali et al., 2018) 4.5 km/h

Bus speed s

(Ishaq and Cats, 2020) 28km/h

Fleet size per line N

Distance between adjacent centroids 1km

Discount factor γ 0.95

5.2 Baselines

We compare the performance of our algorithm to two

baselines. To compare the algorithms, we deﬁne a

maximum running time of 1-hour for each method

and check which is the best bus lines deployment

found. Specially, 1 hour is the training time for our

algorithm, our testing time is too short and can be

ignored. For Baselines, they keep looking for better

graphs within one hour. After one hour, we simply

stop searching and output the current optimal graph

of Baselines.

5.2.1 Random Search Algorithm

Random states of the form S = (l

,. ..,l

) are gen-

erated, each corresponding to a random partition of

set B of candidate stops. At every generated state S =

,. ..,l

), each set l

is sorted as in Section 4.4

to generate the corresponding lines. Then the cor-

responding graph G

rnd

is constructed, and accessi-

bility acc

rnd

) is computed. This process is re-

peated until the running time threshold is exceeded.

The largest value of acc

rnd

) found at that point

is then returned. This random search algorithm has

the advantage over our algorithm to visit very diverse

states and no time for computing node embeddings,

rewards, etc. The number of states visited by this al-

gorithm is much larger than the one visited by our

approach, within the same running time threshold.

5.2.2 Genetic Algorithm

The second baseline is a genetic algorithm (Algo-

rithm 2). It is a popular metaheuristic to solve combi-

natorial problems, and PT design problems in partic-

ular (Farahani et al., 2013). In transit network design,

state-of-the-art algorithms are generally metaheuris-

tic. There are many ﬂavors of GA for transit net-

work design. Our GA algorithm is an effort to repro-

duce those. However, due to difﬁcult reproducibility

of such methods, we cannot claim our GA algorithm

is exactly the same as the one in the state of the art.

We are sure that we did our best to improve our GA

algorithm, in the effort to have it represent the state

of the art. We adopt acc

(G) as the ﬁtness function.

Next, the design of the evolutionary functions must

be done carefully so that the new generations inherit

good genes from their parents. Therefore, the most

important function that must be modiﬁed for that case

is the crossover function. More popular approaches,

like Order Crossover 1 (OX1) preserve relative order

of the states and thus their structure, are used in sim-

ilar problems like TSP (Kora and Yadlapalli, 2017)

and VRP (Prins, 2004). Children can beneﬁt from ad-

vantageous orderings of the parent nodes, as from our

experience, close nodes (sorted by the SORT func-

tion) are often good to increase accessibility.

5.3 Results

For the ﬁrst comparison, we train our Reinforcement

Learning Equality agent and test it on the same bus

stop distribution. The random search baseline run

with different accessibility metric. In Figure 4, the

different colors correspond to different accessibility

metrics adopted as reward of our RL algorithm. Fig-

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning

627

Input: Size n

pop

of the population, number

of lines n

lines

, number of parents n

par

per

generation, timeout t

limit

of the benchmark,

probability P

mut

of an attribute to mutate ;

Result: The best accessibility over all

generations acc

best

Initialization: Initialize

pop

= (I

,. ..,I

pop

) at generation 0 as

individuals with random partitions of the

bus stops between the lines. Sort the lines of

each individual. Compute acc

best

;

while Running time threshold is exceeded do

Select n

par

best parents =

Tournament(pop,acc

) ;

while pop

is ﬁlled with n

pop

children. do

, p

= Sample(parents,2) ;

c = OX(p

, p

) ;

c = Mutate(c,P

mut

) ;

Sort the lines of each child

c = SORT (c) ;

pop

.Append(c) ;

end

Compute acc

best

= max(acc

(pop)) ;

end

Algorithm 2: Genetic algorithm.

ure 4 shows that our approach outperforms the ran-

dom baseline by 10%-15% when trained and tested

on the same accessibility metric (e.g., the agent op-

timizes acc

with its reward function and is tested

on the same metric). Our algorithm also improves

the other different accessibility metrics than the one

it has been trained by an average ratio of 5% over the

baseline. Only the agent trained on acc

performs

worse than the random baseline. Because when we

optimize PT with equality (acc

) as the optimization

goal, we may lose some efﬁciency (acc

100

). Planning

bus lines need to make a trade-off between equality

and efﬁciency. It should be noted that the balance be-

tween equality and efﬁciency is a “political” choice,

which the transport planner should choose, and it is

not possible to deﬁne the “best” value of the quantile.

A practical option for the transport planner could be

to obtain different networks, with different quantiles,

and then compare them a posteriori to check which

one is the most adapted to the scenario at hand. In any

case, our method is agnostic to the “political” choice

of q%.

Our agent is also able to apply to different bus stop

distributions. We assume that each bus stop remains

in the same grid cell, but its position is changed for

different distributions. Now we select acc

as our

accessibility metric for training and testing on a set of

100 PT graphs with different bus stop distributions.

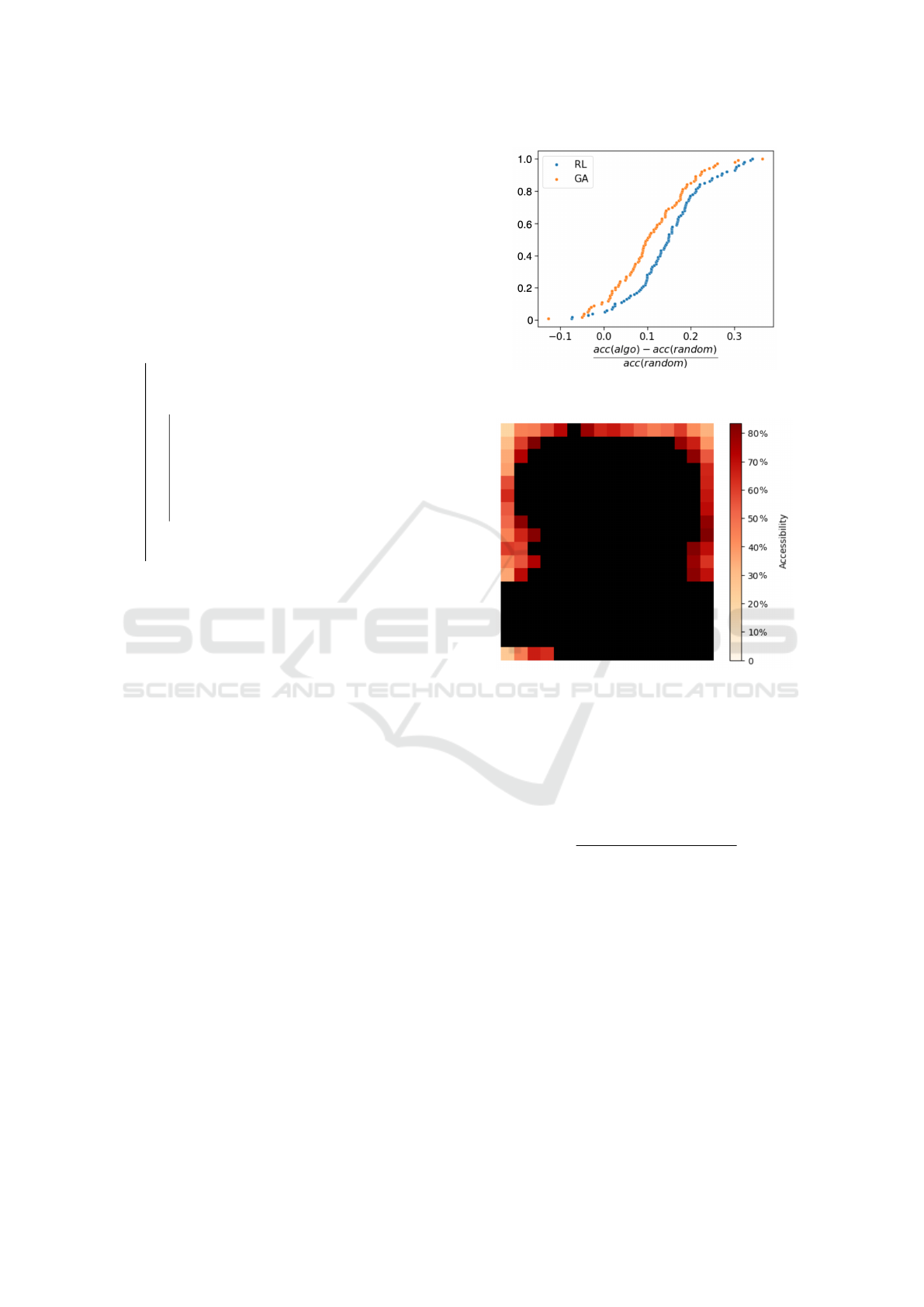
Figure 5: CDF of acc

improvements of different algo-

rithms comparing with random baseline.

Figure 6: Heatmap of percentage improvement of accessi-

bility (%) via Reinforcement Learning Equality algorithm

against the random baseline on underserved areas (The

darker red areas indicate that our approach improves more

obviously than the random baseline in these areas. Black

areas with the best 80% accessibility are not considered).

In Fig. 5, we plot the value of CDF (y-axis) of acc

improvements value

R =

acc(algo) − acc(random)

acc(random)

, (17)

where acc(random) is the optimized acc

value by

the random search, and acc(algo) is the optimized

acc

value by Algorithm 1 or GA. The higher the

value of R (x-axis), the better the Algorithm 1 or the

GA than the random baseline. We observe in both

cases that R follow a normal distribution. Using this

data, we conduct a t-test with the null hypothesis (H

)

that mean(R) = 0. We run the t-test and get a T-

statistic value of 17. From the p-value p = 3 ∗ 10

−31

we can reject H

with conﬁdence more than 99.9%.

Thus, we conﬁrm that our approach work better than

random baseline on graphs with different bus stop

distributions. Similarly, the Genetic Algorithm per-

forms better than the random baseline. Using a sim-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

628

ilar procedure to compare our Reinforcement Learn-

ing Equality algorithm and the Genetic algorithm, we

show that our approach performs better on different

test graphs with conﬁdence > 99.9% (the T-statistic

value is 8).

We next test the performance of our algorithm

on the actual geography of Montreal. Considering

acc

as the objective function, so our algorithm fo-

cuses more on optimizing those areas with the 20%

worst accessibility. We also calculate the value of im-

provements compared to Random Baseline (acc

−

acc

Random

) for each centroid with the lowest accessi-

bility in the initial graph. Figure 6 shows that our ap-

proach preform better than random baseline in these

areas, the improvement in most of these areas ex-

ceeded 40%.

6 CONCLUSION

In this paper, we proposed an approach that combined

Message Passing Neural Networks (MPNN) and Re-

inforcement Learning (RL) to optimize bus line de-

sign. The objective is to reduce the inequality in

the distribution of accessibility provided via Public

Transport (PT). Our results showed that MPNN and

RL are more effective than commonly used meta-

heuristics, as they can capture the PT graph structure

and learn the dependencies between lines and the dis-

tribution of Points of Interest, where meta-heursitcs

restrict themselves to a random exploration of the so-

lution space.

In future work, we will test how our method gener-

alizes to different metro networks, realistically mod-

eled via open data, and how it scales when the prob-

lem involves much more bus stops than considered

here. In fact, different transit modes can be repre-

sented by different graphs. We can connect these

graphs to each other to form a multilayer graph. Then,

our method can be applied with modiﬁcations on the

multilayer graph. Of course, for metro networks, once

the network infrastructure is put in place, it cannot

be easily modiﬁed, as with bus lines. Results from

the algorithm would thus require a thorough “politi-

cal evaluation” of the results of the algorithm before

implementation. For example, We can set different

weights so that the algorithm prefers to modify bus

lines rather than metro lines. Moreover, we expect

even better results when allowing the same bus stop

to be part of multiple bus lines (which is not the case

in this work).

The main takeaway of this paper is that combin-

ing MPNN and RL is promising to solve PT network

design, at a strategic planning phase.

ACKNOWLEDGEMENTS

This work has been supported by the French ANR re-

search project MuTAS (ANR-21-CE22-0025-01) and

by Hi!Paris - Paris Artiﬁcial Intelligence for Society.

REFERENCES

Ali, M. F. M., Abustan, M. S., Talib, S. H. A., Abustan, I.,

Abd Rahman, N., and Gotoh, H. (2018). A case study

on the walking speed of pedestrian at the bus terminal

area. In E3S Web of Conferences, volume 34, page

01023. EDP Sciences.

Anable, J. (2005). ‘complacent car addicts’ or ‘aspir-

ing environmentalists’? identifying travel behaviour

segments using attitude theory. Transport policy,

12(1):65–78.

Barcel

o, J., Grzybowska, H., and Orozco-Leyva, A. (2018).

City logistics.

Barrett, T., Clements, W., Foerster, J., and Lvovsky, A.

(2020). Exploratory combinatorial optimization with

reinforcement learning. In Proceedings of the AAAI

conference on artiﬁcial intelligence, volume 34, pages

3243–3250.

Blakely, D., Lanchantin, J., and Qi, Y. (2021). Time and

space complexity of graph convolutional networks.

Accessed on: Dec, 31:2021.

Calabro, G., Araldo, A., Oh, S., Seshadri, R., Inturri,

G., and Ben-Akiva, M. (2023). Adaptive transit de-

sign: Optimizing ﬁxed and demand responsive multi-

modal transportation via continuous approximation.

Transportation Research Part A: Policy and Practice,

171:103643.

Chakroborty, P. (2003). Genetic algorithms for optimal ur-

ban transit network design. Computer-Aided Civil and

Infrastructure Engineering, 18(3):184–200.

Darwish, A., Khalil, M., and Badawi, K. (2020). Optimis-

ing public bus transit networks using deep reinforce-

ment learning. In 2020 IEEE 23rd International Con-

ference on Intelligent Transportation Systems (ITSC),

pages 1–7. IEEE.

Dekel, O. and Hazan, E. (2013). Better rates for any adver-

sarial deterministic mdp. In International Conference

on Machine Learning, pages 675–683. PMLR.

Duan, L., Zhan, Y., Hu, H., Gong, Y., Wei, J., Zhang, X.,

and Xu, Y. (2020). Efﬁciently solving the practical

vehicle routing problem: A novel joint learning ap-

proach. In Proceedings of the 26th ACM SIGKDD

international conference on knowledge discovery &

data mining, pages 3054–3063.

EU, E. P. (2019). CO

emissions from cars: facts and ﬁg-

ures (infographics). https://www.europarl.europa.eu/

topics/en/article/20190313STO31218.

Farahani, R. Z., Miandoabchi, E., Szeto, W. Y., and Rashidi,

H. (2013). A review of urban transportation network

design problems. European journal of operational re-

search, 229(2):281–302.

Public Transport Network Design for Equality of Accessibility via Message Passing Neural Networks and Reinforcement Learning

629

Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., and

Dahl, G. E. (2017). Neural message passing for quan-

tum chemistry. In International conference on ma-

chine learning, pages 1263–1272. PMLR.

Gkiotsalitis, K. (2022). Public transport optimization.

Springer.

Guti

errez-Jarpa, G., Laporte, G., and Marianov, V. (2018).

Corridor-based metro network design with travel ﬂow

capture. Computers & Operations Research, 89:58–

67.

Hameed, M. S. A. and Schwung, A. (2023). Graph neu-

ral networks-based scheduler for production planning

problems using reinforcement learning. Journal of

Manufacturing Systems, 69:91–102.

Ishaq, R. and Cats, O. (2020). Designing bus rapid transit

systems: Lessons on service reliability and operations.

Case Studies on Transport Policy, 8(3):946–953.

Khalil, E., Dai, H., Zhang, Y., Dilkina, B., and Song, L.

(2017). Learning combinatorial optimization algo-

rithms over graphs. Advances in neural information

processing systems, 30.

oksal Ahmed, E., Li, Z., Veeravalli, B., and Ren, S.

(2022). Reinforcement learning-enabled genetic algo-

rithm for school bus scheduling. Journal of Intelligent

Transportation Systems, 26(3):269–283.

Kora, P. and Yadlapalli, P. (2017). Crossover operators in

genetic algorithms: A review. International Journal

of Computer Applications, 162(10).

Kovalyov, M. Y., Rozin, B. M., and Guschinsky, N. (2020).

Mathematical model and random search algorithm for

the optimal planning problem of replacing traditional

public transport with electric. Automation and Remote

Control, 81:803–818.

Maskey, S., Levie, R., Lee, Y., and Kutyniok, G. (2022).

Generalization analysis of message passing neural

networks on large random graphs. Advances in neural

information processing systems, 35:4805–4817.

Miller, E. J. (2020). Measuring accessibility: Methods and

issues. International Transport Forum Discussion Pa-

per.

OpenStreetMap contributors (2017). Planet dump re-

trieved from https://planet.osm.org . https://www.

openstreetmap.org.

Owais, M. and Osman, M. K. (2018). Complete hierarchical

multi-objective genetic algorithm for transit network

design problem. Expert Systems with Applications,

114:143–154.

Prins, C. (2004). A simple and effective evolutionary algo-

rithm for the vehicle routing problem. Computers &

operations research, 31(12):1985–2002.

Quynh, T. D. and Thuan, N. Q. (2018). On optimization

problems in urban transport. Open Problems in Opti-

mization and Data Analysis, pages 151–170.

Saeidizand et al. (2022). Revisiting car dependency: A

worldwide analysis of car travel in global metropoli-

tan areas. Cities.

Schittekat, P., Kinable, J., S

orensen, K., Sevaux, M.,

Spieksma, F., and Springael, J. (2013). A metaheuris-

tic for the school bus routing problem with bus stop

selection. European Journal of Operational Research,

229(2):518–528.

STM (2023). GTFS data (bus schedules and m

etro fre-

quency) in Montr

eal. https://www.stm.info/en/about/

developers.

Sun, Y., Schonfeld, P., and Guo, Q. (2018). Optimal ex-

tension of rail transit lines. International Journal of

Sustainable Transportation, 12(10):753–769.

UN (2020). Make cities and human settlements inclusive,

safe, resilient and sustainable.

Wang, Z., Di, S., and Chen, L. (2023). A message pass-

ing neural network space for better capturing data-

dependent receptive ﬁelds. In Proceedings of the 29th

ACM SIGKDD Conference on Knowledge Discovery

and Data Mining, pages 2489–2501.

Wei, M., Liu, T., and Sun, B. (2021). Optimal routing

design of feeder transit with stop selection using ag-

gregated cell phone data and open source gis tool.

IEEE Transactions on Intelligent Transportation Sys-

tems, 22(4):2452–2463.

Wei, Y., Jin, J. G., Yang, J., and Lu, L. (2019). Strate-

gic network expansion of urban rapid transit systems:

A bi-objective programming model. Computer-Aided

Civil and Infrastructure Engineering, 34(5):431–443.

Wei, Y., Mao, M., Zhao, X., Zou, J., and An, P. (2020). City

metro network expansion with reinforcement learn-

ing. In Proceedings of the 26th ACM SIGKDD Inter-

national Conference on Knowledge Discovery & Data

Mining, pages 2646–2656.

Welch, T. F. et al. (2013). A measure of equity for public

transit connectivity. Journal of Transport Geography.

Yoo, S., Lee, J. B., and Han, H. (2023). A reinforcement

learning approach for bus network design and fre-

quency setting optimisation. Public Transport, pages

1–32.

Yoon, J., Ahn, K., Park, J., and Yeo, H. (2021). Transferable

trafﬁc signal control: Reinforcement learning with

graph centric state representation. Transportation Re-

search Part C: Emerging Technologies, 130:103321.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

630