Quality Clustering for Reducing the Search Space for Mobile Stroke Unit
Allocation
Muhammad Adil Abid
1 a
, Johan Holmgren
1 b
, Fabian Lorig
1 c
and Jesper Petersson
2,3 d
1
Department of Computer Science and Media Technology, Malm
¨
o University, 21119 Malm
¨
o, Sweden
2
Department of Neurology, Lund University, 221 85 Lund, Sweden
3
Department of Health Care Management, Region Sk
˚
ane, 21428 Malm
¨
o, Sweden
Keywords:
Ambulance Allocation, Optimization, Healthcare, Mobile Stroke Unit, Clustering, Reducing Search Space,
Fast Convergence.
Abstract:
Mobile stroke units (MSUs), which are specialized ambulances equipped with a brain imaging device and
staffed with trained healthcare personnel, have the potential to provide rapid on-site diagnosis and treatment
for stroke patients. To maximize the efficiency of utilizing MSUs, it is crucial to strategically allocate these
units. When solving the MSU allocation problem, the current methods search the whole search space when
looking for the optimal solutions, which causes slow convergence. In the current paper, we propose the Quality
Clustering for Reducing the Search Space (QCRSS) framework to reduce the search space by filtering out
ambulance locations without negatively affecting the quality of the solution too much when solving the MSU
allocation problem. By narrowing down the set of possible locations, the problem becomes more manageable,
leading to faster convergence when solving the MSU problem. Extensive experiments under the multiple
MSU settings show that the QCRSS is largely faster in convergence toward the optimal solution by reducing
the search space by 5x, 11x, 26x, and 67x for two, three, four, and five MSUs, respectively. We illustrate the
performance of the QCRSS through both qualitative and quantitative analyses.
1 INTRODUCTION
A stroke is a severe neurological condition caused by
disrupted blood flow inside the brain, caused by ei-
ther a blockage (ischemic stroke) or a ruptured blood
vessel (hemorrhagic stroke) (Patil et al., 2022). With-
out prompt medical intervention, a stroke can lead to
permanent brain damage, disability, and death. The
global burden of stroke is staggering; it is estimated
that one in six people will experience a stroke during
their lifetime, with an annual incidence of 15 million
cases and 5.8 million deaths (World Stroke Organi-
zation, 2023). In Sweden alone, over 21, 000 indi-
viduals suffer strokes every year, with approximately
3, 900 cases occurring within the Southern Healthcare
Region (SHR) (The Swedish Stroke Register, 2023),
which is the focus area of the current study. The SHR
encompasses both densely populated and rural areas,
a
https://orcid.org/0000-0002-0403-5353
b
https://orcid.org/0000-0001-7773-9944
c
https://orcid.org/0000-0002-8209-0921
d
https://orcid.org/0000-0003-3322-6383
presenting a significant challenge for prehospital care.
Beyond the immediate medical impact, stroke also
poses a significant long-term challenge, as it can
lead to disability and financial strain not only for pa-
tients and their families but also for society (Luengo-
Fernandez et al., 2020) (Majersik and Woo, 2020).
Therefore, the timely treatment of stroke is crucial, as
patients who receive treatment earlier have a signif-
icantly better chance of recovery compared to those
who receive delayed care (Ashraf et al., 2023). How-
ever, providing immediate and effective stroke treat-
ment remains a challenge due to logistical hurdles and
difficulties in accurately diagnosing stroke in the field
(Blacker and Hankey, 2014). Ischemic strokes, the
most common type, require clot-dissolving medica-
tions (thrombolysis) or clot removal (thrombectomy)
to restore the blood flow. Conversely, hemorrhagic
strokes, caused by bleeding blood vessels, necessitate
immediate blood pressure reduction to prevent further
bleeding. Unfortunately, the initial symptoms of both
stroke types are typically similar, making a quick and
precise diagnosis essential to avoid administering the
wrong treatment, which could be life-threatening.
Abid, M. A., Holmgren, J., Lorig, F. and Petersson, J.
Quality Clustering for Reducing the Search Space for Mobile Stroke Unit Allocation.
DOI: 10.5220/0013154000003911
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 18th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2025) - Volume 2: HEALTHINF, pages 105-114
ISBN: 978-989-758-731-3; ISSN: 2184-4305
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
105

Mobile stroke units (MSUs) have emerged as
a promising solution to expedite stroke treatment
(Bowry and Grotta, 2017) (Navi et al., 2022). These
specialized ambulances are equipped with CT scan-
ners, allowing the ambulance personnel on site, to-
gether with stroke experts connected by telemedicine,
to diagnose stroke type and initiate treatments like
thrombolysis directly in the ambulance (Harris,
2021). In many cases, this enables to reduces the
time to treatment, at least corresponding to the time
needed to transport the patient to an acute hospital
with stroke diagnosis facilities. While MSUs offer
significant advantages, their high operational costs
limit the number of units a region can typically deploy
(Southerland and Brandler, 2017). Therefore, strate-
gically positioning MSUs is crucial for maximizing
the patient benefit within a specific geographic area
(Amouzad Mahdiraji et al., 2021)(Nour et al., 2022).
This leads to the MSU allocation problem, which is
the optimization problem that aims to identify the op-
timal locations for a fixed number of MSUs at exist-
ing ambulance station locations within a geographic
area covering the efficiency perspective. Efficiency
refers to covering as many patients as possible to re-
ceive treatment in a shorter window of time.
To efficiently allocate the MSUs in a region,
Amouzad Mahdiraji et al. (Mahdiraji et al., 2021)
apply the exhaustive search. In another study,
Amouzad Mahdiraji et al. (Amouzad Mahdiraji et al.,
2023) propose a mathematical optimization model
(Amouzad Mahdiraji et al., 2023) using mixed integer
linear programming (MILP). However, both of these
approaches face significant computational challenges
for large geographic areas (Abid et al., 2023). In re-
cent studies (Abid et al., 2023) (Abid et al., 2024),
Abid et al. use genetic algorithms to solve the MSU
allocation problem. Typically, the above-mentioned
approaches use the whole search space when search-
ing for the optimal solution. As a result, the conver-
gence can be slow. We hypothesize that if we could
reduce the search space by filtering out ambulance lo-
cations without significantly compromising the qual-
ity of the solution, we can speed up the optimization
process by focusing on the smaller search space, thus
obtaining faster convergence. Therefore, the question
naturally arises: How can we reduce the search space
effectively when solving the MSU allocation prob-
lem?
In the current paper, we propose the Quality
Clustering for Reducing the Search Space (QCRSS)
method to solve the MSU allocation problem. It
is a preprocessing framework for search algorithms
that explicitly exploits the spatial distribution of am-
bulance locations to narrow down the search space.
The ultimate aim is to enable the search algorithm to
traverse a smaller search space instead of the whole
search space. In the QCRSS framework, we first per-
form a preprocessing step using clustering to group
the ambulance locations (or stations). Thereafter, we
select only one representative from each cluster. The
problem is then solved using the selected set of repre-
sentatives. The core idea behind the clustering is that
geographically close ambulance stations are likely to
have similar response times to emergency calls.
The paper’s key contributions are summarized as
follows:
1. An optimization framework, the Quality Clus-
tering for Reducing the Search Space (QCRSS),
which consists of a preprocessing step and a
problem-solving step to solve the MSU allocation
problem. The primary contribution of the pro-
posed method lies in the preprocessing step.
2. An application to a real-world case study of
the Southern Healthcare Region (SHR), Sweden.
This region is a combination of densely populated
and more rural areas, which is the biggest chal-
lenge of pre-hospital care.
3. An illustration through visualization of how the
QCRSS framework can significantly improve the
convergence speed across different MSUs scenar-
ios. We further validate the effectiveness of our
model through a comprehensive quantitative and
qualitative analysis.
The rest of this paper is structured as follows: Sec-
tion 2 presents an overview of related work. Sec-
tion 3 provides the formal definition of the MSU op-
timization problem. Section 4 describes the proposed
methodology, and Section 5 encompasses the compu-
tational study. Finally, Sections 6 and 7 conclude the
paper by summarizing the conclusions and proposing
future areas for research.
2 RELATED WORK
In the field of emergency medical services, re-
searchers have explored various models for optimal
MSUs allocation. Recently, Amouzad Mahdiraji et
al. (Mahdiraji et al., 2021) use exhaustive search (ES)
to solve the MSU allocation problem for one to three
MSUs across 39 potential locations to minimize the
travel time to treatment, covering both the efficiency
and equity perspectives for prehospital stroke care
in the SHR. The ES systematically explores all po-
tential combinations of MSU locations to determine
whether each combination meets the problem’s crite-
ria and assesses its quality using an objective function.
HEALTHINF 2025 - 18th International Conference on Health Informatics
106

However, as the number of possible combinations of
MSU locations increases, with an increasing number
of MSUs, the ES method results in an exponentially
increasing search space. Consequently, the computa-
tional time required for ES often becomes impracti-
cally high.
Another study (Amouzad Mahdiraji et al., 2023)
propose a mathematical optimization model for the
MSU allocation problem, aiming to determine the op-
timal placement of MSUs within a given geographic
region. The model was applied to the SHR in Sweden.
The optimization model is a mixed integer linear pro-
gramming model. Despite the model’s potential, it be-
came apparent when using the Gurobi solver (Gurobi
Optimization, LLC, 2024) that the model’s complex-
ity limited its application to just two counties in the
SHR. In a related study (Abid et al., 2023), Abid et al.
propose a time-efficient genetic algorithm to solve the
MSU allocation problem. This model demonstrates
high efficiency and increased scalability, covering a
broader range of regions. However, the random ini-
tial population selection causes the traditional GA to
converge slowly, necessitating a significantly higher
amount of generations to evolve the randomly se-
lected starting solutions into improved ones. The ran-
dom selection might choose ambulance locations that
are close to each other, leading to poor coverage and a
lack of diversity in the solution space. Hence, the tra-
ditional GA may struggle to explore other, potentially
better regions. To overcome this limitation, Abid et
al. (Abid et al., 2024) introduce a cluster-based GA
model to improve performance. This method uses
clustering to strategically select the initial population
by including MSUs in geographically distant areas to
provide a broader spread and better coverage from the
beginning.
The aforementioned methods consider the whole
search space (every possible ambulance location)
when solving the MSU allocation problem. The
search space may contain many ambulance location
solutions with similar performance. This can slow
down the algorithm’s ability to converge to the best
solution, as it might spend time exploring these re-
dundant options or suboptimal solutions. This limi-
tation can hinder the overall performance, leading to
the inefficient use of computational resources. There-
fore, an efficient method is required to solve the MSU
allocation problem — one that addresses the limita-
tion of the current methods by ensuring a focus on
only the most promising regions of the search space.
By narrowing down the search space to the most rel-
evant ambulance station locations, we can reduce the
search space by filtering out ambulance station loca-
tions without having a significantly negative effect on
the quality of the solution when solving the MSU al-
location problem, thereby improving the convergence
speed.
3 MSU ALLOCATION
OPTIMIZATION PROBLEM
In the current section, we present a mathematical
model for the MSU allocation problem, which aims
to identify the optimal locations of a fixed number of
MSUs at existing ambulance stations within a geo-
graphic area.
Let I represent the set of existing ambulance sta-
tions in the considered region and N the total number
of MSUs to allocate. Each ambulance station is as-
sumed always to have at least one regular ambulance
available. The geographic region R is subdivided into
smaller areas r, where all patients located within sub-
region r ∈ R is assumed to be located at the centroid
of r.
Let t
RA
ir
be the expected time to treatment for a pa-
tient in subregion r when served by a regular ambu-
lance located in i ∈ I, and let t
MSU
ir
be the expected
time to treatment if the patients are served by an MSU
stationed at i. The expected time to treatment for a
patient in subregion r ∈ R when served by a regular
ambulance is given by t
RA
r
= min
i∈I
{t
RA
ir
}. The values of
t
RA
r
(r ∈ R) and t
MSU
ir
(r ∈ R, i ∈ I) can be precomputed
and are parameters in the optimization model.
We let Q
r
(r ∈ R) denote the share of the stroke
cases in R that is expected to take place in subregion
r. The decision variables x
i
∈ {0, 1} (i ∈ I) are defined
as follows:
x
i
=
(
1 if an MSU is placed at location i
0 otherwise.
Using the decision variables x
i
, the minimum ex-
pected time to treatment for a patient in subregion r
when served by an MSU can be calculated as follows:
t
MSU
r
= min
i∈I
{t
MSU
ir
+ (1 − x
i
) · M}, (1)
where M is a sufficiently large constant, such as the
maximum expected time to treatment for any subre-
gion r from any ambulance station i. This equation
ensures that stations without an MSU are assigned
such a long time to treatment that they will be ex-
cluded from consideration.
The objective function is the weighted average
time to treatment across all subregions r ∈ R, which
is formulated as follows:
minz =
∑
r∈R
Q
r
· min{t
RA
r
, t
MSU
r
}, (2)
Quality Clustering for Reducing the Search Space for Mobile Stroke Unit Allocation
107

where the decision variables (x
i
, i ∈ I) are implicitly
included in the calculation of t
MSU
r
(see Eq. 1). The
MSU allocation, represented by the x
i
values, is con-
strained by
∑
i∈I
x
i
= N, (3)
which ensures that exactly N MSUs are allocated
within the region.
4 QUALITY CLUSTERING FOR
REDUCING THE SEARCH
SPACE
The MSU allocation problem is a complex problem
due to the need to search through a large combinato-
rial space of possible placements. In the current pa-
per, we propose the Quality Clustering for Reducing
the Search Space (QCRSS) method for solving the
MSU allocation problem. QCRSS is a preprocess-
ing framework for searching algorithms that explic-
itly exploit the spatial distribution of ambulance loca-
tions to narrow down the search space, particularly by
incorporating a more global perspective and dynam-
ically adjusting clusters to reflect the true geograph-
ical spread of ambulance stations. The ultimate aim
is to enable the search algorithm to consider a smaller
search space instead of the whole search space. The
QCRSS framework includes three key steps: (1) pre-
processing using clustering, (2) selecting representa-
tives for each cluster, and (3) solving the MSU allo-
cation problem using the chosen representatives. In
this step, any suitable solution-finding method can be
applied.
4.1 Preprocessing Using Clustering
In the preprocessing step, we filter out locations that
are very close to other locations. The core idea be-
hind the clustering approach is that geographically
close ambulance stations are likely to have similar re-
sponse times to emergency calls within their vicinity.
By grouping these stations through clustering, we fo-
cus on evaluating a smaller set of representative lo-
cations by considering only one representative from
each cluster. In the preprocessing step, we explore
two clustering mechanisms: (1) K-medoid clustering
and (2) Agglomerative hierarchical clustering (AHC).
4.1.1 K-medoid Clustering
We use the K-medoids clustering method on a set of
ambulance station locations I, where each location
i ∈ I has specific coordinates (x
i
, y
i
). The objective
of K-medoids clustering is to partition I into K clus-
ters, where each cluster is represented by a central
point called a “medoid,” selected from actual ambu-
lance station locations. Let M denote the set of these
medoids, where M ⊆ I. The medoids minimize the to-
tal dissimilarity (sum of distances) between the ambu-
lance stations and their respective medoid locations.
See below for details about how to select the value of
K.
The K-medoids clustering approach achieves min-
imal dissimilarity through two main iterative steps:
1. Assignment Step: Each ambulance location i is
assigned to the nearest medoid m
j
, effectively
minimizing the distance between each location
and its assigned medoid:
C
j
=

i ∈ I | j = arg min
m
j
∈M
d(i, m
j
)

, (4)
where C
j
denotes the set of locations in cluster j,
m
j
is the medoid of cluster C
j
, and d(i, m
j
) is the
dissimilarity measure (distance) between location
i and medoid m
j
.
2. Update Step: Each medoid m
j
is updated to be
the location within C
j
that minimizes the sum of
distances to all other locations in the cluster:
m
j
= arg min
p∈C
j
∑
q∈C
j
d(p, q), (5)
where p represents a candidate medoid, and q
ranges over all locations in cluster C
j
. This step
ensures that each medoid is the location that re-
duces intra-cluster dissimilarity.
These two steps are repeated until the cluster as-
signments and medoid locations stabilize, indicating
convergence. At convergence, the minimum total dis-
similarity across all clusters can be expressed as:
min
K
∑
j=1
∑
i∈C
j
d(i, m
j
), (6)
which represents the total sum of distances from each
location i to its medoid m
j
across all clusters.
Thereafter, we employ a random selection strategy
from the clusters formed by the K-medoids. Specifi-
cally, for each cluster C
j
, we randomly select one lo-
cation i ∈ C
j
as a representative.
4.1.2 Agglomerative Hierarchical Clustering
Consider the set of ambulance locations I =
{i
1
, i
2
, . . . , i
|I|
}, where each location i ∈ I has coordi-
nates (x
i
, y
i
), which represent the geographical coor-
dinates (latitude and longitude) of ambulance station
i.
HEALTHINF 2025 - 18th International Conference on Health Informatics
108

Initially, each ambulance station location is
treated as its own cluster, resulting in k = |I| clusters
(one for each station). We then compute the Euclidean
distance d(i, j) between every pair of ambulance loca-
tions,
d(i, j) =
q
(x
i
− x
j
)
2
+ (y
i
− y
j
)
2
, (7)
to compute the geographical proximity between them.
The next step is to iteratively merge the closest
clusters (ambulance stations) using Ward’s linkage
criterion (Developers, 2024), which minimizes the in-
crease in the sum of squared deviations within clusters
(i.e., variance). The centroid of each cluster C
j
is de-
fined as:
µ
j
=
1
|C
j
|
∑
x∈C
j
x, (8)
where |C
j
| is the size of cluster C
j
, and µ
j
is its cen-
troid.
The increase in the sum of squared deviations
within clusters when merging two clusters C
i
and C
j
is given by:
∆E(C
i
, C
j
) =
|C
i
||C
j
|
|C
i
| + |C
j
|
· d(µ
i
, µ
j
)
2
, (9)
where d(µ
i
, µ
j
) is the Euclidean distance between the
two centroids µ
i
and µ
j
. Upon merging clusters C
i
and C
j
, the new centroid µ
′
of the merged cluster C
′
=
C
i
∪C
j
is computed as:
µ
′
=
|C
i
|µ
i
+ |C
j
|µ
j
|C
i
| + |C
j
|
. (10)
The process iterates until the desired number of
clusters k is reached, where k ≤ |I|. This step refers
to the Chosen Representatives in Step 3 of the pro-
posed method, as discussed in Section 4.3, where the
optimal number of clusters is identified. This ideal
number is based on the consistency of the solutions
in achieving the optimal solutions for different MSU
settings.
4.2 Selection of Representative
Ambulance Station
Once the clusters are formed, the next step is to select
a representative ambulance station from each cluster
C
j
. Given that the ambulance stations within a cluster
are already geographically close to each other, we hy-
pothesize that it is possible to choose any one of them
as representative of the cluster. The most logical and
efficient way is to pick one randomly to serve as a
representative location for the cluster, eliminating the
need for further calculations or sorting. Formally, the
representative ambulance station m
j
is defined as,
m
j
= x
j,r
∈ C
j
, (11)
where x
j,r
is a randomly selected ambulance station
from the cluster C
j
.
Our proposed method preserves the key spa-
tial properties of the cluster and reduces the search
space for the MSU allocation problem, reducing
the number of candidate stations from |I| to k as
we now focus on the representative ambulance lo-
cations {m
1
, m
2
, . . . , m
k
} as candidate locations for
MSU placement.
4.3 Solving the MSU Problem Using the
Chosen Representatives
We determine the ideal number of clusters by con-
structing and evaluating different numbers of clusters
and selecting a number that leads to the best solu-
tion. We evaluate different numbers of clusters (e.g.,
3, 4, 5, etc.) and observe the performance (mini-
mum weighted time to treatment) and consistency in
achieving the targeted object values (optimal time to
treatment) for different numbers of MSUs. Accord-
ingly, we chose the number of clusters that we con-
sider will yield the best results. To determine suitable
ambulance station locations, we focus only on the re-
duced search space determined by the chosen number
of clusters. This reduced search space is then passed
to the objective function (i.e., Eq. 2) as outlined in
Section 3. From this reduced search space, we choose
the solution that gives the minimum weighted time
to treatment as the acceptable solution to place the
MSUs.
5 COMPUTATIONAL STUDY
5.1 Scenario Description
To assess the efficiency of the QCRSS framework in
solving the MSUs allocation problem, we applied the
method to the Sweden’s Southern Healthcare Region
(SHR). The goal was to efficiently find suitable lo-
cations to place N MSUs, ranging from two to five,
in order to maximize coverage while minimizing the
time to treatment. The SHR is a combination of
densely populated and more rural areas, which is the
biggest challenge of pre-hospital care. The SHR en-
compasses four counties, comprising 49 municipali-
ties. The region has a population of around 1.9 mil-
lion and covers an area of 24, 000 square kilometers.
Quality Clustering for Reducing the Search Space for Mobile Stroke Unit Allocation
109

Figure 1: An overview of the SHR, Sweden, where the ambulance locations are indicated by orange dots with a corresponding
ambulance location ID.
The SHR has 13 acute hospitals and 39 ambulance
sites. An overview of the SHR is provided in Figure
1.
5.2 A Comparison Between the
K-medoid and Hierarchical
Clustering
To examine the effectiveness of the two consid-
ered clustering methods for MSU placement using
the QCRSS framework, we conducted a comparative
analysis between the K-medoid clustering (KMC) and
the agglomerative hierarchical clustering (AHC) in
terms of weighted time to treatment (i.e., WATT). The
WATT is calculated using the objective function from
Section 3, Eq. 2. We evaluated various numbers of
clusters ranging from 3 to 27 for two, three, four, and
five MSUs to highlight the impact of solution qual-
ity on the performance convergence of the KMC and
the AHC. The comparison of cluster quality, number
of clusters, and convergence to the optimal solution is
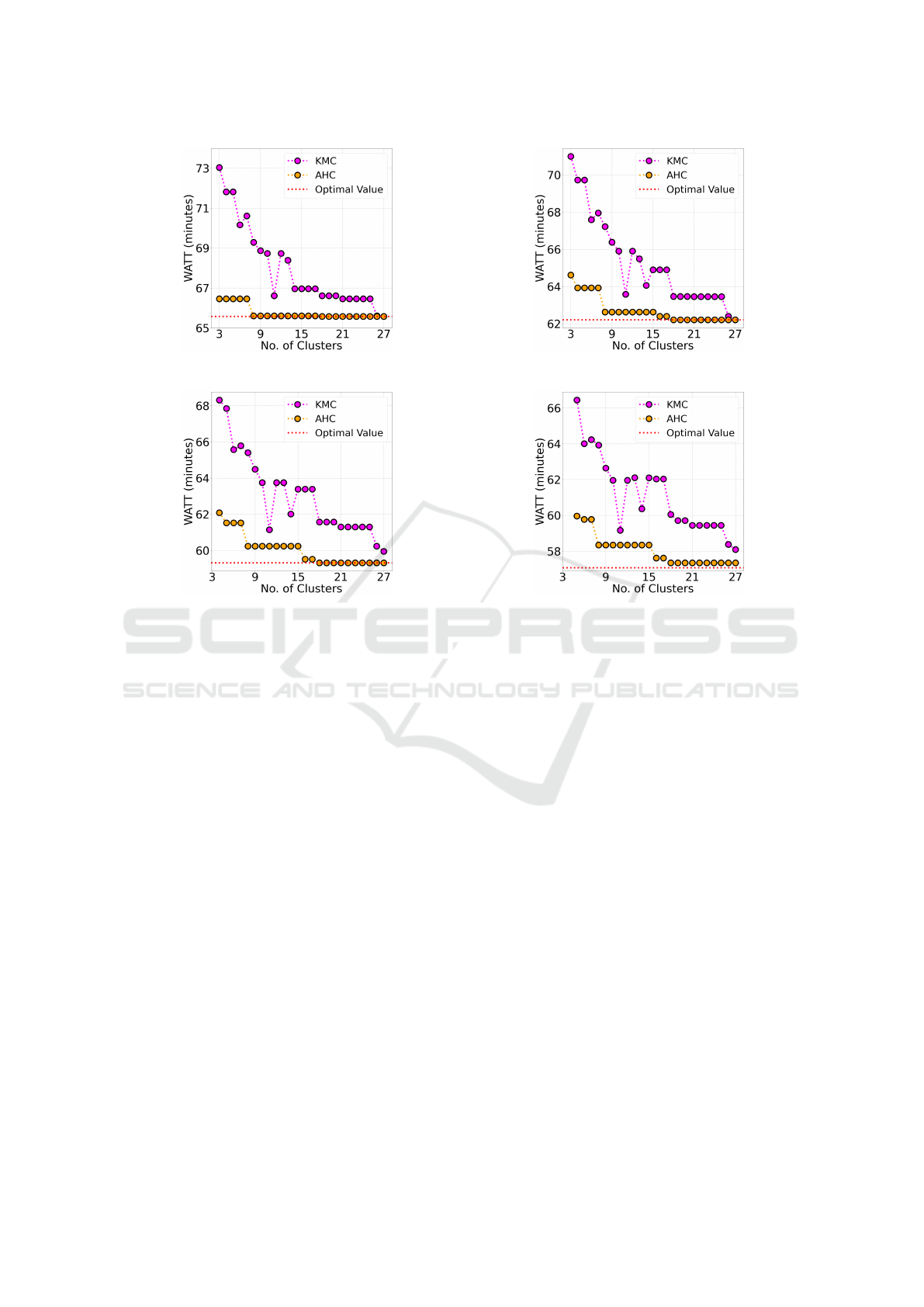
depicted in Figure 2.
5.2.1 Quantitative Results
The results in Figure 2 clearly demonstrate the supe-
riority of the AHC clustering for different numbers
of MSU (i.e., two, three, four, and five) in terms of
both cluster quality and faster convergence. For in-
stance, as shown in Figure 2a, for two MSUs, the
AHC reached the target value with a number of clus-
ters of only 18, making it 1.4x more efficient than
K-medoid clustering, which required 26 clusters to
achieve the same result.
The results clearly show that for all MSUs set-
tings, when the number of clusters is small, the KMC
gives sub-optimal solutions. This trend is evident in
Figure 2, where there is a large difference between
the obtained WATT and the optimal WATT. This indi-
cates that the KMC is affected by underfitting, which
occurs when the method fails to capture the underly-
ing patterns in the data, leading to poor performance.
In contrast, the AHC achieves significantly better re-
sults for a smaller number of clusters, as demonstrated
by the much smaller difference between the obtained
WATT and the optimal WATT.
The results indicate that when we increase the
number of clusters, the solutions improve relatively
in terms of WATT but with noticeable fluctuations for
the KMC. This pattern is seen for all of the MSU set-
tings. For example, for two MSUs, the KMC is a rel-
atively better solution for six clusters, but the perfor-
mance worsens as the number of clusters increases to
seven. A similar trend is observed with an improved
solution at 11 clusters, followed by a decline as the
number of clusters increases to 12, which continues
to worsen through the number of clusters from 13 to
17. Interestingly, for 18 clusters, the KMC achieves
the same solution as it did for 11 clusters. On the other
HEALTHINF 2025 - 18th International Conference on Health Informatics
110

(a) Two MSUs (b) Three MSUs
(c) Four MSUs (d) Five MSUs
Figure 2: Evaluation of different numbers of clusters for the considered MSUs settings to assess their quality in terms of
weighted time to treatment (WATT).
hand, the AHC appears to be more reliable and con-
sistent, with the AHC maintaining stable performance
for different numbers of clusters and delivering signif-
icantly better solutions.
An important observation can be seen from the re-
sults presented in Figure 2 when evaluating the al-
location of MSUs for the considered region (SHR,
Sweden). The KMC achieved optimal value for two
MSUs, with a relatively high number of clusters, that
is, 28. The performance of the KMC worsens as we
increase the number of MSUs as it fails to achieve op-
timal or acceptable solutions for three to five MSUs.
In other words, it appears that the KMC is not produc-
ing quality clusters. However, inconsistency and sub-
optimal clustering could significantly negatively af-
fect the quality of the solution when solving the MSU
allocation problem.
On the other hand, the AHC is showing better per-
formance. It is evident that 18 clusters consistently
yield the best solutions for two, three, and four MSUs.
Even in the case of five MSUs, 18 clusters lead to a
highly acceptable solution. Given this consistent per-
formance across different MSU settings, we can con-
fidently select 18 clusters as the most effective num-
ber of clusters, allowing to filter out of ambulance lo-
cations while maintaining a satisfactory quality solu-
tion for the MSU allocation problem within the SHR
geographic region of Sweden.
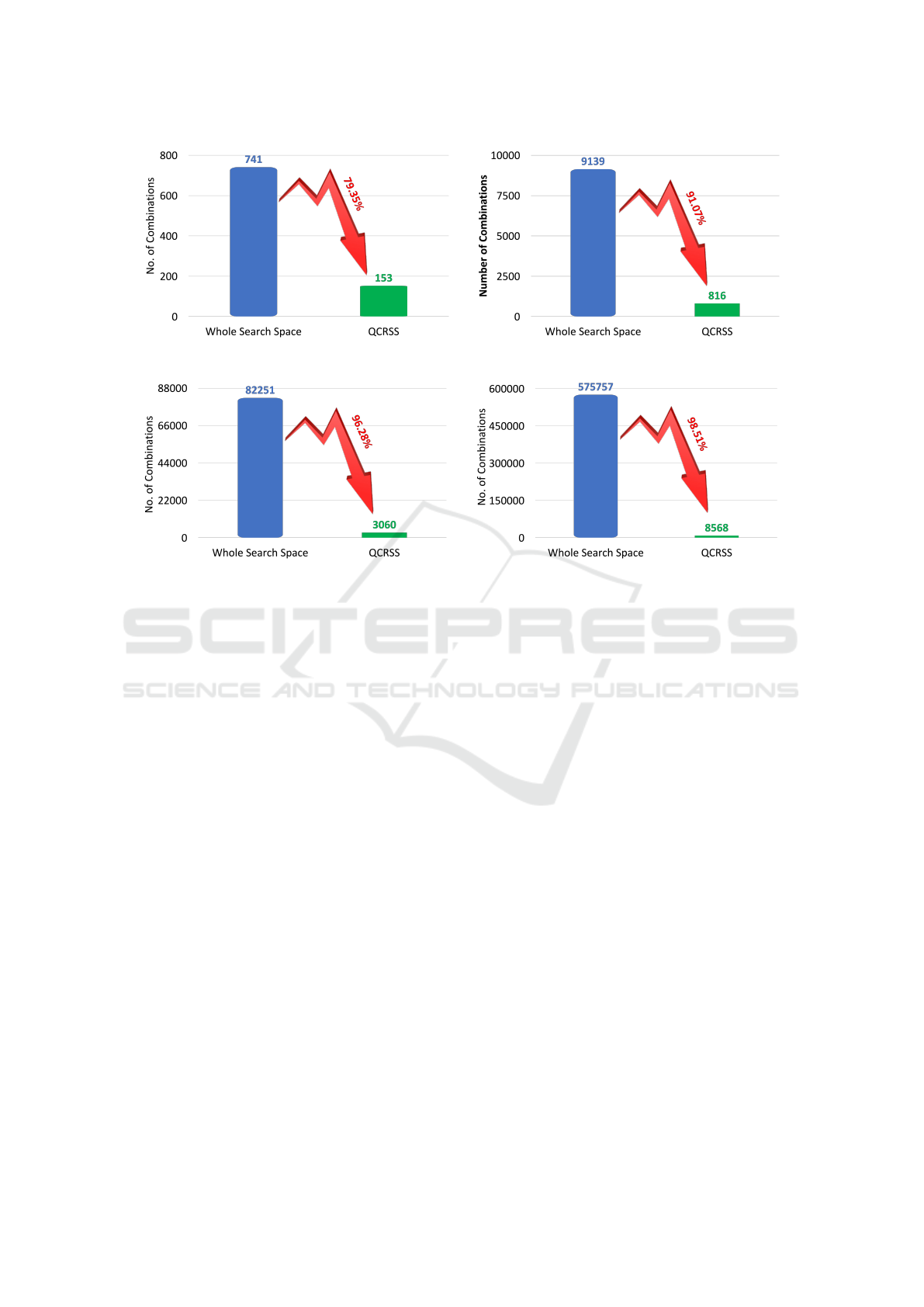
From this observation, we conclude that utilizing
18 clusters within the QCRSS framework allows for a
significant reduction in the search space while main-
taining a high level of quality (see Figure 2). By em-
ploying 18 clusters, the search space for two MSUs
is reduced from 741 to 153 combinations (79.35% of
the whole search space), a 5x reduction. Similarly, for
three MSUs, the search space is reduced from 9, 139
to 816 combinations (91.07% of the whole search
space), an over 11x reduction. For four MSUs, the
search space reduces from 82, 251 to 3, 060 combina-
tions (96.28% of the whole search space), represent-
ing a more than 26x reduction, and for five MSUs, the
search space is reduced from 575, 757 to just 8, 568
combinations (98.51% of the whole search space), a
more than 67x reduction. This substantial decrease in
the search space becomes increasingly significant as
the number of MSUs and potential ambulance station
locations grows. In particular, in scenarios involving
five MSUs, where the original search space consists
Quality Clustering for Reducing the Search Space for Mobile Stroke Unit Allocation
111

(a) Two MSUs (b) Three MSUs
(c) Four MSUs (d) Five MSUs
Figure 3: Comparison of the complete and reduced search spaces for multiple MSU settings. The impact of search space
reduction, achieved by selecting 18 ideal representatives using the QCRSS framework, is illustrated in terms of its effect on
the overall search space.
of over half a million possible combinations, the AHC
reduces this number to a far more practical subset of
8, 568 combinations.
5.2.2 Qualitative Results
In light of the quantitative results (see Figure 2), we
argue that AHC can be more effective than KMC
when solving the MSU allocation problem. In this
section, we present a qualitative analysis to explain
how the AHC and KMC-selected ambulance repre-
sentative locations can contribute to creating quality
clusters. We visually present the geographical loca-
tions of SHR in Figure 4, showcasing 39 potential am-
bulance locations along with their corresponding IDs.
Figure 4a and Figure 4b show one of the possible re-
sults of the use of clustering in the AHC and KMC,
respectively (in this example, the number of clusters
is set to eight).
In the KMC output, shown in Figure 4a, the
groupings are less intuitive, with some clusters con-
taining ambulances spread across relatively large ge-
ographical areas, leading to a suboptimal represen-
tative medoid (ambulance station location) selection.
For example, the clustered data points in teal color
span ambulances across varied coordinates to reduce
their cohesiveness. This can lead to higher objective
values, as poor medoid choices result in increased
travel distances and longer times to treatment. The
random initial selection of medoids further exacer-
bates this issue, as poorly chosen medoids often fail
to represent the true central points of clusters ade-
quately. Consequently, the KMC’s rigidity in fixing
medoids early in the process can lead to suboptimal
and relatively less adaptive clusters.
In contrast, the AHC performs better in forming
geographically coherent clusters (see Figure 4b), with
clusters like clustered data points in purple color and
clustered data points in magenta clearly grouping am-
bulances that are closer together. This creates more
balanced and compact clusters, ensuring that the cho-
sen representative locations more accurately reflect
the central geography of each group. The AHC’s
flexibility in progressively merging clusters based on
geographical closeness allows it to adaptively repre-
sent the spatial distribution of ambulances, making it
more effective for minimizing time to treatment. By
not including a random initialization step, the AHC
provides more stable and interpretable clustering out-
comes than the KMC, particularly when the objective
is to optimize travel distances in real-world ambu-
lance allocation problems.
HEALTHINF 2025 - 18th International Conference on Health Informatics
112

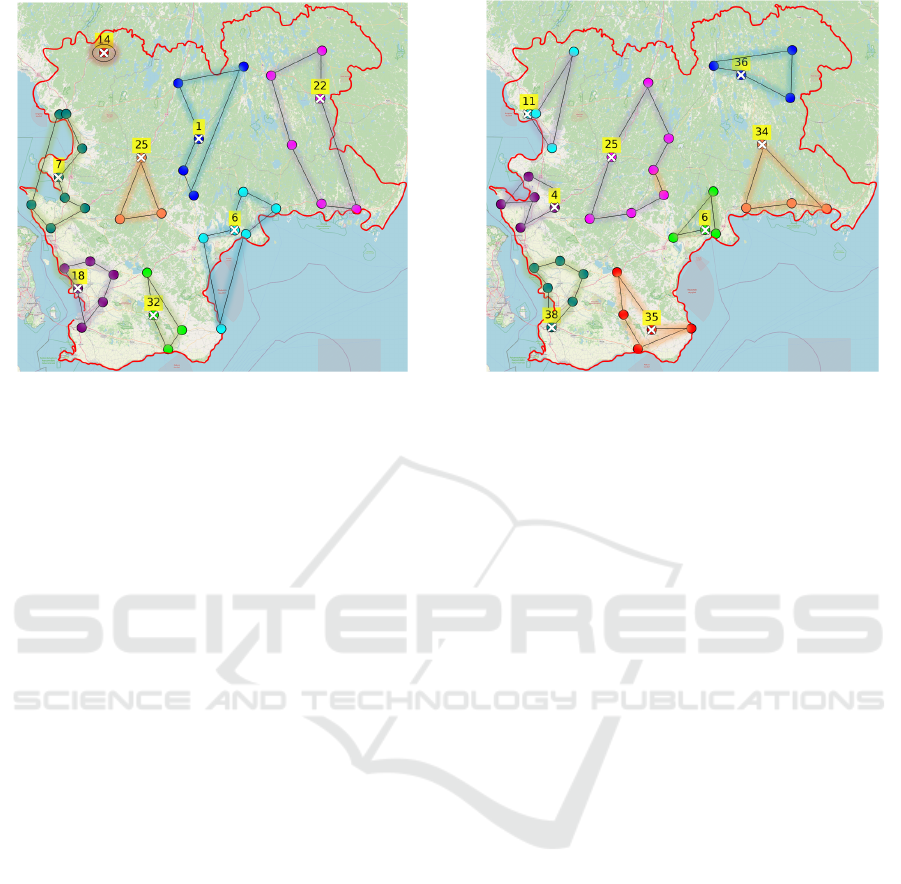
(a) KMC Clustering (b) AHC Clustering
Figure 4: An example of creating ten clusters with their corresponding selected ambulance station’s representative (yellow
label) using the QCRSS framework on the SHR, Sweden map.
6 CONCLUSIONS
In the current paper, we propose the Quality Cluster-
ing for Reducing the Search Space (QCRSS) method
for solving the MSU allocation problem. QCRSS is
a preprocessing framework for searching algorithms
that explicitly exploit the spatial distribution of am-
bulance locations to narrow down the search space.
The ultimate aim is to enable the search algorithm to
traverse a smaller search space instead of the whole
search space. The QCRSS contains three steps: (1)
preprocessing using clustering, (2) selecting repre-
sentatives for each cluster, and (3) solving the prob-
lems using the chosen representatives. The proposed
QCRSS framework filtered out ambulance locations
without negatively affecting the quality of the solu-
tion too much, as it appears that the difference is mi-
nor for the considered scenario. The proposed frame-
work appears to be both reliable and efficient for solv-
ing the MSU allocation problem within the SHR ge-
ographic region of Sweden. The proposed QCRSS
exhibited significantly faster convergence for all con-
sidered MSUs settings. We believe that our method
has the potential to contribute to significant improve-
ments in the healthcare domain, particularly by open-
ing new avenues for further research on optimal MSU
placement and related healthcare logistics challenges.
7 FUTURE WORK
In this study, we considered the efficiency perspec-
tive when solving the MSU allocation problem. Effi-
ciency refers to covering as many patients as possible
to receive treatment in a shorter window of time. In
the future, we plan to extend our proposed method to
consider both efficiency and equity. Equity refers to
contributing to equal care for all patients, regardless
of where they live. In addition, we plan to consider a
trade-off between these two perspectives. Addition-
ally, we plan to investigate our proposed method’s
performance in wider geographic regions and scopes
to obtain more comprehensive insights to improve
future stroke care by providing more efficient pre-
hospital treatment.
REFERENCES
Abid, M. A., Holmgren, J., Lorig, F., and Petersson, J.
(2024). An enhanced genetic algorithm with cluster-
ing for optimizing mobile stroke unit deployment. In
Proceedings of the 24th IEEE International Confer-
ence on Bioinformatics and Bioengineering. IEEE.
Abid, M. A., Mahdiraji, S. A., Lorig, F., Holmgren, J., Mi-
hailescu, R.-C., and Petersson, J. (2023). A genetic
algorithm for optimizing mobile stroke unit deploy-
ment. Procedia Computer Science, 225:3536–3545.
Amouzad Mahdiraji, S., Abid, M. A., Holmgren, J., Mi-
hailescu, R.-C., Lorig, F., and Petersson, J. (2023). An
optimization model for the placement of mobile stroke
units. In International Conference on Advanced Re-
Quality Clustering for Reducing the Search Space for Mobile Stroke Unit Allocation
113

search in Technologies, Information, Innovation and
Sustainability, pages 297–310. Springer.
Amouzad Mahdiraji, S., Dahll
¨
of, O., Hofwimmer, F.,
Holmgren, J., Mihailescu, R.-C., and Petersson, J.
(2021). Mobile stroke units for acute stroke care in the
south of sweden. Cogent Engineering, 8(1):1874084.
Ashraf, S., Masood, S., Shahbaz, A., and Saboor, Q. A.
(2023). Factors responsible for worse outcomes in
stemi patients with early vs delayed treatment present-
ing in a tertiary care center. Pakistan Heart Journal,
56(Supplement 2):S11–S11.
Blacker, D. and Hankey, G. (2014). Pre-hospital stroke
management: an australian perspective. Internal
medicine journal, 44(12a):1151–1153.
Bowry, R. and Grotta, J. C. (2017). Bringing emergency
neurology to ambulances: mobile stroke unit. In Sem-
inars in respiratory and critical care medicine, vol-
ume 38, pages 713–717. Thieme Medical Publishers.
Developers, S. (2024). scipy.cluster.hierarchy.ward. (Ac-
cessed October 2024).
Gurobi Optimization, LLC (2024). Gurobi Optimizer Ref-
erence Manual.
Harris, J. (2021). A review of mobile stroke units. Journal
of Neurology, 268:3180–3184.
Luengo-Fernandez, R., Violato, M., Candio, P., and Leal, J.
(2020). Economic burden of stroke across europe: A
population-based cost analysis. European stroke jour-
nal, 5(1):17–25.
Mahdiraji, S. A., Holmgren, J., Mihailescu, R.-C., and
Petersson, J. (2021). An optimization model for
the tradeoff between efficiency and equity for mobile
stroke unit placement. In Innovation in Medicine and
Healthcare: Proceedings of 9th KES-InMed 2021,
pages 183–193. Springer.
Majersik, J. J. and Woo, D. (2020). The enormous financial
impact of stroke disability.
Navi, B. B., Audebert, H. J., Alexandrov, A. W., Cadil-
hac, D. A., Grotta, J. C., and Group, P. P. S. T. O. W.
(2022). Mobile stroke units: evidence, gaps, and next
steps. Stroke, 53(6):2103–2113.
Nour, M., Vassar, S. D., Brown, A. F., Bosson, N. E.,
Chidester, C., Liebeskind, D. S., Kazan, C., Sanko, S.,
Eckstein, M., Gausche-Hill, M., et al. (2022). Geospa-
tial modeling to optimize mobile stroke unit system
deployment in a large metropolitan region. Stroke,
53(Suppl 1):A22–A22.
Patil, S., Rossi, R., Jabrah, D., and Doyle, K. (2022). Detec-
tion, diagnosis and treatment of acute ischemic stroke:
current and future perspectives. Frontiers in medical
technology, 4:748949.
Southerland, A. M. and Brandler, E. S. (2017). The cost-
efficiency of mobile stroke units: where the rubber
meets the road.
The Swedish Stroke Register (2023). Stroke Registrations.
In Annual Reports and Graphs. The Swedish Stroke
Register. (Accessed October 2024).
World Stroke Organization (2023). Facts and Figures about
Stroke. World Stroke Organization. (Accessed Octo-
ber 2024).
HEALTHINF 2025 - 18th International Conference on Health Informatics
114