Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level

Quantum Programming

Sebastian Bock

1 a

, Raphael Seidel

1 b

, Matic Petri

1 c

, Nikolay Tcholtchev

2,1 d

Andreas Hoffmann

and Niklas Porges

Fraunhofer Institute for Open Communication Systems (FOKUS), Berlin, Germany

RheinMain University of Applied Sciences, Wiesbaden, Germany

ﬁ

Keywords:

Quantum Computing, Meta-Model, High-Level Quantum Programming Language, Quantum Programming

Language Modelling.

Abstract:

Eclipse Qrisp is a high-level programming language designed to simplify quantum programming and make it

accessible to a wider range of developers and end users. Initially developed at Fraunhofer FOKUS and now

part of the Eclipse Foundation, Eclipse Qrisp abstracts complex quantum operations into user-friendly con-

structs, enhancing code readability structure. Currently, Eclipse Qrisp is realized as an extension of the Python

programming language, in the form of an embedded Domain Speciﬁc Language (eDSL), allowing to develop

hybrid quantum algorithms, while at the same time utilizing the potential of the overall Python ecosystem in

terms of libraries and available developer resources. We ﬁrmly believe that the eDSL approach to high-level

quantum programming will prevail over the idea of deﬁning speciﬁc languages - with their own grammar and

ecosystem - due to its ease of integration within available ICT products and services. However, in order to

reach higher levels of scalability and market penetration, the Eclipse Qrisp eDSL should be available for vari-

ous platforms and programming languages beyond Python, e.g. C/C++, Java or Rust. In order to provide the

means for implementing Eclipse Qrisp in other programming languages, this paper speciﬁes a meta-model,

thereby outlining the pursued design philosophy, architecture, and key features, including compatibility with

existing frameworks. The purpose of such a Qrisp meta-model is two-fold: On one hand it formalizes and

standardizes the Eclipse Qrisp programming model. On the other hand, such a meta-model can be used to

formally extend other programming languages and platforms by the capabilities and concepts speciﬁed and

implemented within Eclipse Qrisp.

1 INTRODUCTION

With the rapid progress in quantum computing more

complicated algorithms are required and being devel-

oped. With increasing complexity it is important to

have access to an easy and comprehensible program-

ming language for quantum computing. A high-level

programming language helps with the readability and

structure of the code. This would make getting started

easier for developers especially for those without a

physics background.

In the past years, the Eclipse Qrisp program-

ming framework/language (Seidel et al., 2024) (Sei-

del et al., 2023) (Seidel et al., 2022b) (Seidel et al.,

https://orcid.org/0000-0001-8362-8458

https://orcid.org/0000-0003-3560-9556

https://orcid.org/0009-0008-4482-5270

https://orcid.org/0000-0001-6821-4417

2022a) for quantum computing was developed in vari-

ous national (Bock et al., 2022) and European projects

(Chochliouros et al., 2023) (Cid et al., 2024). In the

course of the development activities, Qrisp has been

contributed and integrated into the Open Source de-

velopment processes of the Eclipse Foundation (Ecl,

2024a) and opened up for a larger community of

developers (Ecl, 2024b) under the EPL 2.0 license

(Eclipse Foundation, 2017). The full name of the

framework is thus Eclipse Qrisp. For simplicity rea-

sons we will mostly use Qrisp throughout the docu-

ment and by that refer to Eclipse Qrisp.

Qrisp is intrinsically designed as an extension of

the Python programming language (Python Software

Foundation, 2024). By utilizing certain properties of

Python, Qrisp introduces new environments and arti-

facts that enable the high-level deﬁnition of quantum

programming ﬂows thereby providing a new high-

Bock, S., Seidel, R., Petri

c, M., Tcholtchev, N., Hoffmann, A. and Porges, N.

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming.

DOI: 10.5220/0013121000003896

In Proceedings of the 13th International Conference on Model-Based Software and Systems Engineering (MODELSWARD 2025), pages 27-39

ISBN: 978-989-758-729-0; ISSN: 2184-4348

level programming paradigm for quantum comput-

ers. In this context, it is important to remark that

Qrisp removes the low-level assembler-like program-

ming of quantum processing units (QPU) by introduc-

ing layers of abstractions that enable coding through

functions, modules, environments and special arti-

facts rather than based on primitive qubit handling

and gate-based programming.

The above considerations clearly position Qrisp

as an eDSL (embedded Domain Speciﬁc Language)

(Dinkelaker et al., 2010) within the Python program-

ming language and its ecosystem of libraries and plat-

forms. We ﬁrmly believe that this approach bears

more chances of success and industrial penetration

than the approach of deﬁning and developing speciﬁc

languages such as Silq (Bichsel et al., 2020), Classiq

(Cla, 2024) or QCL (

Omer, 2005) to mention a few.

These languages come with their own formal gram-

mar, their own lexer, tokenizer, parser and compiler

and face the challenge of building their own ecosys-

tem of modules, libraries and tools. Hence, in order

to reach industrial relevance and exploitation, we ar-

gue that is needed to build on existing platforms and

ecosystems, which are widely adopted in relevant in-

dustrial domains.

The above considerations imply that the Qrisp

concepts must be transferable to other programming

languages and platforms, such as C/C++, Java, PHP

or Rust, to mention a few. In order to achieve this,

there must be a clear and formal deﬁnition of the

Qrisp concepts and programming models, which can

be implemented and transferred to other program-

ming languages and platforms. A possible formaliza-

tion with excellent acceptance in industry is the con-

cept of a meta-model as introduced by MOF (Meta-

Object Facility) (Weisem

oller and Sch

urr, 2008).

Hence, in the current paper we aim at deﬁning a meta-

model for the Qrisp eDSL for high-level program-

ming of quantum computers. We present the struc-

tures and artifacts of the meta-model based on the

UML-notation and give examples for their implemen-

tation and utilization in the Python based Qrisp ver-

sion. We argue that the presented meta-model lays

down a foundation for Qrisp based quantum high-

level programming in the scope of other languages,

such as Java, C/C++, PHP or Rust.

The rest of the paper is structured as follows: Sec-

tion II presents an overview of state-of-the-art re-

garding quantum programming. Section III gives a

brief introduction of the Qrisp eDSL for high-level

programming. In Section IV, we present the key

artifacts of the meta-model and give corresponding

code examples in Python. Section V summarizes the

sub-results to an overall Eclipse Qrisp meta-model.

Lastly, Section VI discusses the presented interrela-

tions and concludes the paper.

2 STATE OF THE ART

In this section, we look at the current state of the art

of existing quantum software frameworks, program-

ming languages and interfaces. For this purpose, we

focus on common solutions and frameworks, as this is

sufﬁcient to get a good overview of the general state

of the art in this area.

Probably the most widely used software frame-

work for writing quantum programs is Qiskit, mainly

developed by IBM (Javadi-Abhari et al., 2024). It

provides support for IBM backends as well as for

some other service providers such as AQT (Qis,

2024). The programming style is strongly based on

the assembler-like circuit model mentioned above. To

overcome this problem, IBM is working on an exten-

sive library with modules for machine learning, simu-

lation of quantum systems or optimisation problems.

However, the underlying style of the quantum pro-

grams still resembles the circuit model. The same

applies to other common software frameworks such

as Cirq developed Google (Cirq Developers, 2024)

(Heim et al., 2020), Quipper (Green et al., 2013), Pen-

nylane from Xanadu (Bergholm et al., 2022) or TKET

by Quantinuum (Sivarajah et al., 2020). The latter in-

cludes a highly competitive compiler based on the ZX

calculus (Coecke and Duncan, 2007). In addition, the

Scaffold programming language (Abhari et al., 2012)

comes with some high-level structures like conditions

and loops, however still requiring to operate on qubit

and gate-level. Moreover, Scaffold is not embedded

in another platform and will suffer the difﬁculty of

integrating into existing products and platforms with

their respective ecosystems.

Another initiative worth mentioning is the higher-

level language Silq (Bichsel et al., 2020) introduced

by ETH Zurich. Silq includes some of the afore-

mentioned features of a high-level programming lan-

guage, but does not provide a compiler. Furthermore,

Silq does not offer a software stack that enables pro-

grams to be executed on physical backends after com-

pilation.

Furthermore, the Q# programming language of

Microsoft should be mentioned (Svore et al., 2018).

Q# is a domain speciﬁc language, which is aligned

to C# from Microsoft and is integrated in the cor-

responding tools and tool-chains like Visual Studio

Code. Q# provides a type system, which mostly fo-

cuses on classical data types, e.g., int, bool, string

and only three quantum related types: Qubit, Result,

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

Pauli. This indicates that Q#, like the other frame-

works mentioned above, also focuses more on qubit

and gate based operations. Q# is declared to be an

Open Source software distribution and, similarly to

Qrisp, comes with a powerful simulator that is easily

accessible to execute and test quantum programs. A

big difference to Qrisp, additional to the different typ-

ing approach, is that Q# is not intrinsically embedded

in a host languages, but needs additional setups, in or-

der to operate inside Python for the purpose of hybrid

quantum computing (Hyb, 2024). With the current

paper, we want to go a step beyond and enable a seam-

less integration of Qrisp concepts in various program-

ming languages and platforms. To summarize: There

is a lot of developments in the domain of quantum

programming languages and frameworks. However,

many of them either still require the manual low-level

handling of qubits and gates (Svore et al., 2018), (Ab-

hari et al., 2012), (Green et al., 2013), or are of a the-

oretical nature (Bichsel et al., 2020), (Voichick et al.,

2023), (Wright et al., 2024), as they provide no means

of compiling/connecting a program to actual quantum

hardware as of now. Currently, there are only pro-

prietary approaches for interfaces and intermediate

representations for connecting to real quantum hard-

ware/backends, i.e. there are no standardised solu-

tions available between the relevant components, e.g.

between compiler and backend. This harbours the

risk of vendor lock-in, and a program written in IBM

Qiskit, for example, is only optimal (after compila-

tion and transpilation) for a QC instance provided by

IBM. Initiatives such as the QIR Alliance (QIR, 2024)

and formats like OpenQASM (Cross et al., 2017a) are

making efforts in this direction, but do not yet offer

standardised interfaces and appear to be difﬁcult to

extend in the context of a completely open business

ecosystem with various stakeholders (e.g. SMEs, in-

dustry and science). We therefore see the need to use

clearly deﬁned interfaces, which should be discussed

within the framework of relevant standardisation bod-

ies such as DIN or CEN/CENELEC.

3 ECLIPSE QRISP: BRIEF

INTRODUCTION

Qrisp was designed with a few key concepts and goals

in mind as depicted in Figure 1. Its goal is to make

developing code for quantum computers easier and

more accessible for a broad spectrum of developers.

After formulating a problem, Qrisp can be used to cre-

ate a circuit to solve this task on a quantum computer

or a simulation on a classical one.

Figure 1: Eclipse Qrisp (Qri, 2024) and its main features

positioning it as a framework/eDSL for high-level quantum

programming.

3.1 High-Level Programming

Quantum computing is an active ﬁeld of research

and requires more and more complicated algorithms.

Qrisp is designed to be a high-level programming lan-

guage, in order to make the development of increas-

ingly complex algorithms easier. Its algorithms con-

stitute of variables and functions instead of qubits and

circuits, which helps with the structure of the code

and reduce the technical debt. Qrisp implemented

so called QuantumVariables, which are the quantum

counterpart to classical variables. Therefore, the de-

veloper does not need to work with single qubits and

can use high-level functionality, such as a smoothly

integrated system of ﬂoating-point arithmetic, arrays

and strings. Qrisp handles the qubit resource manage-

ment and uncomputation (i.e. garbage collection) of

quantum variables in the background. A simple syn-

tax is achieved by combining the concept of Quan-

tum Variables and the simplicity and ﬂexibility that

comes with the Python language. The goal in this pa-

per is to bring the Qrisp programming concepts on a

more abstract level and to enable the implementation

of Qrisp as an embedded DSL in other host languages

(e.g. Java or C/C++).

3.2 Abstraction Levels

Qrisp was developed with different abstraction lev-

els in mind. The lowest level is the quantum cir-

cuit level, where use can create their quantum cir-

cuits by directly assigning gate operations to qubits.

This makes it possible to program close to hardware

speciﬁcations. On the other hand, development with

QuantumVariables and the arithmetic and logic that

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming

comes with them, enables to focus more on the al-

gorithm itself instead of taking care of small details,

e.g., qubit connectivity. Lastly, with the use of a sig-

niﬁcant number of algorithms implemented in Qrisp

(e.g. Grover’s Algorithm, QFT, Shor, QAOA etc.) it

is possible to program on an even higher abstraction

level.

3.3 Compatibility

Qrisp comes with a simulator, that enables direct ex-

ecution and testing of the code. The resulting com-

piled circuits can be run on integrated backends as

well. Furthermore, the compiled circuit objects can be

imported and exported to other common libraries and

formats such as OpenQASM (Cross et al., 2017b).

The compilation of the circuits can be adapted to ac-

count for different hardware architectures by varying

the native gate set the compiler compiles to.

3.4 Visualization

Qrisp has an inbuilt functionality for visualizing

quantum circuits and the state of the simulation,

which is run for a compiled circuit. The circuit vi-

sualization is based on ASCII characters. During the

simulation, the probability distribution can be plotted,

in addition to the possibility to view and print the cur-

rent state vector within the simulation.

3.5 Simulator

The circuits generated can be run on the efﬁcient

Qrisp internal simulator that makes use of sparse ma-

trices. These are used to store and process quantum

states. This makes it possible to run some circuits

that involve more than 100 qubits. Before executing

the simulation, the circuit is further optimized to re-

duce the complexity.

3.6 Modularity and Extensibility

Qrisp users/developers have access to the vast ecosys-

tem of Python libraries. These can assist in the devel-

opment of complicated algorithms. Automated qubit

allocation and handling allows to independently de-

velop and reuse algorithmic modules.

4 DESIGNING THE ECLIPSE

QRISP META-MODEL

In this section, we will guide the reader through the

elements of the high-level Qrisp eDSL, thereby de-

scribing the underlying meta-model and giving code

examples where appropriate.

4.1 Basic Infrastructure

We begin by outlining the basic infrastructure for han-

dling and describing the processes on the QPU. This

infrastructure provides the means to enable the high-

level constructs and abstractions (e.g. QuantumVari-

ables) described in the following sections.

4.1.1 Meta-Model

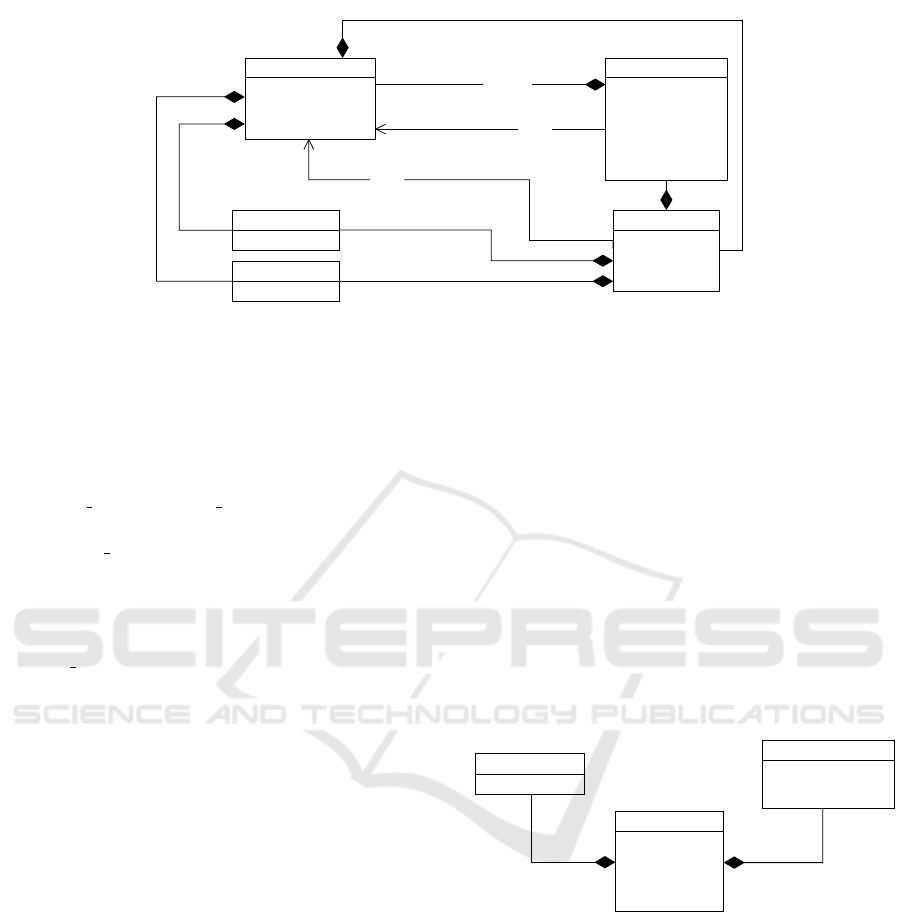
The meta-model for the basic infrastructure is pre-

sented in Figure 2. Thereby, it is possible to observe

a number of classes that interact with each other,

in order to enable the structured representation of a

quantum program/circuit:

Qubit. This class is used to describe qubits.

Qubits are distinguished by an identifier string.

Clbit. The Clbit classe describes classical bits

and can be distinguished by the identifier string.

Operation. This class represents an operation

that can be executed either on a quantum computer or

on a classical computer. An operation can be either

a single gate, such as the X-Gate, a classical logic

gate or a set of gates speciﬁed in the definition

ﬁeld of the class. The operation class can also be

used to describe measurements. It is given a name,

which is used to identify the operation. The class

keeps track of the parameters that further specify the

operation. The number of qubits that are required

for the operation is stored in the num qubits ﬁeld

and the number of classical bits in num clbits. This

class does not specify which Clbit or Qubit it acts

on. This is done in the Instruction class. The

unitary matrix which represents the operation can be

obtained with the get unitary method. An inverted

instance can be created with the inverse method and

a controlled version with the control function.

Instruction. The Instruction class combines an

operation op with a list of qubits qubits and another

list of classical bits clbits, which it operates on.

This class acts as the link between qubits, classical

bits for measurements and the operations. Instruc-

tions can be inverted using the inverse method

and be merged with another instance to form a new

instruction with the merge function.

QuantumCircuit. This class describes a quantum

circuit. The data attribute stores all the instructions,

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

QuantumCircuit

data: list<Instruction>

qubits: list<Qubit>

clbits: list<Clbit>

Operation

num_qubits: int

num_clbits: int

params: list<ﬂoat>

deﬁnition: QuantumCircuit

Instruction

op: Operation

qubits: list<Qubit>

clbits: list<ClBit>

Qubit

identiﬁer: string

Clbit

identiﬁer: string

toOperation()

append()

Figure 2: The Meta-Model for the Eclipse Qrisp Basic Infrastructure for Quantum Processing.

which the circuit consists of. It also keeps track of all

qubits and classical bits in the qubits and clbits

attributes. The circuit can be extended by operations

and instructions via the append method or by another

QuantumCircuit object with the extend function.

A QuantumCircuit can be turned into an operation

via the to gate or the to op function. The unitary

matrix which represents the circuit can be obtained

with the get unitary function. An inverted instance

can be generated using the inverse method. A

QuantumCircuit object is used as the deﬁnition for

operations. The class implements several methods

to evaluate the size and depth of the Circuit such

as cnot count and depth. The run method runs

the quantum circuit on a given backend. Quantum

circuits can be imported and exported to and from

other APIs and formats, such as Qiskit, OpenQASM

and Pennylane.

4.1.2 Example Code

The following listing shows a short piece of Qrisp

code that allows to create a quantum circuit based on

low-level assembler-like repetitive coding approach.

Thereby, a quantum circuit object is created at the

beginning, followed by the appending of different

gates with corresponding parameters to the quantum

circuit. Even though such type of programming is

not the general idea behind Qrisp it is important to

support it, such that the higher abstraction layers can

be compiled to the circuit level, which is described

in the coming sections. Additionally, in some

special cases, e.g., when speciﬁc new gates shall be

implemented or other hardware constraints should be

considered, it is also important to be able to write

programs on a circuit level.

from qrisp import QuantumCircuit, XGate,

CXGate, PGate

qc = QuantumCircuit(2)

qc.append(XGate(), 0)

qc.append(CXGate(), [0,1])

qc.append(PGate(0.5), 1)

synthed_op = qc.to_op()

qc.append(synthed_op, qc.qubits)

4.2 Quantum Variables

After having shed light on the basic infrastructure for

quantum circuit building, the next step is to move to

a higher abstraction level within the Qrisp program-

ming model. The basic ingredient within the higher-

level programming of Qrisp is the QuantumVariable,

which is presented in the following subsections.

QuantumSession

qv: list<QuantumVariable>

env_stack:

list<QuantumEnvironment>

Qubit

identiﬁer: string

QuantumVariable

size: int

reg: list<Qubit>

qs: QuantumSession

Figure 3: The Eclipse Qrisp Meta-Model for

QuantumVariables - the key structure for qubit Manage-

ment.

4.2.1 QuantumVariable Meta-Model

Figure 3 depicts the meta-model around the Qrisp

QuantumVariable, which is the basic abstraction

for managing qubits. This part of the overall Qrisp

meta-model consists of the following classes:

Qubit. Qubit is the basic class for managing

qubits, within the Qrisp meta-model and constitutes

a key part of the basic infrastructure presented

above. Instances of this class are an integral part of a

QuantumVariable as depicted in Figure 3.

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming

QuantumVariable. This is the QuantumVariable

class and the quantum equivalent of a classical

variable. When initializing a QuantumVariable the

number of Qubits it can use has to be speciﬁed but

the speciﬁc management of the qubits, e.g., which

qubit gets assigned to which QuantumVariable or

QuantumSession respectively is done automatically

and hidden from the user. QuantumVariables are

decoded to and encoded from human readable repre-

sentations with the encoder and decoder method.

After its creation the size of the QuantumVariable

can be modiﬁed with the extend and the reduce

method. The outcome of a measurement on a variable

is returned by the get measurement method and the

most likely measurement outcome by most likely.

The measurement outcome can be visualized with the

plot histogram function.

QuantumSession. The class QuantumSession

is the wrapper that manages multiple quantum vari-

ables in one session while steering the execution and

the exchange of data within one run on a quantum

processing unit (in a backend) or in a simulator.

More details on quantum sessions within Qrisp are

provided in the following sections.

4.2.2 QuantumVariable Example Code

The following small code example illustrates the

initialization and utilization of QuantumVariables.

This shows the core concept of Qrisp, which is using

QuantumVariables instead of qubit objects, and in-

terpret the in- and outputs in a human readable format.

In the code example two QuantumVariables, each

consisting of 3 qubits, are created and given unique

identiﬁers. Subsequently, a CX-gate is applied on

the qubits of both variables. Hence, the developer

no longer needs to deal with single qubits but rather

with the human readable representation of the quan-

tum variables.

from qrisp import QuantumSession,

QuantumVariable

example_qv_1 = QuantumVariable(3,

name = "alice")

example_qv_2 = QuantumVariable(3,

name = "bob")

cx(example_qv_1, example_qv_2)

4.3 Quantum Sessions

The QuantumSessions are one of the main ingredi-

ents for effectively managing the execution of quan-

tum code on a backend or a QPU simulator. Assuming

that the quantum related code is executed in a hybrid

setting, where an overall program runs on a CPU and

is having subroutines executed on various computing

architectures (e.g. GPUs, SNNs, HPC-clusters ...), the

quantum sessions are the artifacts encapsulating the

communication and seamless integration of quantum

backend executions within a hybrid program.

Figure 4: The Role of Quantum Sessions in Interacting with

Quantum Processing Units and Backends.

The role of quantum sessions within Qrisp is vi-

sually depicted in Figure 4. On the left side, one

can observe the various quantum variables and data

types, including data structures (more to come in

the following sections) of the Qrisp eDSL, such as

quantum arrays. These variables and data structures

within a program are compiled to a quantum circuit

(see section 4.1), which together with different exe-

cution environments all reside in a quantum session.

The QuantumSession is the main object encapsulat-

ing the various aspects and requests of the quantum

part of a hybrid program and managing the interac-

tions with the quantum backend - e.g. QPU or a (lo-

cal) quantum simulator. The communication proto-

cols between client side and host/ backend side are

not focus of the current publication

. However, it

is important to establish that the QuantumSession is

the one managing the state of the computation within

the interactions with backends, similarly as session

management is conducted in legacy web-technologies

(Wedman et al., 2013).

4.3.1 QuantumSession Meta-Model

The overall meta-model for the Qrisp

QuantumSessions is depicted in Figure 5 and

consists of the following classes:

QuantumSession. This QuantumSession class

extends the QuantumCircuit class. It manages

the life cycle of QuantumVariables by keeping

track of them in a list called qv. If an operation

acts on qubits from different sessions, they are

automatically merged into one. Sessions can also be

merged manually via a special merge function. An

For more details on the communication protocols and

architecture we refer the reader to (Seidel et al., 2022a)

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

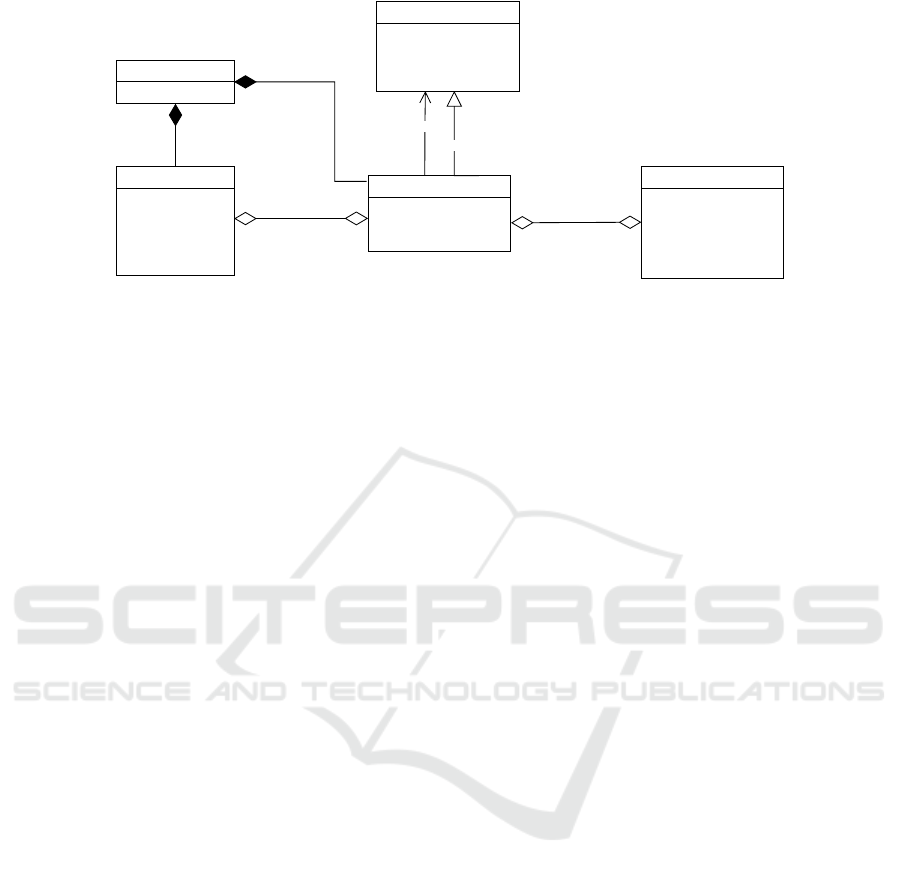
QuantumVariable

size: int

reg: list<Qubit>

qs: QuantumSession

QuantumSession

qv: list<QuantumVariable>

env_stack:

list<QuantumEnvironment>

QuantumArray

qtype: QuantumVariable

QuantumCircuit

data: list<Instruction>

qubits: list<Qubit>

clbits: list<Clbit>

Extends

QuantumEnvironment

env_qs: QuantumSession

env_data: list<Operation>

original_data: list<Operation>

parent: QuantumEnvironment

compile()

Figure 5: The Meta-Model for the Quantum Sessions towards a Quantum Backend.

Operation or Instruction can be appended to a

QuantumSession with a dedicated append method.

A Quantum Session enables the use of additional

features such as QuantumEnvironments and uncom-

putation, which corresponds to garbage collection in

legacy programming languages (Seidel et al., 2023).

Through a method called compile, a Quantum-

Session can be synthesized to a QuantumCircuit

from the basic infrastructure. The class has methods

to evaluate the size of the quantum session, such

as the amount of CNOT gates used or the num-

ber of quantum variables. The representation of

the state vector (e.g. from a simulator) for a quan-

tum session is returned by the statevector function.

QuantumEnvironment. This class denotes special

environments for executing different types of code

within a hybrid programm ﬂow. It is described in

more details in the coming sections.

QuantumArray. The QuantumArray is a class

that consists of many QuantumVariables of a certain

type, much like a classical array consists of classical

variables. It is described in more detail in section 4.5.

4.3.2 QuantumSession Example Code

Following the above description of the meta-model,

the following illustrates a simple example of the ex-

plicit usage of QuantumSessions within Qrisp. The

code snipet demonstrates the initiation of a quantum

session and the creation of a quantum variable as-

signed to this session. At the end, two of the qubits

within the quantum variable are connected over a CX-

gate. This simple example demonstrates how straight

forward it is, to create and operate sessions for quan-

tum program execution within Qrisp.

from qrisp import QuantumSession,

QuantumVariable

qs = QuantumSession()

qv = QuantumVariable(3, qs = qs)

qv.qs.cx(qv[0], qv[1])

4.4 Data Types

Similarly to classical high-level programming lan-

guages, Qrisp provides the possibility to use speciﬁc

(native) data types (such as ﬂoats, integers, characters

...), which can be used to steer the program ﬂow and

ensure quality and soundness of the quantum com-

putations. The meta-model for this typing system is

presented in the following subsection.

4.4.1 Data Types Meta-Model

The meta-model for the Qrisp data types is depicted

in Figure 6 and consists of the following classes:

QuantumFloat. This class extends the

QuantumVariable class and represents the quantum

equivalent of a classical ﬂoating point number with a

predetermined exponent and mantissa size. However,

there are some differences compared to classical

ﬂoating point numbers. Due to the restricted size

of current quantum computers, a QuantumFloat

variable can’t just use 64 qubits as in a classical

setting. For this reason Qrisp is designed in a way

that users have to set the size of the QuantumFloat

and the exponent when initializing them. The

QuantumFloat class supports operations such as

addition, subtraction, multiplication, division and

comparisons. The class adds bit-wise operations and

functionality to change the size and exponent of the

ﬂoating-point number.

QuantumModulus. This class extends

QuantumFloat and is used to model and pro-

cess modular arithmetic which is important for Shor’s

algorithm. It supports the same operations as the

QuantumFloat class.

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming

QuantumVariable

size: int

reg: list<Qubit>

qs: QuantumSession

QuantumSession

qv: list<QuantumVariable>

env_stack:

list<QuantumEnvironment>

QuantumArray

qtype: QuantumVariable

QuantumDictionary

return_type: QuantumVariable

QuantumFloat QuantumBool QuantumChar

QuantumString

Extends

QuantumModulus

modulus: int

Figure 6: The Meta-Model for Quantum Types and Data Structures in Eclipse Qrisp.

QuantumBool. This class inherits from the

QuantumVariable class and is used to represent the

quantum equivalent of a boolean truth value. They

can either be created manually or automatically when

comparing a QuantumVariable with a concrete

value or with another QuantumVariable derivative.

QuantumChar. This class extends

QuantumVariable and represents a single character.

To represent multiple characters the QuantumString

class is used.

QuantumString. This class inherits from

QuantumArray - elaborated on in the section

4.5 - and represents a string of characters. The

class adds functionality for concatenation and string

operations in general. The QuantumString objects

created this way share the same qubits.

4.4.2 Data Types Example Code

The following example shows how two ﬂoating point

numbers in a superposition are added. Firstly, two

instances of QuantumFloat are initialized and subse-

quently a Hadamard gate is applied on the least sig-

niﬁcant qubit of the ﬁrst ﬂoat. In the last step the ad-

dition of the two variables is performed and the result

is stored in a new QuantumFloat variable. The gen-

erated circuit is then executed on the integrated Qrisp

simulator and the result is printed to the console.

# Import Qrisp classes/functions

from qrisp import QuantumFloat

from qrisp.core import h

# Initialize QuantumFloats with 3 Qubits

n = 3

a = QuantumFloat(n, exponent=0, signed=False)

b = QuantumFloat(n, exponent=0, signed=False)

# Set the values of both variables

a[:] = 2

b[:] = 4

# Apply a Hadamard gate on

# the least significant qubit

h(a[0])

# Add both QuantumFloats

res = a+b

# Print the result to the console

print(res)

# returns: {6: 0.5, 7: 0.5}

To elaborate more on the example code: The two

quantum ﬂoats - a and b - are initialized with three

qubits each and assigned with the values of 2 and 4

respectively. Single qubits within a quantum ﬂoat can

be accessed using square brackets. This is used to ap-

ply the Hadamard gate only on the least signiﬁcant

qubit of a. Therefore, the variable a is in an equal

superposition between the values 2 and 3. Mathemat-

ical operations can be used on quantum ﬂoats just as if

they were classical ﬂoats, since they are converted to

the quantum equivalent in the background. The result

of the added ﬂoats is stored in a new variable called

res and is also of type QuantumFloat, automatically

created by Qrisp. By print(res) the result is printed

to the console. To do so, Qrisp actually performs a full

simulation of the quantum program with a measure-

ment in the end. This is also why the result is shown

as a dictionary (i.e. a hash map) with all the possi-

ble outcomes of a measurement with their respective

probability. In this case the possible outcomes are 6

and 7, which are both equally likely.

4.5 Data Structures

Data structures come on top of the data types and al-

low for handling more complex constellations and re-

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

lations between data entities within the quantum part

of a Qrisp program.

4.5.1 Data Structures Meta-Model

The meta-model for Qrisp data structures is depicted

together with the data types in ﬁgure 6 and consists

of the following classes:

QuantumArray. This is a class, which inherits

from ndarray of the popular NumPy python library

(Harris et al., 2020). It can be used to manage mul-

tiple QuantumVariable objects. QuantumArrays

support many convenient array manipulation meth-

ods such as slicing and reshaping. Using the array

for matrix multiplication is possible as long as

the array consists of QuantumFloat objects. It

can be multiplied by another such array or a clas-

sical ndarray which consists of numbers. The

most likely measurement outcome is obtained by in-

voking a special method called most likely method.

QuantumDictionary. This class extends the

python class dict and is the quantum equivalent of a

classical dictionary. This class makes inputing data

into the quantum computer easier. The value of a

dictionary can be loaded into a QuantumVariable

using the load method.

4.5.2 Data Structures Example Code

The following code examples illustrate the us-

age of QuantumDictionaries and QuantumArrays.

The ﬁrst code snippet demonstrates the usage of

QuantumDictionaries. We see the creation of

the QuantumDictionary, followed by storing a nu-

merical value with a numerical key in the dictio-

nary. Afterwards, a tupel (3,4) is stored in the

dictionary with the key of 42. Finally, we store

two words with corresponding string keys in the

QuantumDictionary.

from qrisp import QuantumDictionary,

QuantumVariable

qd = QuantumDictionary()

qd[1] = 2

qd[42] = (3,4)

qd["hello"] = "hallo"

qd["world"] = "welt"

The second code example illustrates the usage

of QuantumArrays. It starts with the creation of a

special QuantumFloat based type, which is subse-

quently used for the creation of theQuantumArray.

The second parameter (shape) determines the size

of the array thereby creating a 3-dimensional array.

The subsequent 2 lines are used to create a superpo-

sition between various array conﬁgurations in the 3-

dimensional space, yielding the ﬁnal outcome shown

as comments at the end of the code example.

import numpy as np

from qrisp import QuantumArray,

QuantumFloat, h

qtype = QuantumFloat(5, -2)

q_array = QuantumArray(qtype = qtype,

shape = (2, 2, 2))

qv = q_array[0,0,1]

h(qv[0])

print(q_array)

# returns:

# {OutcomeArray([[[0., 0.],

# [0., 0.]],

# [[0., 0.],

# [0., 0.]]]): 0.5,

# OutcomeArray([[[0. , 0.25],

# [0. , 0. ]],

# [[0. , 0. ],

# [0. , 0. ]]]): 0.5}

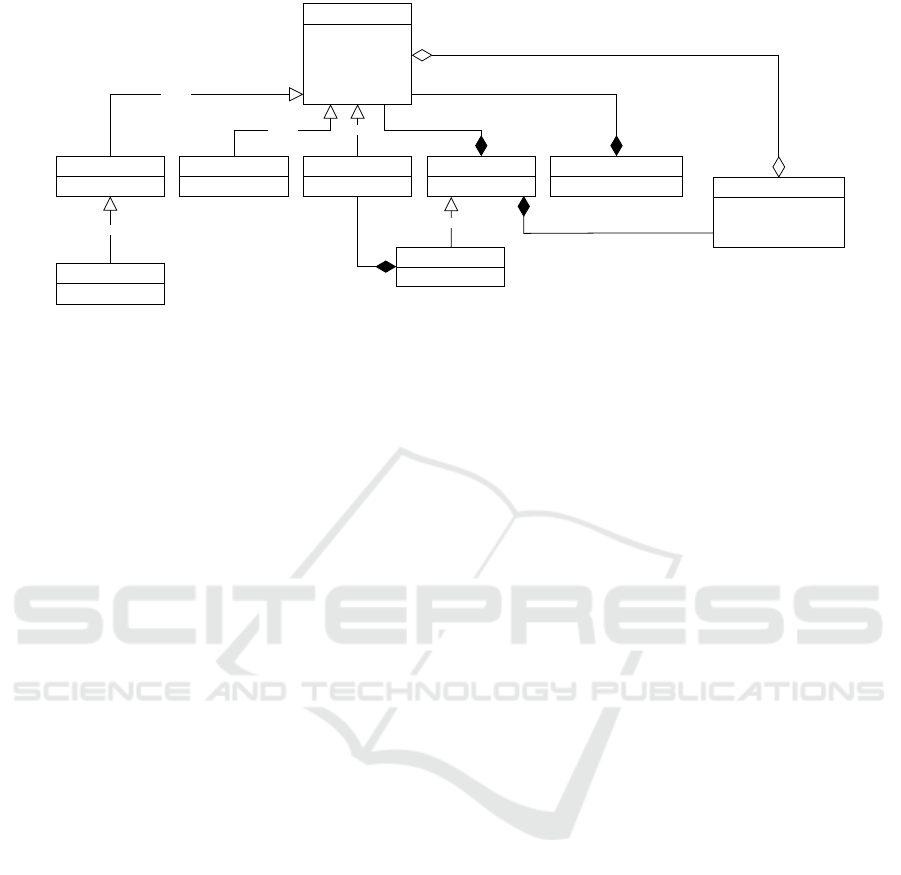
4.6 Quantum Environments

The quantum environments are another key element

of the Qrisp meta-model allowing for the execution of

different ﬂows depending on the speciﬁc environment

surrounding the belonging code snippet.

4.6.1 Quantum Environments Meta-Model

The meta-model for realizing quantum environments

is presented in Figure 7 and consists of the following

classes:

QuantumEnvironment. The main environment

class represents a block of code, which undergoes

a speciﬁc compilation process. After entering an

environment, the resulting circuit data is compiled

into the env data, while keeping the unchanged

part in the original data attribute. The compiling

process is speciﬁed in the compile method. An

environment has references to the QuantumSession

where all the active QuantumVariable objects are

located together at the parent environment.

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming

QuantumSession

qv: list<QuantumVariable>

env_stack:

list<QuantumEnvironment>

ConditionEnvironment

cond_eval_function:

function

args: list

kwargs: dict

ControlEnvironment

ctrl_qubits: list<Qubit>

ctrl_state: string

InversionEnvironmentConjugationEnvironment

conjugation_function:

function

args: iterable

kwargs: dict

GateWrapEnvironment

IterationEnvironment

qs: QuantumSession

iteration_amount: int

GMSEnvironment

QuantumEnvironment

env_qs: QuantumSession

env_data: list<Operation>

original_data: list<Operation>

parent: QuantumEnvironment

Extends

CustomControlEnvironment

control_qb: Qubit

Extends

Figure 7: The Meta-Model for the various Environments in Eclipse Qrisp.

ConditionEnvironment. This class inherits from

QuantumEnvironment and enables if-conditionals

similar to classical programming. The environment

takes a function cond eval function which eval-

uates the truth value as an input. The arguments

and keyword arguments are given by the args and

kwargs attributes. The program part inside of the

environment is activated if the condition function

returns true.

ControlEnvironment. This class extends

QuantumEnvironment and its logic is controlled

on a supplied list of Qubits stored in ctrl qubits.

The environment is activated, if the control Qubits

match the computational basis state given in the

ctrl state argument. A ControlEnvironment can

be activated using the control function.

GateWrapEnvironment.. This class extends

QuantumEnvironment and allows to hide complexity

in the QuantumCircuit visualization. This is done

by bundling the content in a single Instruction

object, which is given the name determined by the

name argument.

CustomControlEnvironment. This class in-

herits from GateWrapEnvironment and allows to

specify the controlled version of a decorated function.

This is done with the custom control decorator. If

the function is called within a ControlEnvironment,

the controlled version is called instead of the regular

one. The controlled version is controlled by a Qubit

stored in the control qb attribute.

IterationEnvironment. This class extends

QuantumEnvironment and can be used to re-

peatedly execute the same quantum circuit, which

can reduce the compilation time. The environment

takes the QuantumSession, in which the repeated

operations should be performed and the iteration

amount as arguments. The logic of the environment

is executed the speciﬁed amount of times, basically

creating a loop type of behaviour.

ConjugationEnvironment. This class extends

QuantumEnvironment and can be used to perform

conjugated operations. An arbitrary unitary matrix

(i.e. quantum operation) can be conjugated by

another unitary quantum operation. This structure

appears in many quantum algorithms such as Grover,

quantum backtracking or Fourier arithmetic. Using

the ConjugationEnvironment not only helps

to structure the code, but can also grant perfor-

mance advantages. The ConjugationEnvironment

takes the conjugation function as an argument.

The arguments and keyword arguments for the

conjugation function are given by the args and

kwargs attributes. The content of the environment

is conjugated by the conjugation function. A

ConjugationEnvironment can be called by using

the conjugate function.

InversionEnvironment. This class inherits from

QuantumEnvironment and can be used to invert a

block of operations or more precisely the content of

the environment. An InversionEnvironment can

be called using the invert function.

GMSEnvironment. This class inherits from

QuantumEnvironment and can be used to conve-

niently construct circuits using GMS-Gates, which

are the native entangling gates of trapped ion quantum

computers. The environment allows only phase-only

Gates and compiles them to GMS-Gates.

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

4.6.2 Quantum Environments Example Code

The following code example demonstrates the us-

age of the ConditionEnvironment. Thereby, it

can be observed how a quantum character is de-

ﬁned, followed by putting the ﬁrst qubit of the char-

acter in a superposition. Subsequently, the with-

clause activates the ConditionEnvironment and ex-

ecutes an if-statement on the previously created quan-

tum character. Based on the if-condition evalu-

ation, different values are assigned to a previous

declared QuantumFloat. Finally, we measure the

QuantumChar and the QuantumFloat and obtain the

probabilities for all possible states, which are consti-

tuted by different values of both variables depending

on the superposition and the with-clause.

from qrisp import QuantumChar, QuantumFloat,

h, multi_measurement

q_ch = QuantumChar()

qf = QuantumFloat(3, signed = True)

h(q_ch[0])

with q_ch == "a":

qf += 2

print(multi_measurement([q_ch,qf]))

# returns: {('a', 2): 0.5, ('b', 0): 0.5

4.7 Quantum Loops

The ﬁnal programming concept we introduce is the

quantum loop construct in Qrisp. Analogous to

for/while and iterator loops in traditional program-

ming languages, quantum loops are implemented

within the previously discussed quantum environ-

ments.

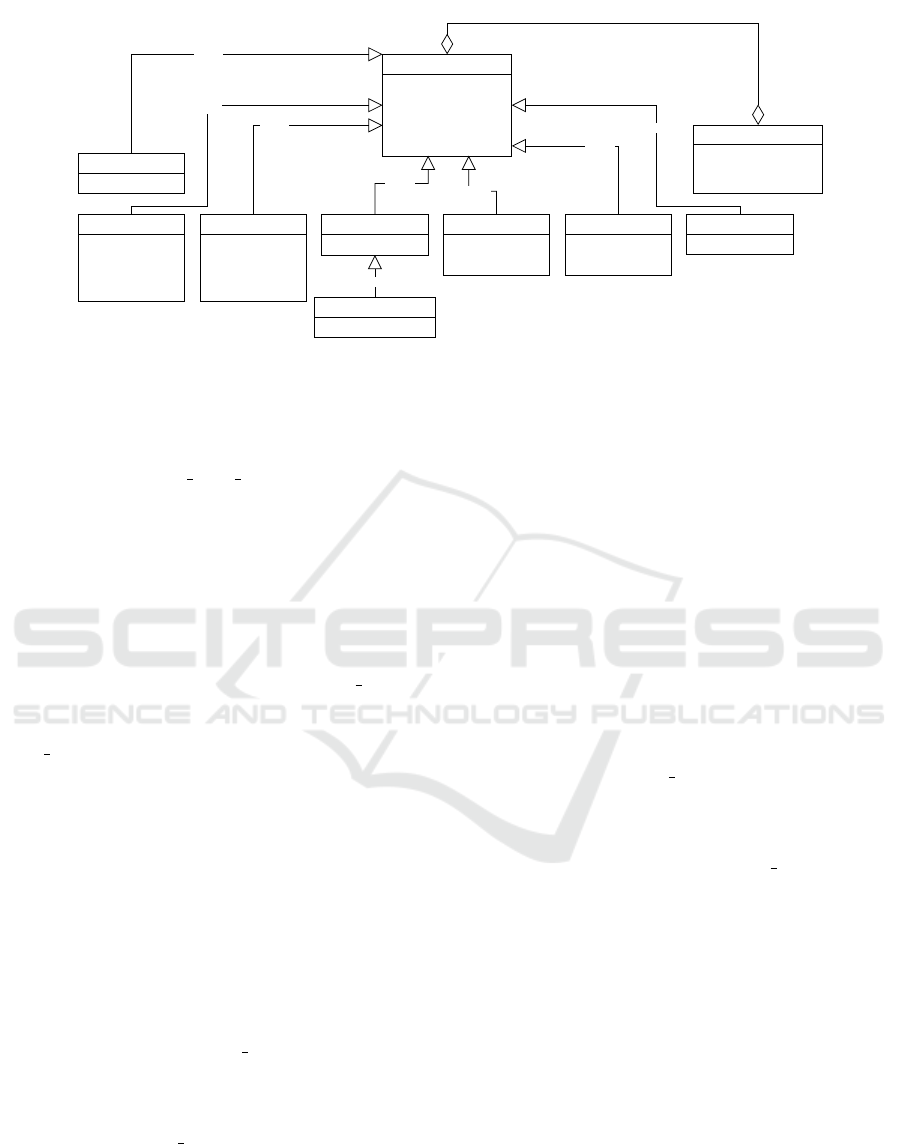
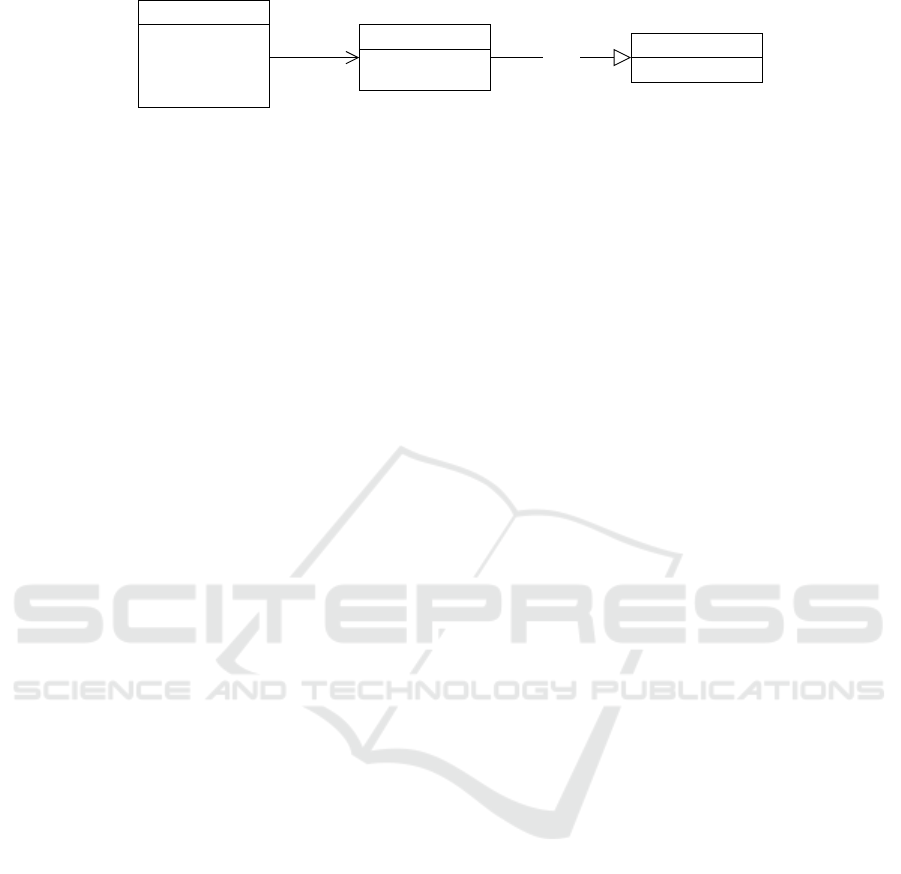
4.7.1 Quantum Loops Meta-Model

The meta-model for quantum loops in Qrisp is illus-

trated in ﬁgure 8. The new component is constituted

by the qRange class, which is the core class to mimic

a loop from classical computing. The end of the loop

is determined by a QuantumFloat stored in the at-

tribute max index qf. The qRange concept embodies

a quantum ControlEnvironment, with its belong-

ing functions to determine the end of a programming

loop.

4.7.2 Quantum Loop Example Code

The following example code demonstrates the usage

of quantum loops. At the beginning, corresponding

ﬂoat variables are deﬁned that are used to demonstrate

the effects of the iterations. Next, the n variable is set

to 4, which is meant to be the upper boundary for the

number of iterations in the loop. Afterwards, the ﬁrst

qubit of n is put in a superposition leading to it being

10 and 15 with a probability of 0.5 for each value.

Having prepared all relevant variables, a qRange

based loop is executed, in which an incremented value

of index variable i is iteratively added to the over-

all sum. Finally, the resulted sum is measured and

printed showing two different values depending on

the loop upper limit, which was put into superposition

in advance. These overall sum values emerge with a

probability of 0.5 each, as expected based on the su-

perposition of the upper boundary.

from qrisp import QuantumFloat, qRange, h

n = QuantumFloat(3, signed = True, name = "n")

qf = QuantumFloat(5, name = "qf")

n[:] = 4

h(n[0])

for i in qRange(n):

qf += i

print(qf)

# returns: {10: 0.5, 15: 0.5}

5 CASE STUDY: GROVER IN

ECLIPSE QRISP

This example shows the level of abstraction - based

on Qrisp - which can be achieved for the implemen-

tation of the Grover search algorithm. The developer

does not need to deal with qubits or gates, but rather

relies on predeﬁned functions and programming con-

structs according to the above described meta-model.

One can observe the deﬁnition of the corresponding

Grover oracle for solving a simple quadratic equation

= 0.25. Based on standard Eclipse Qrisp functions,

we can implement a Grover quantum search for the

suitable solutions of the equation.

from qrisp.grover import diffuser

from qrisp import auto_uncompute, z,

h, QuantumFloat

@auto_uncompute

def sqrt_oracle(qf):

temp_qbool = (qf*qf == 0.25)

z(temp_qbool)

qf = QuantumFloat(3, -1, signed = True)

n = qf.size

iterations = int((2**n/2)**0.5)

h(qf)

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming

QuantumFloat

ConditionEnvironment

cond_eval_function:

function

args: list

kwargs: dict

qRange

max_index_qf:

QuantumFloat

Extends

Figure 8: The Qrisp Meta-Model for Quantum Loops.

for i in range(iterations):

sqrt_oracle(qf)

diffuser(qf)

6 CONCLUSION

In conclusion, the development of Qrisp marks a sig-

niﬁcant advancement in making quantum computing

more accessible to a broad spectrum of developers,

including those without a background in physics.

By providing a high-level programming language

speciﬁcally designed for quantum computing, Qrisp

simpliﬁes the creation and management of com-

plex quantum algorithms. The language’s design

philosophy emphasizes ease of use, abstraction,

compatibility, visualization, and extendibility, which

collectively enhance the development experience

and lower the entry barriers for new users. Qrisp’s

modular architecture, which integrates seamlessly

with Python’s extensive ecosystem, further facili-

tates the development of complex hybrid quantum

applications. This modularity also ensures that

code written by domain experts can interoperate

efﬁciently, leveraging automated qubit management

and optimized resource allocation.

In order to capture, the Qrisp programming model

and to enable the transfer of the Qrisp embedded DSL

to other programming languages and platforms, the

current paper presented a meta-model for the Qrisp

eDSL. By following this meta-model, it becomes fea-

sible to develop new iterations of Qrisp for languages

such as Java, C/C++, Rust, and others. The adaptation

of Qrisp to these languages will be explored in future

research endeavors. Furthermore, this meta-model

holds potential for standardization, which could sig-

niﬁcantly enhance large-scale industrial collaboration

in high-level quantum programming.

ACKNOWLEDGEMENTS

This work was funded by the Federal Ministry

for Economic Affairs and Climate Action (German:

Bundesministerium f

ur Wirtschaft und Klimaschutz)

under the projects Qompiler (01MQ22005A) and

EniQma (01MQ22007A). The authors are responsi-

ble for the content of this publication.

REFERENCES

(2024). AQT Qiskit Provider. https://qiskit-community.

github.io/qiskit-aqt-provider/. Accessed: 14.08.2024.

(2024). Classiq. https://www.classiq.io.

(2024a). Eclipse Foundation. https://www.eclipse.org/org/

foundation/. Accessed: 14.08.2024.

(2024b). Eclipse Qrisp GitHub Repository. https://github.

com/eclipse-qrisp/Qrisp. Accessed: 14.08.2024.

(2024). Hybrid Computing with Q#. https:

//learn.microsoft.com/en-us/azure/quantum/

hybrid-computing-integrated. Accessed: 14.08.2024.

(2024). QIR Alliance. https://www.qir-alliance.org. Ac-

cessed: 14.08.2024.

(2024). Qrisp documentation page. www.qrisp.eu. Ac-

cessed: 26.04.2024.

Abhari, A., Faruque, A., and Dousti, M. J. e. a. (2012).

Scaffold: Quantum programming language.

Bergholm, V. et al. (2022). PennyLane: Automatic differ-

entiation of hybrid quantum-classical computations.

arXiv:1811.04968 [physics, physics:quant-ph].

Bichsel, B., Baader, M., and Gehr, T. e. a. (2020). Silq: A

high-level quantum language with safe uncomputation

and intuitive semantics. In Proceedings of the 41st

ACM SIGPLAN Conference on Programming Lan-

guage Design and Implementation, PLDI 2020, page

286–300, New York, NY, USA. Association for Com-

puting Machinery.

Bock, S., Seidel, R., and Becker, C. K. (2022). Towards a

standardised quantum software stack. ERCIM News,

2022(128).

Chochliouros, I. P. et al. (2023). OASEES: an innovative

scope for a dao-based programmable swarm solution,

for decentralizing AI applications close to data gener-

ation locations. In Maglogiannis, I. et al., editors, AIAI

2023 IFIP WG 12.5 International Workshops, volume

677 of IFIP Advances in Information and Communi-

cation Technology, pages 91–105. Springer.

Cid, M. I. G. et al. (2024). PQ-REACT: Post Quantum

Cryptography Framework for Energy Aware Contexts.

In Proceedings of the 19th International Conference

on Availability, Reliability and Security, ARES 2024,

Vienna, Austria, 30 July 2024 - 2 August 2024, pages

65:1–65:7. ACM.

Cirq Developers (2024). Cirq. https://doi.org/10.5281/

zenodo.11398048.

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

Coecke, B. and Duncan, R. (2007). A graphical calculus for

quantum observables. Preprint.

Cross, A. W., Bishop, L. S., Smolin, J. A., and Gambetta,

J. M. (2017a). Open Quantum Assembly Language.

arXiv:1707.03429 [quant-ph].

Cross, A. W., Bishop, L. S., Smolin, J. A., and Gambetta,

J. M. (2017b). Open quantum assembly language.

Dinkelaker, T., Eichberg, M., and Mezini, M. (2010). An ar-

chitecture for composing embedded domain-speciﬁc

languages. AOSD ’10, page 49–60, New York, NY,

USA. Association for Computing Machinery.

Eclipse Foundation (2017). Eclipse Public License 2.0

(EPL) | The Eclipse Foundation. https://www.eclipse.

org/legal/epl-2.0/. Accessed: 2024-10-02.

Green, A. S., Lumsdaine, P. L., and Ross, N. J. e. a. (2013).

Quipper: A scalable quantum programming language.

SIGPLAN Not., 48(6):333–342.

Harris, C. R. et al. (2020). Array programming with

NumPy. Nature, 585(7825):357–362.

Heim, B. et al. (2020). Quantum programming languages.

Nature Reviews Physics, 2(12):709–722.

Javadi-Abhari et al. (2024). Quantum computing with

Qiskit. arXiv:2405.08810 [quant-ph].

Python Software Foundation (2024). Python Language Ref-

erence. https://www.python.org/.

Seidel, R., Bock, S., Tcholtchev, N., and Hauswirth, M.

(2022a). Qrisp: A framework for compilable high-

level programming of gate-based quantum computers.

In PlanQC - Programming Languages for Quantum

Computing.

Seidel, R., Bock, S., Zander, R., Petri

c, M., Stein-

mann, N., Tcholtchev, N., and Hauswirth, M. (2024).

Qrisp: A Framework for Compilable High-Level

Programming of Gate-Based Quantum Computers.

arXiv:2406.14792 [quant-ph].

Seidel, R., Tcholtchev, N., Bock, S., Becker, C. K.,

and Hauswirth, M. (2022b). Efﬁcient ﬂoating point

arithmetic for quantum computers. IEEE Access,

10:72400–72415.

Seidel, R., Tcholtchev, N., Bock, S., and Hauswirth, M.

(2023). Uncomputation in the Qrisp High-Level

Quantum Programming Framework. In Kutrib, M.

and Meyer, U., editors, Reversible Computation - 15th

International Conference, RC 2023, Giessen, Ger-

many, July 18-19, 2023, Proceedings, volume 13960

of Lecture Notes in Computer Science, pages 150–

165. Springer.

Sivarajah, S., Dilkes, S., and al., A. C. (2020). tket: a retar-

getable compiler for NISQ devices. Quantum Science

and Technology, 6(1):014003.

Svore, K., Roetteler, M., Geller, A., and al., M. T. (2018).

Q#. In Proceedings of the Real World Domain Speciﬁc

Languages Workshop 2018 on - RWDSL2018. ACM

Press.

Voichick, F., Li, L., Rand, R., and Hicks, M. (2023).

Qunity: A Uniﬁed Language for Quantum and Clas-

sical Computing. Qunity: A Uniﬁed Language for

Quantum and Classical Computing (Type Checker),

7(POPL):32:921–32:951.

Wedman, S., Tetmeyer, A., and Saiedian, H. (2013). An

Analytical Study of Web Application Session Man-

agement Mechanisms and HTTP Session Hijacking

Attacks. Information Security Journal: A Global Per-

spective, 22(2):55–67.

Weisem

oller, I. and Sch

urr, A. (2008). Formal deﬁnition

of mof 2.0 metamodel components and composition.

In Czarnecki, K., Ober, I., Bruel, J.-M., Uhl, A., and

olter, M., editors, Model Driven Engineering Lan-

guages and Systems, pages 386–400, Berlin, Heidel-

berg. Springer.

Wright, C. J., Luj

an, M., Petoumenos, P., and Goodacre, J.

(2024). Quff: A dynamically typed hybrid quantum-

classical programming language. In Proceedings of

the 21st ACM SIGPLAN International Conference

on Managed Programming Languages and Runtimes,

MPLR 2024, page 65–81, New York, NY, USA. As-

sociation for Computing Machinery.

Omer, B. (2005). Classical Concepts in Quantum Program-

ming. International Journal of Theoretical Physics,

44(7):943–955.

Designing a Meta-Model for the Eclipse Qrisp eDSL for High-Level Quantum Programming