Computation of 2D Discrete Geometric Moments on Quadtrees

Paola Magillo

1 a

and Lidija

Comi

2 b

Department of Computer Science, Bioengineering, Robotics, and Systems Engineering,

University of Genova, Genova, Italy

Faculty of Technical Sciences, University of Novi Sad, Novi Sad, Serbia

Keywords:

Discrete Geometric Moments, Quadtree, Computation.

Abstract:

We address the problem of computing discrete geometric moments on 2D binary images encoded in the

quadtree data structure. We do this by precomputing central moments of the squares of side length 2

, and

using the connection between ordinary and central moments. Compared with the state of the art for images

encoded as quadtrees, our method considerably improves the efﬁciency of moment computation.

1 INTRODUCTION

Moments have been used in a wide spectrum of ap-

plication domains, ranging from engineering and me-

chanics to image processing and pattern recognition,

as they form a basis for deﬁning shape descriptors in-

variant to similarity transformations (Hu, 1962). Mo-

ments computation is a well-studied ﬁeld with long

history (Flusser et al., 2016), with many existing al-

gorithms based on different computational paradigms

and image data structures. We propose another such

algorithm, based on the quadtree data structure, which

represents images of size 2

× 2

as the union of

squares of side length 2

, 0 ≤ k ≤ n. The algorithm

precomputes the moments of such squares centered at

the origin, and uses the well known connection be-

tween the ordinary and central moments to compute

the moments of the object encoded in the image.

2 BACKGROUND NOTIONS

We consider a binary 2D world, where the object of

interest O is black, and the background is white. This

world can be continuous or digital. In the latter case,

the world is an image, i.e., a raster of pixels, each

either black or white.

https://orcid.org/0000-0001-5088-034X

https://orcid.org/0000-0001-9664-2160

2.1 Geometric (Cartesian) Moments

For an object O in the continuous world, its geometric

(p,q)-moment m

p,q

(O) of order p + q is deﬁned as

p,q

(O) =

dxdy.

For a digital object O, the geometric moment is usu-

ally approximated by

p,q

(O) =

∑

(i, j)∈O

. (1)

The centroid (barycenter) of O is the point ( ¯x, ¯y) =

1,0

0,0

0,1

0,0

). Central moments are deﬁned

p,q

(O) =

(x − ¯x)

(y − ¯y)

dxdy.

and are approximated by

p,q

(O) =

∑

(i, j)∈O

(i − ¯x)

( j − ¯y)

. (2)

Central moments (of order up to three) can be ex-

pressed through ordinary moments, e.g., as

0,0

= m

0,0

1,0

= 0

2,0

= m

2,0

− ¯x m

1,0

3,0

= m

3,0

− 3 ¯xm

2,0

+ 2 ¯x

1,0

0,1

= 0

1,1

= m

1,1

− ¯ym

1,0

= m

1,1

− ¯x m

0,1

2,1

= m

2,1

− 2 ¯xm

1,1

− ¯ym

2,0

+ 2 ¯x

0,1

0,2

= m

0,2

− ¯ym

0,1

1,2

= m

1,2

− 2 ¯ym

1,1

− ¯x m

0,2

+ 2 ¯y

1,0

0,3

= m

0,3

− 3 ¯ym

0,2

+ 2 ¯y

0,1

(3)

Magillo, P. and

Comi

c, L.

Computation of 2D Discrete Geometric Moments on Quadtrees.

DOI: 10.5220/0013119400003905

In Proceedings of the 14th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2025), pages 17-22

ISBN: 978-989-758-730-6; ISSN: 2184-4313

The inverse expressions are

0,0

= µ

0,0

1,0

= ¯xm

0,0

2,0

= µ

2,0

+ ¯x m

1,0

3,0

= µ

3,0

+ 3 ¯xm

2,0

− 2 ¯x

1,0

0,1

= ¯ym

0,0

1,1

= µ

1,1

+ ¯ym

1,0

= µ

1,1

+ ¯x m

0,1

2,1

= µ

2,1

+ 2 ¯xm

1,1

+ ¯ym

2,0

− 2 ¯x

0,1

0,2

= µ

0,2

+ ¯ym

0,1

1,2

= µ

1,2

+ 2 ¯ym

1,1

+ ¯x m

0,2

− 2 ¯y

1,0

0,3

= µ

0,3

+ 3 ¯ym

0,2

+ 2 ¯y

0,1

(4)

2.2 Quadtrees

A quadtree (Samet, 1990) provides a compact hierar-

chical representation of an image. Assuming a square

image of 2

× 2

pixels for some natural n, a quadtree

is a quaternary tree inductively deﬁned as follows:

• if all pixels have the same color, the tree consists

of a single node labelled with that color;

• otherwise the tree consists of a root node and four

children, where each child is the quadtree repre-

sentation of one of the four quadrants obtained by

cutting the given image into half horizontally and

vertically.

The worst case size for a quadtree occurs in a

chessboard image, where the tree consists of n + 1

full levels, the last level having 2

× 2

leaves (one

for each pixel of the image). Instead, if the image

presents large areas of uniform color, the quadtree

may be much more compact than the original image.

Figure 1 shows a quadtree representation of an image

of size 8 × 8.

Although a quadtree can be constructed top-down

following the inductive deﬁnition, the efﬁcient con-

struction algorithm (Samet, 1990) works bottom-up

by merging groups of four pixels (in the ﬁrst itera-

tion) or of four nodes (in the other ones) having the

same color.

3 RELATED WORK

The algorithms for the computation of the geometric

moments of 2D binary objects can broadly be clas-

siﬁed as decomposition-based and boundary-based

(Flusser et al., 2016). The algorithms in the ﬁrst

class decompose the image into non-overlapping sim-

ple shapes (rectangles) for which the moment compu-

tation is straightforward. The algorithms in the sec-

ond class consider only the border black pixels (ad-

jacent to a white pixel). We will review only decom-

position based algorithms, as our algorithm falls into

this category.

Decomposition-based algorithms algorithms work

on a decomposition of the image into runs, rectangles

or squares. A run (a maximal set of contiguous black

pixels in one row of the image) is a rectangle with one

side of length 1, and a square is a rectangle of equal

sides. The algorithms are either based on a speciﬁc

data structure used to encode the image (quadtree, run

length or contour chain code), or they compute a de-

composition of the image into rectangles or squares in

a preprocessing step.

Shneier (Shneier, 1981) proposed an algorithm for

computation of m

1,0

and m

0,1

, based on the quadtree

representation of the image. For each block, the coor-

dinates of upper left pixel are determined (the size of

the block is given by its level in the tree) and the mo-

ments of black blocks (leaves) are computed in O(1)

time. Worst-case time complexity is O(2

) for chess-

board image of size 2

× 2

. No discussion on other

values of p and q has been provided.

Wu et al. (Wu et al., 2001) proposed an algo-

rithm for computing moments of order up to three on

a quadtree decomposition of the image. A detailed

description of a parallel implementation is also given.

Zakaria et al. (Zakaria et al., 1987) proposed

a method for computing the discrete low-order mo-

ments based on run-length encoding of a horizontally

convex image (with at most one run in each row).

Li (Li, 1993) generalized the algorithm by Zakaria et

al. to the computation of low-order moments of non-

convex objects (Flusser and Suk, 1999). Spiliotis and

Mertzios (Spiliotis and Mertzios, 1996; Spiliotis and

Mertzios, 1998) proposed another extension of the

algorithm of Zakaria et al., which ﬁrst decomposes

an image into disjoint rectangular blocks by merging

consecutive runs of equal spread into rectangles and

then computes the discrete moments of arbitrary order

on the rectangles.

Sossa-Azuela et al. (Sossa-Azuela et al., 2001)

proposed to use morphological erosion to decom-

pose the image into a set of non-overlapping squares,

whose moments are computed through closed form

formulas. The squares are of odd side length, be-

cause the structuring element is of size 3 × 3 (but

even side length could be obtained by using structur-

ing element of size 2 × 2 (Suk and Flusser, 2010)).

Many iterations of morphological erosion are needed

to ﬁnd all the squares of the decomposition, from

the largest to the smallest ones (equal to one pixel).

Sossa-Azuela and Flusser (Sossa-Azuela and Flusser,

2004) extended the above decomposition method to

the computation of continuous moments.

Suk and Flusser (Suk and Flusser, 2010) proposed

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

Figure 1: An example of an image quadtree: the image decomposition (left) and the tree (right). Leaf nodes are black or

white, internal nodes are called gray and shown with a pattern in the ﬁgure.

to use the distance transform instead of the morpho-

logical erosion to obtain the decomposition of the im-

age into squares.

4 THE NEW ALGORITHM

We suppose that the object O is contained in an image

of size 2

×2

and encoded in a quadtree. If the image

has a different size, it is completed with white (i.e.,

background) pixels to the nearest larger power of two.

Therefore, O is a set of pixels and the leaves in the

quadtree representing it are (black or white) squares

of side equal to 2

with 0 < k ≤ n or single pixels for

k = 0.

4.1 Idea of the Method

The algorithm precomputes the moments of axis-

aligned black squares with edges equal to a power of

two and centered in (0, 0). Later, such moments will

be used to obtain the moments of the black leaves of

the quadtrees with a limited number of operations.

For a square S of (even) size 2

× 2

, 1 ≤ k ≤ n,

centered at the origin, µ

p,q

(S) = m

p,q

(S), and

p,q

(S) =

k−1

−1

∑

i=−2

k−1

(i +

)

k−1

−1

∑

j=−2

k−1

( j +

)

(5)

and thus its moments of order p + q, with odd p or

q, are equal to 0. Therefore only (central) moments

0,0

,µ

0,2

and µ

2,0

must be computed, with µ

0,2

= µ

2,0

because of the symmetry of S w.r.t. the x- and y-axes.

Given any other square R with same side length

as S and centered at any point ( ¯x, ¯y), the moments of

R can be computed from its central moments, which

are the same as the central moments of S, by using

Formulas (4).

Taking into account that all central moments, with

the exception of µ

0,0

,µ

2,0

,µ

0,2

, are null, the Formulas

(4) for the square R can be rewritten as:

0,0

= µ

0,0

1,0

= ¯xm

0,0

2,0

= µ

2,0

+ ¯x m

1,0

3,0

= 3 ¯xm

2,0

− 2 ¯x

1,0

0,1

= ¯ym

0,0

1,1

= ¯ym

1,0

2,1

= ¯ym

2,0

0,2

= µ

0,2

+ ¯ym

0,1

1,2

= ¯xm

0,2

0,3

= 3 ¯ym

0,2

− 2 ¯y

0,1

(6)

4.2 Algorithm Description

The algorithm computes all the moments m

p,q

of the

object O represented in the image encoded in the

quadtree, for p + q ≤ 3. It consists of three stages:

1. Compute all the central moments µ

0,0

and µ

0,2

2,0

for all the squares having side length equal to

1,2,4,...2

(i.e., for all the possible sizes of the

quadtree nodes). Such values are stored in a table

for later use.

2. Initialize all the moments of the object O to zero.

3. Traverse the quadtree. For each black node, cov-

ering a square R, compute the moments of the

node from the central moments computed in step

1, by using the formulas (6). The moments of the

node are added to the current moments.

4. At the end of the quadtree traversal, the moments

of the object O have been computed.

5 EXPERIMENTAL EVALUATION

This section presents the experiments performed to

compare our new algorithm with the state of the

art. Our comparison is restricted to decomposition-

based algorithms for computing image moments and,

Computation of 2D Discrete Geometric Moments on Quadtrees

among them, to the ones using general-purpose de-

compositions. The quadtree, as well as the run-length

encoding, are general compression schemes for im-

ages, so it is likely that an input image is already

given in this format. Other decompositions (such as

those from morphological erosion or distance trans-

form) do not correspond to an image format, and they

should be constructed ad-hoc for moment computa-

tion. Therefore, they are not considered in this com-

parison. Some preliminary experiments also showed

that the quadtree-based approach is faster than the one

based on runs, so we concentrate our comparison on

methods working with quadtrees.

We compared our new algorithm with the algo-

rithm by Wu et al. (Wu et al., 2001), the only one in

the literature using a quadtree. We used a sequential

implementation of both algorithms.

Both algorithms have been implemented in

Python and share the same module for the manage-

ment of the quadtree. They differ in the main pro-

cedure used for computing the moments. The used

quadtree implementation maintains a list of all the

leaves, therefore it is not necessary to descend the tree

from the root in order to process all the leaves. The

programs were run on a PC equipped with an Intel

CPU i7-2600K CPU at 3.4 Gigahertz with 32 Giga-

bytes of RAM.

We tested the algorithms on 80 im-

ages from the MPEG7 set available at

https://dabi.temple.edu/external/shape/

MPEG7/MPEG7dataset.zip and featuring different

object shapes and sizes. This set contains 70 classes

of object types with 20 elements each. We selected

the ﬁrst four elements of twenty classes. Figure 2

shows an element for each selected class.

Note that each class contains semantically the

same object (e.g., an apple or a camel), but the im-

age sizes, the size of the object inside the image, the

thickness of the set of black pixels, may be very dif-

ferent. The given images present a white object on a

black background, and the colors have been inverted

to meet our convention. Figure 3 shows the four se-

lected images in the ”beetle” class.

The total running time of the two algorithms has

the same order of magnitude, and ranges from 0.04

to to 12.7 seconds depending on the size of the im-

age and on the size of the object contained in the im-

age. As Python is an interpreted language, it is easy

to obtain the running time of each executed function

separately. The execution time is dominated by the

construction of the quadtree, which takes from 87%

to 99% of the total time. Figure 4 shows the plot

of the times for building the quadtree (the graph of

the total running time would be almost superimposed

to this). In the ﬁgure we note three clusters of run-

ning times around 0.6, 3 and 12 seconds, respectively.

These clusters correspond to three different ranges of

image sizes. For example, among the four images of

class ”beetle” (see Figure 3), beetle-1 takes 12.171

seconds (ﬁrst cluster from top), beetle-2 and beetle-

4 take 2.886 and 2.882 seconds, respectively (second

cluster), and beetle-3 takes 0.637 seconds (third clus-

ter).

Disregarding the time for building the quadtree,

the remaining time is the one actually used for com-

puting the moments, and is speciﬁc of each of the two

algorithms. Figure 5 provides a graphic comparison

of the times for computing the moments by our al-

gorithm (on the x-axis) and the algorithm by Wu et

al. (on the y-axis). Each point corresponds to a test

image. Our algorithm is faster where the point lies

over the bisector of the ﬁrst quadrant. This happens

for all the test images, the ratio of our execution time

over that by Wu et. al. being on average 36% and at

most 69%. Indeed in Figure 5 we ﬁnd three clusters

of dots, all aligned on a line of the form y = cx + d

where c ≃ 5 and d is different in each cluster. As the

clusters of Figure 4, also these clusters correspond to

the three different ranges of image sizes. Finally, we

note that the time for computing the central moments

of squares in our algorithm is negligible (less than one

millisecond).

6 SUMMARY AND FUTURE

WORK

We proposed an algorithm for the computation of dis-

crete geometric moments of 2D binary objects en-

coded in the quadtree data structure. It is based on

precomputing the moments of the squares centered

at the origin, and using the connection between cen-

tral and ordinary moments to compute the moments

of the given object. Our algorithm improves the run-

ning time of the previous quadtree-based algorithm

for moments computation by Wu et al. (Wu et al.,

2001) in its sequential form. Both the construction

of the quadtree and the computation of the moments

from it could beneﬁt from a parallel implementation,

as in Wu et al. (Wu et al., 2001).

This work has several possible extensions. It can

be extended to the computation of geometric mo-

ments of

• 3D objects encoded in the octree data structure;

• greyscale images by decomposing the image into

a binary image for each grey level, as done in (Pa-

pakostas et al., 2008);

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

apple-1 beetle-1 bell-1 bird-1 camel-1

(256 x 256) (613 x 660) (252 x 255) (423 x 296) (391 x 355)

crown-1 cup-1 deer-1 dog-1 face-1

(633 x 521) (425 x 383) (693 x 703) (686 x 535) (269 x 337)

ﬂy-1 fork-1 hat-1 jar-1 octopus-1

(308 x 253) (297 x 650) (251 x 216) (512 x 512) (256 x 256)

pocket-1 shoe-1 spring-1 tree-1 watch-1

(147 x 205) (551 x 307) (393 x 318) (256 x 256) (500 x 202)

Figure 2: The ﬁrst element in each of the twenty considered classes.

beetle-1 beetle-2 beetle-3 beetle-4

(613 x 660) (273 x 303) (216 x 217) (258 x 442)

Figure 3: The four elements of class ”beetle”.

Computation of 2D Discrete Geometric Moments on Quadtrees

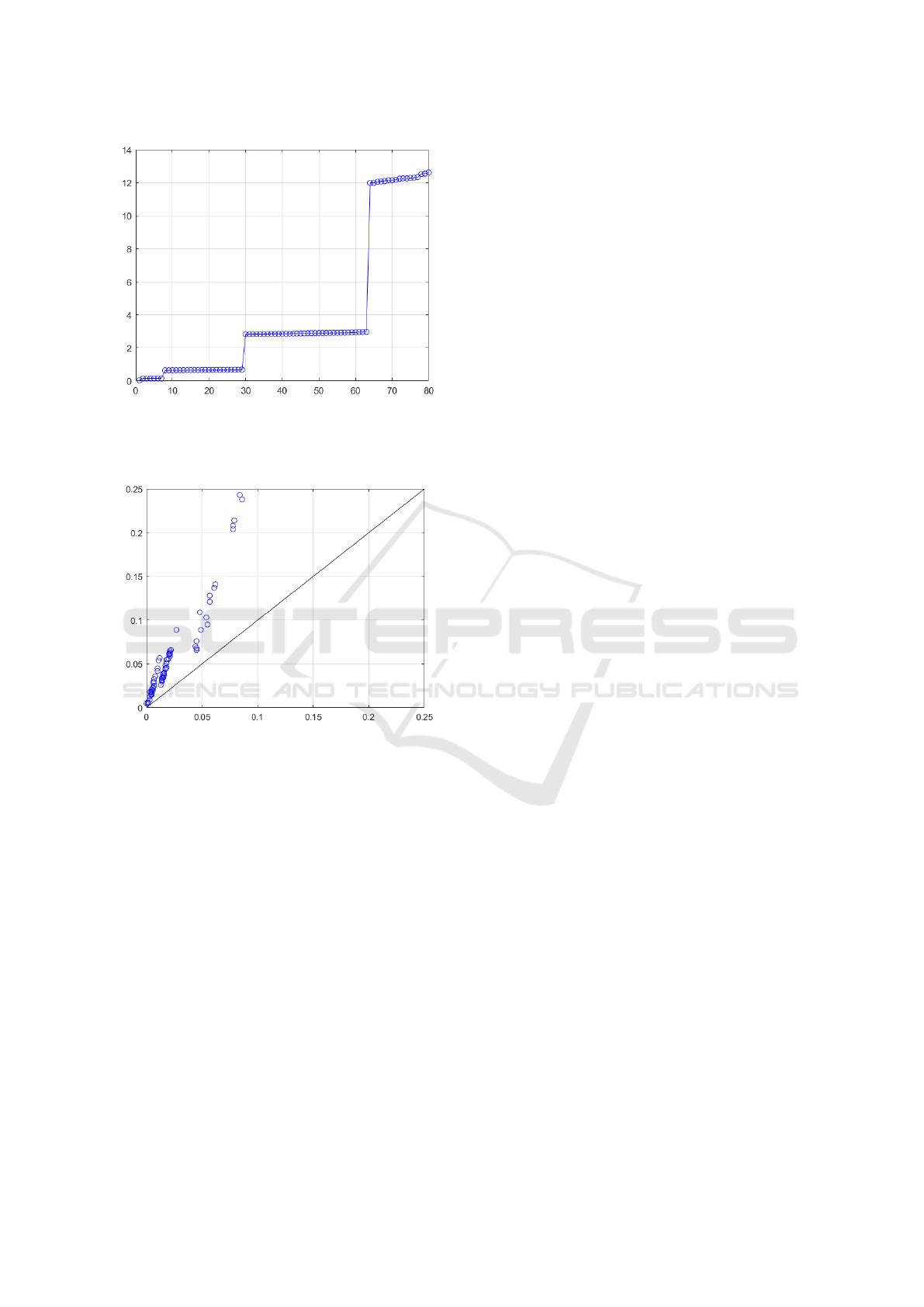
Figure 4: Running times for building the quadtree on the

80 test images, sorted from the one giving the least to the

one giving the largest time. This is a common task in both

considered algorithms.

Figure 5: Comparison of running times for computing the

moments (total running time minus quadtree construction).

The x-axis represents the running time of our algorithm and

the y-axis that of the algorithm by Wu et al.

• moments of higher order by taking into account

that, for any p,q, we can express each µ

p,q

through m

i, j

, 0 ≤ i ≤ p, 0 ≤ j ≤ q as

p,q

∑

i=0

∑

j=0







p−i

1,0

q− j

0,1

(−m

0,0

)

p+q−i− j

i, j

and conversely

p,q

∑

i=0

∑

j=0







p−i

1,0

q− j

0,1

p+q−i− j

0,0

i, j

ACKNOWLEDGEMENTS

This research has been partially supported by the

Science Fund of the Republic of Serbia through

PRIZMA program, GRANT No 7632, Project ”Math-

ematical Methods in Image Processing under Uncer-

tainty” - MaMIPU

REFERENCES

Flusser, J. and Suk, T. (1999). On the calculation of image

moments. Technical Report 1946, Institute of Infor-

mation Theory and Automation, Academy of Sciences

of the Czech Republic.

Flusser, J., Suk, T., and Zitova, B. (2016). 2D and 3D Image

Analysis by Moments. John Wiley & Sons, Ltd.

Hu, M.-K. (1962). Visual pattern recognition by moment

invariants. IRE Trans. Information Theory, 8(2):179–

187.

Li, B. C. (1993). A new computation of geometric mo-

ments. Pattern Recognition, 26(1):109–113.

Papakostas, G., Karakasis, E., and Koulouriotis, D. (2008).

Efﬁcient and accurate computation of geometric mo-

ments on gray-scale images. Pattern Recognition,

41:1895–1904.

Samet, H. (1990). Applications of Spatial Data Structures:

Computer Graphics, Image Progessing, and GIS. Ad-

dison Wesley, Reading, MA.

Shneier, M. (1981). Calculations of geometric properties

using quadtrees. Computer Graphics Image Process-

ing, 16:296–302.

Sossa-Azuela, J. H. and Flusser, J. (2004). Reﬁned method

for the fast and exact computation of moment invari-

ants. In Progress in Pattern Recognition, Image Anal-

ysis and Applications, 9th Iberoamerican Congress on

Pattern Recognition, CIARP, pages 487–494.

Sossa-Azuela, J. H., Y

nez-M

arquez, C., and D

ıaz-de

on S, J. L. (2001). Computing geometric moments

using morphological erosions. Pattern Recognition,

34(2):271–276.

Spiliotis, I. M. and Mertzios, B. G. (1996). Real-time com-

putation of 2-D moments on block represented binary

images on the scan line array processor. In 8th Euro-

pean Signal Processing Conference, EUSIPCO, pages

1–4.

Spiliotis, I. M. and Mertzios, B. G. (1998). Real-time com-

putation of two-dimensional moments on binary im-

ages using image block representation. IEEE Trans.

Image Processing, 7(11):1609–1615.

Suk, T. and Flusser, J. (2010). Reﬁned morphological meth-

ods of moment computation. In 20th International

Conference on Pattern Recognition, ICPR, pages 966–

970.

Wu, C.-H., Horng, S.-J., and Lee, P.-Z. (2001). A new com-

putation of shape moments via quadtree decomposi-

tion. Pattern Recognition, 34(7):1319–1330.

Zakaria, M. F., Vroomen, L. J., Zsombor-Murray, P. J., and

van Kessel, J. M. H. M. (1987). Fast algorithm for the

computation of moment invariants. Pattern Recogni-

tion, 20(6):639–643.

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods