Machine Learning-Driven Monitoring for Early Detection and

Management of Prediabetes

Wesam A. Ali

1 a

and Adeem Ali Anwar

2 b

Department of Chemistry, Khalifa University, P.O. Box 127788, Abu Dhabi, U.A.E.

School of Computing, Macquarie University, 2109, NSW, Australia

Keywords:

Prediabetes, Progression Rate, Machine Learning, Diabetes, Prediction.

Abstract:

Prediabetes is a critical metabolic condition that acts as the precursor for type 2 diabetes (T2D). Early de-

tection and management of prediabetes can prevent the onset of diabetes and associated complications. For

individuals with prediabetes, having a reliable way to estimate their risk of developing T2D is crucial, as it

helps them to keep their glycemic levels on track and may even enable them to regress to normoglycemia.

Building on this, we propose a methodology to predict the progression rate of prediabetes. In this study, we

enhanced the preexisting dataset by incorporating risk progression and risk probability using logistic regres-

sion. Moreover, we predicted the progression rate of prediabetes using machine learning-based approaches

and performed comparative analysis using logistic regression, random forest, decision tree, gradient boosting,

neural networks, and support vector machines. Utilizing key health indicators such as age, body mass index

(BMI), gender, and comorbidities as characteristic factors of prediabetes progression. The results demonstrate

that logistic regression outperforms other models with an accuracy of 99.93%, a precision of 99.92%, and an

AUC-ROC of 1.0000, making it the most suitable model for predicting prediabetes risk. The proposed system

offers a promising solution for real-time prediabetes monitoring.

1 INTRODUCTION

Diabetes mellitus (DM) is a metabolic disorder that

is induced by insufﬁcient insulin production by the

pancreas to decompose the blood glucose (Chauhan

et al., 2023). Resulting in severe damage to multiple

organs and the development of associated health com-

plications such as cardiovascular disease, blindness,

and neuropathy (JhaJay et al., 2016; Klein and Klein,

1995; Mohamed et al., 2016). According to the recent

statistics of the World Health Organization (WHO),

diabetes is the seventh cause of death worldwide (Or-

ganization, 2023). In this work, the term ’diabetes’

speciﬁcally refers to type 2 diabetes (T2D), unless

otherwise speciﬁed. Aside from genetic factors, di-

abetes typically does not develop suddenly (Katsarou

et al., 2017), as it generally progresses from a pre-

liminary stage called prediabetes (intermediate hyper-

glycemia). Prediabetes is a reversible condition where

glucose levels are high but not reaching the diabetic

threshold (Echouffo-Tcheugui and Selvin, 2021). It

occurs due to an inactive lifestyle, unhealthy dietary

https://orcid.org/0000-0003-0569-8615

https://orcid.org/0000-0002-6474-3810

intake, and obesity. If prediabetes is detected and

monitored at the right time, it can be reversed to

normoglycemia with the implementation of necessary

lifestyle changes and appropriate treatment (Bansal,

2015). Despite this, the current glucose monitoring

technologies are concentrated on diabetes manage-

ment rather than prediabetes, shifting attention to the

condition after it has developed instead of address-

ing it at the earlier, more treatable stage (Zhang et al.,

2021; Bruen et al., 2017; Liu et al., 2022; Liu et al.,

2024).

The application of machine learning (ML) tech-

niques for diabetes management and prediction has

received a lot of attention, particularly when it comes

to determining prediabetes progression. Research has

demonstrated that ML models with a variety of health

markers including age, body mass index (BMI), blood

glucose levels, and HbA1c values, may accurately

predict the onset of diabetes. To illustrate the po-

tential of machine learning (ML) in early diagno-

sis and preventive efforts, Cahn et al. (Cahn et al.,

2020) constructed and validated a machine learning

model to predict the progression from prediabetes to

diabetes. Perveen et al. (Perveen et al., 2019) em-

256

Ali, W. A. and Anwar, A. A.

Machine Learning-Driven Monitoring for Early Detection and Management of Prediabetes.

DOI: 10.5220/0013118800003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 3, pages 256-263

ISBN: 978-989-758-737-5; ISSN: 2184-433X

ployed machine learning approaches for predictive

modeling, demonstrating that machine learning may

increase prediction precision by analyzing a range of

features. The basis for the current study’s focus on

the progression of prediabetes has been established by

this research, which demonstrates the beneﬁts of uti-

lizing ML techniques to predict diabetes risk. Several

classiﬁers, such as random forests, neural networks,

and support vector machines have not received much

attention in the literature. These classiﬁers along with

others are used to predict the progression of predi-

abetes using an enhanced dataset that includes risk

probability and progression rate. This is despite the

advancements in the ﬁeld. This study aims to ﬁll

that gap by analyzing the effectiveness of multiple

machine learning models for early detection and risk

management of prediabetes.

In this study, the prediction of the prediabetes pro-

gression rate is achieved using a machine learning-

based approach that leverages patient-speciﬁc health

indicators and comparative analysis of machine learn-

ing algorithms including logistic regression, random

forest, neural networks, support vector machines, de-

cision trees, and gradient boosting has been done. The

dataset (Mustafa, 2021) we used contains gender, age,

hypertension, heart disease, HbA1c, BMI, glucose

levels, and diabetes, which was enhanced by adding

risk progression and risk probability (Anwar, 2024).

To the best of our knowledge, no study has speciﬁ-

cally targeted these key features using these machine

learning algorithms on the considered dataset and pre-

dicted prediabetes progression rate. It is often as-

sumed that glucose monitors designed for diabetes

can be used for prediabetes as well, but this is an in-

accurate assumption since these monitors need to be

speciﬁcally optimized to address the distinct require-

ments of each condition. This assumption arises from

the overlap between prediabetes and diabetes in terms

of insulin resistance (Haffner, 2003) glucose dysreg-

ulation (Lee et al., 2024), and risk factors (Budiastu-

tik et al., 2022). Regarding the latter, the risk factors

can differ statistically between prediabetes and dia-

betes. For instance, the BMI in diabetics aged 20 to

65 tends to have a higher average compared to those

with prediabetes (Menke et al., 2021). Furthermore,

both conditions differ in the metabolites present, as

demonstrated by Long et al. (Long et al., 2020), who

showed variations in the concentration of metabolites

like alanine, glutamate, and palmitic acid between the

two conditions. Additionally, they result in differ-

ent glycemic thresholds as stated by WHO (Organi-

zation, 2023) and the American Diabetes Association

(ADA) (Association, 2010). Building on this, it is

crucial to propose an optimized model speciﬁc to pre-

diabetes standards. Most importantly, the optimiza-

tion must consider key risk factors such as BMI, age,

and gender, which help differentiate individuals and

accurately address prediabetes.

This paper applies state-of-the-art machine learn-

ing approaches to predict the progression rate of pre-

diabetes by incorporating key metrics such as glucose

levels, age, BMI, gender, and comorbidities. The con-

tributions of this work are as follows:

1. Enhanced pre-existing dataset by incorporating

key ﬁelds such as risk progression and probabil-

ity using logistic regression.

2. Conducted a comparative analysis of multiple ma-

chine learning models to evaluate their perfor-

mance in predicting prediabetes progression rate.

The remainder of this paper is organized as fol-

lows: section 2 describes the prediabetes progression

risk model. Section 3 provides a detailed description

of the used dataset. Section 4 demonstrates the exper-

imental setup, results, and analysis. Finally, section 5

concludes the paper and discusses the future work.

2 PREDIABETES PROGRESSION

RISK PREDICTION

In this study, the prediction of the prediabetes pro-

gression rate is achieved using a machine learning-

based approach that leverages patient-speciﬁc health

indicators and a comparative analysis of models has

been done. The objective is to forecast how the risk

of diabetes may evolve over time and hence super-

vised classiﬁcation models are used using both cur-

rent health metrics and the presence of diabetes. The

prediction models estimate the likelihood of predia-

betes progression based on these factors. Moreover,

we enhanced the pre-existing dataset (Mustafa, 2021)

by incorporating key ﬁelds (i.e., risk progression and

probability) using logistic regression (Anwar, 2024).

2.1 Data Preparation

The dataset (Mustafa, 2021) we used contains gender,

age, hypertension, heart disease, BMI, glucose, and

diabetes and it is enhanced by adding risk progres-

sion and risk probability (Anwar, 2024). These fea-

tures are selected because they inﬂuence the progres-

sion of prediabetes, as supported by medical literature

and epidemiological studies (Mansourian et al., 2020;

Bennasar-Veny et al., 2020; Belsky et al., 2023).

Other factors could have contributed to the predia-

betes progression such as the fasting glucose levels or

triglyceride levels. However, recent research shows

Machine Learning-Driven Monitoring for Early Detection and Management of Prediabetes

257

that their impact is relatively insigniﬁcant compared

to the selected features (Bennasar-Veny et al., 2020;

Mansourian et al., 2020).

2.2 Modeling Approach

Several models are trained and evaluated to assess the

progression rate including logistic regression, random

forest, neural networks, support vector machines, de-

cision trees, and gradient boosting. The dataset is

split into training (80%) and testing (20%) sets, with

the models being trained to classify patients as either

“high risk” or “low risk” of prediabetes progression.

The target variable for progression is deﬁned by set-

ting a threshold on the risk probability, where patients

with a risk score of 50% or higher are classiﬁed as

being at high risk of disease progression.

2.3 Model Evaluation

The performance of each model is assessed using

several standard classiﬁcation metrics i.e., Accuracy

(Sokolova and Lapalme, 2009), Precision (Sokolova

and Lapalme, 2009), Recall (Sokolova and Lapalme,

2009), F1-Score (Sokolova and Lapalme, 2009), Area

Under the Receiver Operating Characteristic Curve

(AUC-ROC) (Bradley, 1997), Mean Squared Error

(MSE) (Willmott and Matsuura, 2005), R-squared

(R²) (Barrett, 2000) and Confusion Matrix (Sokolova

and Lapalme, 2009). Based on the evaluation met-

rics, the logistic regression classiﬁer is selected as the

ﬁnal model due to its superior performance across all

evaluation measures (Organization, 2023).

2.4 Prediction of Progression Rate

A logistic regression model is employed to estimate

the progression of prediabetes by utilizing the user

health metrics as inputs. A higher risk probability in-

dicates a more rapid progression, while a lower risk

probability suggests a slower progression or a stable

glycemic level. The process consists of the following

steps:

1. Input Features: The user provides values for

gender, age, BMI, HbA1c level, blood glucose

level, and relevant comorbidities (i.e., hyperten-

sion, heart disease).

2. Risk Calculation: The model processes the in-

puts and calculates the probability of progression

based on patterns learned during training.

3. Output: The model returns a progression proba-

bility, which is interpreted as the likelihood of the

patient’s diabetes risk increasing over time.

This machine learning-based prediction model en-

ables both healthcare providers and patients to gain

insight into the likelihood of prediabetes progression,

allowing for early interventions and personalized care

strategies. The use of health indicators ensures that

predictions are highly tailored to individual patient

proﬁles, helping to identify those at greater risk for

rapid disease progression. Such insights are vital

for making informed decisions about treatment ad-

justments, lifestyle interventions, and monitoring fre-

quency.

3 DATASET DESCRIPTION

The dataset utilized for this study is taken from Kag-

gle (Mustafa, 2021). This dataset is an extensive com-

pilation of patient medical records created with the

express purpose of aiding in the prediction of the on-

set of diabetes.

The dataset has a number of important features

that are useful for prediction, such as:

• Gender: A binary variable that takes gender vari-

ations in risk into account (0 for females and 1 for

males).

• Age: A continuous variable representing the pa-

tient’s age. It is a known feature for inﬂuencing

prediabetes progression.

• Hypertension: A binary variable that indicates if

the patient has hypertension; a common comor-

bidity with diabetes (0 for no, 1 for yes).

• Heart Disease: A binary variable that indicates

whether cardiovascular problems exist and can ac-

celerate the development of prediabetes (0 for no,

1 for yes).

• BMI: A continuous variable that shows the rela-

tionship between height and body weight, which

is crucial for indicating the development and pro-

gression of prediabetes.

• HbA1c Level: A continuous variable that shows

the percentage of glycated hemoglobin during the

preceding two to three months, acting as a gauge

of blood sugar control.

• Blood Glucose Level: A continuous variable that

gauges the bloodstream’s immediate glucose lev-

els.

• Diabetes: A binary variable that indicates if the

patient has received a diabetes diagnosis (0 for no,

1 for yes).

The dataset is characterized by a diverse range

of patient demographics and health conditions, mak-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

258

ing it a robust resource for machine learning appli-

cations in healthcare. Each entry represents a unique

patient proﬁle, allowing for comprehensive analysis

and modeling of diabetes risk factors.

Prior to model training, the dataset undergoes pre-

processing steps, including handling missing values,

feature normalization, and encoding categorical vari-

ables. This ensures the data is clean and suitable for

predictive modeling.

3.1 Risk Progression

In this study, we employed logistic regression

to model the risk progression of diabetes based

on key health factors. The dataset is prepro-

cessed to normalize relevant numerical features

such as age, BMI, HbA1c level, diabetes, and

blood glucose level, while categorical variables like

hypertension, heart disease, and gender are main-

tained in their binary form. After training the lo-

gistic regression model, we extracted the coefﬁcients

and intercept from the trained model to calculate risk

progression and probability for each individual in the

dataset.

The risk progression for an individual is computed

using the following formula:

risk progression = β

+ β

· age +β

· hypertension

+ β

· heart disease + β

· BMI

+ β

· HbA1c level

+ β

· blood glucose level

+ β

· gender

(1)

where β

represents the model intercept and

, β

, . . . , β

represent the coefﬁcients corresponding

to each feature. The coefﬁcients reﬂect the contribu-

tion of each factor toward the predicted log odds of

developing diabetes.

Once the risk progression (log-odds) is calculated,

we transform it into a probability using the logistic

function:

risk probability =

1 + exp(−risk progression)

(2)

This transformation provides the predicted prob-

ability of developing diabetes for each individual.

The probability is then expressed as a percentage

by multiplying the result by 100. After calculating

the risk progression and risk probability, these values

are added as two new columns risk

progression and

risk probability to the original dataset. The updated

dataset is saved as a CSV ﬁle for further analysis and

reporting.

Overall, the diabetes prediction dataset serves as a

valuable foundation for developing machine learning

models aimed at predicting diabetes risk, contributing

to the advancement of personalized healthcare solu-

tions.

4 EMPIRICAL STUDIES

In this section, the experimental settings and experi-

mental results are discussed in detail. The code for

all the experiments including the dataset alteration is

publicly available on (Anwar, 2024).

4.1 Experimental Settings

4.1.1 Datasets

The enhanced dataset (Mustafa, 2021; Anwar, 2024)

is used to predict the prediabetes progression rate and

includes key health indicators i.e., gender, age, hy-

pertension, heart disease, BMI, HbA1c level, blood

glucose level, diabetes are taken as input features and

Risk Probability is taken as target. These features are

selected due to their established inﬂuence on the pro-

gression of prediabetes as previously discussed.

4.1.2 Parameters Selection

The main parameters used in the creation of the pre-

diabetes risk prediction model are compiled in Table

1. Robust performance in the diabetes risk predic-

tion model is largely dependent on parameter selec-

tion. Different parameters are used by each model

to determine how well it performs; also, feature se-

lection and data partitioning are essential for efﬁcient

training and assessment.

4.1.3 Algorithms for Comparative Studies

The following algorithms are used in this study: (1)

Logistic Regression (Seber and Lee, 2003) a statis-

tical method for binary classiﬁcation which repre-

sents input features to probabilities using a sigmoid

function; (2) Random Forest (Breiman, 2001) an en-

semble technique that links multiple decision trees to

boost accuracy and decreases overﬁtting; (3) Decision

Tree Models (Quinlan, 1986) use a ﬂowchart struc-

ture to make predictions based on feature splitting but

may overﬁt complicated datasets; (4) Gradient Boost-

ing (Friedman, 2001) builds trees in sequence to cor-

rect errors and attains superior accuracy in structured

data; (5) Support Vector Machines (SVM) (Drucker

et al., 1996) ﬁnd an optimal hyperplane for classiﬁ-

cation and perform well in both linear and non-linear

Machine Learning-Driven Monitoring for Early Detection and Management of Prediabetes

259

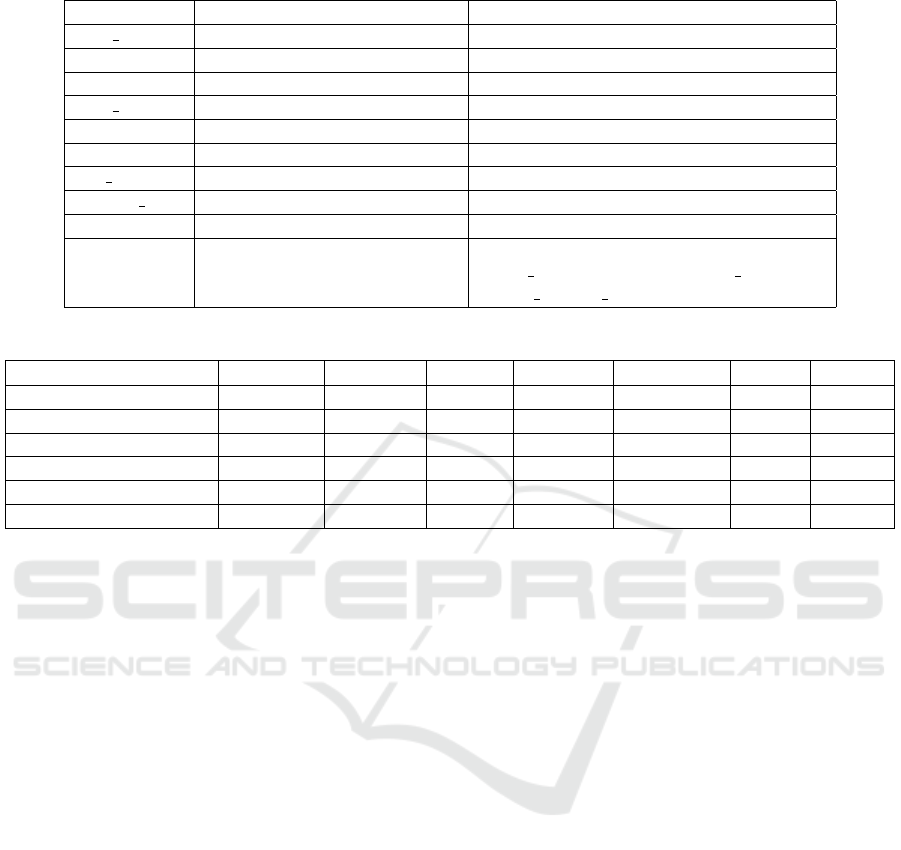
Table 1: Parameters Settings.

Parameter Model/Function Value/Description

max iter Logistic Regression 500 (Maximum iterations for convergence)

probability SVM True (Enables probability estimates)

- Random Forest Default parameters

max iter Neural Network 500 (Maximum iterations for training)

- Decision Tree Default parameters

- Gradient Boosting Default parameters

test size Data Splitting 0.2 (20% data for testing)

random state Data Splitting 42 (Ensures reproducibility)

y Target Variable Transformation apply(lambda x: 1 if x ≥ 50 else 0)

X Feature Selection data[[’gender’, ’age’, ’hypertension,

’heart disease’, ’BMI’, ’HbA1c level’,

’blood glucose level’, ’diabetes’]]

Table 2: Summary of Model Performance.

Model Accuracy Precision Recall F1-Score AUC-ROC MSE R

Logistic Regression 99.93% 99.92% 99.01% 99.46% 1.0000 0.0011 0.9808

Random Forest 99.41% 96.03% 94.13% 95.07% 0.9996 0.0043 0.9245

Neural Network (MLP) 99.40% 99.64% 90.41% 94.80% 0.9997 0.0044 0.9223

SVM 97.14% 94.92% 55.67% 70.18% 0.9971 0.0103 0.8179

Decision Tree 99.28% 93.75% 94.29% 94.02% 0.9694 0.0073 0.8723

Gradient Boosting 99.31% 96.45% 92.06% 94.20% 0.9994 0.0049 0.9136

problems; and (6) Neural Networks (NNs) (Rumel-

hart et al., 1986) inspired by the human brain and suc-

ceed at netting complex patterns in data for tasks in-

cluding image recognition and natural language pro-

cessing.

4.1.4 Evaluation Measures

We used the following evaluation metrics to assess the

performance of the machine learning models. Mean

Squared Error (MSE) measures the average squared

difference between actual and predicted values (Will-

mott and Matsuura, 2005). R-squared (R²), which is

also known as the coefﬁcient of determination shows

how well the model explains the variability in the de-

pendent variable (Barrett, 2000). Accuracy is the ratio

of correctly predicted instances to the total instances

(Sokolova and Lapalme, 2009). Precision measures

the ratio of true positive predictions to the total pre-

dicted positives (Sokolova and Lapalme, 2009). The

recall represents the proportion of actual positives that

are correctly predicted by the model (Sokolova and

Lapalme, 2009). F1-Score is the harmonic mean of

precision and recall (Sokolova and Lapalme, 2009).

The Area Under the Curve (AUC) of the Receiver

Operating Characteristic (ROC) curve measures the

model’s ability to distinguish between classes at vari-

ous threshold levels (Bradley, 1997). Confusion Ma-

trix provides detailed insight into the performance of

the classiﬁcation model by presenting the counts of

true positives, true negatives, false positives, and false

negatives predictions (Sokolova and Lapalme, 2009).

4.2 Experimental Results and

Sensitivity Analysis

The following section describes the experiments, their

discussion, and sensitivity analyses.

4.2.1 Experimental Results

To predict the risk probability of diabetes based on

key health indicators six machine learning models:

Logistic Regression, Random Forest, Neural Net-

works, SVM, Decision Tree, and Gradient Boosting

are used. These models are trained on a dataset con-

taining features such as gender, age, hypertension sta-

tus, heart disease status, BMI, HbA1c level, blood

glucose level, and diabetes status (Mustafa, 2021; An-

war, 2024). The target variable is a binary classiﬁca-

tion of risk probability, where a threshold of 50% is

used to classify instances as high or low risk.

Numerous metrics, such as accuracy, precision,

recall, F1-Score, AUC-ROC, MSE, and R-squared

), are used to evaluate each model’s performance.

Table 2 provides the results for each model. Figure 1

shows the confusion matrix for all algorithms.

With an ideal discriminatory power indicated by

AUC-ROC of 1.0000 and an accuracy of 99.93%,

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

260

Figure 1: Confusion Matrix for all considered algorithms.

Logistic Regression demonstrated the highest overall

performance. With a 99.92% precision and a 99.01%

recall, the model produced an F1-Score of 99.46%.

Additionally, the model explains 98.08% of the vari-

ance (R

= 0.9808) in predicting the risk probability,

and its MSE (0.0011) is the lowest of all the models.

These ﬁndings show that Logistic Regression offers

reliable forecasts with low error rates in addition to

correctly classifying the risk level.

Along with its strong performance, the Random

Forest classiﬁer achieved an accuracy of 99.41% and

an AUC-ROC of 0.9996, indicating almost perfect

classiﬁcation abilities. With a precision of 96.03%

and a recall of 94.13%, the model produced an F1-

Score of 95.07%. Random Forest explained a sig-

niﬁcant amount of the variance in the predictions, as

evidenced by the MSE, which is marginally higher

than Logistic Regression at 0.0043 and the R

value

of 0.9245.

With an accuracy of 99.40% and an AUC-ROC

of 0.9997, the Neural Network model performed sim-

ilarly to Random Forest. The model’s F1-Score is

94.80%, with a precision of 99.64% and a somewhat

lower recall of 90.41%. With an MSE of 0.0044 and

a R

of 0.9223, the prediction stability is marginally

lower than that of Random Forest. In spite of this,

the Neural Network continued to exhibit good perfor-

mance, particularly in differentiating between the two

risk categories.

Performance-wise, the SVM classiﬁer performed

worse than the other models. It obtained an AUC-

ROC of 0.9971 and an accuracy of 97.14%; however,

its precision and recall are only 94.92% and 55.67%,

respectively. With an F1-Score of 70.18%, this in-

dicated that SVM had trouble with recall, especially

when it came to recognizing high-risk cases. When

compared to the other models, the MSE is higher at

0.0103 and the R

is 0.8179, indicating worse predic-

tive power.

With a precision of 93.75%, recall of 94.29%, and

accuracy of 99.28%, the Decision Tree classiﬁer pro-

duced an F1-Score of 94.02%. Although still strong,

the AUC-ROC of 0.9694 is less than that of the lo-

gistic and ensemble models. With an MSE of 0.0073

and a R

of 0.8723, the model demonstrated a moder-

ate level of variance explanation and prediction error.

With an accuracy of 99.31% and an AUC-ROC of

0.9994, the Gradient Boosting model performed ad-

mirably by all measures. The model has an F1-Score

of 94.20% based on its precision of 96.45% and recall

of 92.06%. Its MSE of 0.0049 is marginally higher

than that of Random Forest and Logistic Regression,

and its R

of 0.9136 indicates that it accounts for a

sizable amount of the variance in the predictions.

In conclusion, based on the model performance

metrics, Logistic Regression emerges as the most

effective model for predicting diabetes risk in this

dataset. It achieves the highest values in criti-

cal metrics, including accuracy (99.93%), precision

(99.64%), recall (99.01%), F1-Score (99.46%), AUC-

ROC (1.0000), and R-squared (0.9808), while also

maintaining the lowest MSE (0.0011), indicating

highly accurate and stable predictions. Therefore, Lo-

gistic Regression not only provides superior perfor-

mance across multiple dimensions but also offers a

balance of accuracy, precision, and low error rates,

making it the most suitable choice for this task. This

ideal performance could result from various factors,

including a well-deﬁned decision boundary, over-

ﬁtting, the inherent separability of the classes in the

dataset, and potentially the absence of noise or over-

lap between classes.

4.2.2 Sensitivity Analysis

In this study, a parametric analysis is conducted to in-

vestigate the effect of varying input features on the

predicted risk probability of diabetes progression. A

dataset with features i.e., age, gender, blood pressure,

heart disease, BMI, HbA1c level, blood glucose level,

and diabetes status is used to train a logistic regres-

sion model. Using a threshold value of 50%, the tar-

get variable, risk probability, is converted into a bi-

nary classiﬁcation. Values more than or equal to 50%

are labeled as high risk, while values less than 50%

are labeled as low risk. An 80-20 split ratio is used

to divide the data into training and testing sets. To

guarantee convergence, the logistic regression model

is trained using the training set, up to 500 iterations

total. We change the input for each feature through-

out a predetermined range and assess the effect on the

estimated risk probability. Table 3 lists the ranges that

are used for the parametric analysis.

In the parametric analysis, each feature is taken

one by one while keeping all other features constant

at their mean or usual values. The following con-

Machine Learning-Driven Monitoring for Early Detection and Management of Prediabetes

261

Table 3: Feature Ranges for Parametric Analysis.

Feature Range/Values

Age 30 to 80 years

Gender {0 (Female), 1 (Male)}

Hypertension {0 (No), 1 (Yes)}

Heart Disease {0 (No), 1 (Yes)}

BMI 18.5 to 40.0

HbA1c Level 4.5 to 10.0

Blood Glucose Level 70 to 200 mg/dL

Diabetes {0 (No), 1 (Yes)}

stant values are applied to the non-varied features:

The BMI is ﬁxed at 25.0, the gender is set to male,

the HbA1c level and blood glucose level are set to the

mean value from the training data, and it is assumed

that there is no diabetes, heart disease, or hyperten-

sion. This method makes it possible to evaluate how

each individual feature affects the result.

The predicted probability of risk increases dra-

matically with age, particularly for those over 60.

Another factor is gender, with males often being at

higher risk than women. A larger predicted risk is

shown in people with cardiac disease or hypertension,

which is in line with the correlation between these

conditions and metabolic disorders. Increased BMI

readings, especially those over 30, are linked to in-

creased risk and indicate obesity. The predicted risk is

signiﬁcantly increased by elevated HbA1c levels and

blood glucose levels above 150 mg/dL. Lastly, the fact

that diabetes raises the probability of advancement

signiﬁcantly emphasizes how well the model captures

this important aspect.

Figure 2: Parametric Analysis for all Key Factors.

As shown in the Figure 2, the parametric anal-

ysis demonstrates that the logistic regression model

captures meaningful relationships between the input

features and the predicted risk probability of diabetes

progression. This analysis provides insights into how

each individual feature contributes to the overall risk

and highlights key factors such as age, BMI, HbA1c

level, and the presence of hypertension, heart disease,

and diabetes in inﬂuencing the risk of progression.

5 CONCLUSION AND FUTURE

WORK

This paper presents a comprehensive methodology

for predicting the progression rate of prediabetes us-

ing machine learning models. Moreover, the dataset

has been enhanced by adding key features i.e., risk

progression and probability. With an accuracy of

99.93%, precision of 99.92%, and an AUC-ROC of

1.0000, among the tested models, Logistic Regression

proved to be the most reliable and accurate in pre-

dicting the progression rate of prediabetes. It outper-

formed models like Random Forest, Decision Tree,

Gradient Boosting, Neural Networks, and SVMs.

To lower the risk of developing diabetes, the sug-

gested approach provides a way to implement tailored

healthcare plans and early intervention.

Future efforts will focus on incorporating a sweat-

based wearable device for non-invasive glucose moni-

toring, reﬁning the sensitivity and accuracy of the sen-

sor technology. Furthermore, a more extensive and

varied dataset will be utilized to enhance the model’s

applicability to various demographic groups. The op-

timization of machine learning models to enhance the

trade-off between computing efﬁciency and accuracy

is another area of study, particularly when applied to

real-time healthcare applications. Finally, to assess

the suggested system’s efﬁcacy in practical situations,

clinical trials will be required.

REFERENCES

Anwar, A. A. (2024). Prediabetes progression. https:

//github.com/adeemali/prediabetesProgression. Ac-

cessed: 2024-09-26.

Association, A. D. (2010). Diagnosis and classiﬁca-

tion of diabetes mellitus. Diabetes care, 33(Supple-

ment 1):S62–S69.

Bansal, N. (2015). Prediabetes diagnosis and treatment: a

review. World journal of diabetes, 6(2):296.

Barrett, G. B. (2000). The coefﬁcient of determination: Un-

derstanding r squared and r squared. The Mathematics

Teacher, 93(3):230–234.

Belsky, N., Tamaroff, J., and Shoemaker, A. H. (2023). Risk

factors for progression to type 2 diabetes in a pedi-

atric prediabetes clinic population. Journal of the En-

docrine Society, 7(11):bvad118.

Bennasar-Veny, M., Fresneda, S., L

opez-Gonz

alez, A.,

Busquets-Cort

es, C., Aguil

o, A., and Ya

nez, A. M.

(2020). Lifestyle and progression to type 2 diabetes

in a cohort of workers with prediabetes. Nutrients,

12(5):1538.

Bradley, A. P. (1997). The use of the area under the

roc curve in the evaluation of machine learning algo-

rithms. Pattern recognition, 30(7):1145–1159.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

262

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Bruen, D., Delaney, C., Florea, L., and Diamond, D. (2017).

Glucose sensing for diabetes monitoring: recent de-

velopments. Sensors, 17(8):1866.

Budiastutik, I., Kartasurya, M. I., Subagio, H. W., and Wid-

janarko, B. (2022). High prevalence of prediabetes

and associated risk factors in urban areas of pontianak,

indonesia: A cross-sectional study. Journal of Obe-

sity, 2022(1):4851044.

Cahn, A., Shoshan, A., Sagiv, T., Yesharim, R., Goshen,

R., Shalev, V., and Raz, I. (2020). Prediction

of progression from pre-diabetes to diabetes: de-

velopment and validation of a machine learning

model. Diabetes/Metabolism Research and Reviews,

36(2):e3252.

Chauhan, A. S., Varre, M. S., Izuora, K., Trabia, M. B., and

Dufek, J. S. (2023). Prediction of diabetes mellitus

progression using supervised machine learning. Sen-

sors, 23(10):4658.

Drucker, H., Burges, C. J., Kaufman, L., Smola, A., and

Vapnik, V. (1996). Support vector regression ma-

chines. Advances in neural information processing

systems, 9.

Echouffo-Tcheugui, J. B. and Selvin, E. (2021). Prediabetes

and what it means: the epidemiological evidence. An-

nual review of public health, 42(1):59–77.

Friedman, J. H. (2001). Greedy function approximation: A

gradient boosting machine. Annals of statistics, pages

1189–1232.

Haffner, S. M. (2003). Insulin resistance, inﬂammation, and

the prediabetic state. The American journal of cardi-

ology, 92(4):18–26.

JhaJay, C., ChowBryna, S., CooperMark, E., et al. (2016).

Diabetes and kidney disease: role of oxidative stress.

Antioxidants & redox signaling.

Katsarou, A., Gudbj

ornsdottir, S., Rawshani, A., Dabelea,

D., Bonifacio, E., Anderson, B. J., Jacobsen, L. M.,

Schatz, D. A., and Lernmark,

A. (2017). Type 1

diabetes mellitus. Nature reviews Disease primers,

3(1):1–17.

Klein, R. and Klein, B. E. (1995). Vision disorders in dia-

betes. Diabetes in America, 1:293.

Lee, J., Xue, X., Au, E., McIntyre, W. B., Asgariroozbe-

hani, R., Panganiban, K., Tseng, G. C., Papoulias,

M., Smith, E., Monteiro, J., et al. (2024). Glucose

dysregulation in antipsychotic-naive ﬁrst-episode psy-

chosis: in silico exploration of gene expression signa-

tures. Translational Psychiatry, 14(1):19.

Liu, H., Li, Z., Che, S., Feng, Y., Guan, L., Yang, X., Zhao,

Y., Wang, J., Zvyagin, A. V., Yang, B., et al. (2022).

A smart hydrogel patch with high transparency, ad-

hesiveness and hemostasis for all-round treatment and

glucose monitoring of diabetic foot ulcers. Journal of

Materials Chemistry B, 10(30):5804–5817.

Liu, Y., Yang, L., and Cui, Y. (2024). A wear-

able, rapidly manufacturable, stability-enhancing mi-

croneedle patch for closed-loop diabetes management.

Microsystems & nanoengineering, 10(1):112.

Long, J., Yang, Z., Wang, L., Han, Y., Peng, C., Yan, C.,

and Yan, D. (2020). Metabolite biomarkers of type 2

diabetes mellitus and pre-diabetes: A systematic re-

view and meta-analysis. BMC endocrine disorders,

20:1–17.

Mansourian, M., Yazdani, A., Faghihimani, E., Aminor-

raya, A., Amini, M., and Jafari-Koshki, T. (2020).

Factors associated with progression to pre-diabetes:

a recurrent events analysis. Eating and Weight

Disorders-Studies on Anorexia, Bulimia and Obesity,

25:135–141.

Menke, A., Knowler, W. C., and Cowie, C. C. (2021). Phys-

ical and metabolic characteristics of persons with di-

abetes and prediabetes. Europepmc.

Mohamed, J., Naﬁzah, A. N., Zariyantey, A., and Budin, S.

(2016). Mechanisms of diabetes-induced liver dam-

age: the role of oxidative stress and inﬂammation. Sul-

tan qaboos university medical journal, 16(2):e132.

Mustafa, I. (2021). Diabetes prediction dataset.

https://www.kaggle.com/datasets/iammustafatz/

diabetes-prediction-dataset. Accessed: 2024-09-26.

Organization, W. H. (2023). Diabetes. Accessed: 28-Sep-

2024.

Perveen, S., Shahbaz, M., Keshavjee, K., and Guergachi,

A. (2019). Prognostic modeling and prevention of di-

abetes using machine learning technique. Scientiﬁc

reports, 9(1):13805.

Quinlan, J. R. (1986). Induction of decision trees. Machine

learning, 1(1):81–106.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning representations by back-propagating errors.

Nature, 323(6088):533–536.

Seber, G. A. F. and Lee, A. J. (2003). Linear Regression

Analysis. John Wiley & Sons.

Sokolova, M. and Lapalme, G. (2009). A systematic analy-

sis of performance measures for classiﬁcation tasks.

Information Processing & Management, 45(4):427–

437.

Willmott, C. J. and Matsuura, K. (2005). Advantages of the

mean absolute error (mae) over the root mean square

error (rmse) in assessing average model performance.

Climate research, 30(1):79–82.

Zhang, J., Xu, J., Lim, J., Nolan, J. K., Lee, H., and

Lee, C. H. (2021). Wearable glucose monitor-

ing and implantable drug delivery systems for dia-

betes management. Advanced Healthcare Materials,

10(17):2100194.

Machine Learning-Driven Monitoring for Early Detection and Management of Prediabetes

263