Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised

Image Classiﬁcation

Paul-Dumitru Or

as¸an

, Alexandra-Ioana Albu

and Gabriela Czibula

Department of Computer Science, Babes¸-Bolyai University, M. Kog

alniceanu nr. 1, Cluj-Napoca, Romania

Keywords:

Semi-Supervised Learning, Generative Models, Diffusion Models, Image Classiﬁcation.

Abstract:

Diffusion models have revolutionized the ﬁeld of generative machine learning due to their effectiveness in cap-

turing complex, multimodal data distributions. Semi-supervised learning represents a technique that allows

the extraction of information from a large corpus of unlabeled data, assuming that a small subset of labeled

data is provided. While many generative methods have been previously used in semi-supervised learning

tasks, only few approaches have integrated diffusion models in such a context. In this work, we are adapt-

ing state-of-the-art generative diffusion models to the problem of semi-supervised image classiﬁcation. We

propose Diff-SySC, a new semi-supervised, pseudo-labeling pipeline which uses a diffusion model to learn

the conditional probability distribution characterizing the label generation process. Experimental evaluations

highlight the robustness of Diff-SySC when evaluated on image classiﬁcation benchmarks and show that it

outperforms related work approaches on CIFAR-10 and STL-10, while achieving competitive performance on

CIFAR-100. Overall, our proposed method outperforms the related work in 90.74% of the cases.

1 INTRODUCTION

Semi-supervised learning (SSL) represents a machine

learning (ML) paradigm wherein a model leverages

both labeled and unlabeled data to achieve enhanced

predictive performance. Traditional supervised learn-

ing relies solely on labeled data for training, thus re-

quiring a labour-intensive and costly annotation pro-

cess. In contrast, SSL reduces the labeling effort by

utilizing abundant unlabeled data alongside a smaller

set of labeled samples. The labeled subset provides

explicit guidance for the model, allowing it to learn

from known examples. The unlabeled data is used

to enhance the model’s understanding of the broader

data distribution and to improve generalization. SSL

is particularly valuable in scenarios where obtaining

annotations is resource-intensive or impractical, as it

maximizes the utility of available labeled data while

harnessing the vast, often readily accessible, unla-

beled data for achieving enhanced performance (Yang

et al., 2023).

Generative learning comprises a set of methods

which focus on modeling and understanding the un-

derlying statistical structure of a given dataset. Dif-

https://orcid.org/0009-0008-0474-7095

https://orcid.org/0000-0002-2340-6340

https://orcid.org/0000-0001-7852-681X

fusion models represent a class of generative mod-

els that simulate the diffusion process of particles

through a system, capturing the dynamics of how data

spreads or evolves over time (Dhariwal and Nichol,

2021). While generative models such as Generative

Adversarial Networks (GANs) or Variational Autoen-

coders (VAEs) have been extensively explored in the

past for designing semi-supervised learning proce-

dures (Yang et al., 2023), only few studies have em-

ployed diffusion models for this task (You et al., 2023;

Gong et al., 2023). These approaches use diffusion

models as generative processes for images, by sam-

pling new instances to be added to the training set.

This paper introduces Diff-SySC, a new approach

based on diffusion models for semi-supervised image

classiﬁcation. Our approach uses a diffusion model

for label generation. Our goal is to train a model to

learn the distribution p( ¯y|x), where x denotes the in-

put image, y represents the corresponding target la-

bel of x and ¯y describes an aggregated label obtained

using the neighbors of y. We design a self-training

semi-supervised procedure using the trained diffusion

model to progressively generate pseudo-labels for the

unlabeled data. To the best of our knowledge, our

proposal of directly using diffusion to model the la-

beled data distribution in a semi-supervised fashion

is the ﬁrst of its kind. To summarize, the main con-

132

a¸san, P.-D., Albu, A.-I. and Czibula, G.

Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classiﬁcation.

DOI: 10.5220/0013097100003890

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 3, pages 132-139

ISBN: 978-989-758-737-5; ISSN: 2184-433X

tributions of the paper are the following: (1) integra-

tion of diffusion models for label generation in semi-

supervised learning; and (2) design of an iterative

pseudo-labeling pipeline that is robust to noisy labels.

To achieve the proposed goals, our work aims to an-

swer two research questions: RQ1. How can diffu-

sion models be used for designing a semi-supervised

image classiﬁcation approach? and RQ2. How robust

is the semi-supervised diffusion-based method when

evaluated on literature established image classiﬁca-

tion benchmarks and how does its performance com-

pare to related work?

The rest of the paper is organized as follows. Sec-

tion 2 brieﬂy presents the main literature advance-

ments in the approached ﬁelds. The methodology em-

ployed for designing and validating our Diff-SySC

model is introduced in Section 3. Section 4 presents

the experimental analysis, while a discussion of the

results is conducted in Section 5. Section 6 concludes

the paper and indicates directions for future work.

2 BACKGROUND

2.1 Semi-Supervised Image

Classiﬁcation

In their survey, (Yang et al., 2023) divide the SSL

approaches in several classes of methods: generative

methods, consistency regularization methods, graph-

based methods, pseudo-labeling methods and hy-

brid methods. The ﬁrst category comprises different

methodologies using generative models with the goal

of improving the performance of semi-supervised

classiﬁers. These strategies include the use of GANs

and VAEs for pre-training, the integration of unsuper-

vised training objectives and generative architectural

components in supervised classiﬁers (Springenberg,

2016) or the generation of additional training sam-

ples by class conditioning. Recently, diffusion mod-

els have been incorporated into semi-supervised train-

ing pipelines. (You et al., 2023) employed a diffu-

sion model for augmenting the training set of a semi-

supervised classiﬁer, by generating new images for

multiple labels. The approach was able to outperform

strong baselines on the ImageNet dataset, achieving

an accuracy of 59% using one label per class and

74.4% when using ﬁve labels per class.

The majority of the SSL methods employing con-

sistency regularization (Zhang and Qi, 2020) follow

the Teacher-Student structure that involves training a

Teacher model using the labeled data, and then using

this model to train a Student model using the unla-

beled data. Some approaches opted for using the same

network as both Teacher and Student models. One

such example is the Π-Model (Sajjadi et al., 2016),

which applies a consistency regularizer on the pre-

dictions obtained by the network using two differ-

ent augmentations of the same image. The Mean

Teacher (Tarvainen and Valpola, 2017) method com-

putes an exponential moving average (EMA) of the

network’s parameters to build a teacher model. The

Mean Teacher approach was evaluated on the CIFAR,

SVHN and ImageNet datasets and it signiﬁcantly im-

proved the state-of-the-art results on ImageNet with

10% labels by reaching an error rate of 9.11%. The

pseudo-labeling based SSL methods produce artiﬁ-

cial labels for the unlabeled data and use them in the

following training stages. There are many variations

of this semi-supervised pipeline, with methods such

as Pseudo-label, Noisy Student (Yang et al., 2023),

Meta Pseudo Labels (MPL) (Pham et al., 2021) or

SimCLRv2 (Chen et al., 2020).

Hybrid methods incorporate multiple complemen-

tary techniques in order to achieve improved perfor-

mance. MixMatch (Berthelot et al., 2019) is an ex-

ample of such an approach which produces pseudo-

labels by averaging and sharpening the predictions

for multiple augmentations of a sample. MixMatch

was able to consistently outperform baselines such as

the Π-model, Pseudo-labeling and Mean Teacher on

CIFAR-10 and SVHN. FixMatch (Sohn et al., 2020)

builds on the intuition given by other hybrid methods,

but proposes a simpliﬁed and more effective train-

ing procedure. FixMatch generates pseudo-labels

for unlabeled data by passing weakly augmented im-

ages through the classiﬁcation network. The gen-

erated pseudo-labels are used during training as tar-

gets for strong augmentations of the images. Fix-

Match was evaluated on the CIFAR, SVHN, STL-10

and ImageNet datasets and it was able to outperform

more complex baselines such as MixMatch, Pseudo-

labeling, Mean Teacher and the Π-Model. CRMatch

(Fan et al., 2023) extended FixMatch by adding a

feature loss and a rotation prediction training objec-

tive. CRMatch was able to consistently outperform

other approaches on multiple datasets. (Zheng et al.,

2022) proposed the concept of SSL based on similar-

ity matching (SimMatch). In SimMatch, the key com-

ponent is the integration of consistency regulariza-

tion at both semantic and instance levels. SimMatch

achieved state-of-the-art performance on the CIFAR

and ImageNet benchmarks. SimMatchV2 (Zheng

et al., 2023) introduced multiple consistency regular-

ization terms, by deﬁning a graph in which sample

images and their augmentations represent nodes and

edges are weighted by the similarities between nodes.

Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classiﬁcation

133

2.2 Diffusion Models for Classiﬁcation

Denoising Diffusion Probabilistic Models (DDPM)

(Dhariwal and Nichol, 2021) are generative models

which learn to sample new data points by deﬁning

an iterative denoising procedure. DDPMs consist of

forward and backward diffusion processes. The for-

ward process progressively adds Gaussian noise to

a data sample x

until it becomes indistinguishable

from an isotropic normal distribution. In the back-

ward process, a neural network is trained to approx-

imate the conditional probabilities needed for sam-

pling the original image x

from the corrupted version

The Classiﬁcation and Regression Diffusion

(CARD) framework introduced by (Han et al., 2022)

extended generative diffusion models to classiﬁcation

and regression tasks. The proposed approach ﬁrst

trains a classiﬁer network f

in a supervised man-

ner on the available dataset D to approximate the ex-

pected value of the output y given the input x. Af-

terwards, a diffusion model is trained, by iteratively

corrupting the ground truth label values y

. The for-

ward diffusion process outputs y

, which is character-

ized by a normal conditional probability distribution

centered around the classiﬁer prediction f

(x). Dur-

ing the backward diffusion process, the CARD model

learns to reconstruct the original y

label value.

(Chen et al., 2023) used the innovations brought

by CARD to introduce a new generative perspec-

tive on the task of learning with noisy labels. In

their framework, Label-Retrieval-Augmented Diffu-

sion (LRA-Diffusion), the labeling of a sample is

viewed as a stochastic process. Intuitively, LRA-

Diffusion aims to recreate through a diffusion pro-

cess the true, clean label of a sample starting from

a noisy one. Due to the fact that the clean labels are

not available, the model uses annotations reﬁned by

aggregation over the nearest neighbors. In order to

identify the neighbors of a data point, LRA-Diffusion

computes distances in the embedding space learned

by an unsupervised feature extractor f

. The labels

of the neighbors of a data point are used to construct

an aggregated label, ¯y, which is corrupted throughout

the forward diffusion process. To reconstruct ¯y, the

backward diffusion process makes use of representa-

tions learned by f

. By augmenting the training pro-

cess with labels retrieved from the neighborhood of

the learned representations, the architecture becomes

highly resistant to noisy labels.

3 METHODOLOGY

For answering research question RQ1, this section

introduces the methodology employed in developing

and validating our Diff-SySC approach.

Let us consider the input space X and a set of

given classes/labels C = {c

,... ,c

} (the output

space). Assuming that each input instance belongs

to a class, we are given a single-label classiﬁcation

task formalized as a function f : X → C . In this for-

malization, f (x) represents the class assigned to an

object x ∈ X. In ML, the classiﬁcation task should be

formalized as searching for an approximation of f by

minimizing a loss (error) function L deﬁned on the

input space. We further consider the SSL setting, in

which we have a dataset X ⊂ X consisting of a small

number of labeled samples (X

ℓ

) and a larger number

of unlabeled ones (X

) such that X = X

ℓ

∪ X

and

ℓ

∩ X

0. For each instance x ∈ X

ℓ

its label is

known and is denoted as y

∈ C . Let us denote by

ℓ

= {y

|x ∈ X

ℓ

} the set of available labels for the

instances from X

ℓ

3.1 Overview of Diff-SySC

We introduce the Diff-SySC approach that inte-

grates a LRA-Diffusion model into a semi-supervised

pipeline. Figure 1 provides a high-level overview of

Diff-SySC, highlighting the motivation behind our

proposal. On the left and right sides, we show a rep-

resentation of the feature extractor embedding space.

As with any semi-supervised context, we rely on

several assumptions. The clustering assumption im-

plies that the data samples sharing the same labels

tend to form clusters in a lower-dimensionality man-

ifold. The continuity assumption implies that close

data samples have a strong likelihood of sharing the

same label. The low-density assumption indicates that

decision boundary planes do not intersect with high-

density regions (Yang et al., 2023).

The center of Figure 1 presents the training pro-

cess of the diffusion model. We train a LRA-

Diffusion model through the methodology proposed

in (Chen et al., 2023). The feature embeddings of

the input sample x, obtained using a pre-trained CLIP

(Radford et al., 2021) model, are used as condi-

tioning information in the backward diffusion pro-

cess. Diff-SySC is an iterative procedure that ini-

tially trains a LRA-Diffusion model D

on the avail-

able labeled data



ℓ



. Subsequently, the trained

model is used to generate pseudo-annotations for the

unlabeled dataset X

, which are added to



ℓ



The training stage of the Diff-SySC approach is de-

scribed in Algorithm 1. Thus, for each iteration i, a

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

134

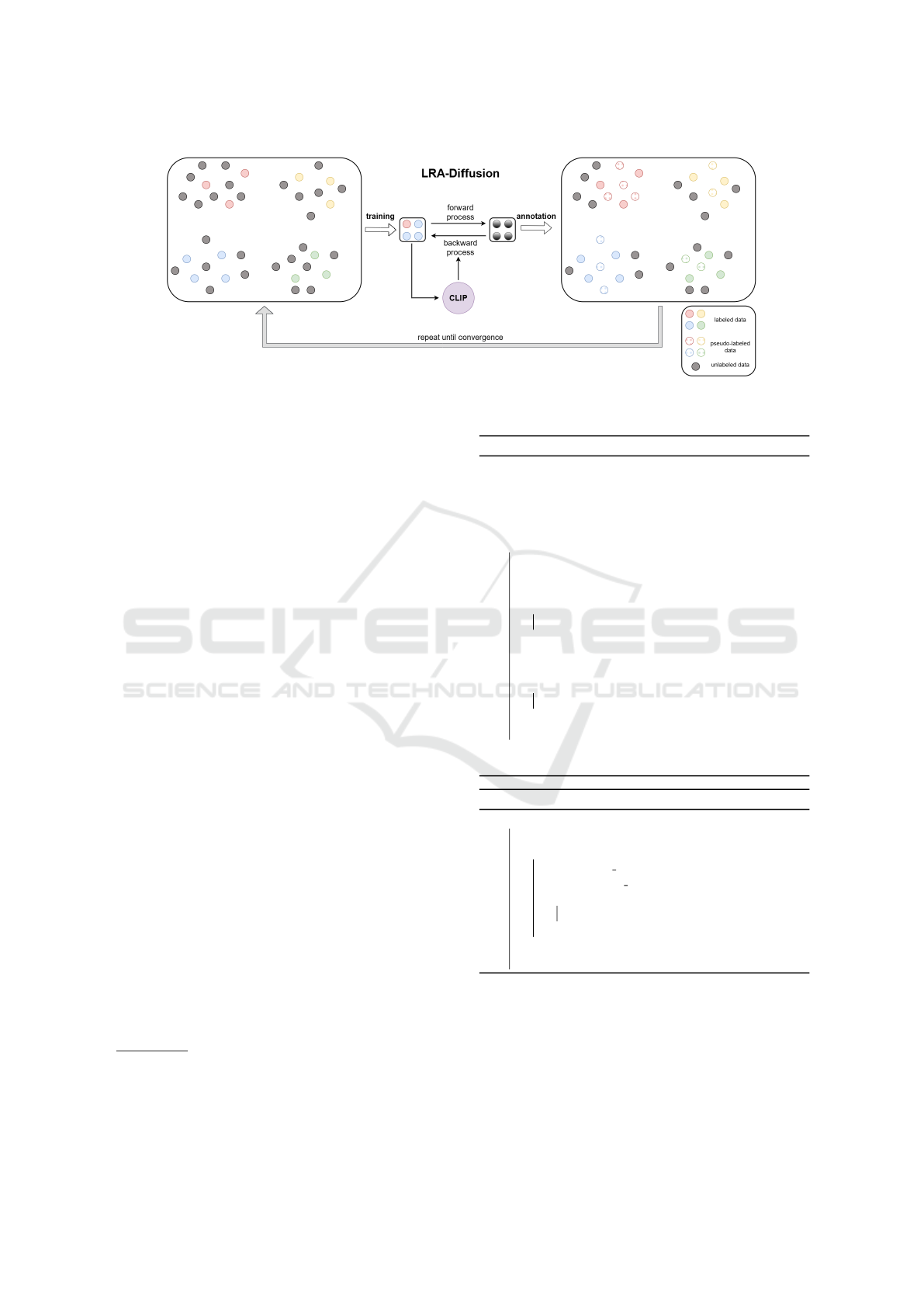
Figure 1: General overview of Diff-SySC. A LRA-Diffusion model is trained on the labeled dataset. The conﬁdent pseudo-

labels generated at the end of one iteration are added to the labeled set and the training is repeated until convergence.

LRA-Diffusion D

is trained on the current labeled

dataset



ℓ



Once the training of the model is ﬁnished, at

the end of an iteration, the predictions of the model

are calibrated using temperature scaling (Guo et al.,

2017). This technique is employed in order to achieve

a better reﬂection of the likelihood that the predicted

classes are correct, by granting a more accurate quan-

tiﬁcation of the model’s conﬁdence in its predictions.

The optimal temperature parameter τ is found using

the validation dataset

⟨

⟩

. More speciﬁcally, a

range of temperature values is considered and the

value which minimizes the Expected Calibration Er-

ror (Guo et al., 2017) on the validation set is selected.

Using the trained model D

and the temperature τ,

the conﬁdent pseudo-labels dataset

⟨

⟩

is con-

structed via annotation. The selection of conﬁdent

predictions aids in limiting the amount of noisy labels

introduced by the usage of pseudo-labels. Concur-

rently, the demonstrated robustness of LRA-Diffusion

to noisy labels represents another strategy for reduc-

ing the impact of incorrect pseudo-labels.

The annotation process is further described in Al-

gorithm 2. For each unlabeled data sample, the

model’s label prediction and its conﬁdence in the

pseudo-label are computed. If the model’s conﬁ-

dence is larger than the threshold γ, the pseudo-label

is stored in the annotated dataset.

The predicted class and its conﬁdence are ob-

tained as follows. For any input image x, we sam-

ple from the model’s learned distribution p( ¯y|x). The

obtained logits z = (z

,..., z

) are further divided by

the temperature τ. The scaled logits z

/τ are given

as input to a Softmax function σ, where σ

(z/τ) =

exp(z

/τ)

∑

j=1

exp(z

/τ)

, in order to obtain the calibrated class

probabilities of the model for input x. Thus, the pre-

dicted conﬁdence for sample x is the maximum entry

in the vector σ(z/τ), while the predicted label y

is the

Algorithm 1: Diff-SySC Training.

Input: labeled set



ℓ



, unlabeled set X

, validation

set

⟨

⟩

, conﬁdence threshold γ, max. no. of

iterations m

Output: the best performing diffusion model

i ← 0; D ←

while i < m do

← Train(X

ℓ

); D ← D ∪

{

}

τ ← Calibrate(D

)

⟨

⟩

← Annotate(D

,τ,γ)

if X

0 then

break

end

ℓ

← X

ℓ

∪ X

; Y

ℓ

← Y

ℓ

∪Y

← X

\ X

if X

0 then

break

end

i ← i + 1

end

return BestModel(D)

Algorithm 2: Diff-SySC Annotation.

Function Annotate(D,X

,τ,γ):

←

0; Y

←

for x in X

← predict label(D , τ, x)

conf ← predict conﬁdence(D,τ,x)

if conf > γ then

← X

∪ {x}; Y

← Y

∪ {y

}

end

return

⟨

⟩

index in the array corresponding to this maximum

value.

The augmented labeled set, obtained after the an-

notation procedure, is further used to train a new

LRA-Diffusion model D

,i ≥ 1 from scratch. The

process is repeated until any of the following conver-

gence criteria are met: (1) all unlabeled samples have

been annotated (X

0); (2) there are no new con-

Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classiﬁcation

135

ﬁdent predictions (X

0); (3) a pre-deﬁned maxi-

mum number of iterations m has been reached. After

the training iterations have been completed, the ob-

tained models are evaluated on the validation set and

the best performing model is selected. This model is

afterwards evaluated on the test set.

3.2 Performance Evaluation

The performance of Diff-SySC is evaluated on im-

age classiﬁcation datasets with various proportions of

labeled data. We randomly sample a ﬁxed number

of data points from each class to form the labeled

dataset



ℓ



. The validation dataset

⟨

⟩

built using 10% of the data, while all the remaining

data samples are used to form the unlabeled subset

. The performance of the trained model D

best

evaluated on a ﬁxed test set. For each dataset and la-

beled set ratio, the training is repeated three times,

using three different random seeds and corresponding

data splits. The performance of the models is mea-

sured using the Error Rate, a standard evaluation met-

ric used for semi-supervised image classiﬁcation. It

is deﬁned as the proportion of incorrect predictions

given by the model: Err = 100 ·

incorrect

total

. The mean

and standard deviation of the obtained error rate val-

ues are reported.

4 EXPERIMENTAL SETUP

4.1 Datasets

Diff-SySC was evaluated on three semi-supervised

image classiﬁcation benchmarks. Table 1 summa-

rizes the characteristics of the datasets: the number

of available samples, the number of classes and the

number of labeled samples used in our experiments.

Table 1: Summary of publicly available image datasets used

for the training and evaluation of Diff-SySC.

Dataset No. of No. of No. of labeled

samples classes data samples

CIFAR-10 60000 10 250 / 4000

CIFAR-100 60000 100 2500 / 10000

STL-10 113000 10 250 / 1000

CIFAR-10 and CIFAR-100 (Krizhevsky, 2009)

represent balanced datasets of images of resolution 32

× 32 containing real world objects and animals. Each

dataset is formed of 50000 training images and 10000

testing images. During the training of the models, we

only use a small percentage of randomly selected la-

bels despite the fact that the datasets are fully labeled.

The STL-10 dataset (Coates et al., 2011) is formed of

images with resolution 96 x 96. The training set con-

tains 5000 labeled images and 100000 unlabeled im-

ages. While the labeled subset is formed of samples

belonging to 10 classes, the unlabeled subset contains

a mixture of in-distribution samples, which are from

these classes, and out-of-distribution examples, which

belong to different categories. Following the protocol

introduced in the literature (Zheng et al., 2023), we

sample 250 and 1000 images from the available train-

ing data to form the labeled set X

and we add the

remaining samples to the unlabeled dataset. The test

set is formed of 8000 images.

4.2 Training Diff-SySC

The experiments were conducted using two Nvidia

RTX 3090 GPUs. Table 2 presents the most important

hyper-parameters used for training Diff-SySC. Addi-

tionally, in all experiments, the number of neighbors

was set to 10 and the maximum number of iterations

m was set to 4. The CLIP feature extractor was used,

speciﬁcally the ViT-L/14 architecture.

Table 2: Overview of the main hyper-parameters: pseudo-

labels conﬁdence threshold γ, batch size and number of

training epochs per iteration.

Dataset No. of labels γ Batch size No. of epochs

CIFAR-10

250

0.95

{

400,30, 30,20

}

4000 200

{

100,20, 20,20

}

CIFAR-100

2500 0.6 25

{

300,400, 450,500

}

10000 0.7 200

STL-10

250

0.95 25

{

300,30, 30,30

}

1000

{

200,30, 20,20

}

The experimental analysis revealed that for large

initial labeled datasets, the model could be trained ef-

fectively using large batch sizes and a relatively small

number of epochs. In these cases, the initial iter-

ation generally produced a diverse set of conﬁdent

pseudo-labels, which beneﬁted the subsequent train-

ing epochs. For CIFAR-10 and STL-10, the best re-

sults were obtained using a conﬁdence threshold of

0.95 and a large number of training epochs for the

ﬁrst iteration. In subsequent iterations, a signiﬁcantly

smaller number of training epochs was used, as con-

vergence was reached faster due to the high labeled

data count.

However, setting a high conﬁdence threshold on

CIFAR-100 (i.e. γ > 0.9) led to overﬁtting in the

last training iterations of Diff-SySC. This was caused

by the fact that the mean conﬁdence of the model’s

predictions on the unlabeled dataset was generally

smaller than 0.7. Therefore, when using large con-

ﬁdence thresholds, the annotation stages would only

label new data samples that were very similar to the

training set, thus affecting the model’s ability to gen-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

136

eralize to the true data distribution. We also observed

that, in contrast to CIFAR-10 and STL-10, using a

small number of epochs for CIFAR-100 led to under-

ﬁtting during the last iterations. This could be caused

by the complexity of this dataset.

5 RESULTS AND DISCUSSION

This section presents the experimental results ob-

tained by evaluating the Diff-SySC model on semi-

supervised image classiﬁcation benchmarks. With

the goal of answering RQ2, we compared our ap-

proach with multiple related work methods presented

in Section 2: the Pseudo-labeling approach (Lee

et al., 2013), consistency regularization methods: Π-

model (Sajjadi et al., 2016), Mean Teacher (Tarvainen

and Valpola, 2017) and hybrid methods: MixMatch

(Berthelot et al., 2019), FixMatch (Sohn et al., 2020),

CRMatch (Fan et al., 2023), SimMatch (Zheng et al.,

2022) and SimMatchV2 (Zheng et al., 2023). One

of the goals of our proposed semi-supervised model

Diff-SySC is to make use of the information present

in unlabeled data to improve the learning process of

a supervised model. In order to validate this hy-

pothesis, we also report the performance obtained by

our framework after the ﬁrst training iteration, i.e., a

LRA-diffusion model trained only on the available la-

beled data.

Table 3 presents the error rate obtained by evalu-

ating Diff-SySC on the datasets described in Section

4.1. The mean and standard deviation are reported

for three different runs of the algorithm. The re-

sults show the consistent improvement of Diff-SySC

over the supervised diffusion model baseline, high-

lighting the beneﬁt of using a dataset augmented with

pseudo-annotations. This result validates that our ap-

proach constitutes an effective semi-supervised learn-

ing technique, producing models capable of leverag-

ing information from the unlabeled data samples. The

largest improvement over the supervised baseline can

be observed on the STL-10 dataset and on the CIFAR-

10 dataset with 250 labels. This could be explained

by the fact that, in these settings, the original labeled

training subset is small and the pseudo-labeling step

signiﬁcantly increases the number of training sam-

ples, leading to a more diverse dataset.

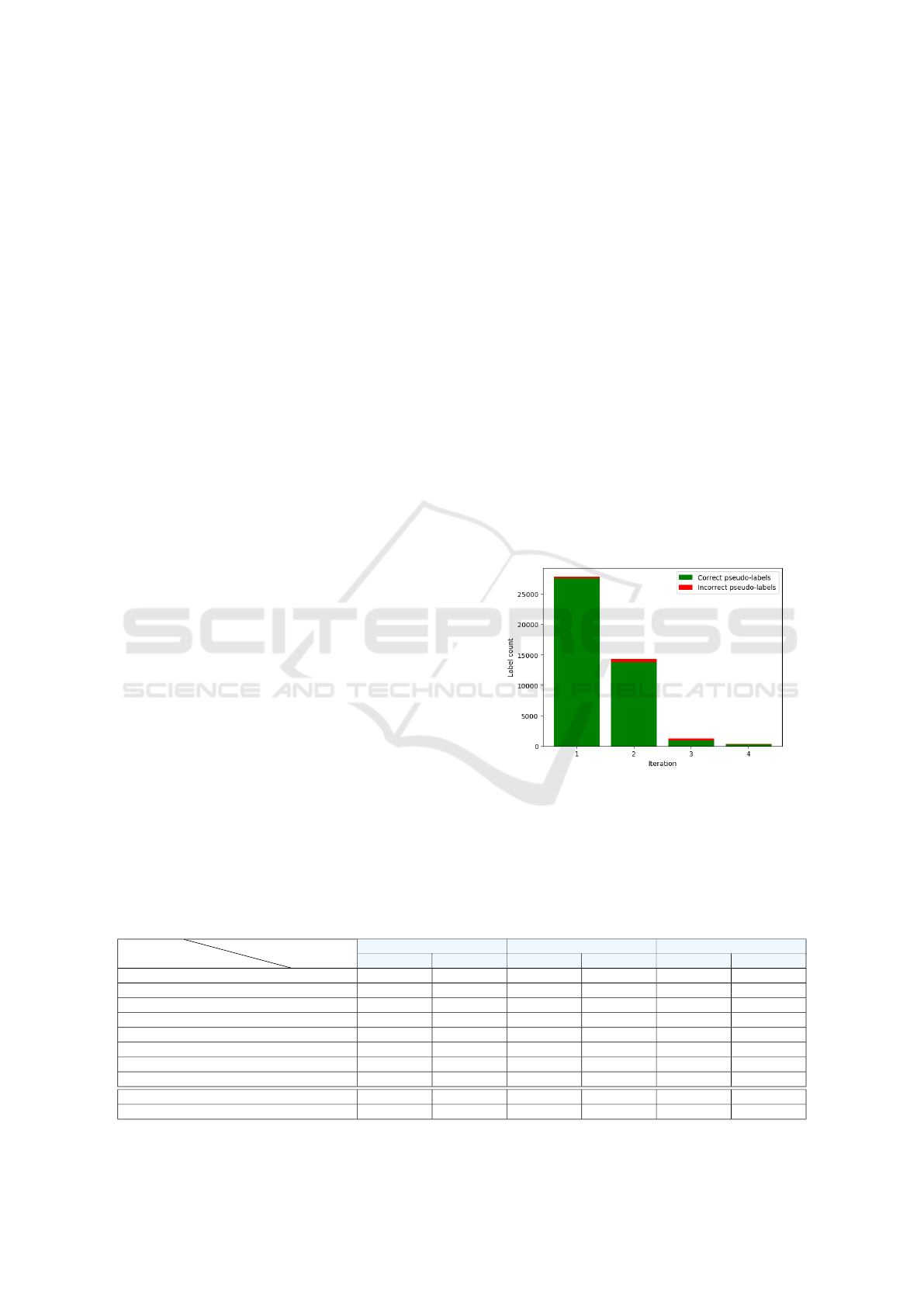
Figure 2 shows the number of conﬁdent pseudo-

labels generated in each iteration for the CIFAR-10

dataset using the 250 label conﬁguration. As illus-

trated in Figure 2, the annotation process produces a

large number of labels after the ﬁrst iteration. More-

over, we observe that in all iterations the great major-

ity of generated pseudo-labels are correct. This sug-

gests that the training protocol is effective in itera-

tively annotating the unlabeled samples, even when

Diff-SySC is exposed to 0.5% of labeled data. This

gradual annotation is controlled via the conﬁdence

threshold γ which helps in mitigating the risk of noisy

labels. Additionally, these results conﬁrm our initial

hypothesis that learning the neighboring labels distri-

bution leads to a more robust mechanism of generat-

ing accurate pseudo-labels.

Figure 2: Number of conﬁdent pseudo-labels generated for

CIFAR-10 (250 initial labels) at the end of each iteration.

When comparing our approach to the results re-

ported in the literature, we note that Diff-SySC is

able to outperform all the related work approaches on

Table 3: Comparison with related work. The mean error rate (%) and the standard deviations over 3 runs are shown for our

Diff-SySC and for the supervised baseline. The methods shown in italic are run by us, while the rest of the results are taken

from (Zheng et al., 2023). The best results are marked in bold.

Method

Dataset CIFAR-10 CIFAR-100 STL-10

250 4000 2500 10000 250 1000

Π-model (Sajjadi et al., 2016) 48.73±1.07 13.63±0.07 56.40±0.69 36.73±0.05 52.20±2.11 31.34±0.64

Pseudo-labeling (Lee et al., 2013) 51.12±2.91 15.32±0.35 55.37±0.48 36.58±0.12 51.90±1.87 30.77±0.04

Mean Teacher (Tarvainen and Valpola, 2017) 37.56±4.90 8.29±0.10 44.37±0.60 31.39±0.11 49.30±2.09 27.92±1.65

MixMatch (Berthelot et al., 2019) 13.00±0.80 6.55±0.05 39.29±0.13 27.74±0.27 32.05±1.16 20.17±0.67

FixMatch (Sohn et al., 2020) 4.95±0.10 4.26±0.01 27.71±0.42 22.06±0.10 8.64±0.84 5.82±0.06

CRMatch (Fan et al., 2023) 4.61±0.17 3.65±0.04 24.13±0.16 19.89±0.23 14.87±5.09 6.53±0.36

SimMatch (Zheng et al., 2022) 5.36±0.08 4.41±0.07 26.21±0.37 21.50±0.11 8.27±0.40 5.74±0.31

SimMatchV2 (Zheng et al., 2023) 5.04±0.09 4.33±0.16 26.66±0.38 21.37±0.20 7.54±0.81 5.65±0.26

Supervised 7.12±0.85 3.70±0.12 31.59±0.06 23.41±1.07 8.58±0.50 9.13±0.47

Diff-SySC 3.65±0.10 3.26±0.06 30.45±0.08 21.36±0.25 1.15±0.49 0.64±0.20

Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classiﬁcation

137

the CIFAR-10 and STL-10 datasets, with the largest

margin of improvement being obtained on the STL-

10 dataset. On CIFAR-100 our method achieves

error rates that are comparable to the results re-

ported in the literature in the 10000-label regime. On

the CIFAR-100 dataset with 2500 labeled samples,

Diff-SySC has a higher error rate than the best litera-

ture approach, CRMatch, but it still is able to outper-

form other methods, such as the Π-Model, Pseudo-

labeling, Mean Teacher and MixMatch. The results

obtained on CIFAR-100 could be due to the larger

number of categories in this dataset and the shared

similarities between classes that belong to the same

super-class. This leads to a more complex label dis-

tribution that the model needs to learn.

To summarize, on CIFAR-100, considering

both datasets (with 2500 and 10000 labels), our

Diff-SySC approach outperforms the related work

depicted in Table 3 in 72.2% of the cases (13 out of

18 comparisons). Overall, considering all datasets

and experiments, a better performance is observed

for Diff-SySC in 90.74% of the cases (49 out of 54

comparisons). We also note small standard devia-

tions of the error rates achieved by our proposed semi-

supervised diffusion-based architecture, thus empha-

sizing the stability and robustness of Diff-SySC.

Figure 3 gives insights into the training dynamics

by showing the accuracy obtained during the train-

ing iterations and the proportions of labeled and un-

labeled data, as progressively more annotations (real

and generated labels) are used for training the model.

The top ﬁgure shows the train and test set accuracy

of the model after each of the training iterations.

Additionally, the proportion of correctly generated

pseudo-labels is depicted in the case of CIFAR-10

and CIFAR-100. This metric is omitted in the case

of STL-10 due to the fact the ground truth labels are

not available for the unlabeled data. Figure 3 high-

lights that the largest number of annotations is gen-

erated at the end of the ﬁrst iterations, with a good

accuracy (over 90% of the pseudo-labels generated

after the ﬁrst iteration are correct), while fewer sam-

ples are annotated during subsequent iterations. Even

though the accuracy of the pseudo-labeling procedure

decreases over the iterations, as it becomes more dif-

ﬁcult to annotate new samples, the test set accuracy

is not affected. This highlights the robustness of our

approach to the presence of noisy pseudo-labels.

Additionally, we analyze how the training con-

vergence is reﬂected within the pseudo-annotation of

the unlabeled dataset. For the CIFAR-10 with 250

labels and STL-10 with 250 labels, only a few un-

labeled samples have not been conﬁdently pseudo-

labeled throughout the training process. Meanwhile,

on CIFAR-100 with 10000 labels, the training does

not conclude with a complete coverage of the unla-

beled dataset. This phenomenon can be attributed to

the higher complexity of the data involved and the

observed overﬁtting accumulated throughout the it-

erations, as shown on the top row. Nonetheless, the

conﬁdent pseudo-labels are predominantly accurate,

with 97.96% aggregated pseudo-labels accuracy on

CIFAR-10 and 87.05% on CIFAR-100.

A potential limitation of our method is the depen-

dence on a pre-trained feature encoder for training the

diffusion model. While general-purpose models like

CLIP can be effective in most cases, other tasks that

involve images sampled from a very different distri-

bution (e.g., medical images, radar or satellite data),

may require more specialized encoders. Nevertheless,

our framework is ﬂexible enough to allow the inte-

gration of any type of feature extractor trained in an

unsupervised manner on the unlabeled data. A sec-

ond limitation is represented by the fact that the unla-

beled data is not used directly during training until it

is pseudo-annotated with conﬁdent predictions. This

could constitute a drawback in scenarios with very

few labels per class, as the initial model, D

, may not

have enough information to be effectively trained. A

possible strategy to alleviate this issue is to integrate

unsupervised objective functions in the training of the

LRA-Diffusion model.

6 CONCLUSIONS

In this work, we introduced a diffusion-based ap-

proach for semi-supervised learning, Diff-SySC. The

method was evaluated on three image benchmarks:

CIFAR-10, CIFAR-100 and STL-10, with varying

ratios of labeled data. The research questions for-

mulated in Section 1 have been answered. RQ1

was answered by introducing the multi-stage semi-

supervised learning approach Diff-SySC which uses

a diffusion model for label generation, unlike the ex-

isting literature approaches that use diffusion mod-

els for enhancing the training dataset. For answer-

ing RQ2, Diff-SySC was compared with multiple

related work methods covering diverse methodolo-

gies and strategies for semi-supervised learning. The

conducted comparison highlighted a performance im-

provement achieved by Diff-SySC over the related

work in 90.74% of the cases. In addition, the robust-

ness and stability of Diff-SySC has been emphasized

through small standard deviations of the error rates

achieved by our model over multiple runs.

Future work will investigate extensions of our

method that integrate unsupervised loss functions,

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

138

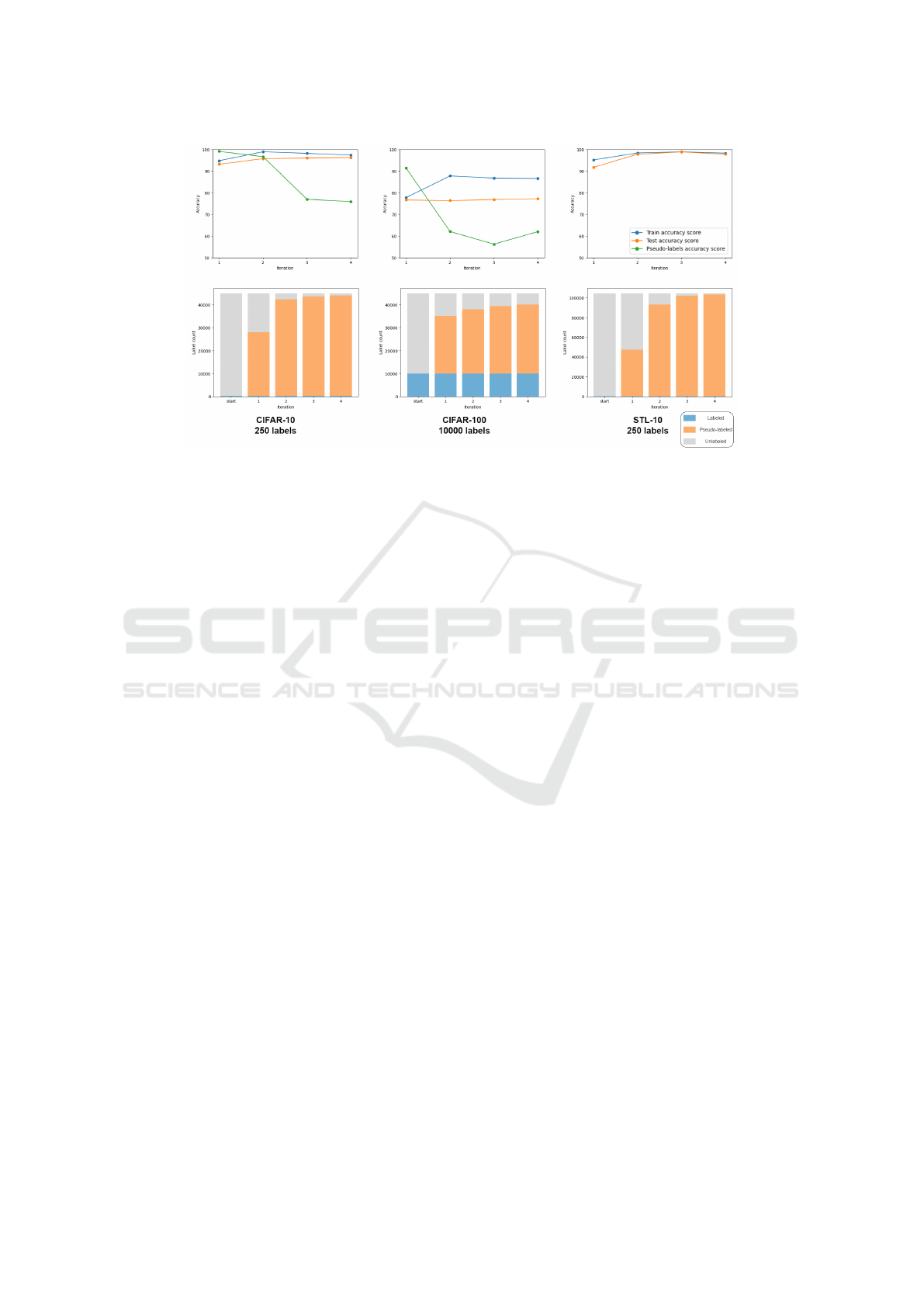
Figure 3: Top: accuracy of Diff-SySC. Bottom: proportions of labeled, pseudo-labeled and unlabeled data per iteration.

such as consistency regularizers. Diff-SySC will

be further evaluated on more challenging real-world

tasks and datasets such as rainfall nowcasting, which

is an important task in meteorology that presents a

particularly difﬁcult annotation process.

ACKNOWLEDGEMENTS

This work was supported by a grant of the Min-

istry of Research, Innovation and Digitization,

CCCDI-UEFISCDI, project number PN-IV-P7-7.1-

PED-2024-0121, within PNCDI IV.

REFERENCES

Berthelot, D. et al. (2019). Mixmatch: A holistic approach

to semi-supervised learning. In Proc. of NeurIPS, vol-

ume 32, pages 1–11.

Chen, J., Zhang, R., et al. (2023). Label-Retrieval-

Augmented Diffusion Models for Learning from

Noisy Labels. In Proc. of NeurIPS, pages 1–19.

Chen, T. et al. (2020). Big Self-Supervised Models are

Strong SS Learners. In NeurIPS, pages 1–13.

Coates, A., Ng, A., and Lee, H. (2011). An analysis of

single-layer networks in unsupervised feature learn-

ing. In Proceedings of PMLR, pages 215–223.

Dhariwal, P. and Nichol, A. Q. (2021). Diffusion Models

Beat GANs on Image Synthesis. In Proceedings of

NeurIPS 2021, pages 8780–8794.

Fan, Y. et al. (2023). Revisiting consistency regularization

for ssl. IJCV, 131(3):626–643.

Gong, S. et al. (2023). Diffusion Model Based SL on Brain

Hemorrhage Images for Efﬁcient Midline Shift Quan-

tiﬁcation. In IPMI, pages 69–81.

Guo, C., Pleiss, G., Sun, Y., and Weinberger, K. Q. (2017).

On calibration of modern neural networks. In Pro-

ceedings of PMLR, pages 1321–1330.

Han, X., Zheng, H., and Zhou, M. (2022). CARD: Classiﬁ-

cation and Regression Diffusion Models. In Proceed-

ings of NeurIPS 2022, pages 1–22.

Krizhevsky, A. (2009). Learning Multiple Layers of Fea-

tures from Tiny Images. Techn. report, Univ. Toronto.

Lee, D.-H. et al. (2013). Pseudo-label: The simple and efﬁ-

cient SSL method for DNNs. In WREPL, page 896.

Pham, H., Dai, Z., et al. (2021). Meta pseudo labels. In

Proceedings of CVPR, pages 11557–11568. IEEE.

Radford, A., Kim, J. W., et al. (2021). Learning Transfer-

able Visual Models From Natural Language Supervi-

sion. In ICML, volume 139, pages 8748–8763.

Sajjadi, M. et al. (2016). Regularization with stochas-

tic transformations and perturbations for deep semi-

supervised learning. In NIPS, pages 1171 – 1179.

Sohn, K., Berthelot, D., et al. (2020). FixMatch: Simplify-

ing Semi-Supervised Learning with Consistency and

Conﬁdence. In Proc. of NeurIPS, pages 596–608.

Springenberg, J. T. (2016). Unsupervised and Semi-

supervised Learning with Categorical Generative Ad-

versarial Networks. In Proc. of ICLR, pages 1–20.

Tarvainen, A. and Valpola, H. (2017). Mean teachers are

better role models: Weight-averaged consistency tar-

gets improve SSL results. In NIPS, pages 1195 – 1204.

Yang, X., Song, Z., et al. (2023). A Survey on Deep Semi-

Supervised Learning. IEEE Transactions on Knowl-

edge and Data Engineering, 35(9):8934–8954.

You, Z., Zhong, Y., et al. (2023). Diffusion Models and

Semi-Supervised Learners Beneﬁt Mutually with Few

Labels. In Proc. of NeurIPS, pages 43479–43495.

Zhang, L. and Qi, G.-J. (2020). WCP: Worst-Case Pertur-

bations for SSL. In CVPR, pages 3911–3920.

Zheng, M., You, S., et al. (2022). SimMatch: Semi-

supervised Learning with Similarity Matching. In

Proceedings of CVPR, pages 14451–14461. IEEE.

Zheng, M., You, S., et al. (2023). Simmatchv2: Semi-

supervised learning with graph consistency. In Pro-

ceedings of ICCV, pages 16432–16442.

Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classiﬁcation

139